Abstract
Semiconductor nano-lasers have been actively investigated both theoretically and experimentally with to the aim of providing a highly compact laser amenable to photonic integration. Such devices are naturally suited for assembly in close-packed one- and two-dimensional arrays. In such arrangements, optical coupling between elements of the array opens opportunities to generate a range of dynamical behaviours. In this paper, we present the first theoretical treatment of the dynamics of electrically pumped nano-laser arrays. Two specific forms of such arrays are analysed in detail: a three-element linear array, and triangular arrays. The former is the basis for extensive one-dimensional arrays, whilst the latter is a building block of many possible geometric configurations of two-dimensional nanolaser arrays. Using these prototypical configurations enables the identification of novel dynamical behaviours, which may be accessed using nano-laser arrays. A distinguishing physical feature of nano-lasers is the enhancement of the spontaneous emission rate via the so-called Purcell effect. Allowing for a range of Purcell enhancement factors, the analysis focusses on the effects of experimentally controllable parameters such as the laser drive current. It is shown that the Purcell enhancement factor is critical to the availability of a range of dynamical behaviours which arise simply due to inter-element optical coupling. Two-dimensional portraits of the regimes of differing dynamics offer a convenient means for determining the dynamics which may be accessed by varying the laser drive current.
1. Introduction
Semiconductor nano-lasers have been of interest for some time [1,2,3,4]. Much progress has been made in the development of optically pumped nano-lasers fabricated in a range of materials [5,6,7,8]. On the other hand, fabrication of electrically driven semiconductor nano-lasers is quite challenging; hence, there have been relatively few reports on their successful implementation [9,10,11,12,13,14]. It is possible that advances in nano-laser fabrication may arise using relatively novel material platforms [15,16]. Significant theoretical work has been undertaken exploring the dynamical behaviour of electrically pumped nano-lasers [17,18,19]. Particular effort has been expended in assessing the impact on the dynamics of semiconductor nanolasers of external perturbations such as: their direct current modulation response [20]; their response to optical injection [21]; and when subject to both regular [22] and phase conjugate [23] optical feedback. Such investigations have been largely confined to the behaviour of stand-alone semiconductor nano-lasers. In addition, attention has been given to the dynamical behaviour in mutually coupled nano-lasers [24]. It is hoped that development of practical electrically pumped semiconductor nanolasers will lead to experimental investigations of the rich dynamics of semiconductor nano-lasers.
By their nature, semiconductor nano-lasers are particularly apposite for the formation of one- and two-dimensional arrays. A recent authoritative survey [25] has highlighted the potential applications of nano-laser arrays and has pioneered the analysis of their dynamics through considering two-element arrays. That work also is able to cite seminal experimental results obtained with optically pumped nano-laser arrays. In such arrays, coupling between array elements can be anticipated to significantly affect both the static and dynamical behaviour of nano-laser arrays. The static behaviour would include the form of the near and far-field emission of the nano-laser array. In [25] attention is, e.g., given to super-mode formation in two-element nano-laser arrays. In contrast, the theme of the present paper is the dynamical behaviour of electrical nano-laser arrays. It is suggested that additional degrees of freedom which become available when use is made of electrical pumping enhance the interest in exploring the dynamics of such arrays. The focus of the analysis provided here is the dynamical behaviours which can be accessed using experimentally variable parameters—without any external perturbations. Even in the absence of such external stimuli it is found that a remarkable diversity of dynamics may arise in electrically pumped nano-laser arrays.
As a means for initiating such studies, the work reported in this paper is concerned with three-element nano-laser arrays: a linear three-element array and a triangular array. These configurations are perceived as building blocks of extensive one- and two-dimensional nano-laser arrays, respectively. Even with such relatively elementary arrays, there are many possibilities for influencing their dynamics; hence, an exhaustive exploration of their dynamics is not tractable. The work undertaken here limits attention to behaviours which may be easily excited using experimentally accessible device parameters. Our aim is to offer a flavour of the rich dynamics available from such arrays whilst hoping that these insights may serve as a further stimulus to the implementation of electrically driven nano-laser arrays.
A distinguishing physical factor which strongly influences the richness of the dynamics in nano-lasers, in general, and nano-laser arrays, in particular, is the possibility of enhancement of spontaneous emission via the so-called Purcell effect. The influence of the Purcell factor on nano-laser array dynamics is explored in some detail here. The model used in this analysis is described in Section 2. Results for linear three-element arrays and triangular arrays are described and interpreted in Section 3 where, in addition, pointers are given to further avenues for exploration. Section 4 provides a conclusion and brief perspective on future analysis.
2. Model
Schematic diagrams of three-element nano-laser linear and triangular arrays are shown in Figure 1. In the arrays, the nano-lasers are laterally coupled which can be modelled using a modified form of coupled rate equations [26,27] with the Purcell enhanced spontaneous emission factor, F and spontaneous emission factor β included, as introduced in [28].
where the subscripts ‘j’ and ‘m’ represent jth and mth laser, respectively. M is the number of lasers in the array, t is the time, S(t) is the photon density, ϕ(t) is the optical phase, and N(t) is the carrier density. Γ is the confinement factor, τn is the carrier lifetime, gn is the differential gain, N0 is the transparency carrier density, τp is the photon lifetime, k is the coupling rate between the two lasers, α is the linewidth enhancement factor, Δω is the frequency detuning between the two lasers, I is the injection current, e is the elementary charge, and Va is the volume of the active region.
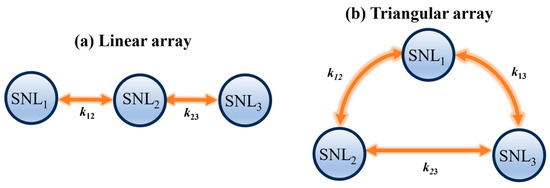
Figure 1.
Schematic diagrams of three-element semiconductor nano-lasers (SNLs) arrays. Circles represent SNLs. The double arrows represent the lateral light coupling between each two lasers. k12, k13 and k23 represent the coupling rate between each two lasers. (a) Linear array; (b) triangular array.
Equations (1)–(3) have been solved numerically using a fourth order Runge–Kutta integration method. The three-element arrays, i.e., M = 3, were simulated which required the solution of 9 coupled rate equations. In the simulations, a temporal resolution of Δt = 0.1 ps is selected and the duration of the time series is set to be 1 μs. The dynamics of the nanolasers are analysed using the device parameters given in Table 1, which are mainly from [12,29].

Table 1.
Nano-laser device parameters.
3. Results
The aim of this paper is to delineate the dynamical behaviour of laterally coupled nano-lasers arrays with non-identical operating parameters and notably taking account variations in the coupling strength between lasers and considering differing laser injection currents. Attention is first given to the behaviour of nano-laser arrays with varying coupling strength. The results presented here have been found using the rate Equations (1)–(3). As already indicated, the salient parameters for nano-lasers include the Purcell factor F. The injection current used to drive the lasers is an important operational parameter. Variations in these parameters lead to the results presented here.
3.1. Linear Array
For definiteness, initial calculations have been performed of the characteristics of three-element linear array when three nano-lasers possess the same Purcell enhancement factor, F = 20 and all are driven at double the threshold, I = 2Ith where Ith is the threshold current. In Figure 2, time series of the three nano-lasers are presented as the coupling rate between nano-laser 1 and nano-laser 2 increases from k12τp = 0 to 3.5 × 10−3, whilst the coupling between nano-lasers 2 and 3 is kept constant at k23τp = 1.8 × 10−5.
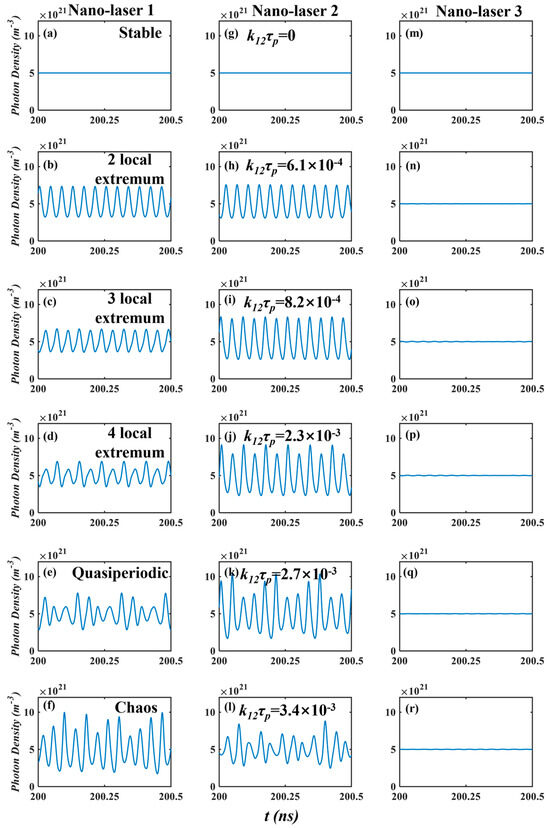
Figure 2.
Dynamics of three−element linear nano−lasers array simulated using Equations (1)–(3) for different coupling rate of k12τp when F = 20, I = 2Ith and k23τp = 1.8 × 10−5. (a–f) Time series of nano−laser 1; (g–l) time series of nano−laser 2; (m–r) time series of nano−laser 3.
From Figure 2, for a relatively small coupling rate, e.g., k12τp = 6.1 × 10−4, 8.2 × 10−4, 2.3 × 10−3 (Figure 2b–d,h–j), nano-lasers 1 and 2 show stable periodic oscillations with 2–4 local extrema. As the coupling between the lasers further increases, nano-lasers 1 and 2 may enter an unstable regime where stable oscillations are finally lost. The results are shown in Figure 2e,k, where quasiperiodic time series of nano-lasers 1 and 2 are presented at a high coupling rate, namely k12τp = 2.7 × 10−3. When the coupling rate increases to a relatively high value, such as k12τp = 3.4 × 10−3, one can observe chaos which is similar to that seen in conventional semiconductor la-sers subject to external perturbations [30,31].
It is worth emphasizing that in the subsequent delineation of the dynamical behaviour of nano-laser arrays, the occurrence of chaotic dynamics has been confirmed by examination of the power spectra of the dynamics. In Figure 3, exemplars of such spectra are provided. In the case of quasi-periodic dynamics many prominent peaks are retained in the spectrum, whereas a broad spectrum characterizes the chaotic dynamics.
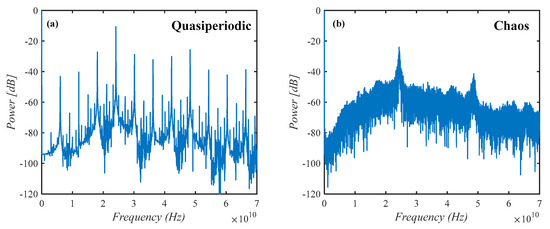
Figure 3.
Exemplar power spectra characterizing (a) quasi−periodic dynamics and (b) chaos.
In the foregoing results, nano-laser 3 remains stable. Due to the latter observation, results for nano-laser 3 are omitted from subsequent results where the behaviour of the nano-laser array is portrayed under a range of operating conditions. Before proceeding to the presentation of those results, it is noteworthy that the dynamics displayed in Figure 2 are merely an exemplar of the array dynamics. Many permutations of drive currents for the three nano-lasers may be envisaged and their detailed dynamics can be expected to differ, albeit one may expect that the generic features of such behaviours retain many similarities.
A parameter of the system which can be easily changed experimentally is the laser injection current. It is of interest, therefore, to further characterize the dynamics of the system as a function of injection current. When considering the response of a dynamical system to variations of a single parameter, it is possible to represent changes of the non-linear dynamics by means of a bifurcation diagram. In the present work, it is wished to explore the appearance of different dynamical behaviours when two parameters are varied viz the inter-element coupling strength and the laser drive current. To represent all those cases would require the use of a large number of bifurcation diagrams. As such, we adopt the approach of displaying the dynamical regimes using two-dimensional portraits parameterized with the coupling strength and laser drive current. Such results are shown in Figure 4 and Figure 5 as 2D maps which were generated for coupling rate in the range 0 < k12τp < 3.5 × 10−3 and injection current 1 < I/Ith < 4 to show the dynamical behaviours of nanolasers for different values of F. Different colors represent different dynamics within the maps.
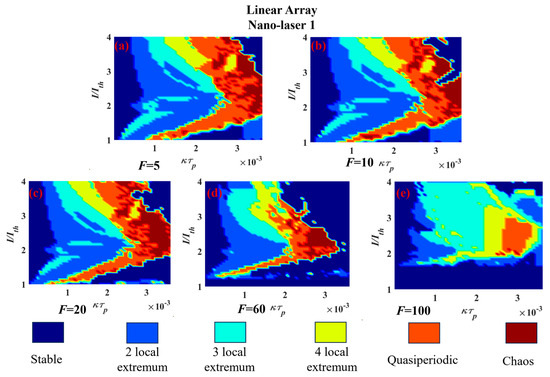
Figure 4.
Two−dimensional maps of dynamics of three−element linear array nano-laser 1 simulated using Equations (1)–(3) for different F, as shown in (a–e), when the other two nano−lasers are driven at double the threshold. The couplings between nano−lasers 2 and 3 are kept constant at k23τp = 1.8 × 10−5.
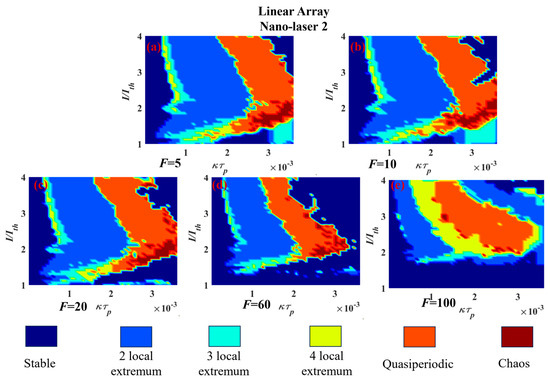
Figure 5.
Two−dimensional maps of dynamics of three−element linear array nano−laser 2 simulated using Equations (1)–(3) for different F, as shown in (a–e), when the other two nano−lasers are driven at double the threshold. The couplings between nano−lasers 2 and 3 are kept constant at k23τp = 1.8 × 10−5.
Echoing the caveat entered after discussion of the results in Figure 2, it is observed that although Figure 4 and Figure 5 capture a wide range of operating conditions, the cases explored are far from a complete catalogue of possible dynamic scenarios. However, they do highlight the richness of the available dynamics. In essence the above portrayals display the forms of dynamics already shown via time series in Figure 2. The critical role of the Purcell enhancement factor in amending the extent of various forms of dynamics is evident with, e.g., the operating regimes in which quasiperiodic behaviour is obtained changing significantly. Clearly, the Purcell enhancement factor and inter-laser coupling factors are largely fixed features of any given device; hence, it is the variation in the drive current which would be the practical means for accessing specific dynamical behaviours.
The convenience provided by these portraits is to offer—at a glance—a summary of the dynamics which may be seen in a given nano-laser array as defined by its normalized coupling factor kτp. Thus, for example, from Figure 4, with a Purcell enhancement of 5 and a normalized coupling factor of 1 × 10−3, increasing the drive current of nano-laser 1 unlocks in turn: quasi-periodic behaviour, and then alternating regimes of three local extremum and two local extremum dynamics. For a normalized coupling factor of 2 × 10−3, the sequence of dynamical regimes is as follows: stable operation; quasi-periodicity (with narrow borders of four local extremum dynamics); two local extremum; three local extremum and four local extremum. These cases exemplify the alacrity with which the kind of dynamics arising can be chosen.
At this stage of electrically driven nano-laser array development it is not possible to be definitive about the practically achievable of Purcell enhancement and coupling rates and hence the scope for further amendment of these regimes of dynamics is unclear. The calculations performed here are constricted to cases where the Purcell enhancement is the same for all lasers. Other opportunities open if non-identical array elements are considered.
In the next section, attention is given to the dynamics of nano-lasers in a triangular configuration as a prototype structure for creating two-dimensional nano-laser arrays. Prior to that it is noted that parallel arrangements of linear arrays may also be used to create two-dimensional arrays. There is considerable scope for calculations of their behaviour.
3.2. Triangular Array
Having established in the preceding section that variation in laser drive current and inter-element coupling strength leads to a wide spectrum of dynamics, the same parameters are used for the case of a triangular nano-laser array. This arrangement delivers a similar mix of dynamical behaviours as found for the linear three-element array but with the boundaries between various behaviours being, not unexpectedly, amended. As in the case of the linear arrangement, with the combination of drive currents used here, nano-laser 3 remains stable and hence its dynamics is omitted from the portraits below. As was discussed in detail for the linear array above, the selection of forms of dynamics available for a given Purcell enhancement factor and specific coupling coefficient can be read off from the portraits below. Similar admixtures of periodic, quasiperiodic and chaotic behaviours can be found.
In respect of the influence of the Purcell enhancement factor, it is apparent from Figure 6 and Figure 7 that in the range of 5–20, relatively little change occurs in the regimes of different dynamics.
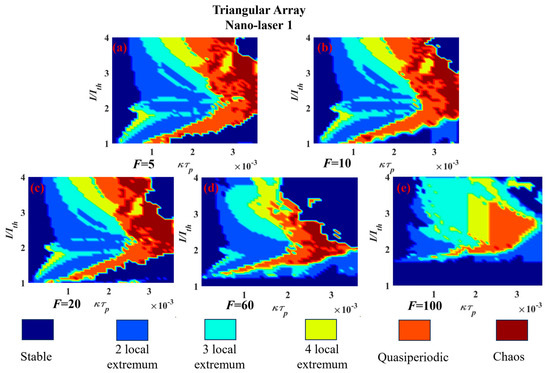
Figure 6.
Two−dimensional maps of dynamics of three element triangular array nano−laser 1 simulated using Equations (1)–(3) for different F, as shown in (a–e), when the other two nano−lasers are driven at double the threshold. The couplings between nano−laser 1 and 3, and nano−laser 2 and 3 are kept constant at k13τp = k23τp = 1.8 × 10−5.
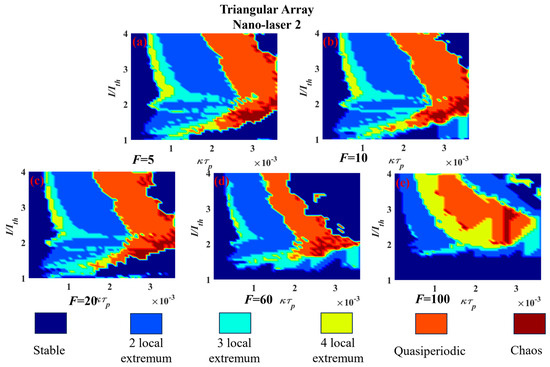
Figure 7.
Two−dimensional maps of dynamics of three−element triangular array nano−laser 2 simulated using Equations (1)–(3) for different F, as shown in (a–e), when the other two nano−lasers are driven at double the threshold. The couplings between nano−laser 1 and 3, and nano−laser 2 and 3 are kept constant at k13τp = k23τp = 1.8 × 10−5.
4. Conclusions
The primary conclusion of this work is that rather simple configurations of nanolasers can provide easy access to many kinds of dynamics. In the case of both the linear three-ement array and the triangular arrays, various forms of periodic dynamics, quasi-periodic dynamics and chaos are generated depending upon the coupling strength between the elements of the array and the laser drive current. It is reiterated that the coupling strength will essentially be fixed at the design and fabrication stage of the arrays whilst the laser drive current is available for variation experimentally. As such, reading the the two-dimensional portraits at fixed coupling strength, the regimes of dynamics which can be accessed in a given device may be identified by examining the regimes encountered as the drive current is varied. Nano-lasers offer the opportunity for enhanced spontaneous emission, which is expressed via the Purcell enhancement factor, F. It is underlined that, as with the inter-element coupling strength the Purcell factor is mainly determined by the geometry of the laser cavity and so is not available for variation when measuring the perfromance of nano-laser arrays. Two-dimensional portraits of the dynamics have been presented for a range of values of the Purcell enhancement factor. In combination, the use of the variation in the inter-element coupling strength and the Purcell factor has provided a wide arnge of dynamical scenarios which are anticipated to arise in nano-laser arrays. Nevertheless, the results presented are necessarily selective and thus illustrative, and are by no means claimed to be exhaustive. The opportunities for expanding the combination of drive currents, coupling coefficients and Purcell enhancement factors have been indicated. It is conjectured that the inclusion of external stimuli will add to the facility with which those varieties of dynamics may be generated. Our future work will examine that proposition.
Author Contributions
Conceptualization, K.A.S.; methodology, Y.F. and K.A.S.; software, Y.F.; validation, Y.F. and K.A.S.; formal analysis, Y.F. and K.A.S.; investigation, Y.F. and K.A.S.; resources, X.S.; data curation, Y.F.; writing—original draft preparation, Y.F. and K.A.S.; writing—review and editing, Y.F., K.A.S. and X.S.; visualization, Y.F.; supervision, K.A.S. and X.S.; project administration, Y.F. and X.S.; funding acquisition, Y.F. and X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Proof of Concept Foundation of Xidian University Hangzhou Institute of Technology under Grant No. GNYZ2023QC0402.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ning, C.Z. Semiconductor Nanolasers: Semiconductor Nanolasers. Phys. Stat. Sol. 2010, 247, 774–788. [Google Scholar] [CrossRef]
- Saxena, D.; Mokkapati, S.; Jagadish, C. Semiconductor Nanolasers. IEEE Photonics J. 2012, 4, 582–585. [Google Scholar] [CrossRef]
- Gu, Q.; Fainman, Y. Semiconductor Nanolasers; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Ma, R.-M.; Oulton, R.F. Applications of Nanolasers. Nature Nanotech. 2019, 14, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Nezhad, M.P.; Simic, A.; Bondarenko, O.; Slutsky, B.; Mizrahi, A.; Feng, L.; Lomakin, V.; Fainman, Y. Room-Temperature Subwavelength Metallo-Dielectric Lasers. Nature Photon. 2010, 4, 395–399. [Google Scholar] [CrossRef]
- Hou, Y.; Renwick, P.; Liu, B.; Bai, J.; Wang, T. Room Temperature Plasmonic Lasing in a Continuous Wave Operation Mode from an InGaN/GaN Single Nanorod with a Low Threshold. Sci. Rep. 2014, 4, 5014. [Google Scholar] [CrossRef]
- Li, C.; Wright, J.B.; Liu, S.; Lu, P.; Figiel, J.J.; Leung, B.; Chow, W.W.; Brener, I.; Koleske, D.D.; Luk, T.-S.; et al. Nonpolar InGaN/GaN Core–Shell Single Nanowire Lasers. Nano Lett. 2017, 17, 1049–1055. [Google Scholar] [CrossRef]
- Song, D.I.; Yu, A.; Samutpraphoot, P.; Lee, J.; Kim, M.; Park, B.J.; Sipahigil, A.; Kim, M.-K. Three-Dimensional Programming of Nanolaser Arrays through a Single Optical Microfiber. Optica 2022, 9, 1424. [Google Scholar] [CrossRef]
- Hill, M.T.; Oei, Y.-S.; Smalbrugge, B.; Zhu, Y.; De Vries, T.; Van Veldhoven, P.J.; Van Otten, F.W.M.; Eijkemans, T.J.; Turkiewicz, J.P.; De Waardt, H.; et al. Lasing in Metallic-Coated Nanocavities. Nat. Photon. 2007, 1, 589–594. [Google Scholar] [CrossRef]
- Lee, J.H.; Khajavikhan, M.; Simic, A.; Gu, Q.; Bondarenko, O.; Slutsky, B.; Nezhad, M.P.; Fainman, Y. Electrically Pumped Sub-Wavelength Metallo-Dielectric Pedestal Pillar Lasers. Opt. Express 2011, 19, 21524. [Google Scholar] [CrossRef]
- Ding, K.; Liu, Z.C.; Yin, L.J.; Hill, M.T.; Marell, M.J.H.; Van Veldhoven, P.J.; Nöetzel, R.; Ning, C.Z. Room-Temperature Continuous Wave Lasing in Deep-Subwavelength Metallic Cavities under Electrical Injection. Phys. Rev. B 2012, 85, 041301. [Google Scholar] [CrossRef]
- Ding, K.; Hill, M.T.; Liu, Z.C.; Yin, L.J.; Van Veldhoven, P.J.; Ning, C.Z. Record Performance of Electrical Injection Sub-Wavelength Metallic-Cavity Semiconductor Lasers at Room Temperature. Opt. Express 2013, 21, 4728. [Google Scholar] [CrossRef] [PubMed]
- Li, K.H.; Liu, X.; Wang, Q.; Zhao, S.; Mi, Z. Ultralow-Threshold Electrically Injected AlGaN Nanowire Ultraviolet Lasers on Si Operating at Low Temperature. Nat. Nanotech. 2015, 10, 140–144. [Google Scholar] [CrossRef] [PubMed]
- Ren, K.; Li, C.; Fang, Z.; Feng, F. Recent Developments of Electrically Pumped Nanolasers. Laser Photonics Rev. 2023, 17, 2200758. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Q.; Su, R.; Do, T.T.H.; Xiong, Q. Halide perovskite semiconductor lasers: Materials, cavity design, and low threshold. Nano Lett. 2021, 21, 1903–1914. [Google Scholar] [CrossRef]
- Yang, C.; Liang, L.; Qin, L.; Tang, H.; Lei, Y.; Jia, P.; Chen, Y.; Wang, Y.; Song, Y.; Qiu, C.; et al. Advances in silicon-based, integrated tunable semiconductor lasers. Nanophotonics 2023, 12, 197–217. [Google Scholar] [CrossRef]
- Lorke, M.; Suhr, T.; Gregersen, N.; Mørk, J. Theory of Nanolaser Devices: Rate Equation Analysis versus Microscopic Theory. Phys. Rev. B 2013, 87, 205310. [Google Scholar] [CrossRef]
- Romeira, B.; Fiore, A. Purcell Effect in the Stimulated and Spontaneous Emission Rates of Nanoscale Semiconductor Lasers. IEEE J. Quantum Electron. 2018, 54, 2000412. [Google Scholar] [CrossRef]
- Fan, Y.; Hong, Y.; Li, P. Numerical Investigation on Feedback Insensitivity in Semiconductor Nanolasers. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1500307. [Google Scholar] [CrossRef]
- Sattar, Z.; Shore, K.A. Analysis of the Direct Modulation Response of Nanowire Lasers. J. Light. Technol. 2015, 33, 3028–3033. [Google Scholar] [CrossRef]
- Jiang, P.; Zhou, P.; Li, N.; Mu, P.; Li, X. Optically Injected Nanolasers for Time-Delay Signature Suppression and Communications. Opt. Express 2020, 28, 26421. [Google Scholar] [CrossRef]
- Rasmussen, T.S.; Mork, J. Theory of Microscopic Semiconductor Lasers with External Optical Feedback. Opt. Express 2021, 29, 14182. [Google Scholar] [CrossRef] [PubMed]
- Abdul Sattar, Z.; Shore, K.A. Phase Conjugate Feedback Effects in Nano-Lasers. IEEE J. Quantum Electron. 2016, 52, 1100108. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Dynamics and Stability of Mutually Coupled Nano-Lasers. IEEE J. Quantum Electron. 2016, 52, 2000306. [Google Scholar] [CrossRef]
- Deka, S.S.; Jiang, S.; Pan, S.H.; Fainman, Y. Nanolaser Arrays: Toward Application-Driven Dense Integration. Nanophotonics 2020, 10, 149–169. [Google Scholar] [CrossRef]
- Wang, S.S.; Winful, H.G. Dynamics of Phase-Locked Semiconductor Laser Arrays. Appl. Phys. Lett. 1988, 52, 1774–1776. [Google Scholar] [CrossRef]
- Jiang, S.; Deka, S.; Pan, S.H.; Fainman, Y. Effects of High β on Phase-Locking Stability and Tunability in Laterally Coupled Lasers. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 1800312. [Google Scholar] [CrossRef]
- Suhr, T.; Gregersen, N.; Yvind, K.; Mørk, J. Modulation Response of NanoLEDs and Nanolasers Exploiting Purcell Enhanced Spontaneous Emission. Opt. Express 2010, 18, 11230. [Google Scholar] [CrossRef]
- Coldren, L.A.; Corzine, S.W. Diode Lasers and Photonic Integrated Circuits; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Mork, J.; Tromborg, B.; Mark, J. Chaos in Semiconductor Lasers with Optical Feedback: Theory and Experiment. IEEE J. Quantum Electron. 1992, 28, 93–108. [Google Scholar] [CrossRef]
- Annovazzi-Lodi, V.; Donati, S.; Manna, M. Chaos and Locking in a Semiconductor Laser Due to External Injection. IEEE J. Quantum Electron. 1994, 30, 1537–1541. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).