Featured Application
This paper demonstrates the effectiveness of high-gain by high-intensity pumping in increasing the efficiency of solid-state lasers. First, using simple theory, it is shown that the temperature increase of the gain medium, which reduces the efficiency of quasi-three-level (quasi-four-level) lasers such as Yb lasers, increases proportionally to the pump power, but the increase is less than proportional to the pump intensity. It is shown that even with a microchip only 1 mm thick and without high cooling efficiency (thermal conductance), a Yb:YAG gain medium with normal thermal conductivity, and a normally used copper heat sink, the local temperature increase in the gain medium is low even at high pump intensity if the pump power is low. Second, it is shown both experimentally and theoretically that the laser mode tunability, which is essential for high efficiency, is well-preserved even under extremely strong thermal focusing due to high-intensity pumping. These tunability properties are sufficient for high-laser efficiency so that the thermal lensing effect of high-intensity pumping does not cause any efficiency reduction. The efficiency of conventional solid-state lasers can be improved by the simple technique of high-intensity pumping, which does not require expensive elements, complex configurations, or skilled adjustments, thus contributing to the cost reduction of high-efficiency solid-state lasers.
Abstract
To increase the efficiency of laser oscillators by overcoming losses, the unsaturated gain must be increased. For this purpose, high-intensity pumping, typically higher than 100 kW/cm2, is effective. However, the temperature increase and strong thermo-optic effects of the gain medium have been pointed out as obstacles to high efficiency in solid-state lasers. Therefore, the effect of high pump intensity on the laser mode tunability required for high efficiency is investigated by studying the dependence of the laser threshold on the cavity length using a continuous-wave hemispherical short-cavity laser. The results show that the laser mode can be tuned with sufficient range and precision for high efficiency under various loss conditions regardless of the high pump intensity and are in qualitative agreement with a simple theory. Furthermore, according to the heat transport theory, microchip Yb:YAG, the gain medium of this study, does not have a high cooling efficiency, but the maximum temperature increase is estimated to be only about 12 K despite the high pump intensity of about 110 kW/cm2. This is because it is the pump power, not the pump intensity, that is proportional to the temperature increase, as the maximum pump power is only 900 mW. These results indicate that high-intensity pumping is a promising approach to achieve efficient lasing at low cost.
1. Introduction
In recent years, there has been an increasing demand for higher efficiency, pulse energy, peak power, and repetition rate of short-pulse lasers to expand their applications from basic to practical. For practical applications, it is better to achieve these characteristics at a low cost. This low cost requires the use of inexpensive but lossy optical elements, such as saturable absorbers, but the efficiency of short-pulse lasers becomes lower when the loss is high. It is also necessary to achieve these characteristics with simple and easily tunable methods. To reduce the cost of the pump source for pulsed lasers, whose repetition rate is sufficiently faster than the fluorescence lifetime, it is better to use CW (continuous wave) lasers instead of pulsed lasers. This is especially important to reduce the cost per average output power of the laser.
It is well-known that to achieve laser efficiencies close to the quantum limit, it is appropriate to lower the laser threshold and increase the slope efficiency [1,2]. However, lasers with high intrinsic residual loss in the cavity tend to have a higher threshold because the total loss tends to be higher, and the slope efficiency tends to be lower because the coupling efficiency between the laser output and the laser power in the cavity tends to be lower [1,2]. On the other hand, if the unsaturated gain is high even at high intrinsic residual losses, the threshold can be lowered and the coupling efficiency can be increased [1,2]. It is well-known that the gain of CW pumping is proportional to the pump intensity (averaged along the laser axis) and, in the case of pulsed pumping, to the pump energy fluence (averaged as in CW pumping). Therefore, high-gain by high-intensity pumping for CW pumping (or high-gain by high-fluence pumping for pulsed pumping) is an excellent way to suppress the reduction in laser efficiency due to high losses. Of course, to avoid damage from pulsed pumping, the pulse width must be broadened to a range shorter than the order of the fluorescence lifetime so as not to reduce the gain. In addition, to avoid damage from high-peak output power, the peak intensity of the pulse must be reduced by expanding the laser mode area and pulse width in the gain medium.
Higher pump intensity is particularly effective in improving the efficiency of lasers using gain media with small gain products and high losses, such as Ti:sapphire crystals and quasi-three-level (quasi-four-level) laser gain media with losses due to the distribution of the lower laser level, such as Yb-based gain media. This loss is referred to as quasi-three-level (quasi-four-level) laser loss. The reasons why both quasi-three-level and quasi-four-level lasers are listed together in this paper are as follows. In general, lasers such as Yb lasers in which the energy difference between the ground level and the lower laser level is smaller than that corresponding to thermal excitation at room temperature are often referred to as quasi-three-level lasers [3]. In these lasers, the more the pump intensity is increased, the more the quasi-three-level (quasi-four-level) loss becomes saturated [3,4,5,6,7]. Therefore, some researchers refer to these lasers as quasi-four-level lasers because they can be regarded as essentially four-level lasers when the pump intensity is high [4,5,6,7]. In this paper, we also study the high pump intensity region. Therefore, we use the terms quasi-three-level laser and quasi-four-level laser here.
Several methods have been investigated to improve laser efficiency, including thin disk lasers [8,9], fiber lasers [10], and cryogenically cooled lasers [11,12]. On the other hand, high optical-to-optical conversion efficiencies of up to for the incident pump power have been achieved for CW Yb:YAG lasers by using high-gain by high-intensity pumping, which are close to the quantum limit of for Yb:YAG lasers [13]. For cavity-dumped Yb:YAG lasers with pulse widths in the nanosecond range, high optical-to-optical conversion efficiencies of up to for the incident pump power have been achieved by using high-gain by high-intensity pumping [14]. For hemispherical short-cavity CW Yb:YAG lasers, optical conversion efficiencies exceeding for the incident pump power have also been achieved [15]. In addition, optical-to-optical conversion efficiencies exceeding for the incident pump power have been achieved for T:sapphire lasers despite the use of commercially available high-loss Ti:sapphire crystals [16,17]. Using a theory that quantitatively reproduces the experimental results of Ti:sapphire lasers, it has been shown that even under conditions of a high intrinsic residual loss of , an optical-to-optical conversion efficiency of , approaching the quantum limit of Ti:sapphire lasers, can be achieved by using high-gain by high-intensity pumping [17]. To the best of our knowledge, as shown in Table 1, the efficiency of CW Yb lasers using high-gain by high-intensity pumping is almost equal to or higher than the efficiency using other technologies [8,9,10,11,12,18,19,20,21,22,23]. In pulsed Yb lasers, also as shown in Table 1, where cavity losses must be high, the efficiency of lasers using high-gain by high-intensity pumping is higher than that of lasers using other technologies [18,24].

Table 1.
Comparison of high-efficiency Yb lasers.
Although high-gain by high-intensity pumping has achieved high efficiencies for CW, pulsed, and short-cavity lasers, as mentioned above, it has been pointed out that high-intensity pumping has some disadvantages. Therefore, the purpose of this article is to address these issues. Three issues commonly associated with high-intensity pumping will be discussed: (1) The possibility of the emitted pulses having a fluence above the damage threshold within the gain medium; (2) The temperature increase within the gain medium, which can affect the efficiency of quasi-three-level (quasi-four-level) lasers; (3) The strong thermo-optic distortion caused by the high pump intensity. First, to avoid damage to the gain medium from the high-energy pulse output, the laser pulse width and the mode area within the gain medium must be expanded to suppress the peak intensity. However, these requirements are not directly related to high-intensity pumping, i.e., increasing the pump intensity within the gain medium. In fact, for lasers without cavities, such as multi-pass amplifiers, the laser beam area in the gain medium is limited by the pump beam area. In contrast, for lasers with cavities, such as laser oscillators, the laser beam area is determined by the stability condition of the cavity and is not limited by the pump beam area. As is well-known, it is easy to expand the laser mode area to be larger than the pump mode area by mode control using the stability condition of the cavity. This is effective for high-energy pulse output. Regardless of the type of laser, it is basically correct to increase the gain as much as possible within the limits of no damage to overcome the reduction in laser efficiency due to losses.
The second point concerns the belief that the higher the pump intensity, the higher the temperature increase in the gain medium. For this reason, it has been pointed out that high pump intensity increases the temperature of the gain medium due to pumping and, thus, reduces the efficiency in quasi-three-level (quasi-four-level) lasers. Of course, as the heat transport equation for the temperature increase in the gain medium indicates, the higher the pump power and pump intensity, the higher the local temperature increase in the pumped region, once the geometry and cooling scheme of the gain medium are determined. However, the heat transport equation explicitly shows that the temperature increase is proportional to the pump power, but the increase is less than proportional to the pump intensity. Therefore, in this paper, the temperature increase of the gain medium due to pumping is theoretically analyzed using the heat transport equation. Even at high pump intensities of about , the maximum temperature increase in the pumped region of the gain medium is estimated to be only about since the maximum pump power in this paper is only about . In other words, when the pump intensity is high but the pump power is low, the temperature increase is also low. By solving the heat transport equation only analytically, we have shown that the effect of the high pump intensity on temperature increase is not necessarily high. As will be discussed in the following sections, it is not necessary to analyze the complex and detailed spatial and temporal dependence of the temperature increase to explain this. These results are considered broadly applicable because they are shown using a microchip that is only 1 mm thick and does not have high cooling efficiency, a Yb:YAG gain medium with normal thermal conductivity, and a commonly used copper heat sink.
According to the heat transport theory, what is needed to increase the cooling efficiency, i.e., the thermal conductance (the heat power per temperature increase), is to expand the cooling area and reduce the distance between the pump and the cooling regions. In general, when the pump density (pump power per unit volume) is high, it is difficult to increase the cooling efficiency because it is difficult to expand the cooling area and reduce the distance. On the other hand, if the pump intensity (pump power per unit area) is only high, it is easy to expand the cooling area and reduce the distance, thus increasing the cooling efficiency and suppressing the temperature increase. Fiber lasers are a typical example of lasers with high pump intensity and high cooling efficiency, and there are also thin or micro-thickness rod or slab lasers.
The third point is the extremely high thermo-optic distortion caused by the high pump intensity required for high-gain. As explained earlier, to achieve near quantum-limited efficiency for high-loss lasers, the laser threshold must be lowered and the slope efficiency must be increased. This requires not only increasing the optimum coupling efficiency but also optimizing the pump and laser beams, i.e., minimizing the effective mode volume between the pump and laser beams and maximizing the mode-matching efficiency between the pump and laser beams. In general, thermo-optic distortion modifies the pump and laser beams. Therefore, it has been pointed out that the higher the thermo-optic distortion, the larger the effective mode volume and the lower the mode-matching efficiency [25,26,27,28,29,30,31,32,33,34,35]. The high-gain technique certainly helps to achieve the lowest laser threshold and the highest optimum coupling efficiency. However, its pump intensity is several orders of magnitude higher than that of other techniques, resulting in a thermal lens focal length that is also several orders of magnitude shorter than that of other techniques. For example, for Yb:YAG, the thermal lens focal lengths of thin disk lasers with a pump intensity of a few and a gain of a few are typically on and above an order of meters. In contrast, when the pump intensity is above the order of , the gain is on the order of tens of or higher, and the thermal lens focal lengths are on the order of or less, also in Yb:YAG. These short thermal lens focal lengths have usually been considered as a strong obstacle preventing the optimization of the pump and laser beams [25,26,27,28,29,30,31,32,33,34,35].
To demonstrate that high-gain by high-intensity pumping is effective in improving laser efficiency, it is necessary to show that the pump and laser beams can be optimized at such high-pump intensities. So far, the thermo-optic effects in solid-state lasers have been studied in many ways, but to the best of our knowledge, their pump intensities have been less than a few tens of [25,26,27,28,29,30,31,32,33,34,35]. It has been noted that compensation of thermo-optic effects is possible when the pump intensity is low and the thermal lens focal length is long but difficult when the pump intensity is high and the thermal lens focal length is short [25,26,28,29,33]. Furthermore, since it has been pointed out that accurate techniques are needed to compensate for thermo-optic distortion, many studies have been conducted to accurately derive the physical quantities associated with thermo-optic distortion [25,26,27,30,31,32,33,34,35]. In this work, we, therefore, investigated how higher pump intensities affect the ease of tuning the laser mode for beam optimization. Specifically, we experimentally and theoretically investigated the dependence of the laser threshold on the cavity length to determine how the pump intensity affects the dependence of the effective mode volume on the cavity length. Since the effective mode volume can be regarded as the sum of the pump mode volume and the laser mode volume under the conditions of this experiment, the tunability of the laser mode can be investigated simply by measuring the cavity length dependence of the laser threshold. From the investigation, we find that the tunability of the laser mode volume is maintained despite the high pump intensity at various cavity loss conditions.
The tunability of these experiments has been qualitatively explained by simply including the thermal lensing effect distributed in the gain medium caused by high pump intensities in the ABCD matrix representing the beam propagation in the laser cavity, despite the uncertainties in the reliability of the parameters used. Thermal lensing effects are well-known as the lowest-order effects in systems with inversion symmetry about the optical axis, where Hermite–Gauss modes are the eigenmodes. In general, when the pump intensity is high and the thermo-optic distortion is extremely high, the higher-order effects should not be negligible. In contrast, this study shows that even under conditions of extremely high thermo-optic distortion due to high pump intensities, the qualitative behavior of the laser mode tunability can be explained by simply ignoring the higher-order effects and including the lowest-order effects. As explained in the following sections, the reason for this is that even at high pump intensities, it is reasonable to assume that if the maximum aperture ratio of the thermal lens is as small as the order of or less, as in this study, the higher-order effects of thermo-optic distortion can be ignored. This means that the conventional compensation for thermo-optic distortion used at low pump intensities [25] can be used at high pump intensities when the maximum aperture ratio is small, as in this study.
The fact that laser mode tunability can be expressed by a simple theory, even if only qualitatively, and that the analysis does not require the actual precise values of physical parameters, which are time-consuming to derive, means that the analysis can be performed inexpensively to achieve high efficiency. A few tens of microns are sufficient for the cavity length adjustment accuracy required to tune the laser mode for high efficiency, and this level of accuracy can be easily achieved with commercially available, inexpensive micrometer stages. This ease of laser mode tuning lends itself to inexpensively achieving high laser efficiencies toward the quantum limit by optimizing the mode overlap between the laser and pump beams by reducing the effective mode volume and increasing the mode-matching efficiency.
2. Materials and Methods
2.1. Experiment
Figure 1 shows a schematic of the experiment. A hemispherical laser cavity with a microchip-structured gain medium was used to measure the laser-threshold intensity because simple cavities are useful to study the effects of high pump intensity for the cavity mode. A slightly wedged Yb:YAG crystal (manufactured by Scientific Materials Corp., Bozeman, MT, USA) with a Yb3+ ion density of and a thickness (gain medium length) of was used as the gain medium. Its surface perpendicular to the <100> axis, which orientation is expected to be effective in reducing thermal birefringence [36,37], has a vertical width of and a horizontal width of . The outer surface (the left side of the Yb:YAG) where the pump beam entered served as the end mirror for the laser cavity and was coated with an anti-reflection coating for the pump wavelengths and a high-reflection coating for the laser wavelengths . The inner surface (the right side) of the Yb:YAG crystal was coated with an anti-reflection coating between the pump and laser wavelengths (). The Yb:YAG crystal was adhered to a slightly wedged sapphire plate with anti-reflection coatings on both surfaces for the pump and laser wavelengths. The sapphire plate is thick and has the same vertical and horizontal width as the Yb:YAG crystal. The adhered surfaces were the outer (left) surface of the Yb:YAG and one of the anti-reflective coated surfaces of the sapphire plate. The ensemble (manufactured by OPTOQUEST Co., Ltd., Saitama, Japan) was mounted on a copper heat sink for cooling. The heat sink was kept at room temperature (approximately 20 °C) by a thermoelectric cooler.
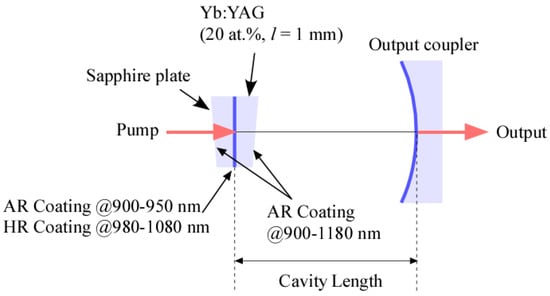
Figure 1.
Schematic of the microchip Yb:YAG laser with hemispherical cavity.
The reflectivity of the output coupler with a radius of curvature of was set to , , and for the experiments, respectively. The diameter of the output mirror was . The pump source was a CW Ti:sapphire laser. The double-pass unsaturated pump absorption efficiency was measured to be . The vertical and horizontal pump spot diameters and in the gain medium were measured to be and , respectively. The vertical and horizontal beam quality factors and were measured to be and , respectively. These values are used to obtain the pump mode volume in the gain medium for analysis. Since the ratios of vertical-to-horizontal spot diameters ( and ) and factors ( and ) are close to unity, the astigmatism of the hemispherical cavity due to thermal focusing was neglected in the theoretical analysis.
2.2. Theory
2.2.1. Quasi-Three-Level (Quasi-Four-Level) Laser Theory
In the theoretical analysis, we used quasi-three-level (quasi-four-level) laser rate equations with CW pumping, which include the spatial distribution of the pump and laser beams [17,38,39,40,41]. In the case of quasi-three-level (quasi-four-level) lasers, as in the case of four-level lasers, for simplicity, we define the normalized incident pump power , which is dimensionless with respect to the incident pump power on the gain medium , as
and the normalized intracavity laser output power , which is dimensionless with respect to the laser output power , as
where the gain medium length is , the pump quantum efficiency is , the pump photon energy is , the laser photon energy is , the output coupler transmission is , and the laser mode volume in the gain medium is [17]. The total loss of the laser cavity, excluding the loss due to the laser ion distribution in the lower laser level of quasi-three-level (quasi-four-level) lasers, is . The sum of the localized Boltzmann distribution of the lower laser level and the upper laser level is defined as .
The optical-to-optical conversion efficiency for the incident pump power is defined by the ratio between the laser output power and the incident pump power and is expressed using the normalized intracavity laser power and the normalized incident pump power from Equations (1) and (2) as
where the coupling efficiency between the laser output and the intracavity laser powers is and the atomic quantum efficiency is . Since the quantum efficiencies and are physical parameters of the gain medium, it is necessary to balance the coupling efficiency , the pump absorption efficiency , and the ratio of the normalized intracavity laser power to the normalized incident pump power to increase the optical-to-optical conversion efficiency of lasers using any particular gain medium [17]. In general, since quasi-three-level (quasi-four-level) lasers have the quasi-three-level (quasi-four-level) losses, there is an optimum value of pump absorption efficiency for high optical-to-optical conversion efficiency. The higher the pump intensity, the higher the optimum pump absorption efficiency, and, thus, the optical-to-optical conversion efficiency can be further increased [42,43].
From the condition that the amplified and lost intracavity laser powers are equal in steady-state laser oscillation, the relationship between the normalized pump power and the normalized intracavity laser power is provided by
where the laser ion doping concentration is . The pump distribution function and the laser distribution function are normalized by the volume integral within the gain medium as . These distributions are defined by the spot positions, radii, and beam qualities of the pump and laser beams. To increase the optical-to-optical conversion efficiency, the ratio of the normalized in-cavity laser power S to the normalized incident pump power F must be increased, which requires optimization of the laser and pump modes. Since the normalized intracavity laser power is zero at the threshold, the laser threshold is obtained from Equation (4) as
where the effective mode volume in the gain medium is defined by .
Equation (5) shows that the laser threshold is proportional to the effective mode volume and the sum of the total loss and the quasi-three-level (quasi-four-level) laser loss . The physical parameters of the gain medium in the analysis, such as the emission cross section and the lifetime , are obtained from [44,45,46]. The gain medium length and laser ion doping concentration are identical to those in the experiment (measured by the manufacturer). The pump distribution was assumed in the analysis to be a Gaussian beam profile with the same beam qualities and spot radii as in the experiment. The pump and laser spot positions were assumed to be at the end face of the gain medium (end face of the cavity). The dependence of the pump distribution on the beam direction was assumed to decay exponentially with an absorption coefficient obtained from the experiment. As for the laser distribution , it was assumed to be a Gaussian beam profile with the same focusing position as the pump beam (the end face of the gain medium and the cavity) and a beam quality of 1.0. Since gain saturation must occur when the laser oscillates, the dependence of the laser distribution function on the beam direction was assumed to be constant.
The intrinsic residual loss used in the analysis was 0.2%, which was obtained from the Findlay and Clay analysis [47]. The reasons for using the analysis result are as follows: There are two known methods for obtaining the intrinsic residual loss, one by Findlay and Clay and the other by Caird [48]. The Findlay and Clay analysis assumes that the effective mode volume remains unchanged when the laser threshold is changed by changing the cavity loss. The Caird analysis, on the other hand, assumes that changing the coupling efficiency changes the slope efficiency, which in turn changes the intracavity laser intensity but not the mode-matching efficiency. In general, at high pump intensities, the effect of thermos-optic distortions on the beam propagation is often non-negligible so that the effective mode volume can vary significantly depending on the pump power. On the other hand, on the stable region side, exactly at the boundary between the unstable and stable regions of the cavity, the laser oscillates in such a way that the laser mode in the gain medium is minimized. This is almost independent of whether the effect of thermo-optic distortion is high or low. For these reasons, our experiments assume that the conditions that satisfy the reliability of the Findlay and Clay analysis hold exactly at the boundary on the side of the stable region, so we used the result of the analysis.
2.2.2. Temperature Increase in the Gain Medium
In order to show in a straightforward way that high-gain by high-intensity pumping is effective at high efficiency, analytical equations are derived below to simplify the theoretical treatment of heat transport as much as possible. Since the experiment is a steady-state continuous-wave laser oscillation with a continuous-wave pump, there is no need to study the time dependence of the temperature increase, as in ref. [32]. The rate of increase of the quasi-three-level (quasi-four-level) laser loss of Yb:YAG lasers with temperature increases almost linearly from about 0 °C to about at any oscillation wavelength, and the rate of increase decreases with the increasing temperature. Therefore, in the range of about 0 °C and above, the maximum increase in the loss with the increasing temperature can be obtained simply by determining the average temperature of the lasing region. Since the temperature increase is highest in the pumped region, the average temperature increase in the lasing region is less than that. Therefore, only the average temperature increase of the pumped region should be determined. In other words, it is not necessary to determine the detailed temperature distribution in the gain medium as in ref. [27,29,32,33,34].
According to the heat transport theory [49], i.e., the heat transport equation, the temperature increase of the laser gain medium by pumping is obtained by the sum of the temperature increase of the heat sink, the temperature increase due to the heat transfer (conductance) between the heat sink and the gain medium, and the temperature increase due to heat diffusion (conduction) within the gain medium. Since the thermal conductivity of the copper heat sink () is extremely high, on the order of two orders of magnitude higher than that of the gain medium ( for 20 at.% Yb:YAG), the temperature increase in the heat sink is almost negligible (less than an order of magnitude in this experiment). Therefore, the temperature increase of the gain medium, , is expressed as the sum of the temperature increase due to the heat transfer between the heat sink and the gain medium, , and the difference between the temperature in the gain medium and the temperature at the cooling surface, , i.e., .
In this experiment, the length of the gain medium () is much shorter than the horizontal and vertical widths of the gain medium (), and the copper heat sinks are attached to the horizontal and vertical sides of the gain medium. Therefore, the dominant heat flow inside the gain medium is in the direction of the horizontal and vertical sides of the gain medium where the heat sinks are attached, i.e., perpendicular to the pump axis, and the flow along the pump axis is negligible [27]. The pump beam diameters and are on the order of two orders of magnitude smaller than the vertical and horizontal widths of the gain medium and . Furthermore, the vertical and horizontal widths of the gain medium and are equal. The ratio of horizontal and vertical pump spot diameters and is close to unity (0.925), and the ratio of horizontal and vertical M2 factors and is also close to unity (1.1). Such heat flow is in a radial direction and can be considered as close to cylindrical symmetry, especially near the pump axis. Therefore, to simplify the analysis, we assume that the system is cylindrical symmetric around the pump axis and neglects the heat flow in the direction of the pump axis.
First, the temperature increase due to the heat transfer between the heat sink and the gain medium is approximately the product of the surface thermal conductance of the heat sink and the gain medium and the contact area of the interface between the heat sink and the gain medium, i.e., the cooling surface [42,49],
In the experiment, the surface thermal conductance was measured to be about . Next, we consider the heat conduction within the gain medium. Assuming that the heat flow is cylindrically symmetric around the pump axis and neglecting the heat flow in the direction of the pump axis, the temperature difference is described by the heat conduction equation
where is the radial coordinate from the pump axis, is the thermal conductivity of the gain medium, is the heat generation efficiency, and is the absorbed pump power per unit volume . As Equation (7) shows, the Laplacian of the temperature difference is proportional to the absorbed pump power density, i.e., the absorbed pump power per unit volume . This means that even if the absorbed power per unit area, i.e., the absorbed pump power intensity, is high, the temperature rise can be reduced by lowering the absorbed pump power density. In the actual experiment, the sapphire plate is attached to the pumping surface (left side) of the gain medium as shown in Figure 1, which causes the heat flow toward the pump axis in the gain medium to reduce the temperature increase. Therefore, the temperature increase in the experiment is lower than the temperature increase if the heat flow toward the pump axis is ignored, so the temperature increase described by the middle and right sides of Equation (7) is an upper limit of the temperature increase in the experiment.
Here, the intensity distribution of the pump beam is assumed to be top-hat; the temperature increase when the intensity distribution of the pump beam is Gaussian has been analyzed in Ref. [27]. The difference in the temperature distribution near the pump axis when the intensity distribution of the pump beam is Gaussian or top-hat is small when the definition of the focused intensity is changed. For simplicity and to obtain an upper limit on the temperature increase in the gain medium, the pump beam diameter along the pump axis is assumed to be constant with the vertical pump spot diameter . Under these conditions, the absorbed pump power per unit volume integrated along the pump axis is the product of the pump absorption efficiency and the pump intensity , where is the cross section of the pump beam, and we obtained the temperatures averaged along the pump axis. From Equation (7), the temperature difference between the pumped region and the cooling surface averaged along the pump axis is
The temperature difference between the coordinate within the pumped region ( and the boundary between the pumped and unpumped regions , averaged along the pump axis, is also obtained from Equation (7) as
In the pumped region, the temperature difference is the sum of the temperature differences and . From Equation (9), the temperature difference averaged over the pumped region is obtained by
As Equations (8)–(10) show, the temperature differences in the gain medium , , and are proportional to the pump power but do not depend on the pump intensity . To reduce the temperature difference , the distance between the pumped region and the cooling surface should be shortened rather than reducing the pump intensity.
From Equations (6) and (10), the temperature increase in the pumped region of the gain medium, averaged in the pump axis, is . Therefore, from Equations (6) and (10), the temperature increase in the pumped region of the gain medium, averaged over the pumped region, is
Equation (11) provides a simple expression for the following well-known fact. To reduce the temperature increase in the pumped region of the gain medium, it is effective to increase the area of the interface between the gain medium and the heat sink, i.e., the cooling surface , and to reduce the distance between the cooling surface and the pumped region . For a cylindrical gain medium, the diameter of the gain medium must be increased to increase the cooling area for cooling , but the diameter must be decreased to reduce the distance between the cooling surface and the pumped region (more precisely, for the cylindrically symmetric system, the ratio of the pumped region to the cooling surface as shown in Equation (11)). The optimum diameter that minimizes the temperature increase is , which is provided that the derivative of the temperature increase with respect to the diameter is zero, i.e., . Therefore, the temperature increase of the optimal diameter is provided by
To further increase the cooling efficiency, i.e., to reduce the thermal resistance and temperature increase, it is necessary to reduce the distance by thinning the gain medium and to expand the cooling area by widening and lengthening the gain medium, as in the case of thin or micro-thickness rods [42,43] or slabs [42,50,51]. The pump intensity has no direct effect on cooling efficiency. The average temperature increase within the gain medium is
where is the cooling surface and and are the thickness and width of the gain medium, respectively [42]. The thickness and width are defined as the widths of the gain medium in the direction of the cooling axis (vertical direction) and in the direction perpendicular to the cooling axis (horizontal direction), respectively. The typical lengths of thin-rod and thin-slab are tens of , the typical thicknesses and widths of thin-rod are less than , and the thicknesses and widths of thin-slab are less than and greater than , respectively. The cooling area resulting from these shapes is several orders of magnitude larger than that of microchips, and the distance between the pumped and cooling regions is smaller, resulting in cooling efficiencies that are several orders of magnitude higher.
2.2.3. Thermal Lens
According to thermo-optic theory, the spatial distribution of the optical path length varies as a result of the interplay between the thermo-optic effect and pumping [25,26,27,28,29,30,31,32,33,34,35]. The thermo-optic effect includes thermally induced variations in refractive index and thermal expansion. Assuming that the system is cylindrically symmetric along the pump and laser axis, the pump intensity distribution is a top-hat profile, i.e., the heat density is uniform in the direction perpendicular to the axis, and the heat flow direction is also perpendicular to the axis as described in Section 2.2.2, while the temperature distribution perpendicular to the axis is ideally quadratic. Therefore, the optical path length distribution in the heated region is also ideally quadratic and is the same as the optical path length distribution where the Hermite–Gaussian mode is an eigenstate. The maximum optical path length difference due to thermo-optic effects is determined by the aperture ratio of the thermal lens, which is defined by the ratio of the laser beam diameter in the gain medium to the thermal focal length. Although the maximum of the quadratic term is proportional to the aperture ratio and the maximum of the quartic term is proportional to the second power of the aperture ratio, the ratio of the quadratic and quartic terms is proportional to the aperture ratio. The maximum in the experiment is on the order of . Since the aperture ratio is sufficiently small, the quadratic approximation is reliable in the analysis.
Using the quadratic approximation for the optical path length distribution perpendicular to the direction of laser beam propagation, the focal length of the thin thermal lens is
where is the refractive index, is the linear expansion coefficient, and is the temperature coefficient of the refractive index. The thermal focus length is inversely proportional to the absorbed top-hat pump intensity . If the radial intensity distribution is assumed to follow a Gaussian profile with an absorbed peak intensity of , the corresponding thermal focal length is equal to Equation (14) because of the quadratic approximation. The quadratic approximation is valid for the gain medium with small optical path length distributions over the optical path. Therefore, we divide the gain medium into several small distribution media. For the pump intensity distribution, the absorption of the gain medium was assumed to be unsaturated (the pump intensity decays exponentially along the pump axis because absorption saturation is resolved during laser oscillation), and the experimental absorption efficiency and corresponding absorption coefficient were used. The pump beam propagation was assumed to be a Gaussian beam with the experimental spot diameters and M2, and the focusing position was also set at the center of the gain medium as in the experiment. The required physical parameters were obtained from various literatures (the refractive index , the linear expansion coefficient , and the temperature coefficient of the refractive index ). The heat conversion efficiency in the gain medium is , which corresponds to the laser wavelength of in the experiment.
3. Experimental Results and Discussions
To achieve high optical-to-optical conversion efficiencies, tunability of the laser mode volume is required to optimize the overlap of the laser and pump modes in the gain medium to achieve high mode-matching efficiency and small effective mode volume. As is well-known, the dependence of the laser mode volume on the cavity length is suitable for this tunability. As shown in Equation (5), the laser threshold intensity is proportional to the effective mode volume and the total cavity loss . The laser threshold intensity increases with increasing cavity loss, and this pump intensity causes thermo-optic effects and varies the laser mode. In our experiments, the maximum pump intensity exceeds and the corresponding thermo-optical distortion is very strong, while the corresponding thermal focal length with the thin lens approximation is very short, less than 10 mm. In general, such a high thermo-optical distortion can have a significant effect on the laser mode. In the experiments, the laser output beam was a near-basic Gaussian beam with near cylindrical symmetry, so the pump and laser beams are considered to be concentric. In this case, the effective mode volume is the sum of the pump mode volume in the gain medium and the laser mode volume in the gain medium , i.e., . Therefore, even under strong thermo-optic effects, the ease of laser mode tuning can be easily investigated by studying the dependence of the laser threshold intensity on the cavity length. Thus, we measured the laser threshold intensity as a function of cavity length for different total cavity losses by changing the output coupler reflectivity, and the results are shown in Figure 2a. The measured wavelength is approximately 1048 nm when the laser oscillates in the stable region near the boundary between the stable and unstable regions (the corresponding cavity length is approximately 99.4 mm) with an output coupler reflectance of . This wavelength was used in the theoretical analysis because the laser is known to oscillate at approximately this wavelength in the range of cavity loss within the stable region in the experiment, and because the theoretical analysis was performed within the stable region.
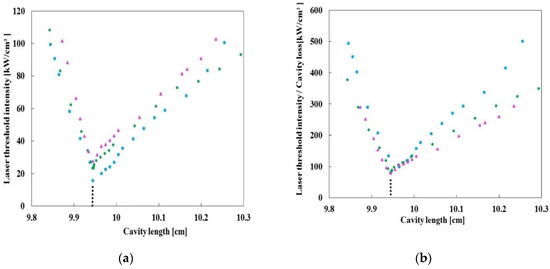
Figure 2.
Experimental results of laser threshold intensity and laser threshold intensity normalized by cavity losses as a function of cavity length. The blue squares, green circles, and purple triangles correspond to results for output coupler reflectivity , , and , respectively. The vertical black dotted line indicates the cavity length at the boundary between stable and unstable regions. (a) Laser threshold intensity as a function of cavity length. (b) Laser threshold intensity normalized by cavity losses as a function of cavity length.
It can be seen from Figure 2a that the laser threshold intensity depends on the total cavity loss but varies significantly, by a factor of several, depending on the laser cavity length for any total cavity loss. Furthermore, as shown in Equation (5), when the laser threshold intensity is normalized by the total cavity loss, the constant of proportionality is provided only by the physical parameters of the gain medium. Therefore, we investigated how the high pump intensity and the corresponding thermo-optic effects affect the laser mode volume by comparing the normalized laser threshold intensities with different cavity losses. The cavity loss was determined in Section 2.2.1 using the Findlay and Clay analysis. The normalized laser threshold intensities are plotted as a function of cavity length in Figure 2b. It can also be seen from Figure 2b that the normalized laser threshold intensity also depends on the total cavity loss, as well as the laser threshold intensity, and varies significantly, by a factor of several, depending on the laser cavity length for any total cavity loss. Overall, it can be seen from Figure 2 that the tunability of the laser mode volume is maintained even when the thermo-optic effect is varied by high pump intensity and cavity loss, as in the experiment.
In general, the stable region of the laser cavity varies with the focal length of the thermal lens [52,53]. For high-gain by high-intensity pumping, the shortest focal lengths of the thermal lens are significantly shorter than those of other solid-state laser techniques (i.e., excluding fiber lasers) where the maximum pump intensities are below a few tens of . For example, the maximum pump intensity in these experiments is about , assuming a top-hat beam profile of the pump spot radius. The corresponding thermal lens focal length of the Yb:YAG crystal is estimated to be about in the thin lens approximation using the theoretical analysis of thermal lensing effects described in Section 2.2.3. In contrast, the thermal-lens focal lengths for the thin disk are typically longer than several meters [8,9,34].
For the laser cavity in our experiments, the thermal lenses are distributed in the gain medium, which also serves as the end mirror of the hemispherical laser cavity. It is known that when the thermal lens focal length of the gain medium (i.e., the focal length when the thermal lens distributed in the gain medium is transformed into a thin lens) is infinite, there is only one stable region [52,53]. The length of the laser cavity corresponding to this stable region ranges from to approximately the radius of curvature. (It is not exactly the radius of curvature because there is a gain medium with a refractive index higher than 1 in the cavity). In this paper, for simplicity, the stable region is expressed as starting at the shortest cavity length (in this case, ) and ending at the longest cavity length (in this case, approximately the radius of curvature); this range of cavity length is expressed as the range of the stable region.
In contrast, when the thermal lens focal length is finite, the stable region is generally divided into two (except when the thermal lens focal length is approximately half the radius of curvature) [52,53]. The stable region with the shorter cavity length is referred to as the first stable region for simplicity as well, and the stable region with the longer cavity length is referred to as the second stable region. When the thermal lens focal length is longer than approximately half of the radius of curvature, the first stable region starts at and ends at approximately the radius of curvature, similar to the stable region when the thermal lens focal length is infinite, and the corresponding range is independent of the thermal lens focal length. In contrast, the second stable region starts at approximately twice the thermal lens focal length and ends at the sum of approximately twice the thermal lens focal length and the radius of curvature. In summary, the range of the first stable region is independent of the thermal lens focal length, while the range of the second stable region depends on the thermal lens focal length. These cavity conditions, where the thermal lens focal length is longer than approximately half the radius of curvature, have been studied by many groups [25,26,27,28,29,30,31,32,33,34,35].
As the thermal lensing effect increases, the behavior of these stable regions changes. That is, when the thermal lens focal length is shorter than approximately half the radius of curvature, the first stable region starts at , which is the same as for other thermal lens focal lengths, but the second stable region starts at approximately the radius of curvature. Furthermore, these stable regions vary to narrow as the thermal lens focal length decreases. To our knowledge, regions with such strong thermal lensing effects have not been well-studied. Here, in the experiments, the pump intensities at the laser thresholds typically exceed about , so that the corresponding thermal lens focal lengths are shorter than about , which is almost half the radius of curvature. Therefore, in Figure 2, the region where the cavity length is approximately or longer is the second stable region, and the region where the cavity length is shorter than that corresponds to the unstable region. It is well-known that laser oscillation in the unstable region is generally difficult due to very high cavity losses caused by diffraction losses. However, as shown in Figure 2, the laser oscillates even in the unstable region in the experiment. This indicates that the high-gain by high-intensity pumping enables oscillation even in the unstable region with high losses.
The cavity loss used in Figure 2b is obtained from the condition that the laser mode volume at the boundary between the unstable and stable regions of the cavity (the cavity length is approximately 99.4 mm) is the same regardless of the loss difference because the laser oscillates in such a way that the laser mode volume is minimized at the boundary regardless of the loss difference, as shown in Section 2.2.1. Therefore, it is natural that just at the boundary, the laser mode volume is the same regardless of the loss difference, i.e., the normalized laser threshold intensity is the same. On the other hand, Figure 2b shows that in the stable region near the boundary (the cavity length between approximately and ), the normalized laser threshold intensity is also almost the same for different losses. Of course, the higher the cavity loss, the higher the laser threshold intensity and, thus, the higher the thermo-optical distortion, i.e., the shorter the thermal lens focal length. This means that within the stable region near the boundary, the laser mode volume is almost the same despite the difference in thermal lens focal length.
In contrast, in the region some distance away from the boundary (the cavity length is longer than about ), the normalized laser threshold intensity becomes dependent on the cavity loss. Namely, the laser mode volume becomes a function of cavity loss. It is well-known that the higher the cavity loss, the higher the laser threshold intensity and, thus, the shorter the thermal lens focal length. In summary, in the range of experimental conditions, in the region some distance away from the boundary, the higher the cavity loss, the shorter the thermal lens focal length and the smaller the laser mode volume. More specifically, the laser mode volume is smaller at higher pump intensities than at lower pump intensities. In general, higher pump intensities lead to stronger thermo-optic effects. Therefore, in the range of experimental conditions, the laser mode volume decreases owing to the thermo-optic effects, which in turn are owing to the high-intensity pumping. This may mean that the ease of tuning the laser mode is reduced to some extent due to the thermal lensing effect caused by the high-intensity pumping. The conventional view that thermal lensing reduces the efficiency of lasers may be based on this fact.
However, as shown in Figure 2b, even under the highest cavity loss condition, the normalized laser threshold intensity varies by a factor of about three within the stable region of the experiment. According to the analysis of laser and pump mode propagation using the ABCD law with thermal lens, the pump and laser modes in the gain medium are almost similar at the boundary between the stable and unstable regions. Therefore, under experimental conditions, the laser mode volume in the gain medium can be controlled by a factor of about three even under high loss conditions. According to the theoretical analysis of the quasi-three-level (quasi-four-level) laser, under the condition of high-intensity pumping, the highest efficiency is obtained when the pump and laser focusing diameters are almost equal. Therefore, the result shown in Figure 2b means that even under the condition of high-intensity pumping, the laser mode tunability remains sufficient to achieve the highest laser efficiency.
4. Theoretical Results and Discussions
4.1. Temperature Increase in the Gain Medium
According to the theory of heat transport, as explained in detail in Section 2.2.2, the temperature increases of the gain medium, e.g., the temperature increase of the gain medium averaged over its pumped region as shown in Equation (11), are proportional to the heat power due to the pump power (not the pump intensity), while the proportionality constant is determined by the thermal resistance between the gain medium and the heat sink and the thermal resistance of the gain medium. In this experiment, the pump power is estimated to be less than , and the thermal resistance is estimated to be less than under the experimental conditions (, , ). Due to this low thermal resistance and the low heat power due to this pump power, the temperature increase obtained from Equation (11) is . The components are: the temperature increase due to the surface conductance is , the temperature difference in the unpumped region is , and the temperature difference is . The temperature increase at the maximum cooling efficiency obtained from Equation (12) under the experimental conditions is at the maximum pump power of , and the corresponding optimum diameter is .
Since most of the temperature increase in the pumped region of the gain medium is due to the temperature difference in the unpumped region , the temperature increase is mostly considered to be caused by the distance between the pumped region and the cooling surface. However, the reason why the temperature rise does not greatly decrease even when the diameter of the gain medium is optimized is that the cooling area becomes smaller in proportion to the diameter, and the thermal resistance between the heat sink and the gain medium becomes larger. As explained in Section 2.2.2, to further reduce the temperature increases, it is necessary to reduce the distance between the pumped and cooling regions by thinning the gain medium and to expand the cooling area by widening and lengthening the gain medium. These temperature increases in the experiment are estimated to be small, and the increase in quasi-three- or four-level laser losses due to these temperature increases is also small (0.25% increase in the local Boltzmann distribution of the lower laser levels at the oscillation for the temperature increase). Therefore, the gain medium temperature in the theoretical analysis was assumed to be the gain medium cooling temperature of 20 °C.
4.2. Dependence of Laser Threshold Intensity on Cavity Length
To explain the experimental dependence of the laser threshold intensity and the laser mode volume on the cavity length and the influence of the high-intensity pumping on these dependences, we have theoretically analyzed the dependence of the laser threshold intensity and the laser mode volume on the cavity length and compared it with the experimental results. The laser and pump mode volumes have been calculated using the ABCD matrix theory for the laser cavity shown in Figure 1, which includes thermo-optic effects distributed in the gain medium. Although the diffraction loss of the output coupler is not included in the theory, when the cavity length is some distance away from the unstable region, the diffraction loss can be ignored. Therefore, the assumptions on which the theory is based are correct at some distance from the unstable region. In conclusion, we can compare the experiment and the theory at some distance from the unstable region.
Note that the product of the emission cross section and the fluorescence lifetime depends on the growth conditions of the gain medium and the theories used to determine their values. Therefore, the exact value of the product in the actual gain medium is difficult to determine. As will be explained later, the assumptions about the pump absorption efficiency in the theory may also be incorrect. As shown in Section 2.2.3, this theory includes only the lowest-order thermo-optic distortion, i.e., thermal lensing effects, for thermo-optic distortions distributed in the gain medium. As a result, the exact value of the laser threshold intensity provided by Equation (5) may be incorrect. In general, the derivation of quantitative values requires a complex and laborious theoretical analysis. In contrast, to improve the efficiency, it is only necessary to be able to control the laser mode within a sufficiently tunable precision and range. Therefore, the efficiency of the laser can be improved if only these behaviors can be obtained qualitatively. Here, if the qualitative behaviors can be explained by a simple theory that does not require labor-intensive analysis, it will lead to a reduction in the cost of high efficiency lasers. Therefore, we investigated whether these qualitative behaviors could be explained by a simple theory.
Figure 3a–c compare the experimental and theoretical results. The theory assumes that the thermal lens distributed in the gain medium is constant with respect to varying the laser threshold intensity (the focal length shown in the figures is the focal length of the thin lens approximation). As shown in the figures, the experimental and theoretical dependence of the laser threshold intensity on the cavity length is qualitatively similar. The theoretical analysis shows that the shorter the thermal lens focal length, between 40 mm and about 10 mm, the lower the dependence of the laser threshold intensity on the cavity length. However, when the thermal lens focal length is shorter than about 10 mm, the dependence of the laser threshold intensity on the cavity length increases with the thermal lens focal length. In other words, the shorter the focal length, the narrower the stable region for thermal lenses with a focal length of about 10 mm or less. This narrowing of the stable region may be one of the reasons why thermal lensing effects have been observed to reduce laser efficiency. According to the efficiency analysis of lasers using the quasi-three-level (quasi-four-level) laser theory in Section 2.2.1, under high-intensity pumping conditions, where the pump intensity is above one hundred , the dependence of laser efficiency on laser spot diameter is also low in the vicinity of the spot diameter near the highest efficiency (even if the spot diameter varies by about 10%, the difference in efficiency is less than a few percent). According to the beam propagation analysis, the cavity length adjustment accuracy required for these appropriate laser spot diameters to achieve high efficiency is tens of microns. Of course, this level of accuracy can be easily achieved using ordinary micrometer stages. Therefore, it is easy to adjust the laser for high efficiency under the condition of high-intensity pumping. This fact indicates that high gain by high-intensity pumping easily enables a low cost for high-efficiency lasers.
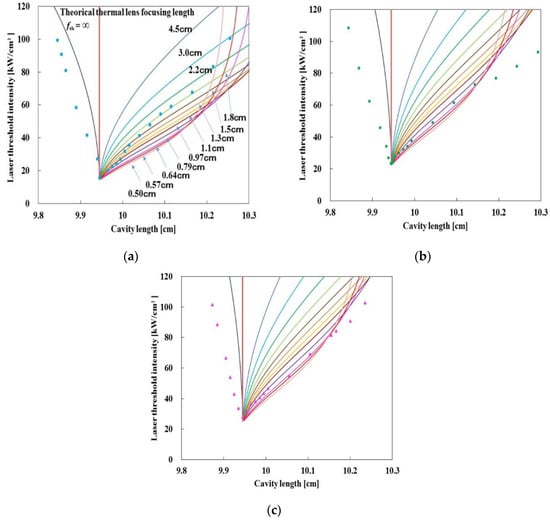
Figure 3.
Laser threshold intensity as a function of cavity length. For these theoretical curves, the focal length of the thermal lens is fixed. The focal length shown in the figures is the focal length of the thin lens approximation. Thermal lens focal lengths range from to infinity. A particular color for the curves corresponds to the same thermal lens focal length. As in Figure 2, the blue squares, green circles, and purple triangles correspond to the experimental results for output coupler reflectivity , , and , respectively. (a) Theoretical and experimental results for output coupler reflectivity . (b) Same as (a) but for . (c) Same as (a) but for .
Figure 4 shows the theoretical results of the laser threshold intensity when the thermal lens distributed in the gain medium is varied as a function of the laser threshold intensity and compares them with the experimental results. As shown in Figure 4, when the thermal lens focal lengths are varied, the stable region in the theoretical results narrows as the cavity loss increases, resulting in a higher laser-threshold intensity. The dependence of the laser threshold intensity on the cavity length and cavity loss in the theory with the thermal lens focal length varied as a function of the laser threshold intensity shown in Figure 4 is qualitatively more similar to the experimental results than the results of the theory with the thermal lens focal length fixed shown in Figure 3.
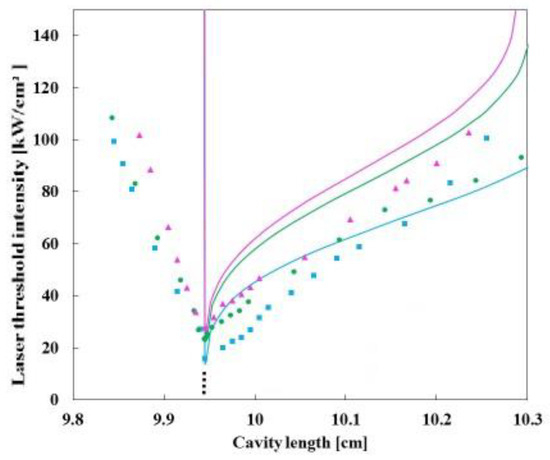
Figure 4.
Laser threshold intensity as a function of cavity length. The theoretical thermal lens focal lengths vary with the laser threshold intensity. As in Figure 2 and Figure 3, the blue squares, green circles, and purple triangles correspond to the experimental results for output coupler reflectivity , , and , respectively. The blue, green, and purple curves are the theoretical results corresponding to the output coupler reflectivity , , and , respectively.
We also investigate theoretically how high-intensity pumping affects the dependence of the laser mode volume on the cavity length by comparing normalized laser threshold intensities with different cavity losses. Figure 5a,b show the theoretical results for the normalized laser threshold intensities. The experimental results are also shown for comparison. In Figure 5a, the thermal lens focal length is fixed as in Figure 3, while in Figure 5b, the thermal lens focal length is varied as a function of the laser threshold intensity as in Figure 4. These results also show that the stable region becomes narrower as the cavity loss increases. In the stable region, the normalized laser threshold intensity is lower at higher cavity losses. This is because the laser mode volume is reduced owing to the strong thermal focusing caused by the high pump intensity.
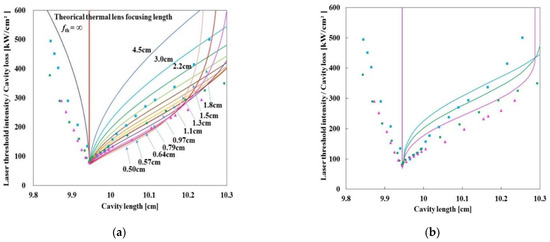
Figure 5.
Normalized laser threshold intensities as a function of cavity length. As in the previous figures, experimental results are also included for comparison. The blue squares, green circles, and purple triangles correspond to the experimental results for output coupler reflectivity , , and , respectively. (a) Theoretical results when the focal length of the thermal lens is fixed as in Figure 3. (b) Theoretical results when the focal length of the thermal lens is varied with the laser threshold intensity as in Figure 4. The blue, green, and purple curves are the theoretical results corresponding to the output coupler reflectivity , , and , respectively.
The quantitative differences between theory and experiment can be attributed to the poor accuracy of the physical parameters described above and the uncertainty in the pump absorption efficiency at the laser threshold. Another possible reason is that the thermo-optic distortion distributed in the gain medium used in the theory to analyze the beam propagation includes only the lowest order effects, namely thermal lensing effects. In general, the saturation of the pump absorption is reduced by lasing, so the assumption in theory that the pump absorption is not saturated is reliable for lasing if the laser mode sufficiently covers the pump mode and the laser mode volume is sufficiently larger than the pump mode volume. In contrast, the pump absorption is more likely to be saturated in the part of the gain medium where there is no lasing. In fact, the pump absorption assumption is reduced when the laser mode volume is smaller than the pump mode volume. Therefore, at the laser threshold, the degree of saturation is not well-known and, therefore, the quantitative reliability of the assumption is not known. The difference between the saturated and unsaturated absorption efficiencies has been measured to be less than a few tens of a percent. Therefore, the uncertainty in the pump absorption efficiency is less than a few tens of a percent. Conversely, if the laser mode volume is sufficiently larger than the pump mode volume, the pump intensity distribution assumption is appropriate because the laser beam de-excites all energized transitions created by pump absorption, and the incident pump intensity distribution is maintained. In contrast, if the laser mode volume is smaller than the pump mode volume, de-excitation of the pump absorption saturation occurs only within the laser beam. At the laser threshold, the accuracy of the pump absorption may decrease when the laser mode volume is smaller than the pump mode volume. By incorporating these effects into the theory, we expect the theoretical dependence of the laser threshold intensity on the cavity length to be in better quantitative agreement with the experimental result.
As explained above, the accuracy of the parameters used in the theory used here is uncertain and the theory is simple. Nevertheless, as shown in these figures, the theory is able to reproduce the qualitative behavior of the experiment. This indicates that even when the pump intensity is very high, as in the experiment, the accuracy of the parameters is not so important if only the qualitative behavior is to be described, and the thermal lensing effect alone is sufficient for the thermo-optic distortion. As shown in Section 2.2.3, the maximum aperture of the thermal lens is small, on the order of , even though the focal length of the shortest experimental thermal lens is very short, estimated to be about . Furthermore, the theory used here treats the gain medium as a quadratic refractive index distribution medium divided into several parts so that the numerical aperture of the thermal lens is further reduced in each part. Therefore, even though the thermo-optic distortion appears to be extremely high compared to previous studies, the thermal lensing effect alone would have been sufficient to qualitatively characterize the experimental results. The fact that a simple theory with such unreliable physical parameters can qualitatively show experimental results is a cost saving for theoretical analysis.
For optimal mode overlap at pump intensities above to achieve quantum-defect limited efficiency, the laser mode volume should be similar to the pump mode volume as mentioned above. As also shown in Figure 5, the laser mode volume, which is linear with the normalized laser threshold intensity, is widely tunable by varying the cavity length, even at different cavity losses. Although the maximum pump intensity in the experiment is about , the theoretical results show that the variability can be maintained for higher pump intensities beyond the experimental conditions. Thus, this variability can be used to obtain the desired laser mode volume to increase the optical-to-optical conversion efficiency. In fact, the influence of strong thermal focusing caused by high-intensity pumping has been shown to be easily controllable both theoretically and experimentally. These results imply that the derivation of precise physical parameters and precise techniques to compensate for thermo-optical distortions, which have also been recently suggested to be necessary [54,55], are not so important for high efficiency using high gain by high-intensity pumping. These results indicate that high-gain by high-intensity pumping can be used to achieve high efficiency lasing for a wide range of cavity loss conditions.
5. Conclusions
Although high-gain by high-intensity pumping achieves high laser efficiency, several issues have been observed. Among these problems, we have studied the effects of high pump intensity on the temperature increase of the gain medium, which leads to an increase in the quasi-three-level (quasi-four-level) laser loss, and on the laser mode tunability, which is necessary to optimize the laser mode and the pumping mode to achieve high efficiency. A hemispherical cavity laser with a thick microchip Yb:YAG gain medium was used. First, the equations analytically derived from the heat transport theory indicate that this microchip gain medium does not have a high cooling efficiency (thermal conductance), but the maximum temperature increase in the pumped region of the gain medium averaged in the pumped region, which is directly related to the increase in the loss, is estimated to be only despite the extremely high pump intensity of about . This is because in heat transport theory, it is the pump power, not the pump intensity, that is proportional to the temperature increase, and the pump power is only . At this level of temperature increase, the increase in the loss at the oscillation wavelength of the experiment is small.
The effect of the pump intensity on the laser mode tunability has also been studied by obtaining the dependence of the laser threshold intensity on the cavity length at different cavity loss conditions. The experimental results on the dependence are in qualitative agreement with the results of the simple theory, which uses physical parameters of unknown reliability and includes only the lowest order thermos-optic distortion, i.e., the thermal lensing effects. The results show that even under conditions of extremely high thermo-optic distortion and short thermal focal length due to high pump intensity, the qualitative behavior of the laser mode tunability can be explained, even if the higher order effects of thermo-optic distortion are ignored. The reason is thought to be that the aperture ratio of the thermal lens is small, on the order of , despite the extremely short minimum focal length of the thermal lens of about . The reliability of the physical parameters is also less important. The fact that the laser mode tunability can be expressed by a simple theory, even if only qualitatively, and that the analysis does not require the actual precise values of the physical parameters, which are time-consuming to derive, means that the analysis can be performed inexpensively. Despite the high pump intensity, the laser mode tunability is maintained over a wide range. Tens of microns are sufficient for the cavity length adjustment accuracy required to optimize the laser mode. This level of accuracy can be easily achieved with commercially available micrometer stages. This ease of tuning has contributed to the low cost of the high-efficiency lasers achieved to date.
Funding
Part of this research was supported by JSPS KAKENHI Grant Numbers JP25390123, JP21K04924; AMADA Co., Ltd. (AF–2018223–B3); and the joint research project of the Institute of Laser Engineering, Osaka University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author thanks Kent Kato for assistance with the experiment and theoretical analysis, Hiroki Kadoya for assistance with the preparation of the manuscript, and Hiroki Goto for assistance with the preparation of the references.
Conflicts of Interest
The author declares no conflict of interest.
References
- Koechner, W. Section 3.4.2. Laser Output. In Solid State Laser Engineering, 6th ed.; Springer: Berlin, Germany, 2006; pp. 118–126. [Google Scholar]
- Yariv, A.; Yeh, P. Section 6.5. Optimum Output Coupling in Laser Oscillators. In Photonics, Optical Electronics in Mordern Communications, 6th ed.; Oxford University Press: New York, NY, USA, 2007; pp. 248–251. [Google Scholar]
- Lacovara, P.; Choi, H.K.; Wang, C.A.; Aggarwal, R.L.; Fan, T.Y. Room-temperature diode-pumped Yb:YAG laser. Opt. Lett. 1991, 16, 1089–1091. [Google Scholar] [CrossRef] [PubMed]
- Taira, T. Yb solid state lasers. Jpn. J. Opt. 1999, 28, 435–442. [Google Scholar]
- Pavel, N.; Saikawa, J.; Taira, T. Radial-Pumped Microchip High-Power Composite Yb:YAG laser: Design and Power Charac-teristics. Jpn. J. Appl. Phys. 2001, 40, 146–152. [Google Scholar] [CrossRef]
- Fan, T.Y. Diode-pumped solid-state lasers. In Laser Sources and Applications; Miller, A., Finlayson, D.M., Eds.; CRC Press: Boca Raton, FL, USA, 2020; pp. 153–193. [Google Scholar]
- White, J.O. Parameters for Quantitative Comparison of Two-, Three-, and Four-Level Laser Media, Operating Wavelengths, and Temperatures. IEEE J. Quantum Electron. 2009, 45, 1213–1220. [Google Scholar] [CrossRef]
- Giesen, A.; Hügel, H.; Voss, A.; Wittig, K.; Brauch, U.; Opower, H. Scalable concept for Diode-Pumped High-Power Solid-state Lasers. Appl. Phys. B 1994, 58, 365–372. [Google Scholar] [CrossRef]
- Peters, R.; Kränkel, C.; Petermann, K.; Huber, G. Broadly tunable high-power Yb:Lu2O3 thin disk laser with 80% slope efficiency. Opt. Express 2007, 15, 7075–7082. [Google Scholar] [CrossRef] [PubMed]
- Jeong, Y.; Sahu, J.K.; Payne, D.N.; Nilsson, J. Ytterbium-doped large-core fiber laser with 1.36 kW continuous-wave output power. Opt. Express 2004, 12, 6088–6092. [Google Scholar] [CrossRef]
- Shoji, T.; Tokita, S.; Kawanaka, J.; Fujita, M.; Izawa, Y. Quantum-defect-limited operation of diode-pumped Yb:YAG laser at low temperature. Jpn. J. Appl. Phys. 2004, 43, L496–L498. [Google Scholar] [CrossRef]
- Ripin, D.J.; Ochoa, J.R.; Aggarwal, R.L.; Fan, T.Y. 165-W cryogenically cooled Yb:YAG laser. Opt. Lett. 2004, 29, 2154–2156. [Google Scholar] [CrossRef]
- Matsubara, S.; Ueda, T.; Kawato, S.; Kobayashi, T. Highly Efficient Continuous-Wave Laser Oscillation in Microchip Yb:YAG Laser at Room Temperature. Jpn. J. Appl. Phys. 2007, 46, L132–L134. [Google Scholar] [CrossRef]
- Takama, M.; Matsubara, S.; Ueda, T.; Inoue, M.; Tanaka, M.; Otani, K.; Kawato, S.; Kobayashi, T. Highly efficient nanosecond-pulse Yb:YAG laser. Smart Process. Technol. 2007, 2, 281–283. [Google Scholar]
- Kawato, S.; Kadoya, H.; Sugiki, F.; Kobayashi, R.; Kanetake, T.; Nakajima, N.; Kataoka, S. Laser efficiency improvement on hemispherical short cavity lasers by high intensity pumping. In Proceedings of the EMN Angkor Meeting & CC Physical Chemistry, Ankor, Cambodia, 12–13 March 2018; p. A14. [Google Scholar]
- Takano, T.; Ogawa, H.; Ohae, C.; Katsuragawa, M. 10 W injection-locked single-frequency continuous-wave titanium:sapphire laser. Opt. Express 2021, 29, 6927–6934. [Google Scholar] [CrossRef] [PubMed]
- Kawato, S.; Kawashima, T. High-Efficiency Continuous-Wave Ti:Sapphire Laser with High-Intensity Pumping Using a Commercially Available Crystal. Appl. Sci. 2022, 12, 4815. [Google Scholar] [CrossRef]
- Liu, J.; Griebner, U.; Petrov, V.; Zhang, H.; Zhang, J.; Wang, J. Efficient continuous-wave and Q-switched operation of a diode-pumped Yb:KLu(WO4)2Yb:KLu(WO4)2 laser with self-Raman conversion. Opt. Lett. 2005, 30, 2427–2429. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wan, Y.; Zhou, Z.; Tian, X.; Han, W.; Zhang, H. Comparative study on the laser perfor-mance of two Yb-doped disordered garnet crystals YbCNGG and YbCLNGG. Appl. Phys. B 2012, 109, 183–188. [Google Scholar] [CrossRef]
- Han, W.; Wu, K.; Tian, X.; Xia, L.; Zhang, H.; Liu, J. Laser performance of ytterbium-doped gallium garnets: Yb:Re_3Ga_5O_12 (Re = Y, Gd, Lu). Opt. Mater. Express 2013, 3, 920–927. [Google Scholar] [CrossRef]
- Dong, J.; Shirakawa, A.; Ueda, K.; Kaminskii, A. Effect of ytterbium concentration on cw Yb:YAG microchip laser performance at ambient temperature—Part I: Experiments. Appl. Phys. B 2007, 89, 359–365. [Google Scholar] [CrossRef]
- Serres, J.M.; Jambunathan, V.; Loiko, P.; Mateos, X.; Yu, H.; Zhang, H.; Liu, J.; Lucianetti, A.; Mocek, T.; Yumashev, K.; et al. Microchip laser operation of Yb-doped gallium garnets. Opt. Mater. Express 2016, 6, 46–57. [Google Scholar] [CrossRef]
- Loiko, P.; Serres, J.M.; Mateos, X.; Xu, X.; Xu, J.; Jambunathan, V.; Navratil, P.; Lucianetti, A.; Mocek, T.; Zhang, X.; et al. Microchip Yb:CaLnAlO_4 lasers with up to 91% slope efficiency. Opt. Lett. 2017, 42, 2431–2434. [Google Scholar] [CrossRef]
- Stolzenburg, C.; Voss, A.; Graf, T.; Larionov, M.; Giesen, A. Advanced pulsed thin disk laser sources. Proc. SPIE 2008, 6871, 68710H. [Google Scholar] [CrossRef]
- Koechner, W. Thermal Lensing in a Nd:YAG Laser Rod. Appl. Opt. 1970, 9, 2548–2553. [Google Scholar] [CrossRef] [PubMed]
- Foster, J.D.; Osterink, L.M. Thermal effects in a Nd:YAG Laser. J. Appl. Phys. 1970, 41, 3656–3663. [Google Scholar] [CrossRef]
- Innocenzi, M.E.; Yura, H.T.; Fincher, C.L.; Fields, R.A. Thermal modeling of continuous-wave end-pumped solid-state lasers. Appl. Phys. Lett. 1990, 56, 1831–1833. [Google Scholar] [CrossRef]
- Song, F.; Zhang, C.; Ding, X.; Xu, J.; Zhang, G.; Leigh, M.; Peyghambarian, N. Determination of thermal focal length and pumping radius in gain medium in laser-diode-pumped Nd:YVO4 lasers. Appl. Phys. Lett. 2002, 81, 2145–2147. [Google Scholar] [CrossRef]
- Chenais, S.; Balembois, F.; Druon, F.; Lucas-Leclin, G.; Georges, P. Thermal lensing in diode-pumped ytterbium Lasers—Part I: Theoretical analysis and wavefront measurements. IEEE J. Quantum Electron. 2004, 40, 1217–1234. [Google Scholar] [CrossRef]
- Chenais, S.; Balembois, F.; Druon, F.; Lucas-Leclin, G.; Georges, P. Thermal lensing in diode-pumped ytterbium Lasers—Part II: Evaluation of quantum efficiencies and thermo-optic coefficients. IEEE J. Quantum Electron. 2004, 40, 1235–1243. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, X.; Wang, Q.; Li, S.; Ding, S.; Su, F. More precise determination of thermal lens focal length for end-pumped solid-state lasers. Opt. Commun. 2006, 266, 620–626. [Google Scholar] [CrossRef]
- Chénais, S.; Druon, F.; Forget, S.; Balembois, F.; Georges, P. On thermal effects in solid-state lasers: The case of ytterbium-doped materials. Prog. Quantum Electron. 2006, 30, 89–126. [Google Scholar] [CrossRef]
- Wang, S.; Eichler, H.J.; Wang, X.; Kallmeyer, F.; Ge, J.; Riesbeck, T.; Chen, J. Diode end pumped Nd:YAG laser at 946 nm with high pulse energy limited by thermal lensing. Appl. Phys. 2009, B95, 721. [Google Scholar] [CrossRef]
- Shang, J.; Zhu, X.; Zhu, G. Analytical approach to thermal lensing in end-pumped Yb:YAG thin-disk laser. Appl. Opt. 2011, 50, 6103–6120. [Google Scholar] [CrossRef]
- Sato, Y.; Taira, T. Highly accurate interferometric evaluation of thermal expansion and dn/dT of optical materials. Opt. Mater. Express 2014, 4, 876–888. [Google Scholar] [CrossRef]
- Shoji, I.; Taira, T. Intrinsic reduction of the depolarization loss in solid-state lasers by use of a (110)-cut crystal. Appl. Phys. Lett. 2002, 80, 3048–3050. [Google Scholar] [CrossRef]
- Shoji, I.; Sato, Y.; Kurimura, S.; Lupei, V.; Taira, T.; Ikesue, A.; Yoshida, K. Thermal-birefringence-induced depolarization in Nd:YAG ceramics. Opt. Lett. 2002, 27, 234–236. [Google Scholar] [CrossRef] [PubMed]
- Kubodera, K.; Otsuka, K. Single-transverse-mode LiNdP4O12 slab waveguide laser. J. Appl. Phys. 1979, 50, 653–659. [Google Scholar] [CrossRef]
- Fan, T.Y.; Byer, R.L. Medeling and CW Operation of a Quasi-Three-Level 946 nm Nd:YAG Laser. IEEE J. Quantum. Electron. 1987, 23, 605–612. [Google Scholar] [CrossRef]
- Risk, W.P. Modeling of longitudinally pumped solid-state lasers exhibiting reabsorption losses. J. Opt. Soc. Am. 1988, B5, 1412–1423. [Google Scholar] [CrossRef]
- Taira, T.; Tuloch, M.W.; Byer, L.R. Modeling of quasi-three-level lases and operation of cw Yb:YAG lasers. Appl. Opt. 1997, 20, 1867–1874. [Google Scholar] [CrossRef]
- Kawato, S.; Sueda, K.; Kobayashi, T. Development of High-Power Micro-Thickness-Slab Yb: YAG Lasers. Rev. Laser Eng. 2005, 33, 236–242. [Google Scholar] [CrossRef]
- Kawato, S.; Kobayashi, T. Design of End-Pumped Thin Rod Yb:YAG Laser Amplifiers. Jpn. J. Appl. Phys. 2003, 42, 2705–2710. [Google Scholar] [CrossRef]
- Sumida, S.D.; Fan, Y.T. Effect of radiation trapping on fluorescence lifetime and emission cross section measurements in solid-state laser media. Opt. Lett. 1994, 19, 1343–1345. [Google Scholar] [CrossRef]
- Krupke, F.W. Ytteribium Solid-State Lasers—The First Decate. IEEE J. Quantum. Electron. 2000, 6, 1287–1296. [Google Scholar] [CrossRef]
- Koechner, W. Section 2.6. Yb:YAG. In Solid State Laser Engineering, 6th ed.; Springer: Berlin, Germany, 2006; pp. 97–101. [Google Scholar]
- Findlay, D.; Clay, R.A. The Measument of internal losses in 4-level lasers. Phys. Lett. 1966, 20, 277–278. [Google Scholar] [CrossRef]
- Caird, J.A.; Payne, S.A.; Staver, P.R.; Ramponi, A.J.; Chase, L.L. Quantum electronic properties of the Na3Ga2Li3F12:Cr3+ laser. IEEE J. Quantum. Electron. 1988, 24, 1077–1099. [Google Scholar] [CrossRef]
- Oezisik, M.N. Heat Conduction, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1993; pp. 18–24. [Google Scholar]
- Sueda, K.; Takahashi, H.; Kawato, S.; Kobayashi, T. High-efficiency laser-diodes-pumped microthickness Yb:Y3Al5O12 slab laser. Appl. Phys. Lett. 2005, 87, 151110. [Google Scholar] [CrossRef]
- Russbueldt, P.; Mans, T.; Rotarius, G.; Weitenberg, J.; Hoffmann, H.D.; Poprawe, R. 400W Yb:YAG Innoslab fs-Amplifier. Opt. Express 2009, 17, 12230–12245. [Google Scholar] [CrossRef]
- Koechner, W. Sections 5.1.3. Resonator Configurations. 5.1.4. Stability of Laser Resonators. In Solid State Laser Engineering, 6th ed.; Springer: Berlin, Germany, 2006; pp. 217–222. [Google Scholar]
- Yariv, A.; Yeh, P. Section 4.4. Mode Stability Criteria. In Photonics, Optical Electronics in Mordern Communications, 6th ed.; Oxford University Press: New York, NY, USA, 2007; pp. 176–177. [Google Scholar]
- Brauch, U.; Röcker, C.; Graf, T.; Ahmed, M.A. High-power, high-brightness solid-state laser architectures and their characteristics. Appl. Phys. B 2022, 128, 58. [Google Scholar] [CrossRef]
- Shang, P.; Bai, L.; Wang, S.; Cai, D.; Li, B. Research progress on thermal effect of LD pumped solid state laser. Opt. Laser Technol. 2023, 157, 108640. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).