Abstract
The phenomena of magneto-optical polarization rotation and circular magnetic dichroism are well known in the Faraday configuration. We present another effect, an odd magneto-optical linear dichroism, arising in nanostructures with polarization-dependent mode Q-factors and magneto-optical components. It reveals itself as the magneto-optical modulation of light intensity for the two opposite magnetization directions in the Faraday configuration. The effect was demonstrated on a magnetophotonic crystal with a cavity mode, the polarization-dependent Q-factor of which is due to oblique incidence. For a polarization angle of 60° (or 120°) and an angle of incidence around 60°, the magneto-optical intensity modulation maximizes and reaches 6%.
1. Introduction
Magneto-optical effects associated with a change in the intensity of reflected or transmitted light, called intensity effects, are widely used in integrated optics devices to create optical non-reciprocal elements [1,2,3], spin wave detectors [4], chemical sensors and biosensors [5,6,7,8,9,10,11,12], magnetometers [13,14,15,16,17] and visualizations of magnetic structures [18,19].
There are several mechanisms leading to magneto-optical intensity modulation in different configurations of the external magnetic field and light. The most known and studied is the intensity transversal magneto-optical Kerr effect (TMOKE) discovered in 1896 [20]. The effect is defined by the relative change in the reflectance or transmittance for the two opposite directions of an in-plane magnetization. The effect occurs in smooth magnetic films due to the influence of the external magnetic field on boundary conditions, and TMOKE typical values are less than 0.1%. TMOKE is only observed with p-polarized oblique incident light. TMOKE is significantly enhanced by up to tens of percent in materials combining gyrotropic, plasmonic and nanostructuring features due to the excitation of surface or guided modes with non-reciprocal dispersion shift [21,22,23,24,25,26,27,28,29,30]. A large TMOKE was demonstrated in all-dielectric nanostructures [31,32]. Recently, a similar effect in transverse configuration was observed for s-polarized light, too, due to the peculiarities of polarization distribution inside a nanostructure [16,33,34,35,36].
In longitudinal and polar configurations, two magneto-optical effects that are odd in magnetization arise in reflected light for an arbitrary linear (p + s) polarization at oblique incidence. These effects originate from the difference in the Fresnel coefficients for p- and s-polarized light and the consequent difference in the intensity of the reflected arbitrary linear polarized light under clockwise and counterclockwise magneto-optical rotations. Such an intensity effect was observed only in single-crystal films of yttrium and bismuth iron garnets, iron, nickel, hematite and yttrium orthoferrite [37] and did not exceed 0.1% in magnitude. Both effects in polar and longitudinal polarizations are odd not only with respect to the magnetization but also with respect to the angle of deviation of the plane of polarization from the p- and s- polarizations. Similar geometries with the light of 45° polarization allow one to obtain dichroic effects and distinguish the domains with opposite magnetization orientations [18].
At the same time, the effects even in magnetization might appear for certain configurations. The orientation effect arising from different refractive indices for linearly polarized light in the two orthogonal in-plane configurations is quite small; however, it is observed in various ferromagnets [38,39]. A larger effect, the so-called longitudinal magnetophotonic intensity effect, was recently observed in nanostructured iron-garnets due to the excitation of the guided modes and the transformation of the mode polarization in the in-plane magnetized medium [24].
Features of the distribution of p and s components inside individual plates (layers) and multilayer structures at large angles of incidence close to the Brewster angle lead to a number of new interesting effects [40,41,42] since the structure transparency and Faraday rotation for the p- and s-polarized light might differ by several times. The ability to switch the transmitted light on and off under the application of the out-of-plane and in-plane fields was theoretically predicted in [40] for magnetophotonic crystals supporting bound states in the continuum. Although the modulation was quite high in this case, it is rather challenging to implement the configuration in practice.
We report the odd magneto-optical linear dichroism arising in a single-cavity all-garnet magnetophotonic crystal (MPC) with the general formula [MA/N]6/2 MA/[N/MA]6 (therein, N and MA denote the garnets of compositions Sm3Ga5O12 and Bi2.97Er0.03Fe4Al0.5Ga0.5O12, respectively) in the Faraday configuration under the oblique incidence of light with arbitrary linear (p + s) polarization. The effect manifests itself in the dependence of light transmittance with arbitrary linear (p + s) polarization in the MPC on the magnetization and the state of polarization. The effective absorption of the MPC becomes an odd function of the magnetization, which allows the light modulation during magnetization reversal. The effect originates due to the Faraday rotation (magnetic circular birefringence) and the different propagation and localization of p- and s-polarized light components inside the MPC and the resulting dependence of the Q-factor of the cavity mode of the MPC on the state of arbitrary linear (p + s) polarization.
2. Materials and Methods
2.1. Materials
Diamagnetic N and ferrimagnetic MA garnet layers of MPC were synthesized via rf-magnetron sputtering on substrate of Gd3Ga5O12 (GGG) with (111) crystallographic orientation. The deposition of the ceramic target material occurred on a hot substrate with a temperature of about 580 °C in an Ar–O2 (4:1) gas mixture at pressure of 25 mTorr. RF-power density was 12 W/cm2. The deposition rate was in a range from 3.6 to 5.5 Å/s. Layer synthesis was finalized with in situ post annealing at 500 Tr oxygen atmosphere and 550 °C for 10 min. Details of experimental conditions and regimes were described in the works [41,43,44,45,46]. According to X-ray diffraction data, layers of such MPCs, as a rule, demonstrate high epitaxial quality [41,45,46]. The GGG substrate sets the orientation for the growth of garnet layers of the entire structure. However, due to the small crystal lattice parameter (aGGG = 1.238 nm) compared with the N (aN = 1.243 nm) and MA layers (aMA = 1.258 nm), GGG leads to accumulation of mismatch strain and magnetostriction-induced uniaxial magnetic anisotropy [45]. Layers of Bi-substituted iron garnets, synthesized as a part of an all-garnet structure, have high values of magneto-optical quality factor, i.e., low absorption and high Faraday rotation, compared with the layers of Bi-substituted iron garnets, synthesized on cold substrates in MPC based on SiO2, TiO2 or Ta2O5 and having a pronounced polycrystalline structure [2]. For epitaxial layers, Bi content in the garnet composition can reach 3 at./f.u. This fact is important, since with an increase in Bi content the magneto-optical effects rise as a result of strengthening in the spin–orbit interaction, which is responsible for the splitting of Fe3+ energy levels [1,47]. However, at the same time, the optical absorption of iron garnet increases. Therefore, Al and Ga substitution was used in composition of the garnet layer MA to reduce optical absorption. Additionally, this substitution induces perpendicular magnetic anisotropy.
The MPC photonic band gap center λ0 and resonant wavelength λR for the cavity mode were matched to 775 nm at normal incidence (Figure A1). So, the thicknesses of MPC layers MA and N corresponded to the optical thickness (λ0/4) and were hMA = 74.5 nm and hN = 99.6 nm, respectively.
2.2. Simulation
Optical and magneto-optical spectra of MPC were obtained by numerically solving Maxwell’s equations using generalized matrix method 4 × 4 [48]. In the simulations, we take into account the initial state of light polarization, characterized by the angle Ψ0 reckoned from the position of p-polarization, angle of incidence θ and the contribution of reflection from the backside of a transparent substrate. The layers of MPC were described by the components of permittivity tensors determined from the optical and magneto-optical spectra of previously synthesized single-layer films and MPCs of similar compositions [45]. In general, the permittivity tensor of magneto-optical layers of iron garnets in optical frequency range for the considered geometries has the form
In the linear in magnetization approximation, the diagonal components are equal to each other, while the non-diagonal ones are determined by the medium gyration g: εxy = i∙g·cos(γ) and εyz = i∙g·sin(γ), respectively, where γ is an angle between the z axis and magnetization direction. The values of tensor component εxx and gyration g for MA layer at resonance wavelengths of MPC are εxx = 6.858 + 0.014·i; g = −0.021 + 0.0002·i at λR = 721 nm (θ = 60°) and εxx = 6.682 + 0.010·i; g = −0.018 + 0.0002·i at λR = 775 nm (θ = 0°). The permittivities of N layer and GGG substrate are well described by a scalar: εN = 3.865, εGGG = 3.948 at λR = 721 nm and εN = 3.844, εGGG = 3.904 at λR = 775 nm.
A software algorithm for calculating the properties of MPC was compiled in MatLab Online. The initial equation of the matrix method is the Maxwell equation written in a 6 × 6 matrix form under the assumption that a monochromatic wave is incident on the MPC:
where and are optical rotation tensors; is the permeability tensor; are the components of electric field strength vector; and are the components of magnetic field strength vector.
Considering purely linear effects and propagation of the light beam in the x − 0 − z plane in the direction from the upper layer of the structure to the lower one bordering the substrate (the wave vector has components kx and kz), according to Berreman [49], Equation (2) can be simplified to the form
where is the dimensionless state vector of a light wave with the following components
Δ is a coefficient matrix with elements dependent on the electromagnetic response of the layer (components of , , and ) [48,49]. Thus, depending on the material parameters for each layer (here, we assume and ), the four eigenmodes, which represent two forward waves (t) and two backward waves (r) propagating in the layer and which can be found as a result of solving the problems of finding and sorting eigenvalues and eigenvectors of the matrix Δ, will exist [48,49,50]. Such solutions will be, in the case of isotropic media, p- and s-polarized waves with electric field amplitudes and, in the case of gyrotropic media, two orthogonal elliptically polarized waves with electric field amplitudes . Having written the electric field vector through the amplitudes of the resulting electric fields of all four modes, we can give its transformation when light passes through a layer of thickness h using the transfer matrix
Here, the transfer matrix includes the matrix and the propagation matrix with components that can be found in [48]. Matrix is the 4 × 4 matrix calculated from the eigenvectors of matrix Δ and represents on the basis of the eigenmodes of the layer. The propagation matrix describes the propagation of all four eigenmodes through the layer.
Matrix is used to write the boundary conditions for electric and magnetic fields (continuity) at the interface of layer (i − 1) and i:
So, the full transfer matrix of all N layers of MPC is
The transmittance T of the structure is determined through the components of the transfer matrix (7) according to expressions taken from [48,51] and generalized for an incident wave with an arbitrary linear polarization Ψ0
Accordingly, the angle of rotation of polarization plane of transmitted light is determined from the relations
It is assumed that the first (air) and last (substrate) medium are isotropic.
The distribution of light intensity inside the layers of the structure was constructed based on calculations of the amplitudes of inside and at the boundaries of the layers of the structure, using the matrices and . The amplitude values were converted into the desired components of the vector [52].
Thus, by setting the initial parameters of MPC under study, the sequence and thickness of the layers, the values of the components of dielectric tensor of the layers and the angles Ψ0, θ and γ, we can determine its optical and magneto-optical characteristics.
2.3. Optical and Magneto-Optical Measurements
Experimental measurements of spectra (transmittance, Faraday rotation angles) were performed using an automated magneto-optical setup ORMS FR/KR2 manufactured by Holmarc (Kochi, India), modified for optical and magneto-optical measurements both in almost any planar geometry and with the possibility of oblique incidence of light on MPC, including the ability to measure with direct light incidence. The light of a halogen lamp was decomposed into a spectrum with a Czerny–Turner monochromator. Then, the resulting monochrome light was guided through the optical fiber using collimators, passed through the first rotating polarizer, the first focusing lens module, the sample, the second lens module, second rotating polarizer and hit the photodetector. The second lens system ensured focusing of the light beam to make the most efficient use of the area of the silicon photodetector. The signal from the photodetector was read with an automated microcontroller system and transferred to a personal computer for further processing. The main control program was written in Lazarus and allows one to automatically record the spectral dependences of transmittance and rotation of the plane of polarization. Both motorized polarizers have the ability to rotate through arbitrary angles to investigate the dependence of properties of the sample on the polarization of incident light and to measure the rotation of the polarization plane of the light passed through the sample. The sample was located in the gap of a liquid cooled electromagnet on a special holder placed at an angle of 60° to the angle of light incidence. For each value of the input polarization, the two spectral intensity dependences of transmittance were recorded in a positive and negative saturating magnetic field (3.5 kOe) with respect to light propagation direction. The value of odd magneto-optical linear dichroism was estimated according to the theory presented in the next section.
To measure the values of Faraday rotation angles for wavelength of cavity mode, a compensation method was used. The method involved searching for a shift in the minimum intensity of light passing through the sample compared with the position of the minimum intensity without the sample using a rotating analyzer. Faraday rotation angles were determined as the half-difference of two values and obtained for two opposite directions of magnetic field of the same strength, respectively:
Based on the measured Faraday rotation values, the Q-factor of cavity mode in the experiment was determined.
The resolution of the monochromator used in the setup is no worse than 0.5 nm. The limit of permissible value of the absolute error of transmittance measurements is ±2%, while the minimum detectable value of transmittance is 0.05%. The measurement range of the rotation angle is ±90° with an accuracy of no worse than 0.005° at transmittance at least 20%.
3. Results
3.1. Model of Odd Magneto-Optical Linear Dichroism and Light Intensity Modulation in the Faraday Configuration
The experimental configuration to observe the effect is shown in Figure 1. The light with an arbitrary linear (p + s) polarization, characterized by an angle Ψ0 between the polarization and plane of light incidence, is incident at an angle θ on the MPC surface and, as a result of refractions and reflections from the interfaces, passes through the MPC at the wavelength of the cavity mode. In this case, the oblique incidence of light leads to a difference in the Fresnel coefficients of s- (Ψ = 90°) and p- (Ψ = 0°) polarizations. As a consequence, at oblique incidence, the Q-factor and the transmittance of the cavity mode of the MPC depend on the state of arbitrary linear (p + s) polarization. The presence of magnetization, which has a non-zero projection on the direction of light zi, leads to the appearance of the magneto-optical Faraday rotation Φ. Since any rotation of an arbitrary linear (p + s) polarization state takes the light to another linear (p + s) state with a different Q-factor, the transmittance of the MPC will change in the presence of magnetization and will generally be a function of two parameters .
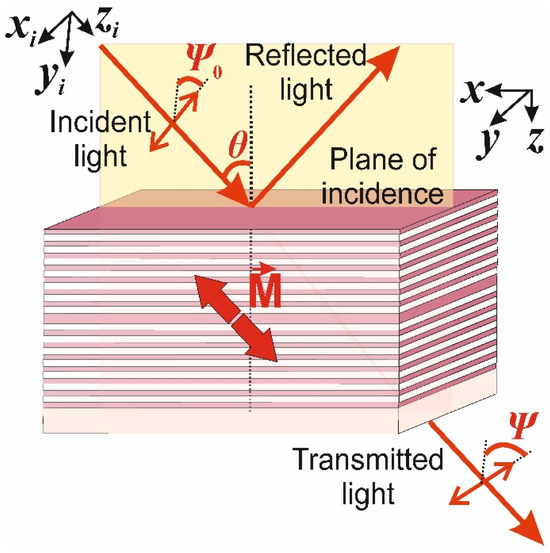
Figure 1.
Configuration for observation of the odd magneto-optical linear dichroism. Red arrows indicate magnetization directions.
The effect can be qualitatively interpreted using the effective length of light propagation. A multiple interference leads to the increase in the effective length inside the MPC. Additionally, due to the violation of spatial symmetry, the effective length inside the MPC depends on its polarization at oblique incidence. We can approximately assume that the effective length L(Ψ) takes the following value:
where Q(Ψ) is the quality factor of cavity mode, showing how many times the light is reflected and passed inside the MPC, and L0 is the real total thickness of the magneto-optical layers in the MPC. The quality factor depends on the state of polarization Ψ, since the Fresnel coefficients depend on Ψ.
Then, we can express the enhancement of the Faraday effect in the MPC as
where Φ(Ψ) is the Faraday rotation angle of cavity mode in the MPC; ϕ is the specific Faraday rotation of garnet magneto-optical layer MA.
Transmittance depends on the passed distance according to the Beer–Lambert–Bouguer law:
where the absorption coefficient does not depend on the magnetization M for linear polarization. However, since the polarization state is transformed due to the Faraday effect in the process of light propagation, changes in the effective length and, as a consequence, in the transmittance occur. In this case, the polarization state can be represented as a function of the coordinate along light incidence:
where Ψ0 is the initial state of polarization at zi = 0 at the interface between the MPC and air. The last approximate equality is valid if Φ is small. Here, we expanded Φ(zi) into a series in zi and took into account only the linear term in zi.
Let us consider the exponent in (15) and its change over an infinitely small segment of the effective optical path d:
Summing up, over the thickness of all the magneto-optical layers passed by the light, we obtain an expression for the transmittance that takes into account the changes introduced by the Faraday rotation:
Thus, since the specific Faraday rotation angle of the medium ϕ depends on the magnetization , the transmittance will depend on . In this case, the effective absorption of the MPC for any arbitrary linear (p + s) polarization will depend oddly on the magnetization:
Let us consider a few special cases. (1) At magnetization = 0, ϕ = 0:
(2) Incident wave with polarization Ψ0 = 0° or Ψ0 = 90°: from symmetry considerations, we obtain , which indicates the absence of an odd effect in . (3) According to (21), it is possible to select and estimate the magnetic contribution to effective absorption if we consider the propagation of two arbitrary linear (p + s) polarizations that experience the Faraday rotation in opposite directions. This is achieved by reversing the magnetization :
In the latter case, the experimentally measured difference in transmittance for arbitrary linear (p + s) polarization Ψ0 will take the form
where and are the transmittance coefficients for the two opposite projections of the magnetization vector on the direction of light zi, , .
Expression (24) shows that in the approximation the transmittance difference oddly depends on for arbitrary linear (p + s) polarization state Ψ0 upon magnetization reversal as well. Thus, by analogy with the odd transverse Kerr effect, we should be able to observe the light intensity modulation when switching the magnetization in opposite directions as a result of the manifestation of odd magneto-optical linear dichroism:
3.2. Simulation and Experimental Observation of the Odd Magneto-Optical Linear Dichroism
To demonstrate the effect, we chose the maximum angle of incidence among all those implemented in the experimental setup, which provides the maximum difference between the Q-factors of p- and s-polarized states, θ = 60°. Figure 2a shows the calculated transmittance spectra of the considered all-garnet MPC for various polarizations of the incident light and wavelength at an oblique incidence. The cavity mode is observed in the middle of the photonic bandgap at λR = 721 nm as the narrow transmittance peak for any polarization of light. At the same time, the transmittance at this resonance significantly depends on the polarization and gradually changes four times from T∼82% for Ψ0 = 0° to T∼17% for Ψ0 = 90° (Figure 2b,c).
As noted above, such a feature arises due to the difference between the Q-factors of the cavity mode for p- and s-polarized light caused by the difference of the Fresnel coefficients. S-polarization is trapped and localized inside the MPC more strongly than p-polarization, as is seen from the optical field distribution along the MPC (Figure 3a). This leads to the fact that the values of the Faraday rotation angle of the MPC Φ will be different for p- and s-polarized light, which, in accordance with formula (14), allows us to estimate the behavior of the dependence Q(Ψ0) (Figure 3b).
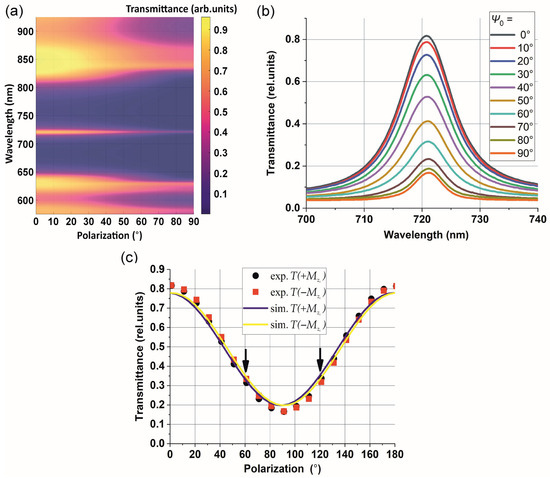

Figure 2.
A color plot for the transmittance calculated for different wavelengths and polarization angles Ψ0 of the arbitrary linearly (s + p) polarized light (a). Measured transmittance of MPC with positive orientation of magnetization versus initial state of polarization Ψ0 (b). Measured (symbol) and simulated (lines) transmittance of MPC at resonance wavelength λR = 721 nm in configurations with opposite orientations of magnetization and versus initial state of polarization Ψ0 (c). The arrows indicate the values of Ψ0 corresponding to the configurations in Figure 4b.
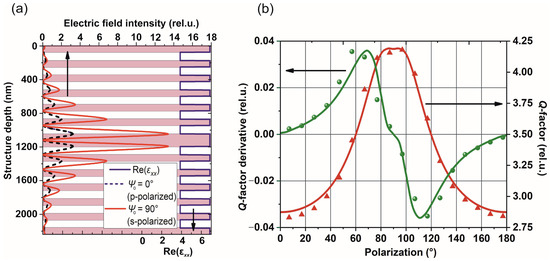
Figure 3.
Simulated distribution of electric field intensity of p- and s-polarized light inside MPC (a) and measured (symbol) and simulated (lines) dependences of the Q-factor and its derivative on the initial state of polarization Ψ0 at λR = 721 nm (b). The angle of incidence is θ = 60°.
When the polarization state changes from p to s, the Faraday rotation angle Φ and Q-factor of the cavity mode increases by 1.5 times. Since, for the arbitrary linearly (s + p) polarized light, clockwise and counterclockwise magneto-optical rotations turn the light to the state with the different Q-factor and transmittance, in accordance with (26), the polarization dependence of the effect of magneto-optical linear dichroism is determined mainly by the multiplication of . This leads to the fact that the maximum effect is observed for the polarization states, in which has a maximum (Figure 3b and Figure 4a). Therefore, the effect reaches 6% for polarizations of Ψ0 = 60° and Ψ0 = 120° and vanishes for Ψ0 = 0° and Ψ0 = 90° ().
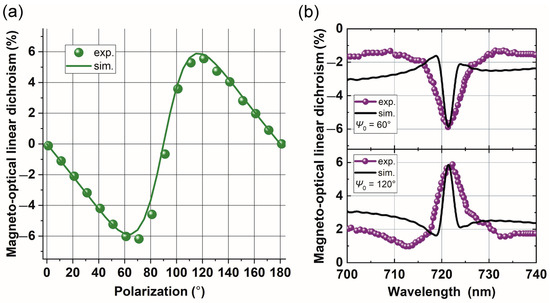
Figure 4.
Measured (symbols) and simulated (lines) values of the odd magneto-optical linear dichroism δT of MPC: (a) at resonance wavelength λR = 721 nm versus initial state of polarization Ψ0, (b) in the vicinity of resonance for different Ψ0: 60° and 120°. The angle of incidence is θ = 60°.
For Ψ0 < 90°, positive magnetization rotates polarization towards s-polarization, while negative magnetization rotates towards p-polarization. Therefore, and (see Figure 4b). The situation is reversed for 90° < Ψ0 < 180°, and the sign of the effect changes to positive.
Similar measurements and simulations were also carried out for the sample located normally to the incident light to ensure the absence of the discussed effect. In this case, the quality factor of the structure ceases to depend on the state of polarization and is constant, i.e.,
4. Discussion
Thus, based on analytical consideration, numerical calculations and experiments, we can postulate that two factors, the presence of Faraday rotation and the polarization dependence of the optical mode Q-factor, lead to the appearance of the odd magneto-optical linear dichroism. These two factors are equally important.
Faraday rotation is the key mechanism that “launches” the effect and leads to the appearance of a magnetically induced contribution to the expression for the transmittance of the MPC (20) and sets the linear dependence of the effect on the magnetization. It is important to note here that the reciprocity of the Faraday rotation also plays a role. If there was no accumulation of the rotation of the plane of polarization during multiple passages, then the effect would be negligible. According to numerical estimates, the dependence of the effect on gyration (or on the magnetization) looks as follows:
where is the saturation magnetization and ξ1 is the coefficient. Thus, the effect is absent at Ψ0 = 0°, 90° or 180°. For the arbitrary linearly (s + p) polarized light with Ψ0 = 30° and Ψ0 = 60°, the coefficient ξ1 is 2.17 and 4.34, respectively. Due to the fact that the linear dependence quite well describes the behavior of δT, we can conclude that the Faraday effect is the main mechanism for the observed intensity effect in the MPC.
The polarization dependence of the Q-factor of the optical mode, as was considered in the experimental part and through numerical calculations, sets the polarization dependence of the magnitude of the effect. The sharper this dependence behaves (that is, the greater the difference between the Q-factors of the modes for p- and s- polarized light), the more intensely the effect will occur. Thus, for pure p and s polarizations, the polarization dependence of the mode quality factor reaches a plateau, which leads to the disappearance of the effect (Figure 4a). It is also worth noting that with oblique incidence and different propagations of p- and s-polarizations (Figure 2a), various optical features in the spectra of any MPC will be accompanied by the effect of odd magneto-optical linear dichroism. In addition to the main resonance corresponding to the microcavity mode, when going from p- to s-polarization, both the width of the photonic band gap and the amplitude of the interference maxima at the edges of the photonic band gap change. Therefore, we should expect that the effect will be observed in the vicinity of the edges of the photonic band gap. Thus, according to the simulation, the maximum effect values are achieved for the arbitrary linearly (s + p) polarized light Ψ0 = 50°: δT = 5% at wavelength 628.5 nm (short wave edge) and δT = 0.9% at wavelength 840 nm (long wave edge). An equally important feature of the effect is its dependence on optical absorption in the iron-garnet layer. It is easy to show that if we consider ideal materials without absorption, then the effect of the modulation of the intensity of transmitted light will also be observed, but will change in sign while keeping the value unchanged. This indicates a strong influence of optical effects in the structure on the formation of the spectral dependence of the magneto-optical effect. The investigation of the spectral features of the effect of odd magneto-optical linear dichroism for various optical modes and for different material parameters deserves special attention and a more thorough analysis.
Thus, we conclude that it is impossible to separate the magneto-optical (Faraday rotation, that is, magnetic circular birefringence) and optical (polarization dependence of the Q-factor of the optical mode, that is, various Fresnel coefficients for p- and s-polarized light) contributions to the effect.
It should be noted that the odd magneto-optical linear dichroism differs from the classical magnetic linear dichroism that is observed in the Voigt effect geometry (or Cotton–Mouton). In the case of classical magnetic linear dichroism, there is a difference in the absorption coefficients of two linear polarizations, the electric field vector of which is oriented parallel and perpendicular to the magnetization vector. The effect is even in the field and is only a consequence of internal mechanisms that arise in strongly absorbing media in a given magnetization geometry. Classical magnetic linear dichroism in the Voigt geometry results in a rotation of the main axis of elliptically polarized light [1]. As noted above, the discussed effect of the linear dichroism arises due to the two factors (magnetic circular birefringence and various Fresnel coefficients for p- and s-polarized light), which, when combined, lead to the appearance of a difference in the effective absorption of the MPC for two arbitrary linear (s + p) polarizations experiencing rotation of the plane of polarization in two opposite directions depending on the orientation of the magnetic field. It is only these two linear polarizations (or, strictly speaking, one linear polarization), according to (20) and (23), that will differ only in the magnetically induced contribution, the magnitude of which is determined by the polarization dependence of the Q-factor of the optical mode and, at the same time, oddly depends on the magnetization. The result of this phenomenon is a change in the intensity of transmitted light during magnetization reversal. In this regard, we called the observed effect «odd magneto-optical linear dichroism in a magnetophotonic crystal». The difference in the effective absorption of any other two arbitrary linear (s + p) polarizations will contain, in addition to the odd magnetic-induced contribution, a purely optical contribution, which does not depend on magnetization but depends on the Q-factor (according to (21), the difference in the initial quality factors Q0). Additionally, in this geometry, effects that are even in magnetization are possible, which, in our case, are excluded by the definitions of (24) and (25).
We suppose that the odd magneto-optical linear dichroism can be applied for modulators and magneto-optical visualization. It can provide more efficient light modulation, by analogy with the effect described in [40], in the case of the optimization of the configuration and MPC structure, for example, when the Faraday rotation angle of the light with polarization Ψ = 45° reaches values close to 45°. In this case, the polarization state can be switched, thereby implementing the maximum possible modulation without the use of an analyzer in the observation system. In magneto-optical microscopy, the effects of linear dichroism can be efficient in situations where the magnetic circular dichroism vanishes, for example, for the visualization of antiferromagnetic domains [18].
5. Conclusions
The odd magneto-optical linear dichroism in the Faraday configuration arises in an MPC at oblique incidence of the light with an arbitrary linear (s + p) polarization. The oblique incidence leads to a polarization-dependent Q-factor of the cavity mode and effective absorption of the MPC, which simultaneously depends on the states of polarization and magnetization. The effect reveals itself as intensity modulation of the transmitted light with an arbitrary linear (s + p) polarization upon magnetization reversal in two opposite directions. In multiple pass mode, the magneto-optical Faraday effect switches the initial state of light polarization with one Q-factor to a state with another Q-factor. It was shown that the increment of the Q-factor of the cavity mode determines the character of the polarization dependence of the odd magneto-optical linear dichroism. Therefore, the maximum magnitude of the effect reaches 6% in the MPC for the polarizations Ψ = 60° (or Ψ = 120°) at the angle of incidence θ = 60°. However, the effect is absent in configurations where the increment of the Q-factor is zero (Ψ = 0°, Ψ = 90° or θ = 0°).
Author Contributions
Conceptualization, T.V.M. and D.O.I.; methodology, T.V.M. and D.O.I.; software, T.V.M. and S.D.L.; validation, D.O.I.; formal analysis, T.V.M.; investigation, S.D.L.; resources, V.N.B. and V.I.B.; writing—original draft preparation, T.V.M.; writing—review and editing, T.V.M., D.O.I., S.D.L., V.I.B. and V.N.B.; visualization, T.V.M. and S.D.L.; supervision, V.I.B.; project administration, V.N.B.; funding acquisition, V.N.B. and V.I.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Ministry of Science and Higher Education of the Russian Federation [Megagrant project No. 075-15-2022-1108] and was partially supported by the MSU Program of Development, project No 23-SCH06-03.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
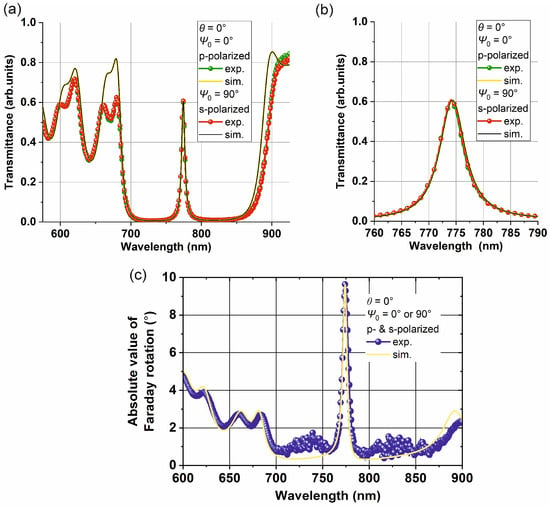
Figure A1.
Spectra of transmittance of MPC at normal incidence θ = 0° for p- and s-polarized light and different scales: (a) in a wide spectral range showing a photonic bandgap, from 575 nm to 925 nm, and (b) in the vicinity of the resonant wavelength, from 760 nm to 790 nm. (c) Spectra of Faraday rotation angle of MPC for p- or s-polarized light at normal incidence θ = 0°.
References
- Zvezdin, A.K.; Kotov, V.A. Modern Magnetooptics and Magnetooptical Materials; IOP Publishing: Bristol, PA, USA, 1997. [Google Scholar]
- Inoue, M.; Levy, M.; Baryshev, A. (Eds.) Magnetophotonics: From Theory to Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hu, S.; Guo, Z.; Dong, L.; Deng, F.; Jiang, H.; Chen, H. Enhanced Magneto-Optical Effect in Heterostructures Composed of Epsilon-Near-Zero Materials and Truncated Photonic Crystals. Front. Mater. 2022, 9, 843265. [Google Scholar] [CrossRef]
- Chernov, A.I.; Kozhaev, M.A.; Ignatyeva, D.O.; Beginin, E.N.; Sadovnikov, A.V.; Voronov, A.A.; Karki, D.; Levy, M.; Belotelov, V.I. All-Dielectric Nanophotonics Enables Tunable Excitation of the Exchange Spin Waves. Nano Lett. 2020, 20, 5259–5266. [Google Scholar] [CrossRef]
- Diaz-Valencia, B.F.; Mejía-Salazar, J.R.; Oliveira Osvaldo, N., Jr.; Porras-Montenegro, N.; Albella, P. Enhanced Transverse Magneto-Optical Kerr Effect in Magnetoplasmonic Crystals for the Design of Highly Sensitive Plasmonic (Bio)sensing Platforms. ACS Omega 2017, 2, 7682–7685. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Valencia, B.F.; Moncada-Villa, E.; Gómez Faustino, R.; Porras-Montenegro, N.; Mejía-Salazar, J.R. Bulk Plasmon Polariton Modes in Hyperbolic Metamaterials for Giant Enhancement of the Transverse Magneto-Optical Kerr Effect Molecules. Molecules 2022, 27, 5312. [Google Scholar] [CrossRef]
- Grunin, A.A.; Mukha, I.R.; Chetvertukhin, A.V.; Fedyanin, A.A. Refractive index sensor based on magnetoplasmonic crystals. J. Magn. Magn. Mater. 2016, 415, 72–76. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, H.; Feng, Y.; Deng, X.; Yang, B.; Xiong, D.; He, M.; Zhang, W. Surface plasmon resonances boost the transverse magneto-optical Kerr effect in a CoFeB slab covered by a subwavelength gold grating for highly sensitive detectors. Opt. Express 2021, 29, 10546–10555. [Google Scholar] [CrossRef] [PubMed]
- Ignatyeva, D.O.; Kapralov, P.O.; Knyazev, G.A.; Sekatskii, S.K.; Dietler, G.; Nur-E-Alam, M.; Vasiliev, M.; Alameh, K.; Belotelov, V.I. High-Q surface modes in photonic crystal/iron garnet film heterostructures for sensor applications. JETP Lett. 2017, 104, 679–684. [Google Scholar] [CrossRef]
- Rizal, C.; Pisana, S.; Hrvoic, I. Improved Magneto-Optic Surface Plasmon Resonance Biosensors. Photonics 2018, 5, 15. [Google Scholar] [CrossRef]
- David, S.; Polonschii, C.; Luculescu, C.; Gheorghiu, M.; Gáspár, S.; Gheorghiu, E. Magneto-plasmonic biosensor with enhanced analytical response and stability. Biosens. Bioelectron. 2015, 63, 525–532. [Google Scholar] [CrossRef]
- Wu, J.; Qing, Y.M. Near-Perfect TMOKE in Photonic Crystal Structures for Sensing Devices with High Figure of Merit. IEEE Sens. J. 2022, 22, 19177–19182. [Google Scholar] [CrossRef]
- Borovkova, O.V.; Ignatyeva, D.O.; Sekatskii, S.K.; Karabchevsky, A.; Belotelov, V.I. High-Q surface electromagnetic wave resonance excitation in magneto-photonic crystals for super-sensitive detection of weak light absorption in near-IR. Photonics Res. 2020, 8, 57–63. [Google Scholar] [CrossRef]
- Rizal, C.; Manera, M.G.; Ignatyeva, D.O.; Mejía-Salazar, J.R.; Rella, R.; Belotelov, V.I.; Pineider, F.; Maccaferri, N. Magnetophotonics for sensing and magnetometry toward industrial applications. J. Appl. Phys. 2021, 130, 230901. [Google Scholar] [CrossRef]
- Ignatyeva, D.O.; Knyazev, G.A.; Kalish, A.N.; Chernov, A.I.; Belotelov, V.I. Vector magneto-optical magnetometer based on resonant all-dielectric gratings with highly anisotropic iron garnet films. J. Phys. D Appl. Phys. 2021, 54, 295001. [Google Scholar] [CrossRef]
- Ignatyeva, D.O.; Krichevsky, D.M.; Belotelov, V.I.; Royer, F.; Dash, S.; Levy, M. All-dielectric magneto-photonic metasurfaces. J. Appl. Phys. 2022, 132, 100902. [Google Scholar] [CrossRef]
- Belyaev, V.K.; Rodionova, V.V.; Grunin, A.A.; Inoue, M.; Fedyanin, A.A. Magnetic field sensor based on magnetoplasmonic crystal. Sci. Rep. 2020, 10, 7133. [Google Scholar] [CrossRef] [PubMed]
- Schafer, R.; Oppeneer, P.M.; Ognev, A.V.; Samardak, A.S.; Soldatov, I.V. Analyzer-free, intensity-based, wide-field magneto-optical microscopy. Appl. Phys. Rev. 2021, 8, 031402. [Google Scholar] [CrossRef]
- McCord, J. Progress in magnetic domain observation by advanced magneto-optical microscopy. J. Phys. D Appl. Phys. 2015, 48, 333001. [Google Scholar] [CrossRef]
- Wind, C.H. On the theory of magneto-optic phenomena. Phys. Rev. 1898, 6, 43. [Google Scholar] [CrossRef]
- Grunin, A.A.; Zhdanov, A.G.; Ezhov, A.A.; Ganshina, E.A.; Fedyanin, A.A. Surface-plasmon-induced enhancement of magneto-optical Kerr effect in all-nickel subwavelength nanogratings. Appl. Phys. Lett. 2010, 97, 261908. [Google Scholar] [CrossRef]
- Torrado, J.F.; González-Díaz, J.B.; González, M.U.; García-Martín, A.; Armelles, G. Magneto-optical effects in interacting localized and propagating surface plasmon modes. Opt. Express 2010, 18, 15635–15642. [Google Scholar] [CrossRef] [PubMed]
- Belotelov, V.I.; Kreilkamp, L.E.; Kalish, A.N.; Akimov, I.A.; Bykov, D.A.; Kasture, S.; Yallapragada, V.J.; Achanta, V.G.; Grishin, A.M.; Khartsev, S.I.; et al. Magnetophotonic intensity effects in hybrid metal-dielectric structures. Phys. Rev. B 2014, 89, 045118. [Google Scholar] [CrossRef]
- Belotelov, V.I.; Bykov, D.A.; Doskolovich, L.L.; Kalish, A.N.; Kotov, V.A.; Zvezdin, A.K. Giant Magnetooptical Orientational Effect in Plasmonic Heterostructures. Opt. Lett. 2009, 34, 398–400. [Google Scholar] [CrossRef]
- Halagacka, L.; Vanwolleghem, M.; Postava, K.; Dagens, B.; Pistora, J. Coupled mode enhanced giant magnetoplasmonics transverse Kerr effect. Opt. Express 2013, 21, 21741–21755. [Google Scholar] [CrossRef]
- Belotelov, V.I.; Zvezdin, A.K. Magnetooptics and extraordinary transmission of the perforated metallic films magnetized in polar geometry. J. Magn. Magn. Mater. 2006, 300, e260–e263. [Google Scholar] [CrossRef]
- Chai, H.; Lu, Y.; Zhang, W. Enhancement of transverse magneto-optical Kerr effects and high sensing performance in a trilayer structure with nanopore arrays. Results Phys. 2021, 31, 105049. [Google Scholar] [CrossRef]
- Barsukova, M.G.; Musorin, A.I.; Shorokhov, A.S.; Fedyanin, A.A. Enhanced magneto-optical effects in hybrid Ni-Si metasurfaces. APL Photon. 2019, 4, 016102. [Google Scholar] [CrossRef]
- Cichelero, R.; Oskuei, M.A.; Kataja, M.; Hamidi, S.M.; Herranz, G. Unexpected large transverse magneto-optic Kerr effect at quasi-normal incidence in magnetoplasmonic crystals. J. Magn. Magn. Mater. 2019, 47, 54–58. [Google Scholar] [CrossRef]
- Carvalho, W.O.F.; Moncada-Villa, E.; Oliveira, O.N., Jr.; Mejía-Salazar, J.R. Beyond plasmonic enhancement of the transverse magneto-optical Kerr effect with low-loss high-refractive-index nanostructures. Phys. Rev. B 2021, 103, 075412. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Hutomo, J.; Kostylev, M. Transverse magneto-optical Kerr effect in subwavelength dielectric gratings. Opt. Express 2014, 22, 8720–8725. [Google Scholar] [CrossRef]
- Royer, F.; Varghese, B.; Gamet, E.; Neveu, S.; Jourlin, Y.; Jamon, D. Enhancement of Both Faraday and Kerr Effects with an All-Dielectric Grating Based on a Magneto-Optical Nanocomposite Material. ACS Omega 2020, 5, 2886–2892. [Google Scholar] [CrossRef]
- Ignatyeva, D.O.; Karki, D.; Voronov, A.A.; Kozhaev, M.A.; Krichevsky, D.M.; Chernov, A.I.; Levy, M.; Belotelov, V.I. All-dielectric magnetic metasurface for advanced light control in dual polarizations combined with high-Q resonances. Nat. Commun. 2020, 11, 5487. [Google Scholar] [CrossRef]
- Yang, W.; Liu, Q.; Wang, H.; Chen, Y.; Yang, R.; Xia, S.; Luo, Y.; Deng, L.; Qin, J.; Duan, H.; et al. Observation of optical gyromagnetic properties in a magneto-plasmonic metamaterial. Nat. Commun. 2022, 13, 1719. [Google Scholar] [CrossRef]
- Voronov, A.A.; Karki, D.; Ignatyeva, D.O.; Kozhaev, M.A.; Levy, M.; Belotelov, V.I. Magneto-optics of subwavelength all-dielectric gratings. Opt. Express 2020, 28, 17988–17996. [Google Scholar] [CrossRef]
- Xia, S.; Ignatyeva, D.O.; Liu, Q.; Wang, H.; Yang, W.; Qin, J.; Chen, Y.; Duan, H.; Luo, Y.; Novák, O.; et al. Circular displacement current induced anomalous magneto-optical effects in high index Mie resonators. Laser Photonics Rev. 2022, 16, 2200067. [Google Scholar] [CrossRef]
- Krinchik, G.S.; Chepurova, E.E.; Ehgamov, S.V. Magneto-optical intensity effects in ferromagnetic metals and dielectrics. Zhurnal Ehksperimental’noj I Teor. Fiz. 1978, 74, 375–378. [Google Scholar]
- Carey, R.; Thomas, B.W.J.; Viney, I.V.F.; Weaver, G.H. Magnetic birefringence in thin ferromagnetic films. J. Phys. D Appl. Phys. 1968, 1, 1679. [Google Scholar] [CrossRef]
- Krinchik, S.S.; Gushchin, V.S. Magnetooptical effect of change of electronic structure of a ferromagnetic metal following rotation of the magnetization vector. JETP Lett. 1969, 10, 24–26. [Google Scholar]
- Ignatyeva, D.O.; Belotelov, V.I. Bound states in the continuum enable modulation of light intensity in the Faraday configuration. Opt. Lett. 2020, 45, 6422–6425. [Google Scholar] [CrossRef] [PubMed]
- Grishin, A.M.; Khartsev, S.I. Waveguiding in All-Garnet Heteroepitaxial Magneto-Optical Photonic Crystals. JETP Lett. 2019, 109, 83–86. [Google Scholar] [CrossRef]
- Lyubchanskii, I.L.; Dadoenkova, N.N.; Lyubchanskii, M.I.; Shapovalov, E.A.; Zabolotin, A.E.; Lee, Y.P.; Rasing, T. Response of two-defect magnetic photonic crystals to oblique incidence of light: Effect of defect layer variation. J. Appl. Phys. 2006, 100, 096110. [Google Scholar] [CrossRef]
- Grishin, A.M. Amplifying magneto-optical photonic crystal, Appl. Phys. Lett. 2010, 97, 061116. [Google Scholar] [CrossRef]
- Dzibrou, D.O.; Grishin, A.M. Fitting transmission and Faraday rotation spectra of [Bi3Fe5O12/Sm3Ga5O12]m magneto-optical photonic crystals. J. Appl. Phys. 2009, 106, 043901. [Google Scholar] [CrossRef]
- Grishin, A.M.; Khartsev, S.I. Luminescent Magneto-Optical Photonic Crystals. J. Phys. Conf. Ser. 2012, 352, 012007. [Google Scholar] [CrossRef]
- Khartsev, S.I.; Grishin, A.M. High performance [Bi3Fe5O12/Sm3Ga5O12]m magneto-optical photonic crystals. J. Appl. Phys. 2007, 101, 053906. [Google Scholar] [CrossRef]
- Levy, M.; Borovkova, O.V.; Sheidler, C.; Blasiola, B.; Karki, D.; Jomard, F.; Kozhaev, M.A.; Popova, E.; Keller, N.; Belotelov, V.I. Faraday rotation in iron garnet films beyond elemental substitutions. Optica 2019, 6, 642–646. [Google Scholar] [CrossRef]
- Passler, N.C.; Paarmann, A. Generalized 4 × 4 matrix formalism for light propagation in anisotropic stratified media: Study of surface phonon polaritons in polar dielectric heterostructures. J. Opt. Soc. Am. B 2017, 34, 2128–2139. [Google Scholar] [CrossRef]
- Berreman, D.W. Optics in stratified and anisotropic media: 4 × 4-matrix formulation. J. Opt. Soc. Am. 1972, 62, 502–510. [Google Scholar] [CrossRef]
- Xu, W.; Wood, L.T.; Golding, T.D. Optical degeneracies in anisotropic layered media: Treatment of singularities in a 4 × 4 matrix formalism. Phys. Rev. B 2000, 61, 1740–1743. [Google Scholar] [CrossRef]
- Yeh, P. Electromagnetic propagation in birefringent layered media. J. Opt. Soc. Am. A 1979, 69, 742–756. [Google Scholar] [CrossRef]
- Passler, N.C.; Jeannin, M.; Paarmann, A. Layer-resolved absorption of light in arbitrarily anisotropic heterostructures. Phys. Rev. B 2020, 101, 165425. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).