Abstract
Chemical and biological detection is now an indispensable task in many fields. On-chip refractive index (RI) optical sensing is a good candidate for mass-scale, low-cost sensors with high performance. While most literature works focus on enhancing the sensors’ sensitivity and detection limit, other important parameters that determine the sensor’s yield, reliability, and cost-effectiveness are usually overlooked. In this work, we present a comprehensive study of the different integrated photonic platforms, namely silica, silicon nitride, and silicon. Our study aims to determine the best platform for on-chip RI sensing, taking into consideration the different aspects affecting not only the sensing performance of the sensor, but also the sensor’s reliability and effectiveness. The study indicates the advantages and drawbacks of each platform, serving as a guideline for RI sensing design. Modal analysis is used to determine the sensitivity of the waveguide to medium (analyte) index change, temperature fluctuations, and process variations. The study shows that a silicon platform is the best choice for high medium sensitivity and a small footprint. On the other hand, silica is the best choice for a low-loss, low-noise, and fabrication-tolerant design. The silicon nitride platform is a compromise of both. We then define a figure of merit (FOM) that includes the waveguide sensitivity to the different variations, losses, and footprint to compare the different platforms. The defined FOM shows that silicon is the best candidate for RI sensing. Finally, we compare the optical devices used for RI sensing, interferometers, and resonators. Our analysis shows that resonator-based devices can achieve much better sensing performance and detection range, due to their fine Lorentzian spectrum, with a small footprint. Interferometer based-sensors allow engineering of the sensors’ performance and can also be designed to minimize phase errors, such as temperature and fabrication variations, by careful design of the interferometer waveguides. Our analysis and conclusions are also verified by experimental data from other published work.
1. Introduction
Chemical and biological detection have become indispensable tasks in many industries, for instance, healthcare, medical diagnosis, environmental monitoring, food quality, and industrial process control [1,2,3]. Chemical and bio-detection have been known about for a long time, but old techniques required bulk equipment and long laboratory processes, in addition to being expensive. Nowadays, with the increasing demand of detection in many applications, these old techniques are no longer applicable. Hence, there is immense need for compact, cost-effective, and rapid detection. Optical sensors are the best candidate that can fulfill the current demand in chemical and biological detection. Optical sensors offer many advantages compared to other sensing techniques, including high sensitivity, wide dynamic range, and multiplexing capability [4,5,6]. In addition, on-chip optical sensors that use mature and cost-effective technologies such as CMOS technology allow for robust, low-cost, and mass-scale production.
Optical sensors can be classified into two main groups: refractive index (RI) sensors and absorption sensors. RI sensors detect the real part of the refractive index n of the sensing medium (analyte) [7,8,9,10]. A change in the real part of the medium index will change the phase of the propagating optical signal, which is then transduced (through an optical device) to a measurable change in either the intensity or the resonance wavelength of the output optical signal. Absorption sensors detect the imaginary part of the refractive index k of the sensing medium [11,12,13,14]. A change in the imaginary part will directly change the intensity of the propagating optical signal. RI sensors are good candidates for integrated on-chip optical sensing as they are well-suited to small-volume samples [5]. Small changes in n over short (micrometer) distances can lead to a large change in the phase of the propagating wave, reaching very high sensitivities through different optical devices. On the other hand, on-chip absorption-based optical sensors suffer from poor sensitivity due to the small interaction length (micrometer to millimeter dimensions) [12].
There is a plethora of work conducted in regard to on-chip optical RI sensing and many interesting review articles can be found in the literature [15,16,17,18,19]. On-chip RI sensing can be classified into two main types; interferometer-based and resonance-based devices. The Mach-Zehnder interferometer (MZI) is the most common format of interferometric sensing. Young, Michelson, and bimodal interferometers are other formats of the interferometric technique [20,21,22]. On the other hand, the micro-ring resonator (MRR) is the most widely used format of resonant sensing. However, there is a large number of micro-resonator structures, such as microdisk, microsphere, microtoroid, microbottle, and microtube resonators [23,24,25,26]. Many studies have also been conducted of RI sensing using plasmonic and photonic crystal waveguides, whereas most of the research conducted on RI sensing is based on conventional dielectric (strip, rib, or slot) waveguides. Many studies have also been conducted using plasmonic and photonic crystal waveguides.
RI sensor performance is determined mainly by its sensitivity and limit of detection (LoD) [18]. The sensitivity of an RI optical sensor is defined as S = Δq/Δnmed, the ratio between the change in the detected (measured) optical quantity Δq, intensity, or wavelength shift, and the change in the medium refractive index Δnmed. LoD is the smallest resolvable index change Δnmed,min that can be detected by the sensor. Although these are the main parameters that determine the sensing performance, there are other important aspects that determine the effectiveness, reliability, and yield of the sensor, for instance, the sensitivity of the sensor to process variations and temperature variations. Although the actual design may achieve exceptional performance, the effect of such variations could significantly deteriorate this performance. Moreover, the sensor footprint is another important aspect for low-cost on-chip sensors. Hence, when evaluating on-chip sensors, all these parameters should be taken into consideration. The mentioned parameters, and hence the performance of on-chip RI optical sensors, is determined by the design of the optical devices, as well as the platform used to implement this design. In most cases, the same design can be implemented on the different platforms. Hence, choosing a suitable platform for a specific application has significant importance.
Today, many integrated photonic platforms are available. Silicon, silicon nitride, silica, and III–V material-based platforms, such as indium phosphide (InP), are the main technologies for integrated photonic circuits [27,28,29,30]. Silicon and silicon nitride photonic platforms are widespread photonic platforms due to their compatibility with the mature CMOS technology. Silicon photonics has been well-known for many decades now; however, silicon nitride has recently emerged as it offers lower losses, better tolerance to process and temperature variations, and a wider operating wavelength range compared to silicon [31,32,33,34]. CMOS compatibility offers a cost-effective and monolithic solution for sensors where both optical and electrical devices can be implemented on a single chip, which results in a more robust sensor and reduces packaging cost, whereas III–V-based technologies are still not widely used for integrated photonics. Their cost is much higher when compared to other platforms, and there is very limited number of foundries. Silica-based platforms, on the other hand, are also a cost-effective platform that can provide acceptable performance, and have a fiber-compatible mode field size and small phase error [35]. However, their chip size is in the order of centimeters [35].
In this work, we present a comparative study of the different photonic platforms that can be used for on-chip RI sensing. As mentioned previously, there is a large number of structures/technologies used for optical RI sensing, such as plasmonic and photonic crystals. The context of this study is mass-scale and low-cost RI sensors; hence, we focus on the standard, dielectric waveguide-based, integrated photonics fabrication process, which is mature and can be easily implemented in many foundries with a high yield. Our study includes silicon, silicon nitride, and silica platforms. Although most of the literature studies focus on enhancing the sensors’ sensitivity and LoD, other parameters affecting the sensor reliability and effectiveness, such as process and temperature variations, are usually overlooked. In this study, we compare the different platforms according to five different aspects that determine the detection performance of the sensor, as well as its yield, reliability, and cost-effectiveness. These aspects are the waveguide sensitivity to medium index change, fabrication tolerance, temperature sensitivity, optical losses, and footprint. A rigorous analysis based on a finite difference eigen-mode (FDE) solver [36] is used to determine and compare the first three aspects for the different platforms, while a literature survey is used to obtain the values of optical losses and footprints. We then define a figure of merit to assess the different platforms and find the most suitable one for RI sensing application. Finally, we compare interferometer-based and resonator-based RI designs in terms of device sensitivity, detection range, and immunity to phase noise. An analysis of the different parameters is presented for both devices.
2. Photonic Platforms
2.1. Comparative Study
In this section we compare the different integrated photonic platforms with respect to five different aspects, i.e., the waveguide sensitivity to medium (analyte) index change, the fabrication tolerance, the temperature sensitivity, optical losses, and footprint. These five aspects determine the performance, yield (robustness), and cost-effectiveness of the RI optical sensor. The waveguide sensitivity is the main parameter for our RI sensing application as it determines both the overall sensor sensitivity and the LoD. RI sensor sensitivity can be divided into two different terms, i.e., the device sensitivity Sdev, which depends on the design of the optical device used (interferometer or resonator dimensions), and the waveguide sensitivity Swg,med, which depends on the waveguide structure, and hence the platform and waveguide dimensions [18]. The overall sensor sensitivity Ssensor, which is the ratio between the shift in the measured optical quantity Δq (intensity or resonance shift) and the change in the sensed medium index Δnmed, is the product of these two terms; see the equation below.
where q is the measured optical quantity, which can be either intensity or (resonance) wavelength. Furthermore, LoD (the smallest resolvable index change) is another essential parameter of any sensor. LoD does not depend only on the sensor itself, but also on the measurement system, such as the source and the detector, in addition to other parameters (such as noise). However, to be able to compare different sensors without these system effects, an intrinsic LOD (iLoD) is defined [18]. iLoD is also proportional to the waveguide sensitivity Swg,med for both interferometric and resonant (cavity-based) devices; see the next section.
The fabrication tolerance determines the degree to which this platform is insensitive to fabrication process variations. This is highly important in RI sensors as a change in waveguide dimensions of just a few nanometers can lead to a significant change in the optical field phase. This will introduce an error in the detected analyte index, limiting the sensors’ accuracy and LoD, and, accordingly, the fabrication yield. Temperature fluctuations are the main source of noise in optical devices. Similar to process variations, changes in temperature will degrade sensors’ accuracy and LoD. On the other hand, optical losses of the sensor will determine the specifications of the source and detector needed for this sensor. Higher losses will require a more powerful source and/or detector, which can significantly increase the price of the sensor. Finally, in the context of mass-scale low-cost optical sensors, a significant part of the sensor’s price depends on its footprint. The footprint will determine how many sensors can be fabricated on a single wafer. Hence, the sensor’s price is proportional to the wafer price over the footprint.
The first three parameters can be assessed for the different platforms using numerical modal analysis. A change in the medium refractive index, temperature, or dimensions will result in a change in the mode effective index Δneff, which will accordingly change the detected optical signal; see Equation (1). Thus, we also define the waveguide sensitivity to temperature variations Swg,T and the waveguide sensitivity to width variation Swg,w as:
Here we use finite difference eigenmode (FDE) solver [36] to calculate the Swg,med, Swg,T, and Swg,w of a strip waveguide structure for the different platforms. For each platform, we sweep the dimensions, width w, and thickness h, and calculate these three parameters for the fundamental quasi-transverse electric (TE) mode. Note that the dimensions used in this analysis always satisfy the single mode operation. The substrate used in all platforms is silicon dioxide and the waveguide is covered with water cladding. The operating wavelength used in the analysis is near-infrared at λ = 1.55 µm. For the silica platform, the index contrast Δ between core and clad is 5.5%. The range of thicknesses used for each platform is different, as a platform with a lower core index, such as silica, needs a higher thickness to be able to support the optical mode.
Figure 1 shows Swg,med at different dimensions for the three different platforms. The waveguide width (single mode) range used at each thickness h for the different platforms is shown in Table 1. As the waveguide thickness decreases, the width increases in the support mode. Note that the minimum waveguide width included in the analysis is 200 nm. FDE results show that as Δn = ncore − nclad increases, we can achieve higher Swg,med = dneff,sens/dnmed. We can see that the silicon platform Swg,med can reach up to 1.2, while the silica maximum Swg,med is only around 0.2. We then calculate the average Swg,med for the different dimensions. The average Swg,med values for the silicon, silicon nitride, and silica platforms are 0.53, 0.23, and 0.09 respectively. Hence, silicon is 5.6 times more sensitive to medium (analyte) change than silica and 2.3 times higher than SiN.
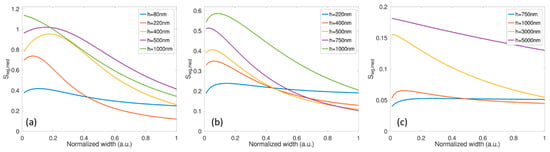
Figure 1.
Swg,med of (a) silicon, (b) silicon nitride and (c) silica platforms versus waveguide width w at different waveguide thicknesses h at λ = 1.55 µm.

Table 1.
The minimum wmin and maximum wmax waveguide widths (single mode range) at each waveguide thickness h for the silicon, silicon nitride, and silica platforms.
Table 2 shows published and experimentally measured sensing performance (sensitivity and LoD) of different MZI-based and MRR-based RI sensors for comparison. The results shown in the table align with our analysis showing that the silicon platform achieves the highest sensitivity among the three platforms, while silica shows the lowest sensitivity. Note that these are just samples from a number of works [15,16,17,18,19] conducted in this field. Much higher sensitivities have also been achieved but with much more complex designs, for instance, cascaded MRRs. However, here we just selected simple MZI or MRR sensors for the sake of comparison. Furthermore, it is important to note that the reported sensitivity includes the device sensitivity, which depends on the device design, and not only the platform. In [37], the authors also compared silicon to other platforms based on the different sensor structures and reached the same conclusion.

Table 2.
Comparison of experimentally measured sensitivity/LoD of RI sensors on different platforms.
For the temperature sensitivity Swg,T we use the thermos-optical (TO) coefficient (dn/dT) of the different materials [46,47] and calculate it as:
where Γ the confinement factor, which is the fraction of the optical power inside a certain medium [48]. Here, the clad medium is water (liquid), the substrate medium is silicon dioxide, and the core is silicon, silicon nitride, and silica, respectively.
For each platform, Γcld, Γcore, and Γsub are determined for different dimensions using modal analysis. Figure 2 shows Swg,T of the three platforms. When we calculate the average over the different waveguide dimensions, we find that the average Swg,T values for the silicon, silicon nitride, and silica platforms are 8.8 ×10−5 RIU/K, 1.1 ×10−5 RIU/K, and 0.6 ×10−5 RIU/K, respectively. The silica platform has the lowest change to temperature fluctuations, which are 15 times lower than those of Si and around 2 times lower than those of SiN. This is expected as silicon has a much higher thermo-optical coefficient 1.8 × 10−4 K−1 than silica and silicon nitride, which are 2.45 × 10−5 K−1 and 8.5 × 10−6 K−1, respectively [46,47]. However, note that some points in Figure 2 have zero Swg,T. This means that at certain dimensions, the sensitivity to temperature variations can be minimized (ideally to zero). This is because the TO coefficient of the water −10−4 K−1 is negative and the other materials have a positive TO coefficient. So, for a certain dimension, the effect of temperature in the mode effective index can be totally compensated for.
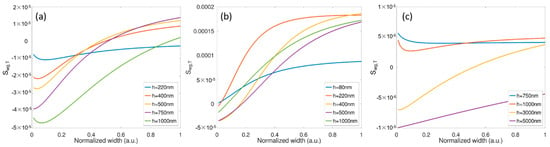
Figure 2.
Swg,T of (a) silicon, (b) silicon nitride and (c) silica platforms versus waveguide width w at different waveguide thicknesses h at λ = 1.55 µm.
Figure 3 shows Swg,w of the different platforms. It can be seen that the silica platform is the most tolerant to process variations, which is expected as it has small Δn = ncore − nclad. As a result, it has relatively large waveguide dimensions, and is hence more tolerant to fabrication variations. FDE results show that the average Swg,w values for the silicon, silicon nitride, and silica platforms are 49 × 10−4 RIU/nm, 3 × 10−4 RIU/nm, and 0.4 × 10−4 RIU/nm, respectively. Hence, the silica platform is 123 times more tolerant than silicon and 8 times more than SiN. Moreover, SiN is 16 times more tolerant than Si.

Figure 3.
Swg,w of (a) silicon, (b) silicon nitride, and (c) silica platforms versus waveguide width w at different waveguide thicknesses h at λ = 1.55 µm.
For the losses and footprint of the different photonic platforms, we gathered different data reported in previously published work. The losses can be divided into two parts, i.e., the propagation loss and the coupling loss. The propagation loss is due to the quality and the absorption of the waveguide materials, as well as the quality of the surfaces (surface roughness). The coupling loss is the loss due to the coupling of the light source to the sensor chip. In most cases, fiber is used to couple the light source to the chip. For the SOI platform, the waveguide dimensions are sub-micron, which results in high coupling loss due to the mode mismatch between the fiber and silicon waveguide. However, because the devices are compact, the propagation losses are low. In contrast, silica waveguides have a low mismatch with fiber and, hence, a low coupling loss. However, silica-based devices are of millimeter lengths, and hence have a large propagation loss. On the other hand, the optical circuit footprint is determined by two parameters, i.e., the phase change per unit length and the waveguide bend size. Both depend mainly on the core-clad index difference. The phase change of the EM field after the propagating distance L is Δφ = 2πneffL/λ, where neff is the mode effective index. The effective index is proportional to the core index. Hence, a waveguide such as silica with a low core index will need a larger length compared to silicon, which has a larger core index. Another thing that determines the footprint is the waveguide bend size. Platforms such as silica with a small core-clad index difference need a large bend radius (in the millimeter range) to route the optical signal with minimal losses. The waveguide bend radius is the parameter that dominates the circuit footprint. Because the phase change per unit length can be two times higher for silicon than for silica, the bend radius can change by three orders of magnitude. Hence, here we compare the footprint using the bend radius of the different platforms. Table 3 below shows the average losses and footprints of the different platforms and the references used to calculate them. The results show that the losses of the silicon platform are around 27 times higher than those of silica, while the footprint of silicon is more than three orders of magnitude smaller. As mentioned before, this will be reflected in a significant reduction in the cost of the silicon-based sensors.

Table 3.
The average losses and bend radius (footprint) of silicon, silicon nitride, and silica photonic platforms as reported in published work; see [28,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67].
2.2. Discussion
Table 4 summarizes the results we presented so far for the three platforms. As we mentioned, silicon is the best choice for compact and high medium sensitivity, while silica is the best choice for low temperature sensitivity and fabrication-tolerant sensor design, with silicon nitride always being a compromise of both.

Table 4.
The average values of the waveguide medium sensitivity Swg,med, temperature sensitivity Swg,T, width variation sensitivity Swg,w, optical losses, and footprints for the three photonic platforms included in this study.
To assess these three platforms and choose the best candidate for on-chip RI sensing and LoC applications, we define a figure of merit (FOM). This FOM takes into account the five different aspects we discussed earlier: the platform sensitivity to medium change, sensitivity to temperature, fabrication tolerance, optical losses, and footprint. Our FOM is defined as:
where L represents the losses and FP is the footprint.
Note that, as previously mentioned, the losses term L has two components, i.e., the propagation loss, which is proportional to the length and is hence multiplied by the footprint, and the coupling loss. Moreover, Swg,med is the main parameter for RI sensing as it affects both the sensor’s sensitivity and LoD, and hence determines its sensing performance; thus, we weighted it more by squaring it. Replacing the results of Table 4 in Equation (5), we find that the FOM values for silicon, silicon nitride, and silica are 13,716, 318, and 13, respectively. Hence, when including the different aspects that affect the performance and robustness of the RI sensor, we find that the silicon platform outperforms the other platforms, with an FOM that is 43 times higher than that of silicon nitride and more than 1000 times higher than that of silica. The FOM may be defined in many different ways by changing the weights of each parameter depending on what is more significant for a specific application. For example, one may assign less weight to width sensitivity if there is very good control of the fabrication process. However, this would not significantly change the conclusion that the silicon platform is the best candidate. This is mainly because of the very high sensitivity and extremely small FP due to the large index contrast. Thus, while silicon is more susceptible to variations than the other two platforms, it is also much more sensitive to medium (analyte) variations and extremely compact, thereby leading to lower propagation losses, even if the loss per unit length is large.
3. Photonic Devices for RI Sensing
3.1. Analysis
In this section we present an analysis of the MZI and micro-ring resonator (MRR) RI sensors. The main performance parameters of RI sensing are derived for both devices, and are then used to compare them. As mentioned in the introduction, there is a plethora of designs, either interferometric based or resonator based, which can further enhance the performance of each of them. However, here we compare the standard interferometer with the resonator RI sensor. This comparison depends on the fundamental difference between resonant-based and interferometric-based devices, which will still be valid even for different (such as a Fabry–Perot resonator or Young interferometer) or more complex designs. The transmissions of an MZI with 3 dB couplers and an all-pass micro-ring resonator are [68,69]:
In the MZI, Δ = βsensLsens − βrefLref is the phase difference between the MZI sensing and reference arm, where βsens, Lsens, and βref, Lref are the propagation constant and the length of the sensing and reference arm, respectively. For the MRR, = βL, L = 2πR and α are the round-trip phase shift, length, and amplitude transmission, respectively, where β is the propagation constant of the circulating mode, r is the self-coupling coefficient, and α2 = e−αL, with α the power loss coefficient.
The resonance (peak) wavelengths of these devices are [68,69]:
Accordingly, the free spectral range (FSR), wavelength sensitivity Smed = dλres/dnmed, and FWHM can be derived as [68,69]:
where Ssens,med = dneff,sens/dnmed is the sensing waveguide sensitivity to the medium index change.
We can also derive the sensitivity of the devices to any parameter x, Sx = dλres/dx as:
where Ssens,x = dneff,sens/dx and Sref,x = dneff,ref/dx represent the waveguide sensitivity to changes in the parameter x of the sensing and the reference waveguides, respectively. This parameter can represent the noise (error) in our detected signal, and hence needs to be minimized. The main noise sources in integrated RI sensors are the temperature and process variations. These variations shift the resonance wavelength, which leads to an error in the detected medium index, limiting the accuracy and LoD of the sensor. We can then determine the ratio between the wavelength sensitivity to medium index change, and the wavelength sensitivity to any other change (error), which represent the signal-to-noise (or error) ratio in the RI sensing application.
The figure of merit (FOM) and minimum detectable refractive index (Δnmin), also known as the intrinsic limit of detection (iLOD) [18], are given by:
The maximum detectable refractive index Δnmax corresponds to the resonance wavelength shift equal to the FSR; hence:
Now we can define the detection range of both MZI and MRR sensors as:
3.2. Discussion
Based on this analysis, we now compare the MZI and MRR with respect to the main features of RI sensing, as derived here. First, the analysis shows that the MRR can achieve a much higher FOM (and hence a low LoD) than the MZI, with a compact footprint. From Equation (13) we can see that, for the same sensing length (Lsens) and sensing waveguide (Ssens,med), FOMMRR is larger than FOMMZI by the factor /(1 − ), owing to the nature of the resonators where the electromagnetic field circulates multiple round trips inside the cavity, which results in a Lorentzian-like spectrum. For a critically coupled MRR (r = α), this factor will depend on the round-trip losses. Typical values for α are between 0.88 and 0.98. Hence, FOMMRR is 4 to 25 times higher than FOMMZI. Furthermore, note that an MRR is more compact than an MZI, even for the same Lsens, due to its ring shape. Next, regarding the detection range in Equation (15), we can see that, for both devices, if we want to reduce Δnmin, Δnmax will also be reduced, because the FWHM is proportional to the FSR in both devices. The maximum detectable index change in the MZI is only 2.2 times its minimum detectable value, which is a very limited range. However, for critically coupled ring resonators (r = α), the detection range depends on the round-trip cavity losses. For typical values of α, the detection range of an MRR-based sensor is much larger than that of an MZI-based sensor. For example, an MRR with α of only 0.9 will have around 7 times higher DR than an MZI. By comparison, for an MRR with better quality, α can be as high as 0.98. In this case, the DRMRR is more than 30 times higher than the DRMZI. On the other hand, for a certain waveguide platform (Ssens,med) and operating wavelength, the wavelength sensitivity Smed,MRR of the MRR sensor is constant and cannot be designed, as shown in Equation (9), and only the FOMMRR can be designed using the radius of the ring R. In contrast, for the MZI-based sensor, the wavelength sensitivity Smed,MZI and FOMMZI can be engineered independently through Lsens and Lref. Hence, MZI sensors can achieve high sensitivities, although at large lengths. Finally, from Equation (12) we can see that the MZI can maximize the signal-to-noise ratio via the design of the interferometer arms. We can design sensing and reference waveguide dimensions, together with their lengths, to minimize the detection error to temperature and process variations. However, in the MRR this ratio cannot actually be designed and is almost fixed for a given platform. This is extremely important as temperature and fabrication variations will have significant effects on the sensor design and can totally degrade its performance.
Table 5 below shows the published and experimentally demonstrated sensing performance (sensitivity and LoD) of different MZI-based and MRR-based RI sensors for comparison. From these results we can see that MZI-based sensors can achieve much higher (wavelength) sensitivity compared to MRR designs. Moreover, we can see that the LoD achieved is comparable or slightly higher in the MZI case, i.e., 10 times higher on average. However, MZI-based sensors have a significantly larger length (footprint) compared to the MRR design, i.e., more than 50 times higher on average. These experimental verified results align well with our analysis and discussion, and further confirm our conclusions.

Table 5.
Comparison of experimentally measured sensitivity, LoD, and length/radius of MZI- and MRR-based RI sensors.
Hence, the MRR sensor is the best choice when a mature technology with very low process variations is used and with a platform that has low temperature dependence, such as silicon nitride or silica (discussed in the previous section). In this case, the MRR will achieve a better LoD than the MZI, while also having a compact size. However, for a technology with non-negligible process variations and with a platform such as silicon, which has high temperature dependence, the MRR sensor design will not be able to compensate for such changes, and hence the MZI will be the device of choice in this case, as discussed.
4. Conclusions
In conclusion, we have presented a comparative study of different photonic platforms and devices for on-chip RI sensing. We first compared the different photonic platforms with respect to waveguide sensitivity to medium index change, fabrication tolerance, temperature sensitivity, optical losses, and footprint. These parameters will determine not only the performance of the sensor, but also its robustness and cost-effectiveness. A rigorous modal analysis was used to determine the waveguide sensitivity and the effect of the process variations and temperature variations for the different platforms. Then, a figure of merit was defined that includes all the parameters for comparison of the different platforms. Our study showed that silicon is the best platform for RI sensing. Next, we presented a detailed analysis of MZI and MRR RI sensors. The sensitivity, LoD, signal-to-noise ratio and detection range were derived for both devices. Finally, a comparison between the two devices, and the selection of the best choice, are discussed. Our analysis and conclusions presented in this study are also supported by experimental data from different published work.
Author Contributions
Conceptualization, M.A.S.; methodology, R.S.E.S. and M.A.S.; software, R.S.E.S.; validation, R.S.E.S.; formal analysis, R.S.E.S.; investigation, R.S.E.S.; resources, M.A.S.; data curation, R.S.E.S.; writing—original draft preparation, R.S.E.S.; writing—review and editing, R.S.E.S., M.A.S. and X.L.; visualization, R.S.E.S.; supervision, M.A.S. and X.L.; project administration, M.A.S. and X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Proll, G.R. R. Narayanaswamy, O.S. Wolfbeis (eds.): Optical Sensors: Industrial, Environmental and Diagnostic Applications. Anal. Bioanal. Chem. 2005, 381, 18–19. [Google Scholar] [CrossRef]
- Wang, M.; Xu, Y.; Yang, Y.; Mu, B.; Nikitina, M.A.; Xiao, X. Vis/NIR optical biosensors applications for fruit monitoring. Biosens. Bioelectron. X 2022, 11, 100197. [Google Scholar] [CrossRef]
- Pires, N.M.M.; Dong, T.; Hanke, U.; Hoivik, N. Recent developments in optical detection technologies in lab-on-a-chip devices for biosensing applications. Sensors 2014, 14, 15458–15479. [Google Scholar] [CrossRef]
- Zaki, A.O.; Kirah, K.; Swillam, M.A. Integrated optical sensor using hybrid plasmonics for lab on chip applications. J. Opt. 2016, 18, 085803. [Google Scholar] [CrossRef]
- Fan, X.; White, I.M.; Shopova, S.I.; Zhu, H.; Suter, J.D.; Sun, Y. Sensitive optical biosensors for unlabeled targets: A review. Anal. Chim. Acta 2008, 620, 8–26. [Google Scholar] [CrossRef] [PubMed]
- Correa-Mena, A.G.; González, L.A.; Quintero-Rodríguez, L.J.; Zaldivar-Huerta, I.E. Review on integrated optical sensors and its applications. In Proceedings of the 2017 IEEE Mexican Humanitarian Technology Conference (MHTC), Puebla, Mexico, 29–31 March 2017; pp. 170–173. [Google Scholar]
- Xie, Y.; Zhang, M.; Dai, D. Design rule of mach-zehnder interferometer sensors for ultra-high sensitivity. Sensors 2020, 20, 2640. [Google Scholar] [CrossRef]
- Zhao, C.; Xu, L.; Liu, L. Ultrahigh sensitivity mach-zehnder interferometer sensor based on a weak one-dimensional field confinement silica waveguide. Sensors 2021, 21, 6600. [Google Scholar] [CrossRef] [PubMed]
- Fard, S.T.; Donzella, V.; Schmidt, S.A.; Flueckiger, J.; Grist, S.M.; Fard, P.T.; Wu, Y.; Bojko, R.J.; Kwok, E.; Jaeger, N.A.F.; et al. Performance of ultra-thin SOI-based resonators for sensing applications. Opt. Express 2014, 22, 14166–14179. [Google Scholar] [CrossRef]
- Jin, L.; Li, M.; He, J.-J. Analysis of wavelength and intensity interrogation methods in cascaded double-ring sensors. J. Light. Technol. 2012, 30, 1994–2002. [Google Scholar] [CrossRef]
- Hodgkinson, J.; Tatam, R.P. Optical gas sensing: A review. Meas. Sci. Technol. 2012, 24, 012004. [Google Scholar] [CrossRef]
- Farca, G.; Shopova, S.I.; Rosenberger, A.T. Cavity-enhanced laser absorption spectroscopy using microresonator whispering-gallery modes. Opt. Express 2007, 15, 17443–17448. [Google Scholar] [CrossRef]
- Nitkowski, A.; Chen, L.; Lipson, M. Cavity-enhanced on-chip absorption spectroscopy using microring resonators. Opt. Express 2008, 16, 11930–11936. [Google Scholar] [CrossRef] [PubMed]
- Armani, A.M.; Vahala, K.J. Heavy water detection using ultra-high-Q microcavities. Opt. Lett. 2006, 31, 1896–1898. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Hu, Z.; Ye, M.; Yu, Z.; Ma, C.; Li, J. On-chip refractive index sensor with ultra-high sensitivity based on sub-wavelength grating racetrack microring resonators and vernier effect. IEEE Photon. J. 2022, 14, 6849007. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Silicon photonic devices realized on refractive index engineered subwavelength grating waveguides—A review. Opt. Laser Technol. 2021, 138, 106863. [Google Scholar] [CrossRef]
- Kazanskiy, N.; Khonina, S.; Butt, M. Plasmonic sensors based on Metal-insulator-metal waveguides for refractive index sensing applications: A brief review. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 117, 113798. [Google Scholar] [CrossRef]
- Luan, E.; Shoman, H.; Ratner, D.M.; Cheung, K.C.; Chrostowski, L. Silicon photonic biosensors using label-free detection. Sensors 2018, 18, 3519. [Google Scholar] [CrossRef]
- Mere, V.; Muthuganesan, H.; Kar, Y.; Van Kruijsdijk, C.; Selvaraja, S.K. On-chip chemical sensing using slot-waveguide-based ring resonator. IEEE Sens. J. 2020, 20, 5970–5975. [Google Scholar] [CrossRef]
- Brandenburg, A.; Krauter, R.; Künzel, C.; Stefan, M.; Schulte, H. Interferometric sensor for detection of surface-bound bioreactions. Appl. Opt. 2000, 39, 6396–6405. [Google Scholar] [CrossRef]
- Schmitt, K.; Schirmer, B.; Hoffmann, C.; Brandenburg, A.; Meyrueis, P. Interferometric biosensor based on planar optical waveguide sensor chips for label-free detection of surface bound bioreactions. Biosens. Bioelectron. 2007, 22, 2591–2597. [Google Scholar] [CrossRef]
- Zinoviev, K.E.; González-Guerrero, A.B.; Domínguez, C.; Lechuga, L.M. Integrated bimodal waveguide interferometric biosensor for label-free analysis. J. Light. Technol. 2011, 29, 1926–1930. [Google Scholar] [CrossRef]
- Zhang, X.; Armani, A.M. Silica microtoroid resonator sensor with monolithically integrated waveguides. Opt. Express 2013, 21, 23592–23603. [Google Scholar] [CrossRef] [PubMed]
- Bianucci, P. Optical microbottle resonators for sensing. Sensors 2016, 16, 1841. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.N.; Zhou, T.; Han, B.; Zhang, A.; Zhao, Y. Optical bio-chemical sensors based on whispering gallery mode resonators. Nanoscale 2018, 10, 13832–13856. [Google Scholar] [CrossRef] [PubMed]
- Madani, A.; Harazim, S.M.; Quiñones, V.A.B.; Kleinert, M.; Finn, A.; Naz, E.S.G.; Ma, L.; Schmidt, O.G. Optical microtube cavities monolithically integrated on photonic chips for optofluidic sensing. Opt. Lett. 2017, 42, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Stojanović, V.; Ram, R.J.; Popović, M.; Lin, S.; Moazeni, S.; Wade, M.; Sun, C.; Alloatti, L.; Atabaki, A.; Pavanello, F.; et al. Monolithic silicon-photonic platforms in state-of-the-art CMOS SOI processes. Opt. Express 2018, 26, 13106–13121. [Google Scholar] [CrossRef] [PubMed]
- Himeno, A.; Kato, K.; Miya, T. Silica-based planar lightwave circuits. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 913–924. [Google Scholar] [CrossRef]
- Rahim, A.; Ryckeboer, E.; Subramanian, A.Z.; Clemmen, S.; Kuyken, B.; Dhakal, A.; Raza, A.; Hermans, A.; Muneeb, M.; Dhoore, S.; et al. Expanding the silicon photonics portfolio with silicon nitride photonic integrated circuits. J. Light. Technol. 2017, 35, 639–649. [Google Scholar] [CrossRef]
- Doerr, C.R. Integrated photonic platforms for telecommunications: InP and Si. IEICE Trans. Electron. 2013, 96, 950–957. [Google Scholar] [CrossRef]
- Porcel, M.A.; Hinojosa, A.; Jans, H.; Stassen, A.; Goyvaerts, J.; Geuzebroek, D.; Geiselmann, M.; Dominguez, C.; Artundo, I. Silicon nitride photonic integration for visible light applications. Opt. Laser Technol. 2019, 112, 299–306. [Google Scholar] [CrossRef]
- Wilmart, Q.; El Dirani, H.; Tyler, N.; Fowler, D.; Malhouitre, S.; Garcia, S.; Casale, M.; Kerdiles, S.; Hassan, K.; Monat, C. A versatile silicon-silicon nitride photonics platform for enhanced functionalities and applications. Appl. Sci. 2019, 9, 255. [Google Scholar] [CrossRef]
- Baets, R.; Subramanian, A.Z.; Clemmen, S.; Kuyken, B.; Bienstman, P.; Le Thomas, N.; Roelkens, G.; Van Thourhout, D.; Helin, P.; Severi, S. Silicon Photonics: Silicon nitride versus silicon-on-insulator. In Optical Fiber Communication Conference; Optical Society of America: Washington, DC, USA, 2016; p. Th3J-1. [Google Scholar]
- Sharma, T.; Wang, J.; Kaushik, B.K.; Cheng, Z.; Kumar, R.; Zhao, W.; Li, X. Review of recent progress on silicon nitride-based photonic integrated circuits. IEEE Access 2020, 8, 195436–195446. [Google Scholar] [CrossRef]
- Suzuki, K.; Matsubara, N.; Hasegawa, J.; Konoike, R.; Matsuura, H.; Kawashima, H.; Ikeda, K. Wavelength (DE) MUX-and-switch based on 5.5%-Δ-silica PLC/silicon photonics hybrid platform. J. Light. Technol. 2022, 40, 1810–1814. [Google Scholar] [CrossRef]
- Optical Waveguide Design Software—Lumerical MODE Solutions. Lumerical. Available online: https://www.lumerical.com/products/mode/ (accessed on 20 August 2023).
- Peng, C.; Yang, C.; Zhao, H.; Liang, L.; Zheng, C.; Chen, C.; Qin, L.; Tang, H. Optical waveguide refractive index sensor for biochemical sensing. Appl. Sci. 2023, 13, 3829. [Google Scholar] [CrossRef]
- Wan, L.; Chandrahalim, H.; Zhou, J.; Li, Z.; Chen, C.; Cho, S.; Zhang, H.; Mei, T.; Tian, H.; Oki, Y.; et al. Demonstration of versatile whispering-gallery micro-lasers for remote refractive index sensing. Opt. Express 2018, 26, 5800–5809. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Shahbaz, M.; Piramidowicz, R. Racetrack Ring Resonator Integrated with Multimode Interferometer Structure Based on Low-Cost Silica–Titania Platform for Refractive Index Sensing Application. Photonics 2023, 10, 978. [Google Scholar] [CrossRef]
- Zuta, Y.; Goykhman, I.; Desiatov, B.; Levy, U. On-chip switching of a silicon nitride micro-ring resonator based on digital microfluidics platform. Opt. Express 2010, 18, 24762–24769. [Google Scholar] [CrossRef]
- Liu, M.; Ma, L.; Qiu, C.; He, Z. Refractive Index Sensor Based on Few-mode Silicon-Nitride Micro-Ring Resonator. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar]
- Gylfason, K.B.; Carlborg, C.F.; Kaźmierczak, A.; Dortu, F.; Sohlström, H.; Vivien, L.; Barrios, C.A.; van der Wijngaart, W.; Stemme, G. On-chip temperature compensation in an integrated slot-waveguide ring resonator refractive index sensor array. Opt. Express 2010, 18, 3226–3237. [Google Scholar] [CrossRef]
- Carlborg, C.F.; Gylfason, K.B.; Kaźmierczak, A.; Dortu, F.; Polo, M.B.; Catala, A.M.; Kresbach, G.M.; Sohlström, H.; Moh, T.; Vivien, L.; et al. A packaged optical slot-waveguide ring resonator sensor array for multiplex label-free assays in labs-on-chips. Lab Chip 2010, 10, 281–290. [Google Scholar] [CrossRef]
- Robinson, J.T.; Chen, L.; Lipson, M. On-chip gas detection in silicon optical microcavities. Opt. Express 2008, 16, 4296–4301. [Google Scholar] [CrossRef]
- Taha, A.M.; Paredes, B.; Khilo, A.; Dahlem, M.S. SOI-based centimeter-scale Mach–Zehnder interferometers for fluid sensing. In Integrated Optics: Devices, Materials, and Technologies XXI; SPIE: Bellingham, WA, USA, 2017; Volume 10106. [Google Scholar]
- Liu, P.; Shi, Y. Simultaneous measurement of refractive index and temperature using a dual polarization ring. Appl. Opt. 2016, 55, 3537–3541. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Goddard, L.L. Measurements of the refractive indices and thermo-optic coefficients of Si3N4 and SiOx using microring resonances. Opt. Lett. 2013, 38, 3878–3881. [Google Scholar] [CrossRef] [PubMed]
- Zengzhi, H.; Zhang, Y.; Zeng, C.; Li, D.; Nisar, M.S.; Yu, J.; Xia, J. High confinement factor ridge slot waveguide for optical sensing. IEEE Photonics Technol. Lett. 2015, 27, 2395–2398. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W.; et al. Review of silicon photonics technology and platform development. J. Light. Technol. 2021, 39, 4374–4389. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, Y.; Qiu, C.; Guo, X.; Sun, L. Silicon photonic platform for passive waveguide devices: Materials, fabrication, and applications. Adv. Mater. Technol. 2020, 5, 1901153. [Google Scholar] [CrossRef]
- Carpenter, L.G.; van Niekerk, M.; Begović, A.; Sundaram, V.S.S.; Deenadayalan, V.; Palone, T.; Fanto, M.; Preble, S.; Baiocco, C.; Leake, G.L.; et al. Towards low propagation losses in active photonic multi-project wafer runs. In Integrated Photonics Research, Silicon and Nanophotonics; Optica Publishing Group: Washington, WA, USA, 2021; p. ITu3A-5. [Google Scholar]
- Carroll, L.; Lee, J.-S.; Scarcella, C.; Gradkowski, K.; Duperron, M.; Lu, H.; Zhao, Y.; Eason, C.; Morrissey, P.; Rensing, M.; et al. Photonic packaging: Transforming silicon photonic integrated circuits into photonic devices. Appl. Sci. 2016, 6, 426. [Google Scholar] [CrossRef]
- Mu, X.; Wu, S.; Cheng, L.; Fu, H.Y. Edge couplers in silicon photonic integrated circuits: A review. Appl. Sci. 2020, 10, 1538. [Google Scholar] [CrossRef]
- Cheng, L.; Mao, S.; Li, Z.; Han, Y.; Fu, H.Y. Grating couplers on silicon photonics: Design principles, emerging trends and practical issues. Micromachines 2020, 11, 666. [Google Scholar] [CrossRef]
- Bahadori, M.; Nikdast, M.; Cheng, Q.; Bergman, K. Universal design of waveguide bends in silicon-on-insulator photonics platform. J. Light. Technol. 2019, 37, 3044–3054. [Google Scholar] [CrossRef]
- Vlasov, Y.A.; McNab, S.J. Losses in single-mode silicon-on-insulator strip waveguides and bends. Opt. Express 2004, 12, 1622–1631. [Google Scholar] [CrossRef]
- Muñoz, P.; Doménech, J.D.; Domínguez, C.; Sánchez, A.; Micó, G.; Bru, L.A.; Pérez, D.; Pastor, D. State of the art of silicon nitride photonics integration platforms. In Proceedings of the 2017 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017; pp. 1–4. [Google Scholar]
- Shaw, M.J.; Guo, J.; Vawter, G.A.; Habermehl, S.; Sullivan, C.T. Fabrication techniques for low-loss silicon nitride waveguides. In Proceedings of the Micromachining Technology for Micro-Optics and Nano-Optics III, San Jose, CA, USA, 22 January 2005; Volume 5720, pp. 109–118. [Google Scholar]
- Lin, T.; Yang, H.; Li, L.; Yun, B.; Hu, G.; Li, S.; Yu, W.; Ma, X.; Liang, X.; Cui, Y. Ultra-broadband and highly efficient silicon nitride bi-layer grating couplers. Opt. Commun. 2023, 530, 129209. [Google Scholar] [CrossRef]
- Zhu, X.; Li, G.; Wang, X.; Li, Y.; Davidson, R.; Little, B.E.; Chu, S.T. Low-loss fiber-to-chip edge coupler for silicon nitride integrated circuits. Opt. Express 2023, 31, 10525–10532. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Halir, R.; Molina-Fernández, Í.; Cheben, P.; He, J.-J. High-efficiency apodized-imaging chip-fiber grating coupler for silicon nitride waveguides. Opt. Lett. 2016, 41, 5059–5062. [Google Scholar] [CrossRef] [PubMed]
- Hibino, Y. Silica-based planar lightwave circuits and their applications. MRS Bull. 2003, 28, 365–371. [Google Scholar] [CrossRef]
- Popovic, M.; Wada, K.; Akiyama, S.; Haus, H.A.; Michel, J. Air trenches for sharp silica waveguide bends. J. Light. Technol. 2002, 20, 1762–1772. [Google Scholar] [CrossRef]
- Takahashi, H. High performance planar lightwave circuit devices for large capacity transmission. Opt. Express 2011, 19, B173–B180. [Google Scholar] [CrossRef]
- Takahashi, M.; Uchida, Y.; Yamasaki, S.; Hasegawa, J.; Yagi, T. Compact and low-loss coherent mixer based on high Δ ZrO2-SiO2 PLC. J. Light. Technol. 2014, 32, 3081–3088. [Google Scholar] [CrossRef]
- Kawachi, M. Silica waveguides on silicon and their application to integrated-optic components. Opt. Quantum Electron. 1990, 22, 391–416. [Google Scholar] [CrossRef]
- Kawachi, M. Recent progress in silica-based planar lightwave circuits on silicon. IEE Proc.-Optoelectron. 1996, 143, 257–262. [Google Scholar] [CrossRef]
- El Shamy, R.S.; Afifi, A.E.; Badr, M.M.; Swillam, M.A. Modelling, characterization, and applications of silicon on insulator loop terminated asymmetric Mach Zehnder interferometer. Sci. Rep. 2022, 12, 3598. [Google Scholar] [CrossRef]
- El Shamy, R.S.; Swillam, M.A.; Li, X. On-chip complex refractive index detection at multiple wavelengths for selective sensing. Sci. Rep. 2022, 12, 9343. [Google Scholar] [CrossRef] [PubMed]
- Tu, X.; Song, J.; Liow, T.Y.; Park, M.K.; Yiying, J.Q.; Kee, J.S.; Yu, M.; Lo, G.Q. Thermal independent silicon-nitride slot waveguide biosensor with high sensitivity. Opt. Express 2012, 20, 2640–2648. [Google Scholar] [CrossRef] [PubMed]
- Densmore, A.; Xu, D.-X.; Janz, S.; Waldron, P.; Mischki, T.; Lopinski, G.; Delâge, A.; Lapointe, J.; Cheben, P.; Lamontagne, B.; et al. Spiral-path high-sensitivity silicon photonic wire molecular sensor with temperature-independent response. Opt. Lett. 2008, 33, 596–598. [Google Scholar] [CrossRef] [PubMed]
- Prieto, F.; Sepúlveda, B.; Calle, A.; Llobera, A.; Domínguez, C.; Abad, A.; Montoya, A.; Lechuga, L.M. An integrated optical interferometric nanodevice based on silicon technology for biosensor applications. Nanotechnology 2003, 14, 907. [Google Scholar] [CrossRef]
- Zinoviev, K.; Carrascosa, L.G.; Sánchez del Río, J.; Sepúlveda, B.; Domínguez, C.; Lechuga, L.M. Silicon photonic biosensors for lab-on-a-chip applications. Adv. Opt. Technol. 2008, 6, 383927. [Google Scholar] [CrossRef]
- Lillie, J.J.; Thomas, M.A.; Jokerst, N.M.; Ralph, S.E.; Dennis, K.A.; Henderson, C.L. Multimode interferometric sensors on silicon optimized for fully integrated complementary-metal-oxide-semiconductor chemical-biological sensor systems. JOSA B 2006, 23, 642–651. [Google Scholar] [CrossRef]
- Sun, D.; Ran, Y.; Wang, G. Label-free detection of cancer biomarkers using an in-line taper fiber-optic interferometer and a fiber bragg grating. Sensors 2017, 17, 2559. [Google Scholar] [CrossRef]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef]
- Iqbal, M.; Gleeson, M.A.; Spaugh, B.; Tybor, F.; Gunn, W.G.; Hochberg, M.; Baehr-Jones, T.; Bailey, R.C.; Gunn, L.C. Label-free biosensor arrays based on silicon ring resonators and high-speed optical scanning instrumentation. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 654–661. [Google Scholar] [CrossRef]
- Claes, T.; Molera, J.G.; De Vos, K.; Schacht, E.; Baets, R.; Bienstman, P. Label-free biosensing with a slot-waveguide-based ring resonator in silicon on insulator. IEEE Photonics J. 2009, 1, 197–204. [Google Scholar] [CrossRef]
- TalebiFard, S.; Schmidt, S.; Shi, W.; Wu, W.; Jaeger, N.A.; Kwok, E.; Ratner, D.M.; Chrostowski, L. Optimized sensitivity of Silicon-on-Insulator (SOI) strip waveguide resonator sensor. Biomed. Opt. Express 2017, 8, 500–511. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Guan, X.; Huang, Q.; Zheng, J.; Shi, Y.; Dai, D. Suspended ultra-small disk resonator on silicon for optical sensing. Opt. Lett. 2013, 38, 5405–5408. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Cao, Z.; Liu, Y.; Zhang, Q.; Zou, J.; Shao, L.; Wang, Y.; He, J.; Li, M. Highlysensitive optical biosensor based on equal fsr cascaded microring resonator with intensity interrogation for detection of progesterone molecules. Opt. Express 2017, 25, 33193–33201. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).