Exploring Data Augmentation and Dimension Reduction Opportunities for Predicting the Bandgap of Inorganic Perovskite through Anion Site Optimization
Abstract
:1. Introduction
- (1)
- Data processing has been approached to clean, null, and duplicate values from 1528 materials. This dataset was characterized by an intricate feature space spanning 130 dimensions, encompassing pertinent attributes including the nature of the bandgap.
- (2)
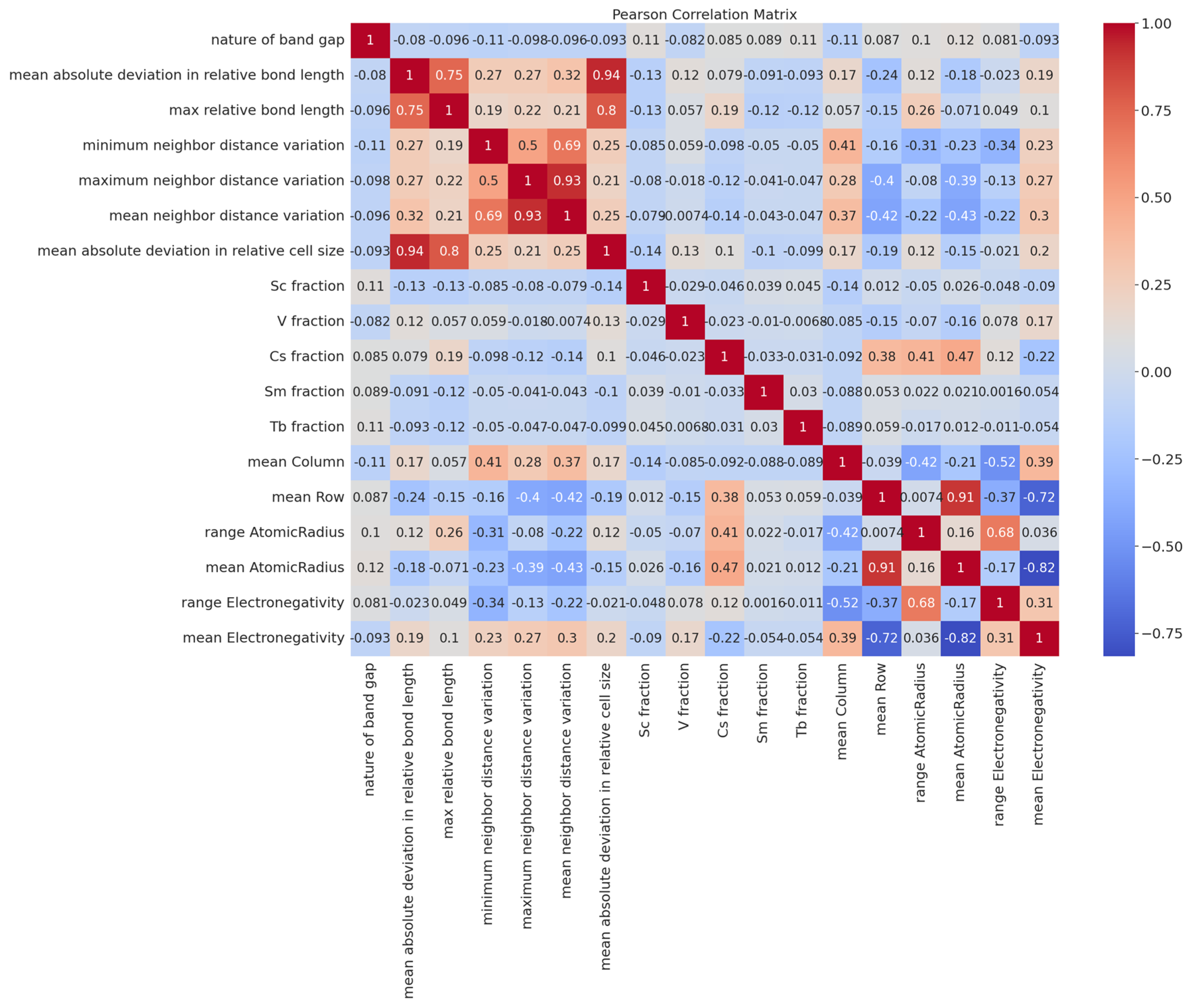
- Through the raw database, the application of the data augmentation methodology was undertaken to enhance the diversity of the dataset. Additionally, the implementation of Pearson Correlation was performed to ascertain the degree of correlation between each individual feature, and, notably, the intrinsic nature of the bandgap, thereby uncovering latent relationships.
- (3)
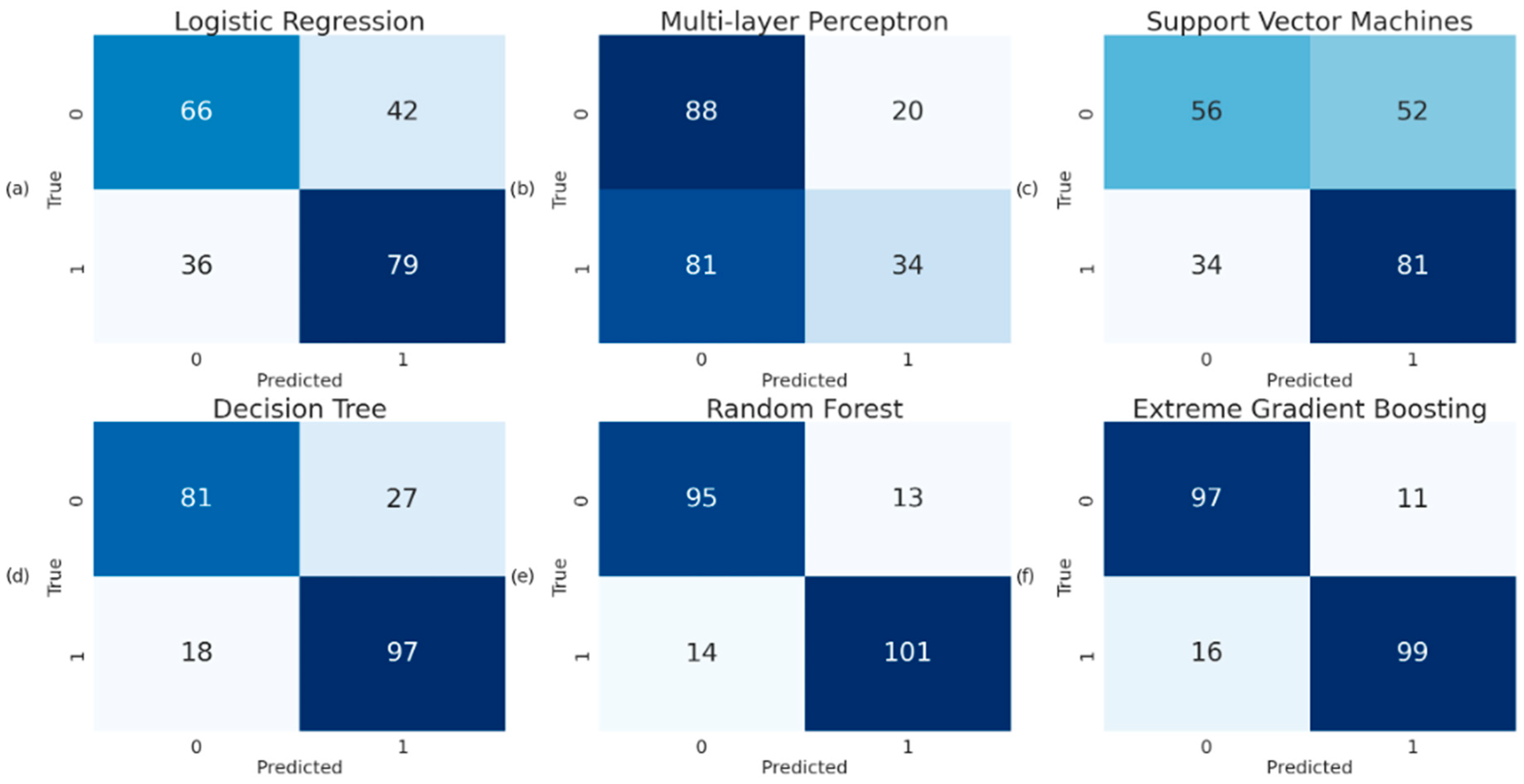
- Following the completion of the data processing pipeline, the refined dataset underwent training across a spectrum of six distinct machine learning algorithms. The selection process was driven by the pursuit of optimal performance as gauged by precision, recall, and F1-score [25] criteria.
- (4)
- Discovering the predictive mechanisms of ML models opens up unexpected findings that can be used to further research directions. By applying game theory to assign credit for the model’s prediction to each feature value based on Shapley Additive exPlanations (SHAP) [26] algorithms, these values can be used to understand the importance of each feature, explain the result of the machine learning model, and represent essential features that can directly affect the natural bandgap. Finally, the investigation reveals that variations in the range neighbor distance hold paramount importance in determining the character of the bandgap, surpassing the influence of other feature values.
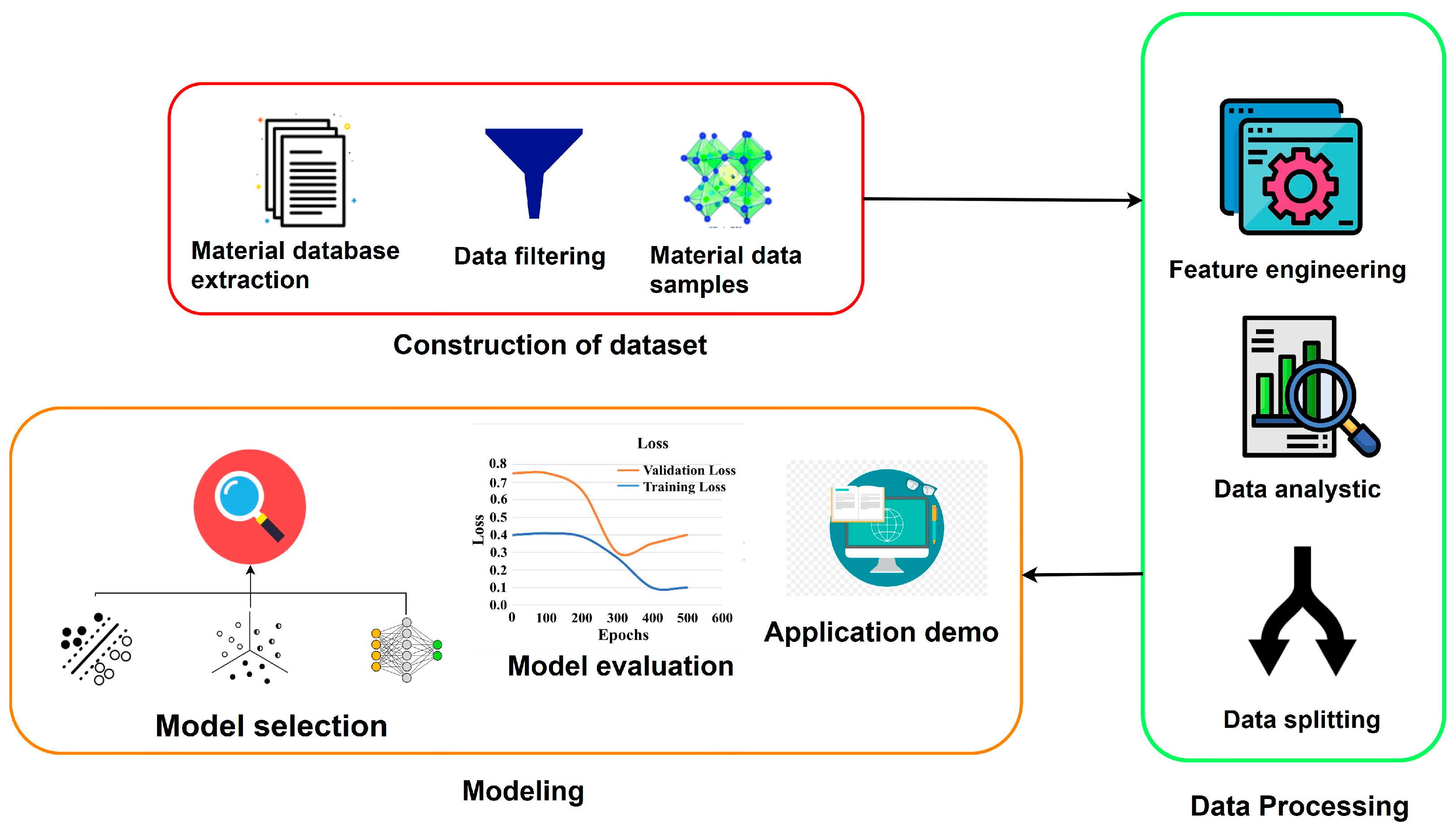
2. Materials and Methods
- Construction of the dataset: This process involves extracting data from an open-source database and filtering it to identify relevant features related to the materials from the raw data.
- Data Processing: This phase is crucial for understanding hidden relationships and identifying important features in the ML algorithms based on numeric information.
- Modeling: This step entails selecting a suitable ML algorithm for the dataset and conducting the final experiments based on the collective results from the previous stages.
2.1. Data Construction
2.2. Data Engineering
2.2.1. Data Augmentation

2.2.2. Feature Engineering
2.3. Machine Learning Algorithms
3. Results
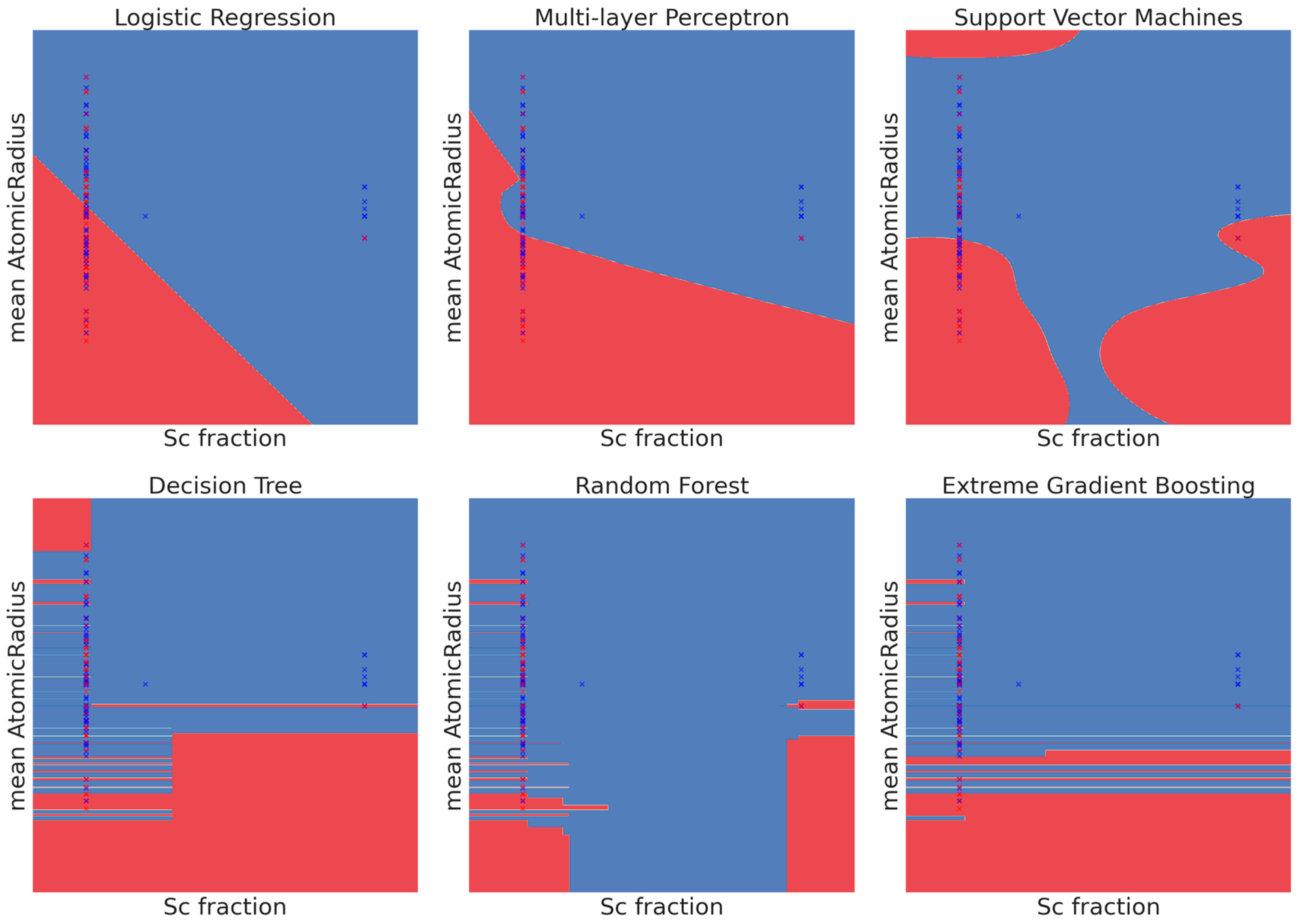
3.1. Model Evaluation
3.2. Discussion
- The minimum neighbor distance variation shows more importance compared to other features, while the Pearson Correlation shows that the most important feature is the mean Atomic Radius. This observation shows that this metric holds significance as it contributes insights into the structural integrity and electronic properties of the perovskite, which are pivotal factors in determining its properties.
- The presence of the Cs, V, Tb, Sc, and Sm factors [40] does not show the importance to the final prediction of the model, which proves that the amount or concentration of ions in the “A” position of perovskite structure does not make a difference to the result of the experiment which is totally opposite to the initial opinion from Pearson Correlation.
- The role of electronic charge density [41] is lower compared to another feature which is known as the pivotal role in understanding various material properties such as the structure of bandgap, mobility, conductivity, and thermal properties.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Roy, P.; Ghosh, A.; Barclay, F.; Khare, A.; Cuce, E. Perovskite Solar Cells: A Review of the Recent Advances. Coatings 2022, 12, 1089. [Google Scholar] [CrossRef]
- Kumar, N.; Rani, J.; Kurchania, R. A review on power conversion efficiency of lead iodide perovskite-based solar cells. Mater. Today Proc. 2020, 46, 5570–5574. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Best Research-Cell Efficiency Chart. 2023. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 27 August 2023).
- Miyata, A.; Mitioglu, A.; Plochocka, P.; Portugall, O.; Wang, J.T.-W.; Stranks, S.D.; Snaith, H.J.; Nicholas, R.J. Direct measurement of the exciton binding energy and effective masses for charge carriers in organic–inorganic tri-halide perovskites. Nat. Phys. 2015, 11, 582–587. [Google Scholar] [CrossRef]
- Romano, V.; Agresti, A.; Verduci, R.; D’angelo, G. Advances in Perovskites for Photovoltaic Applications in Space. ACS Energy Lett. 2022, 7, 2490–2514. [Google Scholar] [CrossRef]
- Singh, R.; Parashar, M.; Sandhu, S.; Yoo, K.; Lee, J.-J. The effects of crystal structure on the photovoltaic performance of perovskite solar cells under ambient indoor illumination. Sol. Energy 2021, 220, 43–50. [Google Scholar] [CrossRef]
- Bera, S.; Saha, A.; Mondal, S.; Biswas, A.; Mallick, S.; Chatterjee, R.; Roy, S. Review of defect engineering in perovskites for photovoltaic application. R. Soc. Chem. 2022, 3, 5234–5247. [Google Scholar] [CrossRef]
- Lekesi, L.; Koao, L.; Motloung, S.; Motaung, T.; Malevu, T. Developments on Perovskite Solar Cells. Appl. Sci. 2022, 12, 672. [Google Scholar] [CrossRef]
- Kurth, S.; Marques, M.A.L.; Gross, E.K.U. Density-Functional Theory. In Encyclopedia of Condensed Matter Physics; Academic Press: Cambridge, MA, USA, 2005; pp. 395–402. [Google Scholar]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into Current Limitations of Density Functional Theory. Science 2020, 321, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Verma, P.; Truhlar, D.G. Status and Challenges of Density Functional Theory. Trends Chem. 2020, 2, 302–318. [Google Scholar]
- Chen, C.; Maqsood, A.; Jacobsson, T.J. The role of machine learning in perovskite solar cell research. J. Alloys Compd. 2023, 960, 170824. [Google Scholar] [CrossRef]
- Yıldırım, C.; Baydoğan, N. Machine learning analysis on critical structural factors of Al:ZnO (AZO) films. Mater. Lett. 2023, 336, 133928. [Google Scholar] [CrossRef]
- Rosen, A.S.; Iyer, S.M.; Ray, D.; Yao, Z.; Aspuru-Guzik, A.; Gagliardi, L.; Notestein, J.M.; Snurr, R.Q. Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery. Matter 2021, 4, 1578–1597. [Google Scholar] [CrossRef]
- Kumar, A.; Upadhyayula, S.; Kodamana, H. A Convolutional Neural Network-based gradient boosting framework for prediction of the band gap of photo-active catalysts. Digit. Chem. Eng. 2023, 8, 100109. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, W.; Han, S.; Zhu, H.; Tu, Y.; Guan, L.; Tan, X. How Machine Learning Predicts and Explains the Performance of Perovskite Solar Cells. Sol. RRL 2022, 6, 2101100. [Google Scholar] [CrossRef]
- Mayr, F.; Harth, M.; Kouroudis, I.; Rinderle, M.; Gagliardi, A. Machine Learning and Optoelectronic Materials Discovery: A Growing Synergy. J. Phys. Chem. Lett. 2022, 13, 1940–1951. [Google Scholar] [CrossRef]
- Jeong, M.; Joung, J.F.; Hwang, J.; Han, M.; Koh, C.W.; Choi, D.H.; Park, S. Deep learning for development of organic optoelectronic devices: Efficient prescreening of hosts and emitters in deep-blue fluorescent OLEDs. npj Comput. Mater. 2022, 8, 147. [Google Scholar] [CrossRef]
- Piprek, J. Simulation-based machine learning for optoelectronic device design: Perspectives, problems, and prospects. Opt. Quantum Electron. 2021, 53, 175. [Google Scholar] [CrossRef]
- Zhang, L.; He, M.; Shao, S. Machine learning for halide perovskite materials. Nano Energy 2020, 78, 105380. [Google Scholar] [CrossRef]
- Cai, X.; Liu, F.; Yu, A.; Qin, J.; Hatamvand, M.; Ahmed, I.; Luo, J.; Zhang, Y.; Zhang, H.; Zhan, Y. Data-driven design of high-performance MASnxPb1-xI3 perovskite materials by machine learning and experimental realization. Light Sci. Appl. 2022, 11, 234. [Google Scholar] [CrossRef]
- Tao, Q.; Xu, P.; Li, M.; Lu, W. Machine learning for perovskite materials design and discovery. npj Comput. Mater. 2021, 7, 23. [Google Scholar] [CrossRef]
- Jianbo, L.; Yuzhong, P.; Lupeng, Z.; Guodong, C.; Li, Z.; Gouqiang, W.; Yanhua, X. Machine-learning-assisted discovery of perovskite materials with high dielectric breakdown. Mater. Adv. 2022, 3, 8639–8646. [Google Scholar]
- Fatourechi, M.; Ward, R.K.; Mason, S.G.; Huggins, J.; Schlögl, A.; Birch, G.E. Comparison of Evaluation Metrics in Classification Applications with Imbalanced Datasets. In Proceedings of the Seventh International Conference on Machine Learning and Applications, San Diego, CA, USA, 11–13 December 2008; pp. 777–782. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, New York, NY, USA, 4–9 December 2017; Volume 30, pp. 4765–4774. [Google Scholar]
- Rath, S.; Priyanga, G.S.; Nagappan, N.; Thomas, T. Discovery of direct band gap perovskites for light harvesting by using machine learning. Comput. Mater. Sci. 2022, 210, 111476. [Google Scholar] [CrossRef]
- Pedregosa, F. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 11, 2825–2830. [Google Scholar]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Hsieh, F.Y.; Bloch, D.A.; Larsen, M.D. A simple method of sample size calculation for linear and logistic regression. Stat. Med. 1998, 17, 1623–1634. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Springer: Boston, MA, USA, 2005; Volume 6, pp. 165–192. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cristianini, N.; Ricci, E. Support Vector Machines. In Encyclopedia of Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 928–932. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Murtagh, F. Multilayer perceptrons for classification and regression. Neurocomputing 1991, 2, 183–197. [Google Scholar] [CrossRef]
- Kohavi, R.; Provost, F. Glossary of terms. Special issue of applications of machine learning and the knowledge discovery process. Mach. Learn. 1998, 30, 271–274. [Google Scholar]
- Gladkikh, V.; Kim, D.Y.; Hajibabaei, A.; Jana, A.; Myung, C.W.; Kim, K.S. Machine Learning for Predicting the Band Gaps of ABX3 Perovskites from Elemental Properties. J. Phys. Chem. C 2020, 124, 8905–8918. [Google Scholar] [CrossRef]
- Chenebuah, E.T.; Nganbe, M.; Tchagang, A.B. Comparative analysis of machine learning approaches on the prediction of the electronic properties of perovskites: A case study of ABX3 and A2BB’X6. Mater. Today Commun. 2021, 27, 102462. [Google Scholar] [CrossRef]
- Oku, T. 23-Crystal structures for flexible photovoltaic application. In Advanced Flexible Ceramics; Elsevier: Amsterdam, The Netherlands, 2023; pp. 493–525. [Google Scholar]
- Le Corre, V.M.; Duijnstee, E.A.; El Tambouli, O.; Ball, J.M.; Snaith, H.J.; Lim, J.; Koster, L.J.A. Revealing Charge Carrier Mobility and Defect Densities in Metal Halide Perovskites via Space-Charge-Limited Current Measurements. ACS Energy Lett. 2021, 6, 1087–1094. [Google Scholar] [CrossRef] [PubMed]



| Name | Data Types | Missing | Uniques | Mean | Standard Deviation |
|---|---|---|---|---|---|
| Nature of bandgap | Int64 | 0 | 2 | 0.270 | 0.444 |
| Max relative bond length | Float64 | 0 | 1368 | 1.095 | 0.041 |
| Min relative bond length | Float64 | 0 | 1369 | 0.806 | 0.069 |
| Frac s valence electrons | Float64 | 0 | 114 | 0.416 | 0.454 |
| Frac p valence electrons | Float64 | 0 | 191 | 0.583 | 0.545 |
| ML Algorithms | Brief Description | Formular |
|---|---|---|
| Linear Regression (LR) [31] | LR is a fundamental machine-learning technique used for classifying data points into distinct categories. This approach seeks to draw a linear decision boundary that effectively separates different classes in the feature space. | where: : input features of data points. : weight of the vectors. : the bias of the function. |
| Decision Tree (DT) [32] | DT is a versatile and intuitive machine-learning algorithm used for both classification and regression tasks. It resembles a flowchart-like structure, where each internal node represents a decision based on a specific feature, and each leaf node represents a predicted outcome. The algorithm works by recursively partitioning the feature space into subsets based on the values of different attributes. At each step, the attribute that best separates the data is chosen, creating a branching structure. | Entropy: Information gain: Gini index: where: S: the dataset calculated using entropy. : the classes in the set, S. : the proportion of data points that belong to class I to the number of total data points in set, S. |
| Random Forest (RF) [33] | RF is a powerful ensemble learning algorithm that leverages the collective wisdom of multiple DTs to enhance prediction accuracy and control overfitting. Each DT in the ensemble is built on a different subset of the data, and its predictions are combined to produce a more robust final prediction. The algorithm introduces randomness at two levels: during data sampling and feature selection. | where: : the total number of decision trees in Random Forest : the class prediction of the dth Random Forest tree. |
| Support Vector Machine (SVM) [34] | SVM is a versatile machine learning algorithm primarily used for classification tasks, although it can be extended to regression as well. SVM aims to find an optimal hyperplane in a high-dimensional space that best separates data points of different classes. This hyperplane maximizes the margin between the two classes, thereby enhancing the algorithm’s generalization capability for new, unseen data. | Linear SVM (Hard Margin): where: : the weight vector perpendicular to the hyperplane : the feature vector of the data point. : the bias term. Linear SVM (Soft Margin): where: : the slack variable associated with the i − th data point Non-Linear SVM (Kernel SVM): where: : the number of support vectors. : Lagrange multipliers assciated with support vectors. : the class labels of support vectors. : the kernel function that computes the similarity between data points |
| Extreme Gradient Boosting (XGBoost) [35] | XGBoost is an advanced and highly optimized machine learning algorithm used for both classification and regression tasks. XGBoost is an enhanced version of gradient boosting that incorporates regularization techniques to improve predictive accuracy while mitigating overfitting. XGBoost employs an ensemble of decision trees, where each new tree is built to correct the errors of the previous ones. | Objective Function: where: : The objective function to minimize L: the loss term that measures the difference between actual target and predict target represent the regularization term, where f_k is the predict of the k − th tree Individual Tree Prediction: where: : is the prediction of the k–th tree for the data point : is the weight assigned to the leaf node that data point Final Prediction: where: : is the final predicted value for the data point xi : total number of values in each tree |
| Multi-layer Perceptron (MLP) [36] | MLP is a foundational type of artificial neural network (ANN) that excels at capturing complex patterns in data. It consists of multiple layers of interconnected nodes (neurons) organized into an input layer, one or more hidden layers, and an output layer. Each neuron in a layer is connected to every neuron in the subsequent layer. MLP leverages activation functions to introduce non-linearity into its computations, enabling it to model intricate relationships in data. | Neuron Activation: where: : the activation of neuron in layer . : the weight connecting neuron I in the layer l − 1 to neuron in layer . : the bias term of neuron in layer : the activation function applied to the weighted sum. Activation Function (Sigmoid): |
| Algorithm | Optimized Hyperparameter |
|---|---|
| Random Forest (RF) | n_estimators: 277, min_samples_split: 5, min_samples_leaf: 1, max_features: ‘sqrt’, max_depth: 28 |
| Precision | Recall | F1-Score | |
|---|---|---|---|
| 0 | 0.85 | 0.85 | 0.85 |
| 1 | 0.86 | 0.86 | 0.86 |
| Accuracy | 0.86 | ||
| Macro avg | 0.86 | 0.86 | 0.86 |
| Weighted avg | 0.86 | 0.86 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-C.-H.; Kim, Y.-U.; Jung, I.; Yang, O.-B.; Akhtar, M.S. Exploring Data Augmentation and Dimension Reduction Opportunities for Predicting the Bandgap of Inorganic Perovskite through Anion Site Optimization. Photonics 2023, 10, 1232. https://doi.org/10.3390/photonics10111232
Nguyen T-C-H, Kim Y-U, Jung I, Yang O-B, Akhtar MS. Exploring Data Augmentation and Dimension Reduction Opportunities for Predicting the Bandgap of Inorganic Perovskite through Anion Site Optimization. Photonics. 2023; 10(11):1232. https://doi.org/10.3390/photonics10111232
Chicago/Turabian StyleNguyen, Tri-Chan-Hung, Young-Un Kim, Insung Jung, O-Bong Yang, and Mohammad Shaheer Akhtar. 2023. "Exploring Data Augmentation and Dimension Reduction Opportunities for Predicting the Bandgap of Inorganic Perovskite through Anion Site Optimization" Photonics 10, no. 11: 1232. https://doi.org/10.3390/photonics10111232
APA StyleNguyen, T.-C.-H., Kim, Y.-U., Jung, I., Yang, O.-B., & Akhtar, M. S. (2023). Exploring Data Augmentation and Dimension Reduction Opportunities for Predicting the Bandgap of Inorganic Perovskite through Anion Site Optimization. Photonics, 10(11), 1232. https://doi.org/10.3390/photonics10111232






