Dynamics Reflects Quantum Phase Transition of Rabi Model

Abstract

As the simplest and most fundamental model describing the interaction between light and matter, a breakdown in the rotating wave approximation of the Rabi model leads to phase transition versus coupling strength when the frequency of the qubit greatly surpasses that of the oscillator. In addition to the phase transition revealed in the ground state, we show that the dynamics of physical quantities can reflect such a phase transition for this model. In addition to the excitation of the bosonic field in the ground state, we show that the witness of inseparability (entanglement), mutual information, quantum Fisher information, and the variance of cavity quadrature can be employed to detect the phase transition in quench. We also reveal the negative impact of temperature on checking the phase transition by quench. This model can be implemented using trapped ions, superconducting artificial atoms coupled bosonic modes, and quantum simulations. By reflecting the phase transition in a fundamental quantum optics model without imposing the thermodynamic limit, this work offers an idea to explore phase transitions by nonequilibrium process for open quantums.

1. Introduction

The interaction between light and matter, as well as between harmonic oscillators and atoms, is pervasive in nature and often associated with quantum phase transitions. Quantum phase transition occurs when a nonthermal parameter scans across a critical point, causing a sudden and significant change in the ground state properties of the system, often accompanied by spontaneous symmetry breaking [1,2]. Such phase transitions can be revealed by various means and have attracted wide attention in quantum information [3,4] and quantum metrology [5,6].

Quantum phase transitions have emerged as a prominent area of research in the field of condensed matter physics. Superradiance is a kind of quantum phase transition that occurs when the coupling strength between the two subsystems exceeds a critical threshold. The exploration of this phenomenon commenced with the Dicke model, a theoretical framework that delves into the collective behavior of a multitude of atoms interacting with a single harmonic oscillator mode of the electromagnetic field. Within this model, the atoms demonstrate quantum-coherent collective behavior, leading to a flurry of captivating dynamics and effects [7]. Namely, the superradiance phase transition is commonly examined under the assumption of the thermodynamic limit, and the interaction between natural atoms and the cavity field is significantly weaker in comparison to the bare atom and cavity frequencies [1]. Recently, significant advancements have been made in superconducting qubit circuits, leading to the achievement of the highly-anticipated strong and ultrastrong coupling regime [8,9,10]. Furthermore, trapped ion quantum simulation presents an opportunity to replicate a similar model by ascribing the oscillatory motion as the harmonic degree of freedom [11]. Given that the artificial atom or ion investigated in these studies plays a role as a two-level system, namely, qubits, the quantum Rabi model (QRM) can showcase behavior that bears resemblance to a superradiance phase transition [12,13,14,15,16,17]. Then, we use quantum phase transition hereafter to represent superradiance phase transition in this work.

In this work, we first show the ground-state quantum phase transition for the Rabi model by several physical quantities, such as the energy-level structure, excitations of the qubit and the cavity field, quantum Fisher information, measures of entanglement (inseparability), mutual information, and variance of the cavity field quadrature. Notably, we explore these quantities without the constraint of a thermodynamic limit, but instead by considering a higher ratio between the eigenfrequency of the qubit and the cavity field. Then, moving beyond this equilibrium by quenching the coupling strength across the critical point of the ground state phase transition, the dynamics of the quantities are examined to indicate the phase. Temperature should be considered for a cavity field interacting with entangled atom pairs in the presence of decoherence [18]. We also check the influence of thermal excitation on the dynamics and propose potential experimental platforms. This comprehensive investigation proposes a method for illuminating the occurrence of phase transition by nonequilibrium processes.

The organization of this study is as follows: In Section 2, we present the Rabi model with a significant disparity in eigenfrequencies between the qubit and cavity field. In Section 3, we show the phase diagram concerning various quantities versus the coupling strength and the eigenfrequency with constraint. In Section 4, we check the behavior of these quantities during a quench to observe and characterize the phase transition. In Section 5, we explore the impact of environmental temperature on the dynamics. In Section 6, we propose potential experimental platforms to realize this work. Finally, we conclude our work in Section 7.

2. The Model

The quantum Rabi model [19,20] with a single-mode bosonic field (such as a cavity mode) coupled to a two-level atom (generic qubit), as depicted in Figure 1, is described by the Hamiltonian ($\hslash =1$ hereafter):

$$\begin{array}{c}\hfill \widehat{H}={\omega }_c{\widehat{a}}^{†}\widehat{a}+\frac{{\omega }_q}{2}{\widehat{\sigma }}_z+g(\widehat{a}+{\widehat{a}}^{†})({\widehat{\sigma }}_{-}+{\widehat{\sigma }}_{+}),\end{array}$$

(1)

where ${\widehat{a}}^{†}$($\widehat{a})$ is the creation (annihilation) operator for the single mode cavity field with frequency ${\omega }_c$, and ${\widehat{\sigma }}_z$ is the Pauli z-basis operator with commutation relation $[{\widehat{\sigma }}_{+},{\widehat{\sigma }}_{-}]={\widehat{\sigma }}_z$. The parameter g represents the coupling strength between the two subsystems. In the case of trapped ion systems, the phase-transition-poisonous vector potential item can be neglected safely [11,12,13].

In the regime of weak coupling ($g\ll {\omega }_c,{\omega }_q$), one can simplify the quantum Rabi model by applying the rotating wave approximation, resulting in the Jaynes–Cummings model [21,22,23], which has been investigated widely in cavity QED system [24]. In scenarios where the coupling strength reaches or exceeds the magnitude of the frequencies of the cavity mode and qubit, the rotating wave approximation becomes invalid. This breakdown paves the way for the emergence of the strong, ultrastrong, and even deep-strong coupling regime, facilitating connections between manifolds characterized by different total excitations [11]. Many exotic physical properties have been investigated in plenty of strong coupling quantum systems such as trapped ions [11,12,13], circuit QED [10,25,26,27,28], and photonic systems [29].

Quantum phase transition is a focus of research usually considered in the thermodynamic limit since this limit leads to the nonanalytic behavior of the free energy or partition function. However, it was recently realized that a quantum phase transition can also occur in a small system with only a two-level atom coupled to a bosonic mode, described by the quantum Rabi model [16]. Due to the smaller ratio of the frequencies $\frac{{\omega }_c}{{\omega }_q}$ in the model, the more obvious of the superradiance phase transition versus the coupling strength, we focus on the situation with ${\omega }_c{\omega }_q=1$ in the Hamiltonian (1).

3. The Phase Diagram

The critical coupling strength for the quantum phase transition of the Hamiltonian (1) is determined to be

$$g_c=\frac{\sqrt{{\omega }_c{\omega }_q}}{2}.$$

(2)

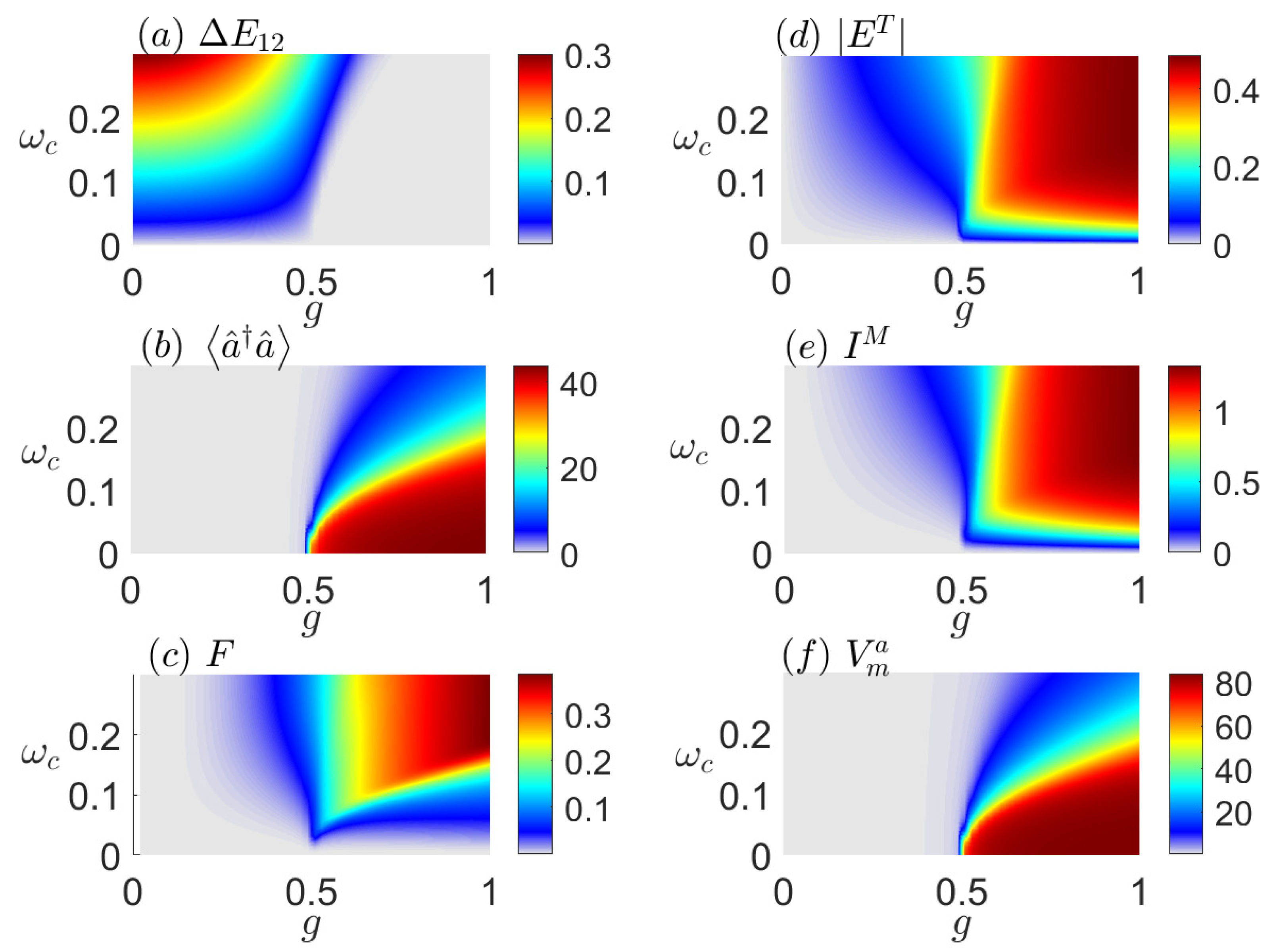
To characterize the quantum phase transition of this model, we examine the behavior of several quantities in the ground state. In addition to the excitations in the cavity traditionally, we check the energy gap between the ground state and the first excited state, the quantum Fisher information (QFI), the partial transposed criteria for entanglement, the mutual information, and the fluctuation of the quadrature of the cavity field. These diverse physical quantities serve as indicators for observing and analyzing the phase transition within the scope of this work.

As ${\omega }_c\to 0$ under the condition ${\omega }_c{\omega }_q=1$, the quantities in the ground state tend to be nonanalytical at the critical point, as shown in Figure 2, which supports a second-order phase transition at zero temperature. As an example, the excitation in the cavity field plays the role as the order parameter being zero in the normal phase while acquiring positive values in the superradiance phase, as shown in Figure 2b.

QFI is a fundamental concept in quantum metrology that stems from the classical Fisher information [30]. It plays a crucial role in quantifying the sensitivity of a quantum state used in parameter estimation, encompassing the critical factors of quantum superposition and entanglement. To improve the precision of parameter estimation in the semiclassical Rabi model, there are works that generalize the approximation expression for maximal QFI in a two-level system [31]. The symmetric aspect of the the rotating-wave and counterrotating-wave terms are discussed in the Rabi model [32]. QFI have been investigated for the atom in Jaynes–Cummings model coupling with the ohmic reservoir [33]. These works show that QFI has been investigated from various aspects in order to benefit parameter estimation. Higher QFI indicates enhanced sensitivity of the quantum system to fluctuations in the measured parameter. We focus on evaluating the QFI pertaining to the state of the cavity field ${\widehat{\rho }}_c$ with respect to ${\widehat{\rho }}_c\left(\theta \right)=e^{i\theta \widehat{G}}{\widehat{\rho }}_c{e}^{-i\theta \widehat{G}}$, where $\theta$ is the parameter that needs to be estimated as accurately as possible with respect to the phase-shift generator $\widehat{G}$, which depends on the target in certain investigation [34,35,36]. The QFI reads

$$F=4\sum _n{p}_n{(\Delta \widehat{G})}_n^2-\sum _{m\ne n}\frac{8p_m{p}_n}{p_m+p_n}|\langle {\psi }_m|\widehat{G}|{\psi }_n{\rangle |}^2,$$

(3)

where ${\widehat{\rho }}_c|{\psi }_n\rangle$=$p_n|{\psi }_n\rangle$. The first term of Equation (3) is an expectation for each pure state $|{\psi }_n\rangle$ with ${(\Delta \widehat{G})}_n^2\equiv \langle {\psi }_n|{\widehat{G}}^2|{\psi }_n\rangle -|\langle {\psi }_n|\widehat{G}|{\psi }_n{\rangle |}^2$. The second term denotes the negative correction. Here, the QFI provides a quantitative measure for the precision attainable in estimating the parameter $\theta$ in experiments conducted on the quantum state. While states with larger QFI are, indeed, valuable for a single-mode linear interferometer and can be treated as a kind of variance, we move beyond their practical utility and view QFI as a witness for the phase transition in this work. When $\frac{{\omega }_c}{{\omega }_q}$ is sufficiently small and ${\omega }_c{\omega }_q=1$, the critical coupling strength equals 0.5. As shown in Figure 2c, the behavior of QFI versus the coupling strength g and ${\omega }_c$ coincides with the phase diagram reflected by the energy gap between the ground state and the first excited state, and that by $\langle {\widehat{a}}^{†}\widehat{a}\rangle$, as shown in Figure 2a,b, respectively. The eigenenergy degeneracy coincides with a spontaneous breaking of the $Z_2$ parity symmetry which provides a fundamental view for this phase transition.

The partial transposed criterion provides a methodology for measuring entanglement in bipartite quantum systems [37,38]. It involves checking the eigenvalues of the partially transposed density matrix of the hybrid system. The presence of negative eigenvalues of the partially transposed density matrix indicates the presence of entanglement. To capture this phenomenon and serve as a witness for the phase transition in this work, we employ the absolute value of the summation of the negative eigenvalues ${\lambda }_i$ of the partially transposed density matrix to witness the phase transition $|E^T|={\sum }_{{\lambda }_i<0}|{\lambda }_i|$ in this work. As shown in Figure 2d, the phase diagram indicated by $|E^T|$ coincides with those indexed by the energy gap between the ground state and the first excited state, $\langle {\widehat{a}}^{†}\widehat{a}\rangle$, and the QFI. However, it is crucial to acknowledge that the partial transposed criterion can only serve as a sufficient condition for entanglement, since there exist entangled states that maintain a positive-definite nature after undergoing partial transposition [37,38]. This means that the superradiance phase offers the source of entangled states which is useful in the quantum information processing.

Mutual information (von Neumann mutual information) is another quantity demonstrating correlation between the subsystems. It characterizes the information of subsystem ‘A’ by exploring its counterpart ‘B’ [3,39,40]. It is defined as $I^M=S_A+S_B-S_{AB}$, where $S_{A\left(B\right)}$ is the entropy for the $A\left(B\right)$ system and $S_{AB}$ is that for the hybrid bipartite system [41]. The entropy can be calculated as $S\left(t\right)=-Tr\left[\rho \right(t\left)log\right(\rho \left(t\right)\left)\right]$, where $Tr[•]$ denotes the trace of •. Although its definition is distinct from the entanglement witness $|E^T|$ mentioned above, its behavior is quite similar in indicating the phase transition in this work, as shown in Figure 2d,e. Entanglement and mutual information provide a quantum resource in the quantum information processing. This inspires us to seek a quantum source in other quantum phase transitions.

In general, it is believed that there is a relationship between phase transitions and fluctuations in physical systems [1,2]. To accurately capture the phase transitions in the strong and ultrastrong coupling regime by using quadrature measurements, it is crucial to define positive and negative frequency cavity–photon operators as ${\widehat{X}}^{+}={\sum }_{j,k>j}{X}_{jk}|j\rangle \langle k|$ and ${\widehat{X}}^{-}={({\widehat{X}}^{+})}^{†}$, with $X_{jk}\equiv \langle j|{\widehat{a}}^{†}+\widehat{a}|k\rangle$, in the dressed eigenbasis $|j\rangle$, $|k\rangle$ of the Hamiltonian (1) with eigenvalues ${\omega }_j$ and ${\omega }_k$, respectively [42,43]. This step is essential for excluding unphysical streams of output photons in experiments. In the limit of weak coupling, these operators coincide with $\widehat{a}$ and ${\widehat{a}}^{†}$, respectively, and the similar operators can be defined for ${\widehat{\sigma }}_{-}$ and ${\widehat{\sigma }}_{+}$ [42,43]. Using the defined operators above, we can assess the minimum variance of the quadrature of the cavity field defined as $\widehat{X}\left(\theta \right)=\frac{{\widehat{X}}^{-}{e}^{i\theta }+{\widehat{X}}^{+}{e}^{-i\theta }}{\sqrt{2}}$, with $\theta \in [0,2\pi )$. The minimum variance reads $V_m^a=\langle {\widehat{X}}^2\left({\theta }_m\right)\rangle -{\langle \widehat{X}\left({\theta }_m\right)\rangle }^2$ versus ${\theta }_m$. The landscape of $V_m^a$ versus g and ${\omega }_c$ coincides with those of the quantities used above by comparing Figure 2f to the other panels in Figure 2. The behaviors of all these quantities approaching the critical point indicate that the smaller the $\frac{{\omega }_c}{{\omega }_q}$ is, the more obvious the phase transition is. Exploring these quantities not only provides additional avenues for studying phase transitions in experiments, but also allows us to understand the essence of phase transitions from multiple perspectives.

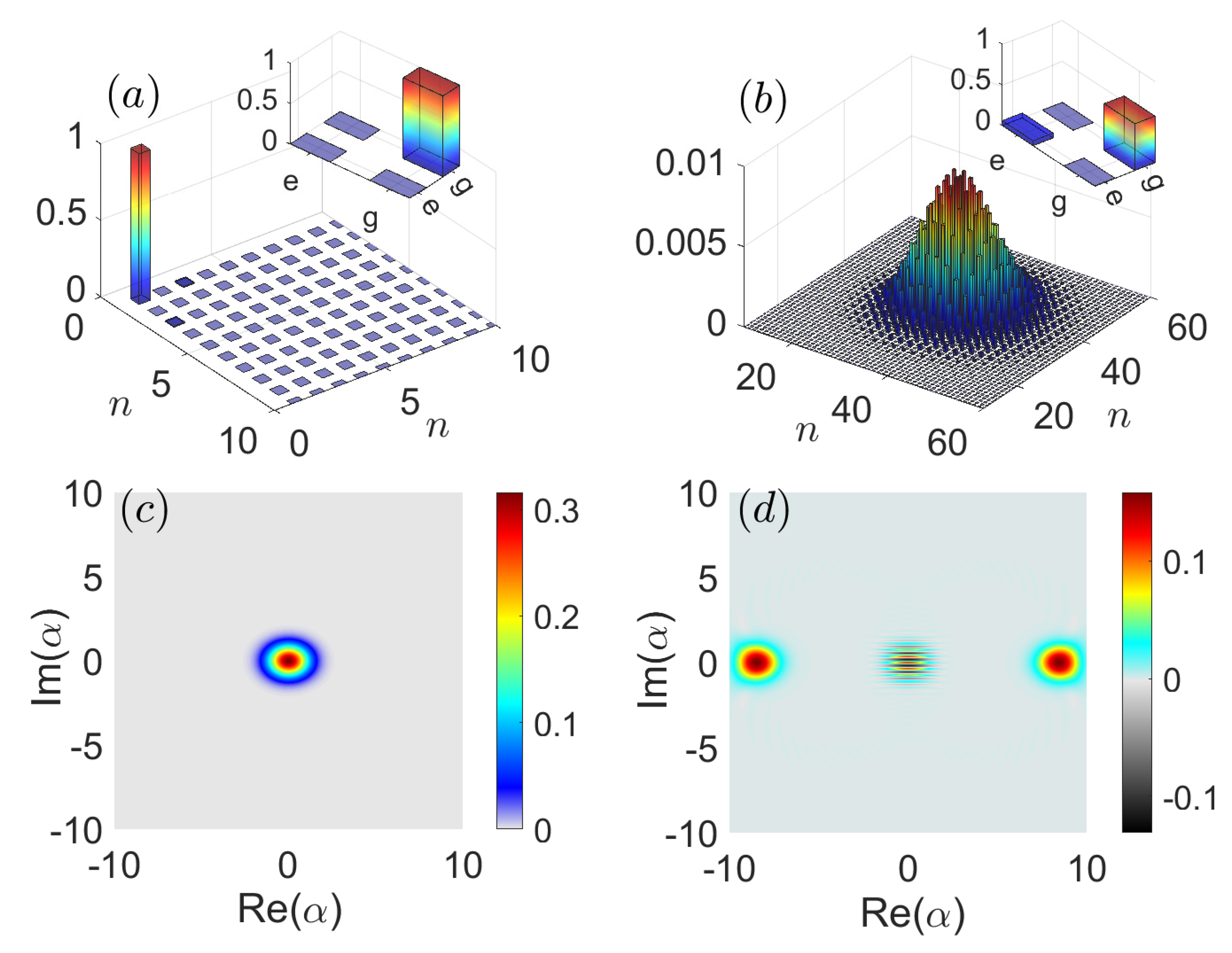
To gain insight into the phase transition, we examine the density matrices of the atom, cavity field, and the Wigner function of the cavity mode in the ground states in different phase regions. It can be seen in Figure 3, in the normal phase, that there is no excitation in both the cavity and the atom (qubit). The Wigner function is that of the vacuum state with Gaussian distribution, as shown in Figure 3c. However, upon entering the strong coupling regime, a distinctive feature emerges in the Wigner function. Negative texture between the two peaks indicates a Schrödinger cat state as shown in Figure 3d, a nonclassical resource which can be used in the quantum information processing [44]. For the condition ${\omega }_c/{\omega }_q=0.1$, one excitation of qubit is equivalent to ten excitations of the cavity field. This leads to the low level of the excitation of the qubit in the superradiance phase, as shown in the inset of Figure 3b.

4. Dynamics Reflect Phase Transition

In this work, we put forward a conjecture that the dynamics of the quantities (including the above quantities) can reveal the quantum phase transition. To verify this idea, we check the dynamics of the quantities in terms of whether the coupling strength quenches across the critical point or not.

Before we check the dynamics in quench, we know that complete isolation of a quantum system from its environment remains a formidable challenge. For the open quantum system, we resort to numerical calculations by solving the master equation under the inherent damping effects of both the cavity field and qubit. However, we implement the finite size of a 50-photon Hilbert space, which imposes certain limits on the accuracy of our numerical calculations.

In the strong and ultrastrong coupling regimes, to exclude unphysical counting of photons, an effective approach for describing the system involves solving the master equations in the eigenbasis of the Hamiltonian (1). In this case, the master equation reads

$$\dot{\rho }\left(t\right)=i[\rho \left(t\right),\widehat{H}]+{\mathcal{L}}_{\widehat{a}}\rho \left(t\right)+{\mathcal{L}}_{{\widehat{\sigma }}^{-}}\rho \left(t\right),$$

(4)

where ${\mathcal{L}}_{\widehat{a}}$ and ${\mathcal{L}}_{{\widehat{\sigma }}^{-}}$ are Liouvillian superoperators describing the decoherence of the cavity field and qubit [45]. They read ${\mathcal{L}}_{\widehat{x}}\rho \left(t\right)={\sum }_{j,k>j}{\mathrm{\Gamma }}_{\widehat{x}}^{jk}\overline{n}({\Delta }_{kj},T)\mathcal{D}\left[\right|k\rangle \langle j\left|\right]\rho \left(t\right)+{\sum }_{j,k>j}{\mathrm{\Gamma }}_{\widehat{x}}^{jk}(1+\overline{n}({\Delta }_{kj},T))\mathcal{D}\left[\right|j\rangle \langle k\left|\right]\rho \left(t\right)$ for $\widehat{x}=\widehat{a},{\widehat{\sigma }}^{-}$ with $\mathcal{D}\left[\mathcal{O}\right]\rho \left(t\right)$ = $\frac{1}{2}(2\mathcal{O}\rho \left(t\right){\mathcal{O}}^{†}-\rho \left(t\right){\mathcal{O}}^{†}\mathcal{O}-{\mathcal{O}}^{†}\mathcal{O}\rho \left(t\right))$. The relaxation coefficients ${\mathrm{\Gamma }}_{\widehat{x}}^{jk}=2\pi d\left({\Delta }_{kj}\right){\alpha }_{\widehat{x}}^2\left({\Delta }_{kj}\right){\left|C_{jk}^{\widehat{x}}\right|}^2$ with $d\left({\Delta }_{kj}\right)$ being the spectral density of the baths, ${\alpha }_{\widehat{x}}\left({\Delta }_{kj}\right)$ denoting the system–bath coupling strength, ${\Delta }_{kj}={\omega }_k-{\omega }_j$, and $C_{jk}^{\widehat{x}}=-i\langle j|(\widehat{x}-{\widehat{x}}^{†})|k\rangle$. $\overline{n}({\Delta }_{kj},T)={[exp({\Delta }_{kj}/T)-1]}^{-1}$ is the mean number of quanta in a mode with frequency ${\Delta }_{kj}$ and temperature T (Boltzmann constant $k_B$=1). When considering a cavity coupling to the momentum quadrature of a field in one-dimension waveguides, the spectral density $d\left({\Delta }_{kj}\right)$ is constant and ${\alpha }_{\widehat{x}}^2\left({\Delta }_{kj}\right)\propto {\Delta }_{kj}$. Then, the relaxation coefficients reduce to ${\mathrm{\Gamma }}_{\widehat{x}}^{jk}={\gamma }_c({\Delta }_{kj}/{\omega }_0){\left|C_{jk}^{\widehat{x}}\right|}^2$, where ${\gamma }_c$ is the standard damping rate. These assumptions can be realized in circuit-QED [46] or a trapped ion system [11,12,13]. The influence of dephasing and Lamb shifts in current experiments can be deemed negligible as they do not exert significant influence [11,12,13].

Dynamics in Quench

The concept of dynamical quantum phase transition has emerged from the analogy between an equilibrium partition function and the return probability in many-body unitary dynamics [47]. This expansion of criticality to nonstationary scenarios involves sudden changes in the macroscopic properties of quantum systems over time. Dynamical phase transition in quantum systems is usually investigated by quench [47,48,49]. However, quench is not limited to investigating dynamical quantum phase transition. The behavior of physical quantities in quench can be used to reveal other intriguing physics. In this work, we check the behaviors of the physical quantities mentioned above in quench to examine whether they can be used to reveal the quantum phase transition. The return rate is usually employed in exploring dynamical phase transition $f\left(t\right)=-\frac{1}{N}lnG\left(t\right)$ [47,48,49]. This quantity behaves nonanalytically versus time when the Loschmidt overlap $G\left(t\right)$ vanishes. Here, the Loschmidt overlap $G\left(t\right)$ is defined as $G\left(t\right)=|\langle {\psi }_{g_0;0}|e^{-i{H}^{\prime }t}|{\psi }_{g_0;0}\rangle |$. $|{\psi }_{g_0;0}\rangle$ denotes the initial state with coupling strength $g_0$ in the Hamiltonian. This quantity measures the overlap between the time-evolved state $e^{-i{H}^{\prime }t}|{\psi }_{g_0;0}\rangle$ and the initial state $|{\psi }_{g_0;0}\rangle$ following a sudden change of the parameter g in the post-quench Hamiltonian, namely, $H\left(g_0\right)\underrightarrow{quench}H\left(g^{\prime }\right)$ in this work. 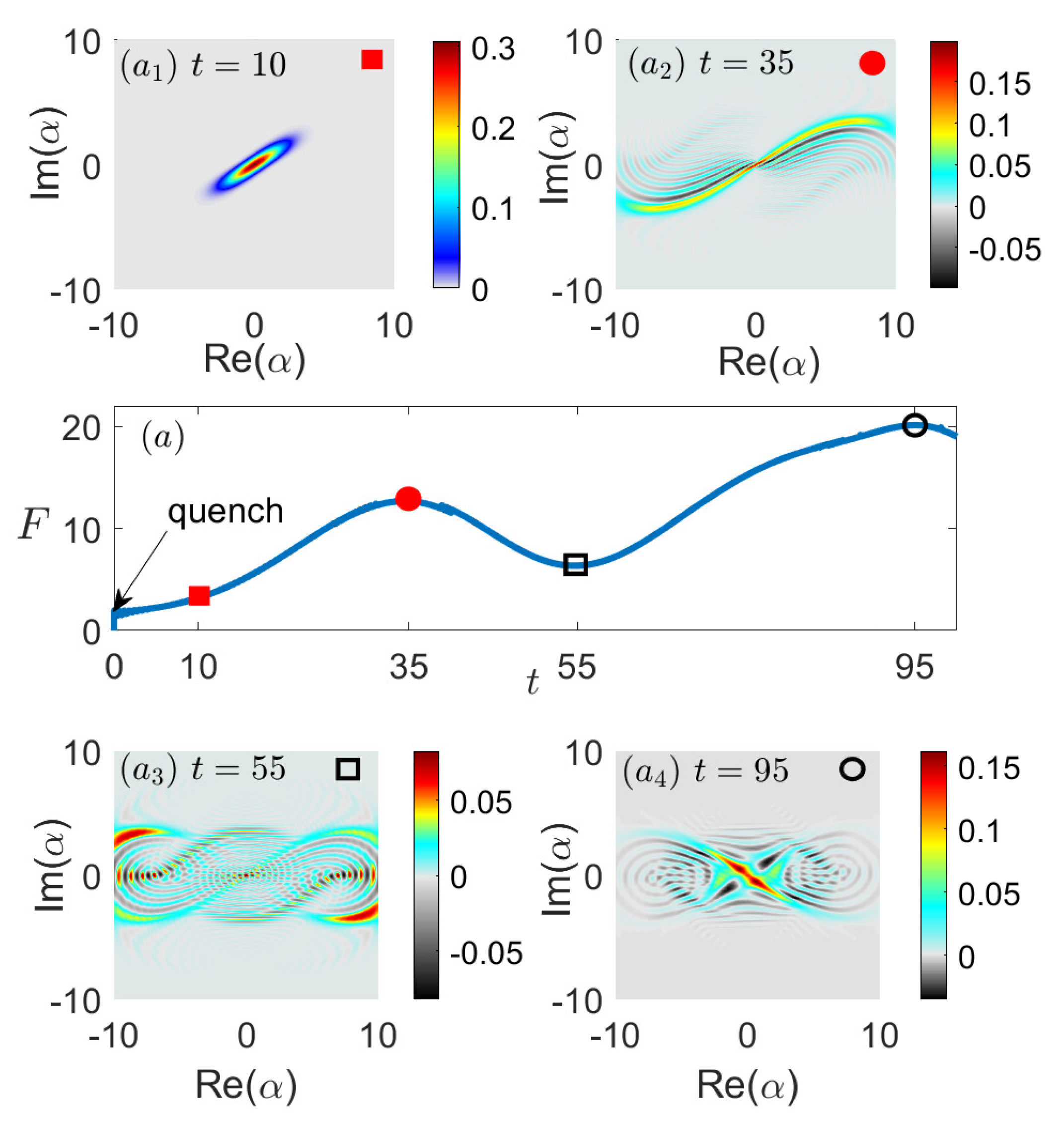To employ this quantity reflecting the phase transition, we check the behavior of $f\left(t\right)$, as shown in Figure 4a, when the coupling strength changes suddenly from $g_0$ to $g^{\prime }=g_0+0.3$. It can be seen that the cusps appear when the coupling strength quenches across the critical point, namely, $g_0\in [0.2,0.5]$.

Figure 4b–f show the dynamics of $\langle {\widehat{X}}^{-}{\widehat{X}}^{+}\rangle$, QFI, entanglement witness $|E^T|$, mutual information $I^M$, and the minimum variance $V_m^a$ versus the initial coupling strength $g_0$ in the quench $H\left(g_0\right)\underrightarrow{quench}H(g_0+0.3)$. In this manner of quench, there are three parameter regions, namely, $g_0<0.2$; $g_0\in [0.2,0.5]$; $g_0>0.5$, with distinct dynamical characters. It depends on whether the coupling strength g quenches across the critical point, namely, $g_c=0.5$, or not for all these quantities. It is interesting to note that the behavior of $\langle {\widehat{X}}^{-}{\widehat{X}}^{+}\rangle$ and $V_m^a$ are similar when $g_0<g_c$. $|E^T|$ and $I^M$ behave similarly versus $g_0$, although their formalisms are different, obviously. This hints at a resemblance between these quantities. These characters of dynamics provide avenues to check such a phase transition in experiments by observing the dynamics of physical quantities, and this suggests a dynamical manner to obtain quantum resources.

To gain insight into the dynamics of the states during the quench, we check examples of the Wigner function for states when $g_0=0.35$ changes to $g^{\prime }=0.65$ abruptly in Figure 5 at zero temperature. Negative scars in the Wigner function indicate the states being nonclassical starting from the vacuum. Such nonclassical states prefer redundancy encoding in quantum information [44].

5. Influence of Temperature

In the results above, a zero-temperature environment is assumed; however, the temperature is, indeed, a factor which should be considered when cavity interacts with atoms [18]. It is necessary to examine the influence of temperature on the dynamics. In Figure 6, we plot the dynamics of the quantities mentioned in Section 4 above versus the temperature. It is clear to see that with increase of the temperature T, the characteristic bends in $f\left(t\right)$, $\langle {\widehat{X}}^{-}{\widehat{X}}^{+}\rangle$, QFI, and variance $V_m^a$, and correlations reflected by $|E^T|$ and $I^M$ during evolution tend to disappear and become gentle for these quantities. According to the master Equation (4), higher temperature leads to more intense incoherent dissipation. These are the negative factors for quantum resource and the application of these quantities as the indicator for the phase transition. This means that low temperatures benefit in revealing the phase transition by the dynamics.

6. Potential Experimental Systems

In this work, we consider the phase transition of the Rabi model with the coupling strength varying across weak and strong regimes and reveal the phase transition by the dynamics of several quantities. There are different quantum platforms to check these results. For instance, within a single trapped ion system, it is feasible to adjust the coupling strength between the atom and the boson mode to achieve the Rabi model. This provides an opportunity to investigate the phase transitions and the dynamics in the ultrastrong and deep-strong coupling regimes, overcoming the limitations of the rotating-wave approximation [11,12]. The entanglement and correlation between the boson mode and the two-level system can be detected in such models. A similar phase transition can be illustrated by employing a ${}^{171}$Yb+ion within a Paul trap through the adiabatic adjustment of the coupling strength between the ion and its spatial mode, without any thermodynamic constraints [13]. In addition to trapped ion systems, the strong coupling regime can also be achieved in circuit quantum electrodynamics setups, where superconducting artificial atoms are coupled to on-chip cavities [10] or coupled to the electromagnetic continuum of a one-dimensional waveguide [26]. These systems offer the tunability that expands the capabilities of quantum optics, enabling exciting investigations into ultrastrong interactions between light and matter. Yet, the quantum Rabi model in the ultrastrong coupling regime can be realized by a superconducting circuit embedded in a cavity QED setup [25]. Through the coupling of a flux qubit and an LC oscillator using Josephson junctions, it is possible to realize the circuits Rabi model with a wide range of coupling strengths [27]. This enables the exploration of the ground-state phase transition and entanglement mentioned in our work. Quantum simulation offers various avenues to realize the Rabi model in diverse systems. One proposal is using a circuit quantum electrodynamics chip with moderate coupling between a resonator and transmon qubit to achieve precise digital quantum simulation of deep-strong coupling dynamics [28]. This proposal will enable the exploration of extreme coupling regimes and quantum phase transitions, as mentioned in our work. A practical implementation of a photonic analog simulator for the quantum Rabi model was achieved using femtosecond laser-written waveguide superlattices. This advancement offers a tangible experimental platform for investigating the intricate physics of light–matter interaction in the deep-strong coupling regime [29]. In these potential platforms, tuning the coupling quickly is necessary to realize quench. In order to make the characteristics of dynamics reflecting the quantum phase transition more pronounced, the temperature should be depressed in the experiments.

7. Conclusions

In addition to traditional indicators such as oscillator occupation and qubit excitation, we first showed that the quantum Fisher information, qubit–oscillator entanglement, mutual information, and the variance of the cavity field quadrature displayed minimal values below the transition point. However, when the coupling strength was tuned across the quantum critical point, these quantities underwent swift and substantial growth. This transition was attributed to the degeneracy between the ground state and the first excited state. The physical quantities displayed singular behavior when the ratio of the frequencies of the oscillator and the qubit approached zero. This behavior is analogous to approaching closer to a thermodynamic limit in superradiant phase transition. The nonclassical Schrödinger cat state was revealed by the Wigner function in the superradiant phase. Then, we examined the dynamics of the Rabi model to investigate the probability of indicating the quantum phase transition by dynamics. The quantities used to witness the phase transition in the ground state all behaved differently depending on whether it quenched across the critical point. It offers avenues to reveal the phase transition by quantities in the nonequilibrium process. It was shown that temperature is poisonous to applying this quench method result from the incoherent process. There are platforms that can be considered to realize our work, for example, the trapped ion system, circuit quantum electrodynamics setups like superconducting artificial atoms coupled boson modes, quantum simulation using circuit quantum electrodynamics chip, or femtosecond laser-written waveguide superlattices. These systems allow researchers to vary the experimental parameters and study their influence on the phase transition.