Nonreciprocal Propagation of Nematicons
Abstract
:1. Introduction
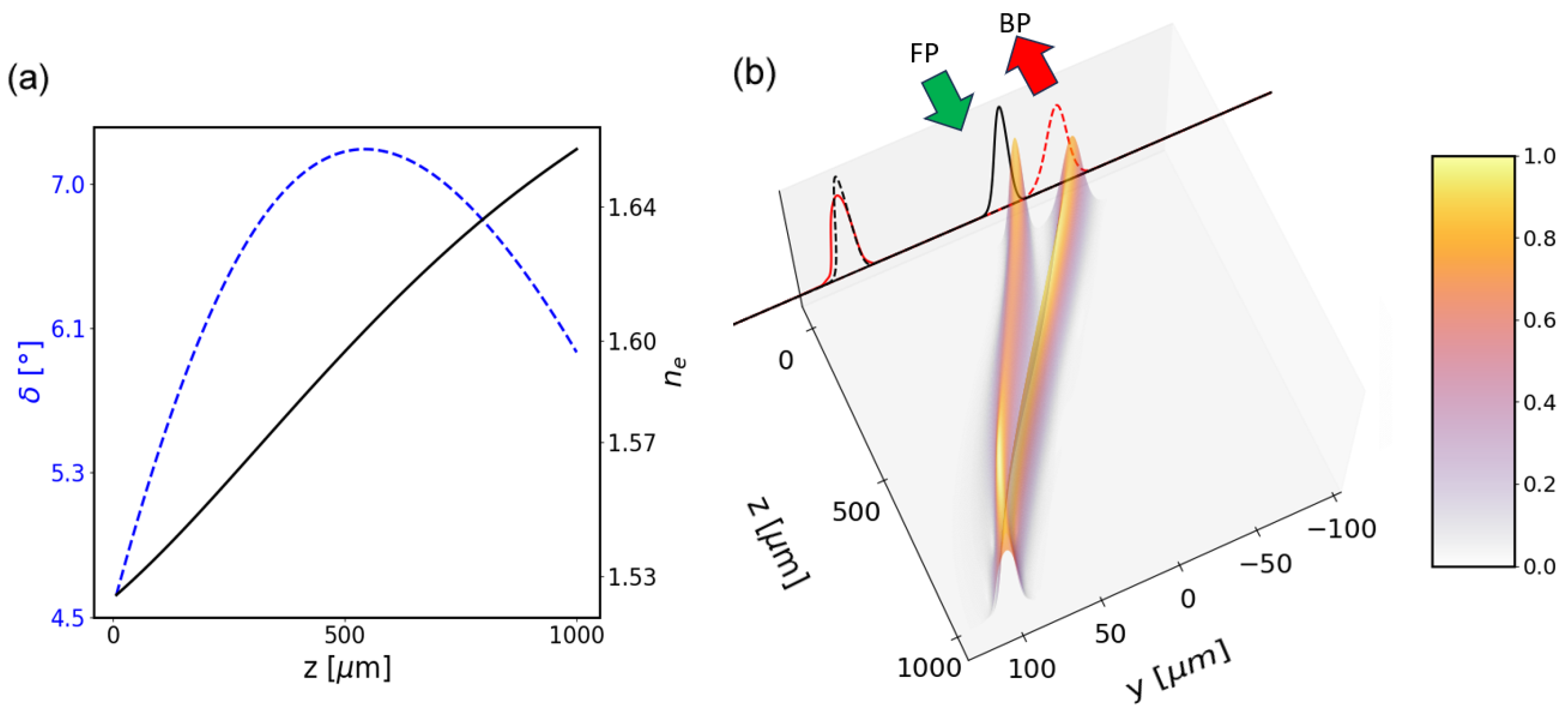
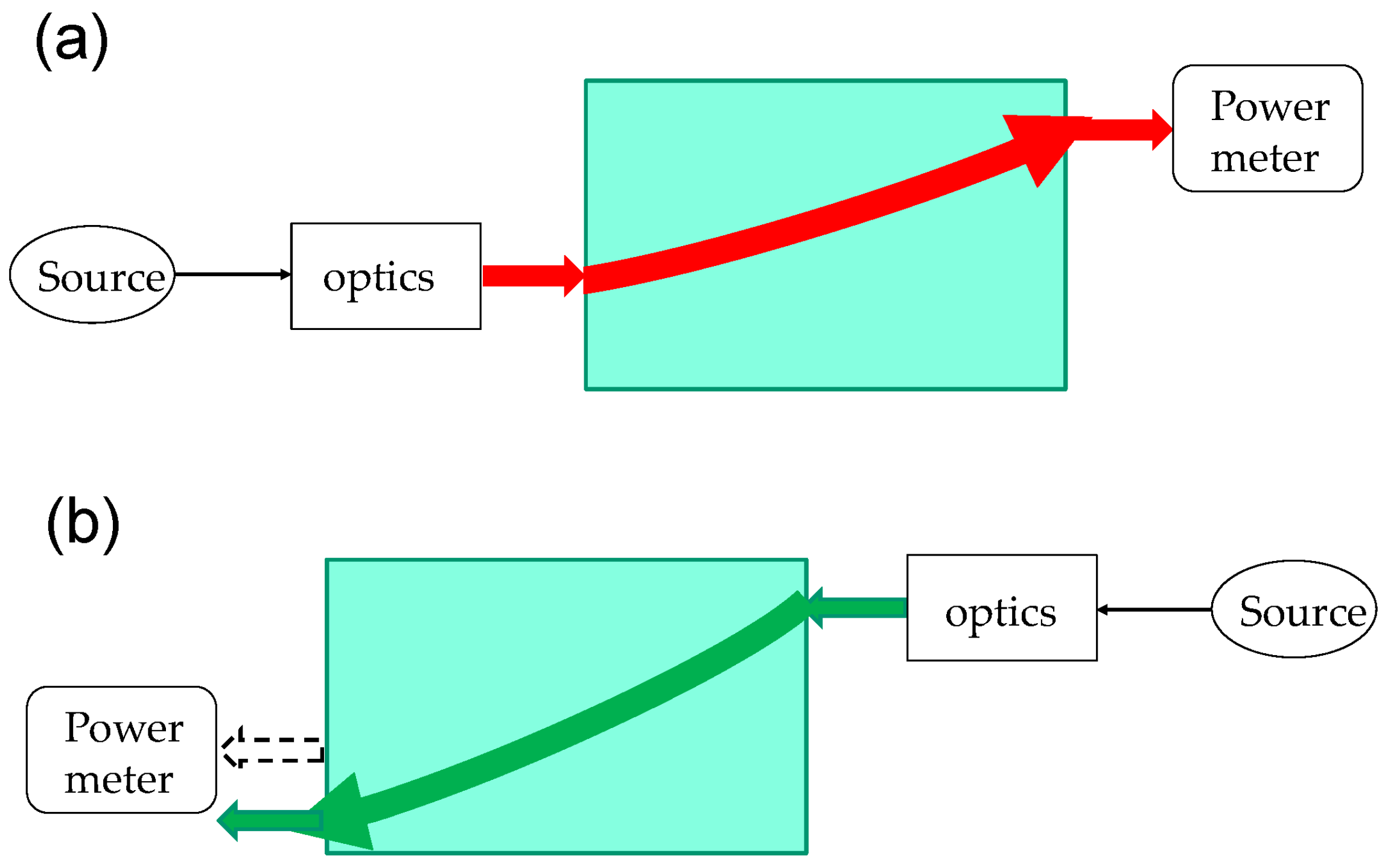
2. Model
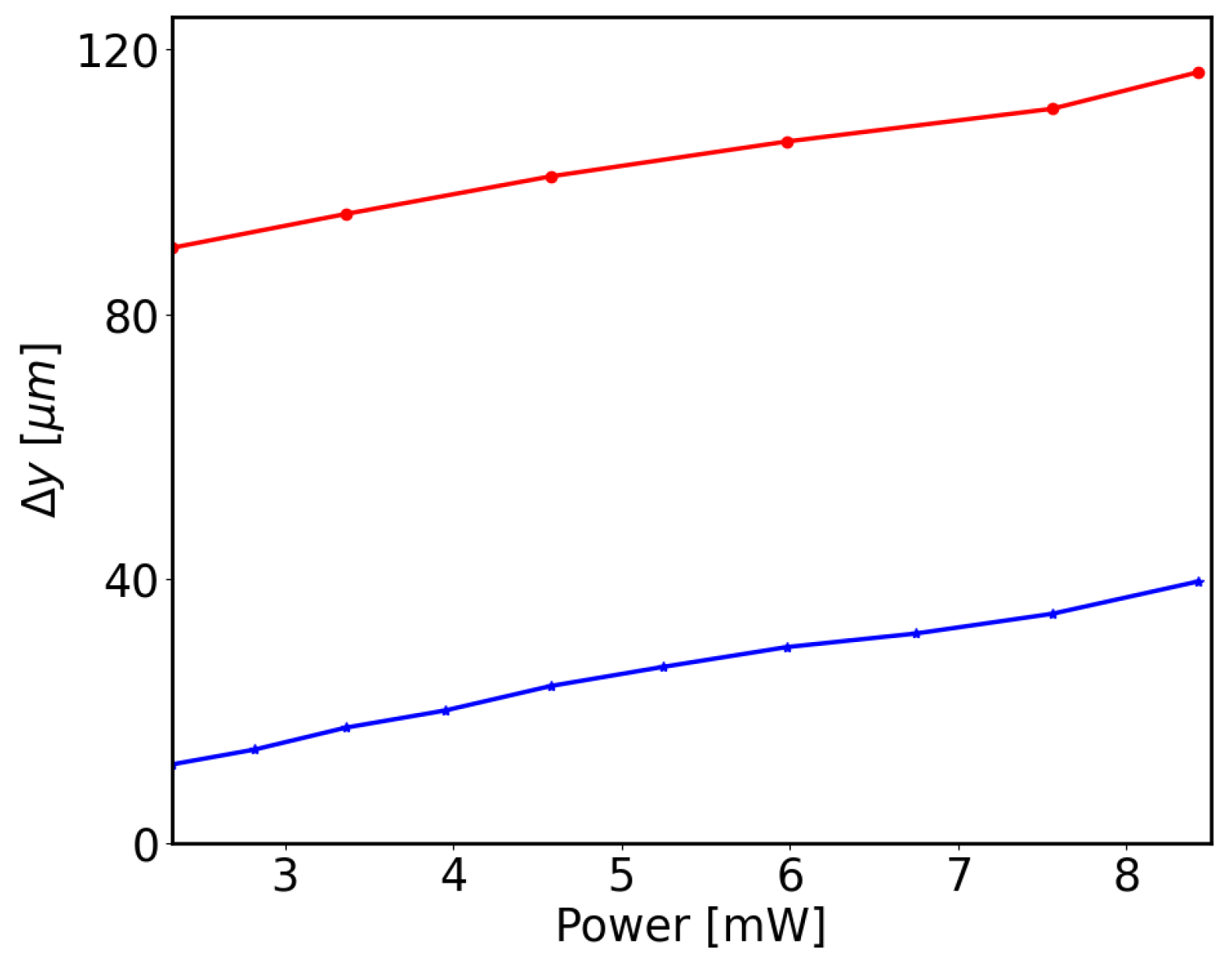
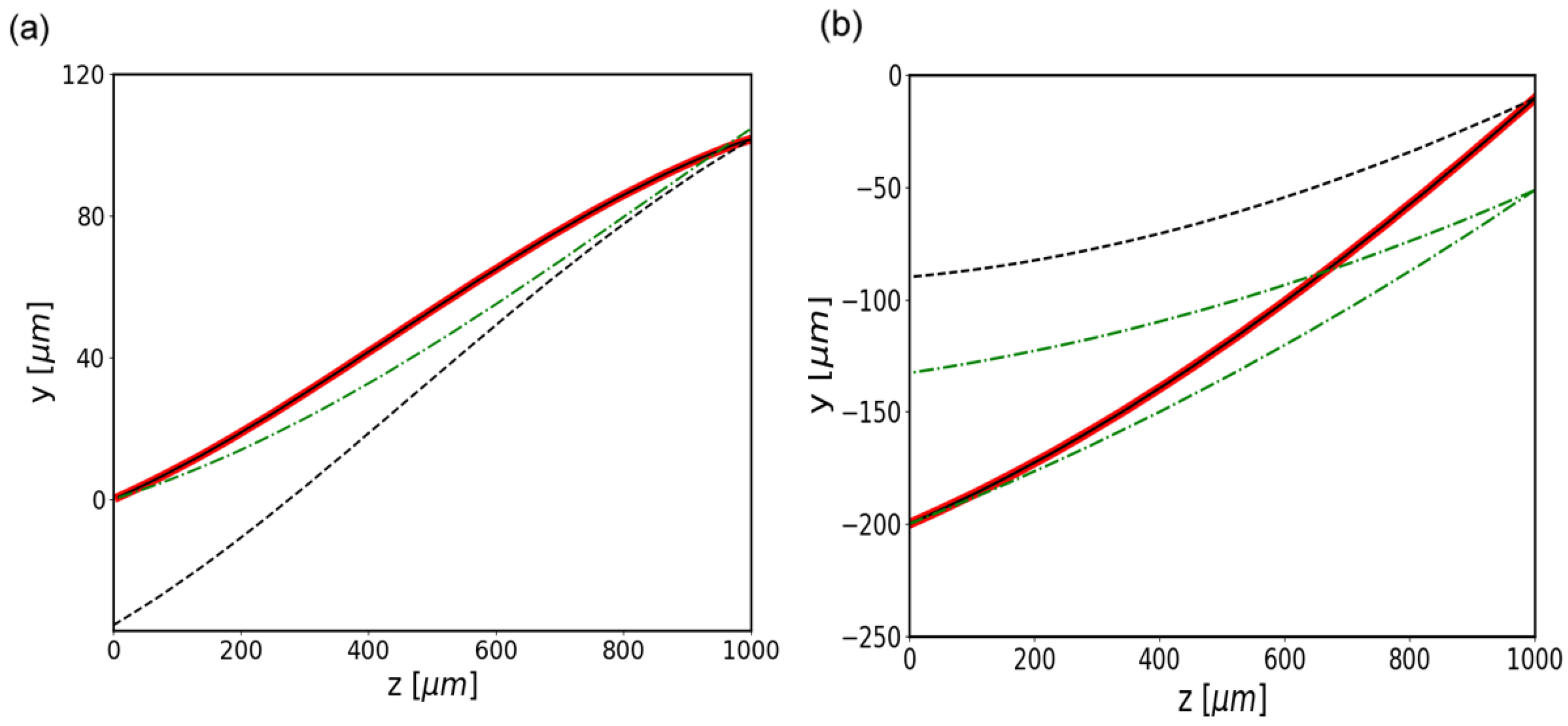
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popović, M.; Melloni, A.; Joannopoulos, J.D.; et al. What is—And what is not—An optical isolator. Nat. Photon. 2013, 7, 579–582. [Google Scholar] [CrossRef]
- Trillo, S.; Wabnitz, S. Nonlinear nonreciprocity in a coherent mismatched directional coupler. Appl. Phys. Lett. 1986, 49, 752. [Google Scholar] [CrossRef]
- Ferro, P.; Trillo, S.; Wabnitz, S. Demonstration of nonlinear nonreciprocity and logic operations with a twisted birefringent optical fiber. Opt. Lett. 1994, 19, 263–265. [Google Scholar] [CrossRef] [PubMed]
- Treviño-Palacios, C.G.; Stegeman, G.I.; Baldi, P. Spatial nonreciprocity in waveguide second-order processes. Opt. Lett. 1996, 21, 1442–1444. [Google Scholar] [CrossRef]
- Gallo, K.; Assanto, G. All-optical diode based on second-harmonic generation in an asymmetric waveguide. J. Opt. Soc. Am. B 1999, 16, 267–269. [Google Scholar] [CrossRef]
- Gallo, K.; Assanto, G.; Parameswaran, K.R.; Fejer, M.M. All-optical diode in a periodically-poled Lithium Niobate waveguide. Appl. Phys. Lett. 2001, 79, 314–316. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, K.F.; Hu, W.; Guo, Q.; Lan, S.; Lin, X.S.; Venu Gopal, A. All-optical diodes based on photonic crystal molecules consisting of nonlinear defect pairs. J. Appl. Phys. 2006, 99, 123111. [Google Scholar] [CrossRef]
- Lin, X.S.; Wu, W.Q.; Zhou, H.; Zhou, K.F.; Lan, S. Enhancement of unidirectional transmission through the coupling of nonlinear photonic crystal defects. Opt. Express 2006, 14, 2429–2439. [Google Scholar] [CrossRef]
- Alexander, D.; Bruce, J.; Zuhlke, C.; Koch, B.; Rudebusch, R.; Deogun, J.; Hamza, H. Demonstration of a nanoparticle-based optical diode. Opt. Lett. 2006, 31, 1957–1959. [Google Scholar] [CrossRef]
- Yu, Z.F.; Wang, Z.; Fan, S.H. One-way total reflection with one-dimensional magneto-optical photonic crystals. Appl. Phys. Lett. 2007, 90, 121133. [Google Scholar] [CrossRef]
- Amemiya, T.; Shimizu, H.; Yokoyama, M.; Hai, P.N.; Tanaka, M.; Nakano, Y. 1.54 μm TM-mode waveguide optical isolator based on the nonreciprocal-loss phenomenon: Device design to reduce insertion loss. Appl. Opt. 2007, 46, 5784–5791. [Google Scholar] [CrossRef] [PubMed]
- Kono, N.; Kakihara, K.; Saitoh, K.; Koshiba, M. Nonreciprocal microresonators for the miniaturization of optical waveguide isolators. Opt. Express 2007, 15, 7737–7751. [Google Scholar] [CrossRef]
- Yazaki, Y.; Shoji, Y.; Mizumoto, T. Demonstration of interferometric waveguide optical isolator with a unidirectional magnetic field. Jpn. J. Appl. Phys. 2007, 46, 5460–5464. [Google Scholar] [CrossRef]
- Lin, X.-S.; Yan, J.-H.; Wu, L.-J.; Lan, S. High transmission contrast for single resonator based all-optical diodes with pump-assisting. Opt. Express 2008, 16, 20949–20954. [Google Scholar] [CrossRef] [PubMed]
- Alberucci, A.; Assanto, G. All-optical isolation by directional coupling. Opt. Lett. 2008, 36, 1641–1643. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photon. 2009, 3, 91–94. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Brasselet, E.; Kivshar, Y.S. Reversible optical nonreciprocity in periodic structures with liquid crystals. Appl. Phys. Lett. 2010, 96, 063302. [Google Scholar] [CrossRef]
- Zhukovsky, S.V.; Smirnov, A.G. All-optical diode action in asymmetric nonlinear photonic multilayers with perfect transmission resonances. Phys. Rev. A 2011, 83, 023818. [Google Scholar] [CrossRef]
- Lira, H.; Yu, Z.; Fan, S.; Lipson, M. Electrically driven nonreciprocity induced by interband photonic transition on a silicon chip. Phys. Rev. Lett. 2012, 109, 033901. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Varghese, L.T.; Wang, J.; Xuan, Y.; Weiner, A.M.; Qi, M. Silicon optical diode with 40 dB nonreciprocal transmission. Opt. Lett. 2013, 38, 1259–1261. [Google Scholar] [CrossRef]
- Wang, D.W.; Zhou, H.T.; Guo, M.J.; Zhang, J.X.; Evers, J.; Zhu, S.Y. Optical diode made from a moving photonic crystal. Phys. Rev. Lett. 2013, 110, 093901. [Google Scholar] [CrossRef] [PubMed]
- Anand, B.; Podila, R.; Lingam, K.; Krishnan, S.R.; Siva Sankara Sai, S.; Philip, R.; Rao, A.M. Optical diode action from axially asymmetric nonlinearity in an all-carbon solid-state device. Nano. Lett. 2013, 13, 5771–5776. [Google Scholar] [CrossRef] [PubMed]
- Sounas, D.L.; Alu, A. Angular-momentum-biased nanorings to realize magnetic-free integrated optical isolation. ACS Photon. 2014, 1, 198–204. [Google Scholar] [CrossRef]
- Sounas, D.L.; Alu, A. Non-reciprocal photonics based on time modulation. Nat. Photon. 2017, 11, 774–783. [Google Scholar] [CrossRef]
- Sounas, D.L.; Soric, J.; Alu, A. Broadband passive isolators based on coupled nonlinear resonances. Nat. Electron. 2018, 1, 113–119. [Google Scholar] [CrossRef]
- Kittlaus, E.A.; Jones, W.M.; Rakich, P.T. Otterstrom, N.T.; Muller, R.E.; Rais-Zadeh, M. Electrically driven acousto-optics and broadband non-reciprocity in silicon photonics. Nat. Photon. 2020, 15, 43–52. [Google Scholar] [CrossRef]
- Yu, M.; Cheng, R.; Reimer, C.; He, L.; Luke, K.; Puma, E.; Shao, L.; Shams-Ansari, A.; Ren, X.; Grant, H.R.; et al. Integrated electro-optic isolator on thin-film lithium niobate. Nat. Photon. 2023, 17, 666–671. [Google Scholar] [CrossRef]
- Lepri, S.; Casati, G. Asymmetric wave propagation in nonlinear systems. Phys. Rev. Lett. 2011, 106, 164101. [Google Scholar] [CrossRef] [PubMed]
- Calisto, E.; Smyth, N.F.; Assanto, G. Optical isolation via direction-dependent soliton routing in birefringent soft-matter. Opt. Lett. 2022, 47, 459564. [Google Scholar] [CrossRef]
- Peccianti, M.; Assanto, G. Nematicons. Phys. Rep. 2012, 516, 147–208. [Google Scholar] [CrossRef]
- Assanto, G. Nematicons: Reorientational solitons from optics to photonics. Liq. Cryst. Rev. 2018, 6, 170–194. [Google Scholar] [CrossRef]
- Assanto, G.; Smyth, N.F. Self-confined light waves in nematic liquid crystals. Phys. D 2020, 402, 132182. [Google Scholar] [CrossRef]
- Peccianti, M.; Fratalocchi, A.; Assanto, G. Transverse dynamics of Nematicons. Opt. Express 2004, 12, 6524–6529. [Google Scholar] [CrossRef] [PubMed]
- Khoo, I.C. Nonlinear optics of liquid crystalline materials. Phys. Rep. 2009, 471, 221–267. [Google Scholar] [CrossRef]
- Conti, C.; Peccianti, M.; Assanto, G. Route to nonlocality and observation of accessible solitons. Phys. Rev. Lett. 2003, 91, 073901. [Google Scholar] [CrossRef] [PubMed]
- Conti, C.; Peccianti, M.; Assanto, G. Observation of optical spatial solitons in a highly nonlocal medium. Phys. Rev. Lett. 2004, 92, 113902. [Google Scholar] [CrossRef]
- Alberucci, A.; Assanto, G. Nematicons beyond the perturbative regime. Opt. Lett. 2010, 35, 2520–2522. [Google Scholar] [CrossRef]
- MacNeil, J.M.L.; Smyth, N.F.; Assanto, G. Exact and approximate solutions for optical solitary waves in nematic liquid crystals. Phys. D 2014, 284, 1–15. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Assanto, G. Soliton self deflection via power-dependent walk-off. Appl. Phys. Lett. 2010, 96, 061105. [Google Scholar] [CrossRef]
- Oswald, P.; Pieranski, P. Nematic and Cholesteric Liquid Crystals, 1st ed.; Taylor and Francis: Oxfordshire, UK, 2005. [Google Scholar]
- Laudyn, U.; Kwasny, M.; Sala, F.; Karpierz, M.; Smyth, N.F.; Assanto, G. Curved solitons subject to transverse acceleration in reorientational soft matter. Sci. Rep. 2017, 7, 12385. [Google Scholar] [CrossRef] [PubMed]
- Alberucci, A.; Piccardi, A.; Peccianti, M.; Kaczmarek, M.; Assanto, G. Propagation of spatial optical solitons in a dielectric with adjustable nonlinearity. Phys. Rev. A 2010, 82, 023806. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, Z.; Fan, S. Limitations of nonlinear optical isolators due to dynamic reciprocity. Nat. Photon. 2015, 9, 388–392. [Google Scholar] [CrossRef]
- Potton, R.J. Reciprocity in optics. Rep. Progr. Phys. 2004, 67, 717–754. [Google Scholar] [CrossRef]
- De Hoop, A.T. Reciprocity of the electromagnetic field. Appl. Sci. Res. 1959, 8, 135. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Available online: https://www.alumni.caltech.edu/in-memoriam/noel-frederick-smyth (accessed on 19 March 2023).




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calisto, E.; Assanto, G. Nonreciprocal Propagation of Nematicons. Photonics 2023, 10, 1144. https://doi.org/10.3390/photonics10101144
Calisto E, Assanto G. Nonreciprocal Propagation of Nematicons. Photonics. 2023; 10(10):1144. https://doi.org/10.3390/photonics10101144
Chicago/Turabian StyleCalisto, Enrique, and Gaetano Assanto. 2023. "Nonreciprocal Propagation of Nematicons" Photonics 10, no. 10: 1144. https://doi.org/10.3390/photonics10101144
APA StyleCalisto, E., & Assanto, G. (2023). Nonreciprocal Propagation of Nematicons. Photonics, 10(10), 1144. https://doi.org/10.3390/photonics10101144





