Microwave Photonic Filters and Applications
Abstract
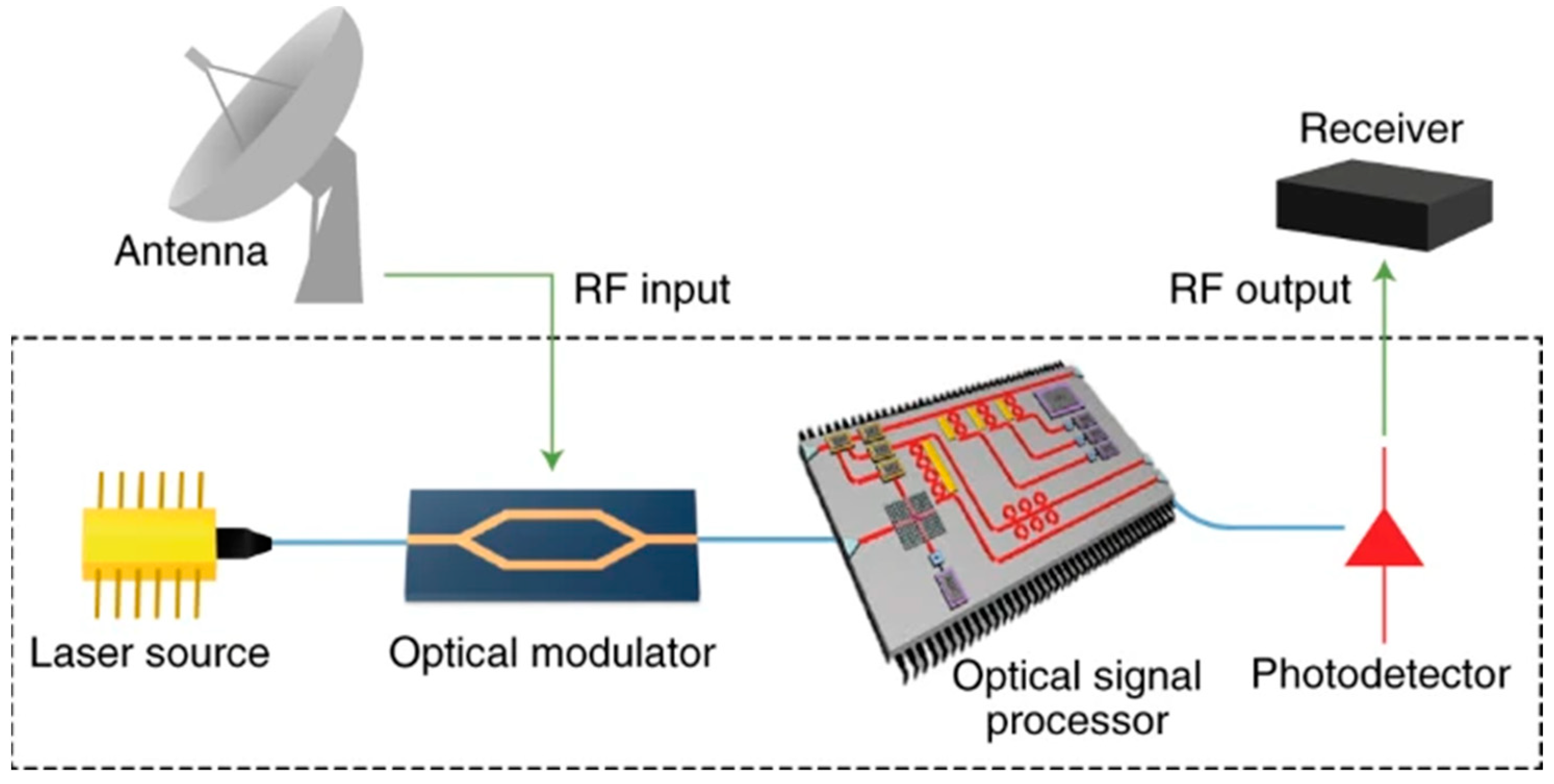
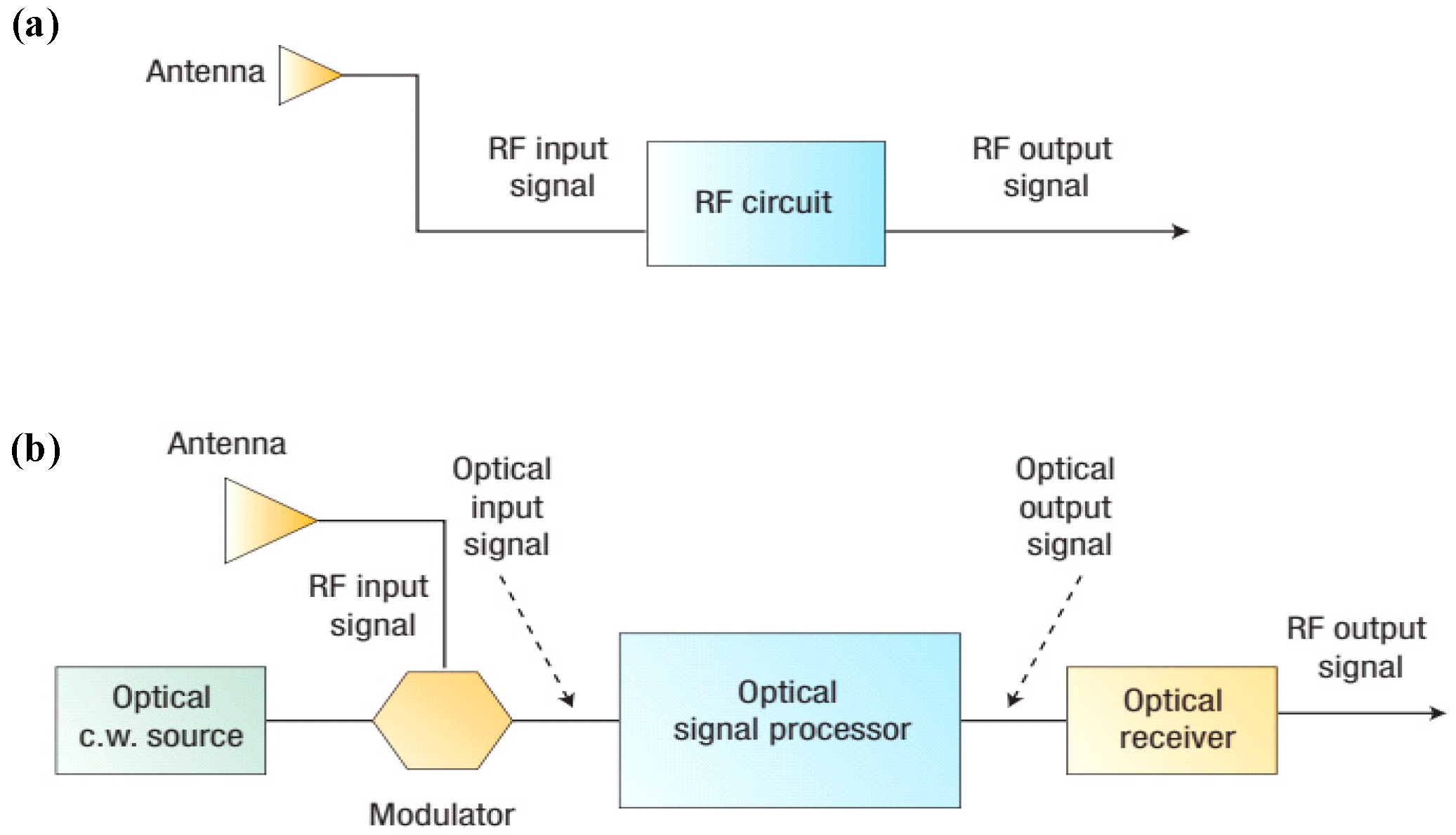
:1. Introduction
2. Fundamental Concepts
2.1. Parameters of the MPF
- (1)
- Free spectral range
- (2)
- Full width at half maximum bandwidth
- (3)
- Quality factor
- (4)
- Rejection ratio
- (5)
- Shape factor
- (6)
- Tunability and reconfigurability
2.2. Classifications of the MPF
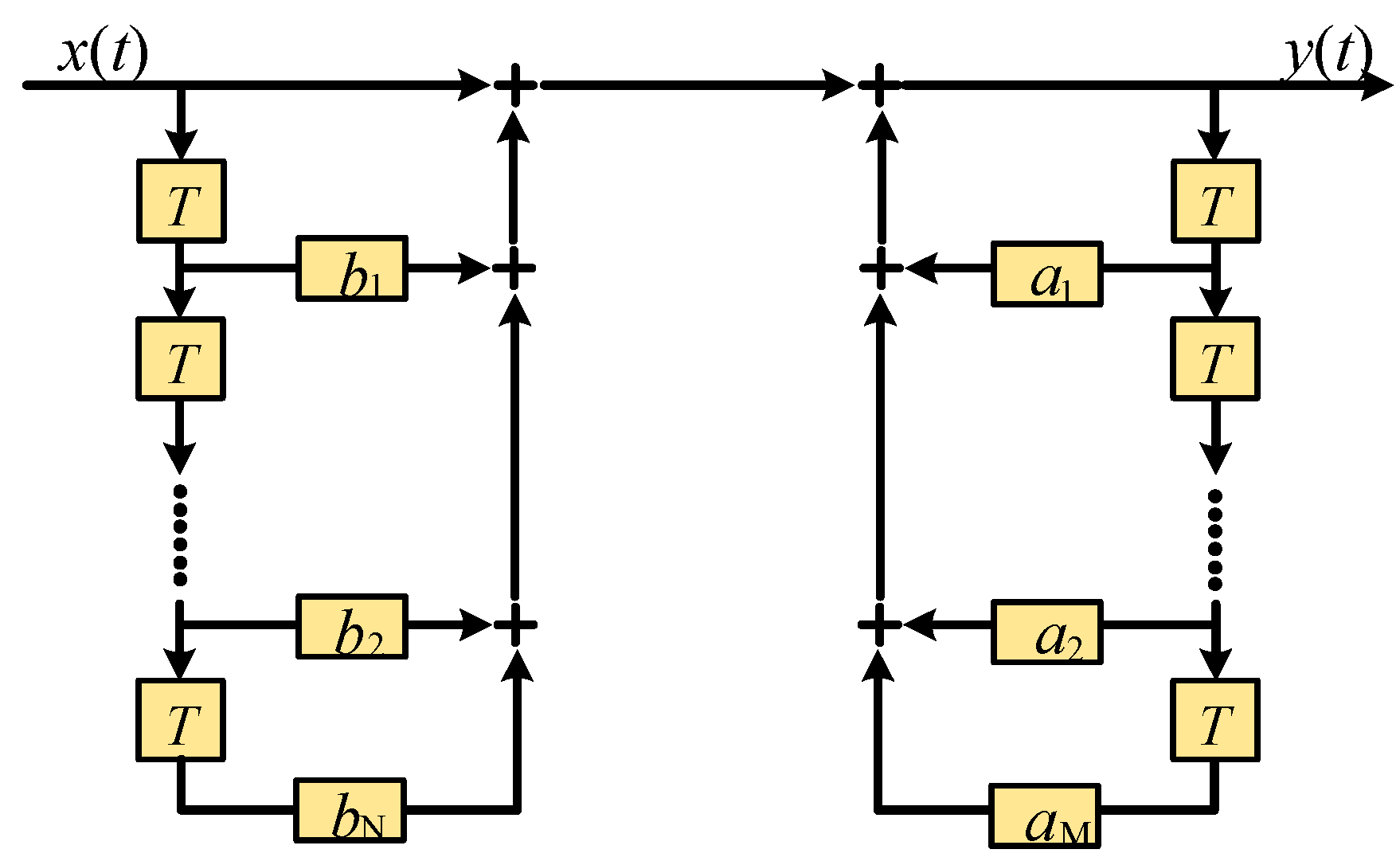
2.2.1. FIR- and IIR-MPFs
2.2.2. Positive, Negative and Complex Coefficient MPF
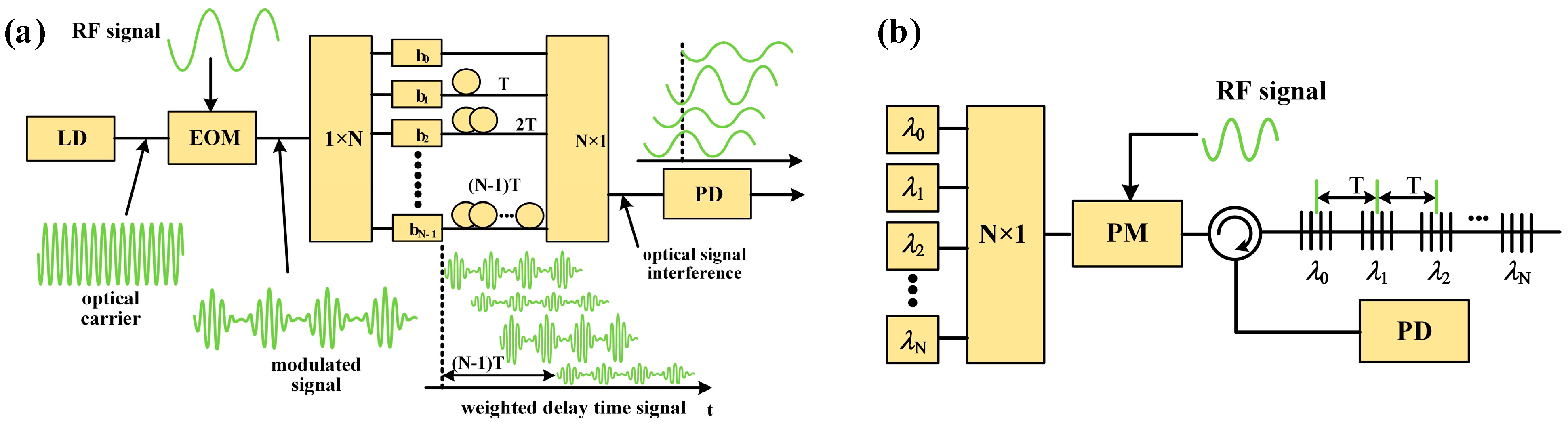
2.2.3. Coherent and Incoherent MPFs
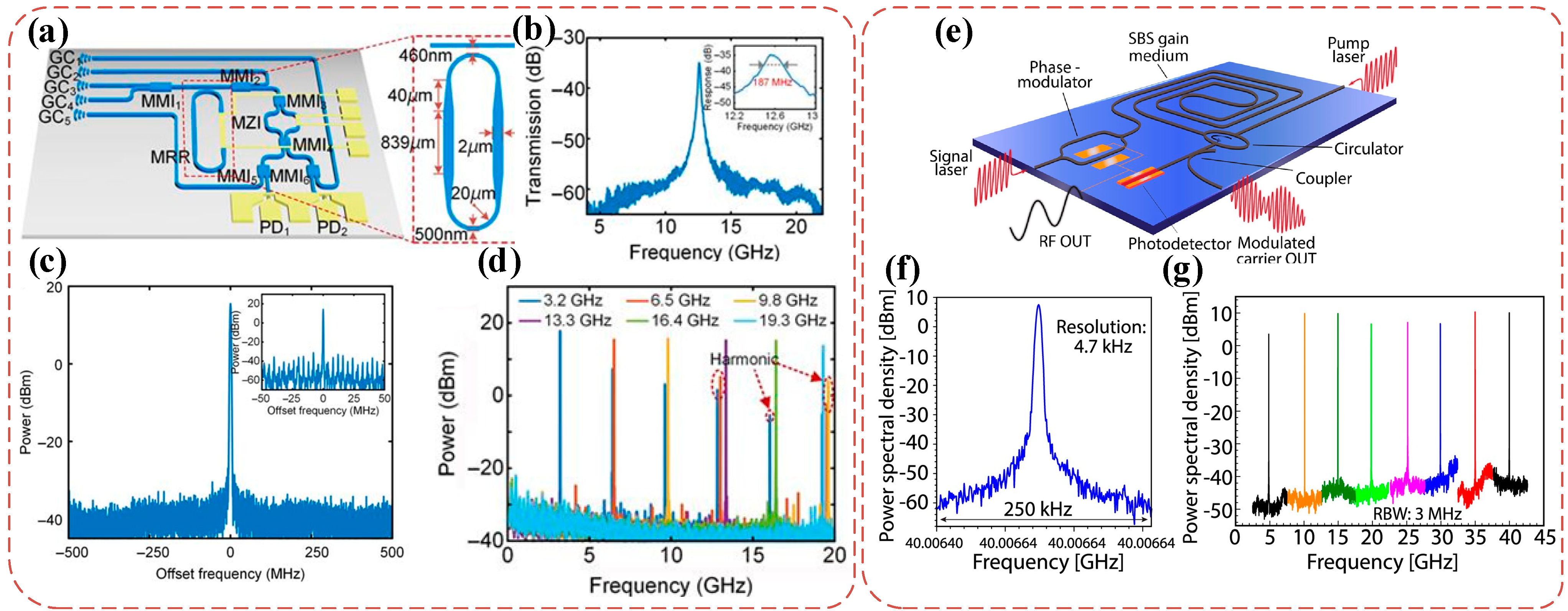
3. Microwave Photonic Integration
3.1. IMPF
3.1.1. Performance Enhancement
3.1.2. High Flexibility
3.1.3. Optical All-Pass Filter
3.1.4. System Integration
3.2. Applications of IMPF
3.2.1. Integrated OEO
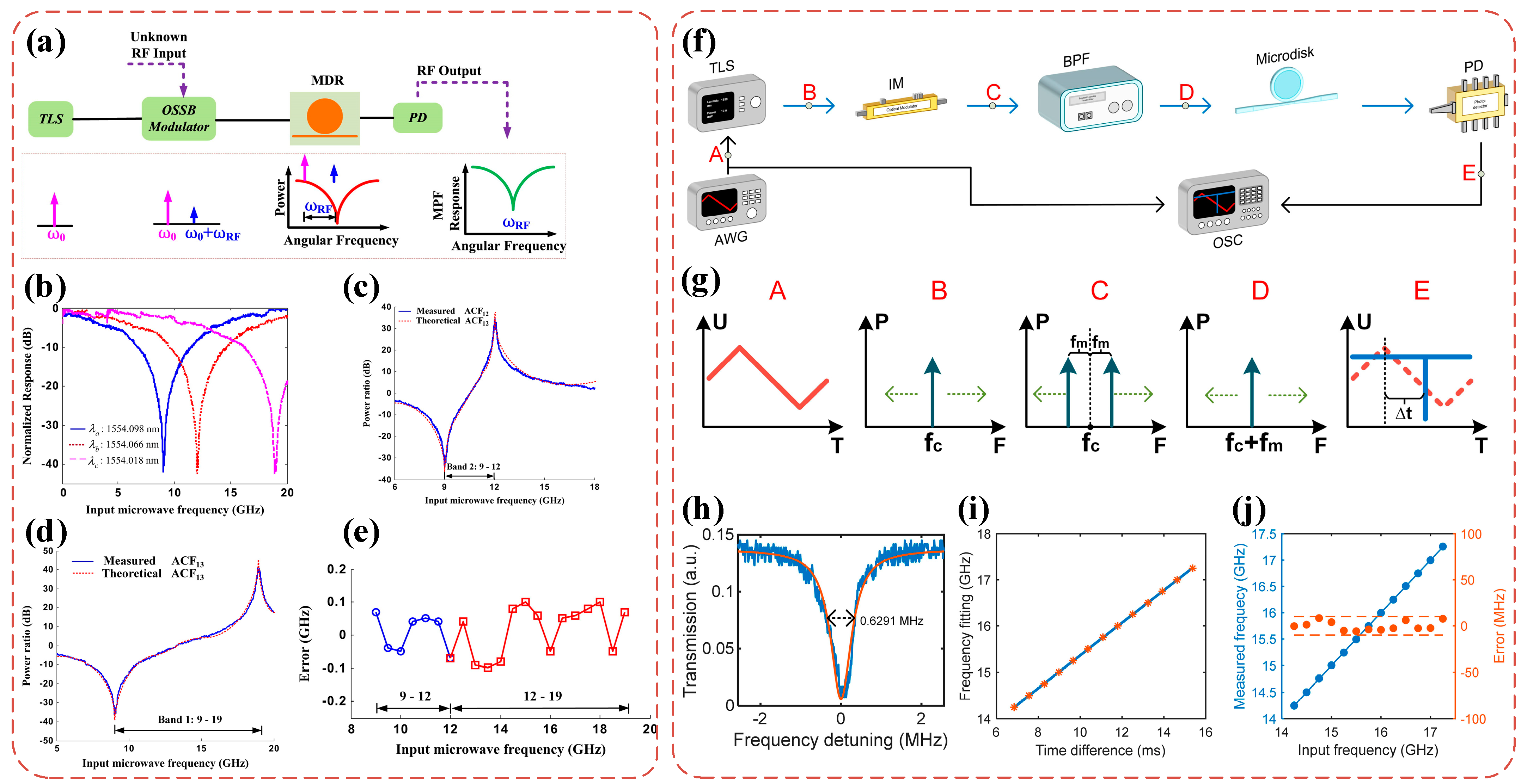
3.2.2. Integrated Microwave Photonic Frequency Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, J. Microwave photonics. J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Seeds, A.J.; Williams, K.J. Microwave Photonics. J. Light. Technol. 2006, 24, 4628–4641. [Google Scholar] [CrossRef]
- Li, M.; Zhu, N. Recent advances in microwave photonics. Front. Optoelectron. 2016, 9, 160–185. [Google Scholar] [CrossRef]
- Borges, R.M.; Muniz, A.L.M.; Sodre, A.C. Development and Performance Analysis of a Photonics-Assisted RF Converter for 5G Applications. Fiber Integr. Opt. 2017, 36, 25–37. [Google Scholar] [CrossRef]
- Waterhouse, R.; Novack, D. Realizing 5G: Microwave photonics for 5G mobile wireless systems. IEEE Microw. Mag. 2015, 16, 84–92. [Google Scholar] [CrossRef]
- Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nat. Photon. 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Yao, J. Microwave Photonic Systems. J. Light. Technol. 2022, 40, 6595–6607. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J.; Capmany, J. Integrated microwave photonics. Nat. Photon. 2019, 13, 80–90. [Google Scholar] [CrossRef]
- Loayssa, A.; Capmany, J.; Sagues, M.; Mora, J. Demonstration of incoherent microwave photonic filters with all-optical complex coefficients. IEEE Photon. Technol. Lett. 2006, 18, 1744–1746. [Google Scholar] [CrossRef]
- Xue, X.; Zheng, X.; Zhang, H.; Zhou, B. Widely tunable single-bandpass microwave photonic filter employing a non-sliced broadband optical source. Opt. Express 2011, 19, 18423–18429. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Sun, W.; Wang, W.; Wang, S.; Zhu, N. Widely tunable single bandpass microwave photonic filter based on Brillouin-assisted optical carrier recovery. Opt. Express 2014, 22, 29304–29313. [Google Scholar] [CrossRef]
- Song, M.; Long, C.; Wu, R.; Seo, D.; Leaird, E.; Weiner, A.M. Reconfigurable and Tunable Flat-Top Microwave Photonic Filters Utilizing Optical Frequency Combs. IEEE Photon. Technol. Lett. 2011, 23, 1618–1620. [Google Scholar] [CrossRef]
- Preussler, S.; Zadok, A.; Stern, Y.; Schneider, T. Microwave-photonic filters. In Proceedings of the 2016 German Microwave Conference (GeMiC), Bochum, Germany, 14–16 March 2016. [Google Scholar]
- Yu, Y.; Xu, E.; Dong, J.; Zhou, L.; Li, X.; Zhang, X. Switchable microwave photonic filter between high Q bandpass filter and notch filter with flat passband based on phase modulation. Opt. Express 2010, 8, 25271–25282. [Google Scholar] [CrossRef]
- Zhang, W.; Minasian, R.A. Switchable and Tunable Microwave Photonic Brillouin-Based Filter. IEEE Photon. J. 2012, 4, 1443–1455. [Google Scholar] [CrossRef]
- Capmany, J.; Ortega, B.; Pastor, D.; Sales, S. Discrete-time optical Processing of microwave signals. J. Light. Technol. 2005, 23, 702–723. [Google Scholar] [CrossRef]
- Xu, E. Microwave Photonic Filters Based on Semiconductor Optical Amplifier. Ph.D. Dissertation, Huazhong University of Science and Technology, Wuhan, China, 2010. [Google Scholar]
- Jiang, F.; Wong, J.H.; Lam, H.Q.; Zhou, J.; Aditya, S.; Lim, P.H.; Lee, K.E.K.; Shum, P.P.; Zhang, X. An optically tunable wideband optoelectronic oscillator based on a bandpass microwave photonic filter. Opt. Express 2013, 21, 16381–16389. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Yu, Y.; Wang, Z.; Xu, L.; Zhang, X. Wideband tunable optoelectronic oscillator based on a microwave photonic filter with an ultra-narrow passband. Opt. Lett. 2018, 43, 2328–2331. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, X.; Xu, L.; Liu, Y.; Chen, Y.; Yu, Y.; Zhang, X. On-chip tunable parity-time symmetric optoelectronic oscillator. Adv. Photon. Nexus 2023, 2, 016004. [Google Scholar] [CrossRef]
- Merklein, M.; Stiller, B.; Kabakova, I.V.; Mutugala, U.S.; Vu, K.; Madden, S.J.; Eggleton, B.J.; Slavík, R. Widely tunable, low phase noise microwave source based on a photonic chip. Opt. Lett. 2016, 41, 4633–4636. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Hao, T.; Li, W.; Dai, Y. Tutorial on optoelectronic oscillators. APL Photon. 2021, 6, 061101. [Google Scholar] [CrossRef]
- Hao, T.; Liu, Y.; Tang, J.; Cen, Q.; Li, W.; Zhu, N.; Dai, Y.; Capmany, J.; Yao, J.; Li, M. Recent advances in optoelectronic oscillators. Adv. Photon. 2020, 2, 044001. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, F.; Yan, S.; Min, S.; He, M.; Gao, D.; Dong, J. Photonic measurement of microwave frequency using a silicon microdisk resonator. Opt. Commun. 2015, 335, 266–270. [Google Scholar] [CrossRef]
- Burla, M.; Wang, X.; Li, M.; Chrostowski, L.; Azana, J. Wideband dynamic microwave frequency identification system using a low-power ultracompact silicon photonic chip. Nat. Commun. 2016, 7, 13004. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.; Ding, Y.; Peucheret, C.; Yang, T.; Dong, J.; Zhang, X. Integrated programmable photonic filter on the silicon-on-insulator platform. Opt. Express 2014, 22, 31993–31998. [Google Scholar] [CrossRef]
- Pérez, D.; Gasulla, I.; Crudgington, L.; Thomson, D.J.; Khokhar, A.Z.; Li, K.; Cao, W.; Mashanovich, G.Z.; Capmany, J. Multipurpose silicon photonics signal processor core. Nat. Commun. 2017, 8, 636. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Zhang, W. Fully Reconfigurable Waveguide Bragg Gratings for Programmable Photonic Signal Processing. J. Light. Technol. 2020, 38, 202–214. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. A fully reconfigurable waveguide Bragg grating for programmable photonic signal processing. Nat. Commun. 2018, 9, 1396. [Google Scholar] [CrossRef]
- Capmany, J.; Ortega, B.; Pastor, D. A Tutorial on Microwave Photonic Filters. J. Light. Technol. 2006, 24, 201–229. [Google Scholar] [CrossRef]
- Vidal, B.; Corral, J.L.; Marti, J. WDM photonic microwave filter using nonuniform wavelength spacing. In Proceedings of the 2004 IEEE International Topical Meeting on Microwave Photonics, Ogunquit, ME, USA, 4–6 October 2004. [Google Scholar]
- Vidal, B.; Polo, V.; Corral, J.L.; Marti, J. Photonic microwave filter with negative coefficients based on WDM techniques. IEEE Photon. Technol. Lett. 2004, 16, 2123–2125. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Mei, H.; Sun, W.; Wang, X.; Zhu, N. Reconfigurable microwave photonic filter based on Brillouin-assisted narrowband rectangular optical amplifier. In Proceedings of the 2015 14th International Conference on Optical Communications and Networks (ICOCN), Nanjing, China, 3–5 July 2015. [Google Scholar]
- Chan, E.H.W.; Minasian, R.A. Coherence-free microwave photonic notch filter with a wide passband and a narrow notch. In Proceedings of the 2008 International Topical Meeting on Microwave Photonics Jointly Held with the 2008 Asia-Pacific Microwave Photonics Conference, Gold Coast, QLD, Australia, 9 September–3 October 2008. [Google Scholar]
- Yost, T.A.; Herczfeld, P.; Rosen, A.; Singh, S. Hybrid transversal filter utilizing MMIC and optical fiber delay lines. IEEE Microw. Guid. Lett. 1995, 5, 287–289. [Google Scholar] [CrossRef]
- Li, X.; Dong, J.; Yu, Y.; Zhang, X. A Tunable Microwave Photonic Filter Based on an All-Optical Differentiator. IEEE Photon. Technol. Lett. 2011, 23, 308–310. [Google Scholar] [CrossRef]
- Vidal, B.; Piqueras, M.A.; Marti, J. Photonic microwave filter based on spectrum slicing with reconfiguration capability. Electron. Lett. 2005, 41, 1286–1287. [Google Scholar] [CrossRef]
- Xu, E.; Li, P.; Wang, F.; Guan, J. Microwave photonic filters based on optical semiconductor amplifier. Front. Optoelectron. China 2011, 4, 270–276. [Google Scholar] [CrossRef]
- Zhang, W.; Williams, J.A.R.; Everall, L.A.; Bennion, I. Fiber-optic radio frequency notch filter with linear and continous tuning by using a chirped fiber grating. Electron. Lett. 1998, 34, 1770–1772. [Google Scholar] [CrossRef]
- Pan, S.; Tang, Z.; Huang, M.; Li, S. Reflective-Type Microring Resonator for On-Chip Reconfigurable Microwave Photonic Systems. IEEE J. Sel. Top. Quant. 2020, 26, 1–12. [Google Scholar] [CrossRef]
- Lu, Z.; Li, J.; Wu, Y.; Chen, H.; Yang, S.; Chen, M. Reconfigurable RF Filter Based on Cascaded Microring Resonators. IEEE Photon. J. 2023, 15, 1–6. [Google Scholar] [CrossRef]
- Li, S.; Cong, R.; He, Z.; Wang, T.; Zhang, F.; Pan, S. Switchable microwave photonic filter using a phase modulator and a silicon-on-insulator micro-ring resonator. Chin. Opt. Lett. 2020, 18, 052501. [Google Scholar] [CrossRef]
- Shahoei, H.; Yao, J. A continuously tunable multi-tap complex-coefficient microwave photonic filter based on a tilted fiber Bragg grating. Opt. Express 2013, 21, 7521–7527. [Google Scholar] [CrossRef] [PubMed]
- Zeng, F.; Wang, J.; Yao, J. All-optical microwave bandpass filter with negative coefficients based on a phase modulator and linearly chirped fiber Bragg gratings. Opt. Lett. 2005, 30, 2203–2205. [Google Scholar] [CrossRef]
- Mora, J.; Ortega, B.; Capmany, J.; Cruz, J.L.; Andrés, M.V.; Pastor, D.; Sales, S. Automatic tunable and reconfigurable fiber-optic microwave filters based on a broadband optical source sliced by uniform fiber Bragg gratings. Opt. Express 2002, 10, 1291–1298. [Google Scholar] [CrossRef]
- Liu, X. Study of Sililcon-Based Integrated Microwave Photonic Filter. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Dai, Y.; Yao, J. Nonuniformly Spaced Photonic Microwave Delay-Line Filters and Applications. IEEE Trans. Microw. Theory Tech. 2010, 58, 3279–3289. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Yao, J. A Microwave Bandpass Differentiator Implemented Based on a Nonuniformly-Spaced Photonic Microwave Delay-Line Filter. J. Light. Technol. 2011, 29, 3470–3475. [Google Scholar]
- Moslehi, B.; Goodman, J.; Tur, M.; Shaw, H.J. Fiber-optic lattice signal processing. Proc. IEEE 1984, 72, 909–930. [Google Scholar] [CrossRef]
- Xu, E.; Zhang, X.; Zhou, L.; Zhang, Y.; Huang, D. A simple microwave photonic notch filter based on a semiconductor optical amplifier. J. Opt. A Pure Appl. Opt. 2009, 11, 085405. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, G.; Williams, J.A.R. Tap multiplexed fibre grating-based optical transversal filter. Electron. Lett. 2000, 36, 1708–1710. [Google Scholar] [CrossRef]
- Pastor, D.; Ortega, B.; Capmany, J.; Sales, S.; Martinez, A.; Muñoz, P. Optical microwave filter based on spectral slicing by use of arrayed waveguide gratings. Opt. Lett. 2003, 28, 1802–1804. [Google Scholar] [CrossRef]
- Vidal, B.; Polo, V.; Corral, J.L.; Marti, J. Cost-effective photonic microwave filter employing tap reusing. In Proceedings of the MWP 2003 Proceedings. International Topical Meeting on Microwave Photonics, Budapest, Hungary, 10–12 September 2003. [Google Scholar]
- Zhou, L.; Zhang, X.; Xu, E.; Yu, Y.; Li, X.; Huang, D. A novel tunable cascaded IIR microwave photonic filter. Opt. Commun. 2010, 283, 2794–2797. [Google Scholar] [CrossRef]
- Chan, E.H.W.; Minasian, R.A. Reflective Amplified Recirculating Delay Line Bandpass Filter. J. Light. Technol. 2007, 25, 1441–1446. [Google Scholar] [CrossRef]
- Pan, S.; Yao, J. Photonics-Based Broadband Microwave Measurement. J. Light. Technol. 2017, 35, 3498–3513. [Google Scholar] [CrossRef]
- Zou, X.; Lu, B.; Pan, W.; Yan, L.; Stöhr, A.; Yao, J. Photonics for microwave measurements. Laser Photon. Rev. 2016, 10, 711–734. [Google Scholar] [CrossRef]
- Wang, W.S.; Davis, R.L.; Jung, T.J.; Lodenkamper, R.; Lembo, L.J.; Brock, J.C.; Wu, M.C. Characterization of a coherent optical RF channelizer based on a diffraction grating. IEEE Trans. Microw. Theory Tech. 2001, 49, 1996–2001. [Google Scholar] [CrossRef]
- Winnall, S.T.; Lindsay, A.C.; Austin, M.W.; Canning, J.; Mitchell, A. A microwave channelizer and spectroscope based on an integrated optical Bragg-grating Fabry–Pérot and integrated hybrid Fresnel lens system. IEEE Trans. Microw. Theory Tech. 2006, 54, 868–872. [Google Scholar] [CrossRef]
- Hunter, D.B.; Edvell, L.G.; Englund, M.A. Wideband microwave photonic channelised receiver. In Proceedings of the 2005 International Topical Meeting on Microwave Photonics, Seoul, Republic of Korea, 14 October 2005. [Google Scholar]
- Nguyen, L.V.T. Microwave photonic technique for frequency measurement of simultaneous signals. IEEE Photon. Technol. Lett. 2009, 21, 642–644. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Chan, E.H.W.; Minasian, R.A. Photonic Multiple Frequency Measurement Using a Frequency Shifting Recirculating Delay Line Structure. J. Light. Technol. 2014, 32, 3831–3838. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, F.; Shi, J.; Pan, S. Deep neural network-assisted high-accuracy microwave instantaneous frequency measurement with a photonic scanning receiver. Opt. Lett. 2020, 45, 3038–3041. [Google Scholar] [CrossRef]
- Zhou, J.; Aditya, S.; Shum, P.P.; Yao, J. Instantaneous Microwave Frequency Measurement Using a Photonic Microwave Filter with an Infinite Impulse Response. IEEE Photon. Technol. Lett. 2010, 22, 682–684. [Google Scholar] [CrossRef]
- Yao, X.S.; Maleki, L. Optoelectronic microwave oscillator. J. Opt. Soc. Am. B 1996, 13, 1725–1735. [Google Scholar] [CrossRef]
- Maleki, L. The optoelectronic oscillator. Nat. Photon. 2011, 5, 728–730. [Google Scholar] [CrossRef]
- Yao, X.S.; Maleki, L. Optoelectronic oscillator for photonic systems. IEEE J. Quantum Electron. 1996, 32, 1141–1149. [Google Scholar] [CrossRef]
- Salik, E.; Yu, N.; Maleki, L. An Ultralow Phase Noise Coupled Optoelectronic Oscillator. IEEE Photon. Technol. Lett. 2007, 19, 444–446. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, L.; Yao, J. Tunable Optoelectronic Oscillator Incorporating a Single Passband Microwave Photonic Filter. IEEE Photon. Technol. Lett. 2014, 26, 326–329. [Google Scholar] [CrossRef]
- Poinsot, S.; Porte, H.; Goedgebuer, J.P.; Rhodes, W.T.; Boussert, B. Continuous radio-frequency tuning of an optoelectronic oscillator with dispersive feedback. Opt. Lett. 2002, 27, 1300–1302. [Google Scholar] [CrossRef]
- Yu, Y. Investigation of All-Optical Microwave Signal Processing Techniques. Ph.D. Dissertation, Huazhong University of Science and Technology, Wuhan, China, 2013. [Google Scholar]
- Yao, J. Photonics to the Rescue: A Fresh Look at Microwave Photonic Filters. IEEE Microw. Mag. 2015, 16, 46–60. [Google Scholar] [CrossRef]
- Sales, S.; Capmany, J.; Marti, J. Experimental demonstration of fibre-optic delay line filters with negative coefficients. Electron. Lett. 1995, 31, 1095–1096. [Google Scholar] [CrossRef]
- Li, J.; Cheung, K.K.Y.; Wong, K.K.Y. Photonic Microwave Filter with Negative Coefficients Using Fiber Optical Parametric Amplifier. In Proceedings of the National Fiber Optic Engineers Conference, San Diego, CA, USA, 22–26 March 2009. [Google Scholar]
- Li, X.; Yu, Y.; Dong, J.; Zhang, X. Widely Tunable Microwave Photonic Filter Based on Semiconductor Optical Amplifier. In Proceedings of the Asia Communications and Photonics Conference and Exhibition, Shanghai, China, 8–12 December 2010. [Google Scholar]
- Mora, J.; Martínez, A.; Manzanedo, M.D.; Capmany, J. Microwave photonic filters with arbitrary positive and negative coefficients using multiple phase inversion in SOA based XGM wavelength converter. Electron. Lett. 2005, 41, 921–922. [Google Scholar] [CrossRef]
- Yi, X.; Fang, W.; Hong, N.J.; Lu, C. Tunable microwave filter design using wavelength conversion technique and high dispersion time delays. IEEE Photon. Technol. Lett. 2001, 13, 857–859. [Google Scholar]
- Zheng, R.; Alameh, K.; Lee, Y.K.; Wang, Z. Multitap coherence-free photonic RF filter employing semiconductor optical amplifier. Microw. Opt. Technol. Lett. 2007, 49, 1103–1106. [Google Scholar] [CrossRef]
- Pastor, D.; Capmany, J.; Ortega, B.; Martinez, A.; Pierno, L.; Varasi, M. Reconfigurable RF photonic filter with negative coefficients and flat-top resonances using phase inversion in a newly designed designed 2×1 integrated Mach-Zehnder modulator. IEEE Photon. Technol. Lett. 2004, 16, 2126–2128. [Google Scholar] [CrossRef]
- Norberg, E.J.; Guzzon, R.S.; Nicholes, S.C.; Parker, J.S.; Coldren, L.A. Programmable Photonic Lattice Filters in InGaAsP–InP. IEEE Photon. Technol. Lett. 2010, 22, 109–111. [Google Scholar] [CrossRef]
- Norberg, E.J.; Guzzon, R.S.; Parker, J.S.; Johansson, L.A.; Coldren, L.A. Programmable Photonic Microwave Filters Monolithically Integrated in InP–InGaAsP. J. Light. Technol. 2011, 29, 1611–1619. [Google Scholar] [CrossRef]
- Guzzon, R.S.; Norberg, E.J.; Parker, J.S.; Johansson, L.A.; Coldren, L.A. Integrated InP-InGaAsP tunable coupled ring optical bandpass filters with zero insertion loss. Opt. Express 2011, 19, 7816–7826. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xu, E.; Zhou, L.; Yu, Y.; Dong, J.; Zhang, X. Microwave photonic filter with multiple taps based on single semiconductor optical amplifier. Opt. Commun. 2010, 283, 3026–3029. [Google Scholar] [CrossRef]
- Coppinger, F.; Yegnanarayanan, S.; Trinh, P.D.; Jalali, B. All-optical RF filter using amplitude inversion in a semiconductor optical amplifier. IEEE Trans. Microw. Theory Tech. 1997, 45, 1473–1477. [Google Scholar] [CrossRef]
- Xu, E.; Zhang, X.; Zhou, L.; Zhang, Y.; Yu, Y.; Li, X.; Huang, D. All-optical microwave filter with high frequency selectivity based on semiconductor optical amplifier and optical filter. J. Light. Technol. 2010, 28, 2358–2365. [Google Scholar]
- Sagues, M.; Loayssa, A.; Capmany, J. Multitap Complex-Coefficient Incoherent Microwave Photonic Filters Based on Stimulated Brillouin Scattering. IEEE Photon. Technol. Lett. 2007, 19, 1194–1196. [Google Scholar] [CrossRef]
- Yan, Y.; Yao, J. A Tunable Photonic Microwave Filter with a Complex Coefficient Using an Optical RF Phase Shifter. IEEE Photon. Technol. Lett. 2007, 19, 1472–1474. [Google Scholar] [CrossRef]
- Li, W.; Zhang, W.; Yao, J. A wideband 360° photonic-assisted microwave phase shifter using a polarization modulator and a polarization-maintaining fiber Bragg grating. Opt. Express 2012, 20, 29838–29843. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, S. Complex Coefficient Microwave Photonic Filter Using a Polarization-Modulator-Based Phase Shifter. IEEE Photon. Technol. Lett. 2013, 25, 187–189. [Google Scholar] [CrossRef]
- Loayssa, A.; Hernandez, R.; Benito, D.; Galech, S. Characterization of stimulated Brillouin scattering spectra by use of optical single-sideband modulation. Opt. Lett. 2004, 29, 638–640. [Google Scholar] [CrossRef]
- Jiang, W.; Xu, L.; Liu, Y.; Chen, Y.; Liu, X.; Yu, Y.; Yu, Y.; Zhang, X. Optical All-Pass Filter in Silicon-on-Insulator. ACS Photon. 2020, 7, 2539–2546. [Google Scholar] [CrossRef]
- Xu, L.; Yu, Y.; Liu, X.; Shu, X.; Zhang, X. Optical All-Pass Filter Realized by Self-Compensation of Loss. ACS Photon. 2021, 8, 3156–3161. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, L.; Jiang, W.; Wang, L.; Cui, S.; Yu, Y.; Yu, Y.; Zhang, X. Reconfigurable second-order optical all-pass filter. Nanophotonics 2022, 11, 3115–3125. [Google Scholar] [CrossRef]
- Pan, S.; Yao, J. Instantaneous Microwave Frequency Measurement Using a Photonic Microwave Filter Pair. IEEE Photon. Technol. Lett. 2010, 22, 1437–1439. [Google Scholar] [CrossRef]
- Xu, E.; Zhang, X.; Zhou, L.; Zhang, Y.; Yu, Y.; Li, X.; Huang, D. Ultrahigh-Q microwave photonic filter with Vernier effect and wavelength conversion in a cascaded pair of active loops. Opt. Lett. 2010, 35, 1242–1244. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Liu, Y.; Chen, Y.; Gou, W.; Cui, C.; Yu, Y.; Xiao, X.; Yu, Y.; Zhang, X. Generation of Reconfigurable Linearly Chirped Microwave Waveforms Based On Fourier domain Mode-Locked Optoelectronic Oscillator. J. Light. Technol. 2022, 40, 85–92. [Google Scholar] [CrossRef]
- Li, W.; Li, M.; Yao, J. A narrow-passband and frequency-tunable microwave photonic filter based on phase-modulation to intensity-modulation conversion using a phase-shifted fiber Bragg grating. IEEE Trans. Microw. Theory Tech. 2012, 60, 1287–1296. [Google Scholar] [CrossRef]
- Yi, X.; Minasian, R.A. Microwave photonic filter with single bandpass response. Electron. Lett. 2009, 45, 362–363. [Google Scholar] [CrossRef]
- Capmany, J.; Pastor, D.; Martinez, A.; Ortega, B.; Sales, S. Microwave photonics filter with negative coefficients based on phase inversion in an electro-optic modulator. Opt. Lett. 2003, 28, 1415–1417. [Google Scholar] [CrossRef]
- Blumenthal, D.J.; Barton, J.; Beheshti, N. Integrated photonics for low-power packet networking. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 458–471. [Google Scholar] [CrossRef]
- Marpaung, D.; Roeloffzen, C.; Heideman, R.; Leinse, A.; Sales, S.; Capmany, J. Integrated microwave photonics. Laser Photon Rev. 2013, 7, 506–538. [Google Scholar] [CrossRef]
- Iezekiel, S.; Burla, M.; Klamkin, J.; Marpaung, D.; Capmany, J. RF Engineering Meets Optoelectronics: Progress in Integrated Microwave Photonics. IEEE Microw. Mag. 2015, 16, 28–45. [Google Scholar] [CrossRef]
- Joshi, H.; Sigmarsson, H.H.; Moon, S.; Peroulis, D.; Chappell, W.J. High- Q Fully Reconfigurable Tunable Bandpass Filters. IEEE Trans. Microw. Theory Tech. 2009, 57, 3525–3533. [Google Scholar] [CrossRef]
- Liu, Y.; Choudhary, A.; Ren, G.; Vu, K.; Morrison, B.; CasasBedoya, A.; Nguyen, T.G.; Choi, D.-Y.; Ma, P.; Mitchell, A.; et al. Integration of Brillouin and passive circuits for enhanced radio-frequency photonic filtering. APL Photon. 2019, 4, 106103. [Google Scholar] [CrossRef]
- Tao, Y.; Shu, H.; Wang, X.; Jin, M.; Tao, Z.; Yang, F.; Shi, J.; Qin, J. Hybrid-integrated high-performance microwave photonic filter with switchable response. Photon. Res. 2021, 9, 1569. [Google Scholar] [CrossRef]
- Liu, X.; Yu, Y.; Tang, H.; Xu, L.; Dong, J.; Zhang, X. Silicon-on-insulator-based microwave photonic filter with narrowband and ultrahigh peak rejection. Opt. Lett. 2018, 43, 1359–1362. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Wang, L.; Yu, Y.; Yu, Y.; Zhang, X. Tunable and Reconfigurable Microwave Photonic Bandpass Filter Based on Cascaded Silicon Microring Resonators. J. Light. Technol. 2022, 40, 4655–4662. [Google Scholar] [CrossRef]
- Liu, Y.; Hotten, J.; Choudhary, A.; Eggleton, B.J.; Marpaung, D. All-optimized integrated RF photonic notch filter. Opt. Lett. 2017, 42, 4631–4634. [Google Scholar] [CrossRef]
- Cui, S.; Cao, K.; Pan, Z.; Gao, X.; Yu, Y.; Zhang, X. Compact microring resonator based on ultralow-loss multimode silicon nitride waveguide. Adv. Photon. Nexus 2023, 2, 046007. [Google Scholar] [CrossRef]
- Marpaung, D.; Morrison, B.; Pant, R.; Roeloffzen, C.; Leinse, A.; Hoekman, M.; Heideman, R.; Eggleton, B.J. Si3N4 ring resonator-based microwave photonic notch filter with an ultrahigh peak rejection. Opt. Express 2013, 21, 23286–23294. [Google Scholar] [CrossRef]
- Rasras, M.S.; Tu, K.Y.; Gill, D.M.; Chen, Y.K.; White, A.E.; Patel, S.S.; Pomerene, A.; Carothers, D.; Beattie, J.; Beals, M.; et al. Demonstration of a Tunable Microwave-Photonic Notch Filter Using Low-Loss Silicon Ring Resonators. J. Light. Technol. 2009, 27, 2105–2110. [Google Scholar] [CrossRef]
- Zhuang, L.; Marpaung, D.; Burla, M.; Beeker, W.; Leinse, A.; Roeloffzen, C. Low-loss, high-index-contrast Si3N4/SiO2 optical waveguides for optical delay lines in microwave photonics signal processing. Opt. Express 2011, 19, 23162–23170. [Google Scholar] [CrossRef]
- Burla, M.; Marpaung, D.; Zhuang, L.; Roeloffzen, C.; Khan, M.R.; Leinse, A.; Hoekman, M.; Heideman, R. On-chip CMOS compatible reconfigurable optical delay line with separate carrier tuning for microwave photonic signal processing. Opt. Express 2011, 19, 21475–21484. [Google Scholar] [CrossRef] [PubMed]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photon Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Dong, J.; Liu, L.; Gao, D.; Yu, Y.; Zheng, A.; Yang, T.; Zhang, X. Compact notch microwave photonic filters using on-chip integrated microring resonators. IEEE Photon. J. 2013, 5, 5500307. [Google Scholar] [CrossRef]
- Song, S.; Chew, S.X.; Yi, X.; Nguyen, L.; Minasian, R.A. Tunable Single-Passband Microwave Photonic Filter Based on Integrated Optical Double Notch Filter. J. Light. Technol. 2018, 36, 4557–4564. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, Y.; Merklein, M.; Daulay, O.; Marpaung, D.; Eggleton, B.J. Positive link gain microwave photonic bandpass filter using Si3N4-ring-enabled sideband filtering and carrier suppression. Opt. Express 2019, 27, 31727–31740. [Google Scholar] [CrossRef] [PubMed]
- Tu, K.Y.; Rasras, M.S.; Gill, D.M.; Patel, S.S.; Chen, Y.K.; White, A.E.; Pomerene, A.; Carothers, D.; Beattie, J.; Beals, M.; et al. Silicon RF-photonic filter and down-converter. J. Light. Technol. 2010, 28, 3019–3028. [Google Scholar] [CrossRef]
- Long, Y.; Wang, J. Ultra-high peak rejection notch microwave photonic filter using a single silicon microring resonator. Opt. Express 2015, 23, 17739–17750. [Google Scholar] [CrossRef]
- Biberman, A.; Shaw, M.J.; Timurdogan, E.; Wright, J.B.; Watts, M.R. Ultralow-loss silicon ring resonators. Opt. Lett. 2012, 37, 4236–4268. [Google Scholar] [CrossRef]
- Jiang, W.C.; Zhang, J.; Usechak, N.G.; Lin, Q. Dispersion engineering of high-Q silicon microresonators via thermal oxidation. Appl. Phys. Lett. 2014, 105, 031112. [Google Scholar] [CrossRef]
- Ji, X.; Barbosa, F.A.; Roberts, S.P.; Dutt, A.; Cardenas, J.; Okawachi, Y.; Bryant, A.; Gaeta, A.L.; Lipson, M. Ultra-low-loss on-chip resonators with sub-milliwatt parametric oscillation threshold. Optica 2017, 4, 619–624. [Google Scholar] [CrossRef]
- Griffith, A.; Cardenas, J.; Poitras, C.B.; Lipson, M. High quality factor and high confinement silicon resonators using etchless process. Opt. Express 2012, 20, 21341–21345. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.W.; Wiederhecker, G.S.; Cardenas, J.; Poitras, C.; Lipson, M. High quality factor etchless silicon photonic ring resonators. Opt. Express 2011, 19, 6284–6289. [Google Scholar] [CrossRef]
- Bauters, J.F.; Heck, M.J.; John, D.; Dai, D.; Tien, M.; Barton, J.S.; Leinse, A.; Heideman, R.G.; Blumenthal, D.J.; Bowers, J.E. Ultra-low-loss high-aspect-ratio Si3N4 waveguides. Opt. Express 2011, 19, 3163–3174. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; Wang, Z.; Bauters, J.; Tien, M.-C.; Heck, M.; Blumenthal, D.; Bowers, J.E. Low-loss Si3N4 arrayed-waveguide grating (de)multiplexer using nano-core optical waveguides. Opt. Express 2011, 19, 14130–14136. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X.; Chen, D.; Wang, L.; Li, M.; Feng, P.; Xiao, X.; Yu, S. Design and demonstration of ultra-high-Q silicon microring resonator based on a multi-mode ridge waveguide. Opt. Lett. 2018, 43, 1586–1589. [Google Scholar] [CrossRef]
- Nijem, J.; Naiman, A.; Zektzer, R.; Frydendahl, C.; Mazurski, N.; Levy, U. High Q-factor microring resonator using local oxidation of silicon (LOCOS) and adiabatic geometry. In Proceedings of the 2021 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 May 2021. [Google Scholar]
- Zhang, L.; Hong, S.; Wang, Y.; Yan, H.; Xie, Y.; Chen, T.; Zhang, M.; Yu, Z.; Shi, Y.; Liu, L.; et al. Ultralow-Loss Silicon Photonics beyond the Singlemode Regime. Laser Photon. Rev. 2022, 16, 2100292. [Google Scholar] [CrossRef]
- Yang, W.; Yi, X.; Song, S.; Chew, S.X.; Li, L.; Nguyen, L. Tunable single bandpass microwave photonic filter based on phase compensated silicon-on-insulator microring resonator. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) Held Jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016. [Google Scholar]
- Xu, L.; Hou, J.; Tang, H.; Yu, Y.; Yu, Y.; Shu, X.; Zhang, X. Silicon-on-insulator-based microwave photonic filter with widely adjustable bandwidth. Photon. Res. 2019, 7, 110–115. [Google Scholar] [CrossRef]
- Liu, Y.; Choudhary, A.; Marpaung, D.; Eggleton, B.J. Integrated microwave photonic filters. Adv. Opt. Photon. 2020, 12, 485–555. [Google Scholar] [CrossRef]
- Hunter, D.B.; Minasian, R.A. Reflectively tapped fibre optic transversal filter using in-fibre Bragg gratings. Electron. Lett. 1995, 31, 1010–1012. [Google Scholar] [CrossRef]
- Yi, X.; Minasian, R.A. Dispersion induced RF distortion of spectrum-sliced microwave-photonic filters. IEEE Trans. Microw. Theory Tech. 2006, 54, 880–886. [Google Scholar] [CrossRef]
- Porzi, C.; Reza, M.; Ghelfi, P.; Sorel, M.; Bogoni, A. Silicon-on-Insulator Microwave Photonic Filter with Widely Tunable and Reconfigurable Flat-Top Bandpass Functionality. J. Light. Technol. 2022, 40, 6666–6675. [Google Scholar] [CrossRef]
- Brunetti, G.; Dell’Olio, F.; Conteduca, D.; Armenise, M.N.; Ciminelli, C. Ultra-Compact Tuneable Notch Filter Using Silicon Photonic Crystal Ring Resonator. J. Light. Technol. 2019, 37, 2970–2980. [Google Scholar] [CrossRef]
- Burla, M.; Cortés, L.R.; Li, M.; Wang, X.; Chrostowski, L.; Azaña, J. Integrated waveguide Bragg gratings for microwave photonics signal processing. Opt. Express 2013, 21, 25120–25147. [Google Scholar] [CrossRef] [PubMed]
- Porzi, C.; Sharp, G.J.; Sorel, M.; Bogoni, A. Silicon photonics high-order distributed feedback resonators filters. IEEE J. Quantum Electron. 2020, 56, 1–9. [Google Scholar] [CrossRef]
- Adams, D.B.; Madsen, C.K. A Novel Broadband Photonic RF Phase Shifter. J. Light. Technol. 2008, 26, 2712–2717. [Google Scholar] [CrossRef]
- Yang, W.J.; Sun, T.B.; Rao, Y.; Megens, M.; Chan, T.; Yoo, B.W.; Horsley, D.A.; Wu, M.C.; Chang Hasnain, C.J. High speed optical phased array using high contrast grating all-pass filters. Opt. Express 2014, 22, 20038–20044. [Google Scholar] [CrossRef]
- Liu, Y.; Marpaung, D.; Choudhary, A.; Eggleton, B.J. Lossless and high-resolution RF photonic notch filter. Opt. Lett. 2016, 41, 5306. [Google Scholar] [CrossRef]
- Lenz, G.; Madsen, C.K. Optical all-pass filters for synchronization in optical time division multiplexed (OTDM) systems. In Proceedings of the Integrated Photonics Research: OSA Trends in Optics and Photonics, Québec City, QC, Canada, 12 July 2000. [Google Scholar]
- Madsen, C.K. Optical all-pass filters for polarization mode dispersion compensation. Opt. Lett. 2000, 25, 878–880. [Google Scholar] [CrossRef]
- Madsen, C.K.; Lenz, G. Optical all-pass filters for phase response design with applications for dispersion compensation. IEEE Photon. Technol. Lett. 1998, 10, 994–996. [Google Scholar] [CrossRef]
- Gupta, S.; Zhang, Q.; Zou, L.; Jiang, L.J.; Caloz, C. Generalized Coupled-Line All-Pass Phasers. IEEE Trans. Microw. Theory Tech. 2015, 63, 1007–1018. [Google Scholar] [CrossRef]
- Guyette, A.C.; Naglich, E.J.; Shin, S. Switched allpass-to-bandstop absorptive filters with constant group delay. IEEE Trans. Microw. Theory Tech. 2016, 64, 2590–2595. [Google Scholar] [CrossRef]
- Naglich, E.J.; Lee, J.; Peroulis, D.; Chappell, W.J. Switchless tunable bandstop-to-all-pass reconfigurable filter. IEEE Trans. Microw. Theory Tech. 2012, 60, 1258–1265. [Google Scholar] [CrossRef]
- Viveiros, D.; Consonni, D.; Jastrzebski, A.K. A tunable all-pass MMIC active phase shifter. IEEE Trans. Microw. Theory Tech. 2002, 50, 1885–1889. [Google Scholar] [CrossRef]
- Minaei, S.; Cicekoglu, O. A Resistorless realization of the first-order all-pass filter. Int. J. Electron. Lett. 2006, 93, 177–183. [Google Scholar] [CrossRef]
- Minaei, S.; Yuce, E. Novel voltage-mode all-pass filter based on using DVCCs. Circuits Syst. Signal Process 2010, 29, 391–402. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Kuntman, H.; Cicekoglu, O. First-order all-pass filter canonical in the number of resistors and capacitors employing a single DDCC. Circuits Syst. Signal Process 2003, 22, 525–536. [Google Scholar] [CrossRef]
- Jablonski, M.; Takushima, Y.; Kikuchi, K. The realization of all-pass filters for third-order dispersion compensation in ultrafast optical fiber transmission systems. J. Light. Technol. 2001, 19, 1194–1205. [Google Scholar] [CrossRef]
- Lunardi, L.M.; Moss, D.J.; Chandrasekhar, S. Tunable dispersion compensation at 40-Gb/s using a multicavity Etalon all-pass filter with NRZ, RZ, and CS-RZ modulation. J. Light. Technol. 2002, 20, 2136–2144. [Google Scholar] [CrossRef]
- Madsen, C.K. Subband all-pass filter architectures with applications to dispersion and dispersion-slope compensation and continuously variable delay lines. J. Light. Technol. 2003, 21, 2412–2420. [Google Scholar] [CrossRef]
- Kim, J.; Ko, Y.; Kim, H.; Chung, Y. Variable Time Delay Experiments in Serially Cascaded Ring Resonator All-Pass Filters. In Proceedings of the 2013 18th OptoElectronics and Communications Conference Held Jointly with 2013 International Conference on Photonics in Switching, Kyoto, Japan, 30 June–4 July 2013. [Google Scholar]
- Liu, W.; Li, M.; Guzzon, R.S.; Norberg, E.J.; Parker, J.S.; Lu, M.; Coldren, L.A.; Yao, J. A fully reconfigurable photonic integrated signal processor. Nat. Photon. 2016, 10, 190–195. [Google Scholar] [CrossRef]
- Fandiño, J.S.; Muñoz, P.; Doménech, D.; Capmany, J. A monolithic integrated photonic microwave filter. Nat. Photon. 2017, 11, 124–129. [Google Scholar] [CrossRef]
- Nagarajan, R.; Kato, M.; Pleumeekers, J.; Evans, P.; Corzine, S.; Hurtt, S.; Dentai, A.; Murthy, S.; Missey, M.; Muthiah, R.; et al. InP photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1113–1125. [Google Scholar] [CrossRef]
- Zhao, H.; Pinna, S.; Song, B.; Megalini, L.; Brunelli, S.S.; Coldren, L.; Klamkin, J. High-power integrated indium phosphide transmitter for free spaceoptical communications. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018. [Google Scholar]
- Letal, G.; Prosyk, K.; Millett, R.; Macquistan, D.; Paquet, S.; Thibault-Maheu, O.; Gagné, J.-F.; Fortin, P.-L.; Dowlatshahi, R.; Rioux, B.; et al. Low loss InP C-band IQ modulator with 40GHz bandwidth and 1.5V Vπ. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 22–26 March 2015. [Google Scholar]
- Lange, S.; Wolf, S.; Lutz, J.; Altenhain, L.; Schmid, R.; Kaiser, R.; Schell, M.; Koos, C.; Randel, S. 100 GBd intensity modulation and direct detection with an InP-based monolithic DFB laser Mach–Zehnder modulator. J. Light. Technol. 2018, 36, 97–102. [Google Scholar] [CrossRef]
- Griffin, R.A.; Jones, S.K.; Whitbread, N.; Heck, S.C.; Langley, L.N. InP Mach–Zehnder modulator platform for 10/40/100/200-Gb/s operation. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 158–166. [Google Scholar] [CrossRef]
- Chen, L.R. Silicon photonics for microwave photonics applications. J. Light. Technol. 2017, 35, 824–835. [Google Scholar] [CrossRef]
- Chen, L.R.; Moslemi, P.; Wang, Z.; Ma, M.; Adams, R. Integrated microwave photonics for spectral analysis, waveform generation, and filtering. IEEE Photon. Technol. Lett. 2018, 30, 1838–1841. [Google Scholar] [CrossRef]
- Qiu, H.; Zhou, F.; Qie, J.; Yao, Y.; Hu, X.; Zhang, Y.; Xiao, X.; Yu, Y.; Dong, J.; Zhang, X. A continuously tunable sub-gigahertz microwave photonic band-pass filter based on an ultra-high-Q silicon microring resonator. J. Light. Technol. 2018, 36, 4312–4318. [Google Scholar] [CrossRef]
- Baba, T.; Akiyama, S.; Imai, M.; Hirayama, N.; Takahashi, H.; Noguchi, Y.; Horikawa, T.; Usuki, T. 50-Gb/s ring-resonator-based silicon modulator. Opt. Express 2013, 21, 11869–11876. [Google Scholar] [CrossRef]
- Tu, X.; Liow, T.Y.; Song, J.; Luo, X.; Fang, Q.; Yu, M.; Lo, G.Q. 50-Gb/s silicon optical modulator with traveling-wave electrodes. Opt. Express 2013, 21, 12776–12782. [Google Scholar] [CrossRef] [PubMed]
- Lischke, S.; Knoll, D.; Mai, C.; Zimmermann, L.; Peczek, A.; Kroh, M.; Trusch, A.; Krune, E.; Voigt, K.; Mai, A. High bandwidth, high responsivity waveguide-coupled germanium pin photodiode. Opt. Express 2015, 23, 27213–27220. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Yao, J. On-chip silicon photonic integrated frequency-tunable bandpass microwave photonic filter. Opt. Lett. 2018, 43, 3622–3625. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Yao, J. Silicon photonic integrated optoelectronic oscillator for frequency-tunable microwave generation. J. Light. Technol. 2018, 36, 4655–4663. [Google Scholar] [CrossRef]
- Kim, J.; Aghaeimeibodi, S.; Carolan, J.; Englund, D.; Waks, E. Hybrid integration methods for on-chip quantum photonics. Optica 2020, 7, 291–308. [Google Scholar] [CrossRef]
- Pant, R.; Poulton, C.G.; Choi, D.-Y.; Mcfarlane, H.; Hile, S.; Li, E.; Thevenaz, L.; Luther-Davies, B.; Madden, S.J.; Eggleton, B.J. On-chip stimulated Brillouin scattering. Opt. Express 2011, 19, 8285–8290. [Google Scholar] [CrossRef]
- Eggleton, B.J.; Poulton, C.G.; Pant, R. Inducing and harnessing stimulated Brillouin scattering in photonic integrated circuits. Adv. Opt. Photon. 2013, 5, 536–587. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, Y.; Wei, Y.; Zhou, F.; Chen, D.; Zhang, Y.; Xiao, X.; Li, M.; Dong, J.; Yu, S.; et al. Highly Integrated Dual-Modality Microwave Frequency Identification System. Laser Photon. Rev. 2022, 16, 2200006. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, W.; Pan, S.; Yao, J. High-Sensitivity Instantaneous Microwave Frequency Measurement Based on a Silicon Photonic Integrated Fano Resonator. J. Light. Technol. 2019, 37, 2527–2533. [Google Scholar] [CrossRef]
- Fandino, J.S.; Munoz, P. Photonics-based microwave frequency measurement using a double-sideband suppressed-carrier modulation and an InP integrated ring-assisted Mach-Zehnder interferometer filter. Opt. Lett. 2013, 38, 4316–4319. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, W.; Liu, J.; Yao, J. On-chip two-step microwave frequency measurement with high accuracy and ultra-wide bandwidth using add-drop micro-disk resonators. Opt. Lett. 2019, 44, 2402–2405. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, W.; Shi, L.; Che, C.; Dong, J. Photonic-Assisted Microwave Frequency Measurement Using High Q-Factor Microdisk with High Accuracy. Photonics 2023, 10, 847. [Google Scholar] [CrossRef]

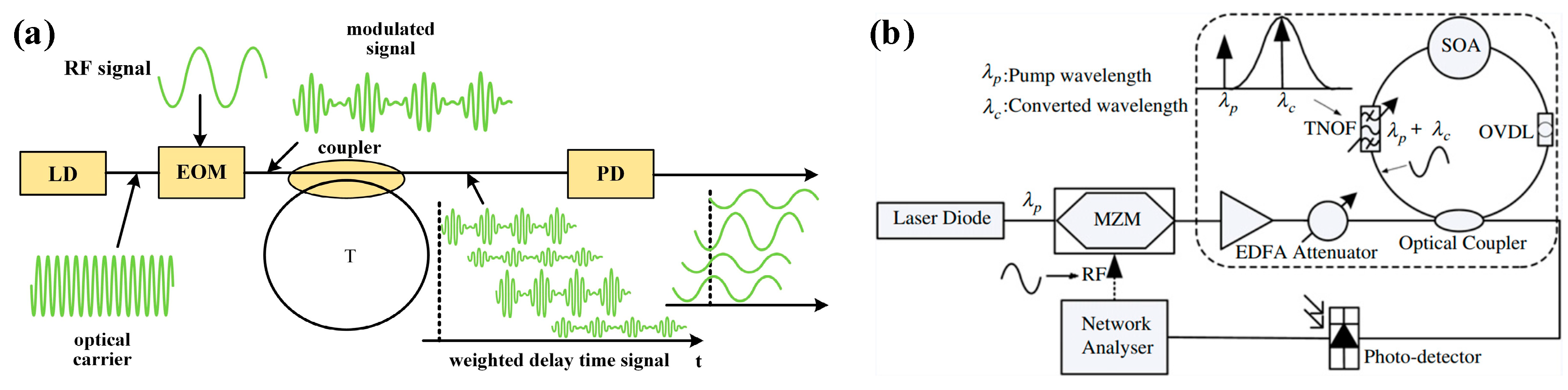
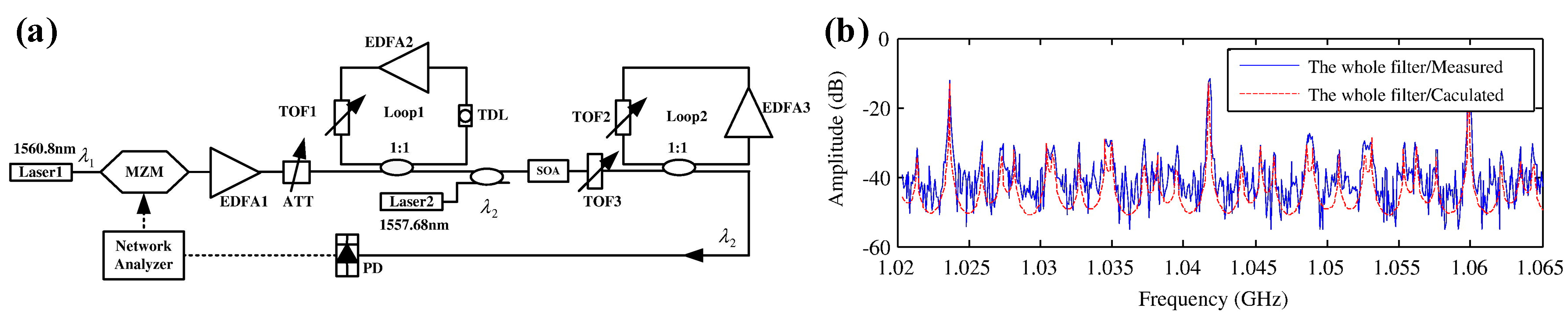
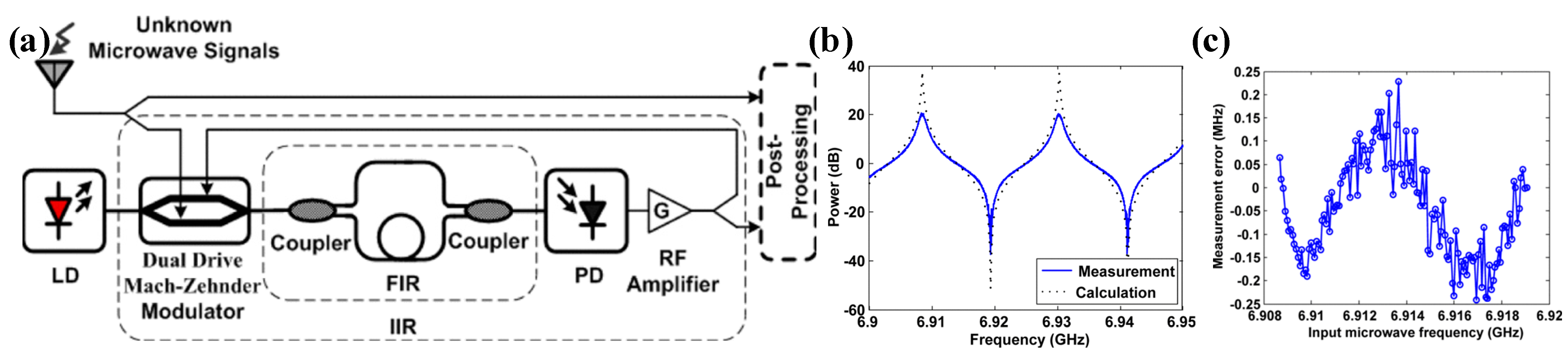
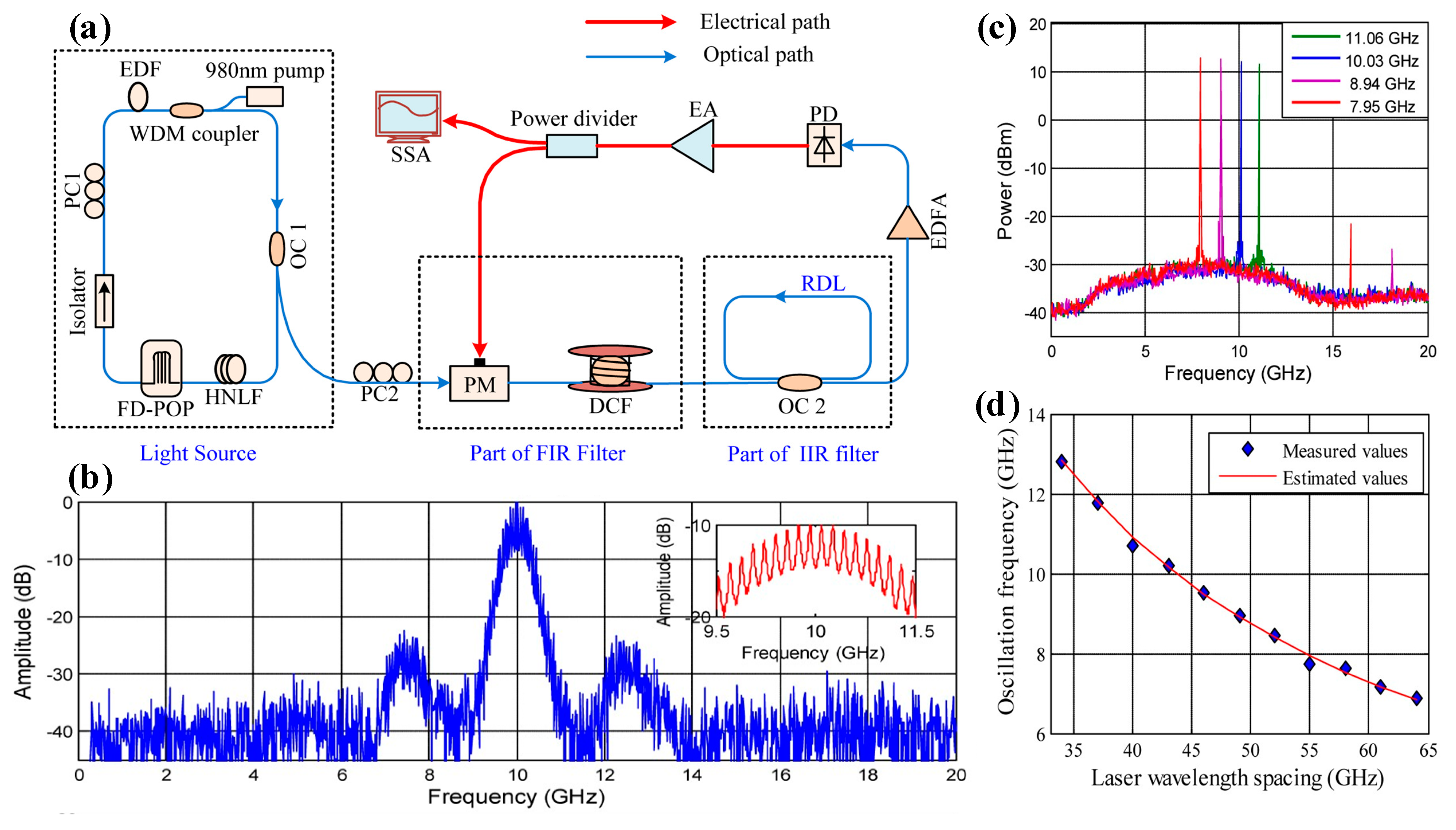
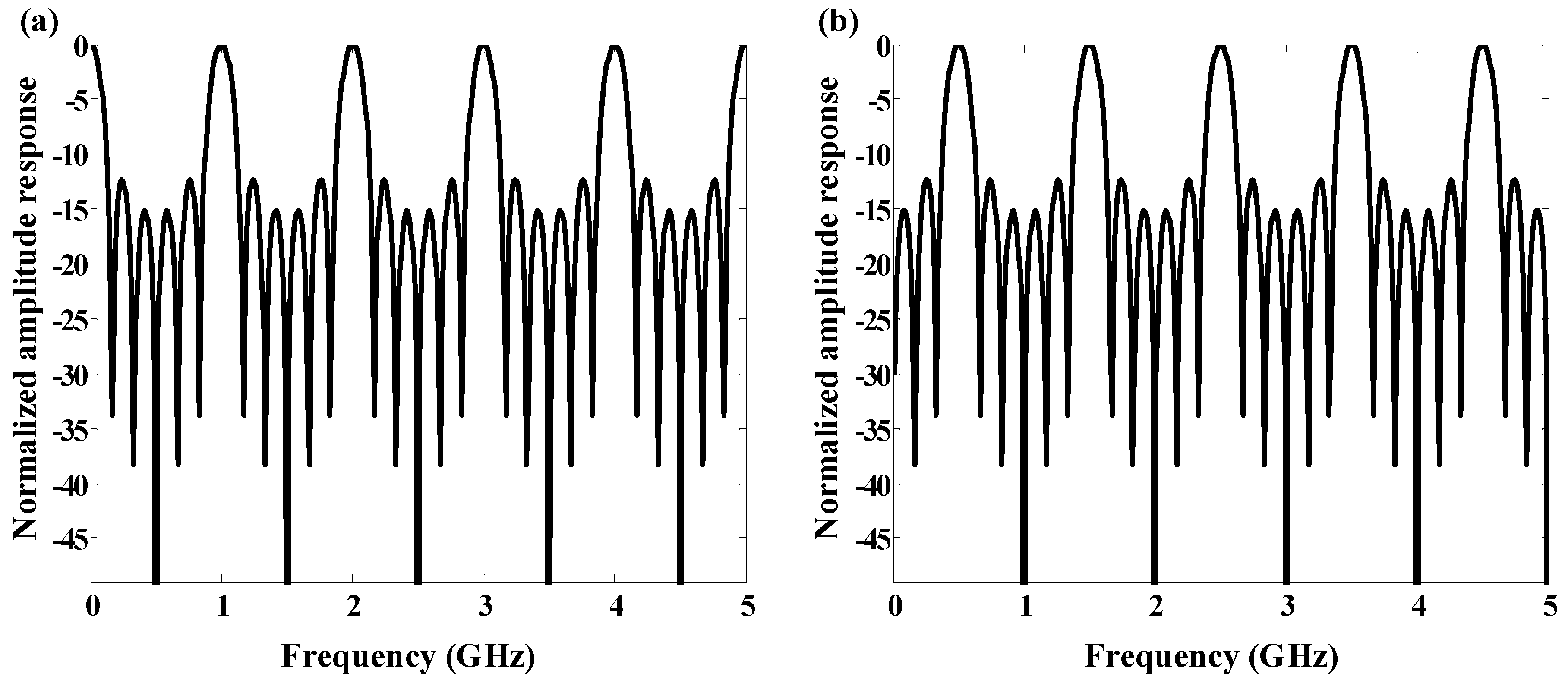
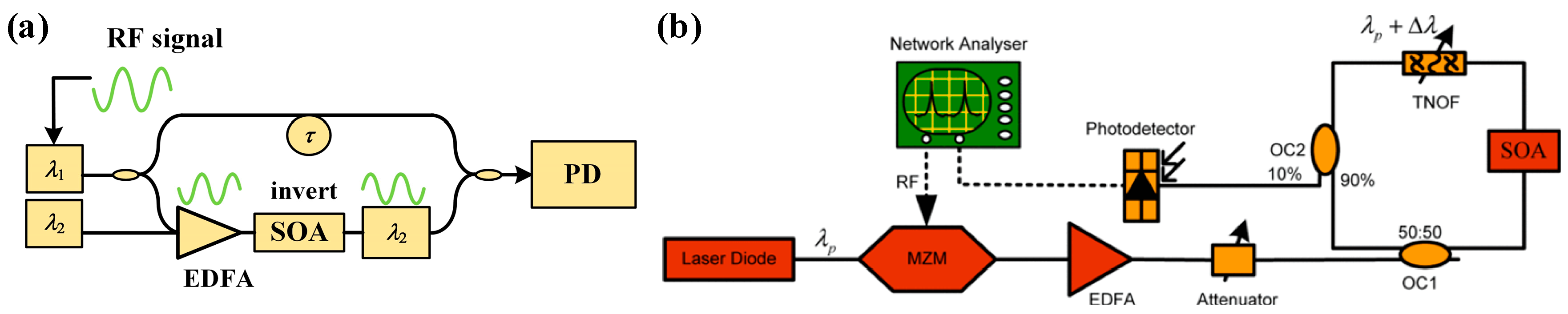


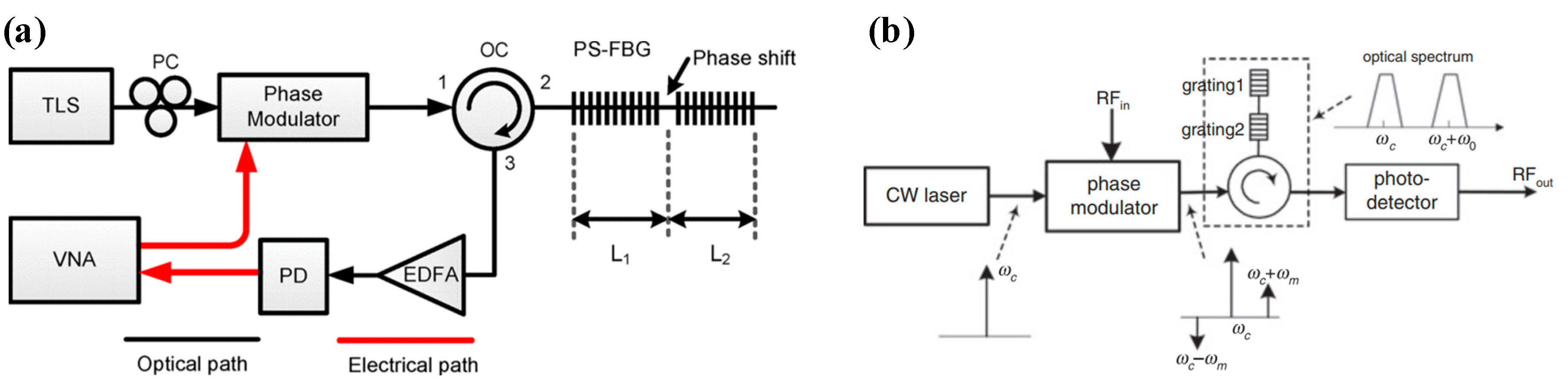
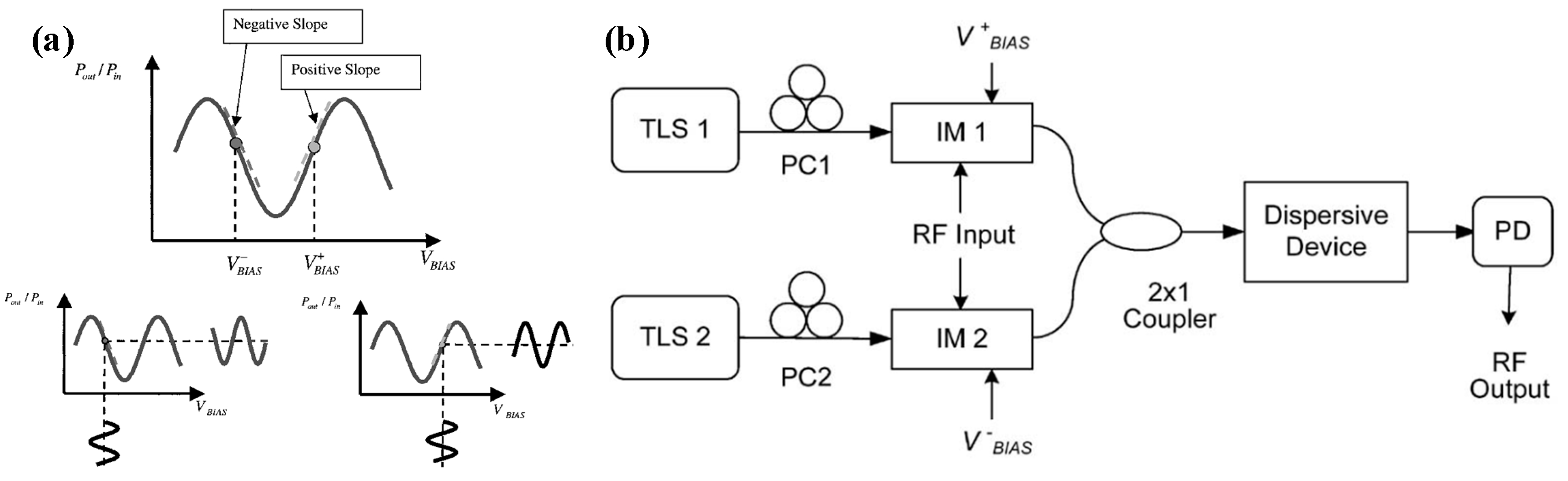
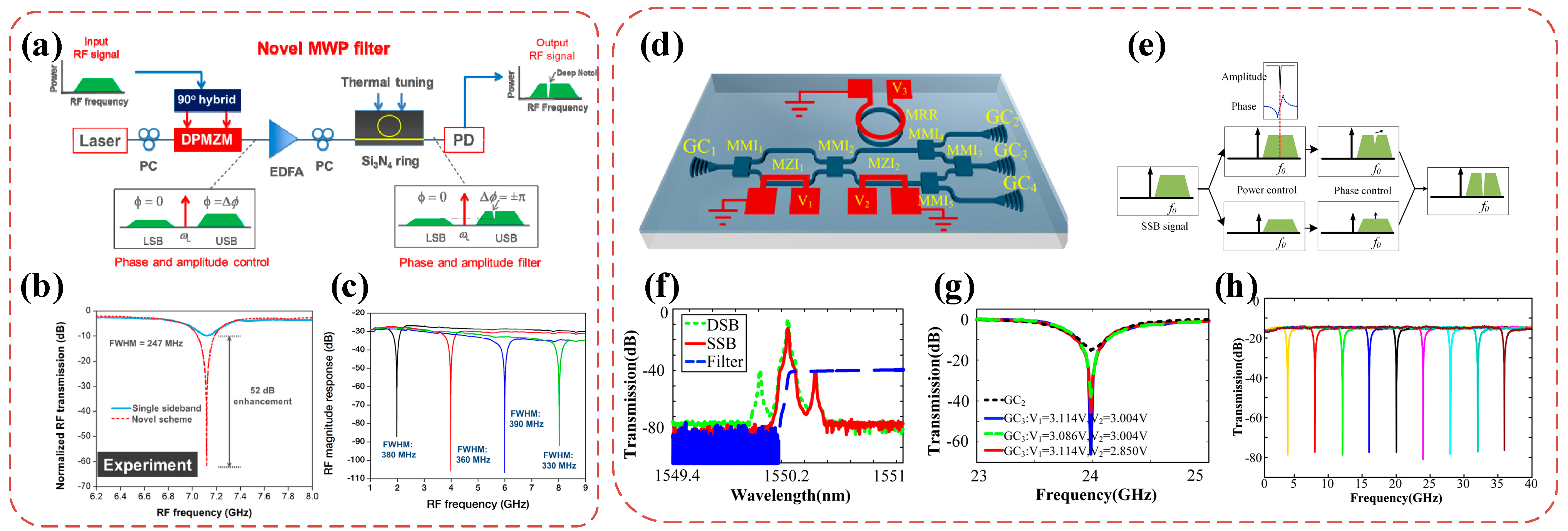

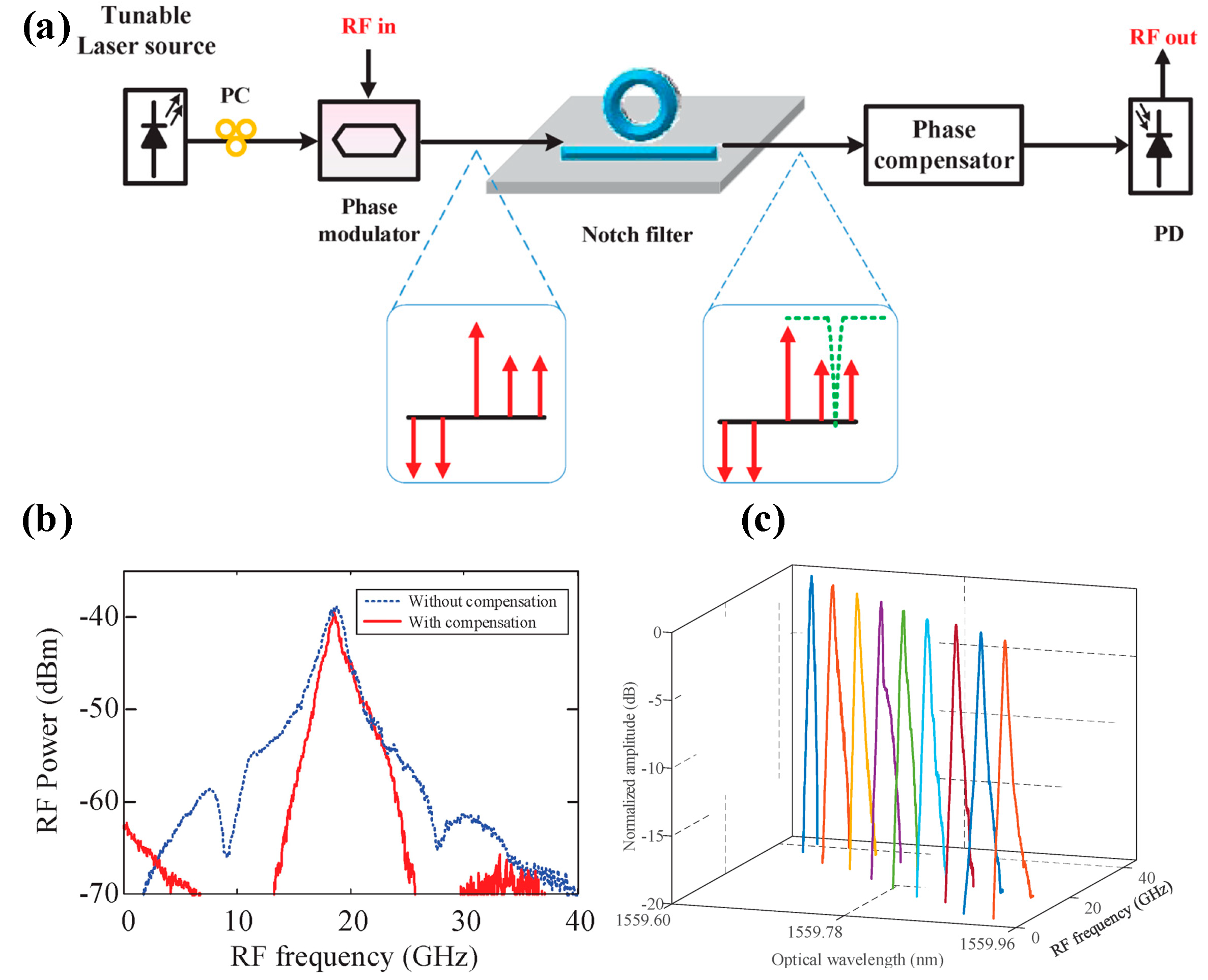
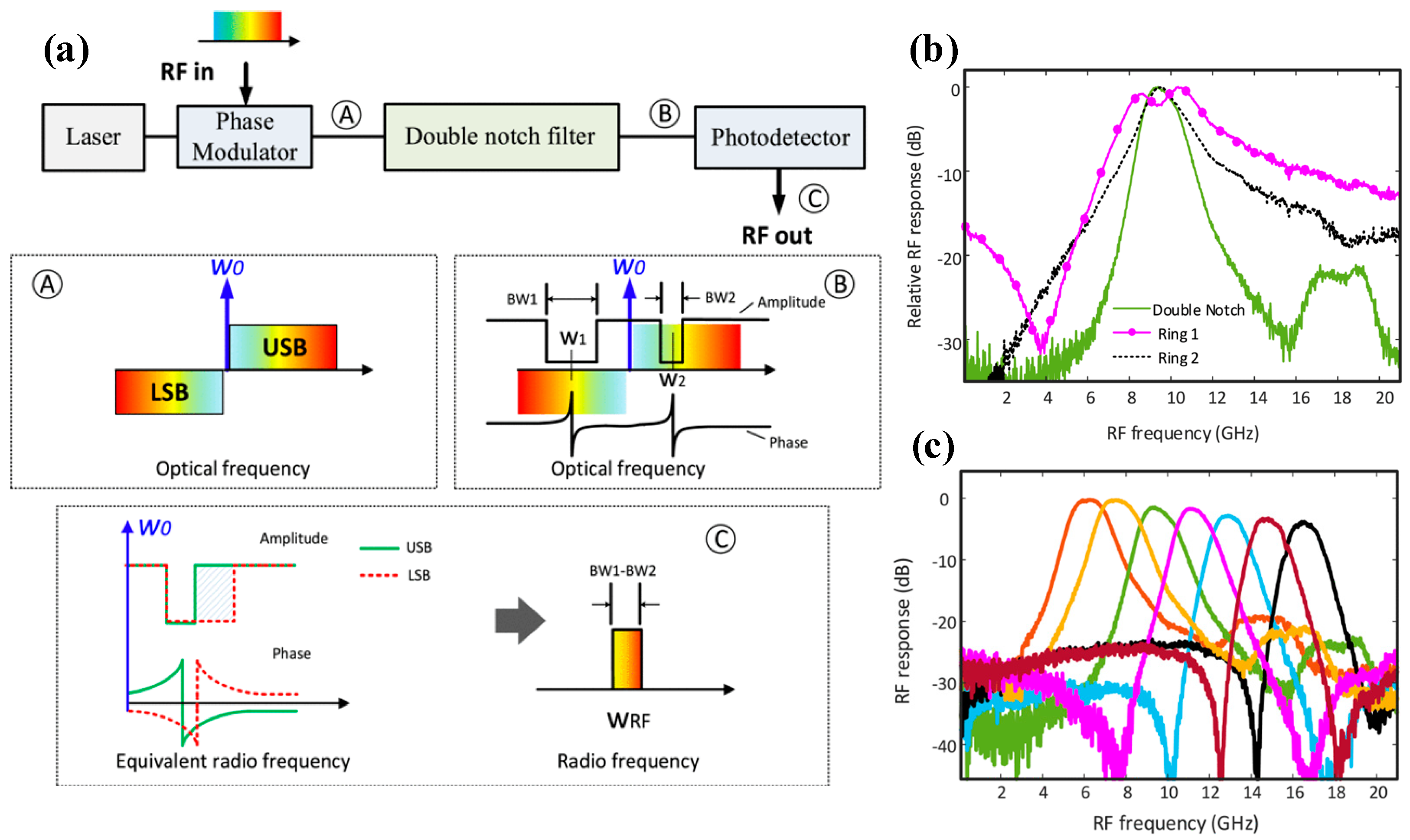
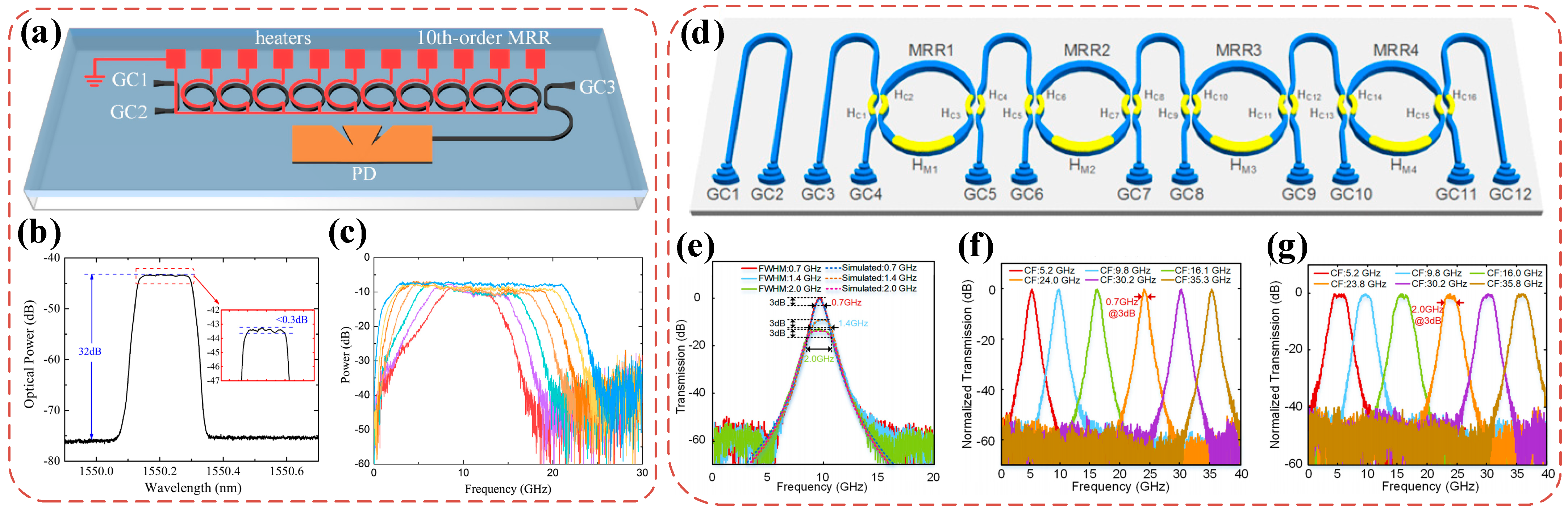
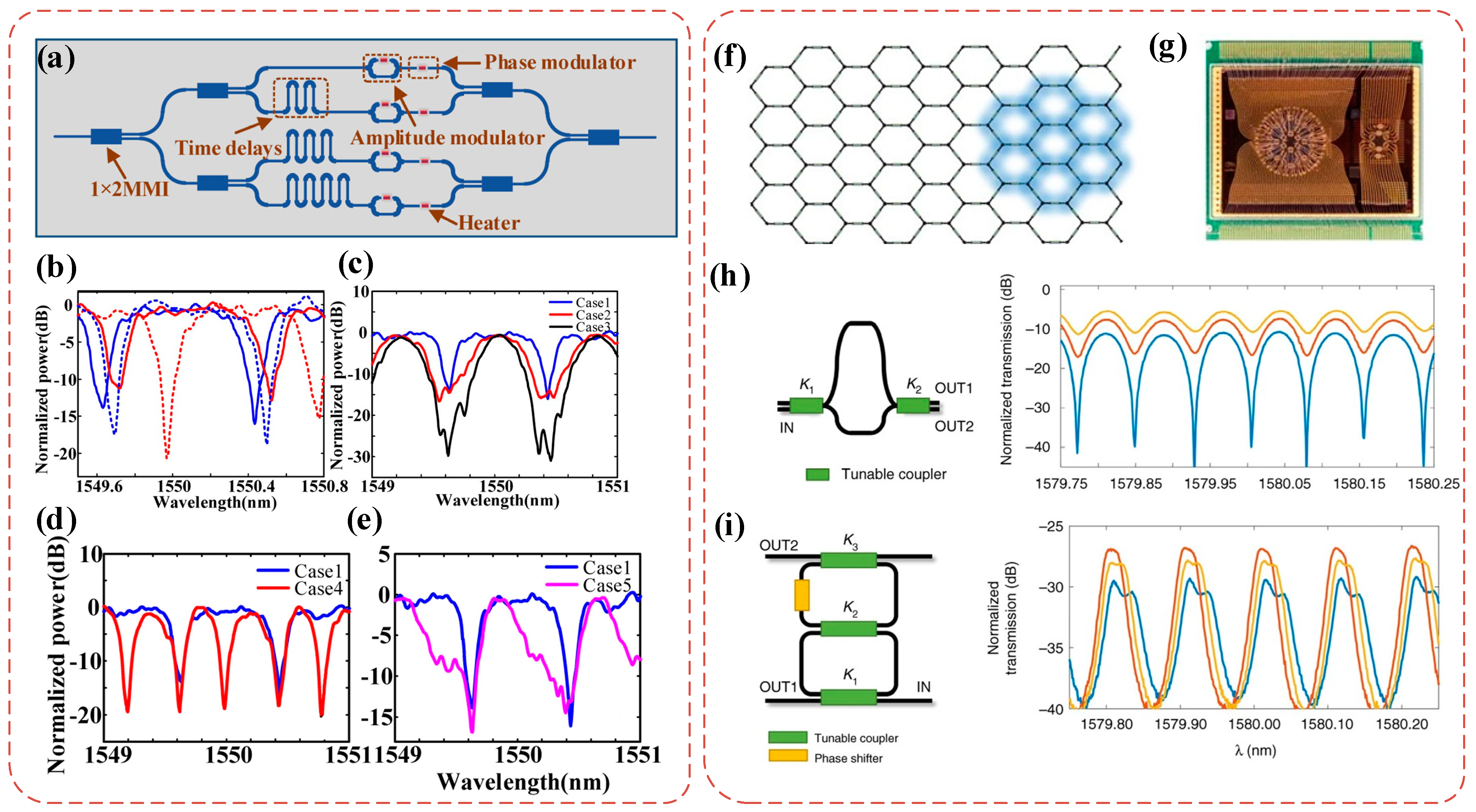
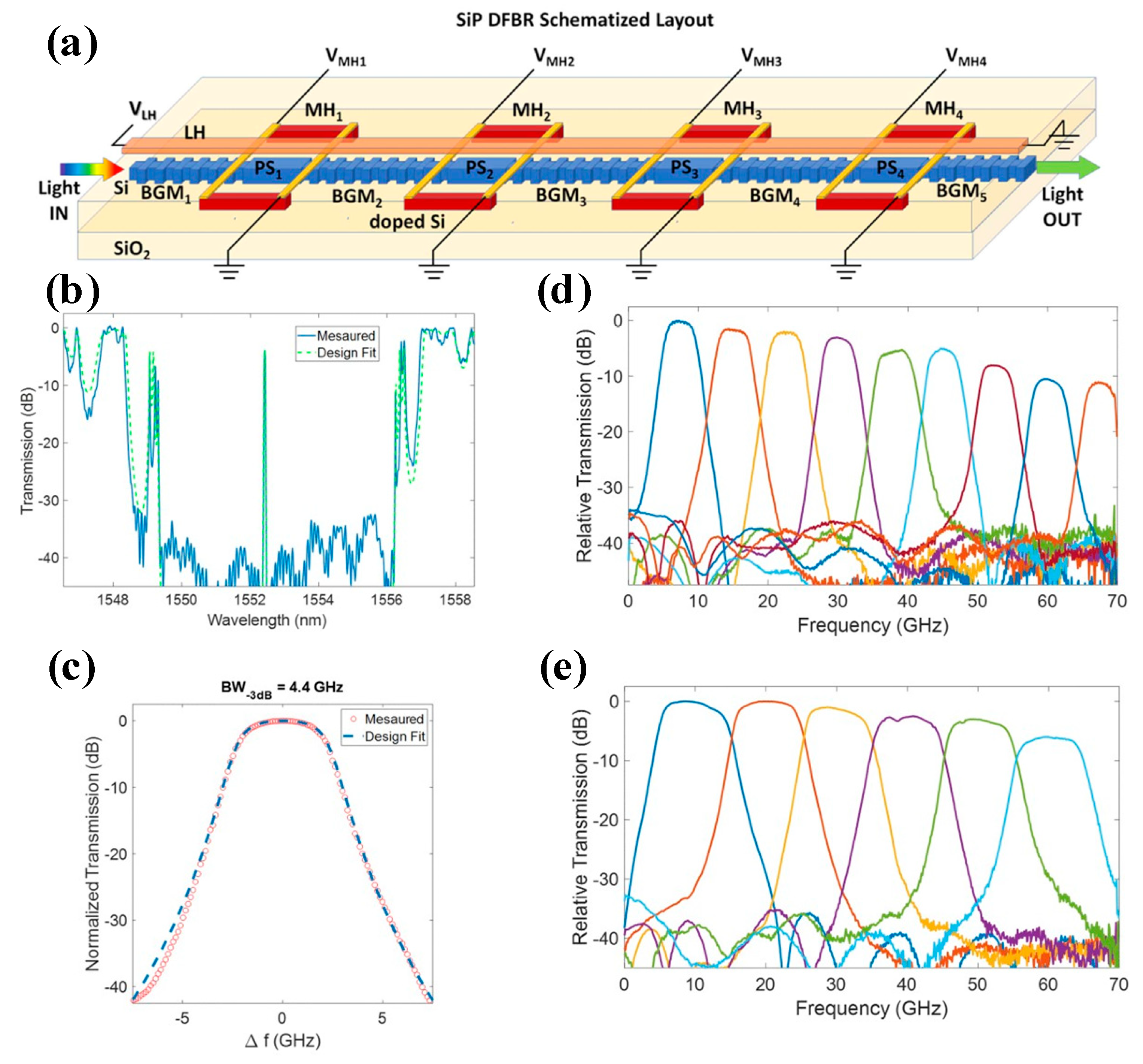


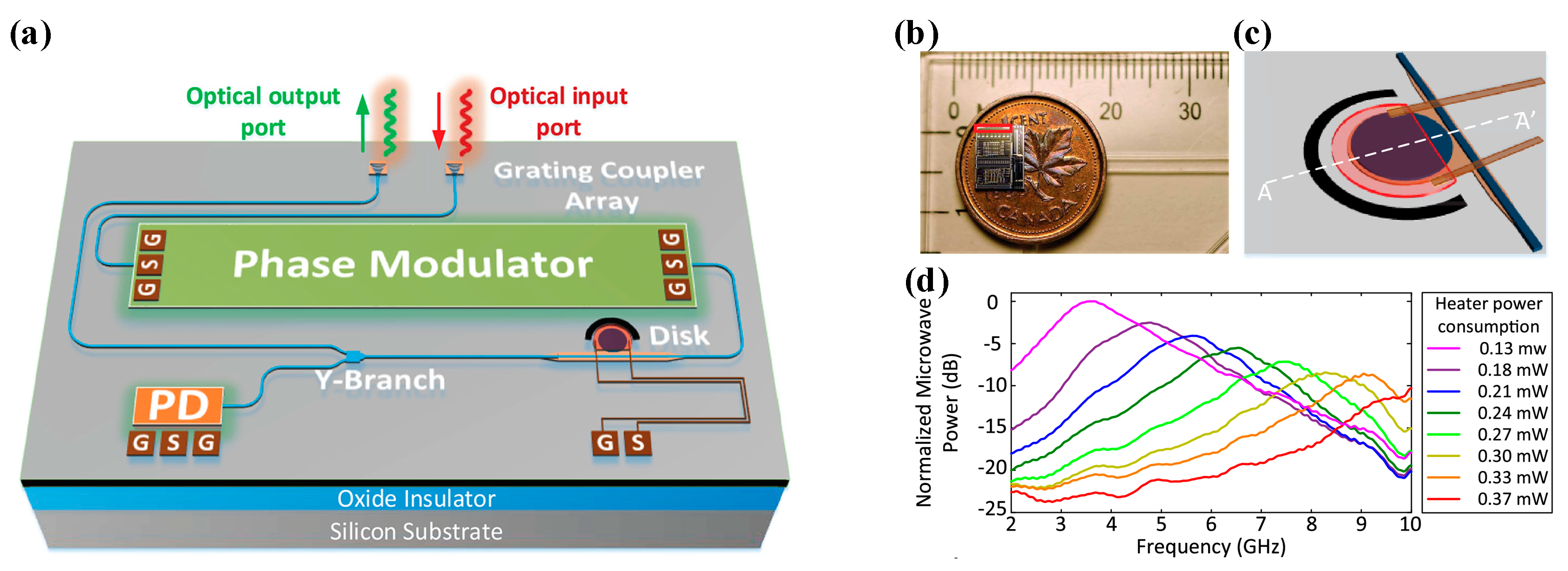
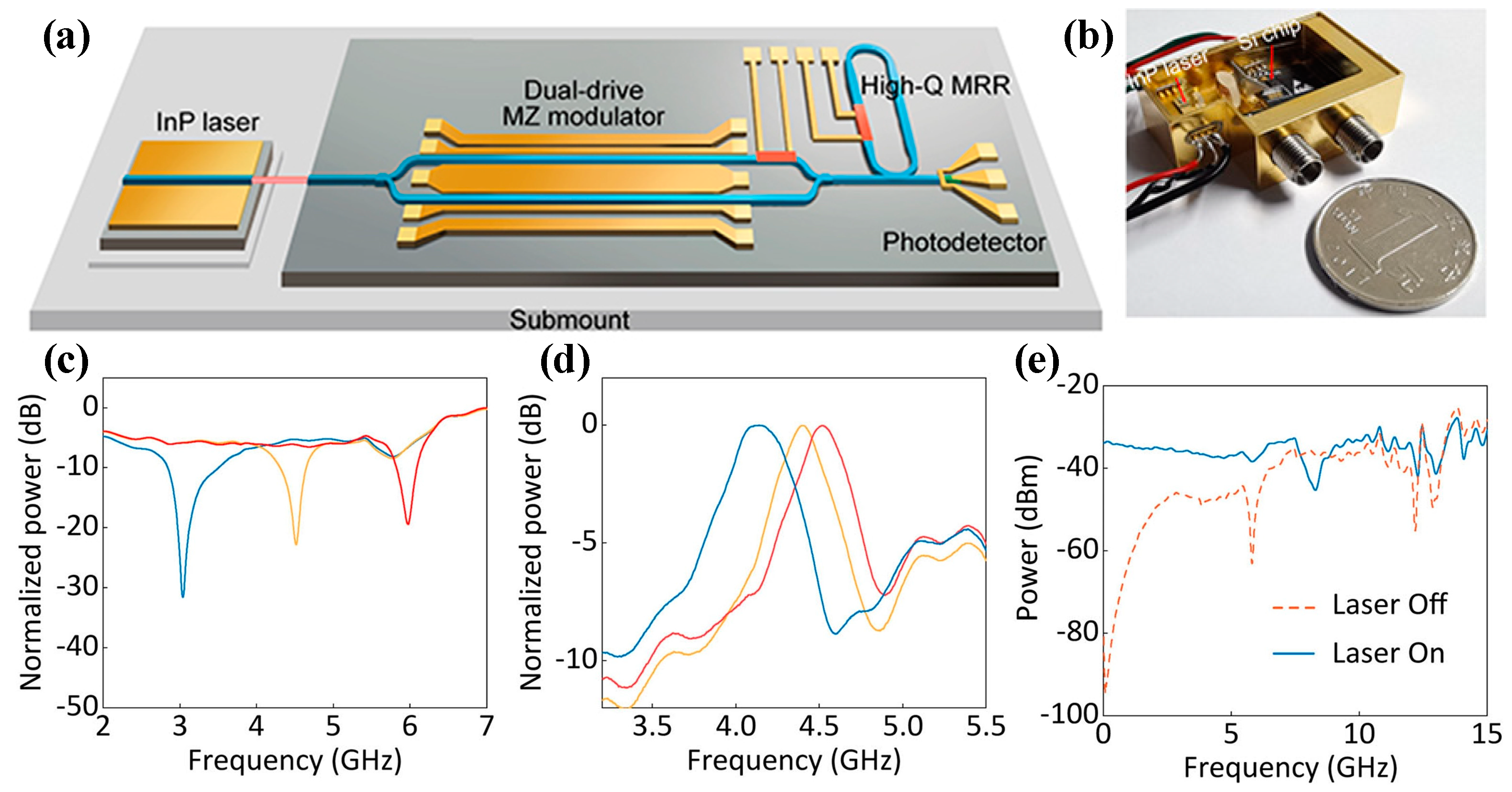
| Platform | Filter Type | FWHM Bandwidth (GHz) | Tunable Range (GHz) | Rejection Ratio (dB) | Gain (dB) | Noise Figure (dB) | SFDR * (dB/Hz2/3) |
|---|---|---|---|---|---|---|---|
| RF [103] | Bandpass | 0.025 | 3–5.6 | 40 | −3.1 | 3.1 | 137 |
| As2S3 [104] | Band-stop | 3 | 0–15 | >40 | −10.1 | 27.1 | 96.5 |
| InP [81] | Bandpass | 1.9–5.4 | 0–27 | 32 | N/A | 23.2 | 86.3 |
| InP + SOI [105] | Bandpass/ Band-stop | 0.36–0.47/ 0.38–0.45 | 3–21/ 3–25 | >10/ >40 | −28.2 | 51.2 | 99.7 |
| SOI [106] | Band-stop | 0.78 | 0–40 | 60 | N/A | N/A | N/A |
| SOI [107] | Bandpass | 0.7–5.2 | 2–35.8 | 51 | 8.97 | 33 | 90.1 |
| Si3N4 [108] | Band-stop | 0.15–0.35 | 0–12 | 50 | 8 | 15.6 | 116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Wang, L.; Liu, Y.; Yu, Y.; Zhang, X. Microwave Photonic Filters and Applications. Photonics 2023, 10, 1110. https://doi.org/10.3390/photonics10101110
Zhou Y, Wang L, Liu Y, Yu Y, Zhang X. Microwave Photonic Filters and Applications. Photonics. 2023; 10(10):1110. https://doi.org/10.3390/photonics10101110
Chicago/Turabian StyleZhou, Yi, Lin Wang, Yifan Liu, Yuan Yu, and Xinliang Zhang. 2023. "Microwave Photonic Filters and Applications" Photonics 10, no. 10: 1110. https://doi.org/10.3390/photonics10101110
APA StyleZhou, Y., Wang, L., Liu, Y., Yu, Y., & Zhang, X. (2023). Microwave Photonic Filters and Applications. Photonics, 10(10), 1110. https://doi.org/10.3390/photonics10101110





