3.2. Sparse Autoencoder Network
Sparse autoencoder [
15] is an unsupervised learning algorithm used for learning feature representation. It is a type of autoencoder neural network that transforms input data into a series of encoding values and reconstructs them back to the original inputs using a decoder. Its main target is to extract important features from high-dimensional data sets by learning a low-dimensional representation. During this process, sparse autoencoder usually imposes sparsity constraints on encoding values to make the learned features more robust and interpretable. A standard sparse autoencoder model typically consists of three parts: encoder; decoder; and loss function.
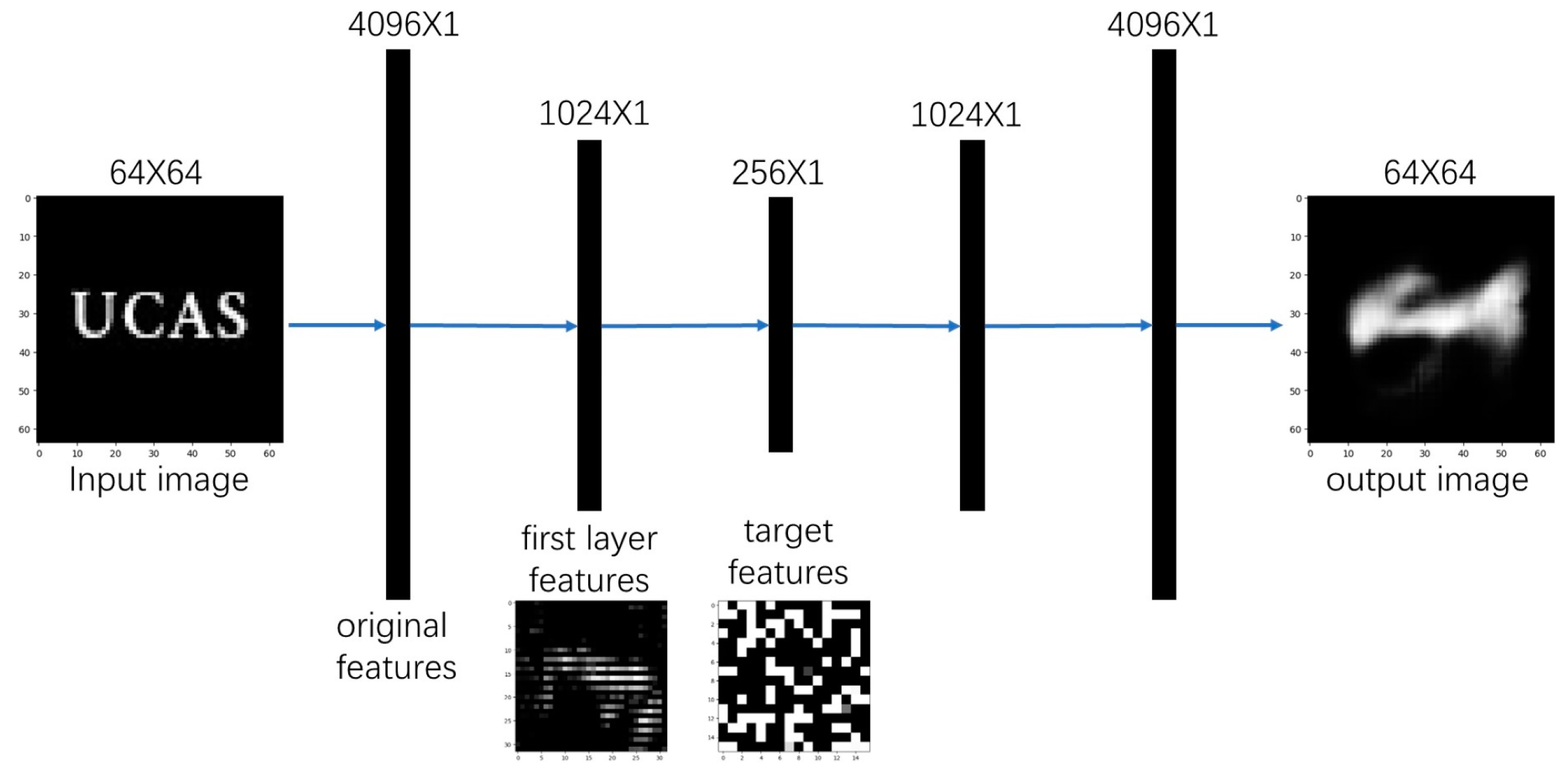
Figure 2 shows a diagram of a simple sparse autoencoder.
In its specific structure, the original image UCAS image is given as input; then, the image is first transformed into a low-dimensional feature vector through the encoder. The encoder consists of fully connected layers, which compress the low-dimensional feature vector in a feature-specific manner. Then, the compressed feature vector is fed into the hidden layer, and the activation function of the hidden layer is usually selected as Sigmoid or ReLU. In the hidden layer, regularization of the activation value is necessary to handle issues caused by insufficient activation leading to overfitting. The activation value is adjusted to the sparsity constraint, and a sparse vector is output to the decoder. When this sparse vector reaches the decoder, it is projected onto a fully connected output layer first, which is equal in size to the pixels of the image. Then, the output of this layer will enter the reversal embedding operation, which remaps the high-dimensional feature vector compressed by the encoder back to the original input space and is used for reconstructing the original image. The feature extraction diagram is shown in
Figure 3.
In a sparse autoencoder, if the dimension of the hidden layer is greater than or equal to the input dimension, its parameters will simply store the input data and output them when required. Although this method achieves high accuracy during training, the neural network will experience overfitting when mapping the data identically. To prevent the autoencoder network from mechanically copying the input to the output, it is necessary to learn an under-complete representation of the input that forces it to capture the most relevant features in the training data. This approach is often used to extract the most useful features from the input signal.
Throughout the encoding and decoding process, to control the activity level of neurons in the hidden layer, the sparse autoencoder introduces a sparsity constraint term in the loss function, which constrains the activation status of the hidden layer to obtain better feature abstractions and sparse representations. The loss function of the sparse autoencoder consists of two key parts: reconstruction error and sparsity penalty. The reconstruction error, named MSE loss, is mainly used to constrain the error of the model’s decoder when reconstructing the sample, while the sparsity penalty forces the encoder model to learn encoding values that conform to a certain sparsity level. This model can optimize the weights of the autoencoder based on the reconstruction error, while sparse regularization can be achieved by restricting the weights of the encoder or adding a penalty term to the loss function. The sparsity coefficient is a hyperparameter in the network that determines how much non-zero encoding should be learned. A low sparsity coefficient means that the network can learn more non-zero encoding to be more adaptive to noise.
Finally, the model training is completed by optimizing the loss function, including the reconstruction error from the decoder output and the sparsity constraint from the hidden layer output. This approach allows for the gradual optimization of the parameters of the encoder and decoder, enabling the autoencoder to learn the characteristics of input data and better reconstruct input images.
In image reconstruction, sparse autoencoder has certain advantages compared to other neural networks such as dual fully connected layer autoencoder and U-Net. Firstly, when the activation rate of the intermediate hidden layer of the sparse autoencoder is limited, it not only increases the compression degree of the image but also improves the modeling of local rules and the effect of eliminating image noise. Secondly, sparse autoencoder has fewer parameters and consumes fewer resources, making them easier to train and infer. Moreover, the feature vectors learned by sparse autoencoder are interpretable and better suited for dimensionality reduction processing of noisy images. Finally, in terms of application range, sparse autoencoders have been successfully applied in various image processing applications and perform better in traditional tasks such as low-noise, denoising, and dimensionality reduction compression.
In choosing the sparse autoencoder as a prior constraint for image reconstruction, this decision is rooted in prior work where Alain et al. [
16] established a connection between the output of a sparse autoencoder network, denoted as
, and the true data density
as described by the following Equation (3).
In the equation above, is a Gaussian kernel with a standard deviation of . This kernel is a smooth function characterized by rotational symmetry and translational invariance.
As evident from this equation, the network output is a weighted average of the image within the input neighborhood. In other words, the neural network can generate a reconstructed image that closely resembles the original image by considering the probabilities of pixel values within the input image regions, as well as the noise present in the image. This implies a smoothed and weighted relationship between the output image of the neural network and the regional pixels of the original image rather than a simple one-to-one correspondence between pixel points. This equation mathematically explains the principles underlying neural network image reconstruction and elucidates the prerequisite for employing the neural network as prior information—the neural network acting as a prior can regulate relationships among regional pixels.
Moreover,
progressively aligns with the input image x as the neural network loss (
) iteratively evolves. The change in
can be derived through simultaneous differentiation of both sides of Equation (3), resulting in Equation (4). This equation shows that the autoencoder error
is directly proportional to the smoothed gradient of the logarithmic likelihood.
This equation implies that when there is a significant variation in the region of , particularly when this region contains texture information, should also exhibit substantial changes. As the autoencoder undergoes successive training iterations, the error approaches a minimum at either local or global extrema. This indicates that within the context of image fidelity term reconstruction in this study, the proposed prior constraint can gradually guide the fidelity term toward an optimal output image that adheres to texture features. This verifies that this prior constraint facilitates the incorporation of texture information into the iterative training process.
Fundamentally, this sparse autoencoder network’s prior constraint resembles the principle of structured sparsity constraint, specifically the one-norm prior constraint. The one-norm prior sets the probabilities of insignificantly contributing pixels to zero, reducing noise and artifacts. Similarly, the sparse autoencoder network’s prior constraint regulates based on the pixel grayscale variations within regions, aiding image reconstruction. Both approaches impact reconstruction at the pixel level. Consequently, the squared autoencoder error can be used as a prior to influence image reconstruction. This motivation has led to the proposal of a single-photon compressed imaging method based on the prior constraint of the sparse autoencoder network.
In order to obtain better prior information from the SAE network, we optimized the training learning rate, network parameters, and loss function parameters, enabling the SAE prior network to better assist in image reconstruction.
3.3. Single-Pixel Imaging Based on the Sparse Autoencoder Network Prior
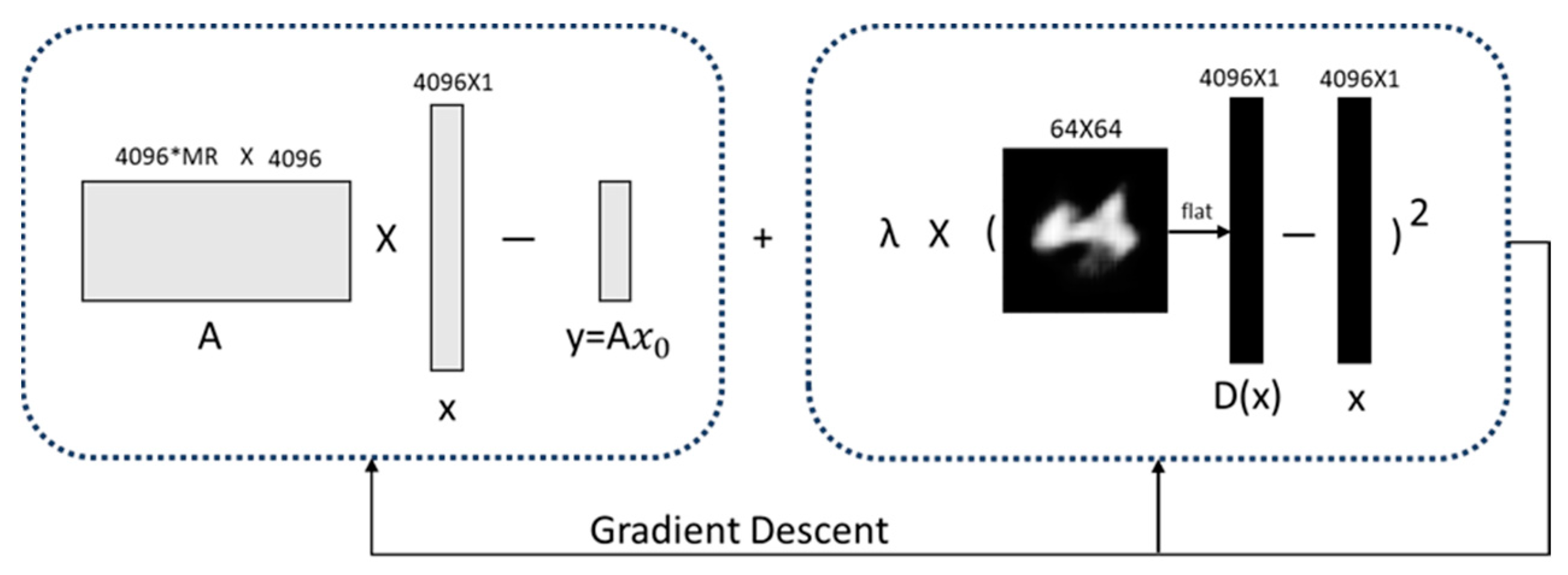
The experimental procedure is shown in
Figure 4. We can obtain the reconstruction of the image by solving the following objective function:
where
is the image to be reconstructed;
represents a partially sampled random matrix;
represents the original data obtained in the single-photon imaging system;
is the output of the network, and
is a hyperparameter, which balances the compressed sensing fidelity term and the prior constraint of the sparse autoencoder network influences.
The entire reconstruction process can be divided into two steps: training the sparse autoencoder network to obtain prior information and solving the objective function to reconstruct the image. The main difference from the classical iterative method is that during the image reconstruction process, we apply a novel prior constraint based on the sparse autoencoder network in addition to the compressive sensing fidelity term. This constraint will result in more desirable results compared to the traditional one-norm prior of the input image. The method of solving this objective function will be discussed in detail later.
The success of the sparse autoencoder prior reconstruction method mainly lies in two aspects:
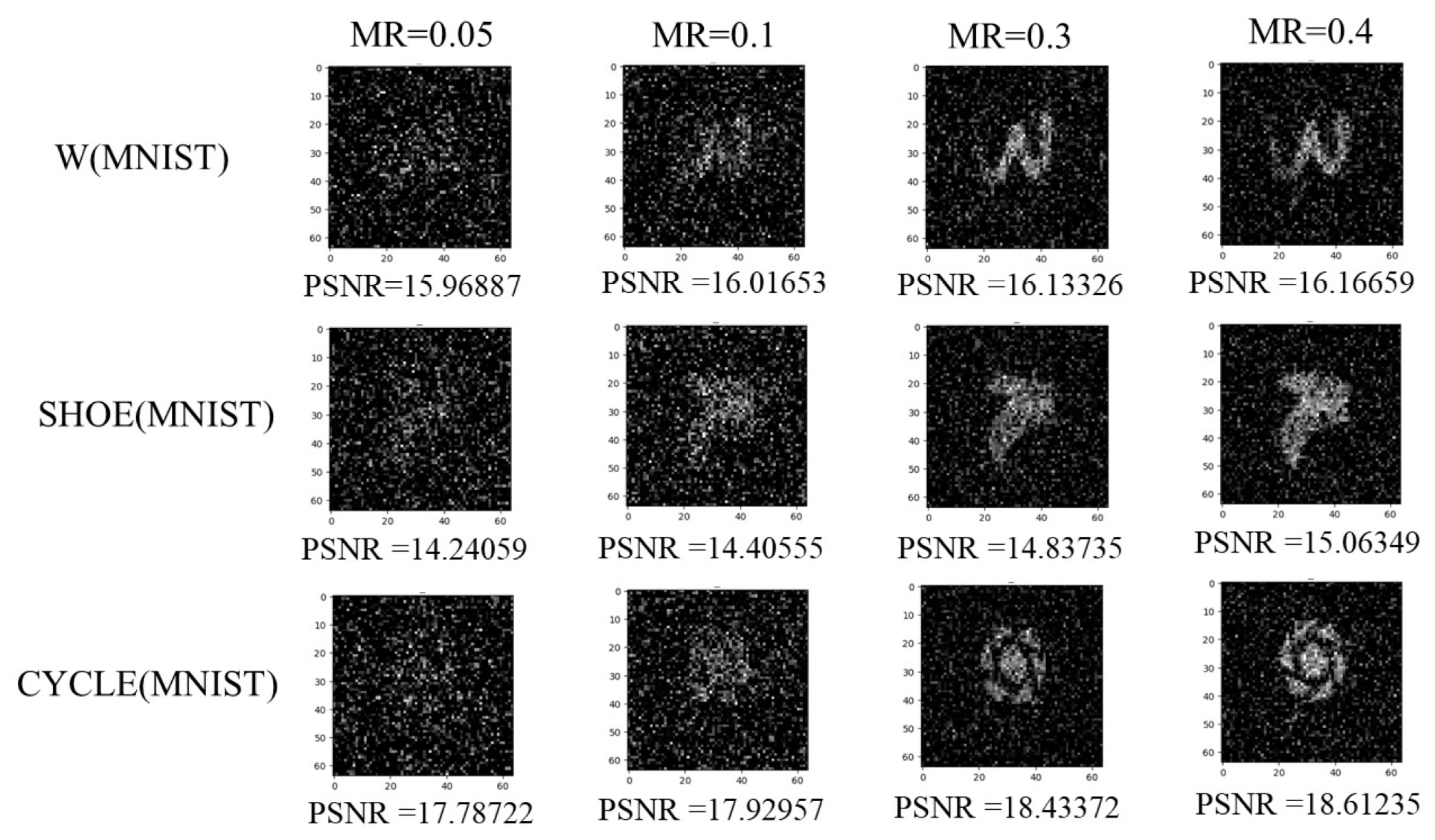
Apart from the single-channel network priors described above, the reconstruction performance can be improved by increasing the number of prior information channels, as shown in
Figure 5. We combine multiple different prior information as constraints for image reconstruction and assign them certain weights of influence. Through experiments, we reach the conclusion that single-channel network priors often have their limitations. For example, the reconstruction effect at low sampling rates is better than that at high sampling rates. The performance of multi-channel network priors can effectively express the advantages of each single-channel network prior while avoiding their shortcomings.