Multi-Channel Visibility Distribution Measurement via Optical Imaging
Abstract
:1. Introduction
2. Principle and Method
2.1. Definition of Visibility
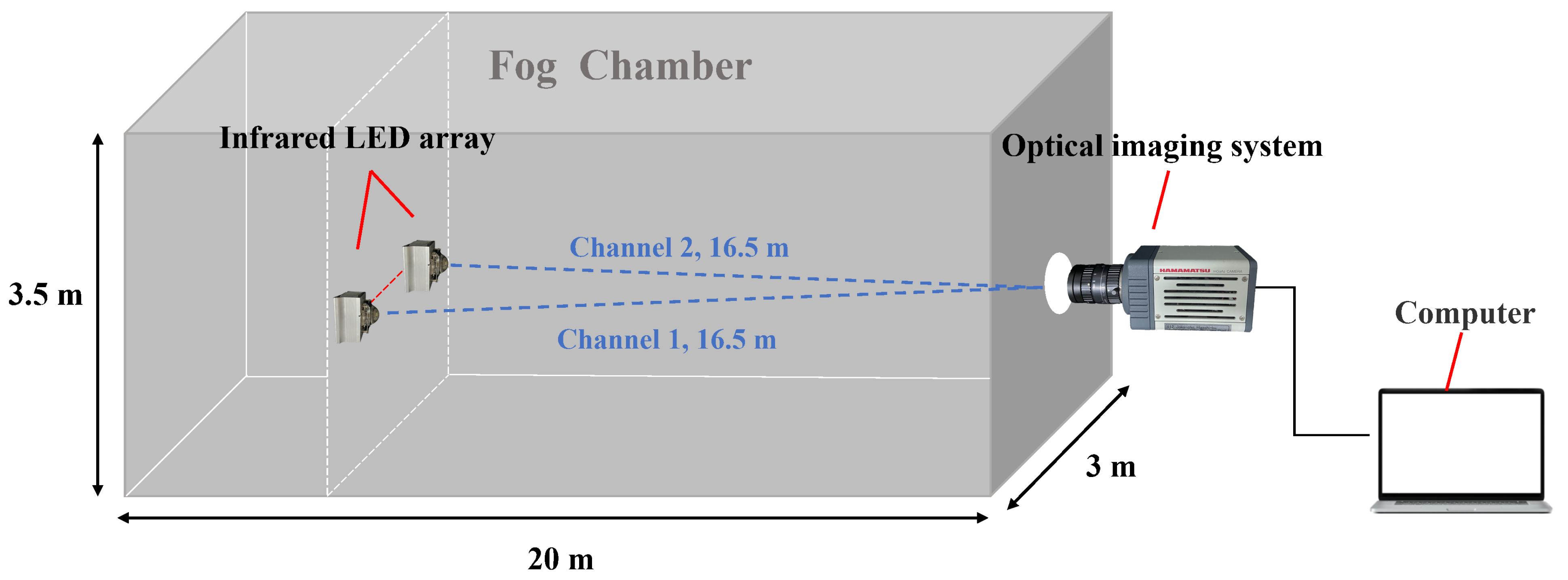
2.2. Experimental Methods
3. Results and Analysis
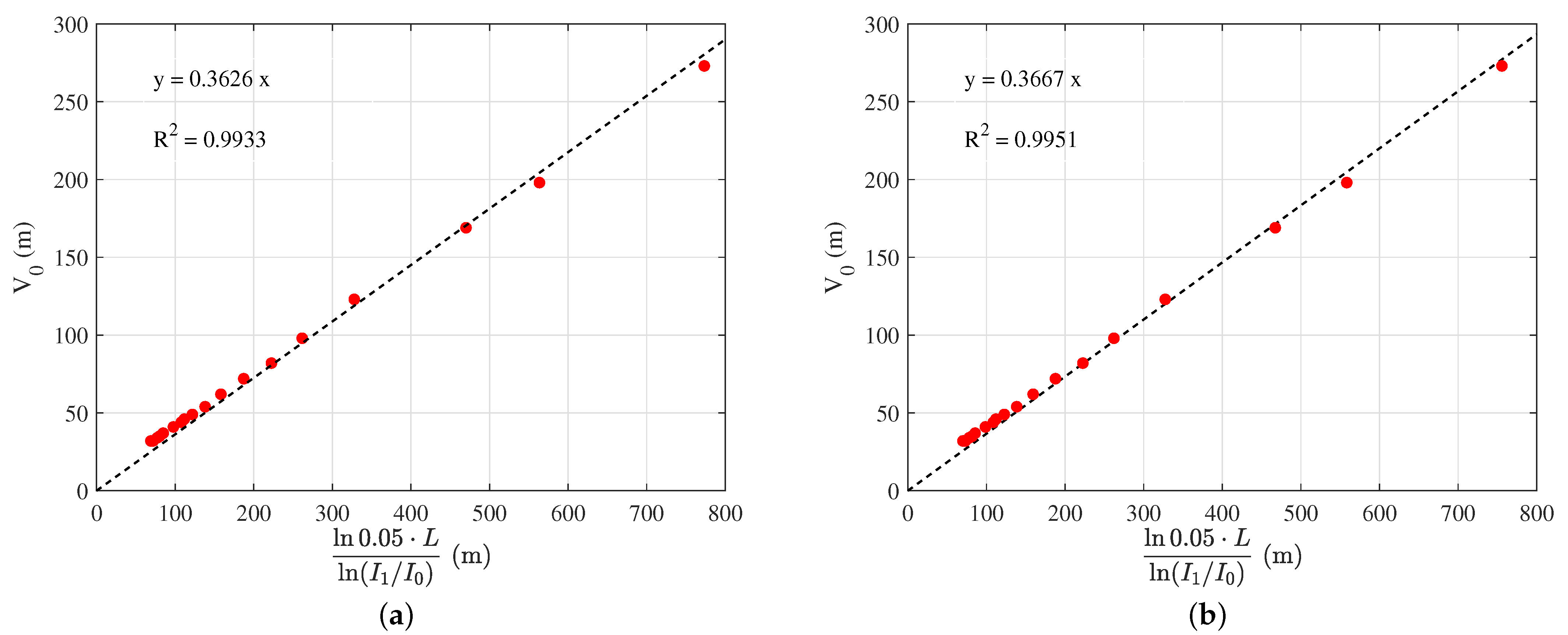
3.1. Coefficient Calibration
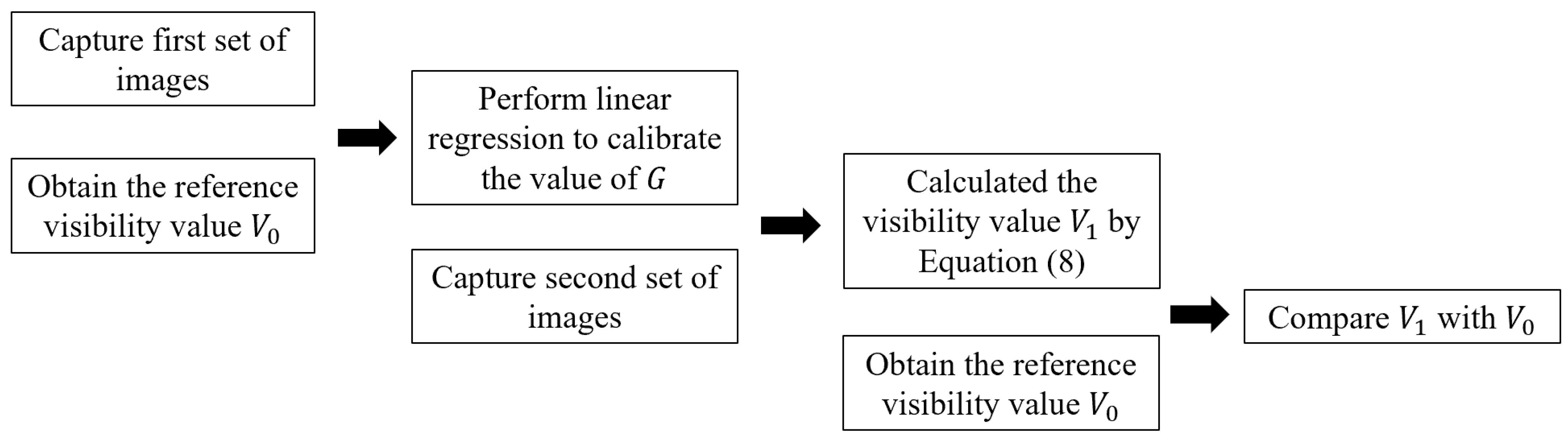
3.2. Data Processing
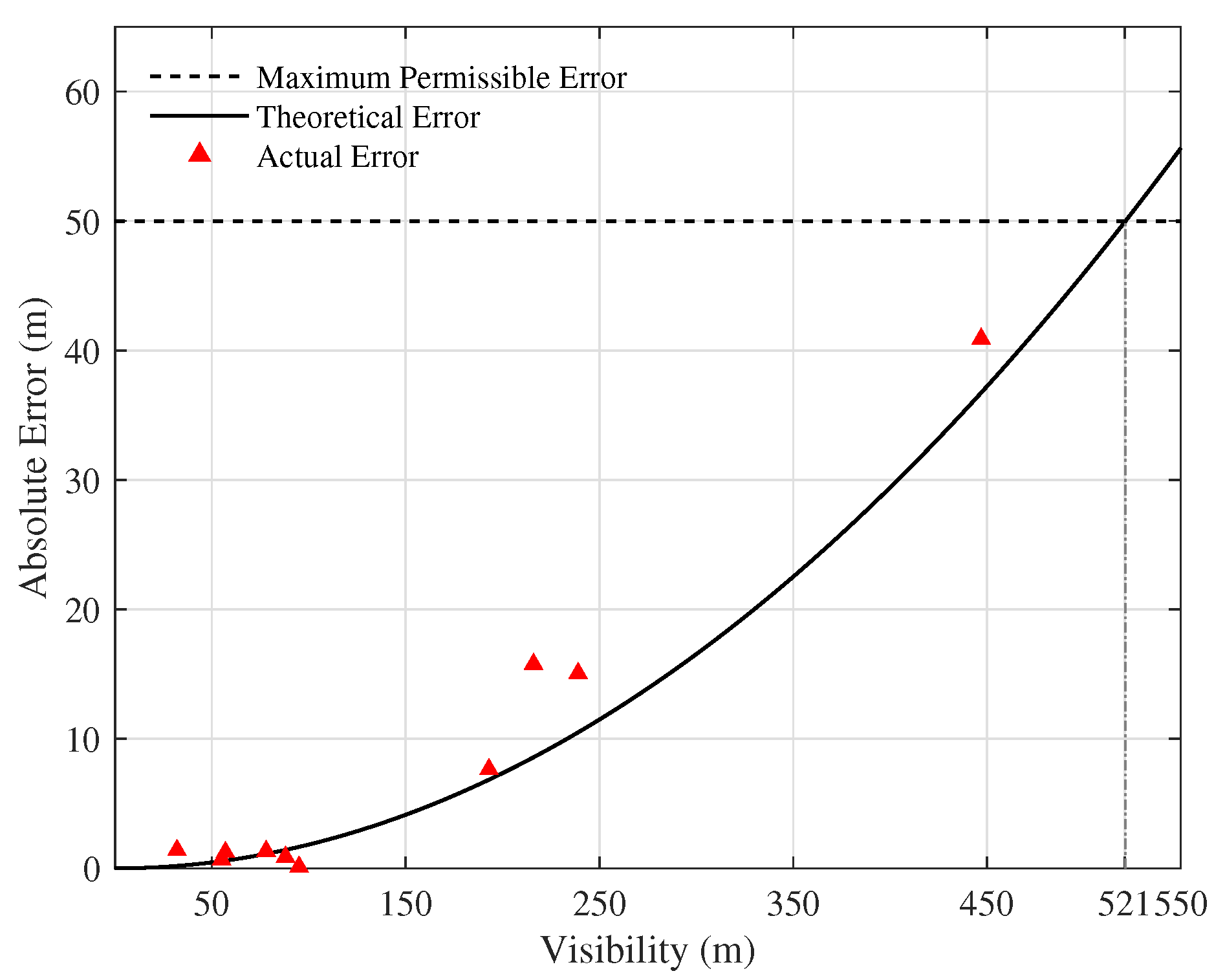
3.3. Error Analysis
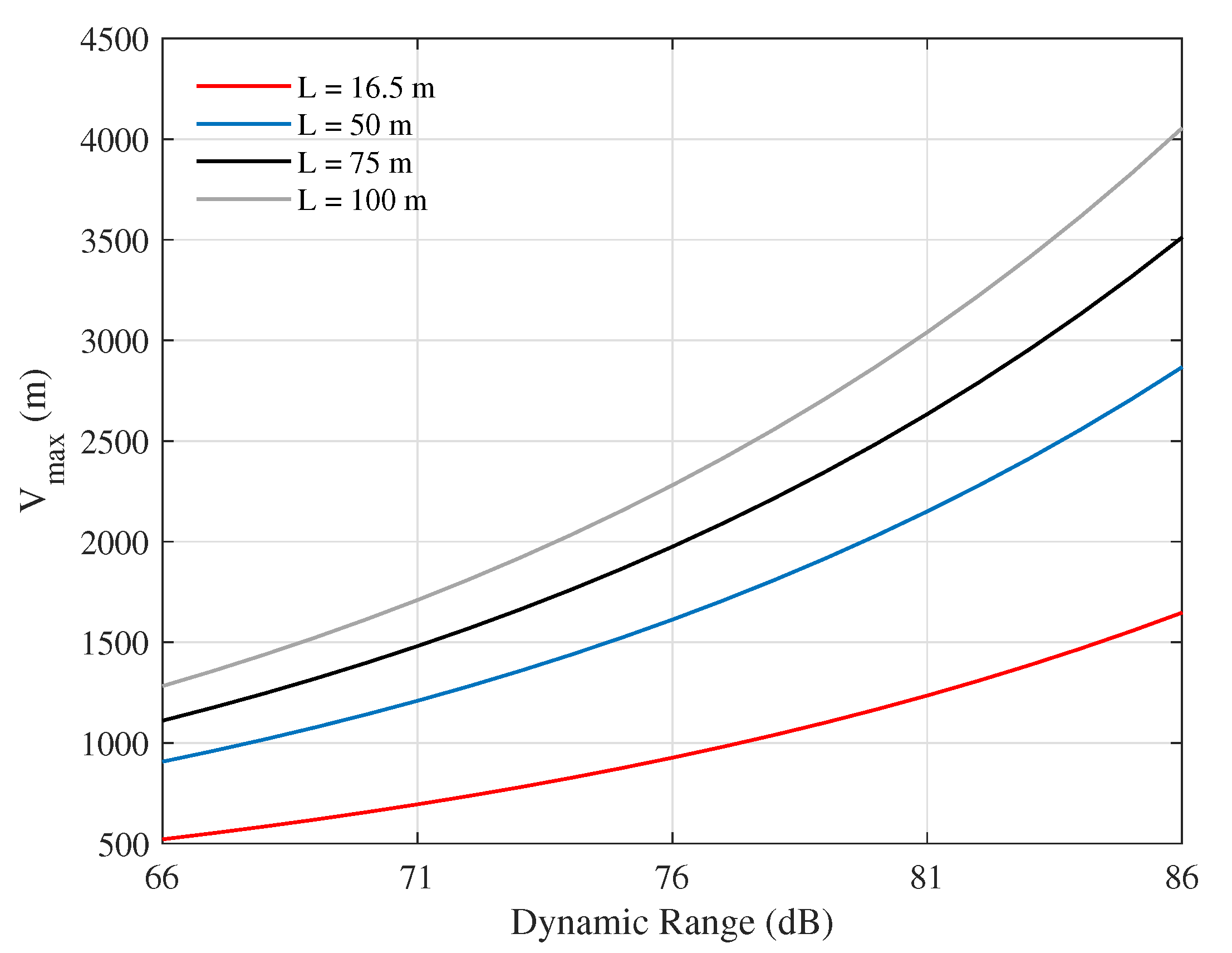
3.4. Discussion on Measurement Limitations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horvath, H. Atmospheric visibility. Atmos. Environ. (1967) 1981, 15, 1785–1796. [Google Scholar] [CrossRef]
- Kim, K.W. The comparison of visibility measurement between image-based visual range, human eye-based visual range, and meteorological optical range. Atmos. Environ. 2018, 190, 74–86. [Google Scholar] [CrossRef]
- Appel, B.; Tokiwa, Y.; Hsu, J.; Kothny, E.; Hahn, E. Visibility as related to atmospheric aerosol constituents. Atmos. Environ. (1967) 1985, 19, 1525–1534. [Google Scholar] [CrossRef]
- Lee, C.G.; Yuan, C.S.; Chang, J.C.; Yuan, C. Effects of aerosol species on atmospheric visibility in Kaohsiung city, Taiwan. J. Air Waste Manag. Assoc. 2005, 55, 1031–1041. [Google Scholar] [CrossRef] [PubMed]
- Charlson, R.J. Atmospheric visibility related to aerosol mass concentration. Environ. Sci. Technol. 1969, 3, 913–918. [Google Scholar] [CrossRef]
- Leung, A.C.; Gough, W.A.; Butler, K.A. Changes in fog, ice fog, and low visibility in the Hudson Bay Region: Impacts on aviation. Atmosphere 2020, 11, 186. [Google Scholar] [CrossRef]
- Chung, W.; Kim, S.; Choi, M.; Choi, J.; Kim, H.; Moon, C.B.; Song, J.B. Safe navigation of a mobile robot considering visibility of environment. IEEE Trans. Ind. Electron. 2009, 56, 3941–3950. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. A combined GPS/GLONASS navigation algorithm for use with limited satellite visibility. J. Navig. 2009, 62, 671–685. [Google Scholar] [CrossRef]
- Huang, S.C.; Chen, B.H.; Cheng, Y.J. An efficient visibility enhancement algorithm for road scenes captured by intelligent transportation systems. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2321–2332. [Google Scholar] [CrossRef]
- Yang, L.; Muresan, R.; Al-Dweik, A.; Hadjileontiadis, L.J. Image-based visibility estimation algorithm for intelligent transportation systems. IEEE Access 2018, 6, 76728–76740. [Google Scholar] [CrossRef]
- WMO. Guide to Instruments and Methods of Observation. Volume I: Measurement of Meteorological Variables; WMO: Geneva, Switzerland, 2020. [Google Scholar]
- Luckiesh, M.; Moss, F.K. Visibility: Its measurement and significance in seeing. J. Frankl. Inst. 1935, 220, 431–466. [Google Scholar] [CrossRef]
- Beuttell, R.; Brewer, A. Instruments for the measurement of the visual range. J. Sci. Instrum. 1949, 26, 357. [Google Scholar] [CrossRef]
- Redmond, H.E.; Dial, K.D.; Thompson, J.E. Light scattering and absorption by wind blown dust: Theory, measurement, and recent data. Aeolian Res. 2010, 2, 5–26. [Google Scholar] [CrossRef]
- Liu, W.T. Progress in scatterometer application. J. Oceanogr. 2002, 58, 121–136. [Google Scholar] [CrossRef]
- Miclea, R.C.; Dughir, C.; Alexa, F.; Sandru, F.; Silea, I. Laser and LIDAR in a system for visibility distance estimation in fog conditions. Sensors 2020, 20, 6322. [Google Scholar] [CrossRef] [PubMed]
- Shui, Y.; Zhou, J.; Huang, Y.; Shen, X.; Chen, L.; Chu, J.; Luo, X.; Liu, Y. Near-Infrared Imaging Optical Visibility Measurement System and Method. Chinese Patent Publication No. CN115326748A, 11 November 2022. [Google Scholar]
- Li, M.; Fan, D.Q.; Yin, C.Y. Study on corresponding relation of laser and infrared transmittivity for smoke screen. J. Infrared Millim. Waves 2006, 25, 127–130. [Google Scholar]
- International Civil Aviation Organization. Meteorological Service for International Air Navigation; International Civil Aviation Organization: Montreal, QC, Canada, 1976. [Google Scholar]
- Schnapf, J.; Kraft, T.; Baylor, D. Spectral sensitivity of human cone photoreceptors. Nature 1987, 325, 439–441. [Google Scholar] [CrossRef] [PubMed]
- Ijaz, M.; Ghassemlooy, Z.; Pesek, J.; Fiser, O.; Le Minh, H.; Bentley, E. Modeling of fog and smoke attenuation in free space optical communications link under controlled laboratory conditions. J. Light. Technol. 2013, 31, 1720–1726. [Google Scholar] [CrossRef]
- Ma, S.; Xu, F.E.; Jietai, M.A.; Liu, D.; Zhang, C.; Ling, Y.; Zhen, X. Experimental Research on Visibility Reference Standard for Blackbody Targets. J. Appl. Meteorol. Sci. 2014, 25, 129–134. [Google Scholar]
- Kim, I.I.; McArthur, B.; Korevaar, E.J. Comparison of laser beam propagation at 785 nm and 1550 nm in fog and haze for optical wireless communications. In Optical Wireless Communications III; SPIE: Bellingham, WA, USA, 2001; Volume 4214, pp. 26–37. [Google Scholar]
- CMA. Test Method for Forward Scattering Visibility Meter; CMA: Beijing, China, 2020. [Google Scholar]



| Channel 1 | Channel 2 | |
|---|---|---|
| G | 0.3626 | 0.3667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Shui, Y.; Chen, L.; Li, M.; Chu, J.; Shen, X.; Liu, Y.; Zhou, J. Multi-Channel Visibility Distribution Measurement via Optical Imaging. Photonics 2023, 10, 945. https://doi.org/10.3390/photonics10080945
Chen L, Shui Y, Chen L, Li M, Chu J, Shen X, Liu Y, Zhou J. Multi-Channel Visibility Distribution Measurement via Optical Imaging. Photonics. 2023; 10(8):945. https://doi.org/10.3390/photonics10080945
Chicago/Turabian StyleChen, Lingye, Yuyang Shui, Libang Chen, Ming Li, Jinhua Chu, Xia Shen, Yikun Liu, and Jianying Zhou. 2023. "Multi-Channel Visibility Distribution Measurement via Optical Imaging" Photonics 10, no. 8: 945. https://doi.org/10.3390/photonics10080945
APA StyleChen, L., Shui, Y., Chen, L., Li, M., Chu, J., Shen, X., Liu, Y., & Zhou, J. (2023). Multi-Channel Visibility Distribution Measurement via Optical Imaging. Photonics, 10(8), 945. https://doi.org/10.3390/photonics10080945






