High-Quality Laser-Accelerated Ion Beams from Structured Targets
Abstract
1. Introduction
2. Methods
3. Results
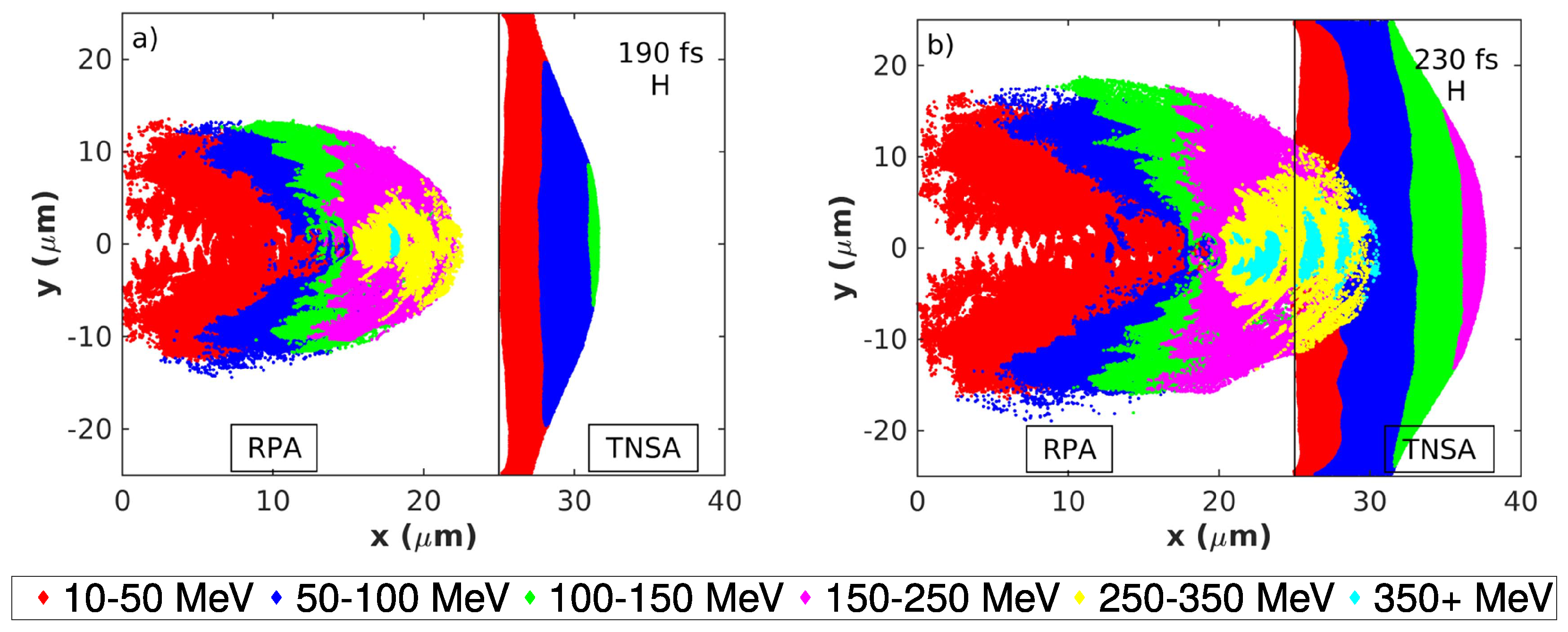
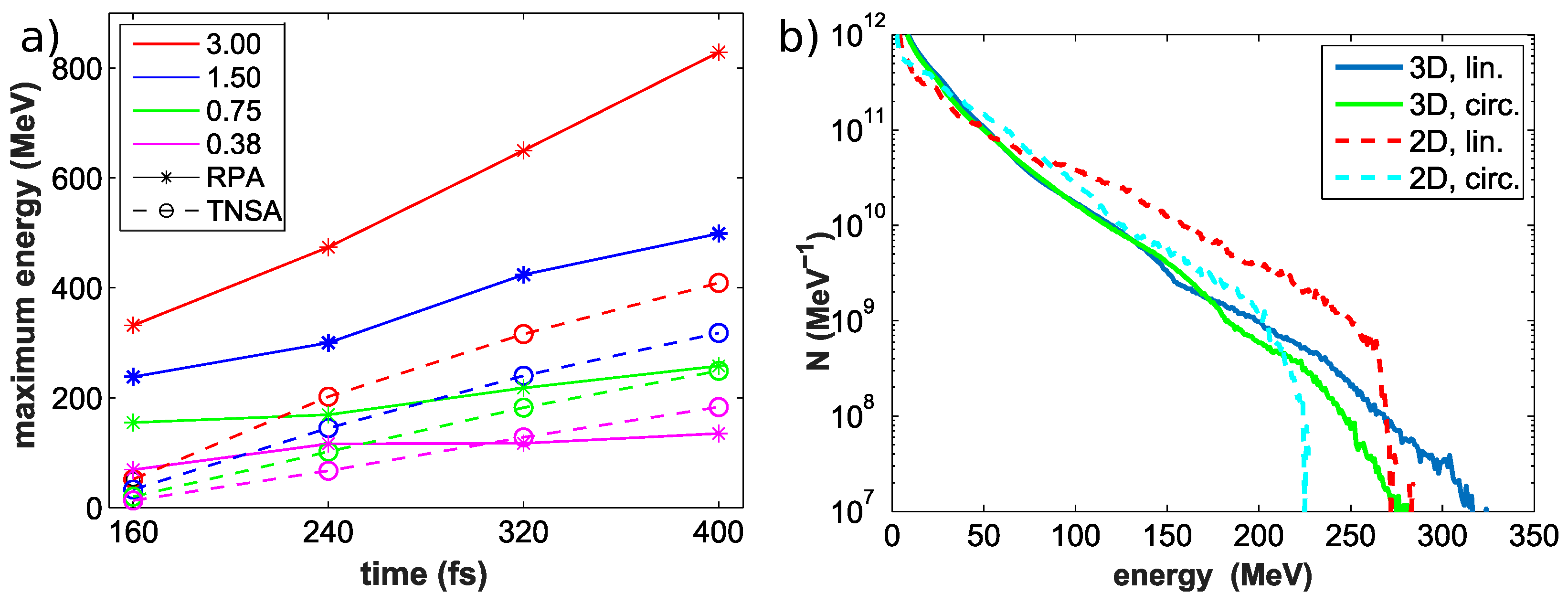
3.1. The Prominence of Different Acceleration Mechanisms Using Cryogenic Targets
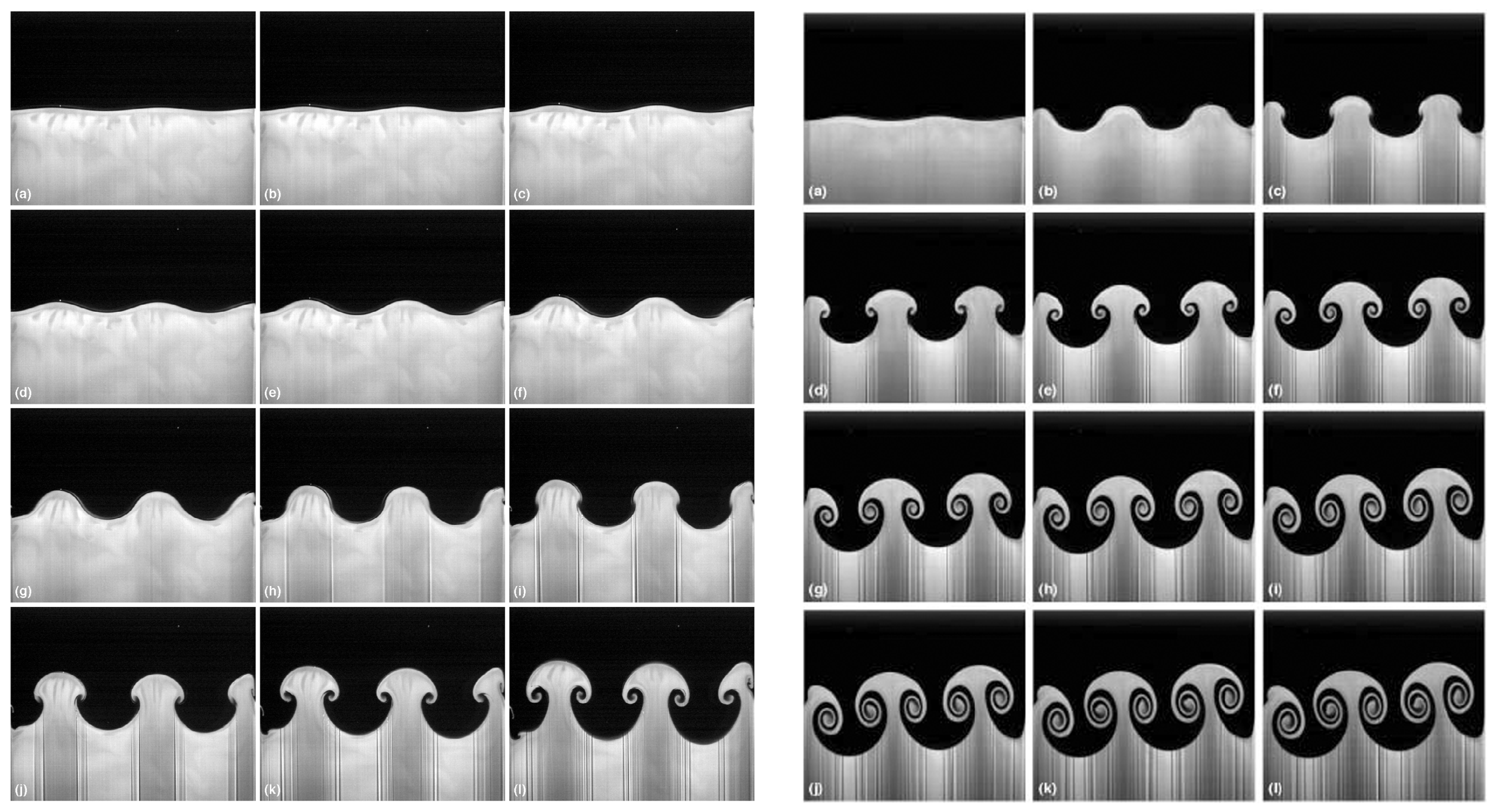
3.2. Improving Ion Properties Using Double-Layer Targets with Interface Corrugation
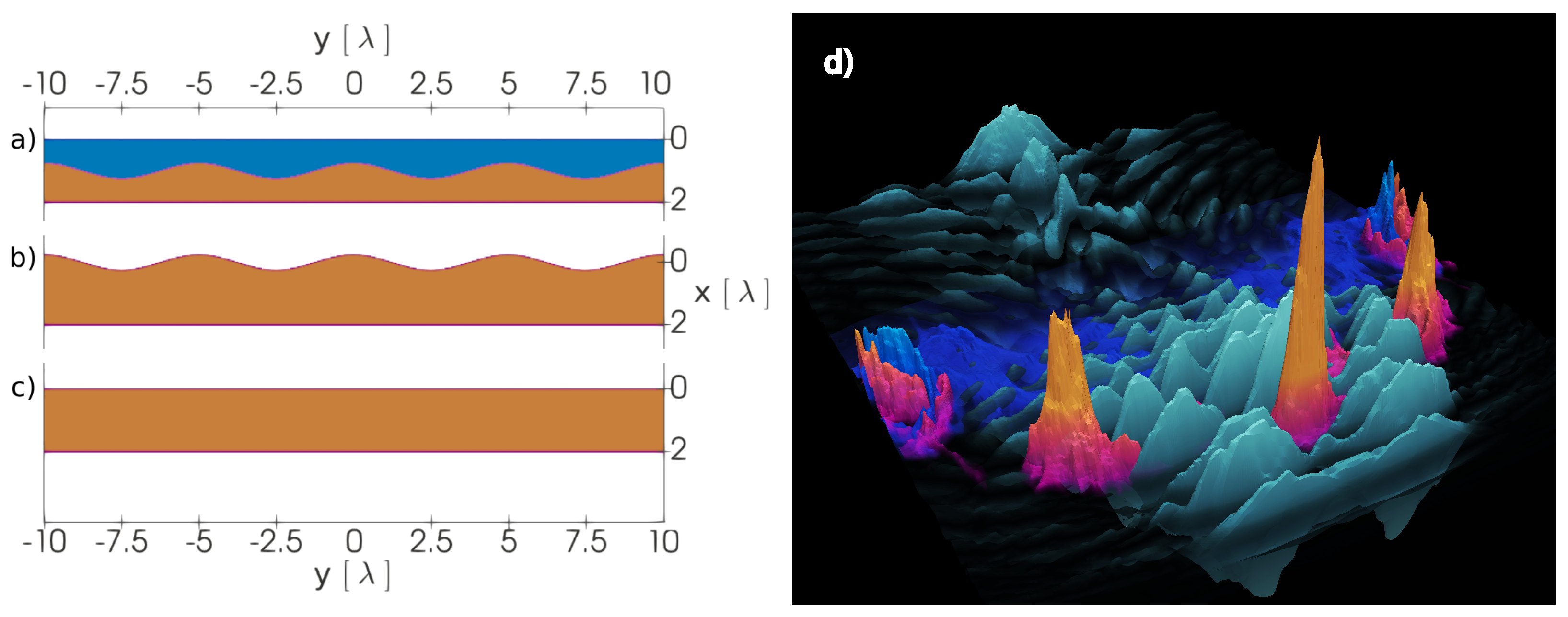
3.3. Target Stability and Generation of the Steep-Front Laser Pulse
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RPA | Radiation Pressure Acceleration |
| TNSA | Target Normal Sheath Acceleration |
| RTI | Rayleigh–Taylor Instability |
| RMI | Richtmyer–Meshkov Instability |
| HL | Heavy-Light |
| LH | Light-Heavy |
| HL-WO | HL without Modulation |
| L2 | Light Single-Layer with the Same Thickness as HL |
| HL-FF | HL with Full-Front Laser Pulse |
| L2-SM | L2 with Surface Modulation |
| W/O-Sh | Without Plasma Shutter |
| W/1xSh | With Plasma Shutter |
| VBL | Virtual BeamLine |
| VR | Virtual Reality |
Appendix A. Virtual Reality Visualization
References
- Bulanov, S.V.; Esirkepov, T.; Khoroshkov, V.S.; Kuznetsov, A.V.; Pegoraro, F. Oncological hadrontherapy with laser ion accelerators. Phys. Lett. A 2002, 299, 240–247. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Wilkens, J.J.; Esirkepov, T.Z.; Korn, G.; Kraft, G.; Kraft, S.D.; Molls, M.; Khoroshkov, V.S. Laser ion acceleration for hadron therapy. Physics-Uspekhi 2014, 57, 1149–1179. [Google Scholar] [CrossRef]
- Tajima, T. Prospect for compact medical laser accelerators. J. Jpn. Soc. Therap. Radiol. Oncol. 1997, 9, 83–85. [Google Scholar]
- Roth, M.; Cowan, T.E.; Key, M.H.; Hatchett, S.P.; Brown, C.; Fountain, W.; Johnson, J.; Pennington, D.M.; Snavely, R.A.; Wilks, S.C.; et al. Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 2001, 86, 436–439. [Google Scholar] [CrossRef] [PubMed]
- Atzeni, S.; Temporal, M.; Honrubia, J.J. A first analysis of fast ignition of precompressed ICF fuel by laser-accelerated protons. Nucl. Fusion 2002, 42, L1. [Google Scholar] [CrossRef]
- Nishiuchi, M.; Sakaki, H.; Esirkepov, T.Z.; Nishio, K.; Pikuz, T.A.; Faenov, A.Y.; Skobelev, I.Y.; Orlandi, R.; Sako, H.; Pirozhkov, A.S.; et al. Acceleration of highly charged GeV Fe ions from a low-Z substrate by intense femtosecond laser. Phys. Plasmas 2015, 22, 033107. [Google Scholar] [CrossRef]
- Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 2012, 75, 056401. [Google Scholar] [CrossRef]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751–793. [Google Scholar] [CrossRef]
- Passoni, M.; Arioli, F.M.; Cialfi, L.; Dellasega, D.; Fedeli, L.; Formenti, A.; Giovannelli, A.C.; Maffini, A.; Mirani, F.; Pazzaglia, A.; et al. Advanced laser-driven ion sources and their applications in materials and nuclear science. Plasma Phys. Control. Fusion 2019, 62, 014022. [Google Scholar] [CrossRef]
- Garcia, S.; Chatain, D.; Perin, J.P. Continuous production of a thin ribbon of solid hydrogen. Laser Part. Beams 2014, 32, 569–575. [Google Scholar] [CrossRef]
- Margarone, D.; Velyhan, A.; Dostal, J.; Ullschmied, J.; Perin, J.P.; Chatain, D.; Garcia, S.; Bonnay, P.; Pisarczyk, T.; Dudzak, R.; et al. Proton acceleration driven by a nanosecond laser from a cryogenic thin solid-hydrogen ribbon. Phys. Rev. X 2016, 6, 041030. [Google Scholar] [CrossRef]
- Margarone, D.; Cirrone, G.A.P.; Cuttone, G.; Amico, A.; Andò, L.; Borghesi, M.; Bulanov, S.S.; Bulanov, S.V.; Chatain, D.; Fajstavr, A.; et al. ELIMAIA: A Laser-Driven Ion Accelerator for Multidisciplinary Applications. Quantum Beam Sci. 2018, 2, 8. [Google Scholar] [CrossRef]
- Chagovets, T.; Stanček, S.; Giuffrida, L.; Velyhan, A.; Tryus, M.; Grepl, F.; Istokskaia, V.; Kantarelou, V.; Wiste, T.; Hernandez Martin, J.; et al. & Margarone, D. Automation of Target Delivery and Diagnostic Systems for High Repetition Rate Laser-Plasma Acceleration. Appl. Sci. 2021, 11, 1680. [Google Scholar] [CrossRef]
- Weber, S.; Bechet, S.; Borneis, S.; Brabec, L.; Bučka, M.; Chacon-Golcher, E.; Ciappina, M.; DeMarco, M.; Fajstavr, A.; Falk, K.; et al. P3: An installation for high-energy density plasma physics and ultra-high intensity laser–matter interaction at ELI-Beamlines. Matter Radiat. Extrem. 2017, 2, 149–176. [Google Scholar] [CrossRef]
- Condamine, F.P.; Jourdain, N.; Hernandez, J.C.; Taylor, M.; Bohlin, H.; Fajstavr, A.; Jeong, T.M.; Kumar, D.; Laštovička, T.; Renner, O.; et al. High-repetition rate solid target delivery system for PW-class laser–matter interaction at ELI Beamlines. Rev. Sci. Instrum. 2021, 92, 063504. [Google Scholar] [CrossRef]
- Jourdain, N.; Chaulagain, U.; Havlík, M.; Kramer, D.; Kumar, D.; Majerová, I.; Tikhonchuk, V.T.; Korn, G.; Weber, S. The L4n laser beamline of the P3-installation: Towards high-repetition rate high-energy density physics at ELI-Beamlines. Matter Radiat. Extrem. 2021, 6, 015401. [Google Scholar] [CrossRef]
- Papadopoulos, D.; Zou, J.; Le Blanc, C.; Cheriaux, G.; Georges, P.; Druon, F.; Mennerat, G.; Martin, L.; Fréneaux, A.; Beluze, A.; et al. The Apollon 10 PW laser: Experimental and theoretical investigation of the temporal characteristics. High Power Laser Sci. Eng. 2016, 4, E34. [Google Scholar] [CrossRef]
- Zamfir, N.V. Nuclear Physics with 10 PW laser beams at Extreme Light Infrastructure-Nuclear Physics (ELI-NP). Eur. Phys. J. Spec. Top. 2014, 223, 1221–1227. [Google Scholar] [CrossRef]
- Shao, B.; Li, Y.; Peng, Y.; Wang, P.; Qian, J.; Leng, Y.; Li, R. Broad-bandwidth high-temporal-contrast carrier-envelope-phase-stabilized laser seed for 100 PW lasers. Opt. Lett. 2020, 45, 2215–2218. [Google Scholar] [CrossRef]
- Esirkepov, T.; Borghesi, M.; Bulanov, S.V.; Mourou, G.; Tajima, T. Highly efficient relativistic-ion generation in the laser-piston regime. Phys. Rev. Lett. 2004, 92, 175003. [Google Scholar] [CrossRef]
- Wilks, S.C.; Langdon, A.B.; Cowan, T.E.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.H.; Pennington, D.; MacKinnon, A.; Snavely, R.A. Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasmas 2001, 8, 542–549. [Google Scholar] [CrossRef]
- Snavely, R.A.; Key, M.H.; Hatchett, S.P.; Cowan, T.E.; Roth, M.; Phillips, T.W.; Stoyer, M.A.; Henry, E.A.; Sangster, T.C.; Singh, M.S.; et al. Intense High-Energy Proton Beams from Petawatt-Laser Irradiation of Solids. Phys. Rev. Lett. 2000, 85, 2945–2948. [Google Scholar] [CrossRef] [PubMed]
- Psikal, J.; Matys, M. Dominance of hole-boring radiation pressure acceleration regime with thin ribbon of ionized solid hydrogen. Plasma Phys. Control. Fusion 2018, 60, 044003. [Google Scholar] [CrossRef]
- Macchi, A.; Cattani, F.; Liseykina, T.V.; Cornolti, F. Laser Acceleration of Ion Bunches at the Front Surface of Overdense Plasmas. Phys. Rev. Lett. 2005, 94, 165003. [Google Scholar] [CrossRef]
- Schwoerer, H.; Pfotenhauer, S.; Jäckel, O.; Amthor, K.U.; Liesfeld, B.; Ziegler, W.; Sauerbrey, R.; Ledingham, K.W.D.; Esirkepov, T. Laser-plasma acceleration of quasi-monoenergetic protons from microstructured targets. Nature 2006, 439, 445–448. [Google Scholar] [CrossRef] [PubMed]
- Hegelich, B.M.; Albright, B.J.; Cobble, J.; Flippo, K.; Letzring, S.; Paffett, M.; Ruhl, H.; Schreiber, J.; Schulze, R.K.; Fernández, J.C. Laser acceleration of quasi-monoenergetic MeV ion beams. Nature 2006, 439, 441–444. [Google Scholar] [CrossRef]
- Kar, S.; Borghesi, M.; Bulanov, S.V.; Key, M.H.; Liseykina, T.V.; Macchi, A.; Mackinnon, A.J.; Patel, P.K.; Romagnani, L.; Schiavi, A.; et al. Plasma Jets Driven by Ultraintense-Laser Interaction with Thin Foils. Phys. Rev. Lett. 2008, 100, 225004. [Google Scholar] [CrossRef]
- Henig, A.; Steinke, S.; Schnürer, M.; Sokollik, T.; Hörlein, R.; Kiefer, D.; Jung, D.; Schreiber, J.; Hegelich, B.M.; Yan, X.Q.; et al. Radiation-Pressure Acceleration of Ion Beams Driven by Circularly Polarized Laser Pulses. Phys. Rev. Lett. 2009, 103, 245003. [Google Scholar] [CrossRef]
- Kar, S.; Kakolee, K.F.; Qiao, B.; Macchi, A.; Cerchez, M.; Doria, D.; Geissler, M.; McKenna, P.; Neely, D.; Osterholz, J.; et al. Ion Acceleration in Multispecies Targets Driven by Intense Laser Radiation Pressure. Phys. Rev. Lett. 2012, 109, 185006. [Google Scholar] [CrossRef]
- Kim, I.J.; Pae, K.H.; Choi, I.W.; Lee, C.L.; Kim, H.T.; Singhal, H.; Sung, J.H.; Lee, S.K.; Lee, H.W.; Nickles, P.V.; et al. Radiation pressure acceleration of protons to 93 MeV with circularly polarized petawatt laser pulses. Phys. Plasmas 2016, 23, 070701. [Google Scholar] [CrossRef]
- Henig, A.; Kiefer, D.; Markey, K.; Gautier, D.C.; Flippo, K.A.; Letzring, S.; Johnson, R.P.; Shimada, T.; Yin, L.; Albright, B.J.; et al. Enhanced Laser-Driven Ion Acceleration in the Relativistic Transparency Regime. Phys. Rev. Lett. 2009, 103, 045002. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.Q.; Lin, C.; Sheng, Z.M.; Guo, Z.Y.; Liu, B.C.; Lu, Y.R.; Fang, J.X.; Chen, J.E. Generating High-Current Monoenergetic Proton Beams by a CircularlyPolarized Laser Pulse in the Phase-StableAcceleration Regime. Phys. Rev. Lett. 2008, 100, 135003. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.Q.; Tajima, T.; Hegelich, M.; Yin, L.; Habs, D. Theory of laser ion acceleration from a foil target of nanometer thickness. Appl. Phys. B 2009, 98, 711–721. [Google Scholar] [CrossRef]
- Tajima, T.; Habs, D.; Yan, X. Laser Acceleration of Ions for Radiation Therapy; World Scientific: Singapore, 2009; pp. 201–228. [Google Scholar] [CrossRef]
- Naumova, N.; Schlegel, T.; Tikhonchuk, V.T.; Labaune, C.; Sokolov, I.V.; Mourou, G. Hole Boring in a DT Pellet and Fast-Ion Ignition with Ultraintense Laser Pulses. Phys. Rev. Lett. 2009, 102, 025002. [Google Scholar] [CrossRef] [PubMed]
- Robinson, A.P.L.; Gibbon, P.; Zepf, M.; Kar, S.; Evans, R.G.; Bellei, C. Relativistically correct hole-boring and ion acceleration by circularly polarized laser pulses. Plasma Phys. Control. Fusion 2009, 51, 024004. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Kando, M.; Pegoraro, F.; Bulanov, S.S.; Geddes, C.G.R.; Schroeder, C.B.; Esarey, E.; Leemans, W.P. Ion acceleration from thin foil and extended plasma targets by slow electromagnetic wave and related ion-ion beam instability. Phys. Plasmas 2012, 19, 103105. [Google Scholar] [CrossRef]
- Macchi, A.; Veghini, S.; Pegoraro, F. “Light Sail” Acceleration Reexamined. Phys. Rev. Lett. 2009, 103, 085003. [Google Scholar] [CrossRef]
- Mackenroth, F.; Bulanov, S.S. Tailored laser pulse chirp to maintain optimum radiation pressure acceleration of ions. Phys. Plasmas 2019, 26, 023103. [Google Scholar] [CrossRef]
- Kar, S.; Kakolee, K.F.; Cerchez, M.; Doria, D.; Macchi, A.; McKenna, P.; Neely, D.; Osterholz, J.; Quinn, K.; Ramakrishna, B.; et al. Experimental investigation of hole boring and light sail regimes of RPA by varying laser and target parameters. Plasma Phys. Control. Fusion 2013, 55, 124030. [Google Scholar] [CrossRef]
- Matys, M.; Nishihara, K.; Kecova, M.; Psikal, J.; Korn, G.; Bulanov, S.V. Laser-driven generation of collimated quasi-monoenergetic proton beam using double-layer target with modulated interface. High Energy Density Phys. 2020, 36, 100844. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Khoroshkov, V.S. Feasibility of using laser ion accelerators in proton therapy. Plasma Phys. Rep. 2002, 28, 453–456. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Kamenets, F.F.; Kato, Y.; Kuznetsov, A.V.; Nishihara, K.; Pegoraro, F.; Tajima, T.; Khoroshkov, V.S. Generation of high-quality charged particle beams during the acceleration of ions by high-power laser radiation. Plasma Phys. Rep. 2002, 28, 975–991. [Google Scholar] [CrossRef]
- Esirkepov, T.; Bulanov, S.V.; Nishihara, K.; Tajima, T.; Pegoraro, F.; Khoroshkov, V.S.; Mima, K.; Daido, H.; Kato, Y.; Kitagawa, Y.; et al. Proposed double-layer target for the generation of high-quality laser-accelerated ion beams. Phys. Rev. Lett. 2002, 89, 175003. [Google Scholar] [CrossRef] [PubMed]
- Pegoraro, F.; Bulanov, S.V. Photon bubbles and ion acceleration in a plasma dominated by the radiation pressure of an electromagnetic pulse. Phys. Rev. Lett. 2007, 99, 065002. [Google Scholar] [CrossRef]
- Echkina, E.Y.; Inovenkov, I.N.; Esirkepov, T.Z.; Pegoraro, F.; Borghesi, M.; Bulanov, S.V. Dependence of the ion energy on the parameters of the laser pulse and target in the radiation-pressure-dominated regime of acceleration. Plasma Phys. Rep. 2010, 36, 15–29. [Google Scholar] [CrossRef]
- Lord Rayleigh. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 1882, 14, 170–177. [Google Scholar] [CrossRef]
- Taylor, G. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 201, 192–196. [Google Scholar] [CrossRef]
- Richtmyer, R.D. Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Math. 1960, 13, 297–319. [Google Scholar] [CrossRef]
- Meshkov, E.E. Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 1969, 4, 101–104. [Google Scholar] [CrossRef]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 2017, 720–722, 1–136. [Google Scholar] [CrossRef]
- Palmer, C.A.; Schreiber, J.; Nagel, S.R.; Dover, N.P.; Bellei, C.; Beg, F.N.; Bott, S.; Clarke, R.J.; Dangor, A.E.; Hassan, S.M.; et al. Rayleigh-Taylor instability of an ultrathin foil accelerated by the radiation pressure of an intense laser. Phys. Rev. Lett. 2012, 108, 225002. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, Q.; Sharp, D.H. Small amplitude theory of Richtmyer-Meshkov instability. Phys. Fluids 1994, 6, 1856–1873. [Google Scholar] [CrossRef]
- Wouchuk, J.G.; Nishihara, K. Asymptotic growth in the linear Richtmyer-Meshkov instability. Phys. Plasmas 1997, 4, 1028–1038. [Google Scholar] [CrossRef]
- Nishihara, K.; Wouchuk, J.G.; Matsuoka, C.; Ishizaki, R.; Zhakhovsky, V.V. Richtmyer-Meshkov instability: Theory of linear and nonlinear evolution. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 1769–1807. [Google Scholar] [CrossRef] [PubMed]
- Mohseni, F.; Mendoza, M.; Succi, S.; Herrmann, H.J. Relativistic effects on the Richtmyer-Meshkov instability. Phys. Rev. D Part. Fields Gravit. Cosmol. 2014, 90, 125028. [Google Scholar] [CrossRef]
- Matsuoka, C.; Nishihara, K.; Sano, T. Nonlinear Dynamics of Non-uniform Current-Vortex Sheets in Magnetohydrodynamic Flows. J. Nonlinear Sci. 2017, 27, 531–572. [Google Scholar] [CrossRef]
- Zhou, Y.; Clark, T.T.; Clark, D.S.; Gail Glendinning, S.; Aaron Skinner, M.; Huntington, C.M.; Hurricane, O.A.; Dimits, A.M.; Remington, B.A. Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities. Phys. Plasmas 2019, 26, 080901. [Google Scholar] [CrossRef]
- Zhou, Y.; Williams, R.J.; Ramaprabhu, P.; Groom, M.; Thornber, B.; Hillier, A.; Mostert, W.; Rollin, B.; Balachandar, S.; Powell, P.D.; et al. Rayleigh–Taylor and Richtmyer–Meshkov instabilities: A journey through scales. Phys. D Nonlinear Phenom. 2021, 423, 132838. [Google Scholar] [CrossRef]
- Hester, J.J. The Crab Nebula: An Astrophysical Chimera. Annu. Rev. Astron. Astrophys. 2008, 46, 127–155. [Google Scholar] [CrossRef]
- Lindl, J.D.; Mccrory, R.L.; Campbell, E.M. Progress toward Ignition and Burn Propagation in Inertial Confinement Fusion. Phys. Today 1992, 45, 32–40. [Google Scholar] [CrossRef]
- Waddell, J.T.; Niederhaus, C.E.; Jacobs, J.W. Experimental study of Rayleigh–Taylor instability: Low Atwood number liquid systems with single-mode initial perturbations. Phys. Fluids 2001, 13, 1263–1273. [Google Scholar] [CrossRef]
- Niederhaus, C.E.; Jacobs, J.W. Experimental study of the Richtmyer-Meshkov instability of incompressible fluids. J. Fluid Mech. 2003, 485, 243–277. [Google Scholar] [CrossRef]
- Velikovich, A.L. Analytic theory of Richtmyer-Meshkov instability for the case of reflected rarefaction wave. Phys. Fluids 1996, 8, 1666–1679. [Google Scholar] [CrossRef]
- Wouchuk, J.G.; Nishihara, K. Linear perturbation growth at a shocked interface. Phys. Plasmas 1996, 3, 3761–3776. [Google Scholar] [CrossRef]
- Klimo, O.; Psikal, J.; Limpouch, J.; Tikhonchuk, V.T. Monoenergetic ion beams from ultrathin foils irradiated by ultrahigh-contrast circularly polarized laser pulses. Phys. Rev. Spec. Top. Accel. Beams 2008, 11, 031301. [Google Scholar] [CrossRef]
- Robinson, A.P.; Zepf, M.; Kar, S.; Evans, R.G.; Bellei, C. Radiation pressure acceleration of thin foils with circularly polarized laser pulses. New J. Phys. 2008, 10, 013021. [Google Scholar] [CrossRef]
- Wan, Y.; Pai, C.H.; Zhang, C.J.; Li, F.; Wu, Y.P.; Hua, J.F.; Lu, W.; Gu, Y.Q.; Silva, L.O.; Joshi, C.; et al. Physical Mechanism of the Transverse Instability in Radiation Pressure Ion Acceleration. Phys. Rev. Lett. 2016, 117, 234801. [Google Scholar] [CrossRef]
- Wan, Y.; Pai, C.H.; Zhang, C.J.; Li, F.; Wu, Y.P.; Hua, J.F.; Lu, W.; Joshi, C.; Mori, W.B.; Malka, V. Physical mechanism of the electron-ion coupled transverse instability in laser pressure ion acceleration for different regimes. Phys. Rev. E 2018, 98, 013202. [Google Scholar] [CrossRef]
- Vshivkov, V.A.; Naumova, N.M.; Pegoraro, F.; Bulanov, S.V. Nonlinear electrodynamics of the interaction of ultra-intense laser pulses with a thin foil. Phys. Plasmas 1998, 5, 2727–2741. [Google Scholar] [CrossRef]
- Reed, S.A.; Matsuoka, T.; Bulanov, S.; Tampo, M.; Chvykov, V.; Kalintchenko, G.; Rousseau, P.; Yanovsky, V.; Kodama, R.; Litzenberg, D.W.; et al. Relativistic plasma shutter for ultraintense laser pulses. Appl. Phys. Lett. 2009, 94, 201117. [Google Scholar] [CrossRef]
- Palaniyappan, S.; Hegelich, B.M.; Wu, H.C.; Jung, D.; Gautier, D.C.; Yin, L.; Albright, B.J.; Johnson, R.P.; Shimada, T.; Letzring, S.; et al. Dynamics of relativistic transparency and optical shuttering in expanding overdense plasmas. Nat. Phys. 2012, 8, 763–769. [Google Scholar] [CrossRef]
- Wei, W.Q.; Yuan, X.H.; Fang, Y.; Ge, Z.Y.; Ge, X.L.; Yang, S.; Li, Y.F.; Liao, G.Q.; Zhang, Z.; Liu, F.; et al. Plasma optical shutter in ultraintense laser-foil interaction. Phys. Plasmas 2017, 24, 113111. [Google Scholar] [CrossRef]
- Matys, M.; Klimo, O.; Psikal, J.; Bulanov, S.V. Simulation studies on transmissivity of silicon nitride plasma shutter for laser pulse contrast enhancement. In Proceedings of the 45th EPS Conference on Plasma Physics, EPS, Prague, Czech Republic, 2–6 July 2018; Coda, S., Berndt, J., Lapenta, G., Mantsinen, M., Michaut, C., Weber, S., Eds.; 2018; pp. 1332–1335. [Google Scholar]
- Jirka, M.; Klimo, O.; Gu, Y.J.; Weber, S. Enhanced photon emission from a double-layer target at moderate laser intensities. Sci. Rep. 2020, 10, 8887. [Google Scholar] [CrossRef] [PubMed]
- Matys, M.; Bulanov, S.; Kecova, M.; Kucharik, M.; Jirka, M.; Janecka, P.; Psikal, J.; Nikl, J.; Grosz, J.; Korn, G.; et al. Ion acceleration enhancement by laser-pulse shaping via plasma shutter. In Proceedings of the Laser Acceleration of Electrons, Protons, and Ions VI, Online, 19–23 April 2021; Bulanov, S.S., Schreiber, J., Schroeder, C.B., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11779. [Google Scholar] [CrossRef]
- Nikl, J.; Jirka, M.; Matys, M.; Kuchařík, M.; Klimo, O. Contrast enhancement of ultra-intense laser pulses by relativistic plasma shutter. In Proceedings of the High Power Lasers and Applications, Online, 19–29 April 2021; Hein, J., Butcher, T.J., Bakule, P., Haefner, C.L., Korn, G., Silva, L.O., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11777, p. 117770X. [Google Scholar] [CrossRef]
- Jirka, M.; Klimo, O.; Matys, M. Relativistic plasma aperture for laser intensity enhancement. Phys. Rev. Res. 2021, 3, 033175. [Google Scholar] [CrossRef]
- Matys, M.; Bulanov, S.V.; Kucharik, M.; Jirka, M.; Nikl, J.; Kecova, M.; Proska, J.; Psikal, J.; Korn, G.; Klimo, O. Design of plasma shutters for improved heavy ion acceleration by ultra-intense laser pulses. New J. Phys. 2022, 24, 113046. [Google Scholar] [CrossRef]
- Arber, T.D.; Bennett, K.; Brady, C.S.; Lawrence-Douglas, A.; Ramsay, M.G.; Sircombe, N.J.; Gillies, P.; Evans, R.G.; Schmitz, H.; Bell, A.R.; et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Control. Fusion 2015, 57, 113001. [Google Scholar] [CrossRef]
- Ridgers, C.P.; Kirk, J.G.; Duclous, R.; Blackburn, T.G.; Brady, C.S.; Bennett, K.; Arber, T.D.; Bell, A.R. Modelling gamma-ray photon emission and pair production in high-intensity laser-matter interactions. J. Comput. Phys. 2014, 260, 273–285. [Google Scholar] [CrossRef]
- Bulanov, S.S.; Esarey, E.; Schroeder, C.B.; Bulanov, S.V.; Esirkepov, T.Z.; Kando, M.; Pegoraro, F.; Leemans, W.P. Radiation pressure acceleration: The factors limiting maximum attainable ion energy. Phys. Plasmas 2016, 23, 056703. [Google Scholar] [CrossRef]
- Matys, M.; Psikal, J.; Danielova, M.; Valenta, P.; Bulanov, S.V. Laser-driven Ion Acceleration Using Cryogenic Hydrogen Targets. In Proceedings of the Supercomputing in Science and Engineering 2017–2018, Ostrava, Czechia, 21–25 January 2019; Pešatová, K., Poláková, B., Cawley, J., Červenková, Z., Eds.; VSB–Technical University of Ostrava: Ostrava, Czechia, 2019; pp. 149–151, ISBN 978-80-248-4289-9. [Google Scholar]
- Laser-Driven Proton Acceleration from Cryogenic Hydrogen Target. Available online: https://vbl.eli-beams.eu/mm-track/ (accessed on 2 June 2022).
- Danielova, M.; Janecka, P.; Grosz, J.; Holy, A. Interactive 3D Visualizations of Laser Plasma Experiments on the Web and in VR. In Proceedings of the EuroVis 2019-Posters, Porto, Portugal, 3–7 June 2019; Madeiras Pereira, J., Raidou, R.G., Eds.; The Eurographics Association: Porto, Portugal, 2019. [Google Scholar] [CrossRef]
- Higginson, A.; Gray, R.J.; King, M.; Dance, R.J.; Williamson, S.D.; Butler, N.M.; Wilson, R.; Capdessus, R.; Armstrong, C.; Green, J.S.; et al. Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme. Nat. Commun. 2018, 9, 724. [Google Scholar] [CrossRef]
- Qiao, B.; Kar, S.; Geissler, M.; Gibbon, P.; Zepf, M.; Borghesi, M. Dominance of Radiation Pressure in Ion Acceleration with Linearly Polarized Pulses at Intensities of 1021 W cm−2. Phys. Rev. Lett. 2012, 108, 115002. [Google Scholar] [CrossRef]
- Yin, L.; Albright, B.J.; Bowers, K.J.; Jung, D.; Fernández, J.C.; Hegelich, B.M. Three-Dimensional Dynamics of Breakout Afterburner Ion Acceleration Using High-Contrast Short-Pulse Laser and Nanoscale Targets. Phys. Rev. Lett. 2011, 107, 045003. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.L.; Chen, M.; Zheng, J.; Sheng, Z.M.; Liu, C.S. Three dimensional effects on proton acceleration by intense laser solid target interaction. Phys. Plasmas 2013, 20, 063107. [Google Scholar] [CrossRef]
- Bulanov, S.S.; Brantov, A.; Bychenkov, V.Y.; Chvykov, V.; Kalinchenko, G.; Matsuoka, T.; Rousseau, P.; Reed, S.; Yanovsky, V.; Litzenberg, D.W.; et al. Accelerating monoenergetic protons from ultrathin foils by flat-top laser pulses in the directed-Coulomb-explosion regime. Phys. Rev. E 2008, 78, 026412. [Google Scholar] [CrossRef] [PubMed]
- Stark, D.J.; Yin, L.; Albright, B.J.; Guo, F. Effects of dimensionality on kinetic simulations of laser-ion acceleration in the transparency regime. Phys. Plasmas 2017, 24, 053103. [Google Scholar] [CrossRef]
- Chen, M.; Pukhov, A.; Yu, T.P.; Sheng, Z.M. Enhanced collimated GeV monoenergetic ion acceleration from a shaped foil target irradiated by a circularly polarized laser pulse. Phys. Rev. Lett. 2009, 103, 024801. [Google Scholar] [CrossRef]
- Matys, M.; Nishihara, K.; Danielova, M.; Psikal, J.; Korn, G.; Bulanov, V.S. Generation of collimated quasi-mono-energetic ion beams using a double layer target with interface modulations. In Proceedings of the Laser Acceleration of Electrons, Protons, and Ions V, Prague, Czech Republic, 1–3 April 2019; Esarey, E., Schroeder, C., Schreiber, J., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11037, p. 110370Z. [Google Scholar] [CrossRef]
- Matys, M.; Valenta, P.; Kecova, M.; Nishihara, K.; Psikal, J.; Esirkepov, T.Z.; Koga, J.K.; Necas, A.; Grittani, G.M.; Lazzarini, C.M.; et al. Laser-Driven Acceleration of Charged Particles. In Supercomputing in Science and Engineering 2019–2020; Vondrak, V., Tomas Kozubek, B.J., Eds.; VSB–Technical University of Ostrava: Ostrava, Czechia, 2021; pp. 86–88. ISBN 978-80-248-4567-8. [Google Scholar]
- Floettmann, K. Some basic features of the beam emittance. Phys. Rev. Spec. Top. Accel. Beams 2003, 6, 80–86. [Google Scholar] [CrossRef]
- Zhang, T.; Peng, S.X.; Wu, W.B.; Ren, H.T.; Zhang, J.F.; Wen, J.M.; Ma, T.H.; Jiang, Y.X.; Sun, J.; Guo, Z.Y.; et al. Practical 2.45-GHz microwave-driven Cs-free H- ion source developed at Peking University. Chin. Phys. B 2018, 27, 105208. [Google Scholar] [CrossRef]
- Cowan, T.E.; Fuchs, J.; Ruhl, H.; Kemp, A.; Audebert, P.; Roth, M.; Stephens, R.; Barton, I.; Blazevic, A.; Brambrink, E.; et al. Ultralow emittance, multi-MeV proton beams from a laser virtual-cathode plasma accelerator. Phys. Rev. Lett. 2004, 92, 204801. [Google Scholar] [CrossRef]
- Gu, Y.J.; Zhu, Z.; Li, X.F.; Yu, Q.; Huang, S.; Zhang, F.; Kong, Q.; Kawata, S. Stable long range proton acceleration driven by intense laser pulse with underdense plasmas. Phys. Plasmas 2014, 21, 063104. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Inovenkov, I.N.; Kirsanov, V.I.; Naumova, N.M.; Sakharov, A.S. Nonlinear depletion of ultrashort and relativistically strong laser pulses in an underdense plasma. Phys. Fluids B 1992, 4, 1935–1942. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Kirsanov, V.I.; Naumova, N.M.; Sakharov, A.S.; Shah, H.A.; Inovenkov, I.N. Stationary shock-front of a relativisticaily strong electromagnetic radiation in an underdense plasma. Phys. Scr. 1993, 47, 209–213. [Google Scholar] [CrossRef]
- Decker, C.D.; Mori, W.B.; Tzeng, K.C.; Katsouleas, T. The evolution of ultra-intense, short-pulse lasers in underdense plasmas. Phys. Plasmas 1996, 3, 2047–2056. [Google Scholar] [CrossRef]
- Wang, H.; Lin, C.; Sheng, Z.; Liu, B.; Zhao, S.; Guo, Z.; Lu, Y.; He, X.; Chen, J.; Yan, X. Laser Shaping of a Relativistic Intense, Short Gaussian Pulse by a Plasma Lens. Phys. Rev. Lett. 1996, 107, 265002. [Google Scholar] [CrossRef] [PubMed]
- Bin, J.; Ma, W.; Wang, H.; Streeter, M.; Kreuzer, C.; Kiefer, D.; Yeung, M.; Cousens, S.; Foster, P.; Dromey, B.; et al. Ion Acceleration Using Relativistic Pulse Shaping in Near-Critical-Density Plasmas. Phys. Rev. Lett. 2015, 115, 064801. [Google Scholar] [CrossRef] [PubMed]
- Fedeli, L.; Formenti, A.; Cialfi, L.; Pazzaglia, A.; Passoni, M. Ultra-intense laser interaction with nanostructured near-critical plasmas. Sci. Rep. 2018, 8, 3834. [Google Scholar] [CrossRef]
- Horný, V.; Chen, S.; Davoine, X.; Lelasseux, V.; Gremillet, L.; Fuchs, J. High-flux neutron generation by laser-accelerated ions from single- and double-layer targets. Sci. Rep. 2022, 12, 19767. [Google Scholar] [CrossRef]
- Park, J.; Bulanov, S.; Bin, J.; Ji, Q.; Steinke, S.; Vay, J.; Geddes, C.; Schroeder, C.; Leemans, W.; Schenkel, T.; et al. Ion acceleration in laser generated megatesla magnetic vortex. Phys. Plasmas 2019, 26, 103108. [Google Scholar] [CrossRef]
- Hakimi, S.; Obst-Huebl, L.; Huebl, A.; Nakamura, K.; Bulanov, S.; Steinke, S.; Leemans, W.; Kober, Z.; Ostermayr, T.; Schenkel, T.; et al. Laser–solid interaction studies enabled by the new capabilities of the iP2 BELLA PW beamline. Phys. Plasmas 2022, 29, 083102. [Google Scholar] [CrossRef]
- Yogo, A.; Daido, H.; Bulanov, S.; Nemoto, K.; Oishi, Y.; Nayuki, T.; Fujii, T.; Ogura, K.; Orimo, S.; Sagisaka, A.; et al. Laser ion acceleration via control of the near-critical density target. Phys. Rev. E 2008, 77, 016401. [Google Scholar] [CrossRef]
- Zwickl, B.M.; Shanks, W.E.; Jayich, A.M.; Yang, C.; Bleszynski Jayich, A.C.; Thompson, J.D.; Harris, J.G.E. High quality mechanical and optical properties of commercial silicon nitride membranes. Appl. Phys. Lett. 2008, 92, 103125. [Google Scholar] [CrossRef]
- Kaloyeros, A.E.; Jové, F.A.; Goff, J.; Arkles, B. Review—Silicon Nitride and Silicon Nitride-Rich Thin Film Technologies: Trends in Deposition Techniques and Related Applications. ECS J. Solid State Sci. Technol. 2017, 6, P691–P714. [Google Scholar] [CrossRef]
- Gonzalez-Izquierdo, B.; Gray, R.; King, M.; Dance, R.; Wilson, R.; McCreadie, J.; Butler, N.; Capdessus, R.; Hawkes, S.; Green, J.; et al. Optically controlled dense current structures driven by relativistic plasma aperture-induced diffraction. Nat. Phys. 2016, 12, 505–512. [Google Scholar] [CrossRef]
- Plasma Shutter for Heavy ION Acceleration Enhancement. Available online: https://vbl.eli-beams.eu/mm-shutter/ (accessed on 7 December 2022).
- Parisi, T. WebGL: Up and Running, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2012; ISBN 144932357X. [Google Scholar]
- Virtual BeamLine. Available online: https://vbl.eli-beams.eu/ (accessed on 2 June 2022).
- Pezoa, F.; Reutter, J.L.; Suarez, F.; Ugarte, M.; Vrgoč, D. Foundations of JSON schema. In Proceedings of the 25th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, Montreal, QC, Canada, 11–15 May 2016; pp. 263–273. [Google Scholar] [CrossRef]
- Valenta, P.; Grittani, G.M.; Lazzarini, C.M.; Klimo, O.; Bulanov, S.V. On the electromagnetic-electron rings originating from the interaction of high-power short-pulse laser and underdense plasma. Phys. Plasmas 2021, 28, 122104. [Google Scholar] [CrossRef]
- Electromagnetic-Electron Rings. Available online: https://valenpe7.github.io/on_the_electromagnetic-electron_rings/ (accessed on 2 June 2022).


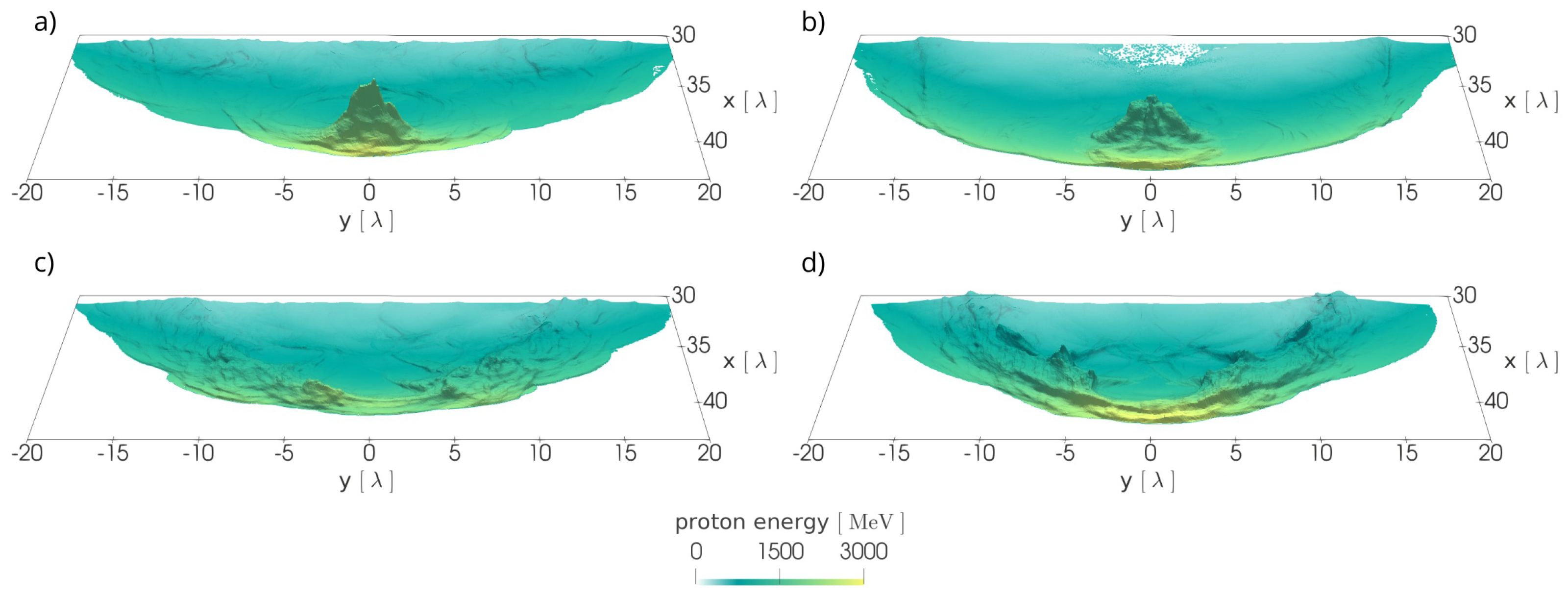
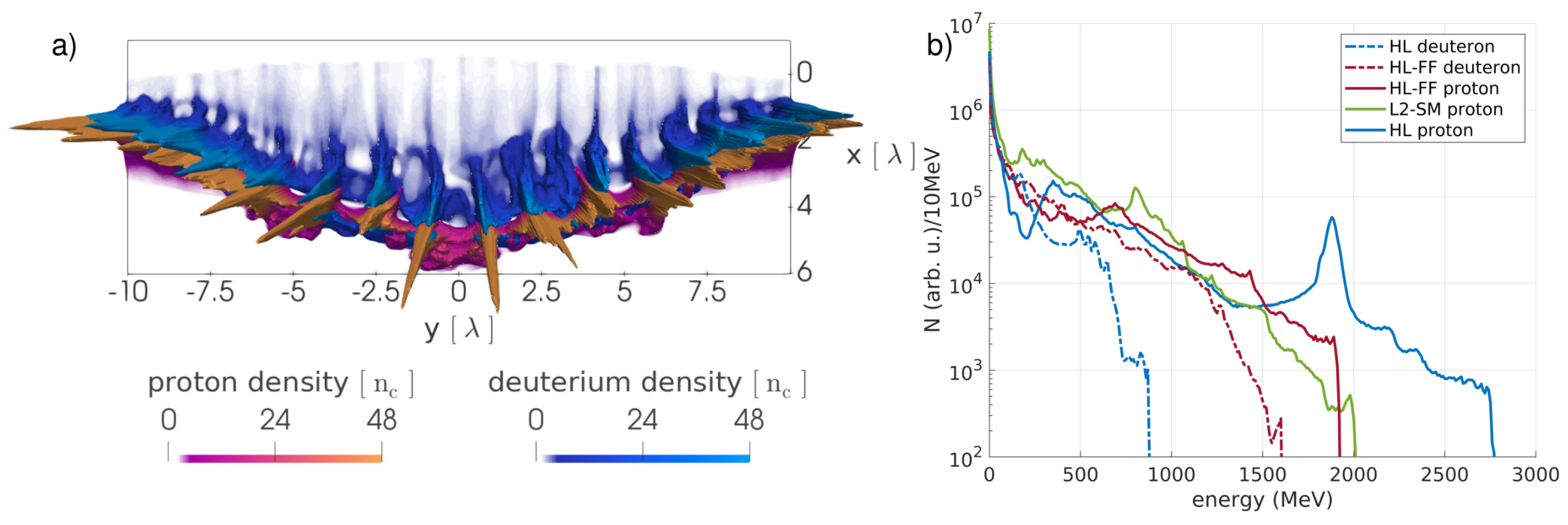


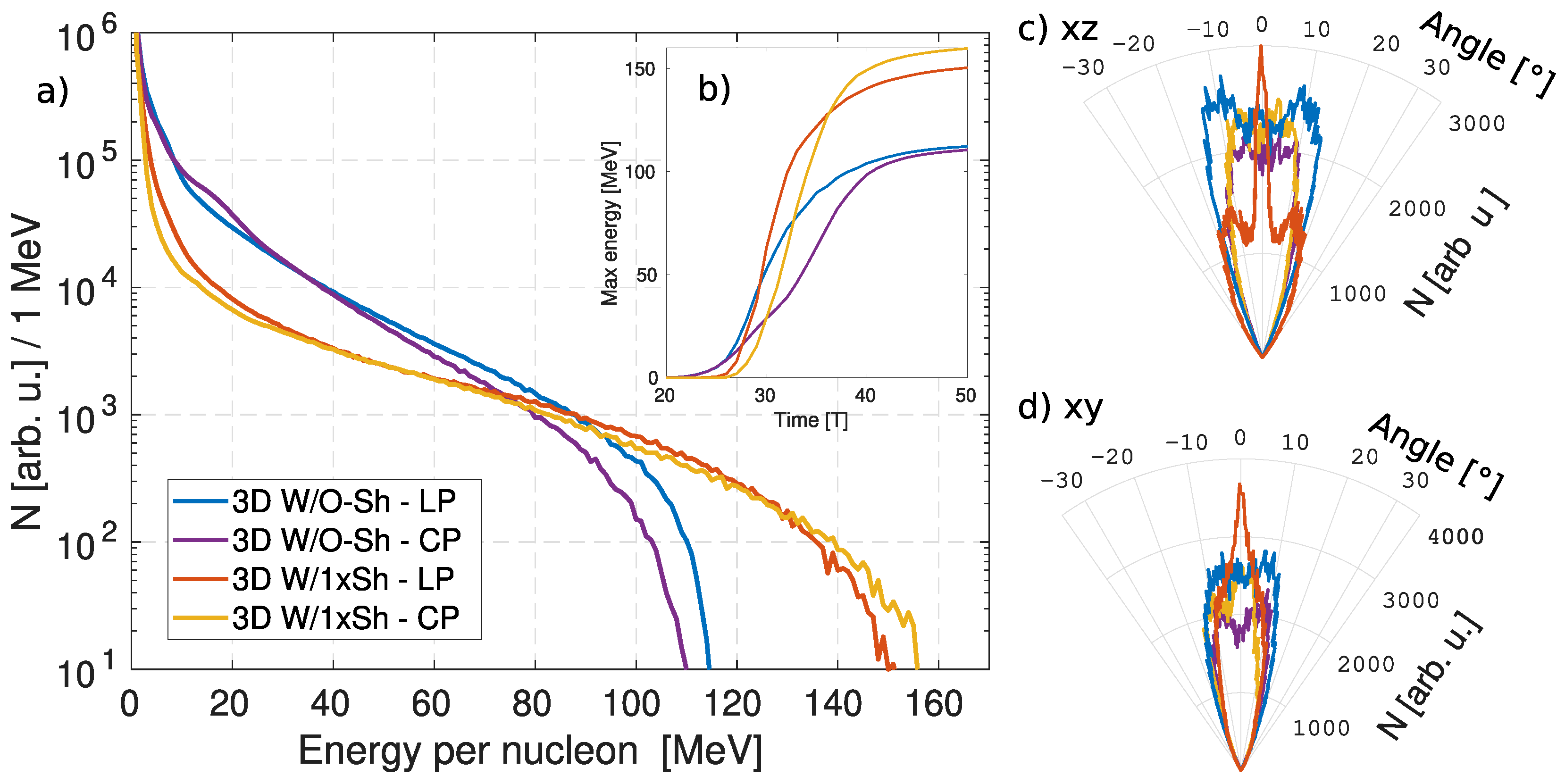
| Section | I [] | Pol. | [m] | Width [m] | t-Shape | Target | Thickness | [] |
|---|---|---|---|---|---|---|---|---|
| 3.1-2D | p | 1.1 | 5 | 320 fs | H | 25 | 56 | |
| 3.1-3D | p | 1.1 | 5 | 200 fs | H | 15 | 56 | |
| 3.1-VR | p | 1.1 | 5 | 200 fs | H | 15 | 56 | |
| 3.2-2D | s | 1.0 | 10 | Gauss 26.7 fs | H-H | (1 + 1) | 48 | |
| 3.3-3D | p | 1.0 | 3 | 64 fs | Shutter SiN | 20 nm | 835 | |
| Target Ag | 20 nm | 2100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matys, M.; Psikal, J.; Nishihara, K.; Klimo, O.; Jirka, M.; Valenta, P.; Bulanov, S.V. High-Quality Laser-Accelerated Ion Beams from Structured Targets. Photonics 2023, 10, 61. https://doi.org/10.3390/photonics10010061
Matys M, Psikal J, Nishihara K, Klimo O, Jirka M, Valenta P, Bulanov SV. High-Quality Laser-Accelerated Ion Beams from Structured Targets. Photonics. 2023; 10(1):61. https://doi.org/10.3390/photonics10010061
Chicago/Turabian StyleMatys, Martin, Jan Psikal, Katsunobu Nishihara, Ondrej Klimo, Martin Jirka, Petr Valenta, and Sergei V. Bulanov. 2023. "High-Quality Laser-Accelerated Ion Beams from Structured Targets" Photonics 10, no. 1: 61. https://doi.org/10.3390/photonics10010061
APA StyleMatys, M., Psikal, J., Nishihara, K., Klimo, O., Jirka, M., Valenta, P., & Bulanov, S. V. (2023). High-Quality Laser-Accelerated Ion Beams from Structured Targets. Photonics, 10(1), 61. https://doi.org/10.3390/photonics10010061






