Optimal Design of Segmented Planar Imaging System Based on Rotation and CLEAN Algorithm
Abstract
1. Introduction
2. Theoretical Model
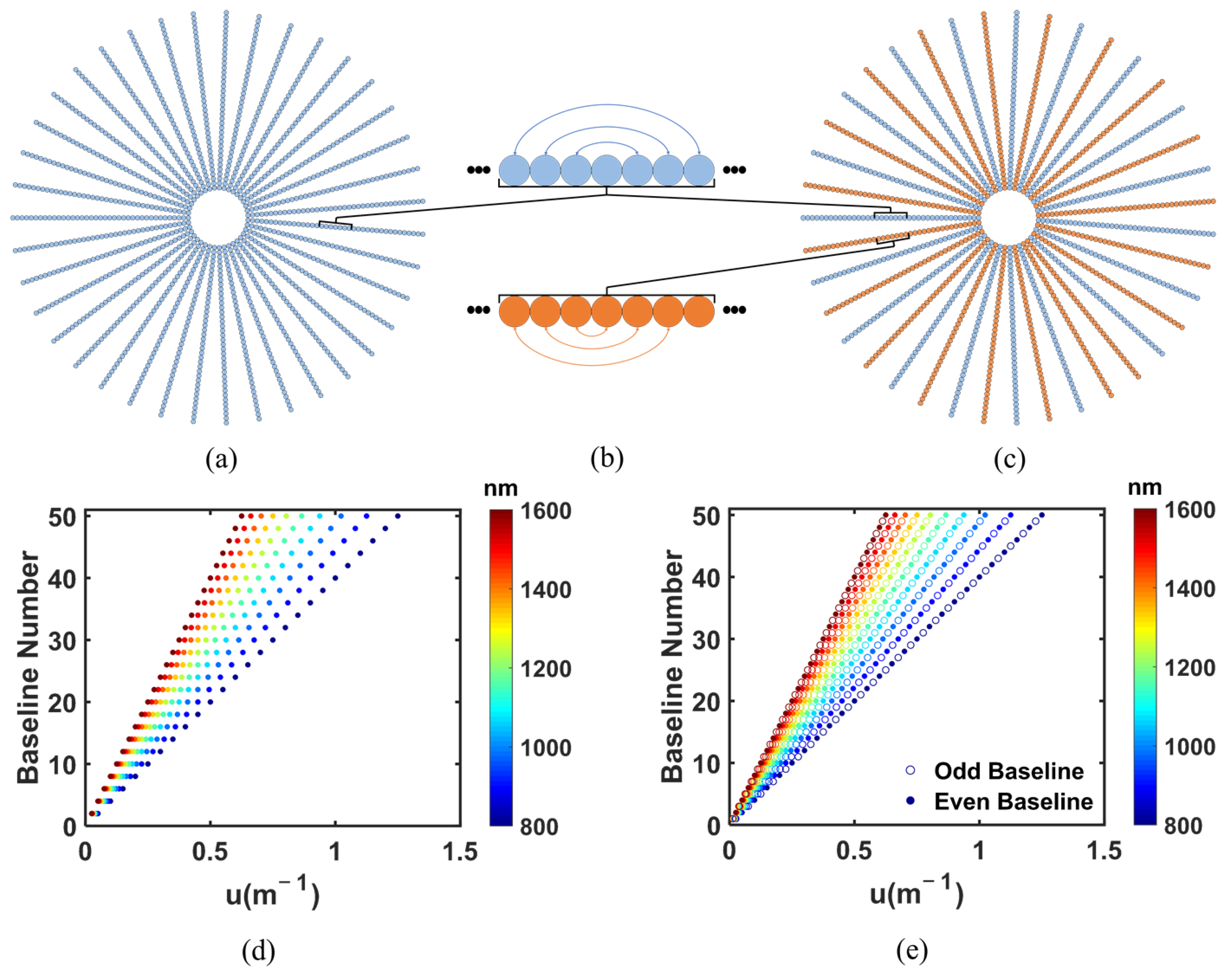
2.1. Parity Baseline Selection
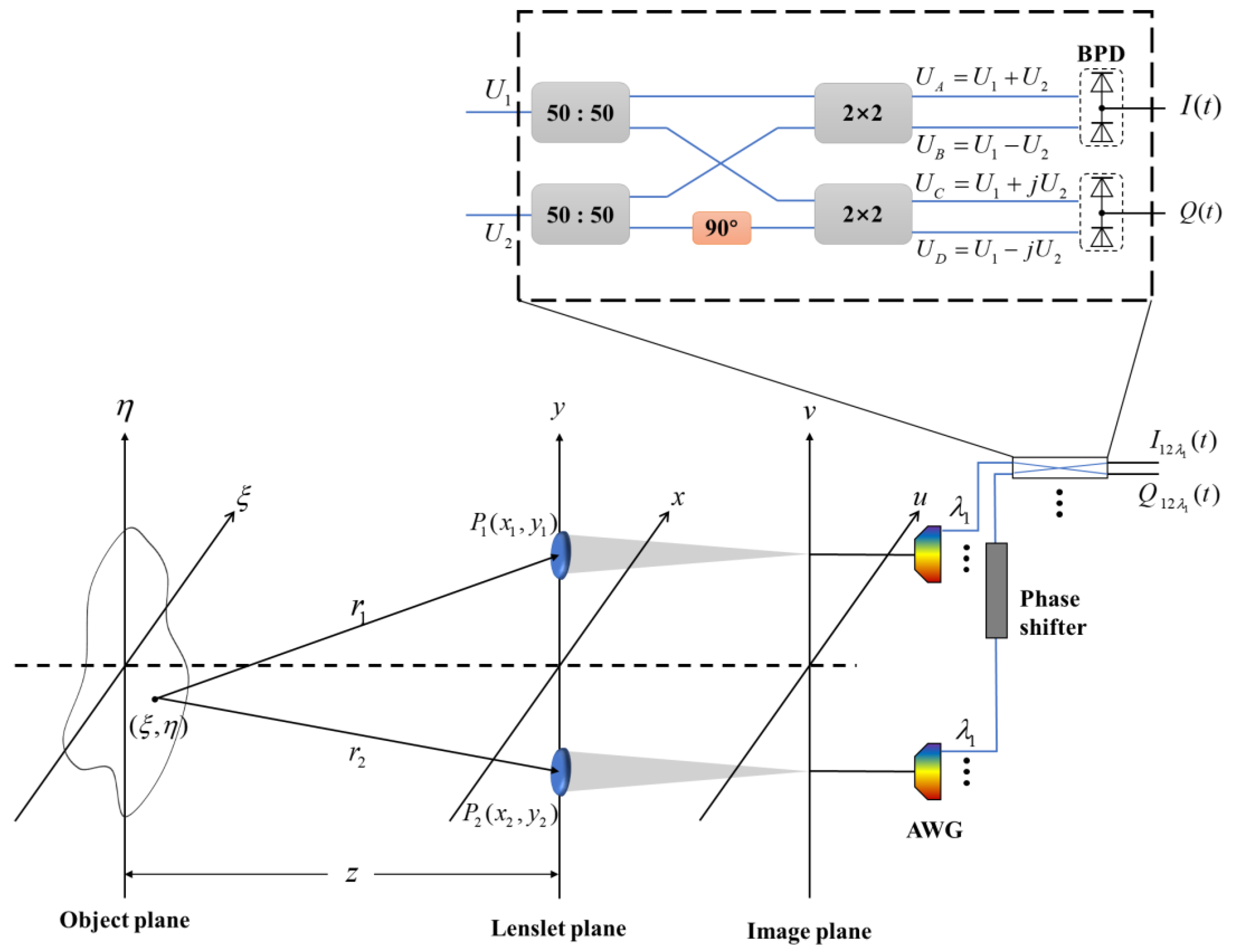
2.2. Signal Transmission Model
2.3. Rotational Imaging
3. Results and Discussion
3.1. Parameter Effects
3.2. Rotational Imaging
3.3. MP-CLEAN Algorithm
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koekemoer, A.M.; Aussel, H.; Calzetti, D.; Capak, P.; Giavalisco, M.; Kneib, J.P.; Leauthaud, A.; Le Fèvre, O.; McCracken, H.J.; Massey, R.; et al. The cosmos survey: Hubble space telescope advanced camera for surveys observations and data processing. Astrophys. J. Suppl. Ser. 2007, 172, 196. [Google Scholar] [CrossRef]
- Gehrels, N.; Fichtel, C.E.; Fishman, G.J.; Kurfess, J.D.; Schönfelder, V. The Compton Gamma Ray Observatory. Sci. Am. 1993, 269, 68–77. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Tananbaum, H.D.; Van Speybroeck, L.P.; O’Dell, S.L. Chandra X-ray Observatory (CXO): Overview. In Proceedings of the Astronomical Telescopes and Instrumentation, Munich, Germany, 27 March–1 April 2000. [Google Scholar]
- Borucki, W.J. KEPLER Mission: Development and overview. Rep. Prog. Phys. 2016, 79, 036901. [Google Scholar] [CrossRef] [PubMed]
- Pilbratt, G.L.; Riedinger, J.R.; Passvogel, T.; Crone, G.; Doyle, D.; Gageur, U.; Heras, A.M.; Jewell, C.; Metcalfe, L.; Ott, S.; et al. Herschel Space Observatory-An ESA facility for far-infrared and submillimetre astronomy. Astron. Astrophys. 2010, 518, L1. [Google Scholar] [CrossRef]
- Yoo, S.J. Low-Mass Planar Photonic Imaging Sensor; No. HQ-E-DAA-TN56002; NASA: Washington, DC, USA, 2014.
- Duncan, A.; Kendrick, R.; Thurman, S.; Wuchenich, D.; Scott, R.P.; Yoo, S.J.B.; Su, T.; Yu, R.; Ogden, C.; Proiett, R. Spider: Next Generation Chip Scale Imaging Sensor. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 15–18 September 2015. [Google Scholar]
- Kendrick, R.L.; Duncan, A.; Ogden, C.; Wilm, J.; Thurman, S.T. Segmented Planar Imaging Detector for EO Reconnaissance. In Proceedings of the Computational Optical Sensing and Imaging, Arlington, VA, USA, 23–27 June 2013. [Google Scholar]
- Badham, K.; Kendrick, R.L.; Wuchenich, D.; Ogden, C.; Chriqui, G.; Duncan, A.; Thurman, S.T.; Yoo, S.J.B.; Su, T.; Lai, W.; et al. Photonic Integrated Circuit-Based Imaging System for SPIDER. In Proceedings of the 2017 Conference on Lasers and Electro-Optics Pacific Rim (CLEO-PR). IEEE, Sands Expo and Convention Centre, Singapore, 31 July–4 August 2017; pp. 1–5. [Google Scholar]
- Scott, R.P.; Su, T.; Ogden, C.; Thurman, S.T.; Kendrick, R.L.; Duncan, A.; Yu, R.; Yoo, S.J.B. Demonstration of a Photonic Integrated Circuit for Multi-Baseline Interferometric Imaging. In Proceedings of the 2014 IEEE Photonics Conference, Hyatt Regency, La Jolla, San Diego, CA, USA, 12–16 October 2014. [Google Scholar]
- Sacher, W.D.; Huang, Y.; Lo, G.Q.; Poon, J.K.S. Multilayer silicon nitride-on-silicon integrated photonic platforms and devices. J. Light. Technol. 2015, 33, 901–910. [Google Scholar] [CrossRef]
- Guo-Mian, L.; Qi, L.; Yue-Ting, C.; Hua-Jun, F.; Zhi-Hai, X.; Jingjing, M. An improved scheme and numerical simulation of segmented planar imaging detector for electro-optical reconnaissance. Opt. Rev. 2019, 26, 664–675. [Google Scholar] [CrossRef]
- Chu, Q.; Shen, Y.; Yuan, M.; Gong, M. Numerical simulation and optimal design of segmented planar imaging detector for electro-optical reconnaissance. Opt. Commun. 2017, 405, 288–296. [Google Scholar] [CrossRef]
- Gao, W.P.; Wang, X.R.; Ma, L.; Yuan, Y.; Guo, D.F. Quantitative analysis of segmented planar imaging quality based on hierarchical multistage sampling lens array. Opt. Express 2019, 27, 7955–7967. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Yuan, Y.; Wang, X.; Ma, L.; Zhao, Z.; Yuan, H. Quantitative analysis and optimization design of the segmented planar integrated optical imaging system based on an inhomogeneous multistage sampling lens array. Opt. Express 2021, 29, 11869–11884. [Google Scholar] [CrossRef]
- Clark, B.G. An efficient implementation of the algorithm ‘CLEAN’. Astron. Astrophys. 1980, 89, 377. [Google Scholar]




| Parameter | Symbol | Value |
|---|---|---|
| Number of PICs | M | 37 |
| Number of lenslets per PIC | N | 51 |
| Lenslet diameter | d | 2 mm |
| Length of the longest baseline | Bmax | 100 mm |
| Wavelength | λ | 800~1600 nm |
| Channel number | q | 10 |
| Object distance | z | 100 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, Z.; Liu, Y.; Li, S.; Zhou, M.; Du, H.; Zhang, X.; Zuo, Y.; Qiu, J.; Wu, J.; Gao, L.; et al. Optimal Design of Segmented Planar Imaging System Based on Rotation and CLEAN Algorithm. Photonics 2023, 10, 46. https://doi.org/10.3390/photonics10010046
Ming Z, Liu Y, Li S, Zhou M, Du H, Zhang X, Zuo Y, Qiu J, Wu J, Gao L, et al. Optimal Design of Segmented Planar Imaging System Based on Rotation and CLEAN Algorithm. Photonics. 2023; 10(1):46. https://doi.org/10.3390/photonics10010046
Chicago/Turabian StyleMing, Zhizi, Yang Liu, Shanchuang Li, Mengchen Zhou, Haoran Du, Xiaochun Zhang, Yong Zuo, Jifang Qiu, Jian Wu, Lu Gao, and et al. 2023. "Optimal Design of Segmented Planar Imaging System Based on Rotation and CLEAN Algorithm" Photonics 10, no. 1: 46. https://doi.org/10.3390/photonics10010046
APA StyleMing, Z., Liu, Y., Li, S., Zhou, M., Du, H., Zhang, X., Zuo, Y., Qiu, J., Wu, J., Gao, L., & Zhang, Z. (2023). Optimal Design of Segmented Planar Imaging System Based on Rotation and CLEAN Algorithm. Photonics, 10(1), 46. https://doi.org/10.3390/photonics10010046







