Dispersive Fourier Transformation for Versatile Microwave Photonics Applications
Abstract
:1. Introduction
2. Dispersive Fourier Transformation Technique
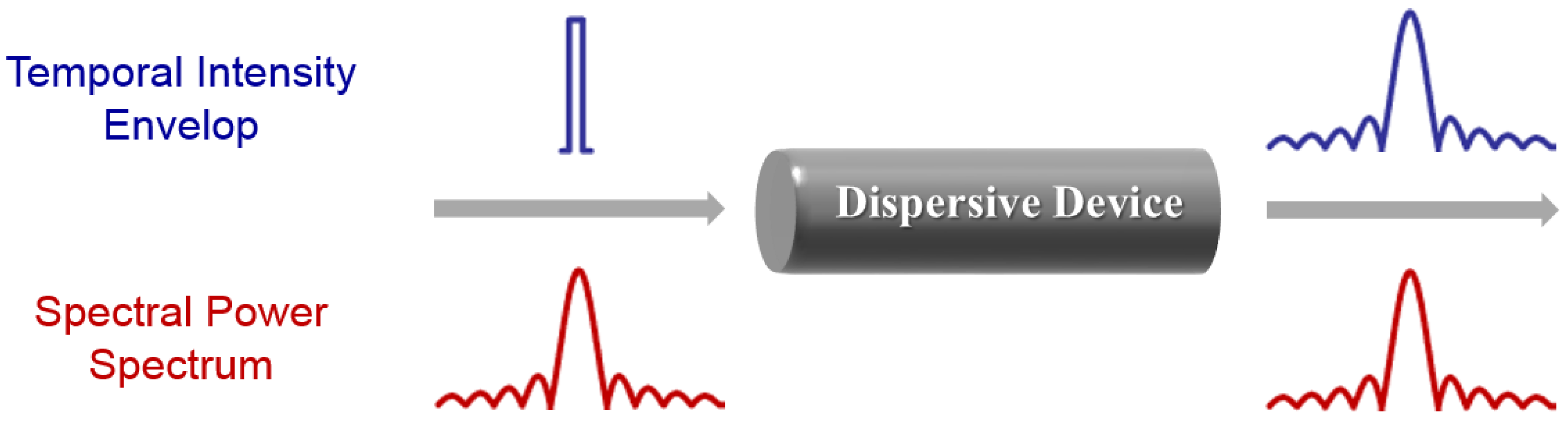
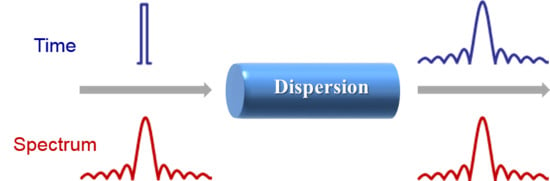
2.1. Theory of DFT
2.1.1. Mathematical Description
2.1.2. Impact of Higher-Order Dispersion
2.1.3. Near-Field Condition
2.2. Implementation of DFT
2.2.1. Optical Source
2.2.2. Dispersive Devices
2.2.3. Operational Wavelength Bands of DFT
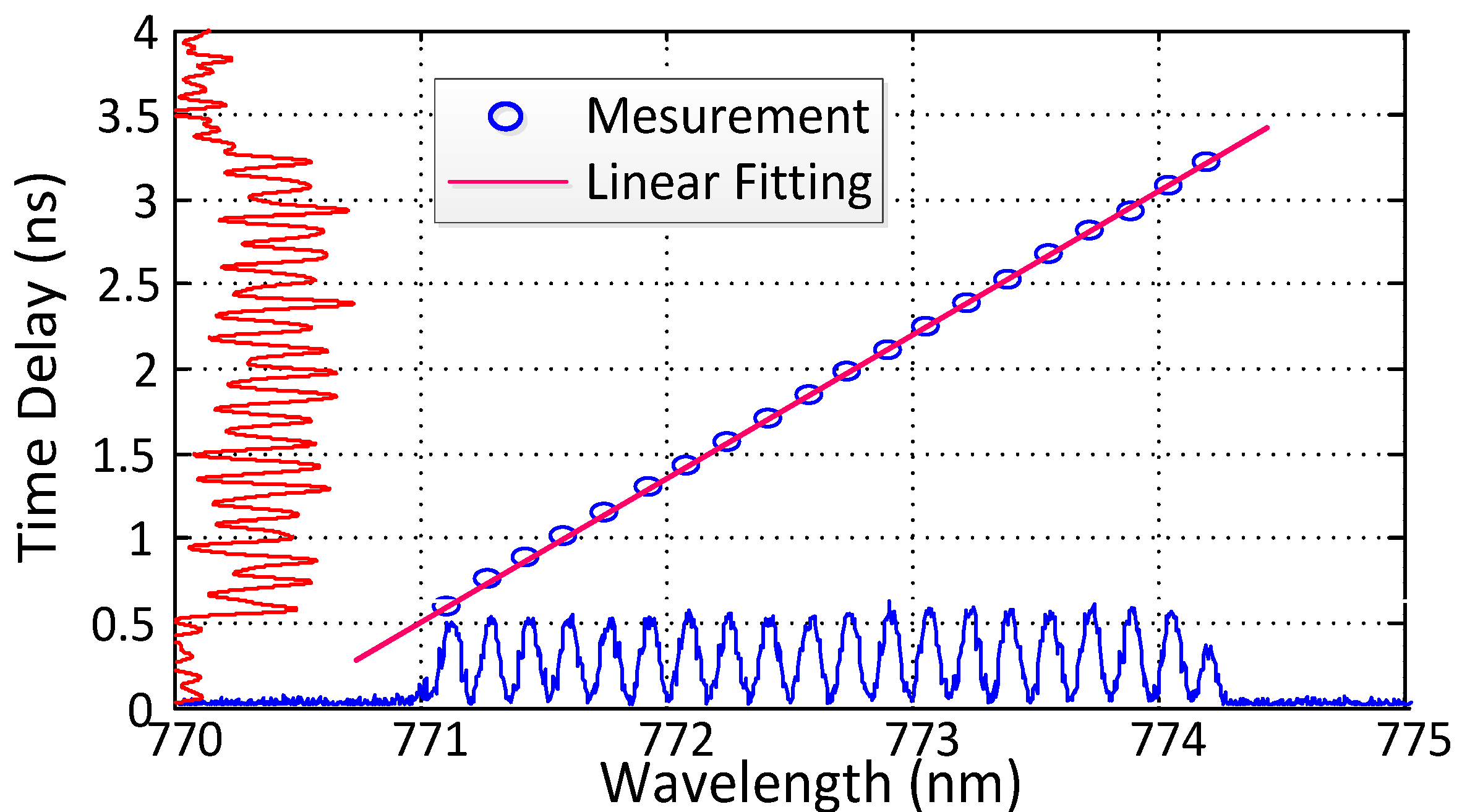
2.2.4. Incoherent DFT
3. Microwave Photonics Applications of DFT
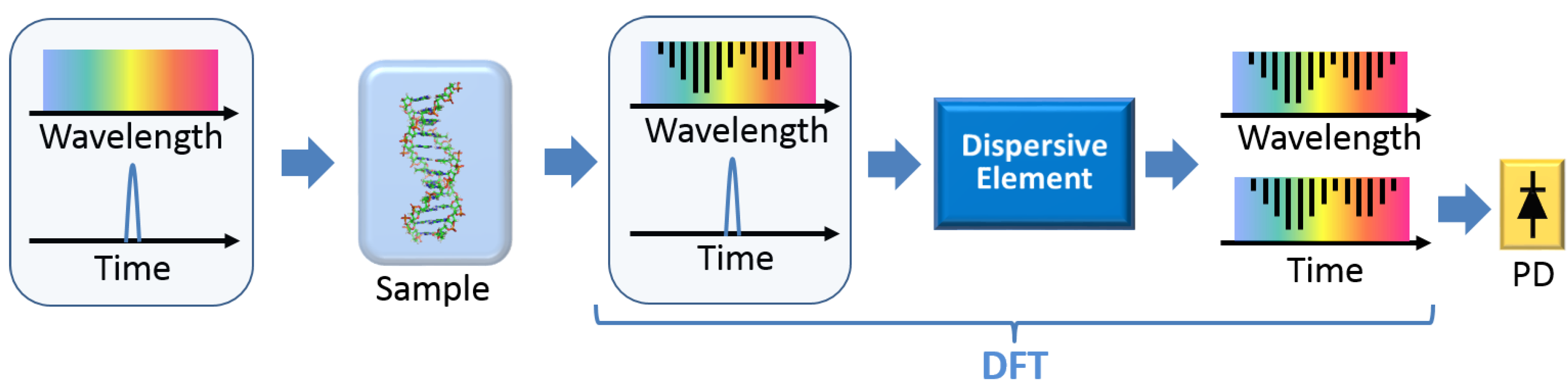
3.1. DFT for Real-Time Spectroscopy
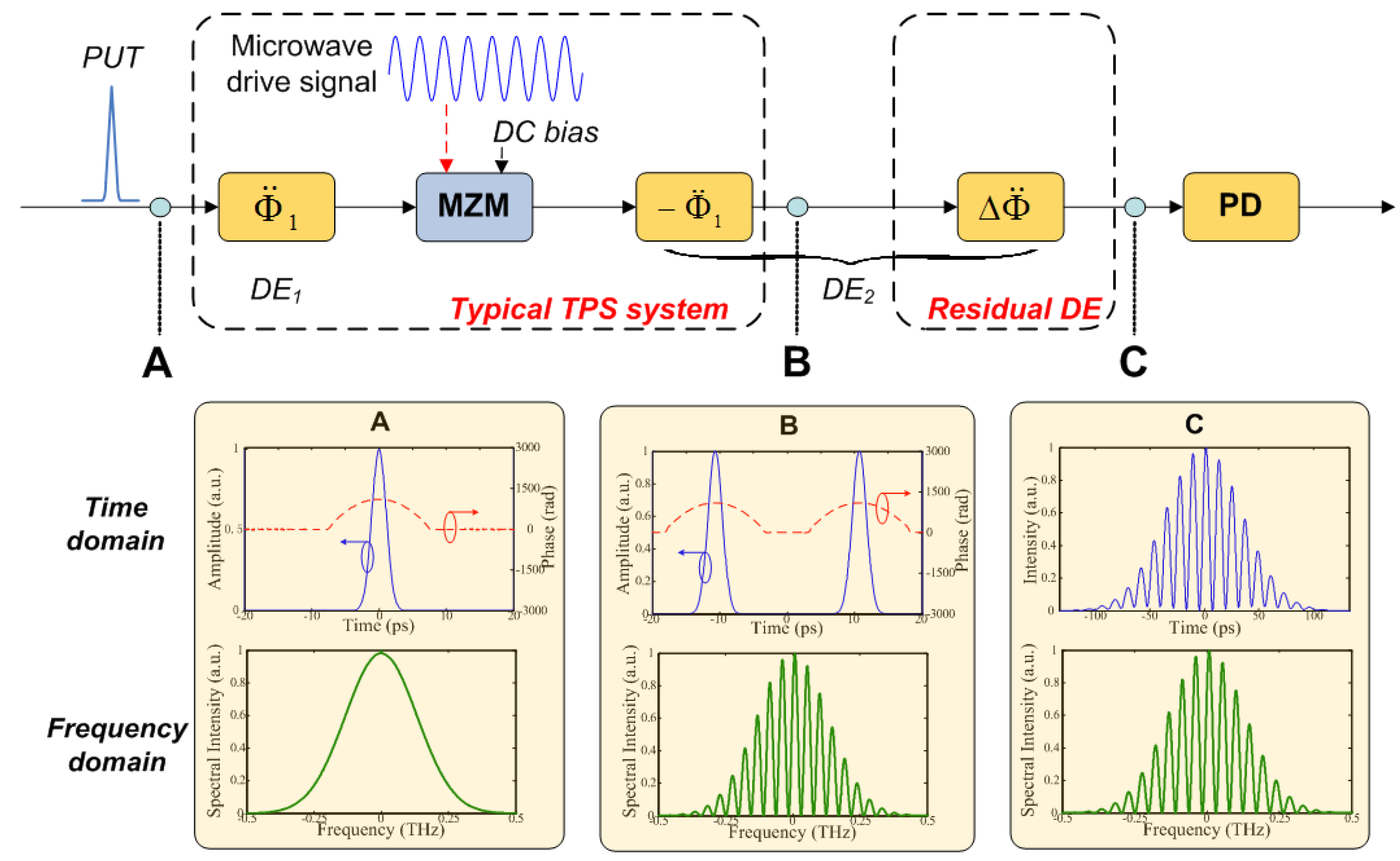
3.2. DFT for Microwave Arbitrary Waveform Generation
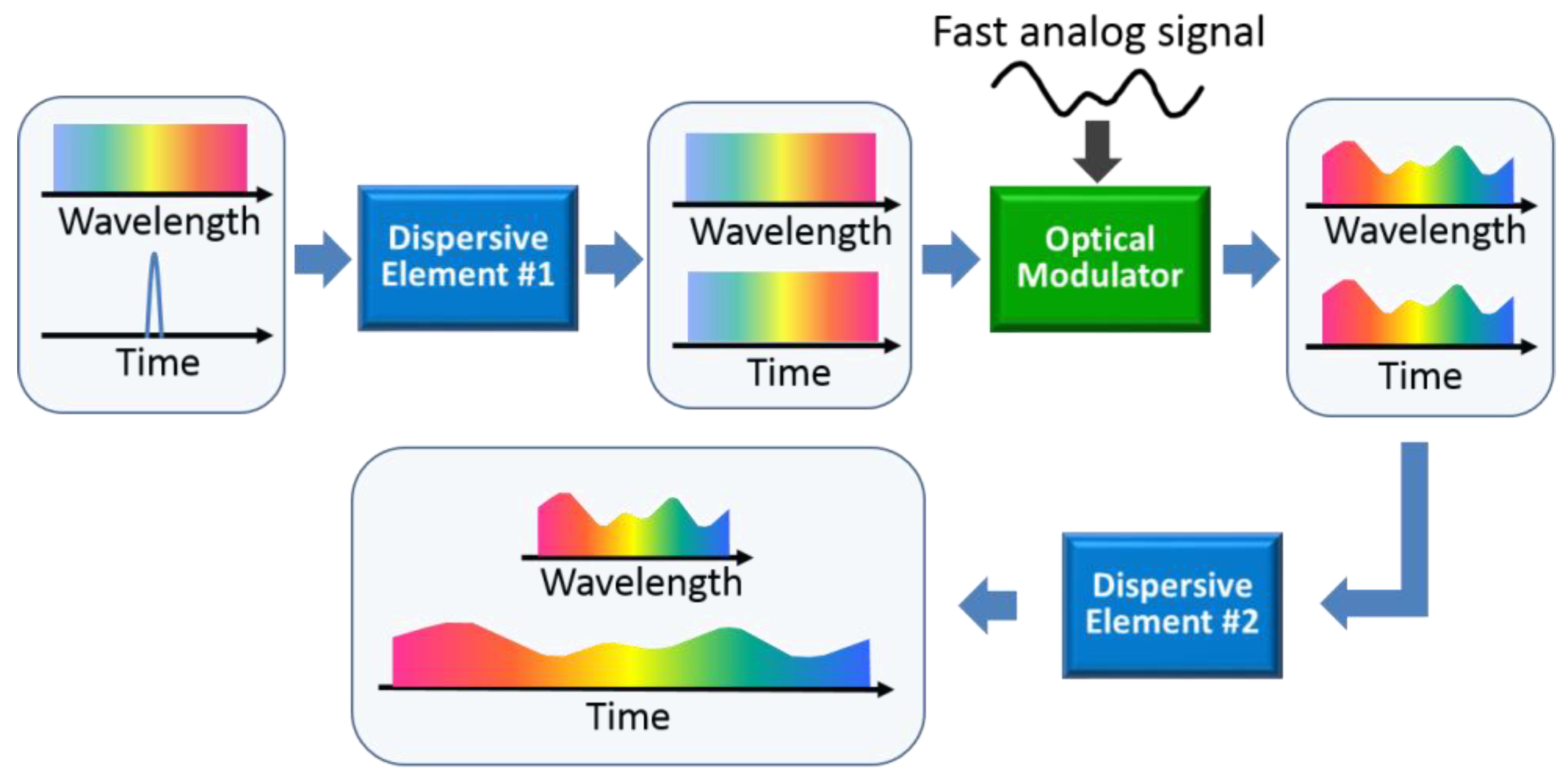
3.2.1. General Concept
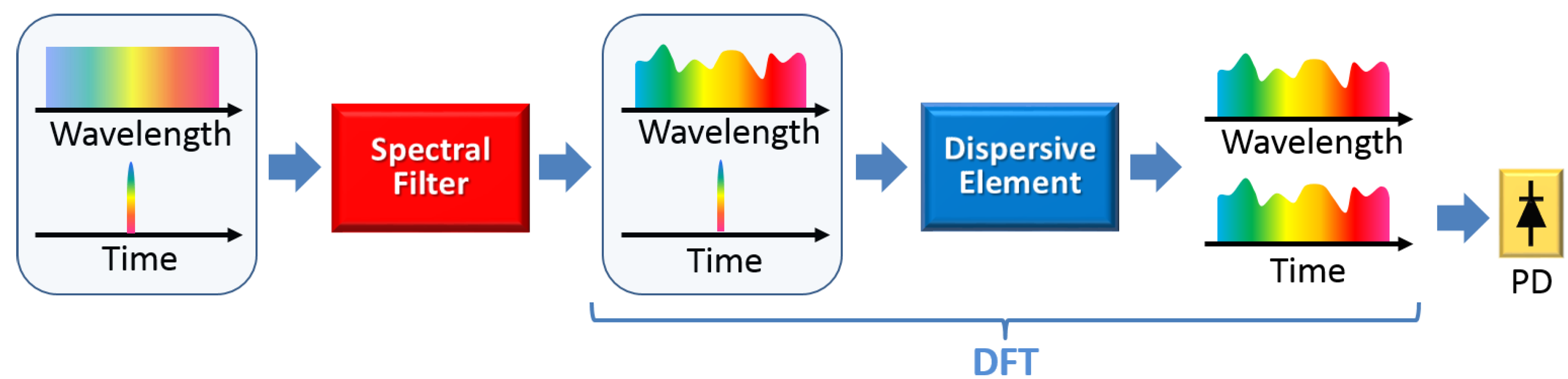
3.2.2. All-Fiber DFT-Based Microwave AWG
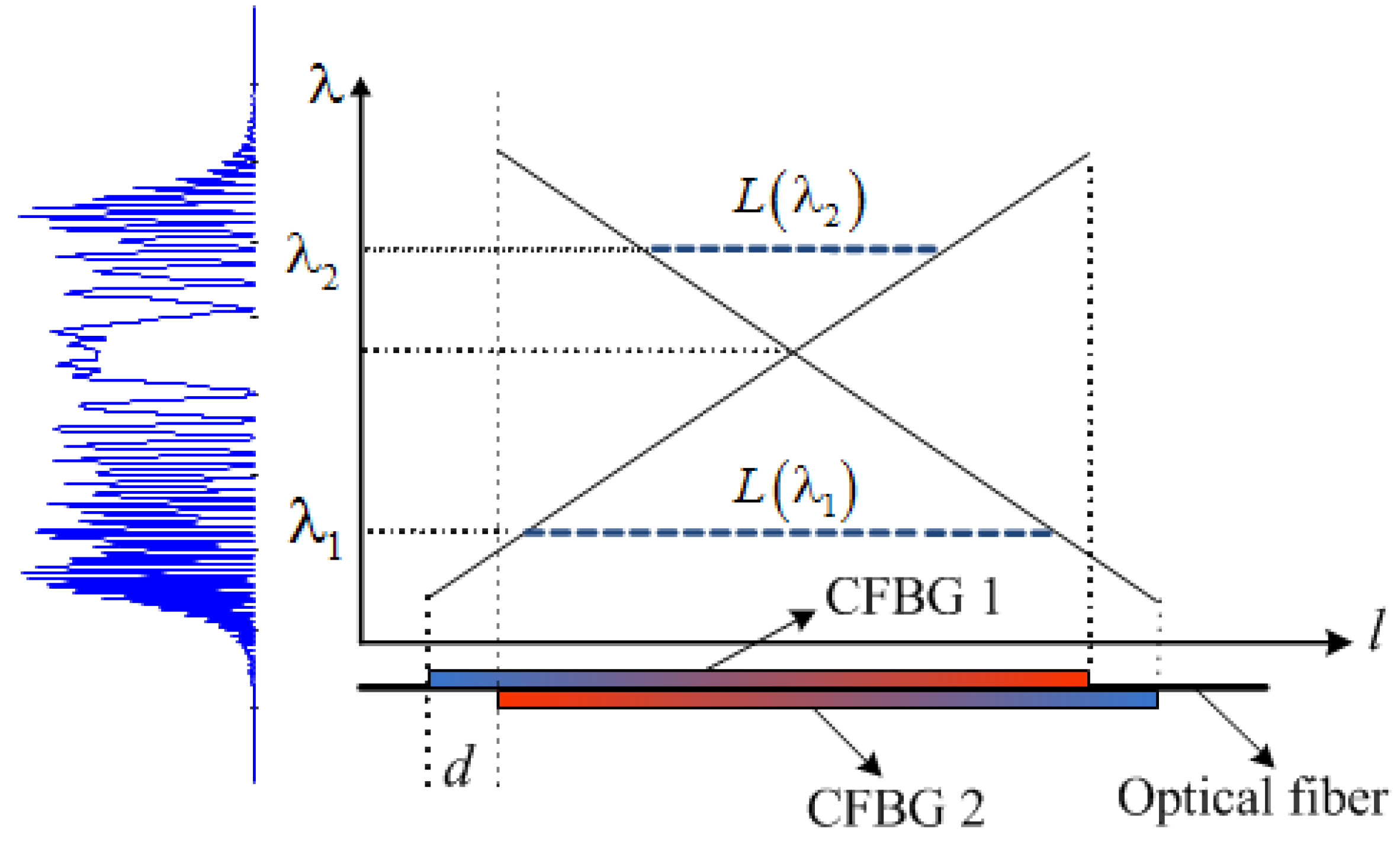
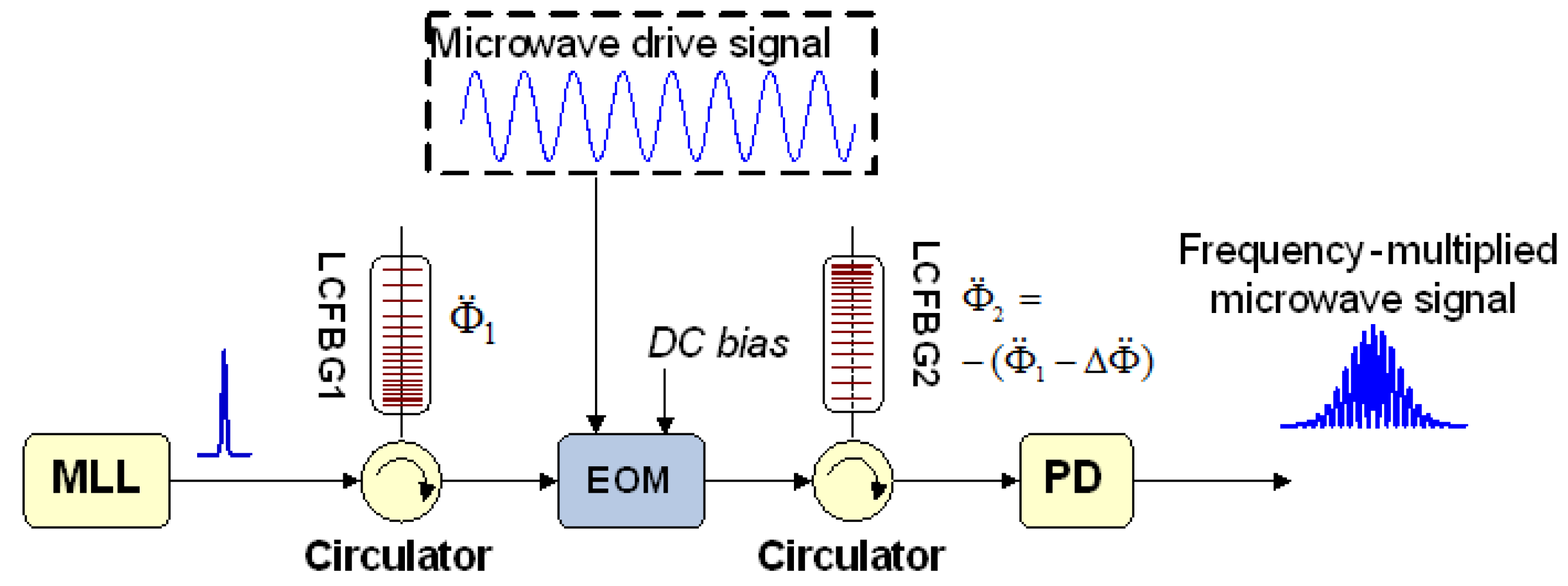
3.2.3. Nonlinear DFT for Photonic Microwave AWG
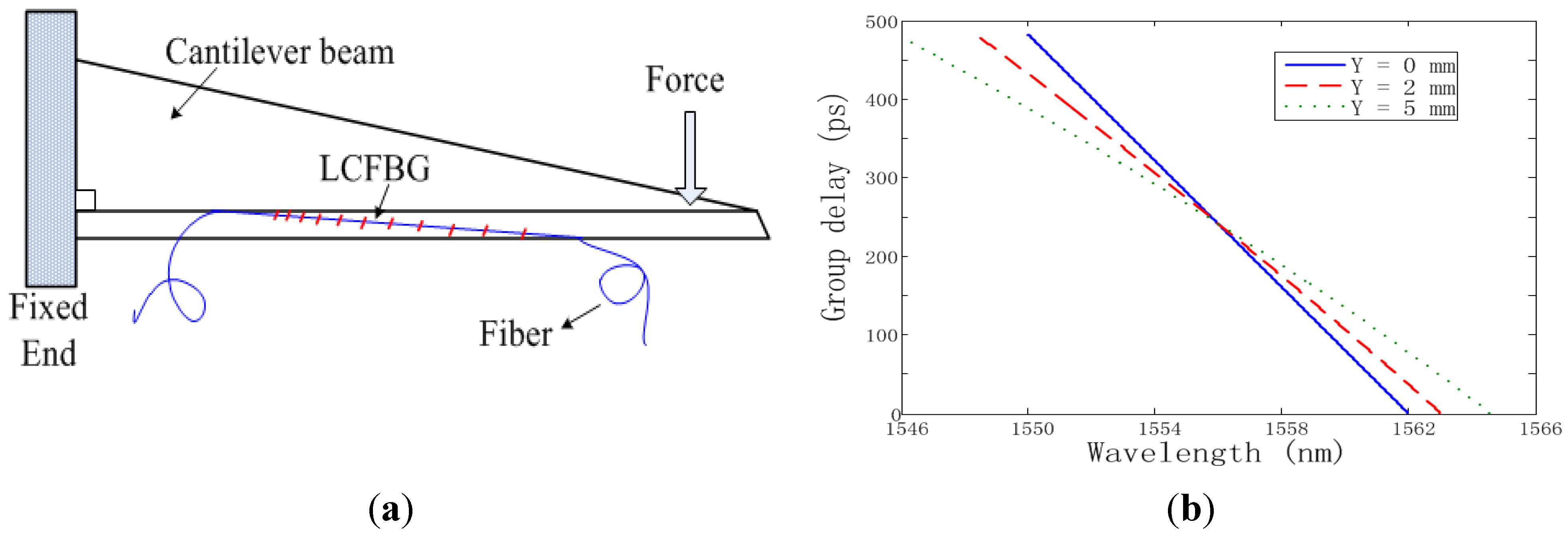
3.2.4. “Two-in-One” Design
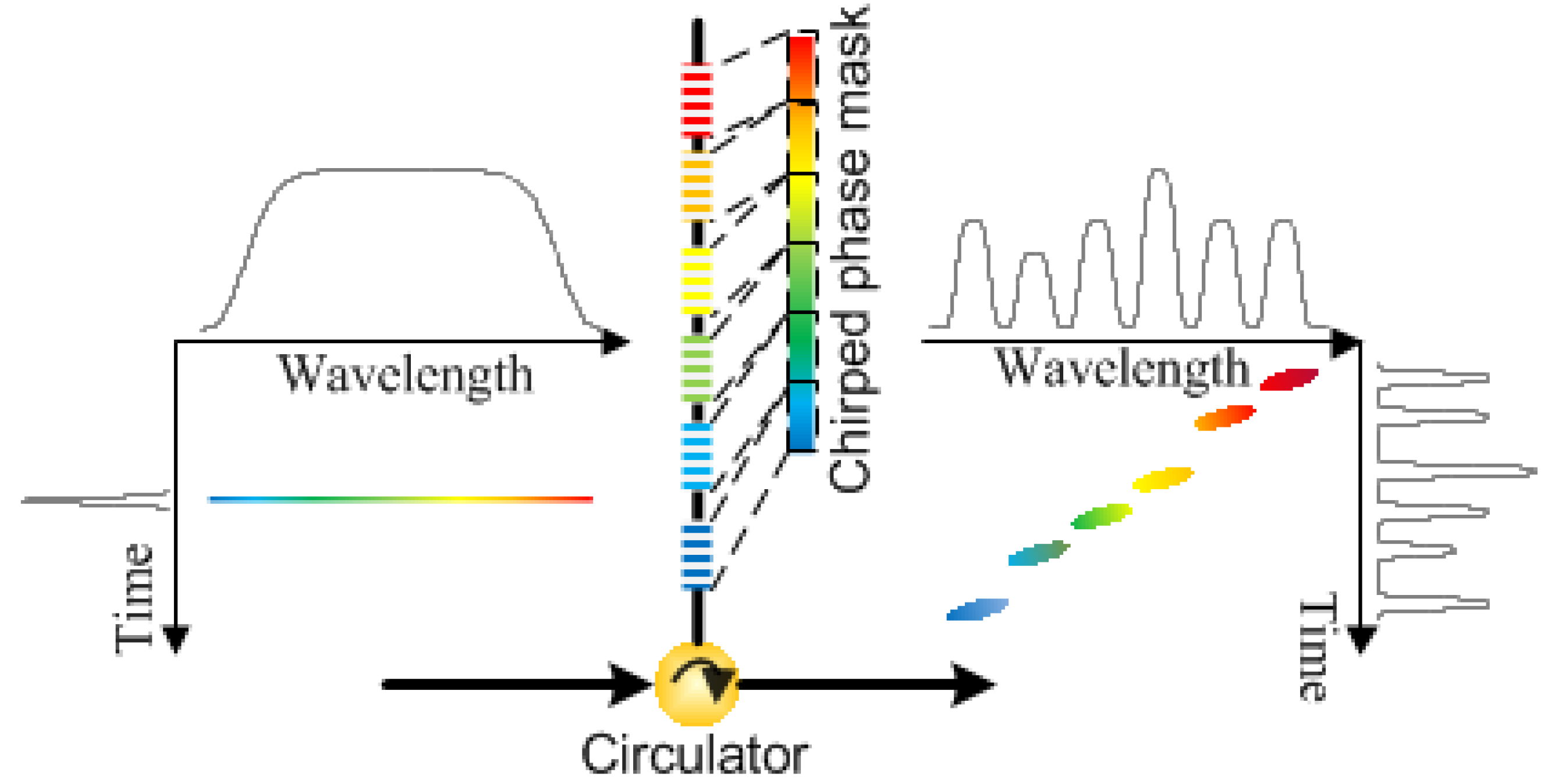
3.2.5. Temporal Fourier Transform Pulse Shaping for Photonic Microwave AWG
| Systems for Generating Chirped Microwave Waveforms | TBWP | Chirp Rate |
|---|---|---|
| Based on superimposed chirped FBGs [103] | 37.5 | 23.8 GHz/ns |
| Based on Sagnac loop mirror with a chirped FBG [104] | 44.8 | 22 GHz/ns |
| Based on nonlinear DFT [56] | 8.4 | 74 GHz/ns |
| Based on spatially-discrete chirped FBG [39] | 16.8 and 23.2 | 11.2–93.6 GHz/ns |
| Based on temporal Fourier transform pulse shaping [114] | 1.8 | 0.715 GHz/ns |
3.3. DFT for Microwave Spectrum Sensing

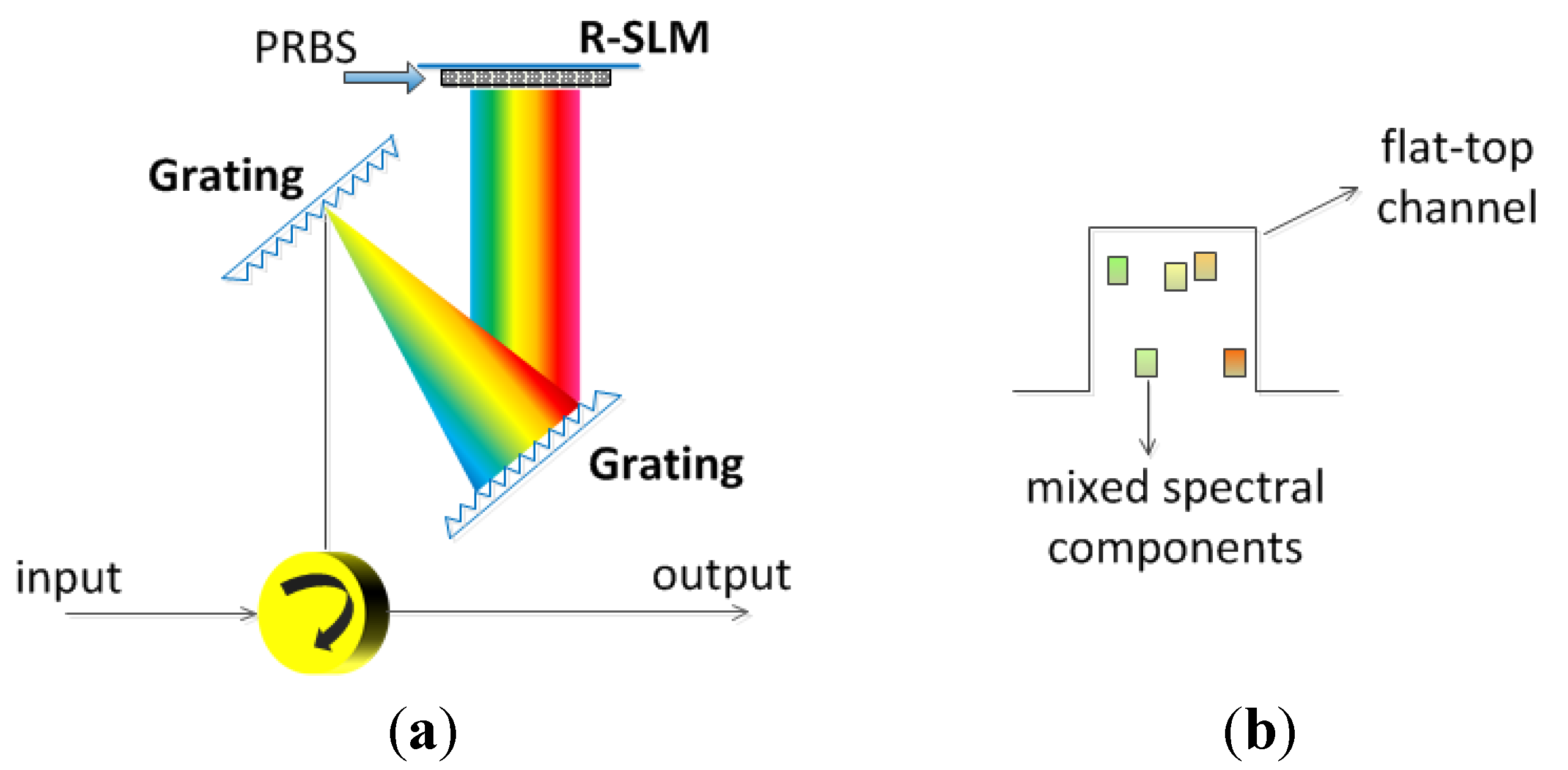
3.4. DFT for Photonic Analog-to-Digital Conversion (ADC)
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Seeds, A.J. Microwave photonics. IEEE Trans. Microw. Theory Tech. 2002, 50, 877–887. [Google Scholar] [CrossRef]
- Seeds, A.J.; Williams, K.J. Microwave photonics. J. Lightwave Technol. 2006, 24, 4628–4641. [Google Scholar] [CrossRef]
- Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nature Photon. 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Yao, J.P. Microwave Photonics. J. Lightwave Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Ghelfi, P.; Laghezza, F.; Scotti, F.; Serafino, G.; Capria, A.; Pinna, S.; Onori, D.; Porzi, C.; Scaffardi, M.; Malacarne, A.; et al. A fully photonics-based coherent radar system. Nature 2014, 507, 341–345. [Google Scholar] [CrossRef] [PubMed]
- Zmuda, H.; Toughlian, E.N. Photonic Aspects of Modern Radar; Artech House: Norwood, MA USA, 1994. [Google Scholar]
- Manka, M.E. Microwave photonics for Electronic Warfare applications. In Proceedings of the international topical meeting on Microwave photonics, 2008 jointly held with the 2008 asia-pacific microwave photonics conference, Gold Coast, Qld, Australia; 2008; pp. 275–278. [Google Scholar]
- Mjeku, M.; Gomes, N.J. Performance analysis of 802.11e transmission bursting in fiberfed networks. In Proceedings of the 2008 IEEE Radio and Wireless Symposium, 22–24 January 2008; pp. 133–136.
- Business News. Wireless future drives microwave photonics. Nat. Photon. 2011, 5, 724. [Google Scholar]
- Sotom, M.; Benazet, B.; Le Kernec, A.; Maignan, M. Microwave photonic technologies for flexible satellite telecom payloads. In Proceedings of the 35th European Conference on Optical Communication, Vienna, Austria, 20–24 September 2009; pp. 1–4.
- Isogawa, T.; Kumashiro, T.; Ho-Jin, S.; Ajito, K.; Kukutsu, N.; Iwatsuki, K.; Nagatsuma, T. Tomographic Imaging Using Photonically Generated Low-Coherence Terahertz Noise Sources. IEEE Trans. Terahertz Sci. Technol. 2012, 2, 485–492. [Google Scholar] [CrossRef]
- Chi, H.; Zou, X.H.; Yao, J.P. An approach to the measurement of microwave frequency based on optical power monitoring. IEEE Photon. Technol. Lett. 2008, 20, 1249–1251. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Fiber Bragg gratings for microwave photonics subsystems. Opt. Express 2013, 21, 22868–22884. [Google Scholar] [CrossRef] [PubMed]
- Guohua, Q.; Jianping, Y.; Seregelyi, J.; Paquet, S.; Belisle, C. Generation and distribution of a wide-band continuously tunable millimeter-wave signal with an optical external modulation technique. IEEE Trans. Microw. Theory Tech. 2005, 53, 3090–3097. [Google Scholar] [CrossRef]
- Minasian, R.A.; Chan, E.H.W.; Yi, X. Microwave photonic signal processing. Opt. Express 2013, 21, 22918–22936. [Google Scholar] [CrossRef]
- Capmany, J.; Mora, J.; Gasulla, I.; Sancho, J.; Lloret, J.; Sales, S. Microwave Photonic Signal Processing. J. Lightwave Technol. 2013, 31, 571–586. [Google Scholar] [CrossRef]
- Frigyes, I.; Seeds, A.J. Optically Generated True-Time Delay in Phased-Array Antennas. IEEE Trans. Microw. Theory Tech. 1995, 43, 2378–2386. [Google Scholar] [CrossRef]
- Ortega, B.; Cruz, J.L.; Capmany, J.; Andres, M.V.; Pastor, D. Variable delay line for phased-array antenna based on a chirped fiber grating. IEEE Trans. Microw. Theory Tech. 2000, 48, 1352–1360. [Google Scholar] [CrossRef]
- Wake, D.; Nkansah, A.; Gomes, N.J. Radio Over Fiber Link Design for Next Generation Wireless Systems. J. Lightwave Technol. 2010, 28, 2456–2464. [Google Scholar] [CrossRef]
- Koonen, A.M.; Larrodé, M.G.; Ng'oma, A.; Wang, K.; Yang, H.; Zheng, Y.; Tangdiongga, E. Perspectives of Radio-over-Fiber Technologies. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference, San Diego, CA, USA, 24 February 2008; p. OThP3.
- McKinney, J.D.; Leaird, D.E.; Weiner, A.M. Millimeter-wave arbitrary waveform generation with a direct space-to-time pulse shaper. Opt. Lett. 2002, 27, 1345–1347. [Google Scholar] [CrossRef] [PubMed]
- Chou, J.; Han, Y.; Jalali, B. Adaptive RF-photonic arbitrary waveform generator. IEEE Photon. Technol. Lett. 2003, 15, 581–583. [Google Scholar] [CrossRef]
- Yao, J.P. Photonic generation of microwave arbitrary waveforms. Opt. Commun. 2011, 284, 3723–3736. [Google Scholar] [CrossRef]
- Han, Y.; Jalali, B. Photonic time-stretched analog-to-digital converter: Fundamental concepts and practical considerations. J. Lightwave Technol. 2003, 21, 3085–3103. [Google Scholar]
- Valley, G.C. Photonic analog-to-digital converters. Opt. Express 2007, 15, 1955–1982. [Google Scholar] [CrossRef]
- Marpaung, D.; Roeloffzen, C.; Heideman, R.; Leinse, A.; Sales, S.; Capmany, J. Integrated microwave photonics. Laser Photonics Rev. 2013, 7, 506–538. [Google Scholar] [CrossRef]
- Coldren, L.A. Photonic Integrated Circuits for microwave photonics. In Proceedings of the 2010 IEEE Topical Meeting on Microwave Photonics (MWP), Montreal, QC, Canada, 5–9 October 2010; pp. 1–4.
- Burla, M.; Cortés, L.R.; Li, M.; Wang, X.; Chrostowski, L.; Azaña, J. Integrated waveguide Bragg gratings for microwave photonics signal processing. Opt. Express 2013, 21, 25120–25147. [Google Scholar] [CrossRef] [PubMed]
- Burla, M.; Marpaung, D.; Zhuang, L.M.; Roeloffzen, C.; Khan, M.R.; Leinse, A.; Hoekman, M.; Heideman, R. On-chip CMOS compatible reconfigurable optical delay line with separate carrier tuning for microwave photonic signal processing. Opt. Express 2011, 19, 21475–21484. [Google Scholar] [CrossRef] [PubMed]
- Pant, R.; Marpaung, D.; Kabakova, I.V.; Morrison, B.; Poulton, C.G.; Eggleton, B.J. On-chip stimulated Brillouin Scattering for microwave signal processing and generation. Laser Photonics Rev. 2014, 1–14. [Google Scholar]
- Goda, K.; Solli, D.R.; Tsia, K.K.; Jalali, B. Theory of amplified dispersive Fourier transformation. Phys. Rev. A 2009, 80, 043821. [Google Scholar] [CrossRef]
- Goda, K.; Jalali, B. Dispersive Fourier transformation for fast continuous single-shot measurements. Nat. Photon. 2013, 7, 102–112. [Google Scholar] [CrossRef]
- Jannson, T. Real-Time Fourier Transformation in Dispersive Optical Fibers. Opt. Lett. 1983, 8, 232–234. [Google Scholar] [CrossRef] [PubMed]
- Muriel, M.A.; Azana, J.; Carballar, A. Real-time Fourier transformer based on fiber gratings. Opt. Lett. 1999, 24, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Azana, J.; Chen, L.R.; Muriel, M.A.; Smith, P.W.E. Experimental demonstration of real-time Fourier transformation using linearly chirped fibre Bragg gratings. Electron. Lett. 1999, 35, 2223–2224. [Google Scholar] [CrossRef]
- Wang, C.; Zeng, F.; Yao, J.P. All-fiber ultrawideband pulse generation based on spectral-shaping and dispersion-induced frequency-to-time conversion. IEEE Photon. Technol. Lett. 2007, 19, 137–139. [Google Scholar] [CrossRef]
- Torres-Company, V.; Leaird, D.E.; Weiner, A.M. Dispersion requirements in coherent frequency-to-time mapping. Opt. Express 2011, 19, 24718–24729. [Google Scholar] [CrossRef] [PubMed]
- Jalali, B.; Solli, D.R.; Goda, K.; Tsia, K.; Ropers, C. Real-time measurements, rare events and photon economics. Eur Phys. J.-Spec. Top. 2010, 185, 145–157. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Large time-bandwidth product microwave arbitrary waveform generation using a spatially discrete chirped fiber Bragg grating. J. Lightwave Technol. 2010, 28, 1652–1660. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Ultrahigh-Resolution Photonic-Assisted Microwave Frequency Identification Based on Temporal Channelization. IEEE Trans. Microw. Theory Tech. 2013, 61, 4275–4282. [Google Scholar] [CrossRef]
- Wang, C.; Gomes, N.J. Photonics-enabled sub-Nyquist radio frequency sensing based on temporal channelization and compressive sensing. In Proceedings of the 2014 IEEE Topical Meeting on Microwave Photonics (MWP), Sapporo, Japan, 20–23 October 2014; pp. 1–4.
- Bhushan, A.S.; Coppinger, F.; Jalali, B. Time-stretched analogue-to-digital conversion. Electron. Lett. 1998, 34, 839–841. [Google Scholar] [CrossRef]
- Chou, J.; Boyraz, O.; Solli, D.; Jalali, B. Femtosecond real-time single-shot digitizer. Appl. Phys. Lett. 2007, 91, 161105. [Google Scholar] [CrossRef]
- Hult, J.; Watt, R.S.; Kaminski, C.F. High bandwidth absorption spectroscopy with a dispersed supercontinuum source. Opt. Express 2007, 15, 11385–11395. [Google Scholar] [CrossRef] [PubMed]
- Chou, J.; Solli, D.R.; Jalali, B. Real-time spectroscopy with subgigahertz resolution using amplified dispersive Fourier transformation. Appl. Phys. Lett. 2008, 92, 111102. [Google Scholar] [CrossRef]
- Sych, Y.; Engelbrecht, R.; Schmauss, B.; Kozlov, D.; Seeger, T.; Leipertz, A. Broadband time-domain absorption spectroscopy with a ns-pulse supercontinuum source. Opt. Express 2010, 18, 22762–22771. [Google Scholar] [CrossRef]
- Solli, D.R.; Chou, J.; Jalali, B. Amplified wavelength-time transformation for real-time spectroscopy. Nature Photon. 2008, 2, 48–51. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Ultrafast and Ultrahigh-Resolution Interrogation of a Fiber Bragg Grating Sensor Based on Interferometric Temporal Spectroscopy. J. Lightwave Technol. 2011, 29, 2927–2933. [Google Scholar] [CrossRef]
- Xia, H.Y.; Wang, C.; Blais, S.; Yao, J.P. Ultrafast and Precise Interrogation of Fiber Bragg Grating Sensor Based on Wavelength-to-Time Mapping Incorporating Higher Order Dispersion. J. Lightwave Technol. 2010, 28, 254–261. [Google Scholar] [CrossRef]
- Goda, K.; Tsia, K.K.; Jalali, B. Serial time-encoded amplified imaging for real-time observation of fast dynamic phenomena. Nature 2009, 458, 1145–1149. [Google Scholar] [CrossRef] [PubMed]
- Goda, K.; Mahjoubfar, A.; Wang, C.; Fard, A.; Adam, J.; Gossett, D.R.; Ayazi, A.; Sollier, E.; Malik, O.; Chen, E.; et al. Hybrid Dispersion Laser Scanner. Sci. Rep. 2012, 2, 445. [Google Scholar] [CrossRef] [PubMed]
- Kolner, B.H. Space-Time Duality and the Theory of Temporal Imaging. IEEE J. Quant. Electron. 1994, 30, 1951–1963. [Google Scholar] [CrossRef]
- Papoulis, A. Pulse compression, fiber communications, and diffraction: A unified approach. J. Opt. Soc. Am. A 1994, 11, 3–13. [Google Scholar] [CrossRef]
- Xia, H.Y.; Yao, J.P. Characterization of Subpicosecond Pulses Based on Temporal Interferometry with Real-Time Tracking of Higher Order Dispersion and Optical Time Delay. J. Lightwave Technol. 2009, 27, 5029–5037. [Google Scholar] [CrossRef]
- Gupta, S.; Jalali, B. Time-warp correction and calibration in photonic time-stretch analog-to-digital converter. Opt. Lett. 2008, 33, 2674–2676. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yao, J.P. Photonic generation of chirped millimeter-wave pulses based on Nonlinear frequency-to-time mapping in a nonlinearly chirped fiber bragg grating. IEEE Trans. Microw. Theory Tech. 2008, 56, 542–553. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, Z.; Chi, H.; Jin, X.; Zheng, S.; Zhang, X. Relaxed dispersion requirement in the generation of chirped RF signals based on frequency-to-time mapping. Opt. Commun. 2014, 331, 278–281. [Google Scholar] [CrossRef]
- Solli, D.R.; Gupta, S.; Jalali, B. Optical phase recovery in the dispersive Fourier transform. Appl. Phys. Lett. 2009, 95, 231108. [Google Scholar] [CrossRef]
- Dezfooliyan, A.; Weiner, A.M. Photonic synthesis of high fidelity microwave arbitrary waveforms using near field frequency to time mapping. Opt. Express 2013, 21, 22974–22987. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-P.; Kapteyn, H.C.; McIntosh, J.W.; Murnane, M.M. Generation of transform-limited 32-fs pulses from a self-mode-locked Ti:sapphire laser. Opt. Lett. 1992, 17, 139–141. [Google Scholar] [CrossRef]
- Kobayashi, T.; Yao, H.; Amano, K.; Fukushima, Y.; Morimoto, A.; Sueta, T. Optical pulse compression using high-frequency electrooptic phase modulation. IEEE J. Quant. Electron. 1988, 24, 382–387. [Google Scholar]
- Komukai, T.; Yamamoto, T.; Kawanishi, S. Optical pulse generator using phase modulator and linearly chirped fiber Bragg gratings. IEEE Photon. Technol. Lett. 2005, 17, 1746–1748. [Google Scholar] [CrossRef]
- Saperstein, R.E.; Panasenko, D.; Fainman, Y. Demonstration of a microwave spectrum analyzer based on time-domain optical processing in fiber. Opt. Lett. 2004, 29, 501–503. [Google Scholar] [CrossRef]
- Chi, H.; Yao, J. All-fiber chirped microwave pulses generation based on spectral shaping and wavelength-to-time conversion. IEEE Trans. Microw. Theory Tech. 2007, 55, 1958–1963. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Complete Characterization of an Optical Pulse Based on Temporal Interferometry Using an Unbalanced Temporal Pulse Shaping System. J. Lightwave Technol. 2011, 29, 789–800. [Google Scholar] [CrossRef]
- Hill, K.O.; Malo, B.; Bilodeau, F.; Johnson, D.C.; Albert, J. Bragg gratings fabricated in monomode photosensitive optical fiber by UV exposure through a phase mask. Appl. Phys. Lett. 1993, 62, 1035–1037. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Lightwave Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Capmany, J.; Pastor, D.; Ortega, B.; Cruz, J.L.; Andres, M.V. Applications of fiber Bragg gratings to microwave photonics. Fiber Integrated Opt. 2000, 19, 483–494. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Fiber Bragg gratings for microwave photonics applications. In Microwave Photonics, 2nd ed.; Lee, C.H., Ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 125–174. [Google Scholar]
- Kashyap, R. Fiber Bragg Gratings; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Chi, H.; Yao, J. Chirped RF Pulse Generation Based on Optical Spectral Shaping and Wavelength-to-Time Mapping Using a Nonlinearly Chirped Fiber Bragg Grating. J. Lightwave Technol. 2008, 26, 1282–1287. [Google Scholar] [CrossRef]
- Kashyap, R.; de Lacerda Rocha, M. On the group delay characteristics of chirped fibre Bragg gratings. Opt. Commun. 1998, 153, 19–22. [Google Scholar] [CrossRef]
- Tan, Z.W.; Wang, C.; Diebold, E.D.; Hon, N.K.; Jalali, B. Real-time wavelength and bandwidth-independent optical integrator based on modal dispersion. Opt. Express 2012, 20, 14109–14116. [Google Scholar] [CrossRef] [PubMed]
- Diebold, E.D.; Hon, N.K.; Tan, Z.; Chou, J.; Sienicki, T.; Wang, C.; Jalali, B. Giant tunable optical dispersion using chromo-modal excitation of a multimode waveguide. Opt. Express 2011, 19, 23809–23817. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.T.W.; Lau, A.K.S.; Wong, K.K.Y.; Tsia, K.K. Optical time-stretch confocal microscopy at 1 mu m. Opt. Lett. 2012, 37, 3330–3332. [Google Scholar] [CrossRef] [PubMed]
- Lau, A.K.S.; Wong, T.T.W.; Ho, K.K.Y.; Tang, M.T.H.; Chan, A.C.S.; Wei, X.; Lam, E.Y.; Shum, H.C.; Wong, K.K.Y.; Tsia, K.K. Interferometric time-stretch microscopy for ultrafast quantitative cellular and tissue imaging at 1 mu m. J. Biomed. Opt. 2014, 19, 076001. [Google Scholar] [CrossRef]
- Wang, C.; Goda, K.; Ibsen, M.; Jalali, B. Dispersive Fourier transformation in the 800 nm spectral range. In Proceedings of the Conference on Lasers and Electro-Optics 2012, San Jose, CA, USA, 6–11 May 2012; p. ATu2G.2.
- Torres-Company, V.; Lancis, J.; Andrés, P. Incoherent frequency-to-time mapping: application to incoherent pulse shaping. J. Opt. Soc. Am. A 2007, 24, 888–894. [Google Scholar] [CrossRef]
- Torres-Company, V.; Lancis, J.; Andres, P.; Chen, L.R. 20 GHz arbitrary radio-frequency waveform generator based on incoherent pulse shaping. Opt. Express 2008, 16, 21564–21569. [Google Scholar] [CrossRef] [PubMed]
- Dorrer, C. Statistical analysis of incoherent pulse shaping. Opt. Express 2009, 17, 3341–3352. [Google Scholar] [CrossRef] [PubMed]
- Azana, J.; Muriel, M.A. Real-time optical spectrum analysis based on the time-space duality in chirped fiber gratings. IEEE J. Quant. Electron. 2000, 36, 517–526. [Google Scholar] [CrossRef]
- Tong, Y.C.; Chan, L.Y.; Tsang, H.K. Fibre dispersion or pulse spectrum measurement using a sampling oscilloscope. Electron. Lett. 1997, 33, 983–985. [Google Scholar] [CrossRef]
- Kelkar, P.V.; Coppinger, F.; Bhushan, A.S.; Jalali, B. Time-domain optical sensing. Electron. Lett. 1999, 35, 1661–1662. [Google Scholar] [CrossRef]
- Chou, J.; Han, Y.; Jalali, B. Time-wavelength spectroscopy for chemical sensing. IEEE Photon. Technol. Lett. 2004, 16, 1140–1142. [Google Scholar] [CrossRef]
- Dennis, M.L.; Putnam, M.A.; Kang, J.U.; Tsai, T.E.; Duling, I.N.; Friebele, E.J. Grating sensor array demodulation by use of a passively mode-locked fiber laser. Opt. Lett. 1997, 22, 1362–1364. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Wang, C. Superimposed Oppositely Chirped FBGs for Ultrafast FBG Sensor Interrogation with Significantly Improved Resolution. In Proceedings of the Sensor and Signal Processing Applications (BThB), Karlsruhe Germany, 21–24 June 2010.
- Liu, W.L.; Li, M.; Wang, C.; Yao, J.P. Real-Time Interrogation of a Linearly Chirped Fiber Bragg Grating Sensor Based on Chirped Pulse Compression With Improved Resolution and Signal-to-Noise Ratio. J. Lightwave Technol. 2011, 29, 1239–1247. [Google Scholar] [CrossRef]
- Fu, H.Y.; Liu, H.L.; Dong, X.; Tam, H.Y.; Wai, P.K.A.; Lu, C. High-speed fibre Bragg grating sensor interrogation using dispersion-compensation fibre. Electron. Lett. 2008, 44, 618–619. [Google Scholar] [CrossRef]
- Rao, Y.J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355–375. [Google Scholar] [CrossRef]
- Iaconis, C.; Walmsley, I.A. Self-referencing spectral interferometry for measuring ultrashort optical pulses. IEEE J. Quant. Electron. 1999, 35, 501–509. [Google Scholar] [CrossRef]
- Berger, N.K.; Levit, B.; Smulakovsky, V.; Fischer, B. Complete characterization of optical pulses by real-time spectral interferometry. Appl. Opt. 2005, 44, 7862–7866. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Li, M.; Yao, J.P. Continuously Tunable Photonic Microwave Frequency Multiplication by Use of an Unbalanced Temporal Pulse Shaping System. IEEE Photon. Technol. Lett. 2010, 22, 1285–1287. [Google Scholar] [CrossRef]
- Wang, C.; Chi, H.; Yao, J. Photonic generation and processing of millimeter-wave arbitrary waveforms. In Proceedings of the 21st Annual Meeting of the IEEE Lasers and Electro-Optics Society, Newport Beach, CA, USA, 9–13 November 2008; pp. 346–347.
- McKinney, J.D.; Seo, D.S.; Weiner, A.M. Photonically assisted generation of continuous arbitrary millimetre electromagnetic waveforms. Electron. Lett. 2003, 39, 309–311. [Google Scholar] [CrossRef]
- Leaird, D.E.; Weiner, A.M. Femtosecond direct space-to-time pulse shaping in an integrated-optic configuration. Opt. Lett. 2004, 29, 1551–1553. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.T.; Yao, J.P. Nonuniformly Spaced Photonic Microwave Delay-Line Filters and Applications. IEEE Trans. Microw. Theory Tech. 2010, 58, 3279–3289. [Google Scholar] [CrossRef]
- Dai, Y.T.; Yao, J.P. Chirped Microwave Pulse Generation Using a Photonic Microwave Delay-Line Filter With a Quadratic Phase Response. IEEE Photon. Technol. Lett. 2009, 21, 569–571. [Google Scholar] [CrossRef]
- Weiner, A.M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 2000, 71, 1929–1960. [Google Scholar] [CrossRef]
- Lin, I.S.; McKinney, J.D.; Weiner, A.M. Photonic synthesis of broadband microwave arbitrary waveforms applicable to ultra-wideband communication. IEEE Microw. Wireless Compon. Lett. 2005, 15, 226–228. [Google Scholar]
- Khan, M.H.; Shen, H.; Xuan, Y.; Zhao, L.; Xiao, S.; Leaird, D.E.; Weiner, A.M.; Qi, M. Ultrabroad-bandwidth arbitrary radiofrequency waveform generation with a silicon photonic chip-based spectral shaper. Nature Photon. 2010, 4, 117–122. [Google Scholar] [CrossRef]
- Yao, J.P. Photonics for Ultrawideband Communications. IEEE Microw. Mag. 2009, 10, 82–95. [Google Scholar] [CrossRef]
- Zeitouny, A.; Stepanov, S.; Levinson, O.; Horowitz, M. Optical generation of linearly chirped microwave pulses using fiber Bragg gratings. IEEE Photon. Technol. Lett. 2005, 17, 660–662. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Photonic generation of chirped microwave pulses using superimposed chirped fiber Bragg gratings. IEEE Photon. Technol. Lett. 2008, 20, 882–884. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Chirped Microwave Pulse Generation Based on Optical Spectral Shaping and Wavelength-to-Time Mapping Using a Sagnac Loop Mirror Incorporating a Chirped Fiber Bragg Grating. J. Lightwave Technol. 2009, 27, 3336–3341. [Google Scholar] [CrossRef]
- Li, M.; Yao, J.P. Photonic Generation of Continuously Tunable Chirped Microwave Waveforms Based on a Temporal Interferometer Incorporating an Optically Pumped Linearly Chirped Fiber Bragg Grating. IEEE Trans. Microw. Theory Tech. 2011, 59, 3531–3537. [Google Scholar] [CrossRef]
- Chi, H.; Yao, J.P. All-fiber chirped microwave pulses generation based on spectral shaping and wavelength-to-time conversion. IEEE Trans. Microw. Theory Tech. 2007, 55, 1958–1963. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Simultaneous Optical Spectral Shaping and Wavelength-to-Time Mapping for Photonic Microwave Arbitrary Waveform Generation. IEEE Photon. Technol. Lett. 2009, 21, 793–795. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Phase-coded millimeter-wave waveform generation using a spatially discrete chirped fiber Bragg grating. IEEE Photon. Technol. Lett. 2012, 24, 1493–1495. [Google Scholar] [CrossRef]
- Heritage, J.P.; Weiner, A.M. Optical systems and methods based upon temporal stretching, modulation and recompression of ultrashort pulses. U.S. patent 4,928,316, 1990. [Google Scholar]
- Saperstein, R.E.; Alic, N.; Panasenko, D.; Rokitski, R.; Fainman, Y. Time-domain waveform processing by chromatic dispersion for temporal shaping of optical pulses. J. Opt. Soc. Am. B 2005, 22, 2427–2436. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.P. Fourier Transform Ultrashort Optical Pulse Shaping Using a Single Chirped Fiber Bragg Grating. IEEE Photon. Technol. Lett. 2009, 21, 1375–1377. [Google Scholar] [CrossRef]
- Chi, H.; Yao, J.P. Symmetrical waveform generation based on temporal pulse shaping using amplitude-only modulator. Electron. Lett. 2007, 43, 415–417. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Yang, J.L.; Yao, J.P. Continuous true-time-delay beamforming for phased array antenna using a tunable chirped fiber grating delay line. IEEE Photon. Technol. Lett. 2002, 14, 1172–1174. [Google Scholar] [CrossRef]
- Li, M.; Wang, C.; Li, W.Z.; Yao, J.P. An unbalanced temporal pulse-shaping system for chirped microwave waveform generation. IEEE Trans. Microw. Theory Tech. 2010, 58, 2968–2975. [Google Scholar] [CrossRef]
- Hogan, J. Microwave data refine picture of Universe. Nature 2006, 440, 395–395. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.V.T.; Hunter, D.B. A photonic technique for microwave frequency measurement. IEEE Photon. Technol. Lett. 2006, 18, 1188–1190. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Li, M.; Chi, H.; Zhang, X.; Yao, J. Instantaneous microwave frequency measurement using a special fiber Bragg grating. IEEE Microw. Wireless Compon. Lett. 2011, 21, 52–54. [Google Scholar] [CrossRef]
- Winnall, S.T.; Lindsay, A.C.; Austin, M.W.; Canning, J.; Mitchell, A. A microwave channelizer and spectroscope based on an integrated optical Bragg-grating Fabry-Perot and integrated hybrid fresnel lens system. IEEE Trans. Microw. Theory Tech. 2006, 54, 868–872. [Google Scholar] [CrossRef]
- Wang, W.; Davis, R.L.; Jung, T.J.; Lodenkamper, R.; Lembo, L.J.; Brock, J.C.; Wu, M.C. Characterization of a coherent optical RF channelizer based on a diffraction grating. IEEE Trans. Microw. Theory Tech. 2001, 49, 1996–2001. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J. High-resolution microwave frequency measurement based on temporal channelization using a mode-locked laser. In Proceedings of the 2012 IEEE MTT-S International Microwave Symposium Digest (MTT), Montreal, Canada, 17–22 June 2012; pp. 1–3.
- Wang, C.; Yao, J. Ultrahigh-resolution photonic-assisted microwave frequency identification based on temporal channelization. IEEE Trans. Microw. Theory Tech. 2013, 61, 4275–4282. [Google Scholar]
- Chou, P.C.; Haus, H.A.; Brennan Iii, J.F. Reconfigurable time-domain spectral shaping of an optical pulse stretched by a fiber Bragg grating. Opt. Lett. 2000, 25, 524–526. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive Sensing [Lecture Notes]. IEEE Signal. Process. Mag. 2007, 24, 118–121. [Google Scholar]
- Nichols, J.M.; Bucholtz, F. Beating Nyquist with light: a compressively sampled photonic link. Opt. Express 2011, 19, 7339–7348. [Google Scholar] [CrossRef] [PubMed]
- Chi, H.; Mei, Y.; Chen, Y.; Wang, D.; Zheng, S.; Jin, X.; Zhang, X. Microwave spectral analysis based on photonic compressive sampling with random demodulation. Opt. Lett. 2012, 37, 4636–4638. [Google Scholar] [PubMed]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. Ieee J.-Stsp. 2007, 1, 586–597. [Google Scholar]
- Walden, R.H. Analog-to-digital converter survey and analysis. IEEE J. Sel. Areas Commun. 1999, 17, 539–550. [Google Scholar] [CrossRef]
- Taylor, H.F. An optical analog-to-digital converter−Design and analysis. IEEE J. Quantum Electron. 1979, 15, 210–216. [Google Scholar] [CrossRef]
- Jalali, B.; Xie, Y.M. Optical Folding-Flash Analog-to-Digital Converter with Analog Encoding. Opt. Lett. 1995, 20, 1901–1903. [Google Scholar] [CrossRef] [PubMed]
- Coppinger, F.; Bhushan, A.S.; Jalali, B. Photonic time stretch and its application to analog-to-digital conversion. IEEE Trans. Microw. Theory Tech. 1999, 47, 1309–1314. [Google Scholar] [CrossRef]
- Fard, A.; Gupta, S.; Jalali, B. Digital broadband linearization technique and its application to photonic time-stretch analog-to-digital converter. Opt. Lett. 2011, 36, 1077–1079. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C. Dispersive Fourier Transformation for Versatile Microwave Photonics Applications. Photonics 2014, 1, 586-612. https://doi.org/10.3390/photonics1040586
Wang C. Dispersive Fourier Transformation for Versatile Microwave Photonics Applications. Photonics. 2014; 1(4):586-612. https://doi.org/10.3390/photonics1040586
Chicago/Turabian StyleWang, Chao. 2014. "Dispersive Fourier Transformation for Versatile Microwave Photonics Applications" Photonics 1, no. 4: 586-612. https://doi.org/10.3390/photonics1040586
APA StyleWang, C. (2014). Dispersive Fourier Transformation for Versatile Microwave Photonics Applications. Photonics, 1(4), 586-612. https://doi.org/10.3390/photonics1040586