Dissolution-Driven Convection in a Porous Medium Due to Vertical Axis of Rotation and Magnetic Field
Abstract
1. Introduction
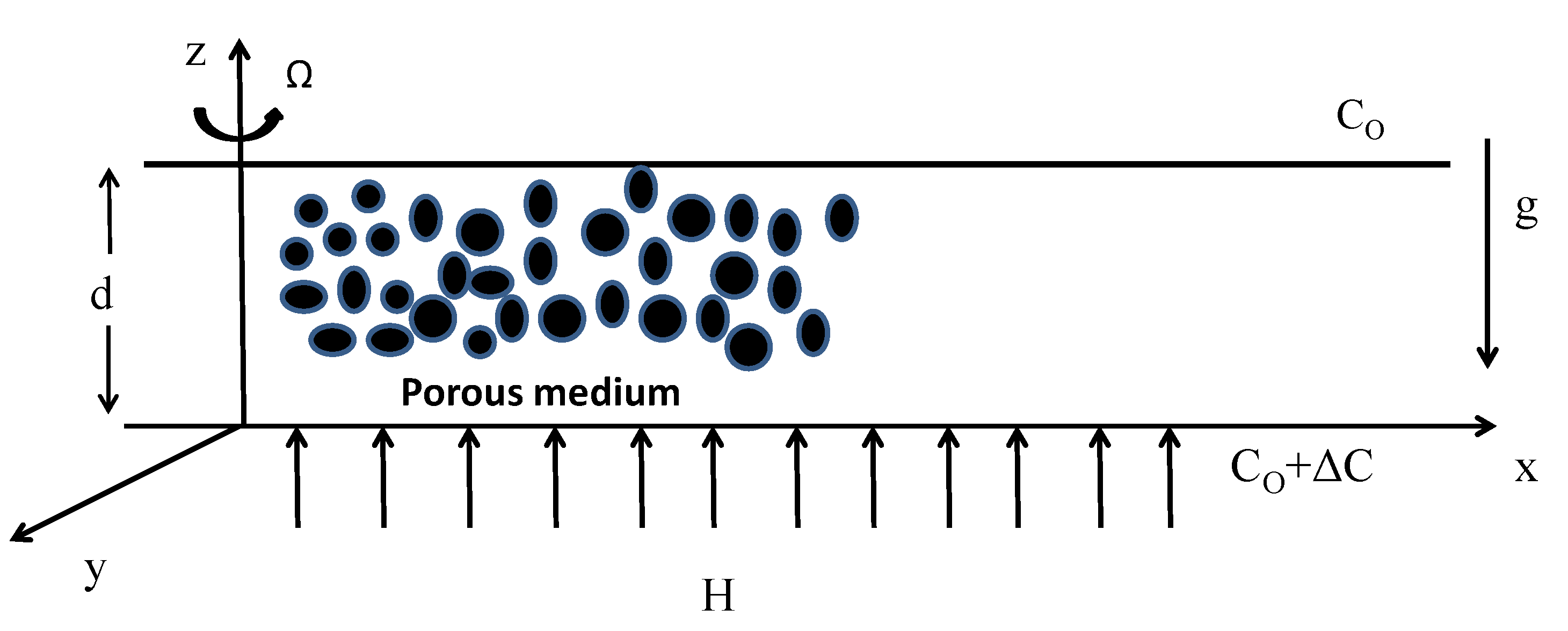
2. Mathematical Modeling
2.1. Basic Equations
2.2. Basic Flow
2.3. Linear Stability Analysis
2.4. Stationary Mode
2.5. Oscillatory Mode
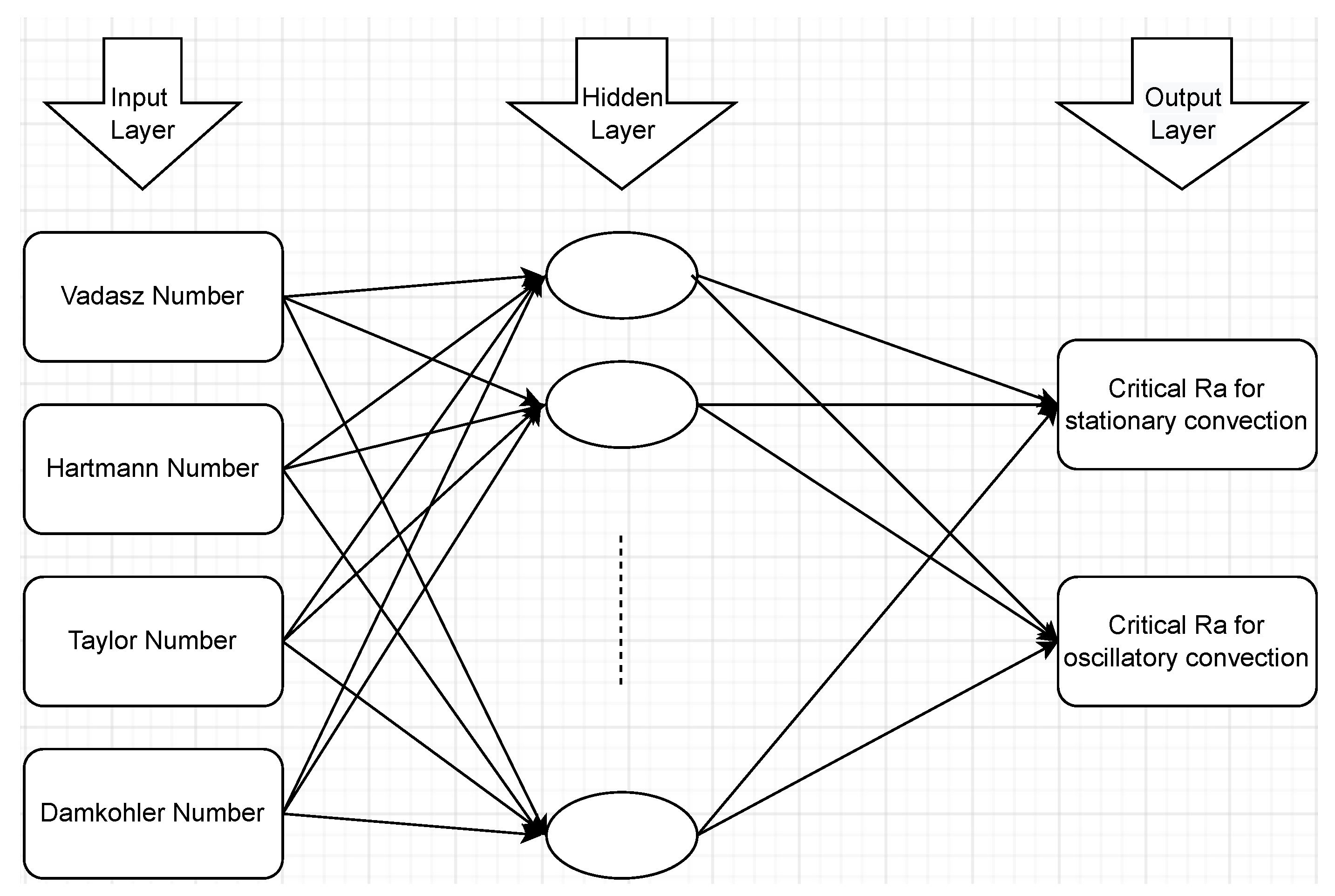
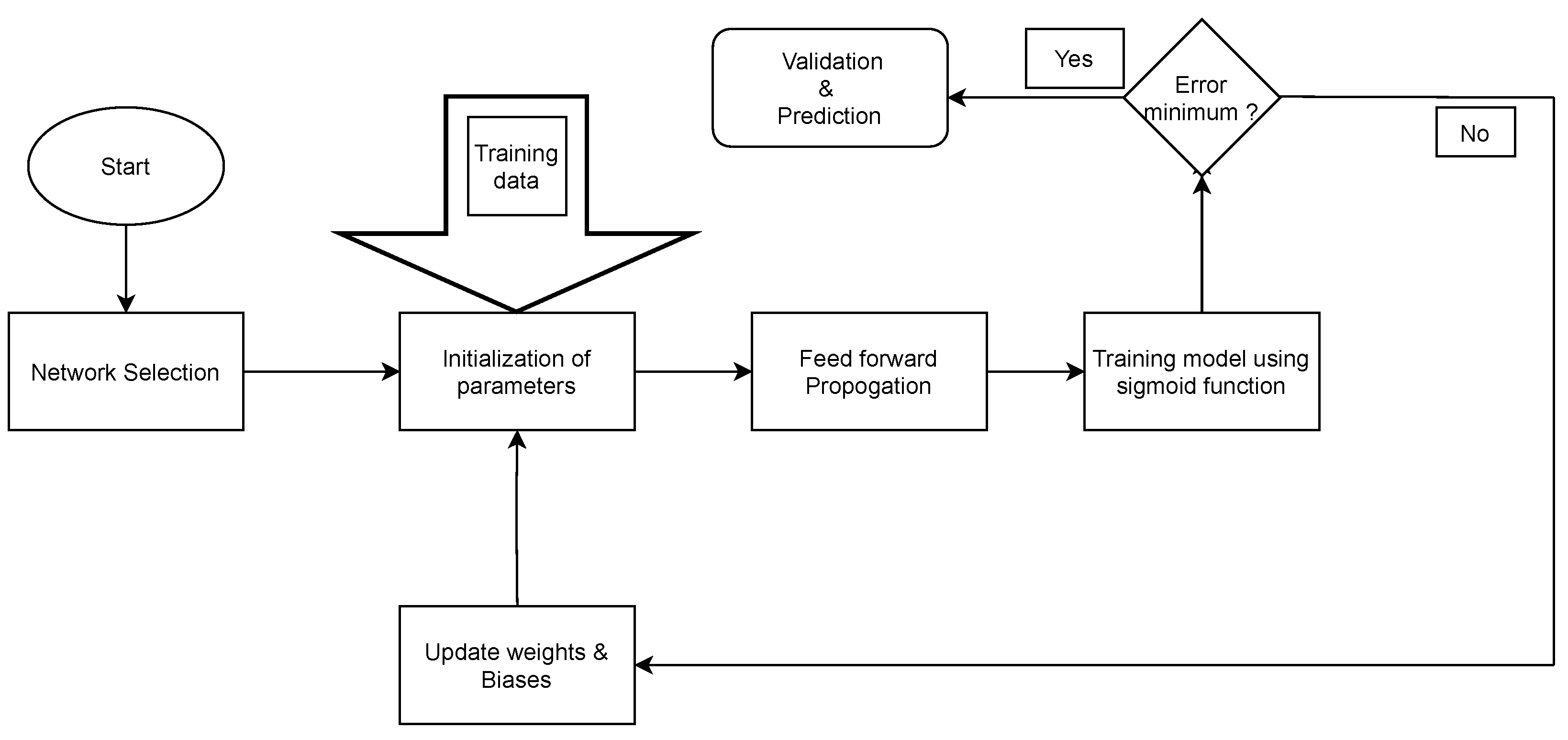
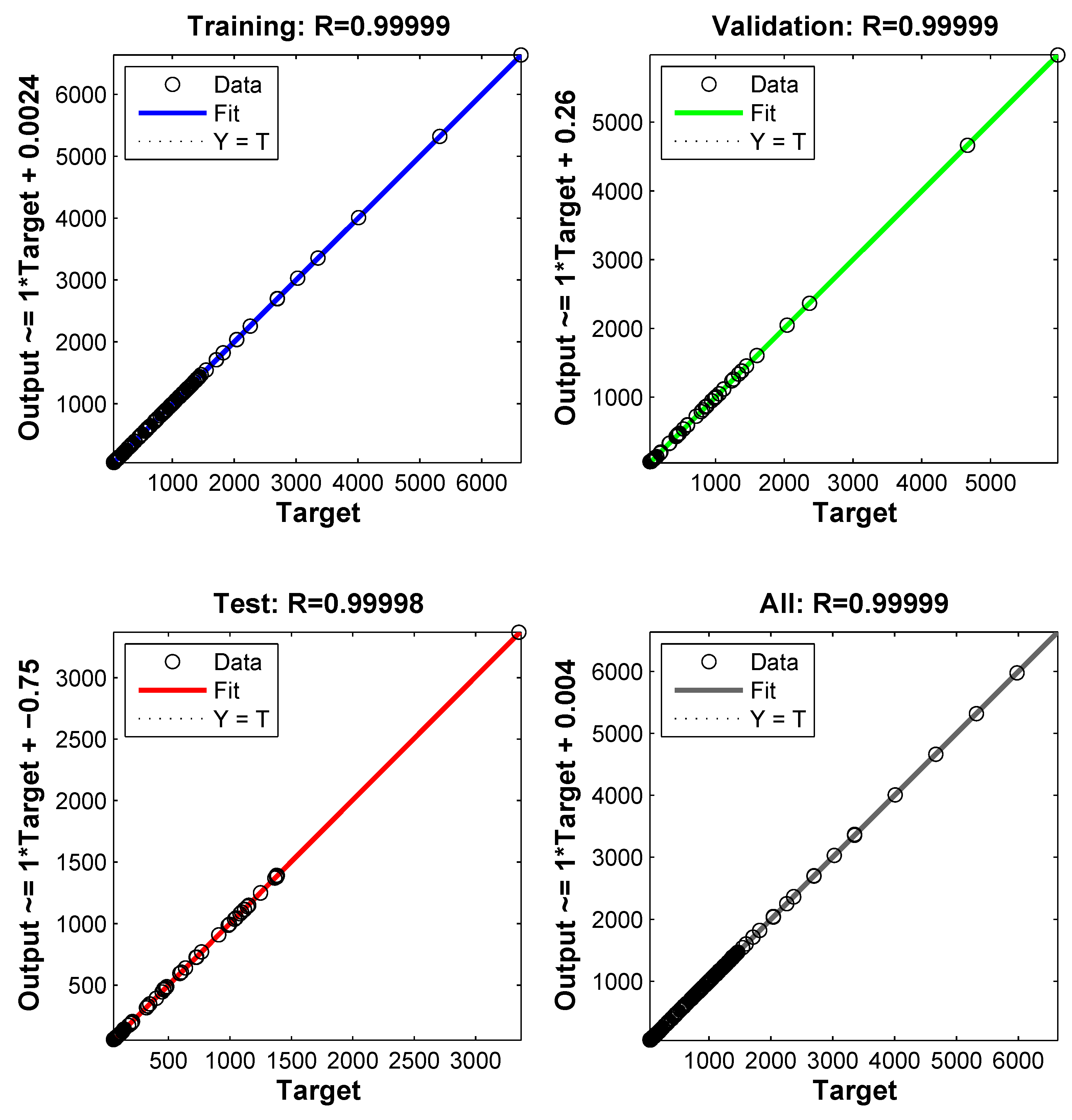
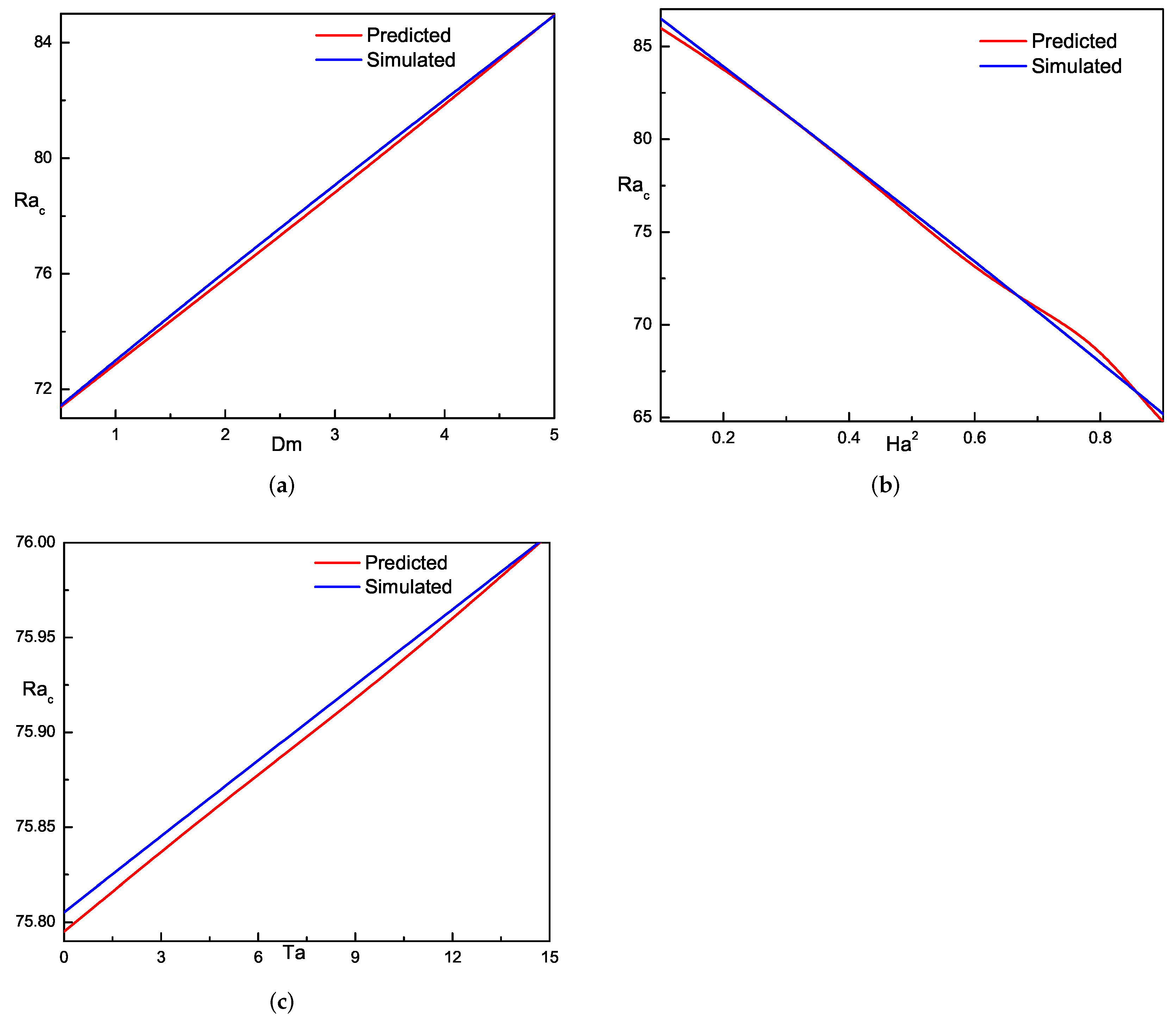
3. Artificial Neural Network Modeling
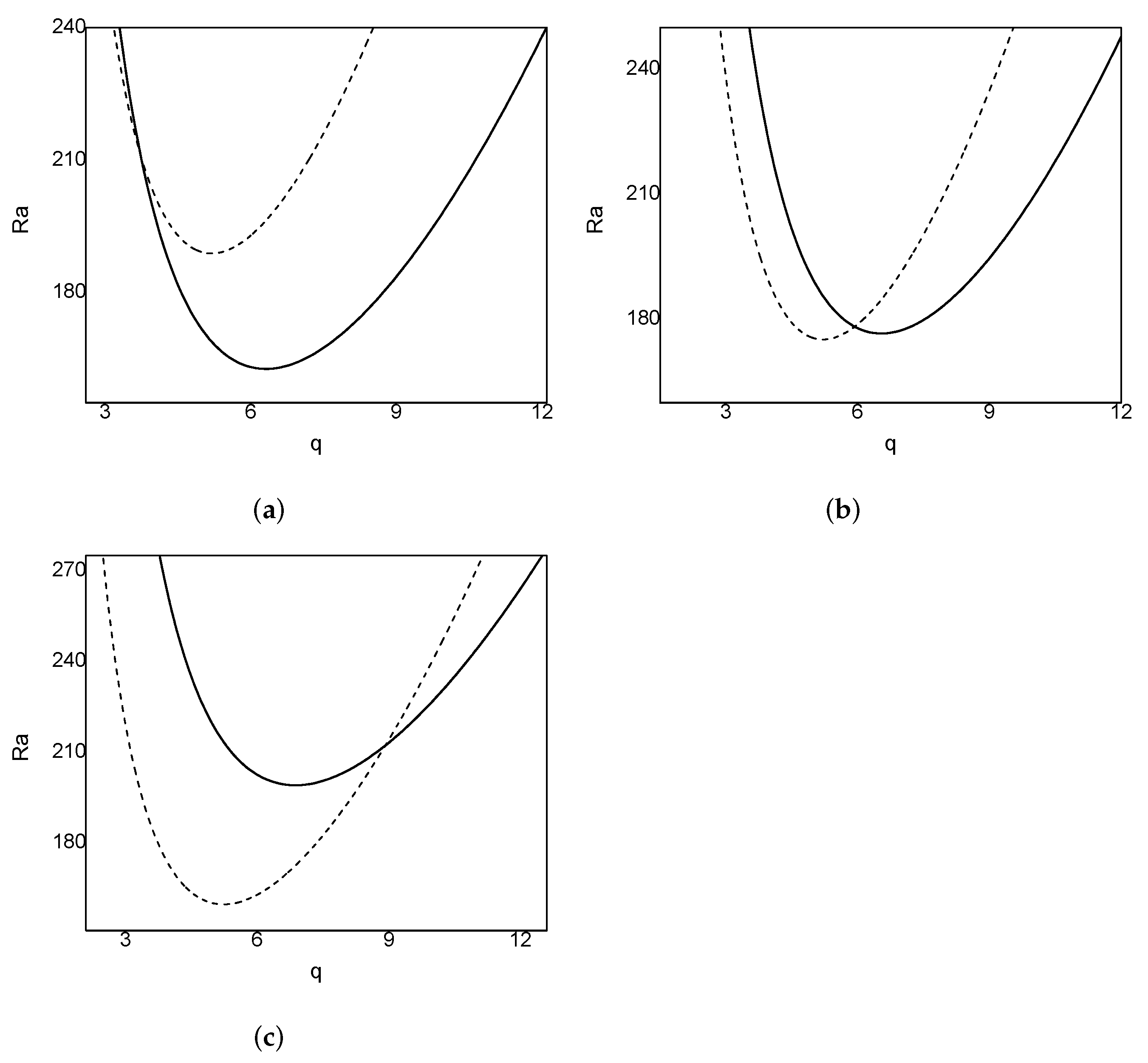
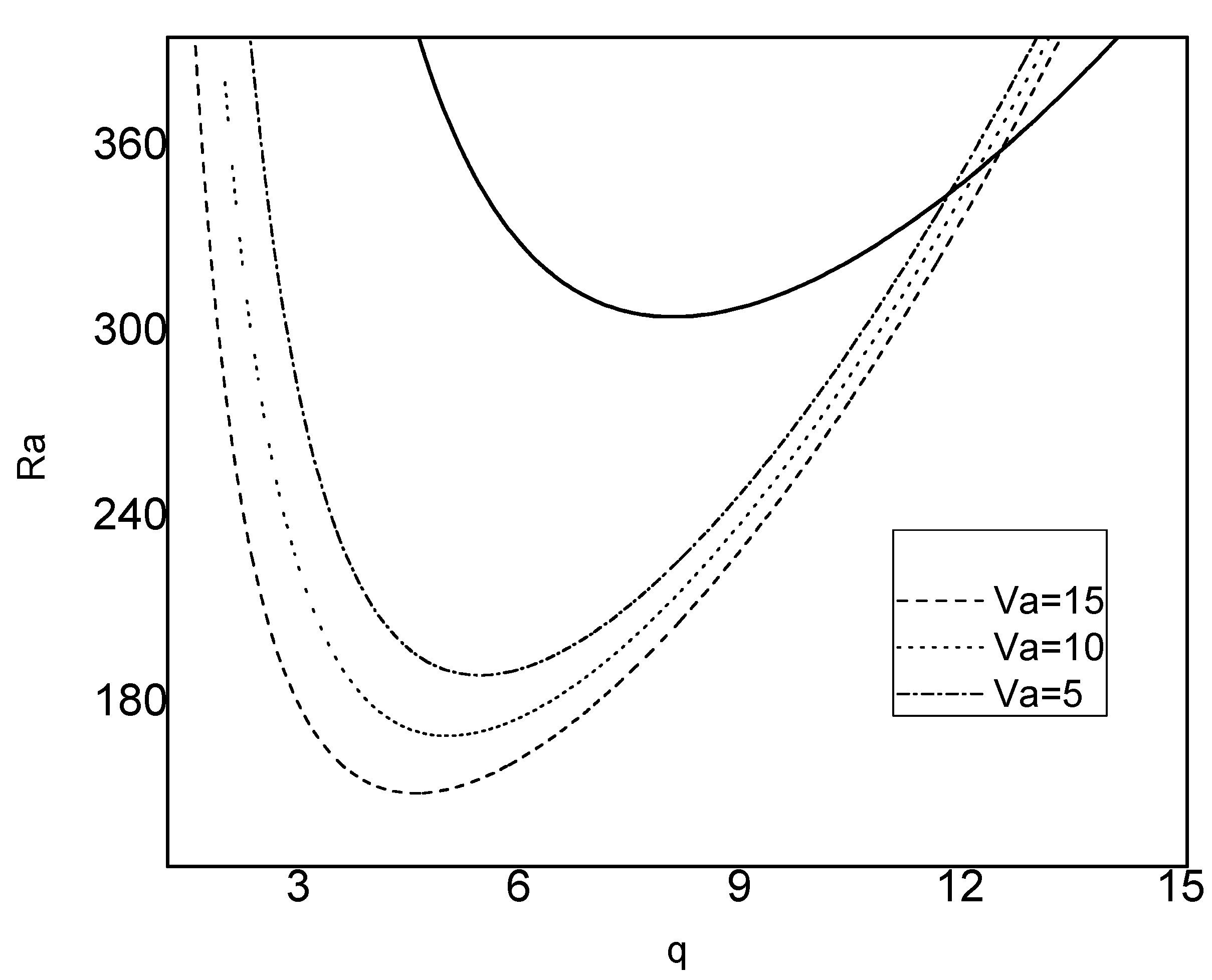
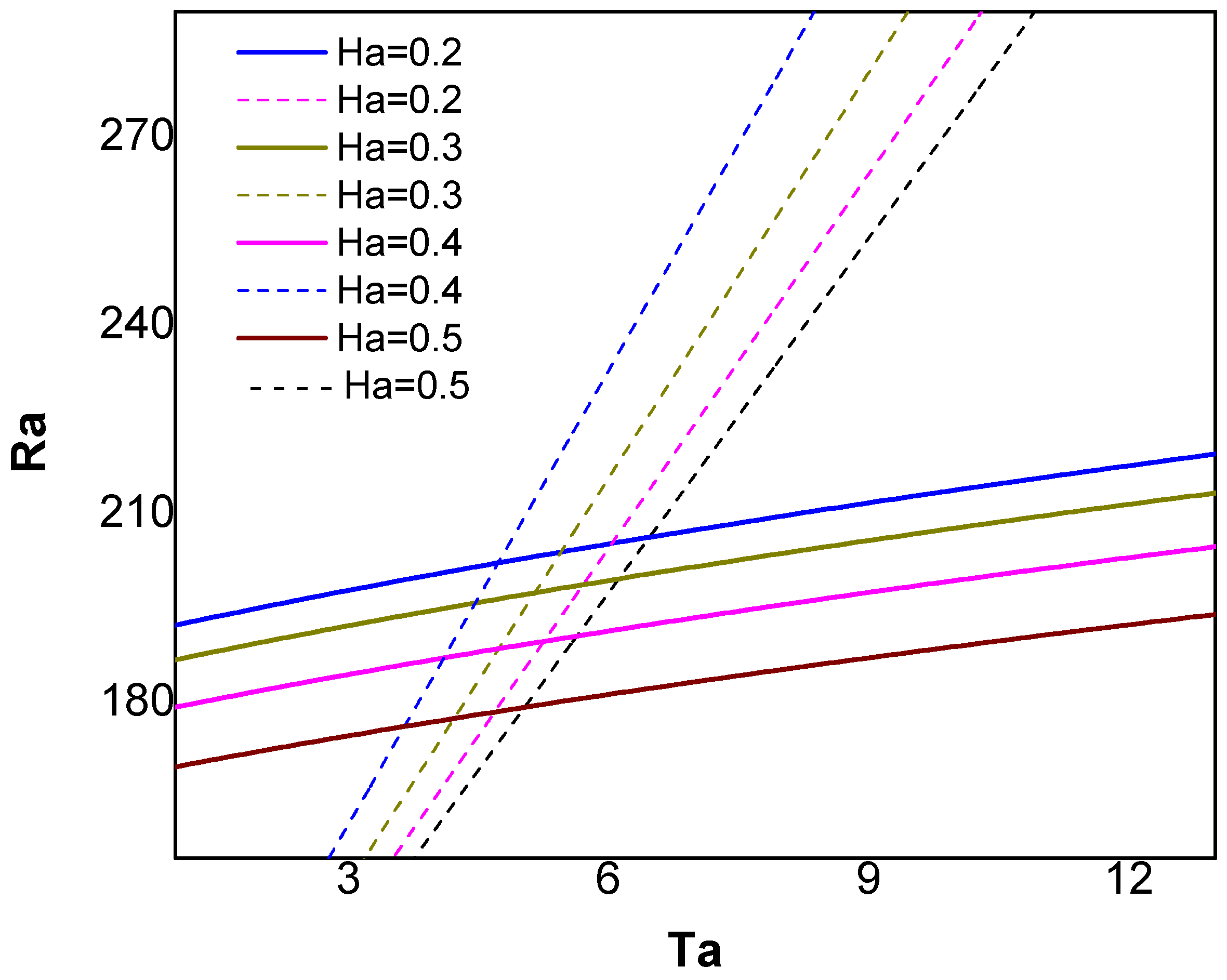
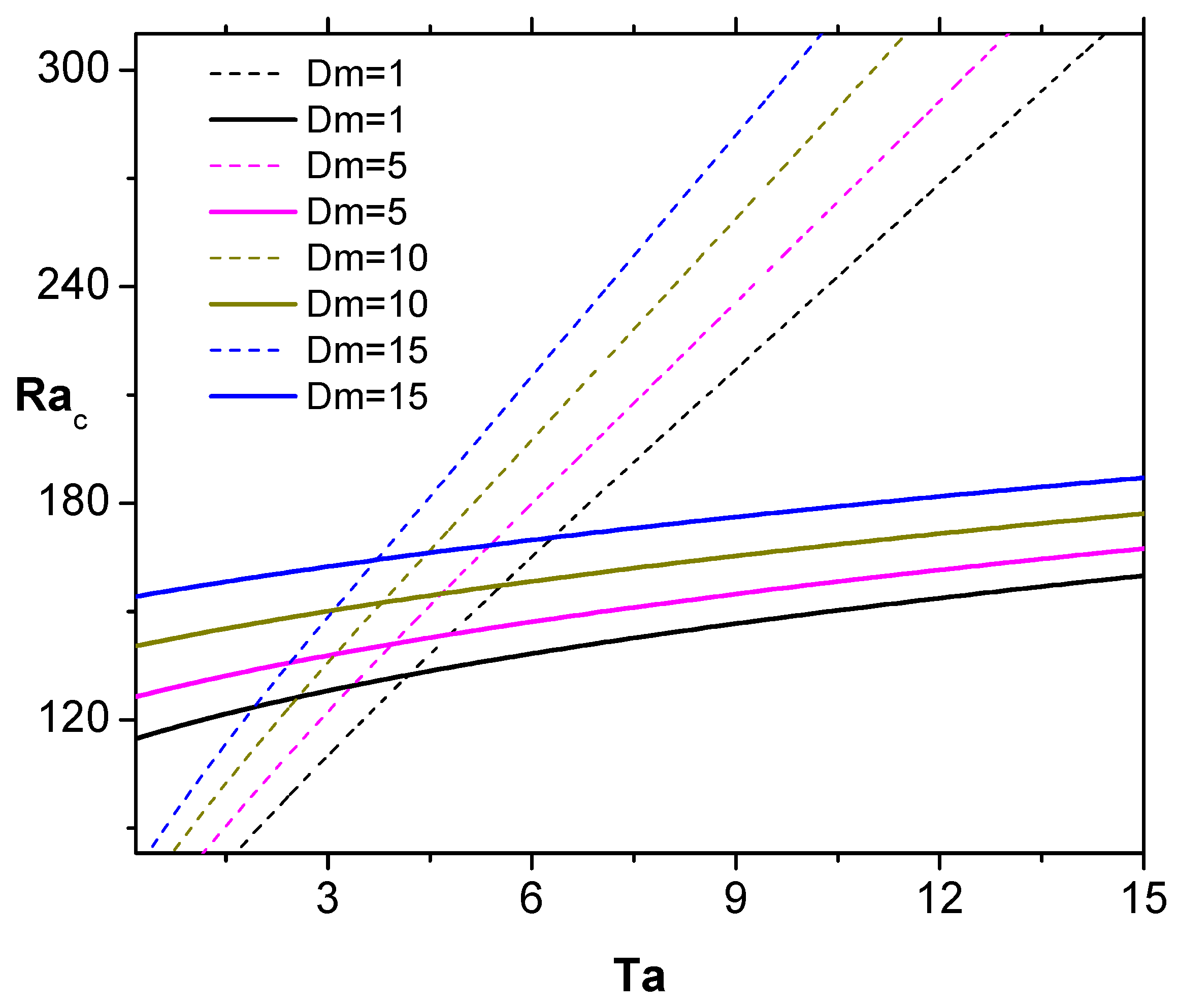
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghoshal, P.; Kim, M.C.; Cardoso, S.S. Reactive–convective dissolution in a porous medium: The storage of carbon dioxide in saline aquifers. Phys. Chem. Chem. Phys. 2017, 19, 644–655. [Google Scholar] [CrossRef] [PubMed]
- Ilya, A.; Ashraf, M.; Ali, A.; Shah, Z.; Kumam, P.; Thounthong, P. Heat source and sink effects on periodic mixed convection flow along the electrically conducting cone inserted in porous medium. PLoS ONE 2021, 16, e0260845. [Google Scholar] [CrossRef] [PubMed]
- Alshehri, A.; Shah, Z. Computational analysis of viscous dissipation and Darcy-Forchheimer porous medium on radioactive hybrid nanofluid. Case Stud. Therm. Eng. 2022, 30, 101728. [Google Scholar] [CrossRef]
- Vo, D.D.; Shah, Z.; Sheikholeslami, M.; Shafee, A.; Nguyen, T.K. Numerical investigation of MHD nanomaterial convective migration and heat transfer within a sinusoidal porous cavity. Phys. Scr. 2019, 94, 115225. [Google Scholar] [CrossRef]
- Jamshed, W.; Şirin, C.; Selimefendigil, F.; Shamshuddin, M.D.; Altowairqi, Y.; Eid, M.R. Thermal Characterization of Coolant Maxwell Type Nanofluid Flowing in Parabolic Trough Solar Collector (PTSC) Used Inside Solar Powered Ship Application. Coatings 2021, 11, 1552. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Rekha, M.B.; Kumar, P.N.V.; Selimefendigil, F.; Sakanaka, P.H.; Lorenzini, G.; Nayakar, S.N.R. Mass transfer characteristics of MHD casson fluid flow past stretching/shrinking sheet. J. Eng. Thermophys. 2020, 29, 285–302. [Google Scholar] [CrossRef]
- Steinberg, V.; Brand, H. Convective instabilities of binary mixtures with fast chemical reaction in a porous medium. J. Chem. Phys. 1983, 78, 2655–2660. [Google Scholar] [CrossRef]
- Steinberg, V.; Brand, H.R. Amplitude equations for the onset of convection in a reactive mixture in a porous medium. J. Chem. Phys. 1984, 80, 431–435. [Google Scholar] [CrossRef]
- Gatica, J.E.; Viljoen, H.J.; Hlavacek, V. Interaction between chemical reaction and natural convection in porous media. Chem. Eng. Sci. 1989, 44, 1853–1870. [Google Scholar] [CrossRef]
- Pritchard, D.; Richardson, C.N. The effect of temperature-dependent solubility on the onset of thermosolutal convection in a horizontal porous layer. J. Fluid Mech. 2007, 571, 59–95. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Selim, A.; Ennis-King, J. The Instability of Unsteady Boundary Layers in Porous Media; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Slim, A.C.; Ramakrishnan, T. Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 2010, 22, 124103. [Google Scholar] [CrossRef]
- Bestehorn, M.; Firoozabadi, A. Effect of fluctuations on the onset of density-driven convection in porous media. Phys. Fluids 2012, 24, 114102. [Google Scholar] [CrossRef]
- Kim, M.C.; Choi, C.K. Effect of first-order chemical reaction on gravitational instability in a porous medium. Phys. Rev. E 2014, 90, 053016. [Google Scholar] [CrossRef] [PubMed]
- Hill, A.A.; Morad, M.R. Convective stability of carbon sequestration in anisotropic porous media. Proc. R. Soc. Math. Phys. Eng. Sci. 2014, 470, 20140373. [Google Scholar] [CrossRef]
- Al-Sulaimi, B. The energy stability of Darcy thermosolutal convection with reaction. Int. J. Heat Mass Transf. 2015, 86, 369–376. [Google Scholar] [CrossRef]
- Emami-Meybodi, H. Stability analysis of dissolution-driven convection in porous media. Phys. Fluids 2017, 29, 014102. [Google Scholar] [CrossRef]
- Salibindla, A.K.; Subedi, R.; Shen, V.C.; Masuk, A.U.; Ni, R. Dissolution-driven convection in a heterogeneous porous medium. J. Fluid Mech. 2018, 857, 61–79. [Google Scholar] [CrossRef]
- Gautam, K.; Narayana, P.A.L. On the stability of carbon sequestration in an anisotropic horizontal porous layer with a first-order chemical reaction. Proc. R. Soc. A 2019, 475, 20180365. [Google Scholar] [CrossRef]
- Babu, A.B.; Koteswararao, N.V.; Reddy, G.S. Instability conditions in a porous medium due to horizontal magnetic field. In Numerical Heat Transfer and Fluid Flow; Springer: Singapore, 2019; pp. 621–628. [Google Scholar]
- Babu, A.B.; Rao, N.; Tagare, S.G. Weakly nonlinear thermohaline convection in a sparsely packed porous medium due to horizontal magnetic field. Eur. Phys. J. Plus 2021, 136, 795. [Google Scholar] [CrossRef]
- Babu, A.B.; Anilkumar, D.; Rao, N.V.K. Weakly nonlinear thermohaline rotating convection in a sparsely packed porous medium. Int. J. Heat Mass Transf. 2022, 188, 122602. [Google Scholar] [CrossRef]
- Reddy, G.S.K.; Ragoju, R. Thermal instability of a Maxwell fluid saturated porous layer with chemical reaction. Spec. Top. Rev. Porous Media Int. J. 2022, 13, 33–47. [Google Scholar] [CrossRef]
- Yin, Y.; Qu, Z.; Zhu, C.; Zhang, J. Visualizing gas diffusion behaviors in three-dimensional nanoporous media. Energy Fuels 2021, 35, 2075–2086. [Google Scholar] [CrossRef]
- Yin, Y.; Qu, Z.; Prodanović, M.; Landry, C.J. Identifying the dominant transport mechanism in single nanoscale pores and 3D nanoporous media. Fundam. Res. 2022. [Google Scholar] [CrossRef]
- Utech, H.P.; Flemmings, M.C. Elimination of solute banding in indium antimonide crystals by growth in a magnetic field. J. Appl. Phys. 1966, 37, 2021–2024. [Google Scholar] [CrossRef]
- Vives, C.; Perry, C. Effects of magnetically damped convection during the controlled solidification of metals and alloys. Int. J. Heat Mass Transf. 1987, 30, 479–496. [Google Scholar] [CrossRef]
- Garandet, J.P.; Alboussiere, T.; Moreau, R. Buoyancy driven convection in a rectangular enclosure with a transverse magnetic field. Int. J. Heat Mass Transf. 1992, 35, 741–748. [Google Scholar] [CrossRef]
- Alboussiere, T.; Garandet, J.P. Buoyancy-driven convection with a uniform magnetic field. Part 1. Asymptotic analysis. J. Fluid Mech. 1993, 253, 545–563. [Google Scholar] [CrossRef]
- Rudraiah, N.; Venkatachalappa, M.; Subbaraya, C.K. Combined surface tension and buoyancy-driven convection in a rectangular open cavity in the presence of a magnetic field. Int. J. Non-Linear Mech. 1995, 30, 759–770. [Google Scholar] [CrossRef]
- Davoust, L.; Cowley, M.D.; Moreau, R.; Bolcato, R. Buoyancy-driven convection with a uniform magnetic field. Part 2. Experimental investigation. J. Fluid Mech. 1999, 400, 59–90. [Google Scholar] [CrossRef]
- Priede, J.; Gerbeth, G. Hydrothermal wave instability of thermocapillary-driven convection in a transverse magnetic field. J. Fluid Mech. 2000, 404, 211–250. [Google Scholar] [CrossRef]
- Pirmohammadi, M.; Ghassemi, M.; Sheikhzadeh, G.A. The effect of a magnetic field on buoyancy-driven convection in differentially heated square cavity. In Proceedings of the 2008 14th Symposium on Electromagnetic Launch Technology, Victoria, BC, Canada, 10–13 June 2008; pp. 1–6. [Google Scholar]
- Sankar, M.; Venkatachalappa, M.; Do, Y. Effect of magnetic field on the buoyancy and thermocapillary driven convection of an electrically conducting fluid in an annular enclosure. Int. J. Heat Fluid Flow 2011, 32, 402–412. [Google Scholar] [CrossRef][Green Version]
- Erglis, K.; Tatulcenkov, A.; Kitenbergs, G.; Petrichenko, O.; Ergin, F.G.; Watz, B.B.; Cbers, A. Magnetic field driven micro-convection in the Hele–Shaw cell. J. Fluid Mech. 2013, 714, 612–633. [Google Scholar] [CrossRef]
- Babu, A.B.; Reddy, G.S.K.; Tagare, S.G. Nonlinear magneto convection due to horizontal magnetic field and vertical axis of rotation due to thermal and compositional buoyancy. Results Phys. 2019, 12, 2078–2090. [Google Scholar] [CrossRef]
- Govender, S.; Vadasz, P. The effect of mechanical and thermal anisotropy on the stability of gravity driven convection in rotating porous media in the presence of thermal non-equilibrium. Transp. Porous Media 2007, 69, 55–66. [Google Scholar] [CrossRef]
- Babu, A.B.; Reddy, G.S.K.; Tagare, S.G. Nonlinear magnetoconvection in a rotating fluid due to thermal and compositional buoyancy with anisotropic diffusivities. Heat Transf. Asian Res. 2020, 49, 335–355. [Google Scholar] [CrossRef]
- Wang, S.; Wenchang, T. The onset of Darcy–Brinkman thermosolutal convection in a horizontal porous media. Phys. Lett. A 2009, 373, 776–780. [Google Scholar] [CrossRef]
- Deepika, N.; Murthy, P.V.S.N.; Narayana, P.A.L. The effect of magnetic field on the stability of double-diffusive convection in a porous layer with horizontal mass throughflow. Transp. Porous Media 2020, 134, 435–452. [Google Scholar] [CrossRef]
- Horton, C.W.; Rogers, F.T. Convection currents in a porous medium. J. Appl. Phys. 1945, 16, 367–370. [Google Scholar] [CrossRef]
- Lapwood, E.R. Convection of a fluid in a porous medium. Math. Proc. Camb. Philos. Soc. 1948, 44, 508–521. [Google Scholar] [CrossRef]
- Dey, P.; Abhijit, S.; Das, A.K. Development of GEP and ANN model to predict the unsteady forced convection over a cylinder. Neural Comput. Appl. 2016, 27, 2537–2549. [Google Scholar] [CrossRef]
- Rana, P.; Gupta, V.; Kumar, L. LTNE magneto-thermal stability analysis on rough surfaces utilizing hybrid nanoparticles and heat source with artificial neural network prediction. Appl. Nanosci. 2021. [Google Scholar] [CrossRef]
- Seo, Y.M.; Pandey, S.; Lee, H.U.; Choi, C.; Park, Y.G.; Ha, M.Y. Prediction of heat transfer distribution induced by the variation in vertical location of circular cylinder on Rayleigh-Bénard convection using artificial neural network. Int. J. Mech. Sci. 2021, 209, 106701. [Google Scholar] [CrossRef]
- Yu, H.; Wilamowski, B.M. Levenberg–Marquardt training. In Intelligent Systems; CRC Press: Boca Raton, FL, USA, 2018; Chapter 12; pp. 1–16. [Google Scholar]
- Seo, Y.M.; Luo, K.; Ha, M.Y.; Park, Y.G. Direct numerical simulation and artificial neural network modeling of heat transfer characteristics on natural convection with a sinusoidal cylinder in a long rectangular enclosure. Int. J. Heat Mass Transf. 2020, 152, 119564. [Google Scholar] [CrossRef]
- Khosravi, R.; Rabiei, S.; Bahiraei, M.; Teymourtash, A.R. Predicting entropy generation of a hybrid nanofluid containing graphene–platinum nanoparticles through a microchannel liquid block using neural networks. Int. Commun. Heat Mass Transf. 2019, 109, 104351. [Google Scholar] [CrossRef]
- Amani, M.; Amani, P.; Bahiraei, M.; Wongwises, S. Prediction of hydrothermal behavior of a non-Newtonian nanofluid in a square channel by modeling of thermophysical properties using neural network. J. Therm. Anal. Calorim. 2019, 135, 901–910. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S.; Keshavarzi, M. Multi-criterion optimization of thermohydraulic performance of a mini pin fin heat sink operated with ecofriendly graphene nanoplatelets nanofluid considering geometrical characteristics. J. Mol. Liq. 2019, 276, 653–666. [Google Scholar] [CrossRef]
- Bahiraei, M.; Mazaheri, N.; Hosseini, S. Neural network modeling of thermo-hydraulic attributes and entropy generation of an ecofriendly nanofluid flow inside tubes equipped with novel rotary coaxial double-twisted tape. Powder Technol. 2020, 369, 162–175. [Google Scholar] [CrossRef]



| Values | Stationary | |||
|---|---|---|---|---|
| 0.999992 | 0.301510 | 0.549099 | ||
| 0.999991 | 0.316226 | 0.562340 | ||
| 0.999996 | 0.333332 | 0.5773497 | ||
| Values | Oscillatory | |||
|---|---|---|---|---|
| 0.999999 | 0.447213 | 0.668740 | ||
| 0.999994 | 0.316226 | 0.562340 | ||
| 0.999966 | 0.333327 | 0.577345 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reddy, G.S.K.; Koteswararao, N.V.; Ravi, R.; Paidipati, K.K.; Chesneau, C. Dissolution-Driven Convection in a Porous Medium Due to Vertical Axis of Rotation and Magnetic Field. Math. Comput. Appl. 2022, 27, 53. https://doi.org/10.3390/mca27030053
Reddy GSK, Koteswararao NV, Ravi R, Paidipati KK, Chesneau C. Dissolution-Driven Convection in a Porous Medium Due to Vertical Axis of Rotation and Magnetic Field. Mathematical and Computational Applications. 2022; 27(3):53. https://doi.org/10.3390/mca27030053
Chicago/Turabian StyleReddy, Gundlapally Shiva Kumar, Nilam Venkata Koteswararao, Ragoju Ravi, Kiran Kumar Paidipati, and Christophe Chesneau. 2022. "Dissolution-Driven Convection in a Porous Medium Due to Vertical Axis of Rotation and Magnetic Field" Mathematical and Computational Applications 27, no. 3: 53. https://doi.org/10.3390/mca27030053
APA StyleReddy, G. S. K., Koteswararao, N. V., Ravi, R., Paidipati, K. K., & Chesneau, C. (2022). Dissolution-Driven Convection in a Porous Medium Due to Vertical Axis of Rotation and Magnetic Field. Mathematical and Computational Applications, 27(3), 53. https://doi.org/10.3390/mca27030053








