Double-Diffusive Convection in Bidispersive Porous Medium with Coriolis Effect
Abstract
:1. Introduction
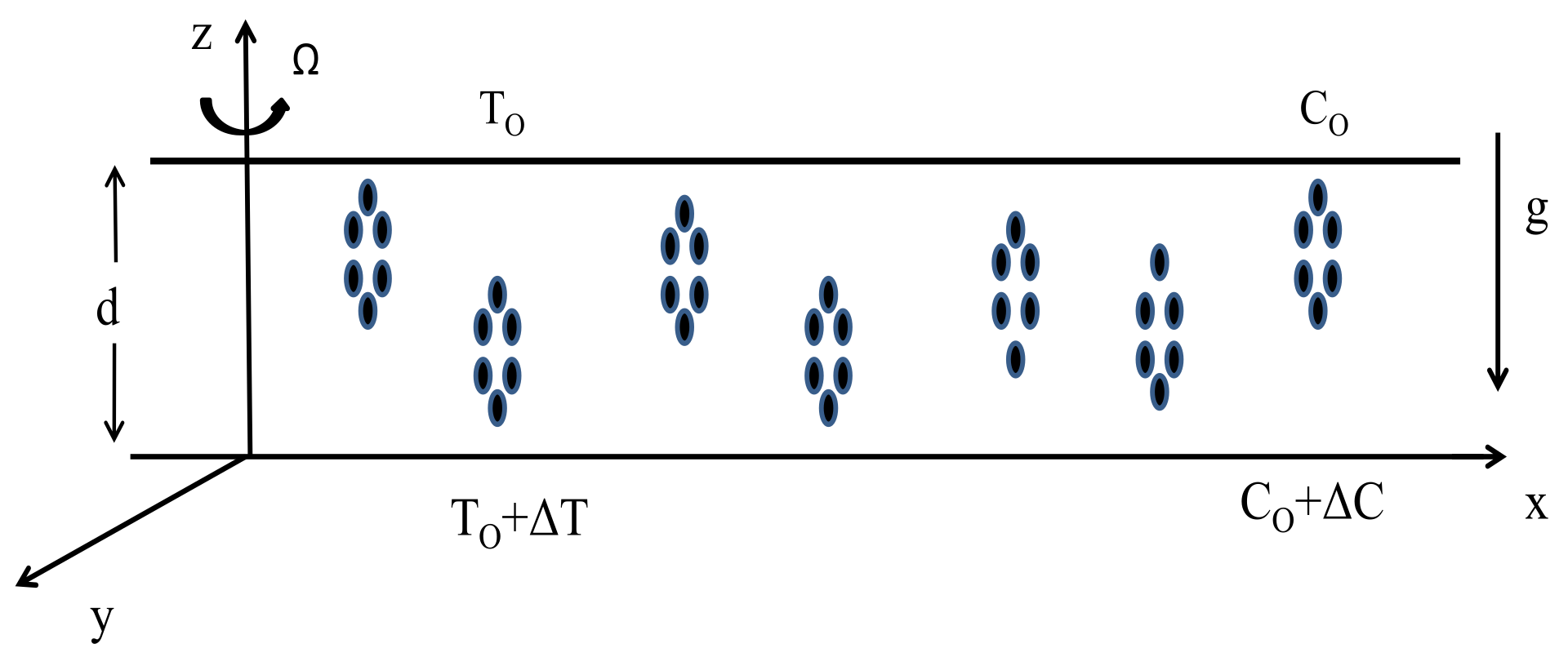
2. Mathematical Formulation
3. Linear Stability Analysis
3.1. Stationary Convection:
3.2. Oscillatory Convection
4. Discussion
5. Conclusions
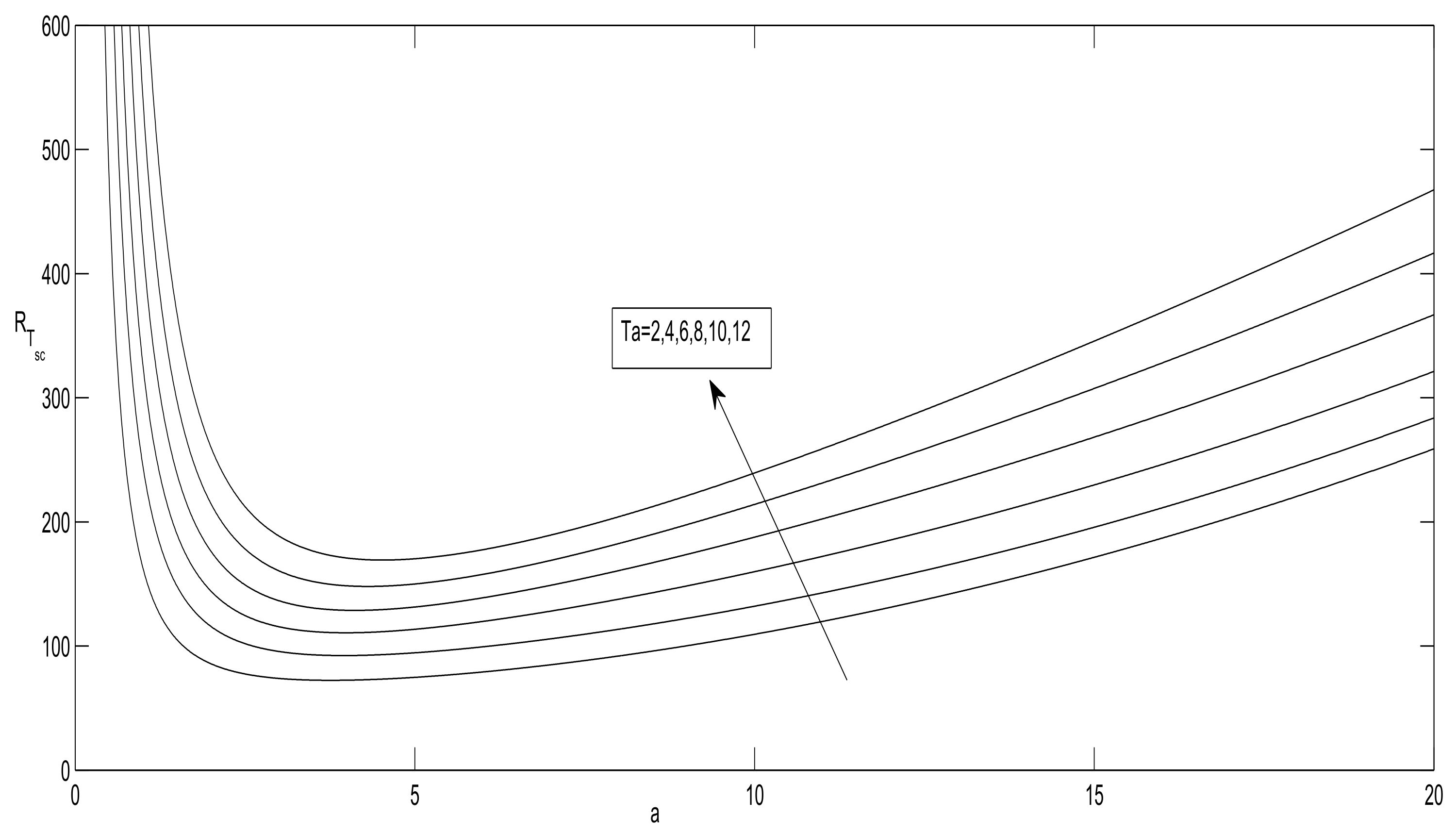
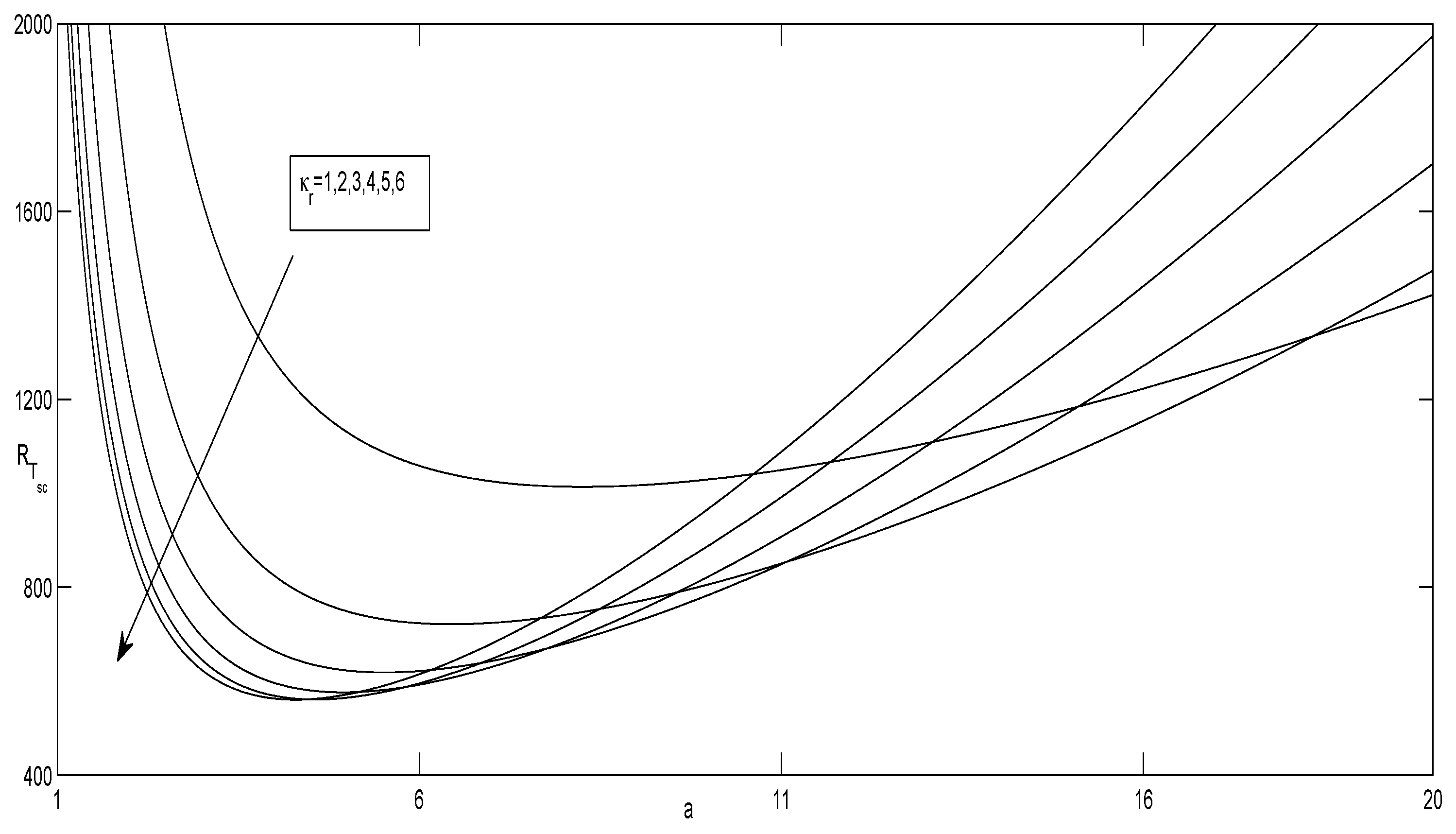
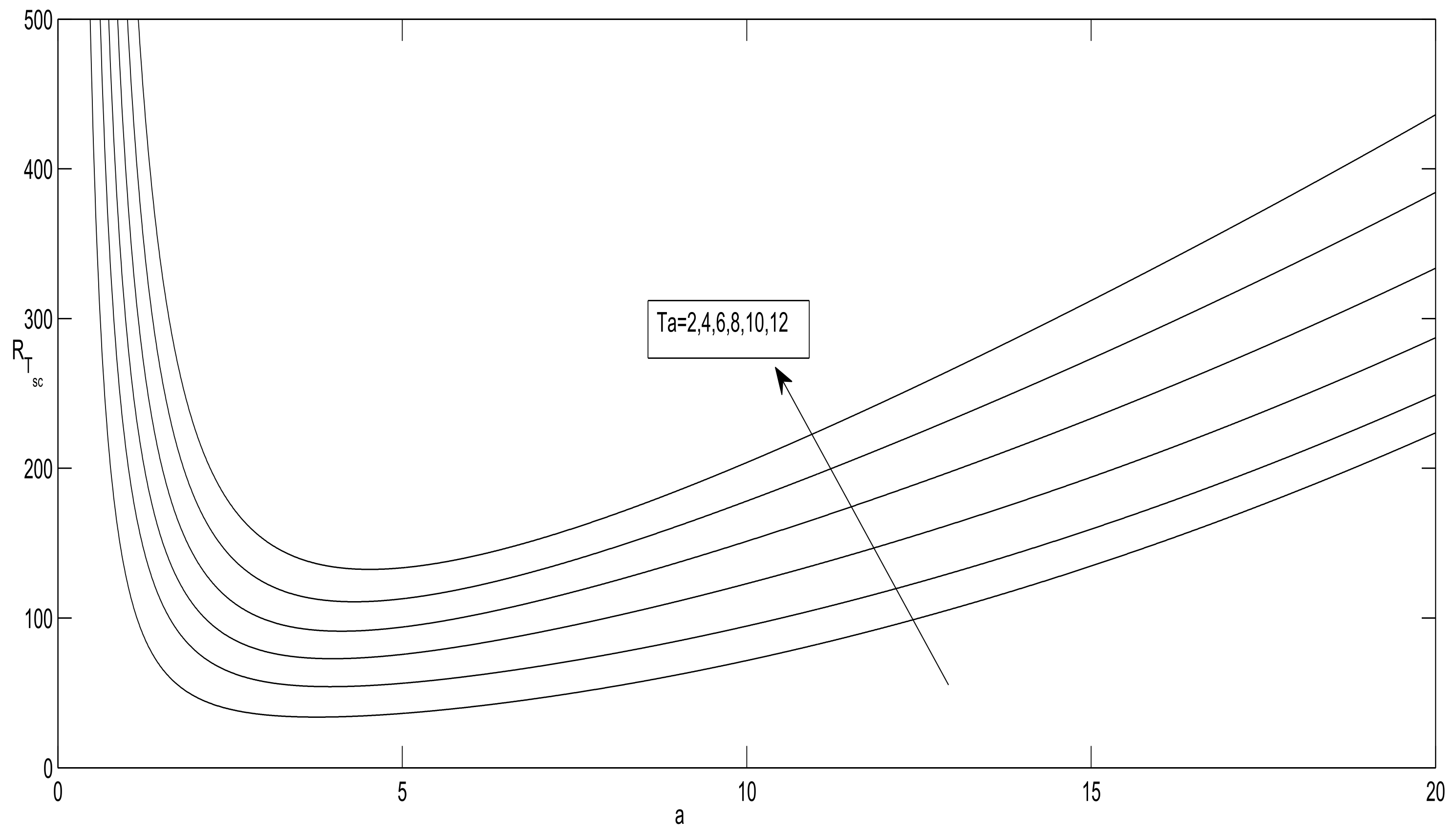
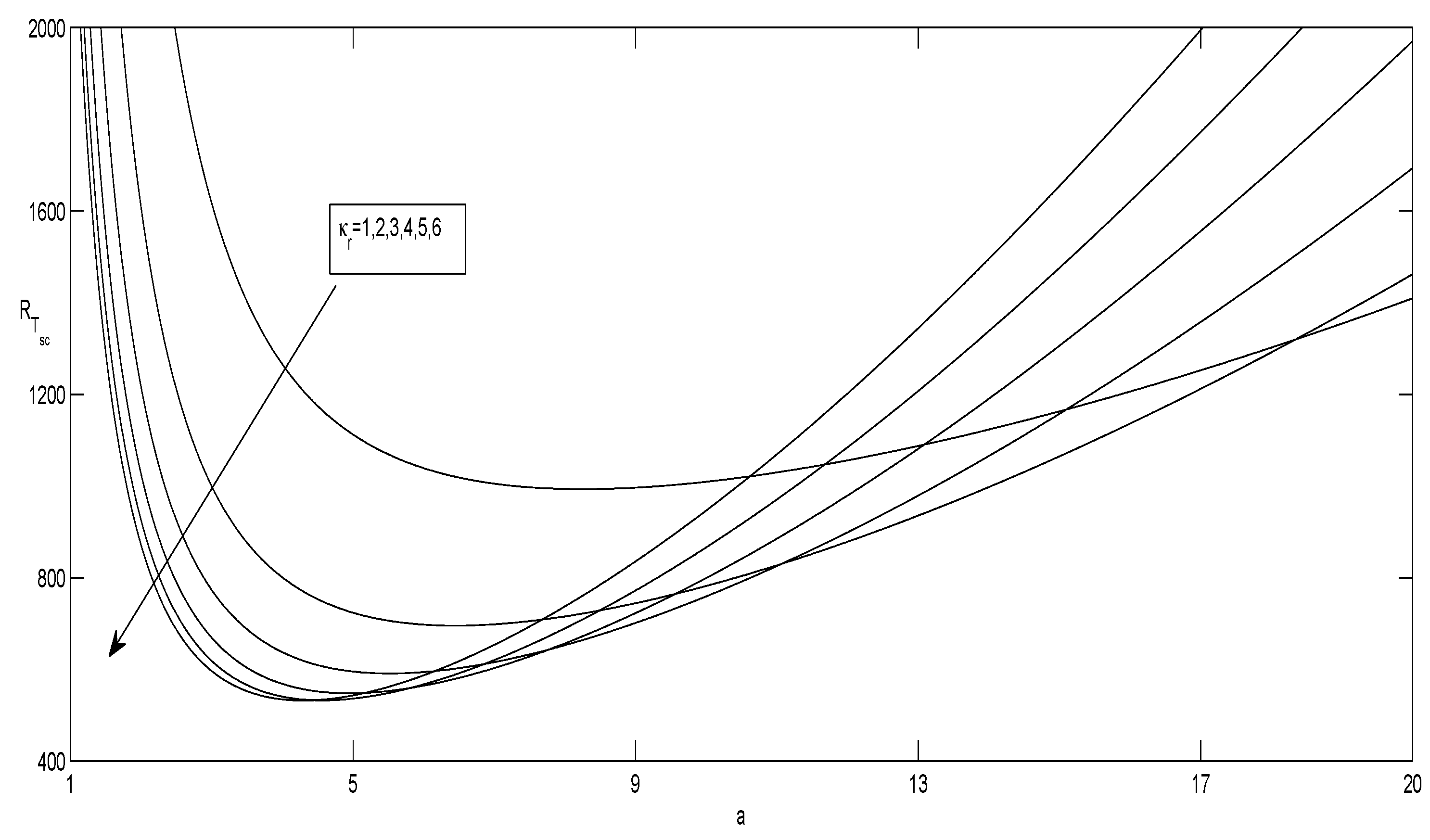
- and increase as the Taylor number increases, indicating that has a stabilizing effect on the onset of convection.
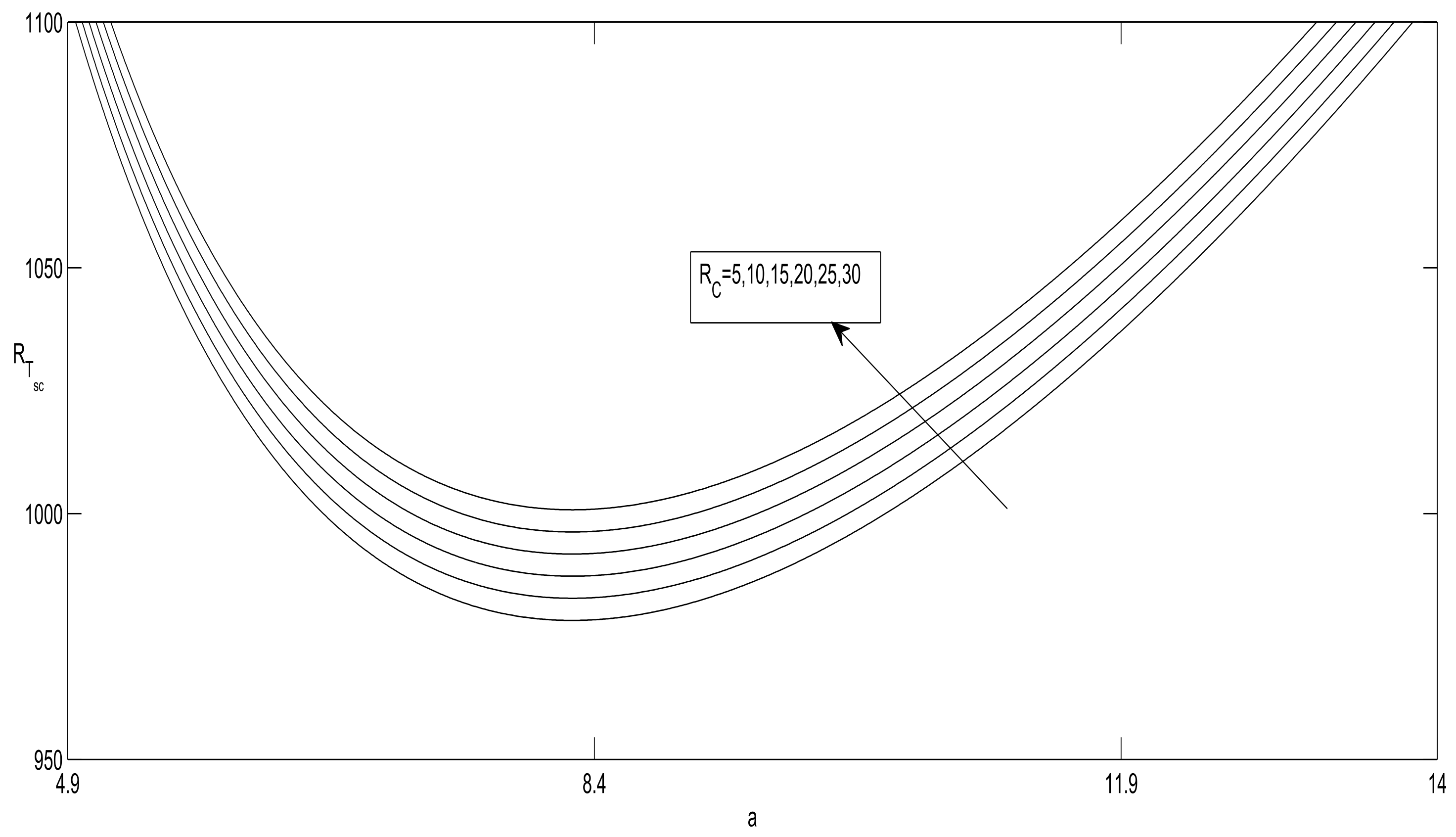
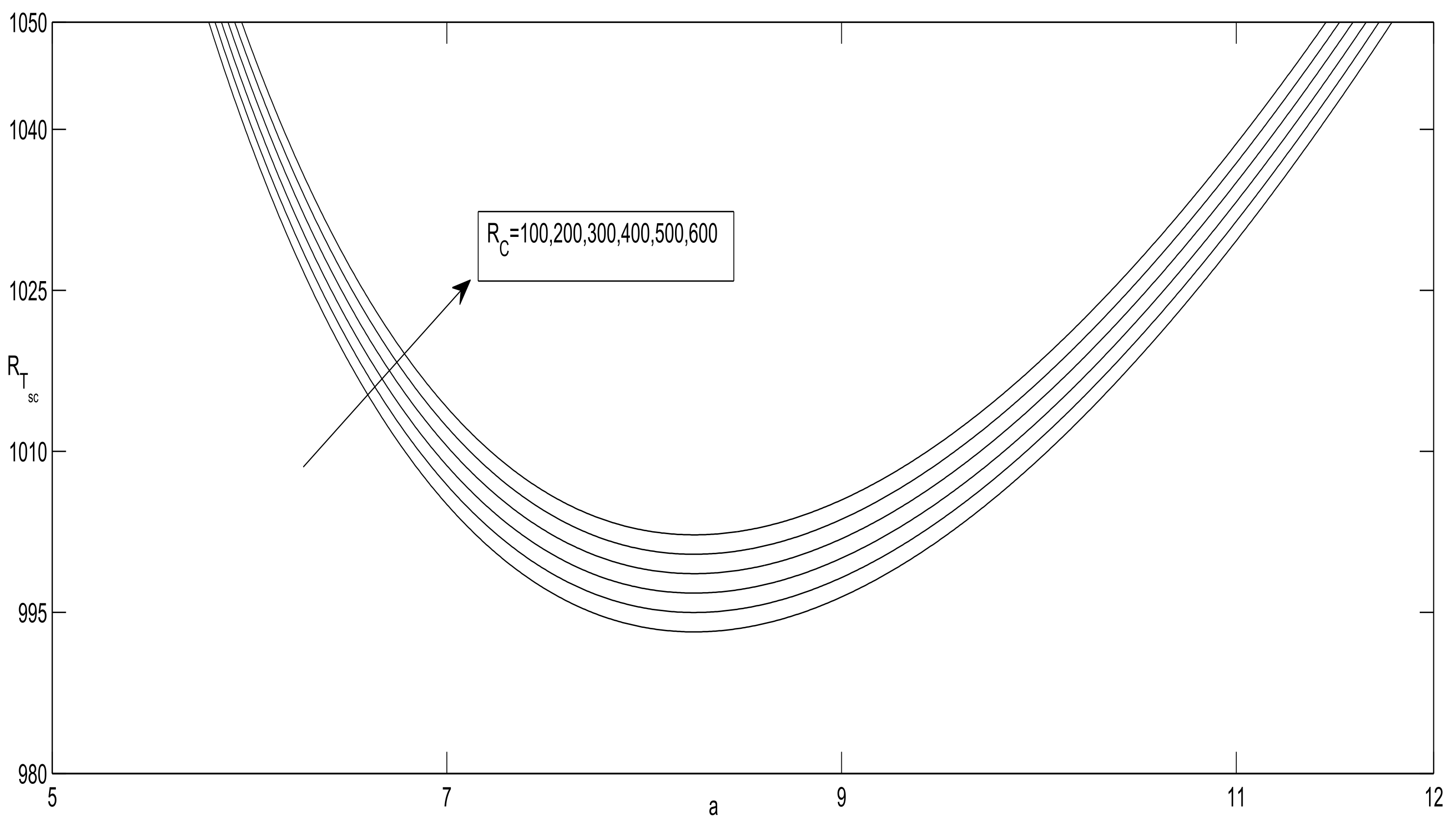
- and are increasing functions of and decreasing functions of .
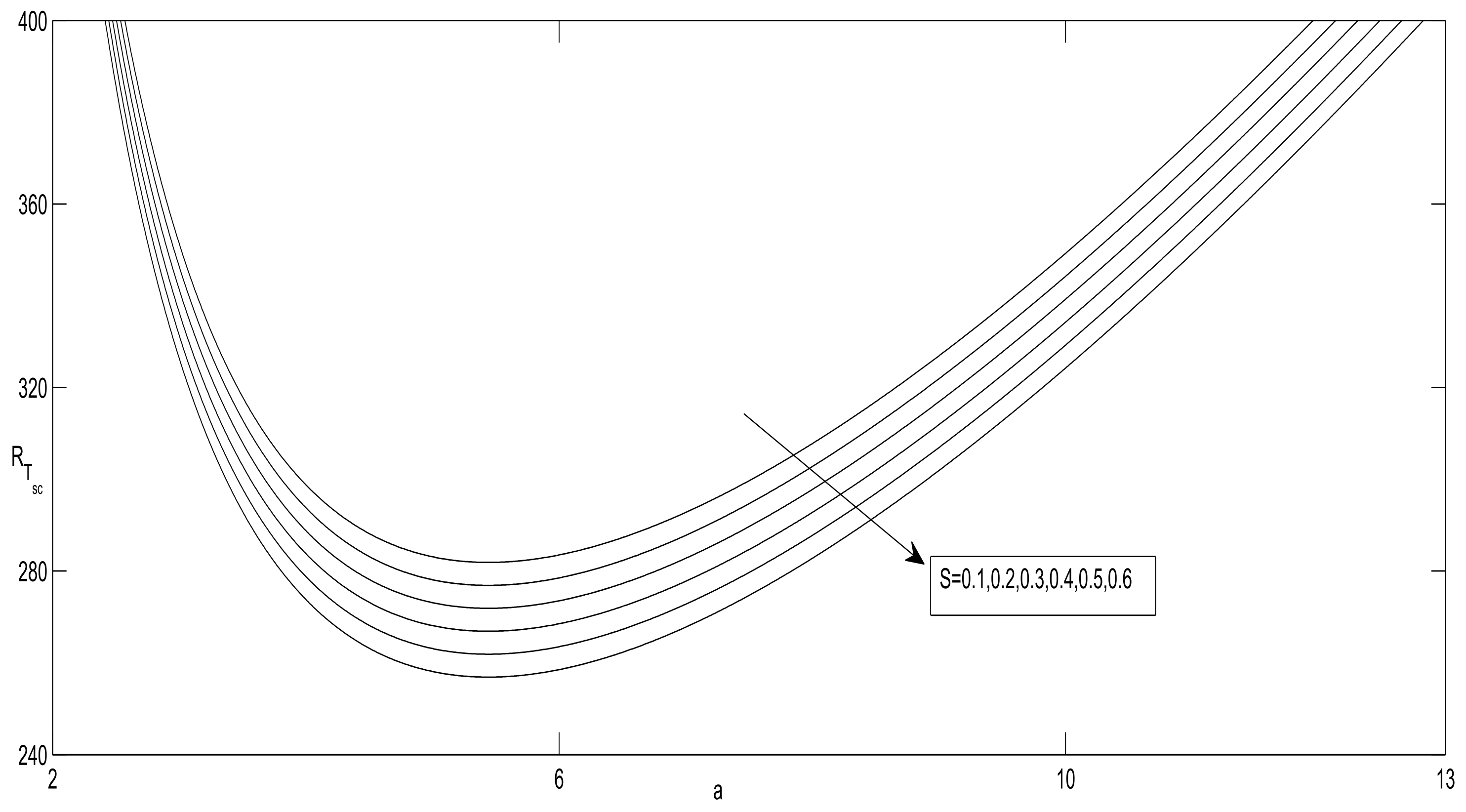
- S does not show any effect on , as is independent of S.
- There exists a threshold for the solute Rayleigh number such that, if , then the convection arises via an oscillatory mode.
- The oscillatory convection sets in and, as soon as the value of S attains a critical value (∈(0.6, 0.7)), the convection ceases to be oscillatory, and stationary convection occurs as the first bifurcation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Acceleration coefficient | |
| Permeability in macro pores | |
| Permeability in micro pores | |
| Interaction coefficient | |
| Fluid viscosity | |
| g | Gravity |
| Coefficient of thermal expansion | |
| Density coefficient for salinity | |
| Heat capacity ratio | |
| Macro porosity | |
| Micro porosity | |
| Density | |
| Thermal conductivity of the solid | |
| Thermal conductivity of the fluid | |
| Product of density and specific heat in the solid skeleton | |
| Product of density and specific heat in the pores | |
| Reference density | |
| Thermal conductivity | |
| Pressure in macro pores | |
| Pressure in micro pores | |
| T | Temperature |
| C | Salt concentration field |
| R | Rayleigh number |
| Solutal Rayleigh number | |
| Taylor number | |
| Lewis number | |
| S | Soret number |
| d | Length |
| Superscripts | |
| ′ | Perturbated quantity |
| c | Critical value |
| Subscripts | |
| b | Base state |
| 0 | Reference valve |
References
- Chen, Z.Q.; Cheng, P.; Hsu, C.T. A theoretical and experimental study on stagnant thermal conductivity of bi-dispersed porous media. Int. Commun. Heat Mass Transf. 2000, 27, 601–610. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Cheng, P.; Zhao, T.S. An experimental study of two phase flow and boiling heat transfer in bi-disperse porous channels. Int. Commun. Heat Mass Transf. 2000, 27, 293–302. [Google Scholar] [CrossRef]
- Gérard, A.; Genter, A.; Kohl, T.; Lutz, P.; Rose, P.; Rummel, F. The deep EGS (Enhanced Geothermal System) project at Soultz-sous-Forêts (Alsace, France). Geothermics 2006, 35, 473–483. [Google Scholar] [CrossRef]
- Nie, R.S.; Meng, Y.F.; Jia, Y.L.; Zhang, F.X.; Yang, X.T.; Niu, X.N. Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir. Transp. Porous Med. 2012, 92, 213–235. [Google Scholar] [CrossRef] [Green Version]
- Nield, D.; Kuznetsov, A. Forced convection in a bidisperse porous medium channel: A conjugate problem. Int. J. Heat Mass Transf. 2004, 47, 53755380. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. A twovelocity twotemperature model for a bidispersed porous medium: Forced convection in a channel. Transp. Porous Media 2005, 59, 325339. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of convection in a bidispersive porous medium. Int. J. Heat Mass Transf. 2006, 49, 3068–3074. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. A note on modeling high speed flow in a bidisperse porous medium. Transp. Porous Media 2013, 96, 495499. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. The effect of combined vertical and horizontal heterogeneity on the onset of convection in a bidisperse porous medium. Int. J. Heat Mass Transf. 2007, 50, 33293339. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. Natural convection about a vertical plate embedded in a bidisperse porous medium. Int. J. Heat Mass Transf. 2008, 51, 16581664. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. Forced convection in a channel partly occupied by a bidisperse porous medium: Symmetric case. J. Heat Transf. 2011, 133, 072601. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D. Thermally developing forced convection in a bidisperse porous medium. J. Porous Media 2006, 9, 393402. [Google Scholar]
- Straughan, B. On the NieldKuznetsov theory for convection in bidispersive porous media. Transp. Porous Media 2009, 77, 159168. [Google Scholar] [CrossRef]
- Straughan, B. Convection with Local Thermal NonEquilibrium and Microfluidic Effects; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Falsaperla, P.; Mulone, G.; Straughan, B. Bidispersiveinclined convection. Proc. R. Soc. A 2016, 472, 20160480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gentile, M.; Straughan, B. Bidispersive thermal convection. Int. J. Heat Mass Transf. 2017, 114, 837840. [Google Scholar] [CrossRef] [Green Version]
- Gentile, M.; Straughan, B. Bidispersive vertical convection. Proc. R. Soc. A 2017, 473, 20170481. [Google Scholar] [CrossRef]
- Capone, F.; De Luca, R.; Gentile, M. Coriolis effect on thermal convection in a rotating bidispersive porous layer. Proc. R. Soc. A 2020, 476, 20190875. [Google Scholar] [CrossRef] [Green Version]
- Capone, F.; De Luca, R. The Effect of the Vadasz Number on the Onset of Thermal Convection in Rotating Bidispersive Porous Media. Fluids 2020, 5, 173. [Google Scholar] [CrossRef]
- Rionero, S. Onset of convection in porous layers salted from above and below. Note Mat. 2012, 32, 159173. [Google Scholar]
- Rionero, S. Global nonlinear stability for a triply diffusive convection in a porous layer. Contin. Mech. Thermodyn. 2012, 24, 629641. [Google Scholar] [CrossRef]
- Rionero, S. Triple diffusive convection in porous media. Acta Mech. 2013, 224, 447458. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Hypo- and hyperthermia effects on LDL deposition in a curved artery. Comput. Therm. Sci. Int. J. 2019, 11, 95–103. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Low-density lipoprotein transport through an arterial wall under hyperthermia and hypertension conditions—An analytical solution. J. Biomech. 2016, 49, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Maiti, S.; Shaw, S.; Shit, G.C. Fractional order model for thermochemical flow of blood with Dufour and Soret effects under magnetic and vibration environment. Colloids Surf. Biointerfaces 2021, 197, 111395. [Google Scholar] [CrossRef] [PubMed]
- Reddy, G.S.K.; Ragoju, R. Thermal instability of a Maxwell fluid saturated porous layer with chemical reaction. Spec. Top. Rev. Porous Media Int. J. 2022, 13, 33–47. [Google Scholar] [CrossRef]
- Babu, A.B.; Reddy, G.S.K.; Tagare, S.G. Nonlinear magneto convection due to horizontal magnetic field and vertical axis of rotation due to thermal and compositional buoyancy. Results Phys. 2019, 12, 2078–2090. [Google Scholar] [CrossRef]
- Benerji Babu, A.; Reddy, G.S.K.; Tagare, S.G. Nonlinear magnetoconvection in a rotating fluid due to thermal and compositional buoyancy with anisotropic diffusivities. Heat Transf. Asian Res. 2020, 49, 335–355. [Google Scholar] [CrossRef]
- Straughan, B. Bidispersive double diffusive convection. Int. J. Heat Mass Transf. 2018, 126, 504–508. [Google Scholar] [CrossRef] [Green Version]
- Straughan, B. Effect of inertia on double diffusive bidispersive convection. Int. J. Heat Mass Transf. 2019, 129, 389–396. [Google Scholar] [CrossRef] [Green Version]
- Badday, A.J.; Harfash, A.J. Double-diffusive convection in bidispersive porous medium with chemical reaction and magnetic field effects. Transp. Porous Media 2021, 139, 45–66. [Google Scholar] [CrossRef]
- Capone, F.; Rionero, S. Inertia effect on the onset of convection in rotating porous layers via the auxiliary system method. Int. J. Nonlinear Mech. 2013, 57, 192–200. [Google Scholar] [CrossRef]
| Rc | Stationary R | Stationary a | Oscillatory R | Oscillatory a | Instability |
|---|---|---|---|---|---|
| 0 | 61.6464 | 3.9578 | 62.7612 | 3.9578 | Stationary |
| 1 | 62.1464 | 3.9578 | 62.7793 | 3.9578 | Stationary |
| 2 | 62.6464 | 3.9578 | 62.7973 | 3.9578 | Stationary |
| 3 | 63.1464 | 3.9578 | 62.8154 | 3.9578 | Oscillatory |
| 4 | 63.6464 | 3.9578 | 62.8335 | 3.9578 | Oscillatory |
| 5 | 64.1464 | 3.9578 | 62.8516 | 3.9578 | Oscillatory |
| S | Stationary R | Stationary a | Oscillatory R | Oscillatory a | Instability |
|---|---|---|---|---|---|
| 0.1 | 1018.7706 | 8.2527 | 992.2842 | 8.2527 | Oscillatory |
| 0.2 | 1013.7706 | 8.2527 | 992.2842 | 8.2527 | Oscillatory |
| 0.3 | 1008.7706 | 8.2527 | 992.2842 | 8.2527 | Oscillatory |
| 0.4 | 1003.7706 | 8.2527 | 992.2842 | 8.2527 | Oscillatory |
| 0.5 | 998.7706 | 8.2527 | 992.2842 | 8.2527 | Oscillatory |
| 0.6 | 993.7706 | 8.2527 | 992.2842 | 8.2527 | Oscillatory |
| 0.7 | 988.7706 | 8.2527 | 992.2842 | 8.2527 | Stationary |
| 0.8 | 983.7706 | 8.2527 | 992.2842 | 8.2527 | Stationary |
| 0.9 | 978.7706 | 8.2527 | 992.2842 | 8.2527 | Stationary |
| Stationary R | Stationary a | Oscillatory R | Oscillatory a | Instability | |
|---|---|---|---|---|---|
| 1 | 983.7706 | 8.2540 | 992.2842 | 8.2540 | Stationary |
| 2 | 691.3454 | 6.4421 | 694.5709 | 6.4421 | Stationary |
| 3 | 588.8136 | 5.5171 | 590.1849 | 5.5171 | Stationary |
| 4 | 546.4455 | 4.9469 | 547.0506 | 4.9469 | Stationary |
| 5 | 531.2631 | 4.5668 | 531.5936 | 4.5668 | Stationary |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramchandraiah, C.; Kishan, N.; Reddy, G.S.K.; Paidipati, K.K.; Chesneau, C. Double-Diffusive Convection in Bidispersive Porous Medium with Coriolis Effect. Math. Comput. Appl. 2022, 27, 56. https://doi.org/10.3390/mca27040056
Ramchandraiah C, Kishan N, Reddy GSK, Paidipati KK, Chesneau C. Double-Diffusive Convection in Bidispersive Porous Medium with Coriolis Effect. Mathematical and Computational Applications. 2022; 27(4):56. https://doi.org/10.3390/mca27040056
Chicago/Turabian StyleRamchandraiah, Chirnam, Naikoti Kishan, Gundlapally Shiva Kumar Reddy, Kiran Kumar Paidipati, and Christophe Chesneau. 2022. "Double-Diffusive Convection in Bidispersive Porous Medium with Coriolis Effect" Mathematical and Computational Applications 27, no. 4: 56. https://doi.org/10.3390/mca27040056
APA StyleRamchandraiah, C., Kishan, N., Reddy, G. S. K., Paidipati, K. K., & Chesneau, C. (2022). Double-Diffusive Convection in Bidispersive Porous Medium with Coriolis Effect. Mathematical and Computational Applications, 27(4), 56. https://doi.org/10.3390/mca27040056







