1. Introduction
Wind energy offers an important supply of electricity without pollution problems presented by conventional forms of energy. There is a global interest for the development and use of alternative energy sources, including geothermal, photovoltaic, hydroelectric, tidal wave, biomass and others [
1]. Unlike other technologies, wind farms have a very low impact on their environment, which has resulted in increased use worldwide, with some countries obtaining as much as 20 percent of their energy from the wind [
2].
Wind turbines can be categorized, for example, based on their rotation axis, which can be vertical or horizontal [
3]. Horizontal axis turbines are the most common and can be classified according to the rotation of the rotor with respect to the tower. These machines are composed of a foundation, a tower, a rotor, nacelle with power train and the blades. The blades are one of the most important components, if not the most, since they are in charge of collecting the energy from the wind, converting the linear movement of the wind into a rotary movement of the rotor. This energy is transmitted to the hub, from the hub it proceeds to a mechanical transmission system and from there it proceeds to the generator that transforms it into electrical energy.
Blades can suffer different types of failures due to a variety of phenomena [
4], such as the following: bending, twisting, cracks and erosion. Detecting these types of faults, particularly at early stages, is important for avoiding catastrophic failures, reducing down times and taking corrective actions in a timely manner [
5]. In particular, automatically detecting erosion at the leading edge of the blade tip presents a challenge because it is not trivial to properly measure erosion without direct access to the blade [
4]. Typically, fault detection in wind turbine blades has been carried out by visual means (
https://energy.sandia.gov/programs/renewable-energy/wind-power/, accessed on 29 December 2021), but it is also possible to use different sensor schemes implemented via a SCADA system [
5,
6]. Afterward, these data can be analyzed by computational models, such as those derived by means of machine learning (ML), which have been found to be of great utility in the detection of damages in a variety of complex scenarios [
7,
8,
9]. One approach of note, for example, is the use of sound to detect such damage [
10]. Moreover, to implement ML methods, sufficient data are required to model blades with and without erosion; however, extracting these data from the field or in controlled scenarios can be a complex task to perform [
11]; thus, one possible alternative is to exploit simulation software such as QBlade [
12].
The goal of this work is two fold. First, it presents a detailed analysis of the effects that erosion has on wind turbine blades, considering modal and numerical analysis, with respect to the physical stress caused by erosion on the blades and the power-generating capacity of a wind turbine. Second, this work presents a methodology to construct ML models that can detect the presence and location of erosion in a blade and measure the amount of erosion as well. The paper makes two important contributions. First, we show for the first time that AutoML can be successfully applied in this problem domain, which has not been considered before for this problem. Second, we show that it is possible to detect the presence of erosion on the blade, determine its location and predict the amount of damage caused by erosion.
The remainder of this paper is organized as follows.
Section 2 presents wind turbine blades and the aerodynamic, modal and numerical analysis of the blades studied in this work.
Section 3 deals with the detection of erosion with ML methods, including an overview of related works and our experimental approach and results. Finally, conclusions and future work are presented in
Section 4.
3. Erosion Detection with Machine Learning
This section deals with the automatic detection of erosion in wind turbine blades. The goal is to detect where erosion has occurred using a classification model, considering the three different cases of where erosion can appear on the blade tip: on the bottom edge, the top edge or both. Moreover, we predict, using regression models, the amount of erosion on the blade. Both tasks are posed as supervised learning problems and solved using ML algorithms by performing feature extraction on the power and vibration response of the blade through QBlade simulation. However, before presenting our proposal, we briefly survey related works in this domain.
3.1. Related Work
Several works have applied ML towards the detection of different types of problems in wind turbines. For instance, static and dynamic regression models have previously been used to detect failures in wind turbines based on vibration analysis [
5]. Another example is [
17], which presents an approach to predict when preventive maintenance should be performed, focusing on the remaining useful life of a wind turbine before a failure occurs and diagnosing the type of failure. The proposal involves low implementation costs because it is based solely on information collected from the very common SCADA system. A recent example also includes forecasting of wind speed assessment using satellite data and ML [
18], specifically a neural network.
In [
11], the authors classify the occurrence of different types of failures in blades, using a piezoelectric accelerometer to measure the vibration of the blade. That work considered five types of damage to the top of the leading edge of the blades, namely bending, cracks, looseness, pitch, twist and erosion. To classify the signals time-domain, feature extraction is performed on the vibration signals, focusing on different types of summary statistics. In a more recent study by the same authors [
19], they also use vibration signals, histogram features and ML to monitor the condition of wind turbine blades, in this case using
lazy classifiers.
ML has also been applied to maintenance management of blades in [
20]. The work is based on the detection of delamination, a common structural problem that can generate large costs. Continuous monitoring of turbines is the focus of [
21], using real data from a SCADA system to predict damage to the structure and blades of wind turbines. The authors present two models for this: the first is the use of multilayer neural network, and the second is adaptive networks with a fuzzy inference system. The proposal is to monitor the power curve signal, achieving good precision. Sound analysis, a unique approach, has also been used for fault detection, extracting descriptive feature of acoustic waves and detecting damage using common ML methods [
10]. A related work can be found in [
22], where ML is used to estimate turbine energy yield losses due to erosion on the leading edge of the blade.
In general, few works deal specifically with erosion, and those that do not focus on a detailed analysis of this type of failure.
3.2. Data Set
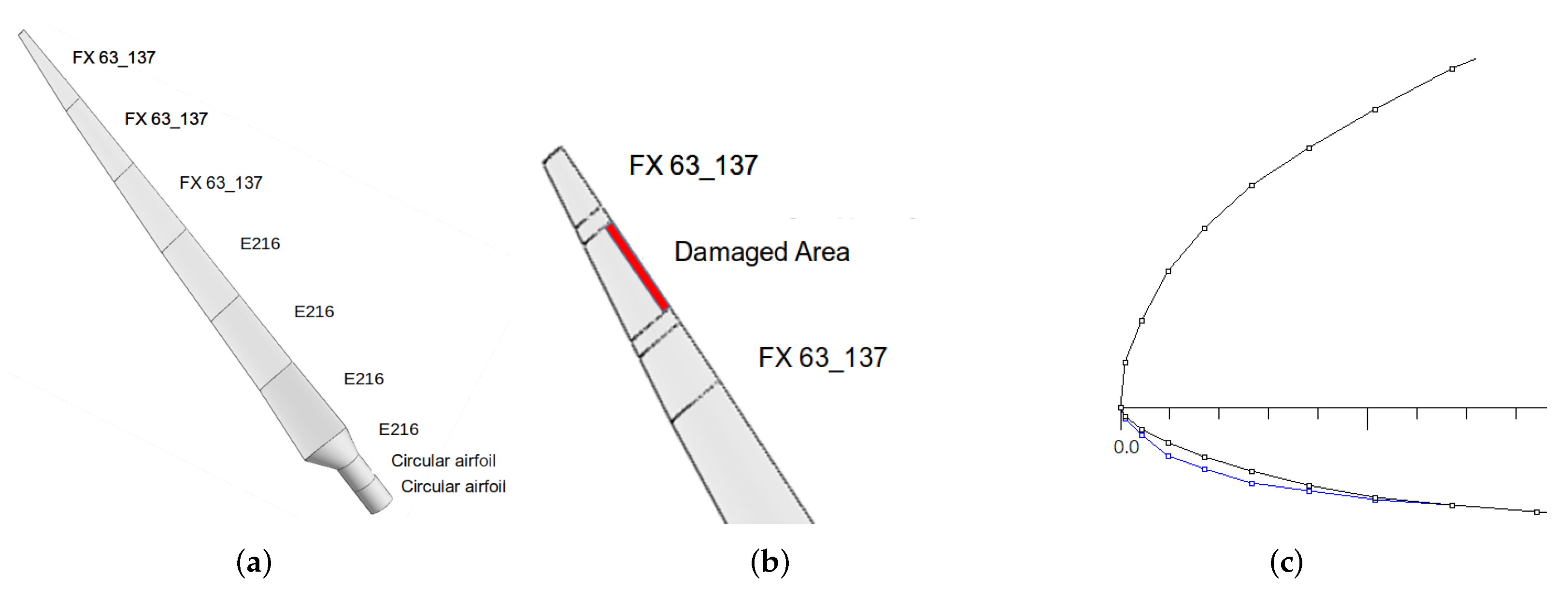
The dataset was generated with QBlade and the procedure outlined in
Section 2.2. A total of 100 blades were simulated for each type of erosion of the blade tip (bottom edge, top edge or both), producing a dataset with 300 samples, similar to [
11]. This work assumes that all blades used in a real-world setting will have a certain amount of erosion in at least one of the edges of the tip. Therefore, we do not consider the case in which the blade is completely clean. It must be stated that, while we are relying on simulated data, it has been shown that simulated results of wind turbine blade performance are reliable predictors of on site behavior [
22,
23].
In order to simulate an eroded blade, each of the contour points of the blade profile was perturbed, adding displacements within the range of 8% to 18%. The same seven contour points on the tip of the blade were modified to model different levels of erosion. Half of the samples were generated using uniform grid sampling, while the other half of samples were generated with random values within the specified range. For example, for the lower edge cases, 8% of erosion was removed from the Y-axis coordinate value; subsequently, the percentage of erosion increased by 0.2% up to 18% to generate 50 samples. For the remaining 50 samples, the amount of erosion was determined randomly by using a uniform distribution
. Random samples were used to simulate a rugged surface on the blade, which can be caused by random events such as contact with insects or large sand particles. Our approach is justified since roughness on a blade is often simulated with a random surface [
24,
25].
Each blade was simulated with QBlade using the settings in
Section 2.1. The acceleration response at the blade tip was obtained, using the QFEM tool for structural design and modal analysis of each blade. The NREL FAST tool [
26] was used to carry out analysis of the dynamic response of wind turbines. The vibration of the acceleration signal at the tip of the blade is selected as output. The simulation parameters are as follows: time step of 0.1, 3 blades, a rotor speed of 296 rpm and air density of 1.225 k/m
. The wind fields are specified in
Table 6 by mostly using the same simulation values used to determine power output. The difference is simulation time and air density.
3.3. Feature Extraction
After obtaining the samples of both power and acceleration for the different blades, we proceeded to perform feature extraction. For this work, feature detection was carried out in the time domain given the success of such measures in similar work [
11] and in the analysis of other complex signals [
27,
28].
Let denote the vector containing a time series from a single signal, and T denotes the number of samples in . A feature of is denoted by x, while the matrix contains all features from all samples, is the vector of a single feature, and F is the total number of features extracted.
The feature extracted from the signals include six statistical descriptors, namely mean, median, maximum, minimum, sum, standard deviation, variance and kurtosis. Moreover, we also extract the following:
Power: ;
First difference: ;
Normalized first difference: ;
Second difference: ;
Normalized second difference: .
Power
measures the strength of the signal or the energy consumed per unit of time. The first and second differences show the changes of a signal in time. The normalized first difference is also known as the Normalized Length Density and is used to quantify the self-similarities contained in a signal. Additionally, we also extract what is referred to as Hjorth features [
29]. These include the following: Activity, Mobility and Complexity. The Activity feature represents the variance of the signal and is computed by the following.
The Mobility feature is defined by the standard deviation of the slope of the EEG signal using as reference the standard deviation of the amplitude expressed as the following ratio by time unit.
The Complexity feature measures the signal’s variation using a smooth curve as reference provided by the following.
Another time domain feature is the Non-Stationary Index (NSI) [
30]. Signal
is divided into segments, and their respective
is computed. NSI is defined as the standard deviation of the segments’
. When NSI is high, the signal is considered to be “less stationary.”
The last feature includes Higher Order Crossings (HOC) [
31]. The feature describes the oscillatory nature of signal counting the number of sign changes over multiple variants of the signal. A total of 10 distinct featur HOC features were extracted.
In total, this work considers 27 time domain features to characterize the signals of interest extracted from the wind turbine blade.
Classification and Regression Problems
The above feature extraction process produces a total of 27 time domain features for each signal. These features are used to pose three classifications by using the following: (1) the features from the power signal; and (2) adding the features from the acceleration signal. An ML model will learn to use these features to determine what edge of the blade is affected by erosion.
Moreover, the same feature set will be used to generate a regression model to estimate the exact amount of erosion. In this scenario, the objective is to predict the level of erosion, which ranges from 8 to 18 percent. In this case, the location of the erosion (top, bottom or both) is not taken into account, and the percentage of erosion is the target of the learning process.
3.4. Auto Machine Learning with H2O-DAI
AutoML is an approach for automating the design, tuning, implementation and evaluation of complete ML pipelines. The goal is to simplify the manner in which ML models are tested and evaluated such that the process by which the models are generated provide a comprehensive evaluation of the best possible approach to solve a given problem. In this proposal, we use H2O-DAI, which stands for H2O Driverless AI, which offers a very simple user interface and a comprehensive set of tools to perform AutoML [
32]. For instance, it makes a choice from a set of state-of-the-art models, such as XGBoost [
33], Generalized Linear Models [
34] and Deep Learning [
35].
There are basically four tuning hyperparameters that are used to configure the AutoML process of H2O-DAI; these include the following. Accuracy refers to the amount of effort to find the best possible pipeline in the range (1–10); it is set to 7 in these experiments. Time controls the duration of the search process, it is set to 2 in our experiments. Interpretability controls the amount of feature engineering performed by the AutoML system. In this case, since a diverse set of features is already being used, it is set to 8. Moreover, to evaluate performance, 6-fold cross validation was used. All experiments were carried out on an IBMP Power 8 Server for High-Performance Computing with two Power 8 processors and two NVIDIA Tesla P100 GPUs.
3.4.1. Classification Results
Summary of the results are presented as an average confusion matrix based on the classification achieved on the testing folds of the cross validation process. Results are shown in
Table 7 when using the power output for feature extraction, where class labels are shown as Bottom, Top and Both for each of the three types of erosion. Other noteworthy classifier performance scores include (given as the average ± standard deviation over all the testing folds) the following: Area Under the Receiver Operating Characteristic Curve of
and an F1-Score of
.
H2O DAI converged to an XGBoost model for classification [
36], using a total of seven input features, four of which are raw features from the 27 time domain features and three automatically engineered features. In particular, for this version of the problem, H2O DAI focused on statistical features, such as the variance, mean and median, but it also used the power feature.
Extending the feature set, incorporating the features computed on the acceleration signal produced optimal results, as shown in the confusion matrix of
Table 8. In this case, H2O DAI also converged to an XGBoost model, using a total of 10 input features, including five automatically engineered features. It is notable that all of the features used in this case are features extracted from the acceleration signal, including the first differential, the NSI and the power features.
3.4.2. Regression Results
The same configuration of H2O DAI is used, which was reported above for classification, with the exception that the scoring function is the root mean squared error (RMSE). Results are presented in
Table 9, showing the average performance on the test sets of the 6-fold cross validation. H2O DAI was applied on three groups of features: power signal, acceleration signal and both, showing the mean absolute error (MAE), coefficient of determination
and the root mean square percentage error loss (RMSPE). In all cases, H2O DAI converged to a Light Gradient Boosting Machine (Light GBM) [
37]. Results show that using both signals for feature extraction produced a highly accurate model in terms of both
and RMSPE.
4. Concluding Remarks
This study presents an in-depth analysis of the aerodynamic and modal response of an eroded wind turbine blade. Efficiently and effectively detecting erosion on a blade can have substantial impacts in preventative and timely maintenance of wind turbines. Results show that it is possible to accurately determine where the erosion is present on the blade (top edge, bottom edge or both) and to estimate the level of erosion (between 8 and 18 percent). This is accomplished by analyzing the power signal of the wind turbine and the vibrations of the blade tip. A large set of time domain features was extracted, and the modeling process is carried out by using an AutoML system, namely H2O DAI. As such, this study represents the first contribution that tackles both the detection, localization and estimation of erosion level on the leading edge of a blade using ML. Moreover, this work is the first to apply AutoML in this domain. The process of designing the ML pipeline was carried out in an automatic fashion, without hampering performance and requiring very little human intervention in the design process. This could motivate further collaborative and multidisciplinary research between applied ML and wind energy maintenance and production.
The results presented in this work are consistent with those reported by [
11,
19], with the slight performance difference probably due to working with simulated data in our case, which is nonetheless a good predictor of real-world performance, as shown by [
22,
23] and partially validated by our experiments with a physical model.
Among both signals that were analyzed, the accelerometer readings seem to be more informative relative to the power signal, based both on the classification (erosion detection) and regression (erosion level estimation) problems, with small but consistent differences. Moreover, the best performance was achieved when both signals are used for feature extraction. It should be possible to use both models to automatically detect the presence and level of erosion in a properly instrumented wind turbine blade. Future work will focus on applying the same experimental procedure in a fully working prototype: first in a wind tunnel and then in the field.