Taming Hyperchaos with Exact Spectral Derivative Discretization Finite Difference Discretization of a Conformable Fractional Derivative Financial System with Market Confidence and Ethics Risk
Abstract
:1. Introduction
2. Preliminaries
2.1. The Conformable Derivative ESDDFD Discrete Model Construction Fundamentals
2.2. The Conformable Derivative Hyperchaotic Financial System and Its CEFD Model
3. ESDDFD Discretization of the Conformable Derivative System and Its Reductions
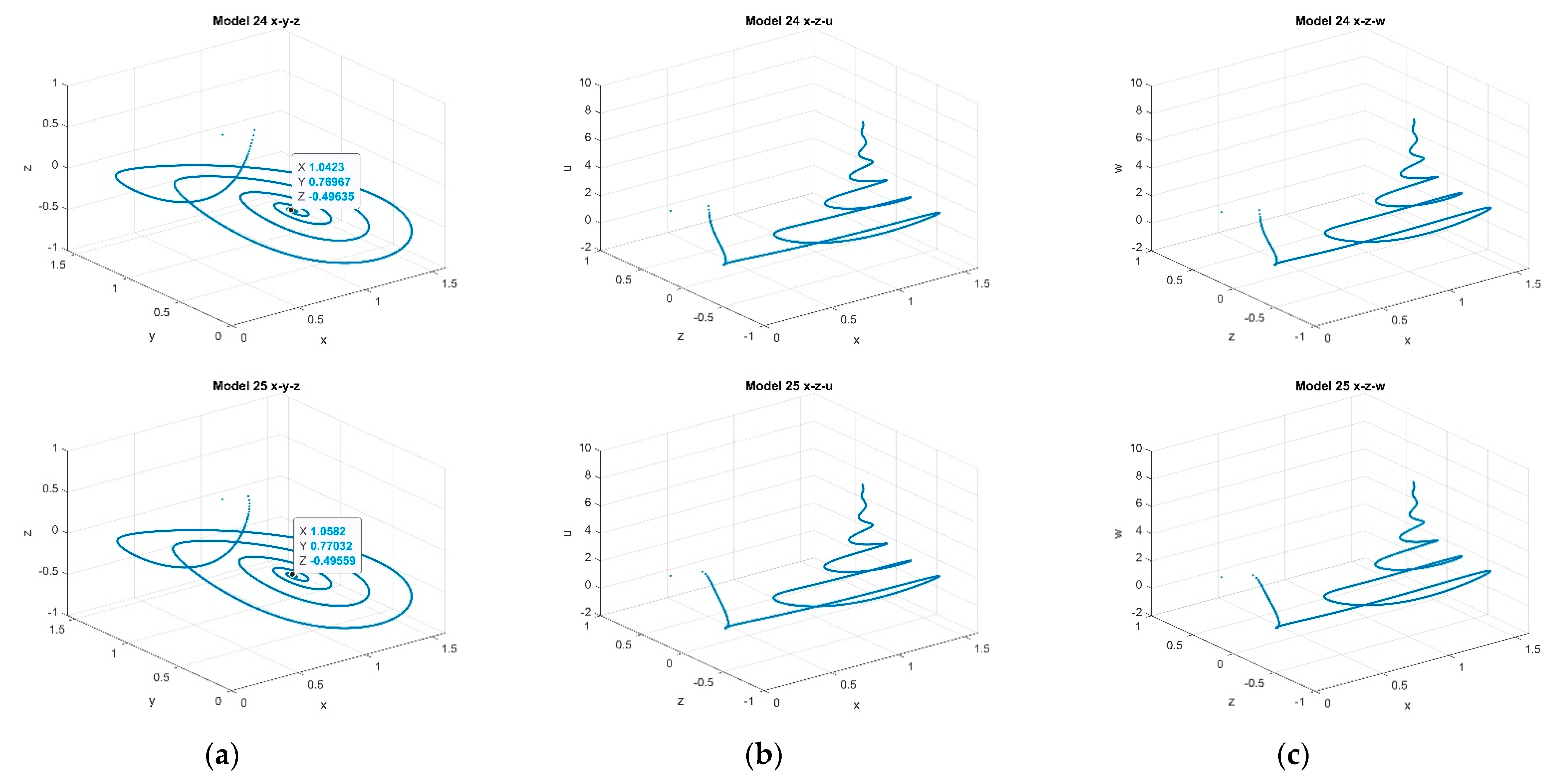
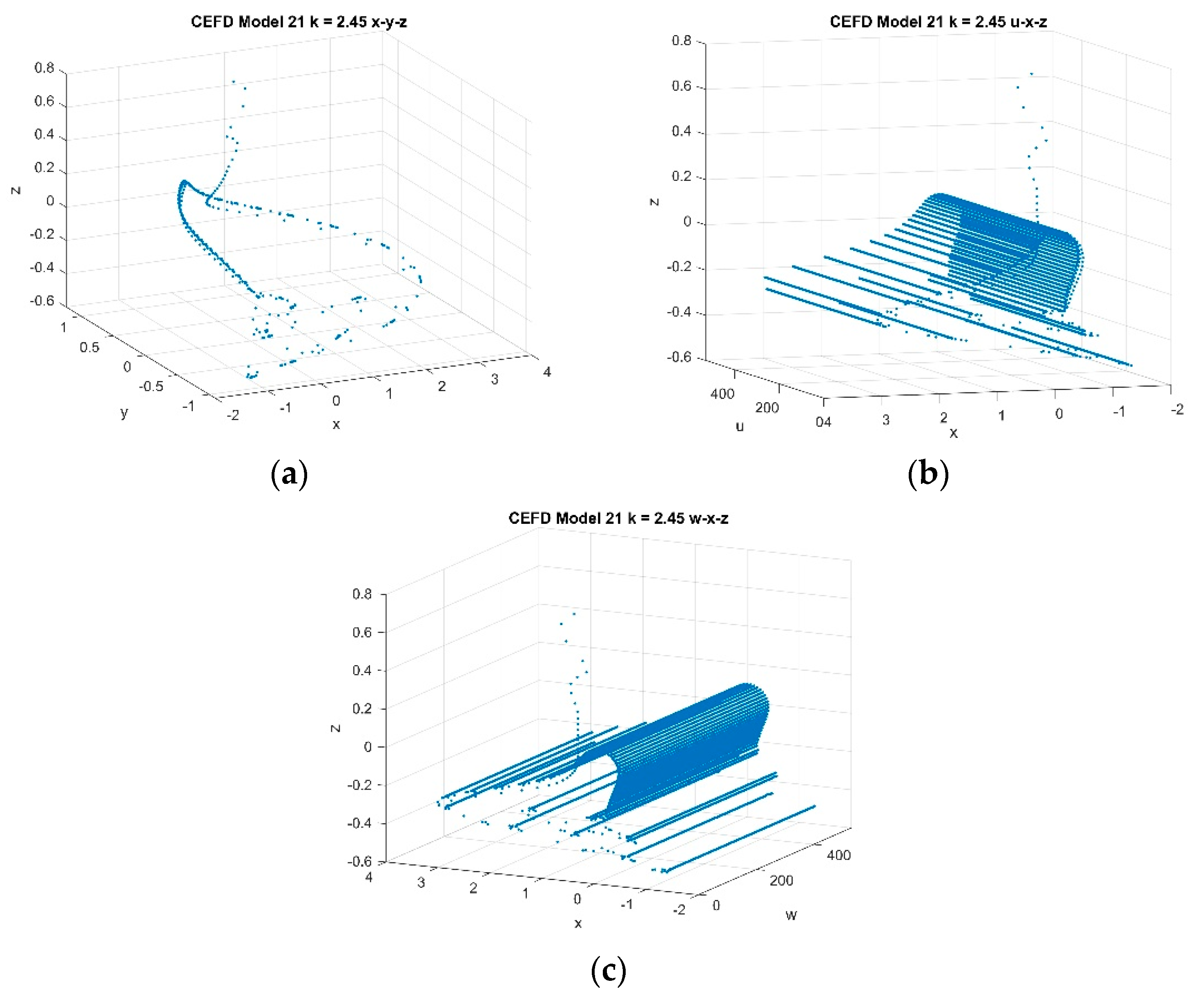
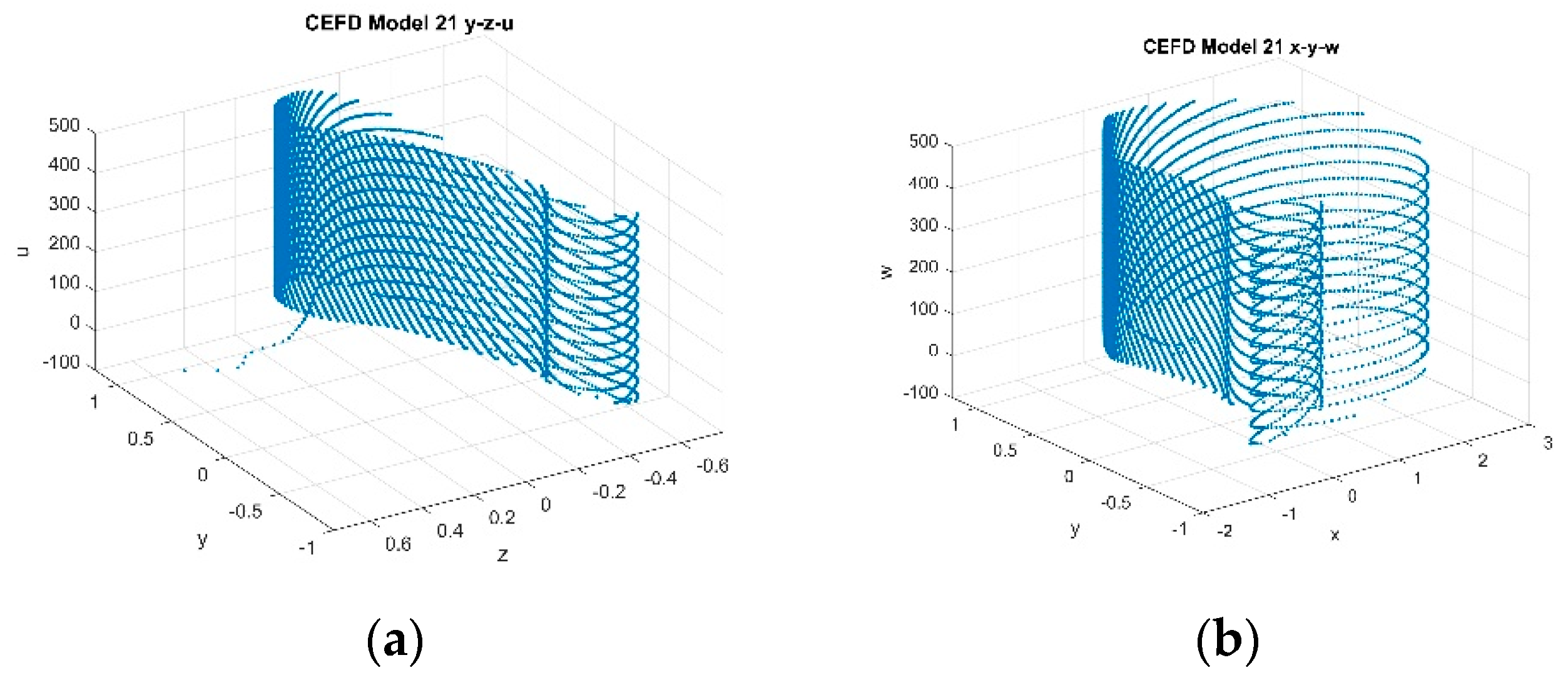
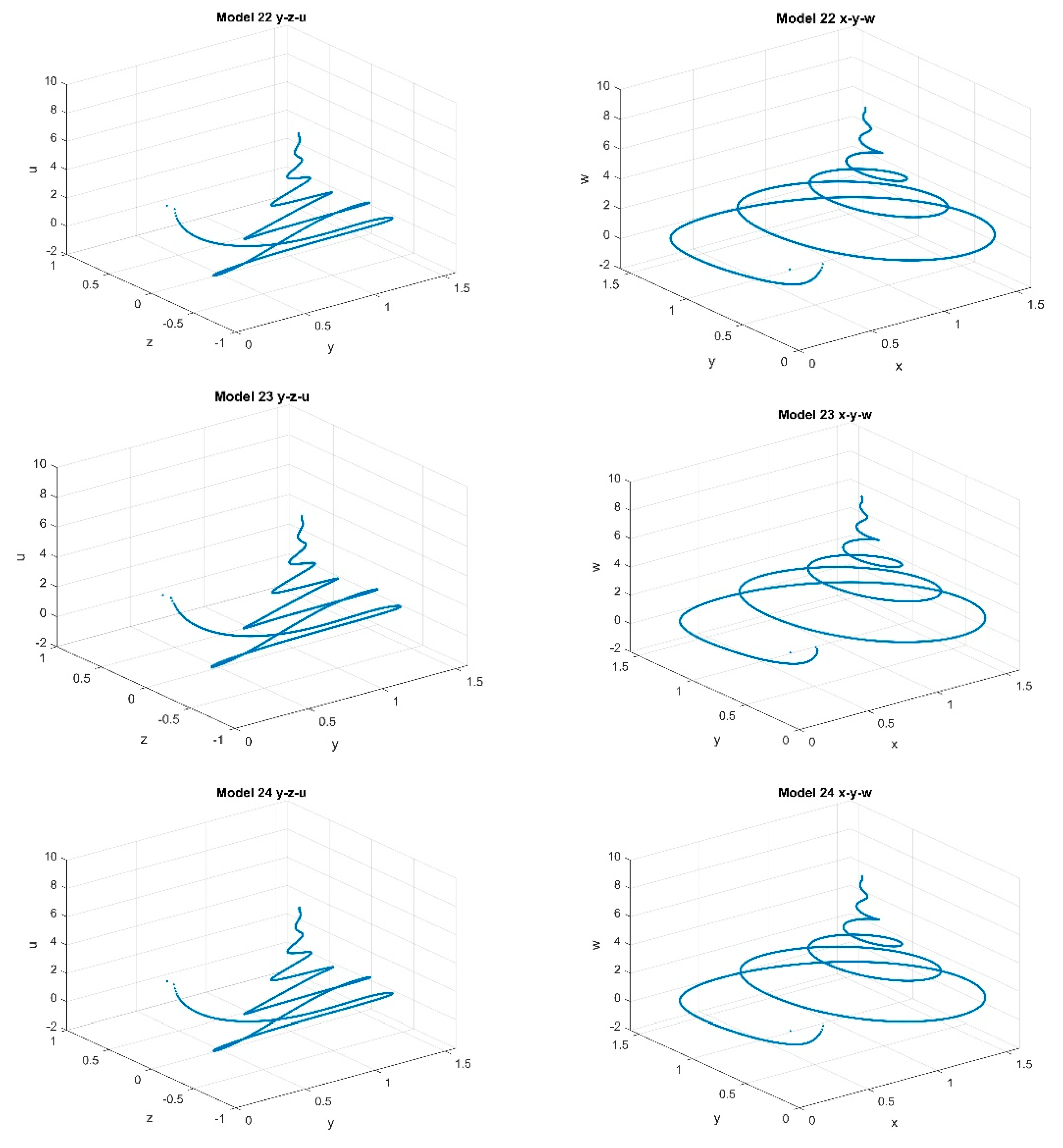
4. Numerical Experiments
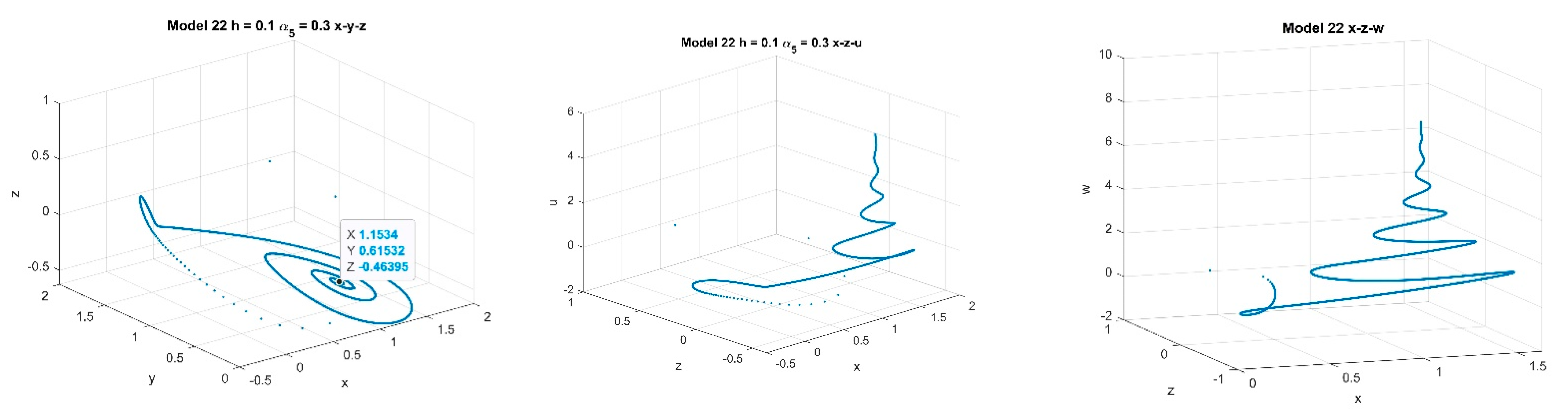
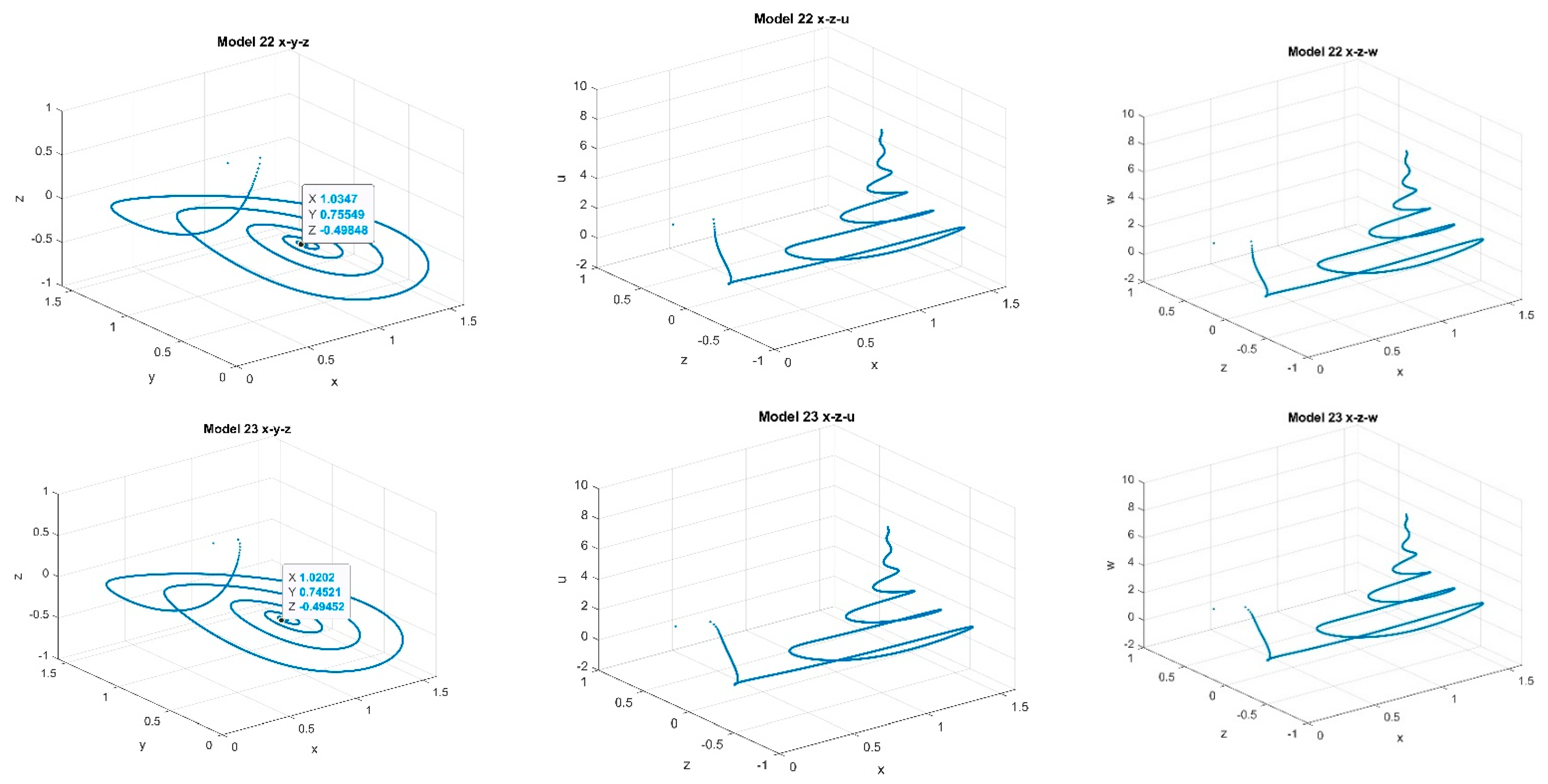
4.1. Three-Dimensional Systems Comparison
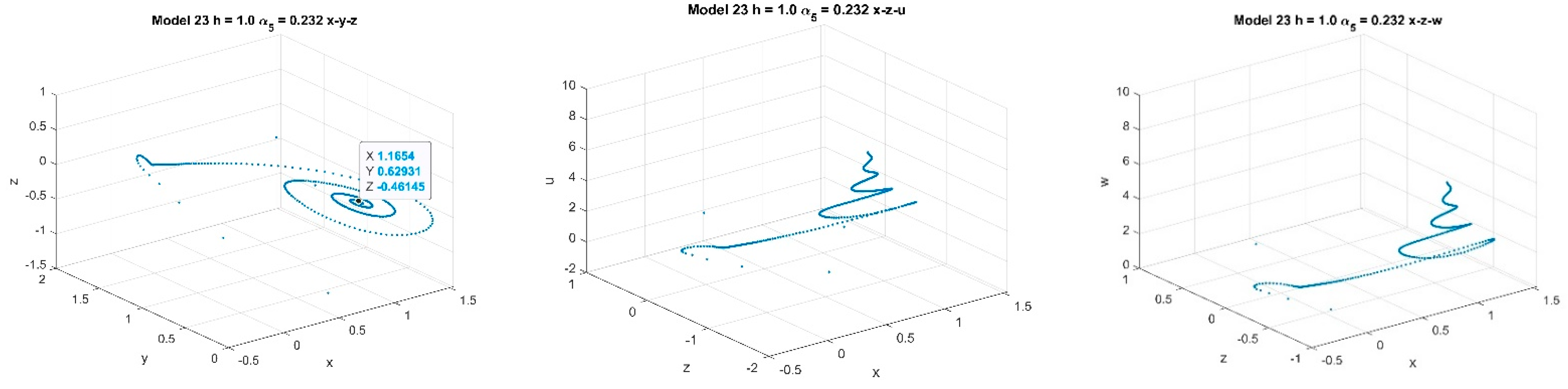
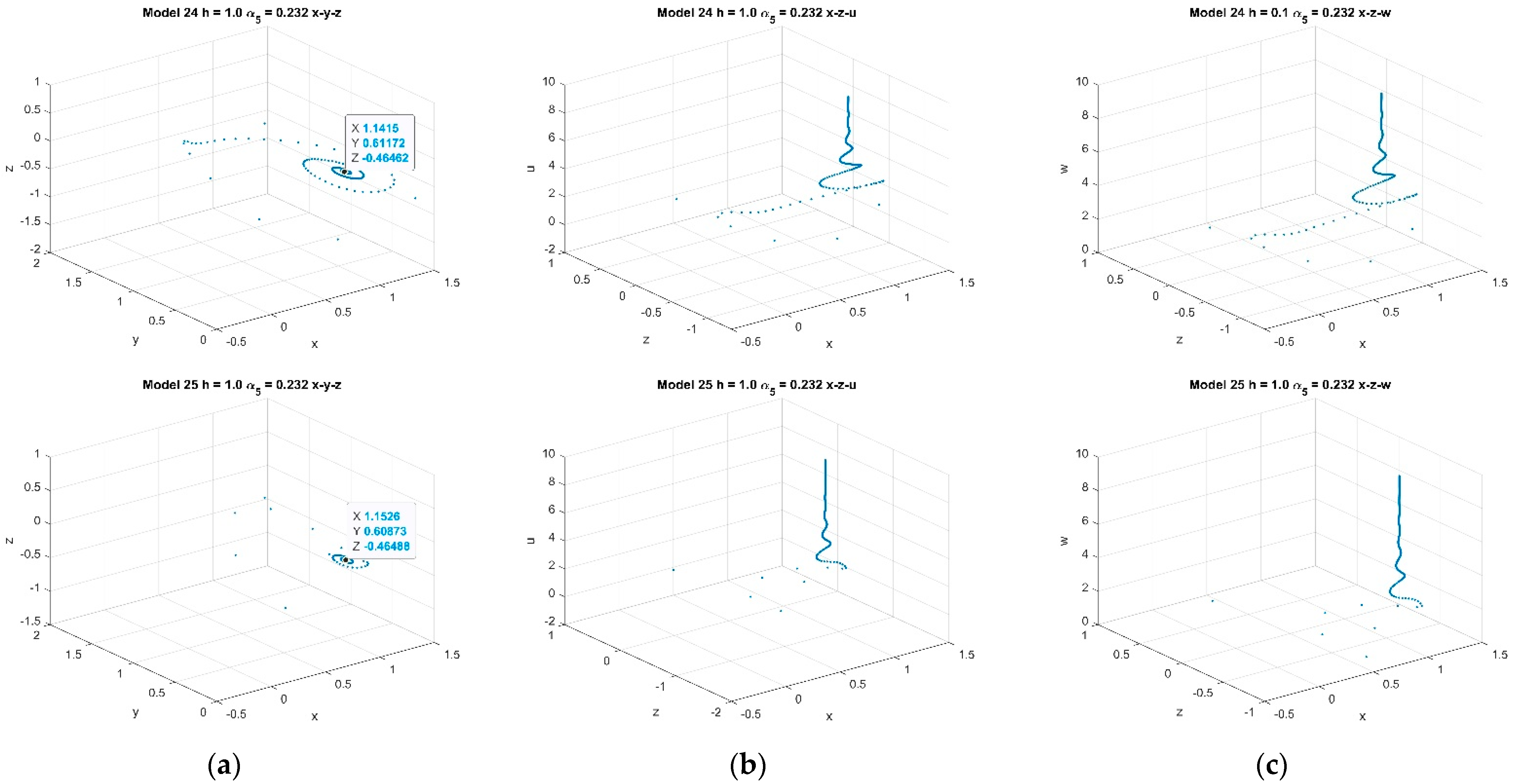
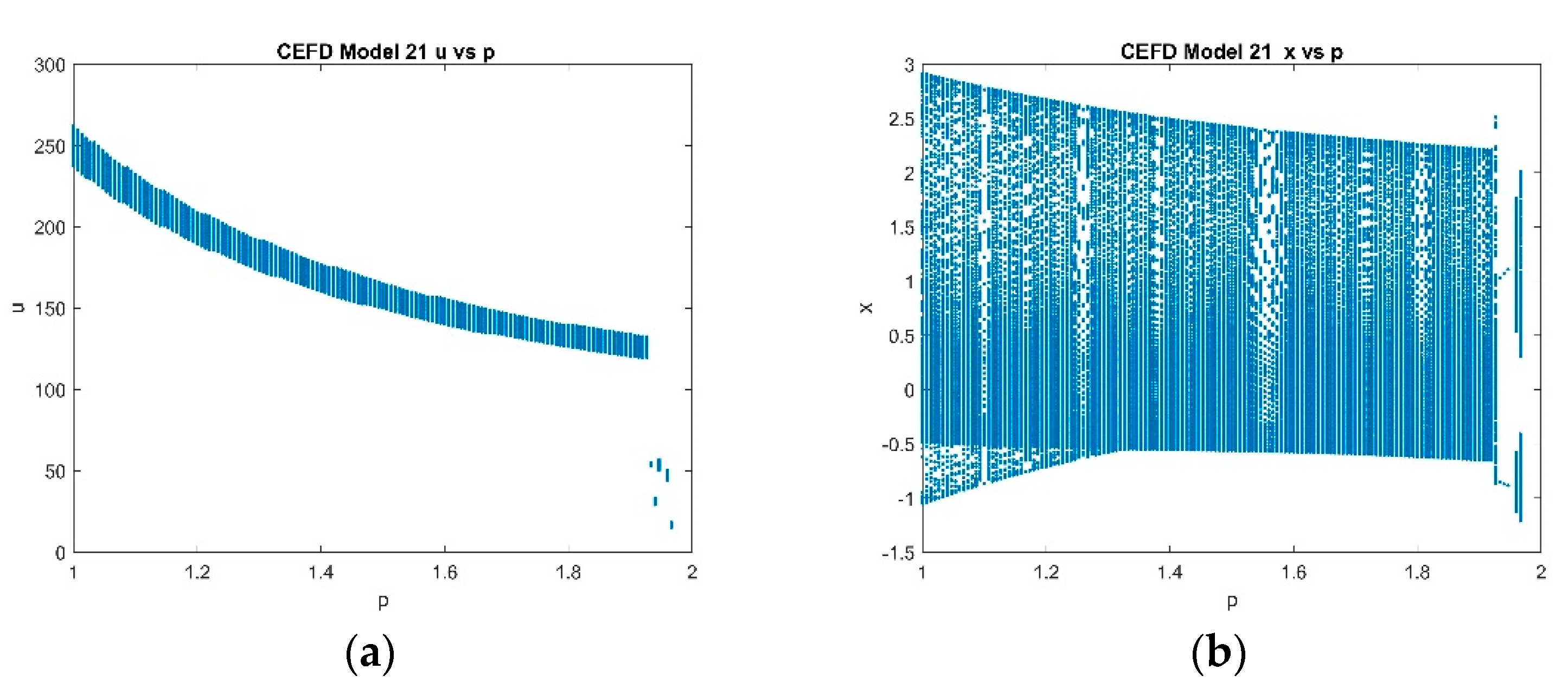
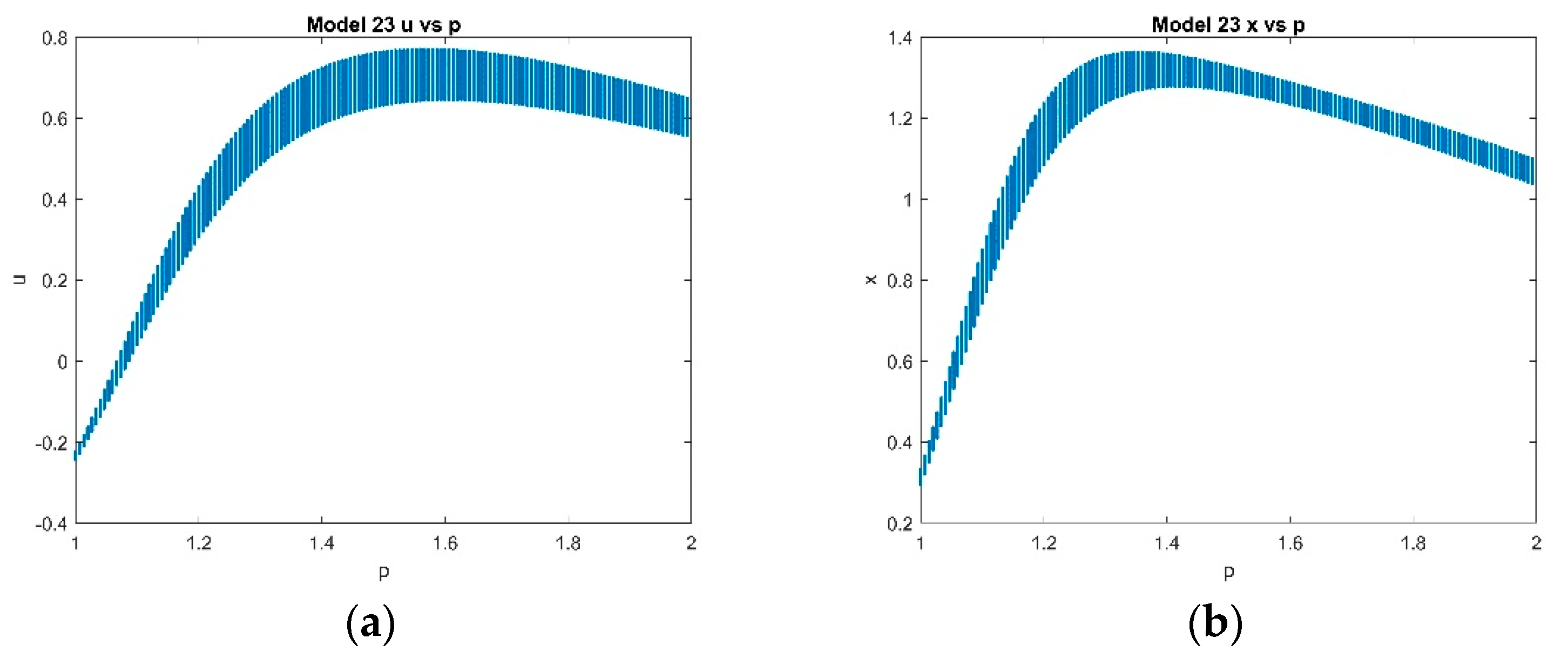
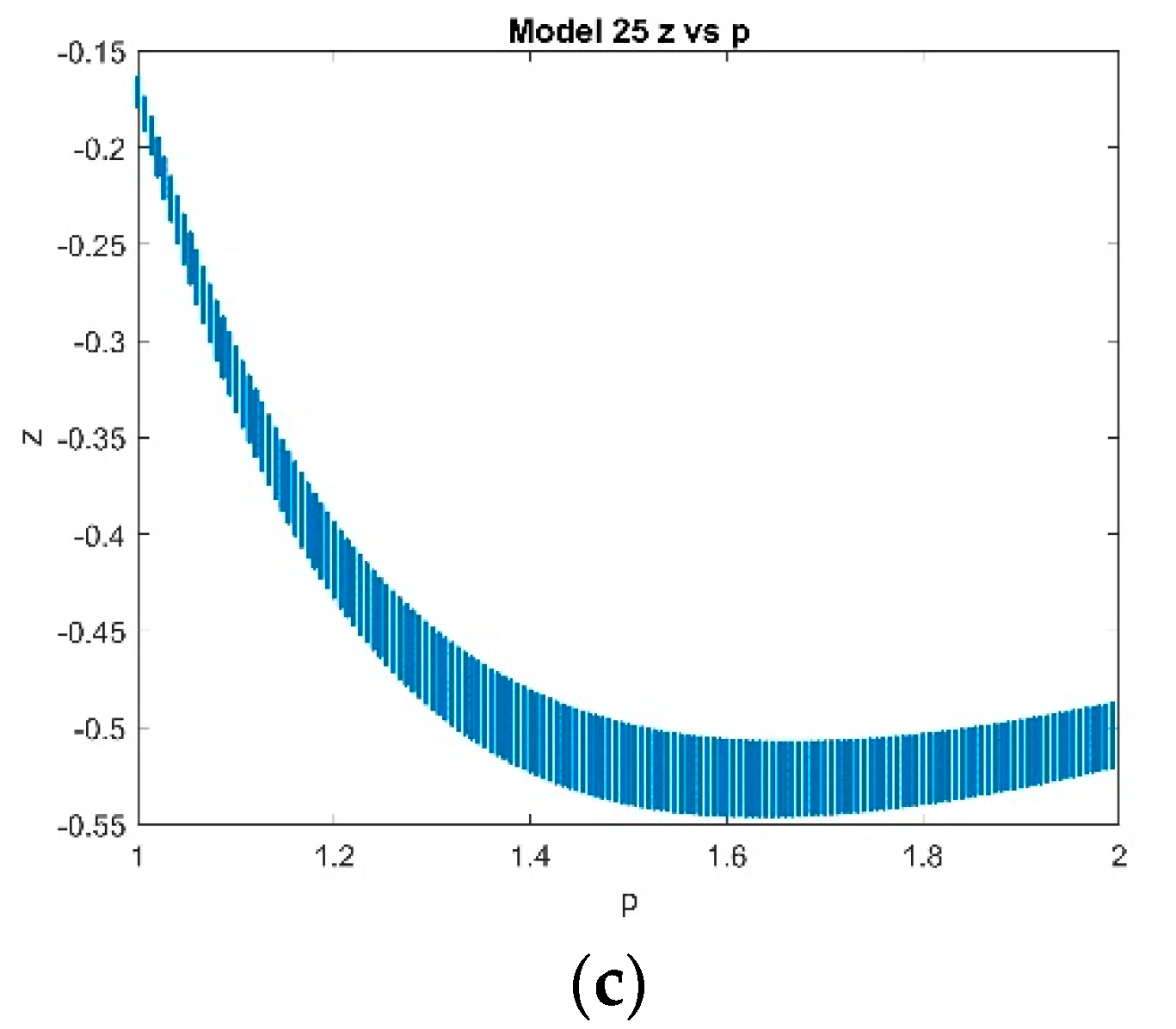
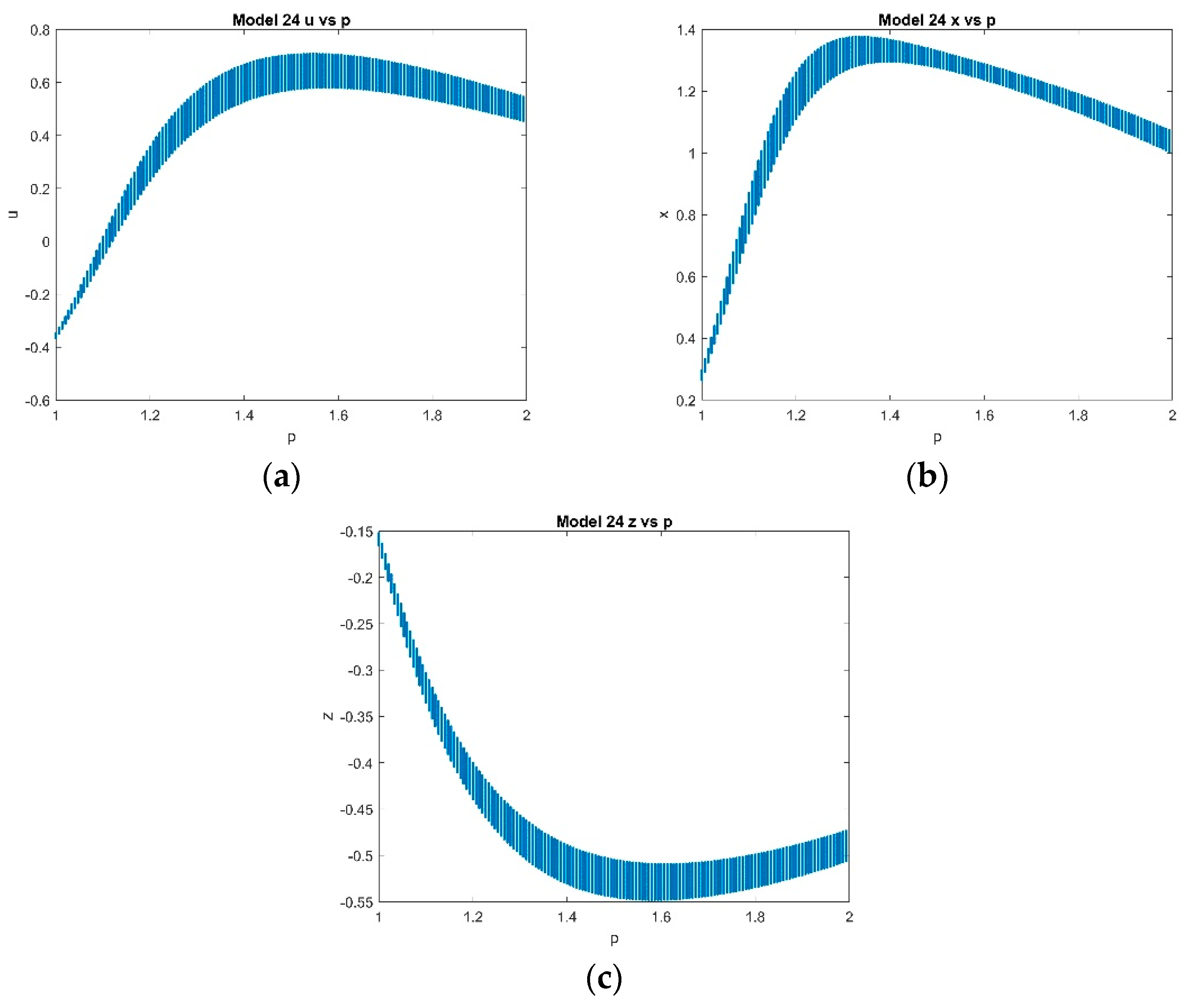
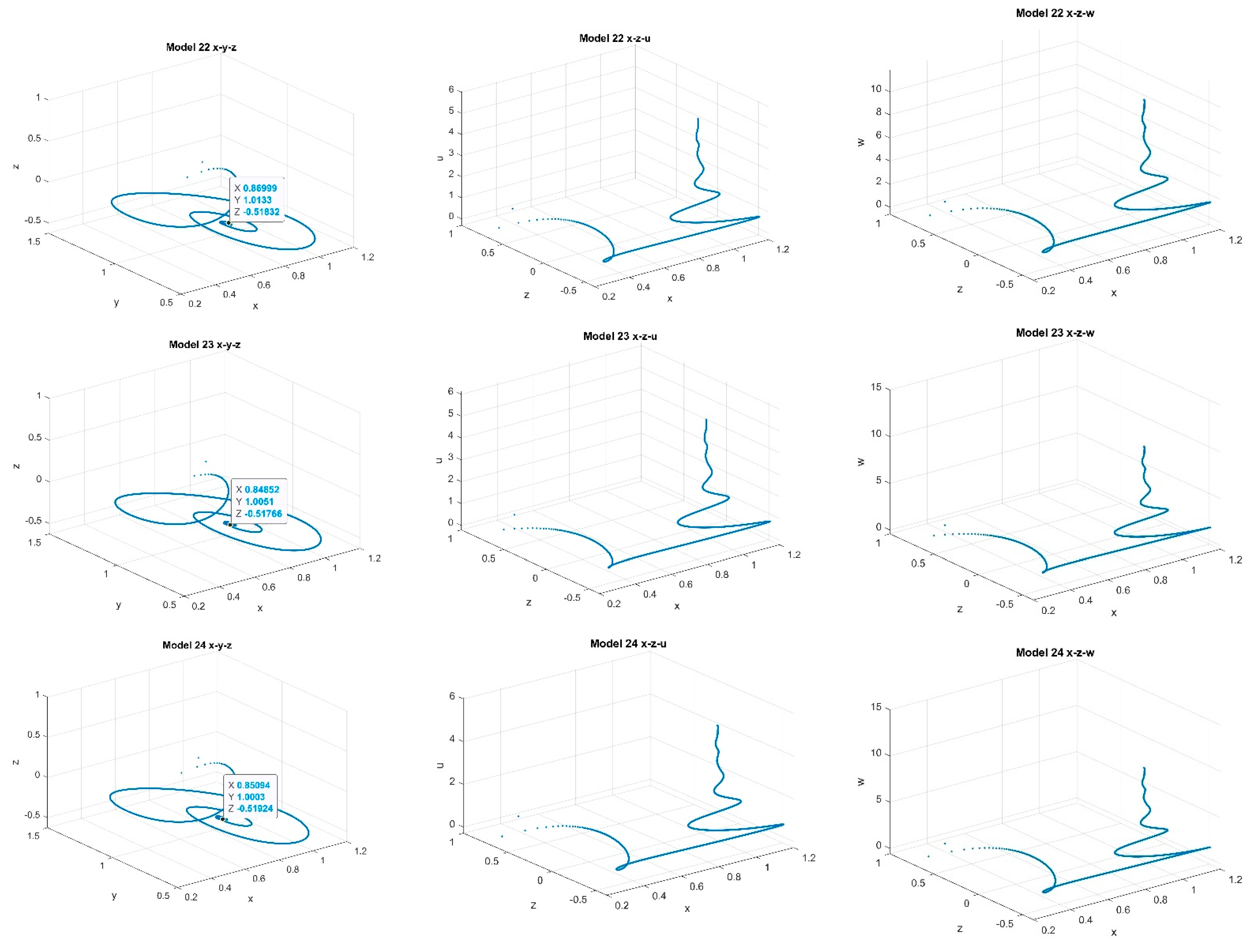
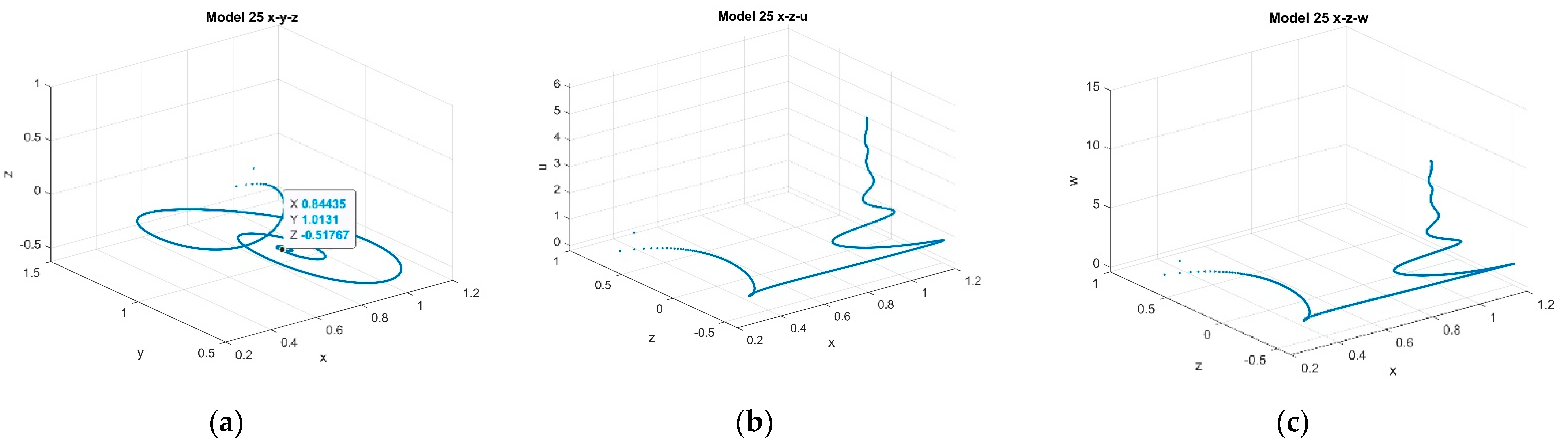
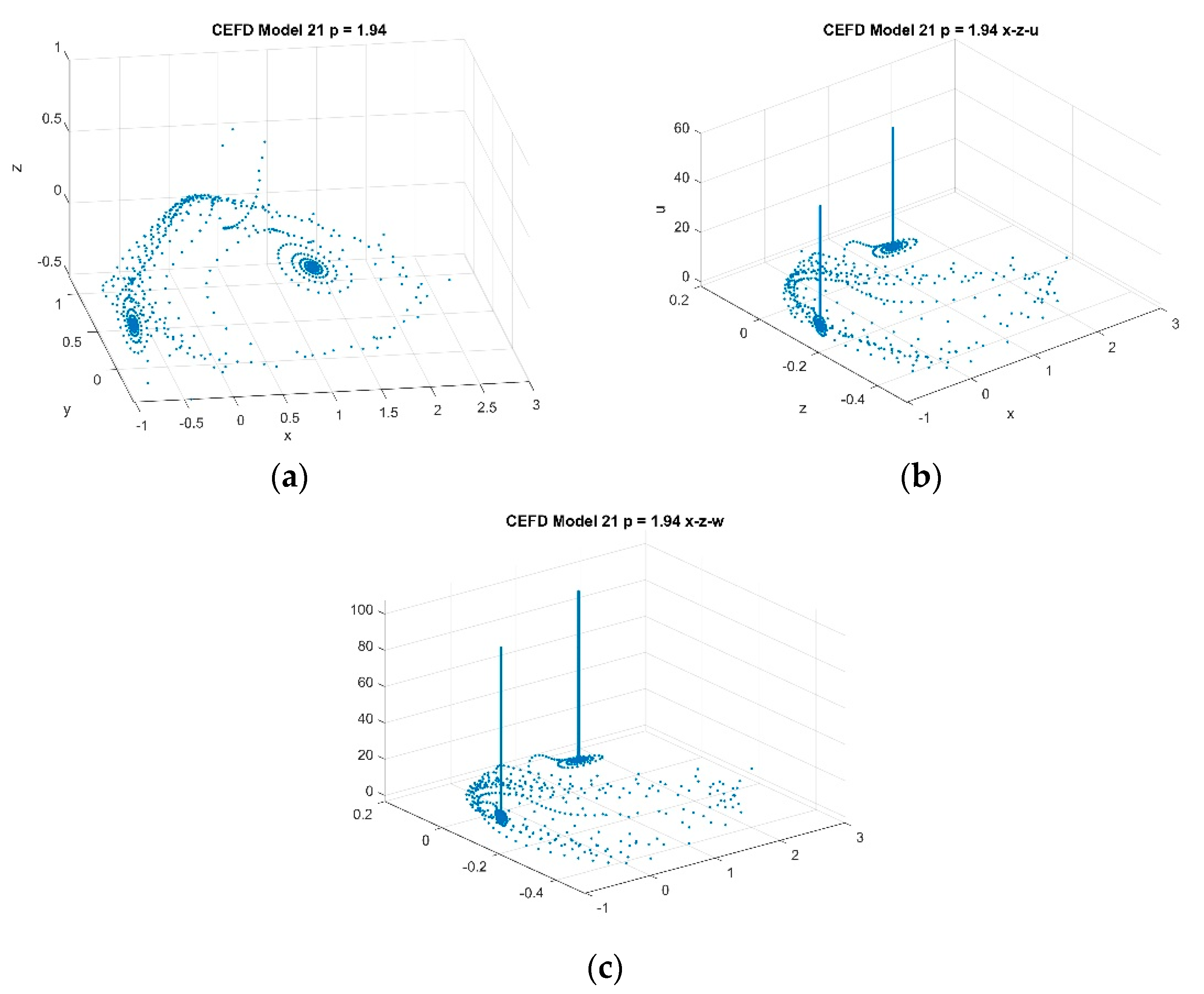
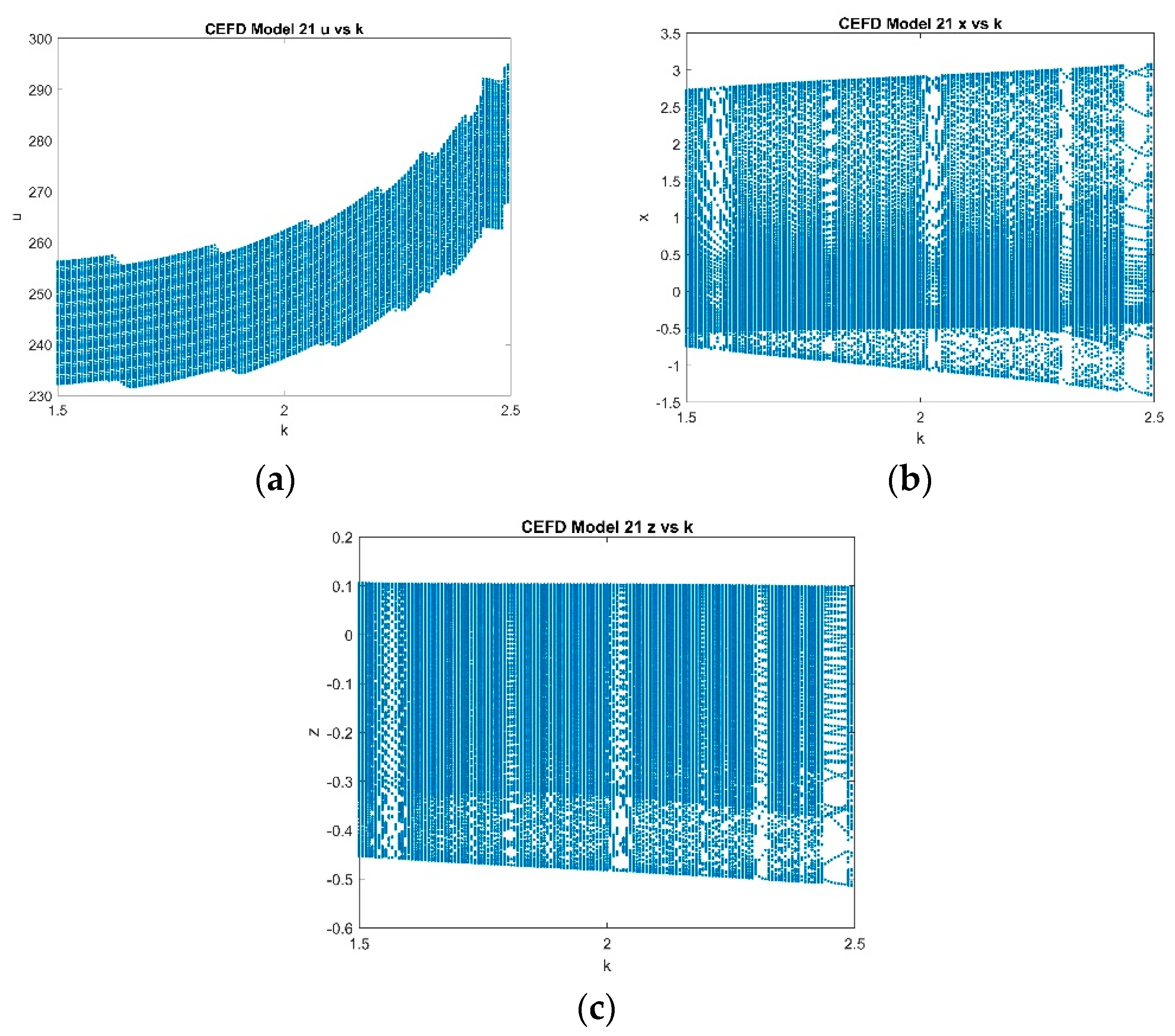
4.2. Five-Dimensional Systems Comparison: Varying , and
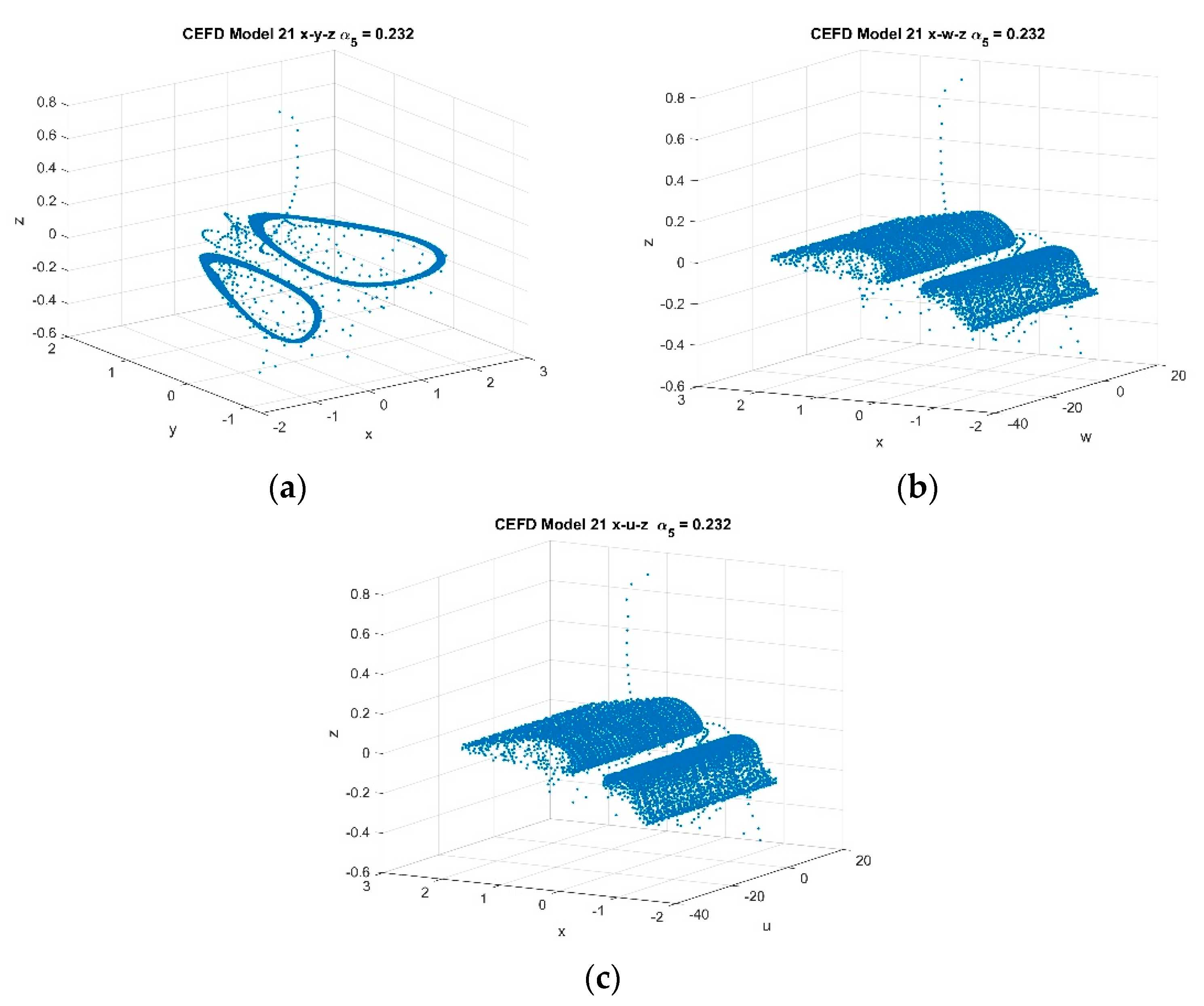
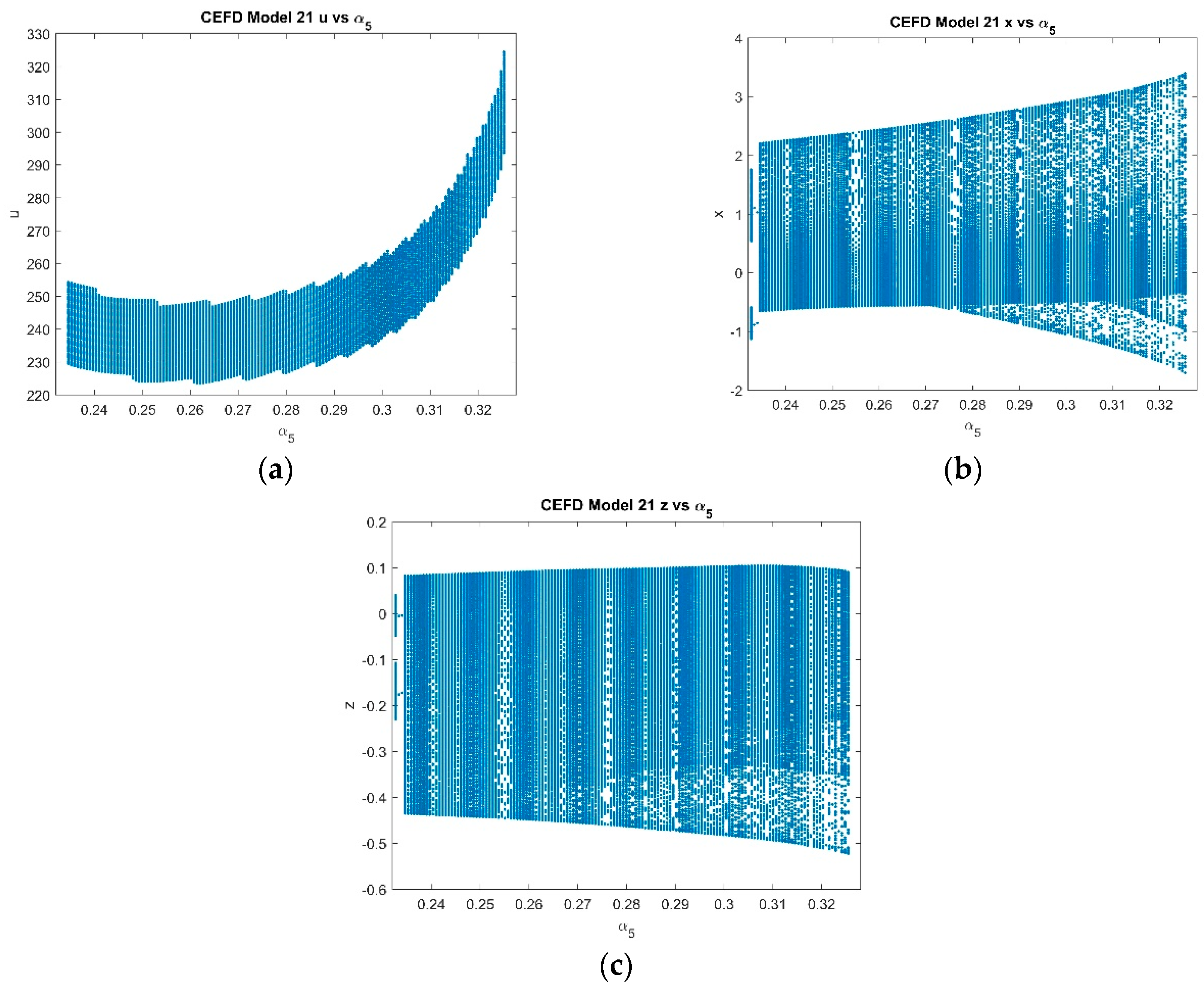
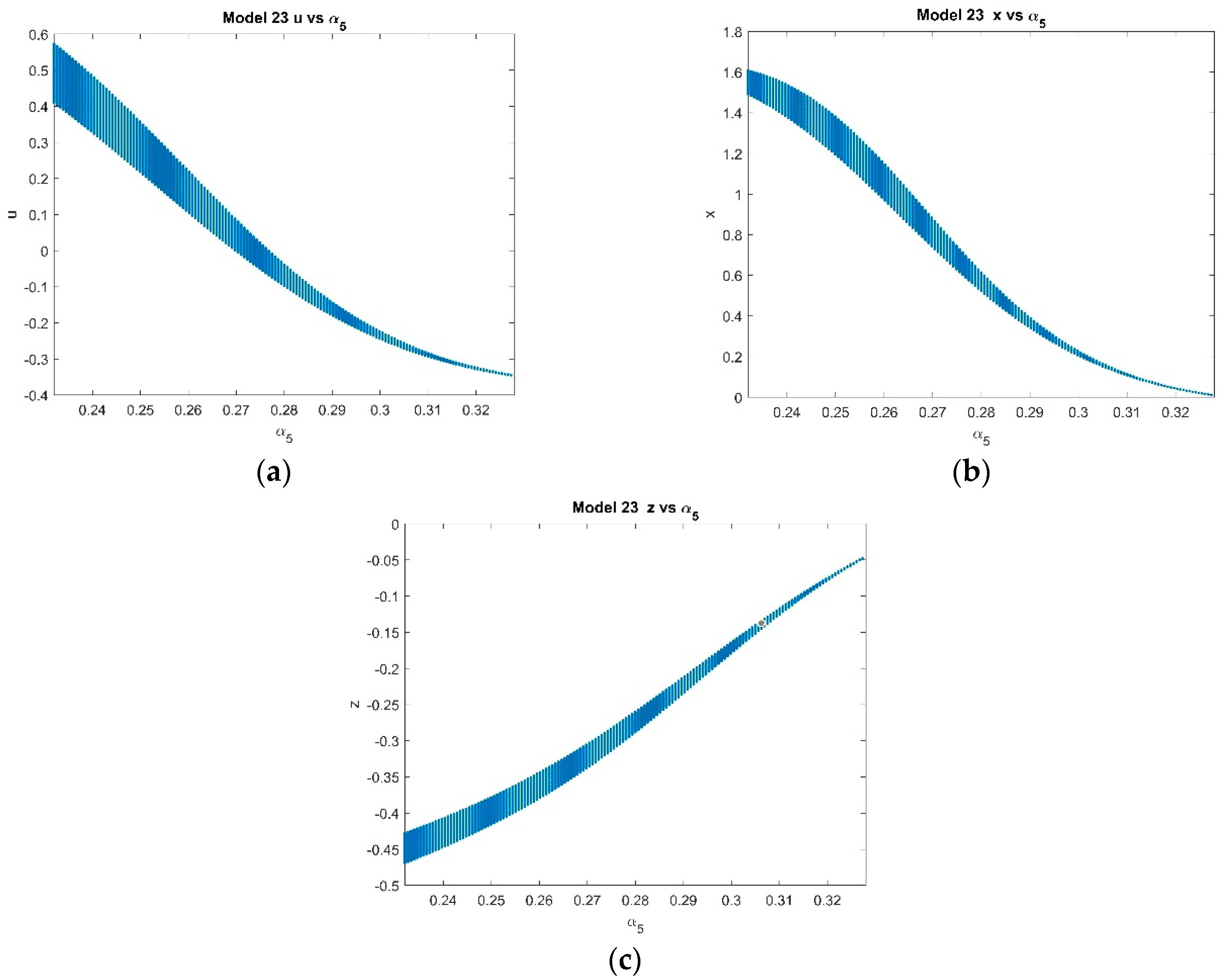
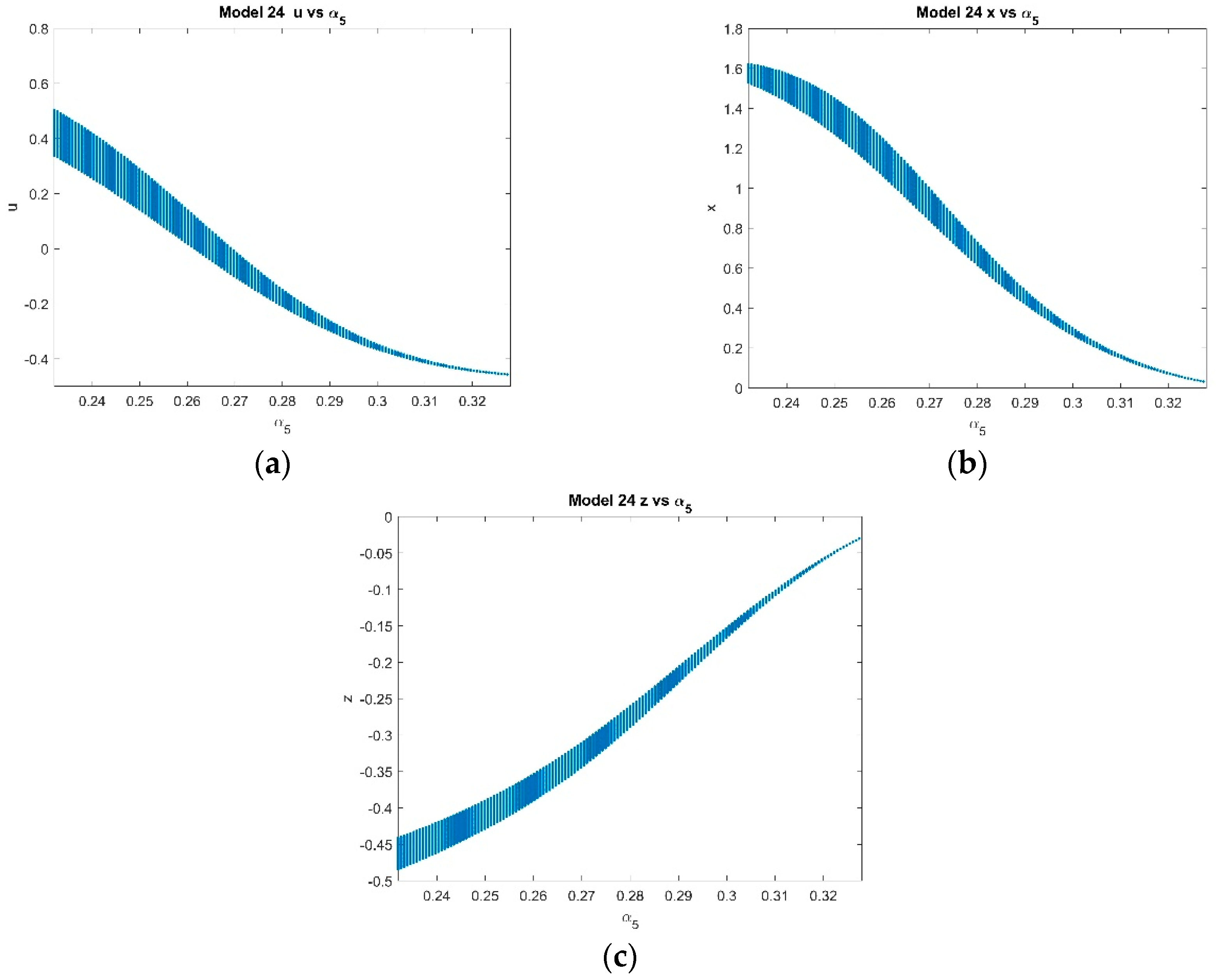
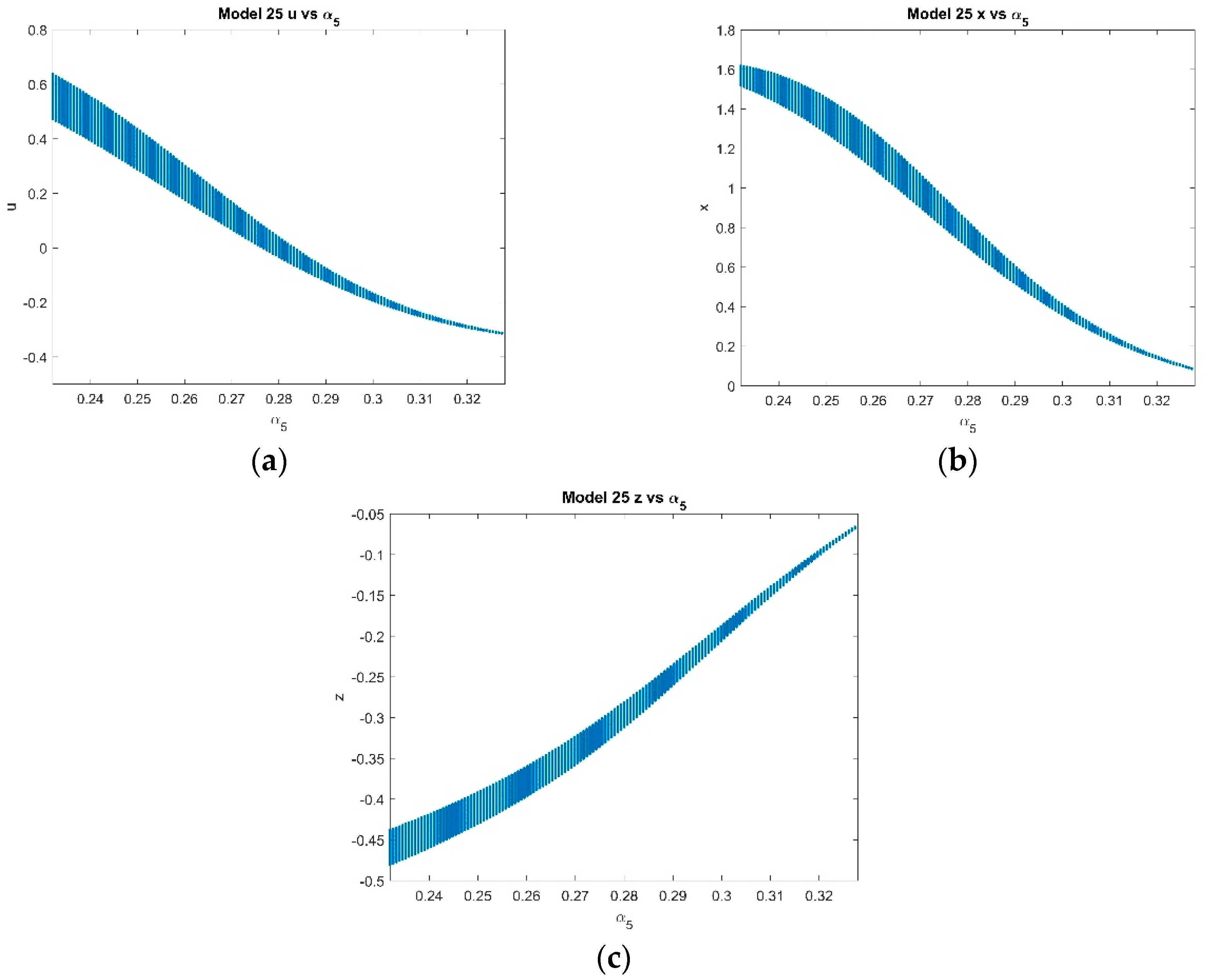
4.2.1. Varying α5 with Fixed k = 2 and p = 1 and α5 ∈ [0.232, 0.328]
4.2.2. Varying p with Fixed and
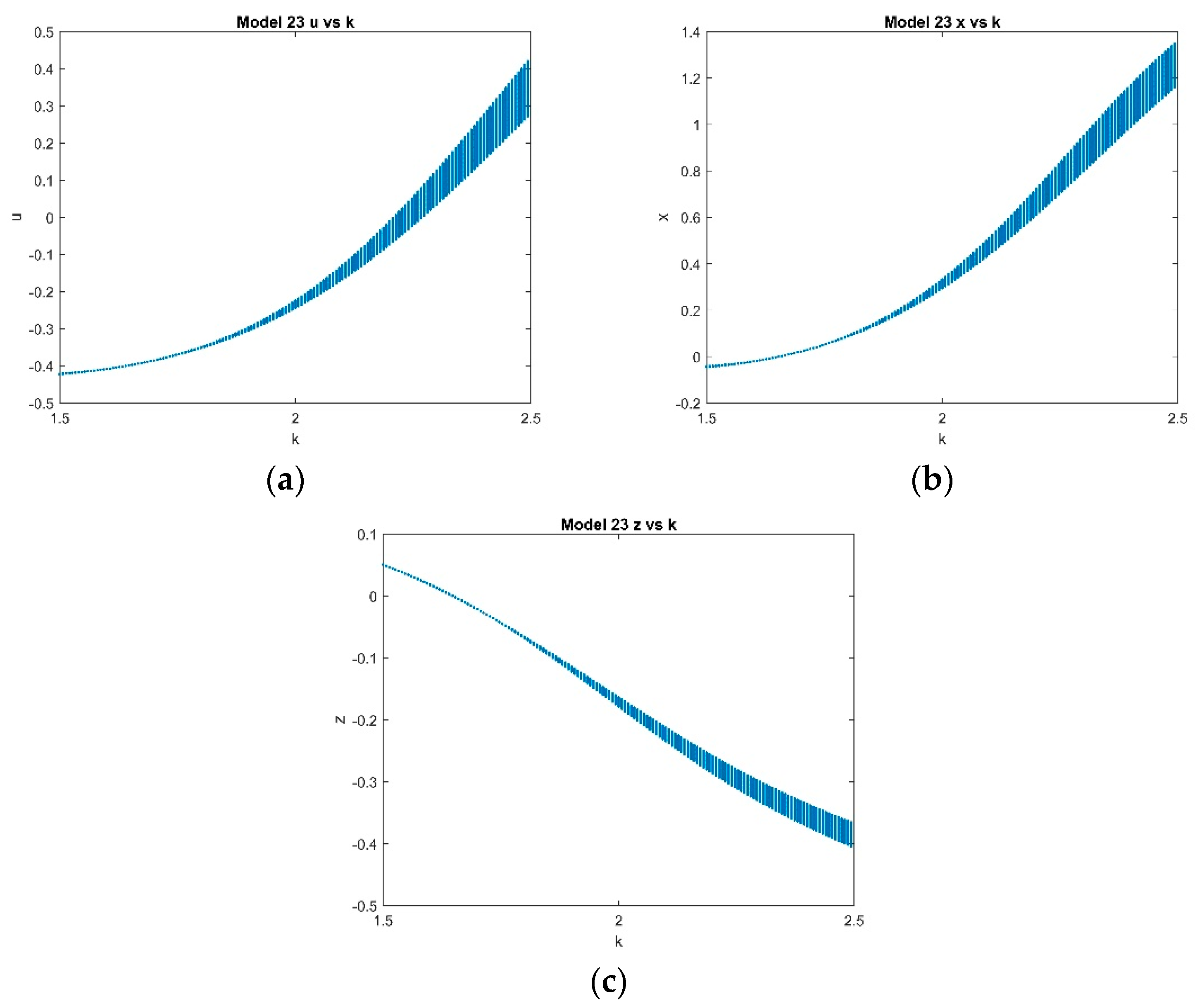
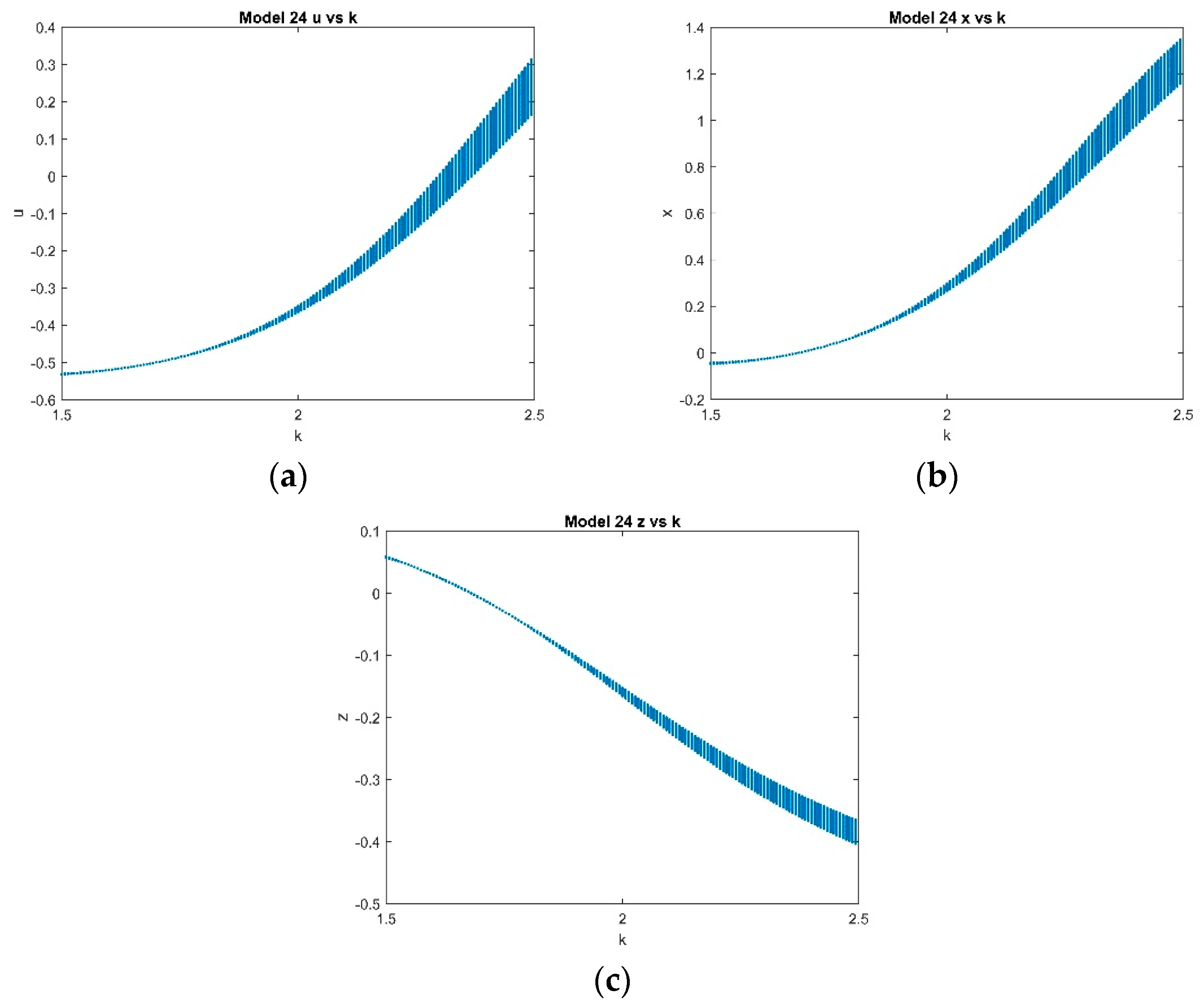
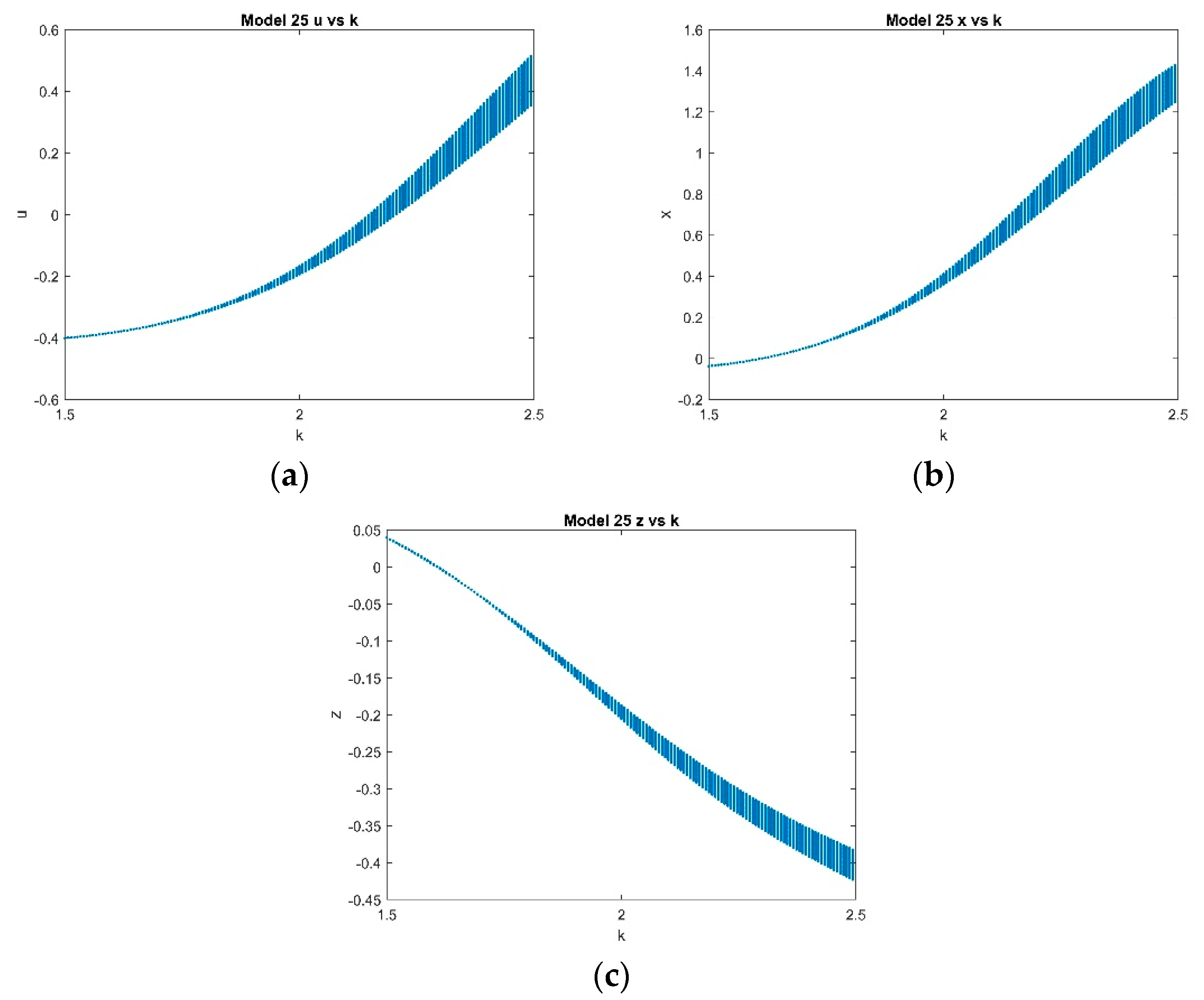
4.2.3. Varying k with Fixed and with k ∈ [1.5, 2.5]
4.2.4. With Fixed k = 2, p = 1 and
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, L.; Sun, K.; He, S.; Wang, H.; Xu, Y. Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings. Eur. Phys. J. Plus 2017, 132, 31. [Google Scholar] [CrossRef]
- Wang, S.; Wu, R. Dynamic analysis of a 5D fractional-order hyperchaotic system. Int. J. Control Autom. Syst. 2017, 15, 1003–1010. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Wei, Z.; Moroz, I. Bifurcation analysis and integrability in the segmented disc dynamo with mechanical friction. Adv. Differ. Equ. 2018, 2018, 210. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Moroz, I.; Sprott, J.C.; Akgul, A.; Zhang, W. Hidden hyperchaos and electronic circuit application in a 5D self-exciting homopolar disc dynamo. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 033101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, Z.; Rajagopal, K.; Zhang, W.; Kingni, S.T.; Akgül, A. Synchronisation, electronic circuit implementation, and fractional-order analysis of 5D ordinary differential equations with hidden hyperchaotic attractors. Pramana 2018, 90, 50. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Chaos and hyperchaos in the fractional-order Rössler equations. Phys. A Stat. Mech. Appl. 2004, 341, 55–61. [Google Scholar] [CrossRef]
- Wang, Y.; He, S.; Wang, H.; Sun, K. Bifurcations and Synchronization of the Fractional-Order Simplified Lorenz Hyperchaotic System. J. Appl. Anal. Comput. 2015, 5, 210–219. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Duraisamy, P. Hyperchaotic Chameleon: Fractional Order FPGA Implementation. Complexity 2017, 2017, 8979408. [Google Scholar] [CrossRef] [Green Version]
- El-Sayed, A.M.A.; Nour, H.M.; Elsaid, A.; Matouk, A.E.; Elsonbaty, A. Dynamical behaviors, circuit realization, chaos control, and synchronization of a new fractional-order hyperchaotic system. Appl. Math. Model. 2016, 40, 3516–3534. [Google Scholar] [CrossRef]
- El-Sayed, A.; Elsonbaty, A.; Elsadany, A.; Matouk, A. Dynamical Analysis and Circuit Simulation of a New Fractional-Order Hyperchaotic System and Its Discretization. Int. J. Bifurc. Chaos 2016, 26, 1650222. [Google Scholar] [CrossRef]
- Mou, J.; Sun, K.; Wang, H.; Ruan, J. Characteristic Analysis of Fractional-Order 4D Hyperchaotic Memristive Circuit. Math. Probl. Eng. 2017, 2017, 2313768. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Zhao, Z.; Wang, Z.; Li, Y. Chaos and hyperchaos in fractional-order cellular neural networks. Neurocomputing 2012, 94, 13–21. [Google Scholar] [CrossRef]
- Xin, B.; Peng, W.; Kwon, Y.; Liu, Y. Modeling, discretization, and hyperchaos detection of conformable derivative approach to a financial system with market confidence and ethics risk. Adv. Differ. Equ. 2019, 2019, 138. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Li, H. Theory and Method of the Nonlinear Economics; Sichuan University Press: Chengdu, China, 1993. [Google Scholar]
- Chen, W.-C. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 2008, 36, 1305–1314. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Shen, H. Control of an uncertain fractional order economic system via adaptive sliding mode. Neurocomputing 2012, 83, 83–88. [Google Scholar] [CrossRef]
- Mircea, G.; Neamţu, M.; Bundău, O.; Opriş, D. Uncertain and Stochastic Financial Models with Multiple Delays. Int. J. Bifurc. Chaos 2012, 22, 1250131. [Google Scholar] [CrossRef]
- Xin, B.; Chen, T.; Ma, J. Neimark–Sacker Bifurcation in a Discrete-Time Financial System. Discret. Dyn. Nat. Soc. 2010, 2010, 405639. [Google Scholar] [CrossRef]
- Yu, H.; Cai, G.; Li, Y. Dynamic analysis and control of a new hyperchaotic finance system. Nonlinear Dyn. 2011, 67, 2171–2182. [Google Scholar] [CrossRef]
- Xin, B.; Li, Y. 0-1 Test for Chaos in a Fractional Order Financial System with Investment Incentive. Abstr. Appl. Anal. 2013, 2013, 876298. [Google Scholar] [CrossRef]
- Xin, B.; Zhang, J. Finite-time stabilizing a fractional-order chaotic financial system with market confidence. Nonlinear Dyn. 2015, 79, 1399–1409. [Google Scholar] [CrossRef]
- Pérez, J.E.S.; Gómez-Aguilar, J.F.; Baleanu, D.; Tchier, F. Chaotic Attractors with Fractional Conformable Derivatives in the Liouville–Caputo Sense and Its Dynamical Behaviors. Entropy 2018, 20, 384. [Google Scholar] [CrossRef] [Green Version]
- Eslami, M.; Rezazadeh, H. The first integral method for Wu–Zhang system with conformable time-fractional derivative. Calcolo 2016, 53, 475–485. [Google Scholar] [CrossRef]
- Ilie, M.; Biazar, J.; Ayati, Z. The first integral method for solving some conformable fractional differential equations. Opt. Quantum Electron. 2018, 50, 55. [Google Scholar] [CrossRef]
- Hosseini, K.; Bekir, A.; Ansari, R. New exact solutions of the conformable time-fractional Cahn–Allen and Cahn–Hilliard equations using the modified Kudryashov method. Optik 2017, 132, 203–209. [Google Scholar] [CrossRef]
- Ünal, E.; Gökdoğan, A. Solution of conformable fractional ordinary differential equations via differential transform method. Optik 2017, 128, 264–273. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Srivastava, H.; Gunerhan, H. Analytical and approximate solutions of fractional-order susceptible-infected-recovered epidemic model of childhood disease. Math. Methods Appl. Sci. 2019, 42, 935–941. [Google Scholar] [CrossRef]
- Kaplan, M. Applications of two reliable methods for solving a nonlinear conformable time-fractional equation. Opt. Quantum Electron. 2017, 49, 312. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 2018, 13, 12. [Google Scholar] [CrossRef] [Green Version]
- Kartal, S.; Gurcan, F. Discretization of conformable fractional differential equations by a piecewise constant approximation. Int. J. Comput. Math. 2018, 96, 1849–1860. [Google Scholar] [CrossRef]
- Iyiola, O.; Tasbozan, O.; Kurt, A.; Cenesiz, Y. On the analytical solutions of the system of conformable time-fractional Robertson equations with 1-D diffusion. Chaos Solitons Fractals 2017, 94, 1–7. [Google Scholar] [CrossRef]
- Ruan, J.; Sun, K.; Mou, J.; He, S.; Zhang, L. Fractional-order simplest memristor-based chaotic circuit with new derivative. Eur. Phys. J. Plus 2018, 133, 3. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Mei, X.; Yan, B.; Xu, S. Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative. Eur. Phys. J. Plus 2017, 132, 36. [Google Scholar] [CrossRef]
- Yokus, A. Comparison of Caputo and conformable derivatives for time-fractional Korteweg-de Vries equation via the finite differencemethod. Int. J. Mod. Phys. B 2018, 32, 1850365. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Ziabarya, B. Sub-equation method for the conformable fractional generalized Kuramoto–Sivashinsky equation. Comput. Res. Prog. App. Sci. Eng. 2016, 2, 106–109. [Google Scholar]
- Zhong, W.; Wang, L. Basic theory of initial value problems of conformable fractional differential equations. Adv. Differ. Equ. 2018, 2018, 321. [Google Scholar] [CrossRef]
- Tayyan, B.A.; Sakka, A.H. Lie symmetry analysis of some conformable fractional partial differential equations. Arab. J. Math. 2018, 9, 201–212. [Google Scholar] [CrossRef] [Green Version]
- Yaslan, H. Numerical solution of the conformable space-time fractional wave equation. Chin. J. Phys. 2018, 56, 2916–2925. [Google Scholar] [CrossRef]
- Kurt, A.; Çenesiz, Y.; Tasbozan, O. On the Solution of Burgers’ Equation with the New Fractional Derivative. Open Phys. 2015, 13, 355–360. [Google Scholar] [CrossRef] [Green Version]
- Khalil, R.; Abu-Shaab, H. Solution of some conformable fractional differential equations. Int. J. Pure Appl. Math. 2015, 103, 667–673. [Google Scholar] [CrossRef] [Green Version]
- Unal, E.; Gokdogan, A.; Celik, E. Solutions of sequential conformable fractional differential equations around an ordinary point and conformable fractional Hermite differential equation. arXiv 2015, arXiv:1503.05407. [Google Scholar]
- Liu, S.; Wang, H.; Li, X.; Li, H. The extremal iteration solution to a coupled system of nonlinear conformable fractional differential equations. J. Nonlinear Sci. Appl. 2017, 10, 5082–5089. [Google Scholar] [CrossRef] [Green Version]
- Çenesiz, Y.; Kurt, A. The solutions of time and space conformable fractional heat equations with conformable Fourier transform. Acta Univ. Sapientiae Math. 2015, 7, 130–140. [Google Scholar] [CrossRef] [Green Version]
- El-Sayed, A.; Salman, S. On a discretization process of fractional-order Riccati differential equation. J. Fract. Calc. Appl. 2013, 4, 251–259. [Google Scholar]
- Agarwal, R.; El-Sayed, A.; Salman, S. Fractional-order Chua’s system: Discretization, bifurcation and chaos. Adv. Differ. Equ. 2013, 1, 320. [Google Scholar] [CrossRef]
- Mohammadnezhad, V.; Eslami, M.; Rezazadeh, H. Stability analysis of linear conformable fractional differential equations system with time delays. Bol. Soc. Parana. Mat. 2020, 38, 159–171. [Google Scholar] [CrossRef]
- Micken, R.E. Nonstandard Finite Difference Schemes: Methodology and Applications; World Scientific Publishing Company: Singapore, 2020. [Google Scholar]
- Garba, S.; Gumel, A.; Lubuma, J. Dynamically-consistent non-standard finite difference method for an epidemic model. Math. Comput. Model. 2011, 53, 131–150. [Google Scholar] [CrossRef]
- Clemence-Mkhope, D.P.; Clemence-Mkhope, B.G.B. The Limited Validity of the Conformable Euler Finite Difference Method and an Alternate Definition of the Conformable Fractional Derivative to Justify Modification of the Method. Math. Comput. Appl. 2021, 26, 66. [Google Scholar] [CrossRef]
- Clemence-Mkhope, D.P. The Exact Spectral Derivative Discretization Finite Difference (ESDDFD) Method for Wave Models. arXiv 2021, arXiv:2106.07609. [Google Scholar]
- Clemence-Mkhope, D.P. Spectral Non-integer Derivative Representations and the Exact Spectral Derivative Discretization Finite Difference Method for the Fokker–Planck Equation. arXiv 2021, arXiv:2106.02586. [Google Scholar]
- Zheng, R.; Jiang, X. Spectral methods for the time-fractional Navier-Stokes equation. Appl. Math. Lett. 2019, 91, 194–200. [Google Scholar] [CrossRef]
- Xu, H.; Jiang, X. Creep constitutive models for viscoelastic materials based on fractional derivatives. Comput. Math. Appl. 2017, 73, 1377–1384. [Google Scholar] [CrossRef]
- Fan, W.; Qi, H. An efficient finite element method for the two-dimensional nonlinear time–space fractional Schrödinger equation on an irregular convex domain. Appl. Math. Lett. 2018, 86, 103–110. [Google Scholar] [CrossRef]
- Yang, X.; Qi, H.; Jiang, X. Numerical analysis for electroosmotic flow of fractional Maxwell fluids. Appl. Math. Lett. 2018, 78, 1–8. [Google Scholar] [CrossRef]
- Gao, X.; Chen, D.; Yan, D.; Xu, B.; Wang, X. Dynamic evolution characteristics of a fractional order hydropower station system. Mod. Phys. Lett. B 2018, 32, 1750363. [Google Scholar] [CrossRef]
- Wang, F.; Chen, D.; Zhang, X.; Wu, Y. Finite-time stability of a class of nonlinear fractional-order system with the discrete time delay. Int. J. Syst. Sci. 2017, 48, 984–993. [Google Scholar] [CrossRef]
- Wu, G.-C.; Baleanu, D.; Huang, L.-L. Novel Mittag–Leffler stability of linear fractional delay difference equations with impulse. Appl. Math. Lett. 2018, 82, 71–78. [Google Scholar] [CrossRef]
- Wu, G.-C.; Baleanu, D.; Luo, W.-H. Analysis of fractional non-linear diffusion behaviors based on Adomian polynomials. Therm. Sci. 2017, 21, 813–817. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Al-Mdallal, Q.; Jarad, F. Fractional logistic models in the frame of fractional operators generated by conformable derivatives. Chaos Solitons Fractals 2019, 119, 94–101. [Google Scholar] [CrossRef]
- Imbert Alberto, F. Contributions to Conformable and Non-Conformable Calculus. Ph.D. Thesis, Universidad Carlos III de Madrid, Madrid, Spain, 2019. Available online: https://www.researchgate.net/publication/342654962_Contributions_to_Conformable_and_non-Conformable_Calculus (accessed on 28 May 2021).
- Acan, O.; Firat, O.; Keskin, Y. Conformable variational iteration method, conformable fractional reduced differential transform method and conformable homotopy analysis method for non-linear fractional partial differential equations. Waves Random Complex Media 2018, 8, 1–19. [Google Scholar] [CrossRef]
- Attia, R.A.M.; Lu, D.; Khater, M.M.A. Chaos and Relativistic Energy-Momentum of the Nonlinear Time Fractional Duffing Equation. Math. Comput. Appl. 2019, 24, 10. [Google Scholar] [CrossRef] [Green Version]
- Bohner, M.; Hatipoğlu, V.F. Dynamic cobweb models with conformable fractional derivatives. Nonlinear Anal. Hybrid Syst. 2018, 32, 157–167. [Google Scholar] [CrossRef]
- Tarasov, V. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Rosales, J.; Godínez, F.; Banda, V.; Valencia, G. Analysis of the Drude model in view of the conformable derivative. Optik 2018, 178, 1010–1015. [Google Scholar] [CrossRef]
- Akbulut, A.; Melike, K. Auxiliary equation method for time-fractional differential equations with conformable derivative. Comput. Math. Appl. 2018, 75, 876–882. [Google Scholar] [CrossRef]
- Martínez, L.; Rosales, J.; Carreño, C.; Lozano, J. Electrical circuits described by fractional conformable derivative. Int. J. Circuit Theory Appl. 2018, 46, 1091–1100. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Khodadad, F.; Manafian, J. New structure for exact solutions of nonlinear time fractional Sharma–Tasso–Olver equation via conformable fractional derivative. Appl. Appl. Math. 2017, 12, 13–21. [Google Scholar]
- Korkmaz, A. Explicit exact solutions to some one-dimensional conformable time fractional equations. Waves Random Complex Media 2017, 29, 124–137. [Google Scholar] [CrossRef]
- He, S.; Banerjee, S.; Yan, B. Chaos and Symbol Complexity in a Conformable Fractional-Order Memcapacitor System. Complexity 2018, 2018, 4140762. [Google Scholar] [CrossRef]
- Xin, B.; Chen, T.; Liu, Y. Synchronization of chaotic fractional-order WINDMI systems via linear state error feedback control. Math. Probl. Eng. 2010, 2010, 859685. [Google Scholar] [CrossRef] [Green Version]
- Yavuz, M.; Özdemir, N. European Vanilla Option Pricing Model of Fractional Order without Singular Kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef] [Green Version]
- Baskonus, H.M.; Mekkaoui, T.; Hammouch, Z.; Bulut, H. Active Control of a Chaotic Fractional Order Economic System. Entropy 2015, 17, 5771–5783. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Ren, W. Complexity and Hopf Bifurcation Analysis on a Kind of Fractional-Order IS-LM Macroeconomic System. Int. J. Bifurc. Chaos 2016, 26, 1650181. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wang, N.; Zhang, J.; Guo, F. Controlling and synchronizing a fractional-order chaotic system using stability theory of a time-varying fractional-order system. PLoS ONE 2018, 13, e0194112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xin, B.; Chen, T.; Liu, Y. Projective synchronization of chaotic fractional-order energy resources demand–supply systems via linear control. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4479–4486. [Google Scholar] [CrossRef]
- Almeida, R.; Malinowska, A.B.; Monteiro, T. Fractional differential equations with a Caputo derivative with respect to a Kernel function and their applications. Math. Methods Appl. Sci. 2017, 41, 336–352. [Google Scholar] [CrossRef] [Green Version]
- Anderson, D.R.; Camrud, E.; Ulness, D.J. On the nature of the conformable derivative and its applications to physics. J. Fract. Calc. Appl. 2019, 10, 92–135. [Google Scholar]
- Mainardi, F. A Note on the Equivalence of Fractional Relaxation Equations to Differential Equations with Varying Coefficients. Mathematics 2018, 6, 8. [Google Scholar] [CrossRef] [Green Version]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clemence-Mkhope, D.P.; Gibson, G.A. Taming Hyperchaos with Exact Spectral Derivative Discretization Finite Difference Discretization of a Conformable Fractional Derivative Financial System with Market Confidence and Ethics Risk. Math. Comput. Appl. 2022, 27, 4. https://doi.org/10.3390/mca27010004
Clemence-Mkhope DP, Gibson GA. Taming Hyperchaos with Exact Spectral Derivative Discretization Finite Difference Discretization of a Conformable Fractional Derivative Financial System with Market Confidence and Ethics Risk. Mathematical and Computational Applications. 2022; 27(1):4. https://doi.org/10.3390/mca27010004
Chicago/Turabian StyleClemence-Mkhope, Dominic P., and Gregory A. Gibson. 2022. "Taming Hyperchaos with Exact Spectral Derivative Discretization Finite Difference Discretization of a Conformable Fractional Derivative Financial System with Market Confidence and Ethics Risk" Mathematical and Computational Applications 27, no. 1: 4. https://doi.org/10.3390/mca27010004
APA StyleClemence-Mkhope, D. P., & Gibson, G. A. (2022). Taming Hyperchaos with Exact Spectral Derivative Discretization Finite Difference Discretization of a Conformable Fractional Derivative Financial System with Market Confidence and Ethics Risk. Mathematical and Computational Applications, 27(1), 4. https://doi.org/10.3390/mca27010004





