Multi-Physics Inverse Homogenization for the Design of Innovative Cellular Materials: Application to Thermo-Elastic Problems
Abstract
:1. Introduction
2. Methods
2.1. Inverse Homogenization
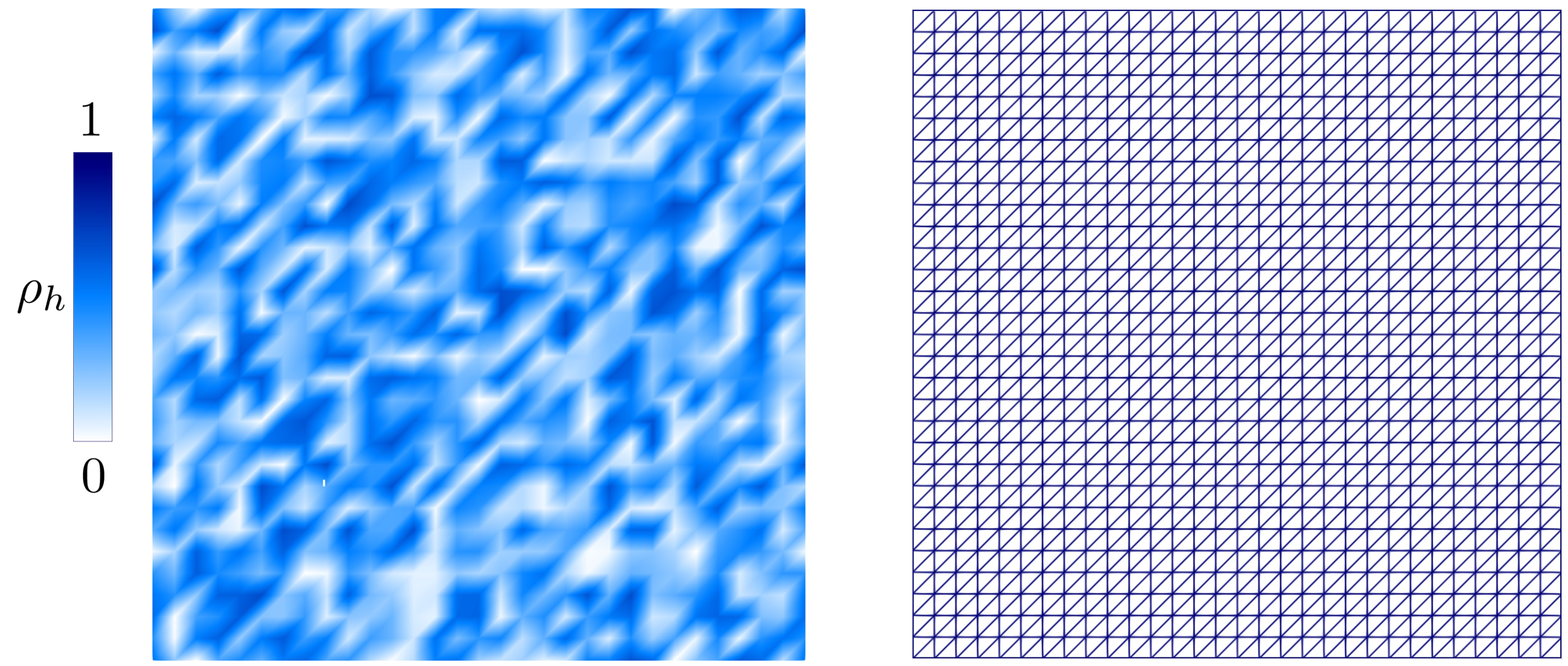
2.2. Discretization on Anisotropic Adapted Meshes
2.3. Multi-Physics Optimization Algorithm
| Algorithm 1 MultiP-microSIMPATY |
|
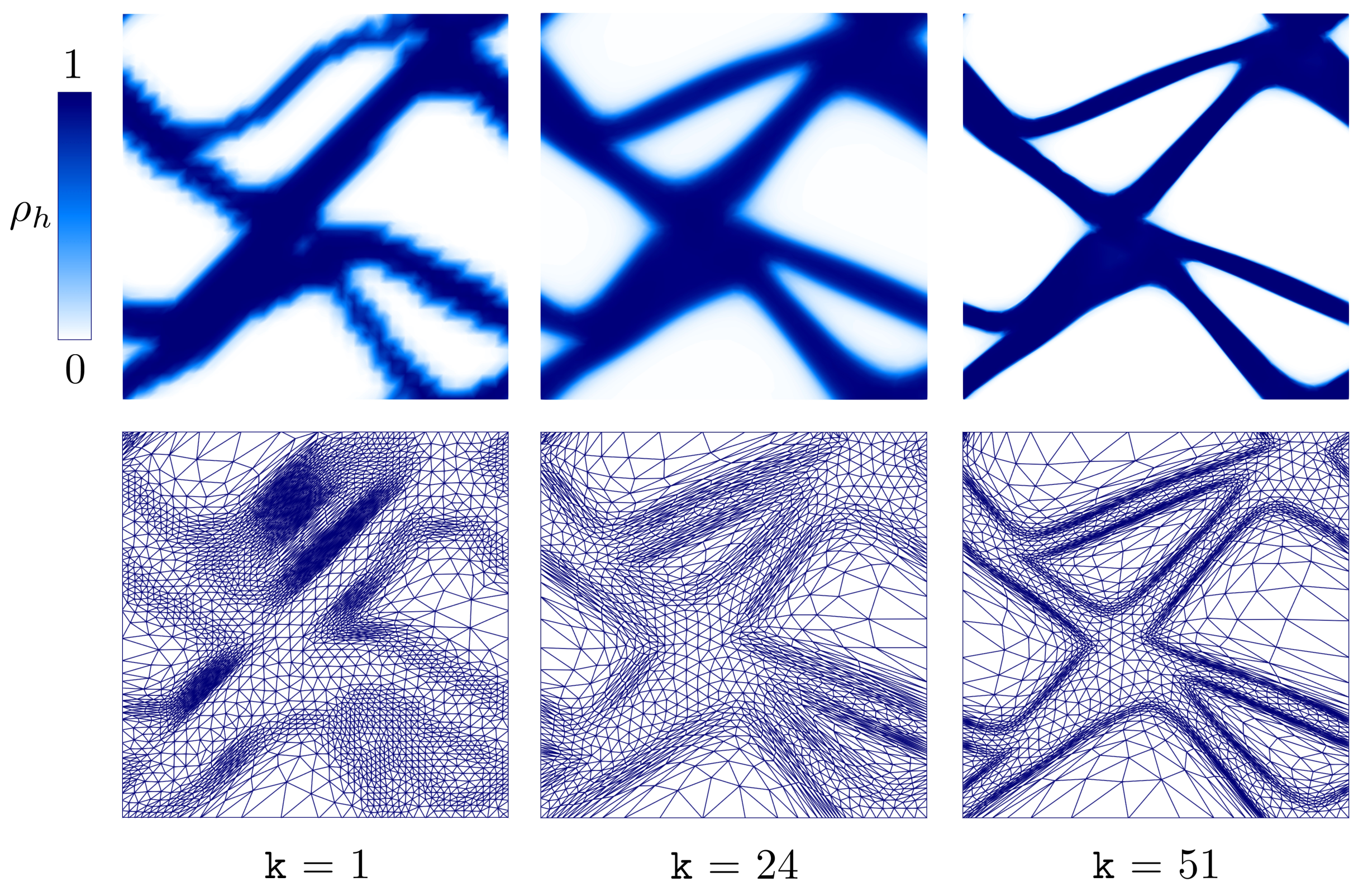
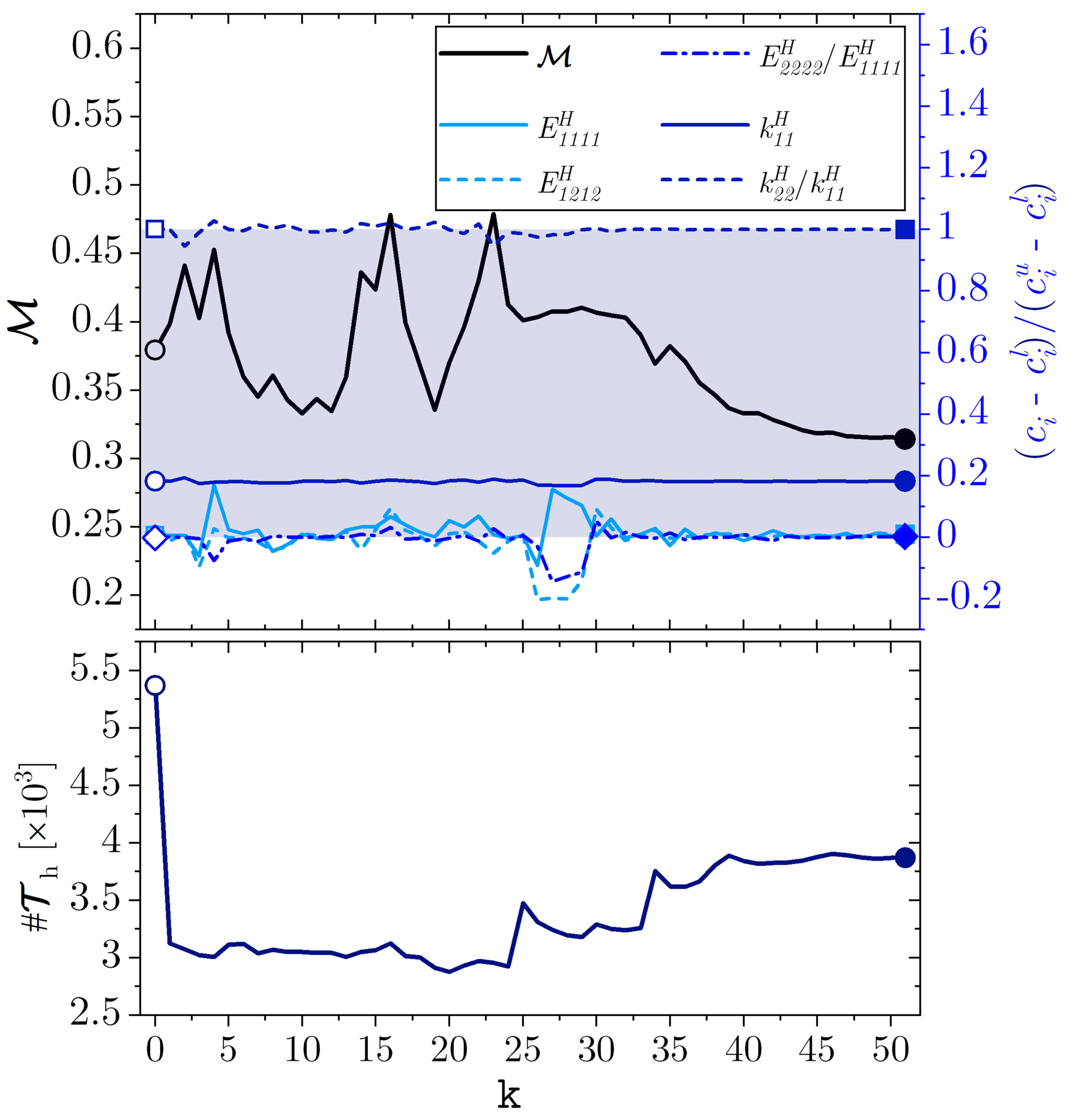
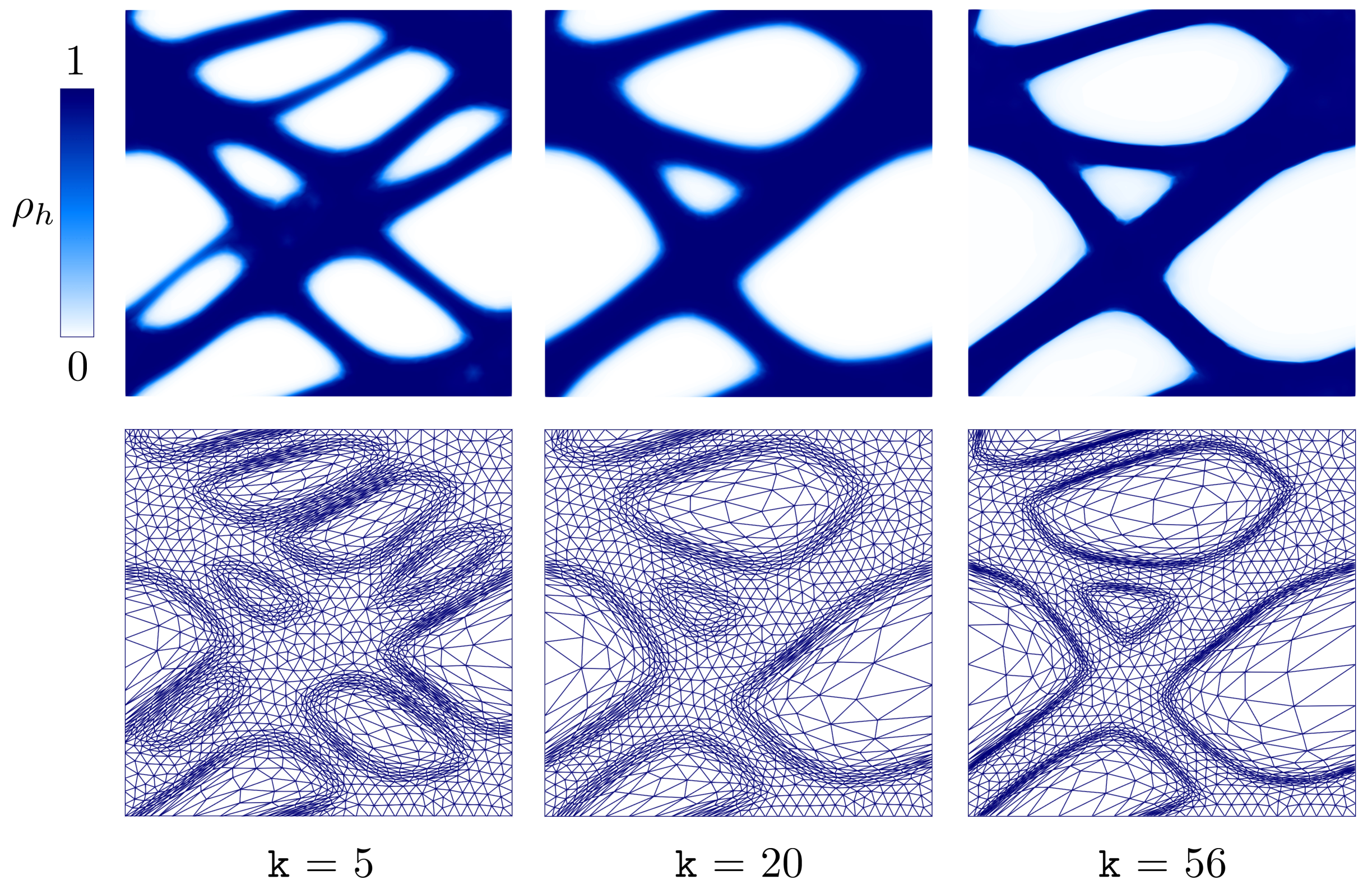
3. Results
3.1. Design Case 1
3.2. Design Case 2
3.3. Design Case 3
4. Discussion of Results
4.1. Comparison with Off-The-Shelf Designs
4.2. Comparison with Standard Inverse Homogenization
5. Conclusions and Perspectives
- (i)
- The MultiP-microSIMPATY algorithm provides original design solutions, complying also with conflicting requirements;
- (ii)
- The good performance of microSIMPATY has been confirmed also in a thermo-elastic context. Standard issues typical of topology optimization, such as the presence of intermediate densities, of jagged boundaries, and of too complex structures, is mitigated by the employment of a mesh customized to the design process (see Figure 7 and Table 3);
- (iii)
- The new cellular materials have been successfully compared with consolidated solutions in terms of mechanical and thermal properties (see Table 2);
- (iv)
- Filtering can be considerably limited thanks to the use of mesh adaptation. This turns into an improvement in terms of accuracy of the optimization process (see Figure 8);
- (v)
- The employment of an anisotropic mesh adaptation provides advantages with a view to a manufacturing phase. Indeed, the unit cells designed by MultiP-microSIMPATY exhibit very smooth geometries which demand for a very limited post-processing;
- (vi)
- The procedure here settled turns out to be fully general with respect to the selected multi-physics context.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Rashed, M.G.; Ashraf, M.; Mines, R.A.; Hazell, P.J. Metallic microlattice materials: A current state of the art on manufacturing, mechanical properties and applications. Mater. Des. 2016, 95, 518–533. [Google Scholar] [CrossRef]
- Bauer, J.; Hengsbach, S.; Tesari, I.; Schwaiger, R.; Kraft, O. High-strength cellular ceramic composites with 3D microarchitecture. Proc. Natl. Acad. Sci. USA 2014, 111, 2453–2458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schaedler, T.A.; Carter, W.B. Architected Cellular Materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Campoli, G.; Amin Yavari, S.; Sajadi, B.; Wauthle, R.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Mechanical behavior of regular open-cell porous biomaterials made of diamond lattice unit cells. J. Mech. Behav. Biomed. Mater. 2014, 34, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Hao, L.; Hussein, A.; Young, P. Ti-6Al-4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J. Mech. Behav. Biomed. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef] [Green Version]
- Taniguchi, N.; Fujibayashi, S.; Takemoto, M.; Sasaki, K.; Otsuki, B.; Nakamura, T.; Matsushita, T.; Kokubo, T.; Matsuda, S. Effect of pore size on bone ingrowth into porous titanium implants fabricated by additive manufacturing: An in vivo experiment. Mater. Sci. Eng. C 2016, 59, 690–701. [Google Scholar] [CrossRef] [Green Version]
- Arabnejad, S.; Burnett Johnston, R.; Pura, J.A.; Singh, B.; Tanzer, M.; Pasini, D. High-strength porous biomaterials for bone replacement: A strategy to assess the interplay between cell morphology, mechanical properties, bone ingrowth and manufacturing constraints. Acta Biomater. 2016, 30, 345–356. [Google Scholar] [CrossRef] [Green Version]
- Bandaru, P.R.; Vemuri, K.P.; Canbazoglu, F.M.; Kapadia, R.S. Layered thermal metamaterials for the directing and harvesting of conductive heat. AIP Adv. 2015, 5, 053403. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.P.; Chen, P.J.; Huang, H.H. Realization of a thermal cloak-concentrator using a metamaterial transformer. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Attarzadeh, R.; Rovira, M.; Duwig, C. Design analysis of the “Schwartz D” based heat exchanger: A numerical study. Int. J. Heat Mass Transf. 2021, 177, 121415. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, P. State-of-the-art in heat exchanger additive manufacturing. Int. J. Heat Mass Transf. 2021, 178, 121600. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Sigmund, O. Materials with prescribed constitutive parameters: An inverse homogenization problem. Int. J. Solids Struct. 1994, 31, 2313–2329. [Google Scholar] [CrossRef]
- Andreassen, E.; Andreasen, C.S. How to determine composite material properties using numerical homogenization. Comp. Mater. Sci. 2014, 83, 488–495. [Google Scholar] [CrossRef] [Green Version]
- Allaire, G.; Geoffroy-Donders, P.; Pantz, O. Topology optimization of modulated and oriented periodic microstructures by the homogenization method. Comput. Math. Appl. 2019, 78, 2197–2229. [Google Scholar] [CrossRef] [Green Version]
- Vigliotti, A.; Pasini, D. Mechanical properties of hierarchical lattices. Mech. Mat. 2013, 62, 32–43. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Xu, H.; Pasini, D. Multiscale isogeometric topology optimization for lattice materials. Comput. Methods. Appl. Mech. Eng. 2017, 316, 568–585. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Liu, J.; Liang, X.; To, A.C. Coupling lattice structure topology optimization with design-dependent feature evolution for additive manufactured heat conduction design. Comput. Methods Appl. Mech. Eng. 2018, 332, 408–439. [Google Scholar] [CrossRef]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for Additive Manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Moussa, A.; Rahman, S.; Xu, M.; Tanzer, M.; Pasini, D. Topology optimization of 3D-printed structurally porous cage for acetabular reinforcement in total hip arthroplasty. J. Mech. Behav. Biomed. Mater. 2020, 105, 103705. [Google Scholar] [CrossRef]
- Coelho, P.G.; Fernandes, P.R.; Guedes, J.M.; Rodrigues, H.C. A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct. Multidiscip. Optim. 2008, 35, 107–115. [Google Scholar] [CrossRef]
- Nakshatrala, P.B.; Tortorelli, D.A.; Nakshatrala, K.B. Nonlinear structural design using multiscale topology optimization. Part I: Static formulation. Comput. Methods Appl. Mech. Eng. 2013, 261/262, 167–176. [Google Scholar] [CrossRef]
- Djourachkovitch, T.; Blal, N.; Hamila, N.; Gravouil, A. Multiscale topology optimization of 3D structures: A micro-architectured materials database assisted strategy. Comput. Struct. 2021, 255, 106574. [Google Scholar] [CrossRef]
- Ferrer, A.; Oliver, J.; Cante, J.C.; Lloberas-Valls, O. Vademecum-based approach to multi-scale topological material design. Adv. Model. Simul. Eng. Sci. 2016, 3, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferro, N.; Micheletti, S.; Perotto, S. Density-Based Inverse Homogenization with Anisotropically Adapted Elements. Lect. Notes Comput. Sci. Eng. 2020, 132, 211–221. [Google Scholar]
- di Cristofaro, D.; Galimberti, C.; Bianchi, D.; Ferrante, R.; Ferro, N.; Mannisi, M.; Perotto, S. Adaptive topology optimization for innovative 3D printed metamaterials. In Proceedings of the WCCM—ECCOMAS 2020 Conference, Volume 1200-Modeling and Analysis of Real World and Industry Applications, Online, 11–15 January 2021. [Google Scholar]
- Auricchio, F.; Bonetti, E.; Carraturo, M.; Hömberg, D.; Reali, A.; Rocca, E. A phase-field-based graded-material topology optimization with stress constraint. Math. Model. Methods Appl. Sci. 2020, 30, 1461–1483. [Google Scholar] [CrossRef]
- Huang, X.; Radman, A.; Xie, Y.M. Topological design of microstructures of cellular materials for maximum bulk or shear modulus. Comput. Mater. Sci. 2011, 50, 1861–1870. [Google Scholar] [CrossRef]
- Xia, L.; Breitkopf, P. Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Comput. Methods Appl. Mech. Eng. 2014, 278, 524–542. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Zhang, N.; Kang, Z. Topological shape optimization of microstructural metamaterials using a level set method. Comput. Mater. Sci. 2014, 87, 178–186. [Google Scholar] [CrossRef]
- Torquato, S.; Hyun, S.; Donev, A. Optimal design of manufacturable three-dimensional composites with multifunctional characteristics. J. Appl. Phys. 2003, 94, 5748–5755. [Google Scholar] [CrossRef] [Green Version]
- de Kruijf, N.; Zhou, S.; Li, Q.; Mai, Y.W. Topological design of structures and composite materials with multiobjectives. Int. J. Solids Struct. 2007, 44, 7092–7109. [Google Scholar] [CrossRef]
- Challis, V.J.; Roberts, A.P.; Wilkins, A.H. Design of three dimensional isotropic microstructures for maximized stiffness and conductivity. Int. J. Solids Struct. 2008, 45, 4130–4146. [Google Scholar] [CrossRef] [Green Version]
- Vineyard, E.; Gao, X.L. Topology and shape optimization of 2-d and 3-d micro-architectured thermoelastic metamaterials using a parametric level setmethod. CMES-Comput. Model. Eng. Sci. 2021, 127, 819–854. [Google Scholar]
- Sigmund, O.; Petersson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Micheletti, S.; Perotto, S.; Soli, L. Topology optimization driven by anisotropic mesh adaptation: Towards a free-form design. Comput. Struct. 2019, 214, 60–72. [Google Scholar] [CrossRef]
- Ferro, N.; Perotto, S.; Bianchi, D.; Ferrante, R.; Mannisi, M. Design of cellular materials for multiscale topology optimization: Application to patient-specific orthopedic devices. Struct. Multidiscip. Optim. 2021, 28, 2021. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology optimization I—homogenization theory for media with periodic structure. Comput. Struct. 1998, 69, 707–717. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology opimization II—analytical and numerical solution of homogenization equations. Comput. Struct. 1998, 69, 719–738. [Google Scholar] [CrossRef]
- Terada, K.; Hori, M.; Kyoya, T.; Kikuchi, N. Simulation of the multi-scale convergence in computational homogenization approaches. Int. J. Solids Struct. 2000, 37, 2285–2311. [Google Scholar] [CrossRef]
- Gould, P.L. Introduction to Linear Elasticity; Springer: New York, NY, USA, 1994. [Google Scholar]
- Noël, L.; Duysinx, P. Shape optimization of microstructural designs subject to local stress constraints within an XFEM-level set framework. Struct. Multidiscip. Optim. 2017, 55, 2323–2338. [Google Scholar] [CrossRef]
- Ern, A.; Guermond, J.L. Theory and Practice of Finite Elements; Springer: New York, NY, USA, 2004. [Google Scholar]
- Formaggia, L.; Perotto, S. New anisotropic a priori error estimates. Numer. Math. 2001, 89, 641–667. [Google Scholar] [CrossRef]
- Ainsworth, M.; Oden, J.T. A Posteriori Error Estimation in Finite Element Analysis; John Wiley & Son: New York, NY, USA, 2000. [Google Scholar]
- Bangerth, W.; Rannacher, R. Adaptive Finite Element Methods for Differential Equations; Birkhäuser Verlag: Basel, Germany, 2003. [Google Scholar]
- Zienkiewicz, O.C.; Zhu, J.Z. A simple error estimator and adaptive procedure for practical engineerng analysis. Int. J. Numer. Methods Eng. 1987, 24, 337–357. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Zhu, J.Z. The superconvergent patch recovery and a posteriori error estimates. I: The recovery technique. Int. J. Numer. Meth. Eng. 1992, 33, 1331–1364. [Google Scholar] [CrossRef]
- Rodríguez, R. Some remarks on Zienkiewicz-Zhu estimator. Numer. Methods Partial. Differ. Equations 1994, 10, 625–635. [Google Scholar] [CrossRef]
- Maisano, G.; Micheletti, S.; Perotto, S.; Bottasso, C.L. On some new recovery-based a posteriori error estimators. Comput. Methods Appl. Mech. Eng. 2006, 195, 4794–4815. [Google Scholar] [CrossRef]
- Li, X.D.; Wiberg, N.E. A posteriori error estimate by element patch post-processing, adaptive analysis in energy and L2 norms. Comput. Struct. 1994, 53, 907–919. [Google Scholar] [CrossRef]
- Micheletti, S.; Perotto, S. Anisotropic adaptation via a Zienkiewicz-Zhu error estimator for 2D elliptic problems. In Numerical Mathematics and Advanced Applications; Kreiss, G., Lötstedt, P., Målqvist, A., Neytcheva, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 645–653. [Google Scholar]
- Farrell, P.E.; Micheletti, S.; Perotto, S. An anisotropic Zienkiewicz-Zhu-type error estimator for 3D applications. Int. J. Numer. Meth. Eng. 2011, 85, 671–692. [Google Scholar] [CrossRef]
- Micheletti, S.; Perotto, S. Reliability and efficiency of an anisotropic Zienkiewicz-Zhu error estimator. Comput. Methods Appl. Mech. Eng. 2006, 195, 799–835. [Google Scholar] [CrossRef]
- Ferro, N.; Micheletti, S.; Perotto, S. Compliance-stress constrained mass minimization for topology optimization on anisotropic meshes. SN Appl. Sci. 2020, 2, 1–11. [Google Scholar] [CrossRef]
- Ferro, N.; Micheletti, S.; Perotto, S. An optimization algorithm for automatic structural design. Comput. Methods Appl. Mech. Eng. 2020, 372, 113335. [Google Scholar] [CrossRef]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]
- Wächter, A.; Lorenz, T. Biegler. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes-a new method for structural optimization. Int. J. Numer. Meth. Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Lazarov, B.S.; Sigmund, O. Filters in topology optimization based on Helmholtz-type differential equations. Int. J. Numer. Meth. Eng. 2011, 86, 765–781. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef] [Green Version]
- Caicedo, M.; Mroginski, J.L.; Toro, S.; Raschi, M.; Huespe, A.; Oliver, J. High performance reduced order modeling techniques based on optimal energy quadrature: Application to geometrically non-linear multiscale inelastic material modeling. Arch. Comput. Methods Eng. 2019, 26, 771–792. [Google Scholar] [CrossRef]
- Ferro, N.; Micheletti, S.; Perotto, S. POD-assisted strategies for structural topology optimization. Comput. Math. Appl. 2019, 77, 2804–2820. [Google Scholar] [CrossRef]
- Chi, H.; Zhang, Y.; Tang, T.L.E.; Mirabella, L.; Dalloro, L.; Song, L.; Paulino, G.H. Universal machine learning for topology optimization. Comput. Methods. Appl. Mech. Eng. 2021, 375, 112739. [Google Scholar] [CrossRef]

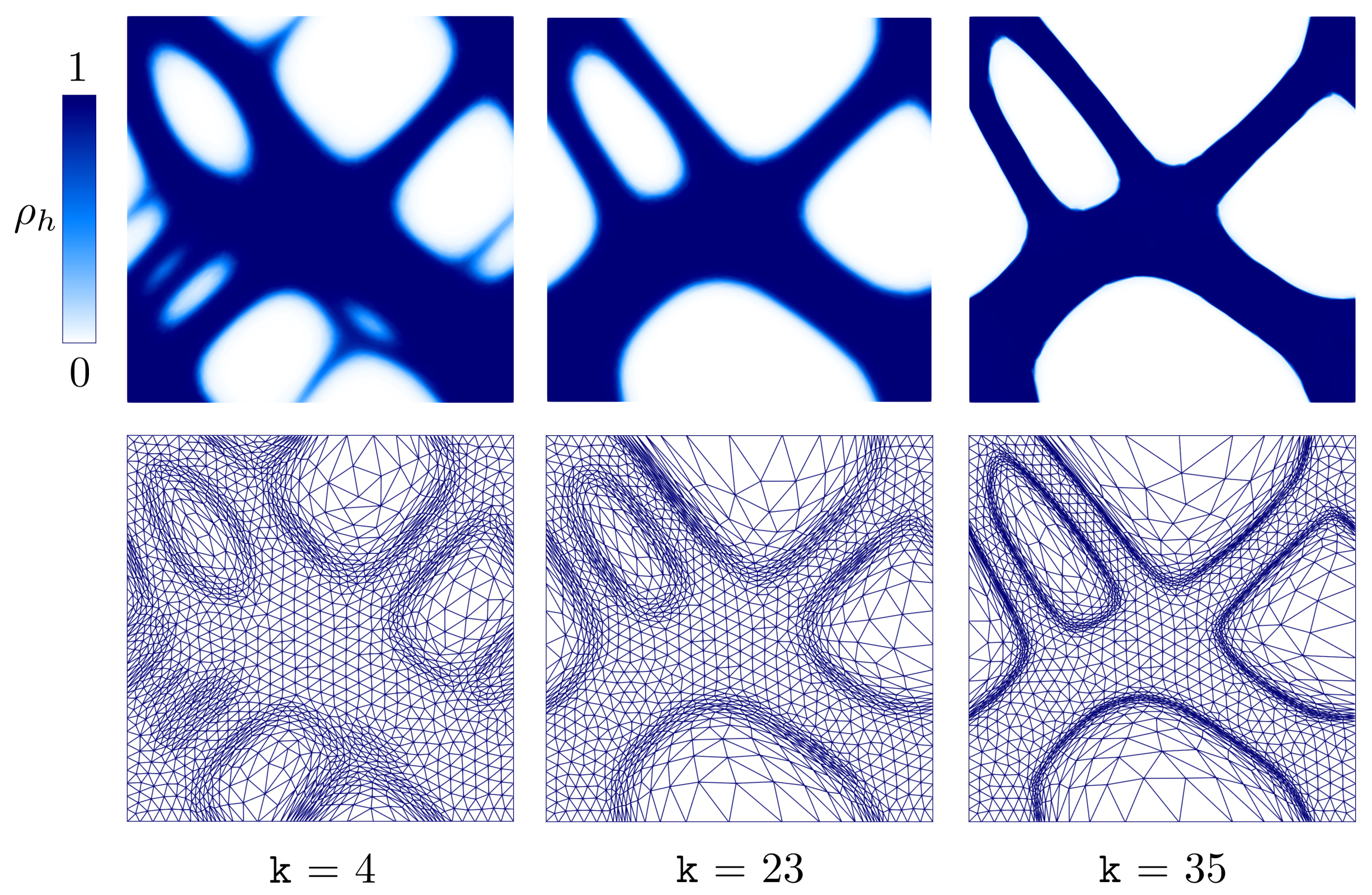

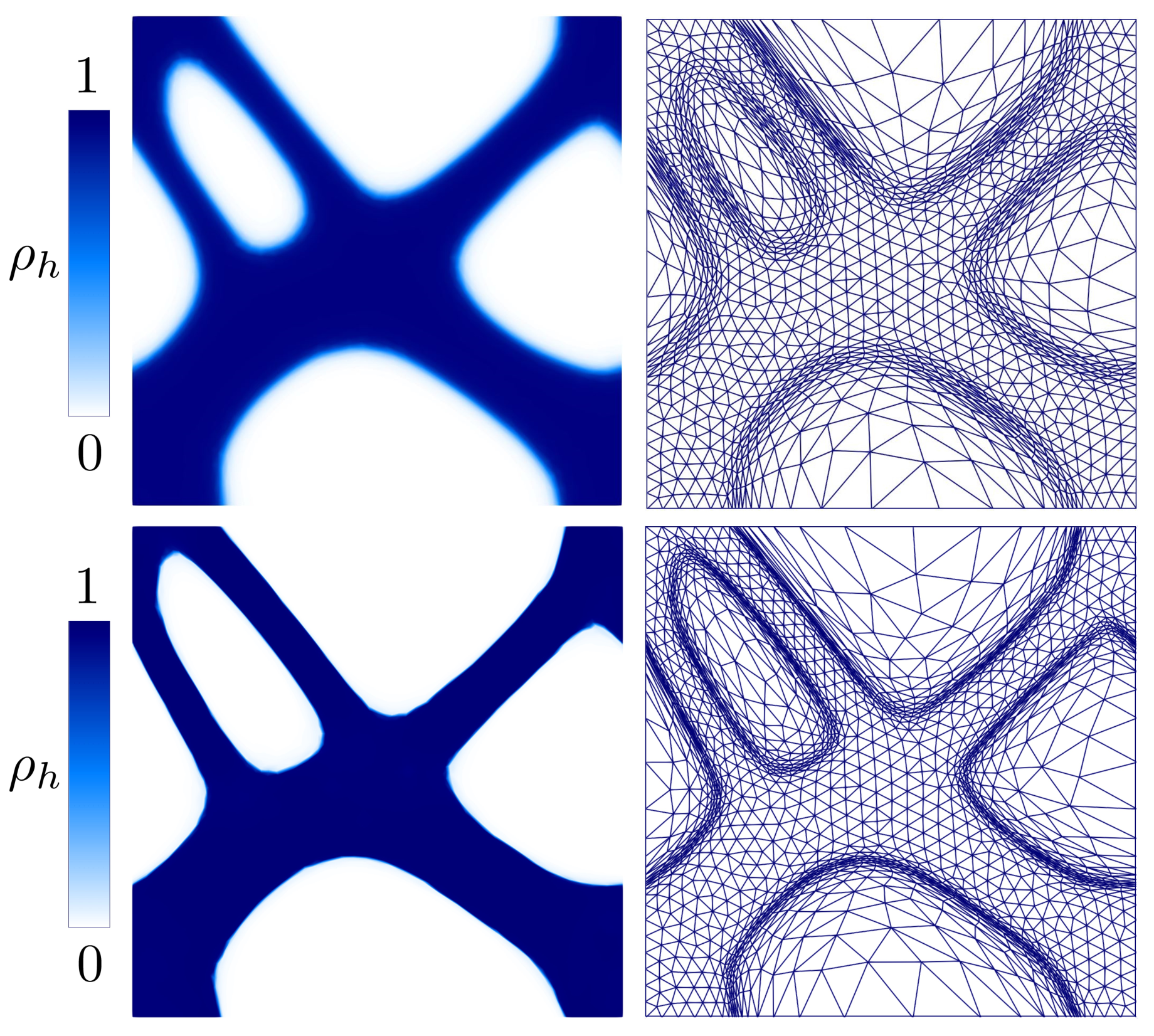
| Design Case 1 | ||||||
| 0.080 | 0.080 | 2.000 | 1.000 | 0.580 | ||
| c | 0.038 | 0.056 | 1.299 | 0.199 | 0.566 | |
| 0.050 | 0.055 | 1.000 | 0.010 | 0.000 | 0.292 | |
| Design Case 2 | ||||||
| 0.350 | 0.150 | 2.000 | 1.000 | 2.000 | ||
| c | 0.250 | 0.086 | 0.299 | 0.317 | 0.597 | |
| 0.230 | 0.080 | 0.300 | 0.300 | 0.000 | 0.412 | |
| Design Case 3 | ||||||
| 0.150 | 0.100 | 1.100 | 0.400 | 1.100 | ||
| c | 0.151 | 0.083 | 1.074 | 0.260 | 1.002 | |
| 0.100 | 0.080 | 1.000 | 0.250 | 1.000 | 0.415 |
| Design Case 1 | ||||||
| D1 |  | 0.012 | 0.015 | 0.056 | 0.200 | 0.113 |
| A |  | 0.009 | 0.009 | 0.075 | 0.163 | 0.163 |
| B |  | 0.095 | 0.042 | 0.059 | 0.198 | 0.131 |
| Design Case 2 | ||||||
| D2 |  | 0.126 | 0.039 | 0.082 | 0.317 | 0.126 |
| C |  | 0.341 | 0.116 | 0.002 | 0.432 | 0.125 |
| Design Case 3 | ||||||
| D3 |  | 0.070 | 0.070 | 0.082 | 0.260 | 0.261 |
| L |  | 0.188 | 0.188 | 0.072 | 0.255 | 0.255 |
| D1 | D2 | D3 | |
|---|---|---|---|
| MultiP-microSIMP | 0.330 | 0.443 | 0.486 |
| MultiP-microSIMPATY | 0.292 | 0.412 | 0.415 |
| Mass reduction [%] | 11.5% | 7.0% | 14.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavazzoni, M.; Ferro, N.; Perotto, S.; Foletti, S. Multi-Physics Inverse Homogenization for the Design of Innovative Cellular Materials: Application to Thermo-Elastic Problems. Math. Comput. Appl. 2022, 27, 15. https://doi.org/10.3390/mca27010015
Gavazzoni M, Ferro N, Perotto S, Foletti S. Multi-Physics Inverse Homogenization for the Design of Innovative Cellular Materials: Application to Thermo-Elastic Problems. Mathematical and Computational Applications. 2022; 27(1):15. https://doi.org/10.3390/mca27010015
Chicago/Turabian StyleGavazzoni, Matteo, Nicola Ferro, Simona Perotto, and Stefano Foletti. 2022. "Multi-Physics Inverse Homogenization for the Design of Innovative Cellular Materials: Application to Thermo-Elastic Problems" Mathematical and Computational Applications 27, no. 1: 15. https://doi.org/10.3390/mca27010015
APA StyleGavazzoni, M., Ferro, N., Perotto, S., & Foletti, S. (2022). Multi-Physics Inverse Homogenization for the Design of Innovative Cellular Materials: Application to Thermo-Elastic Problems. Mathematical and Computational Applications, 27(1), 15. https://doi.org/10.3390/mca27010015







