Modified Representations for the Close Evaluation Problem
Abstract
1. Introduction
2. Motivation for Modified Representations
3. Modified Representations
3.1. Modified Representation for the Laplace Double-Layer Potential
3.2. Modified Representation for the Laplace Single-Layer Potential
- The linear function ;
- The function based on Green’s function;
- The quadratic product function , ;
- The quadratic difference function ,
3.3. Modified Representation for the Helmholtz Double- and Single-Layer Potentials
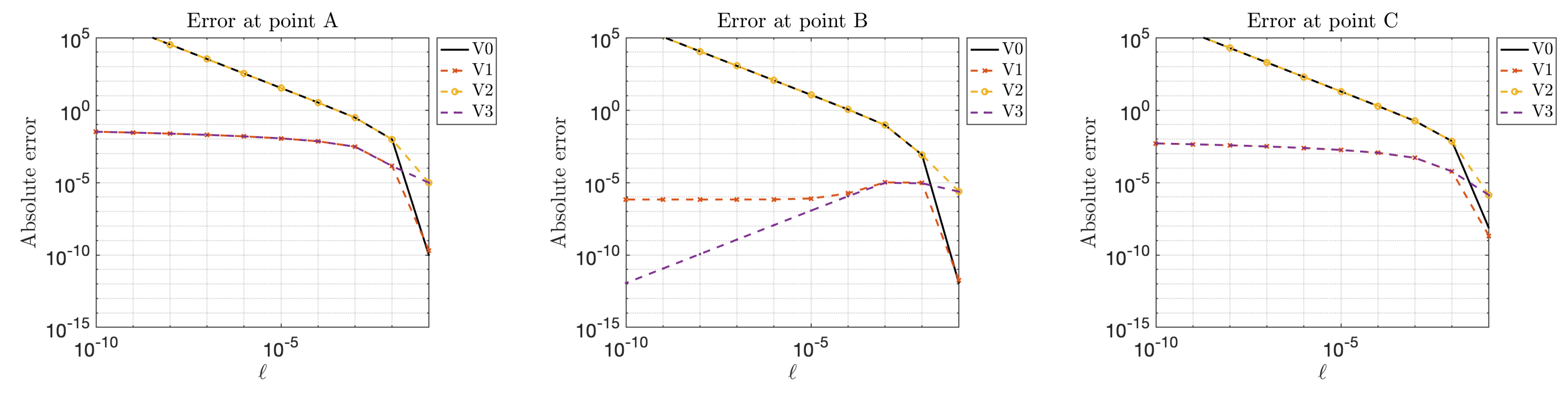
4. Numerical Examples
4.1. Exterior Neumann Laplace Problem
4.1.1. Example 1: Exterior Laplace in Two Dimensions
4.1.2. Example 2: Exterior Laplace in Three Dimensions
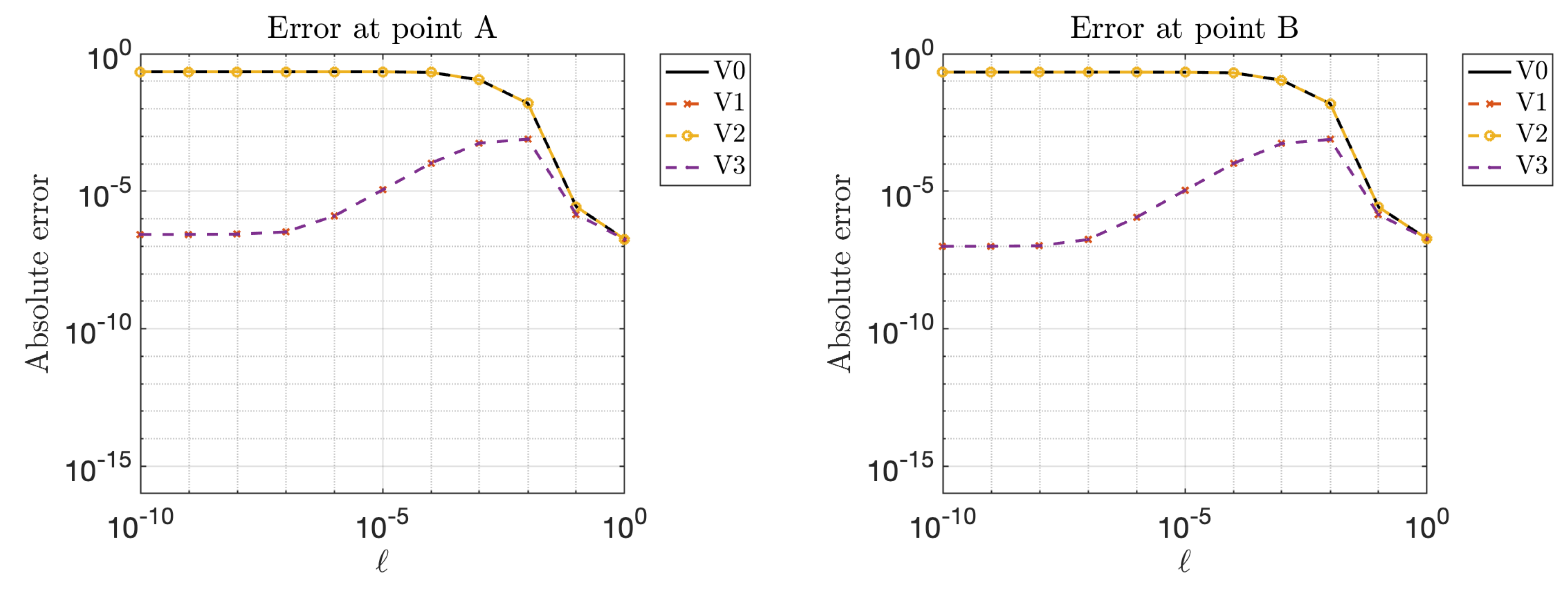
4.2. Scattering Problem
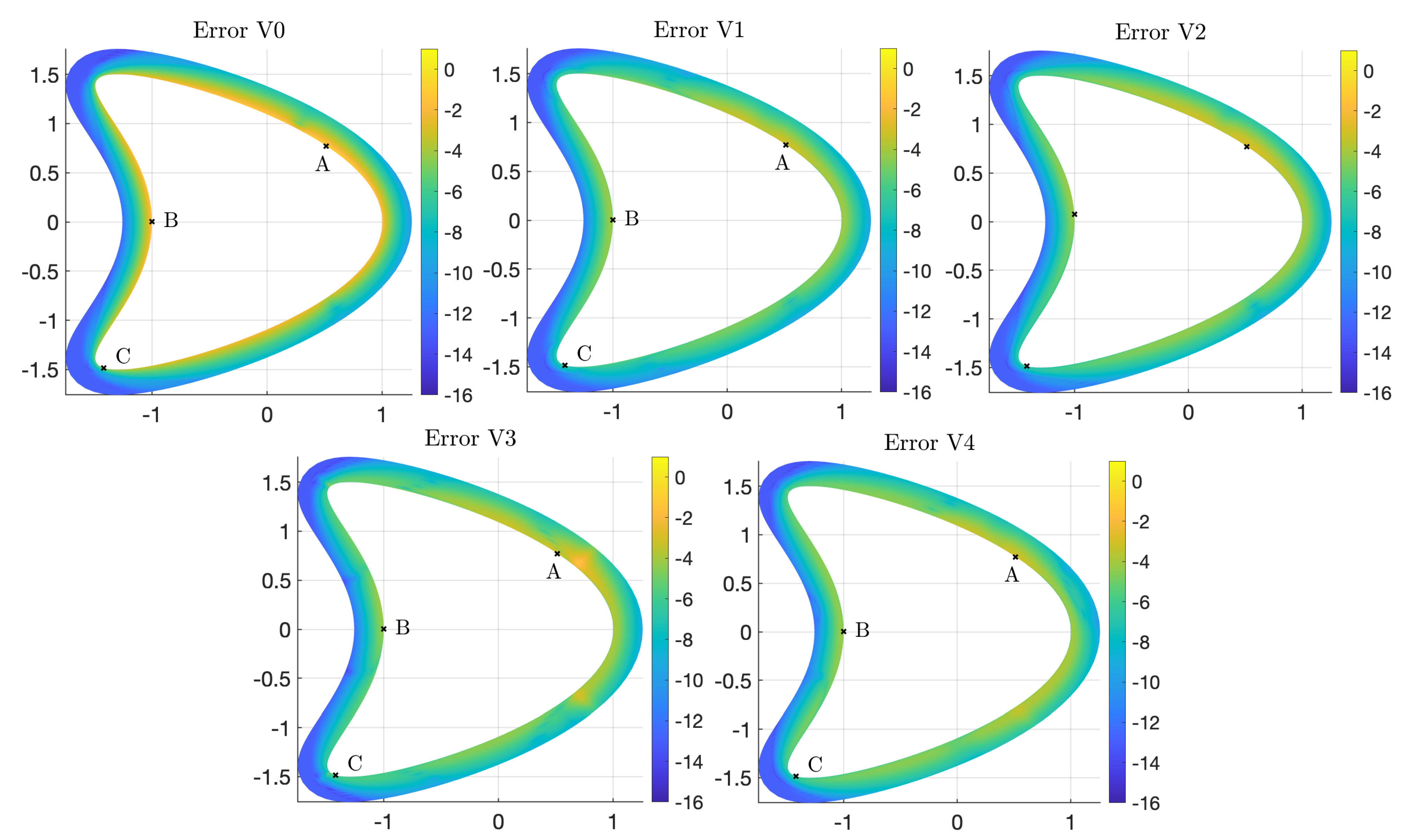
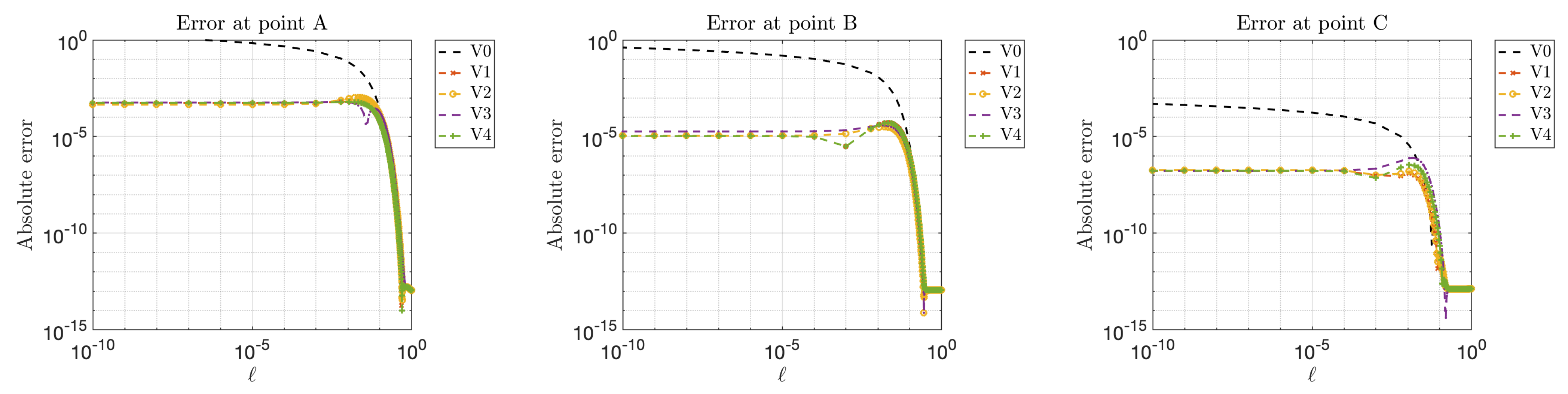
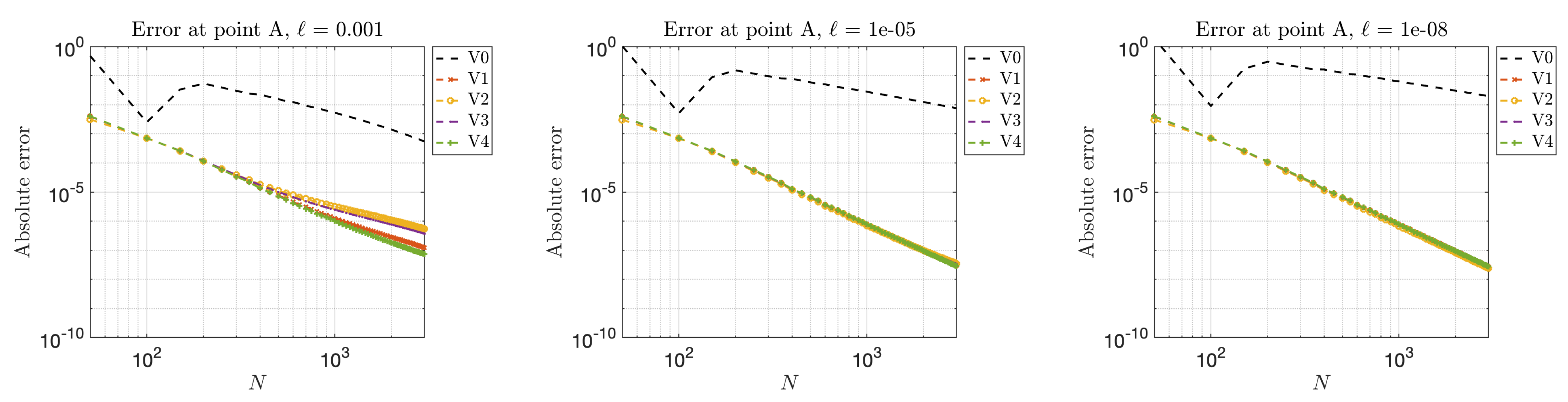
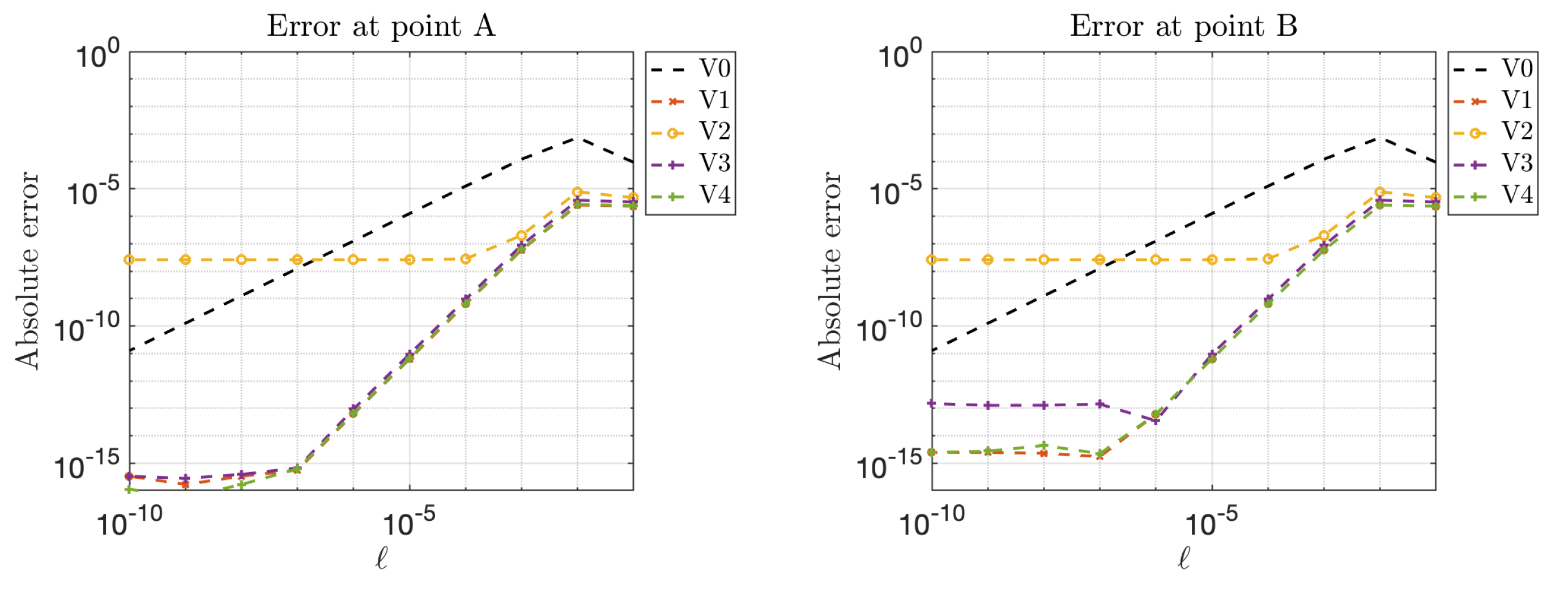
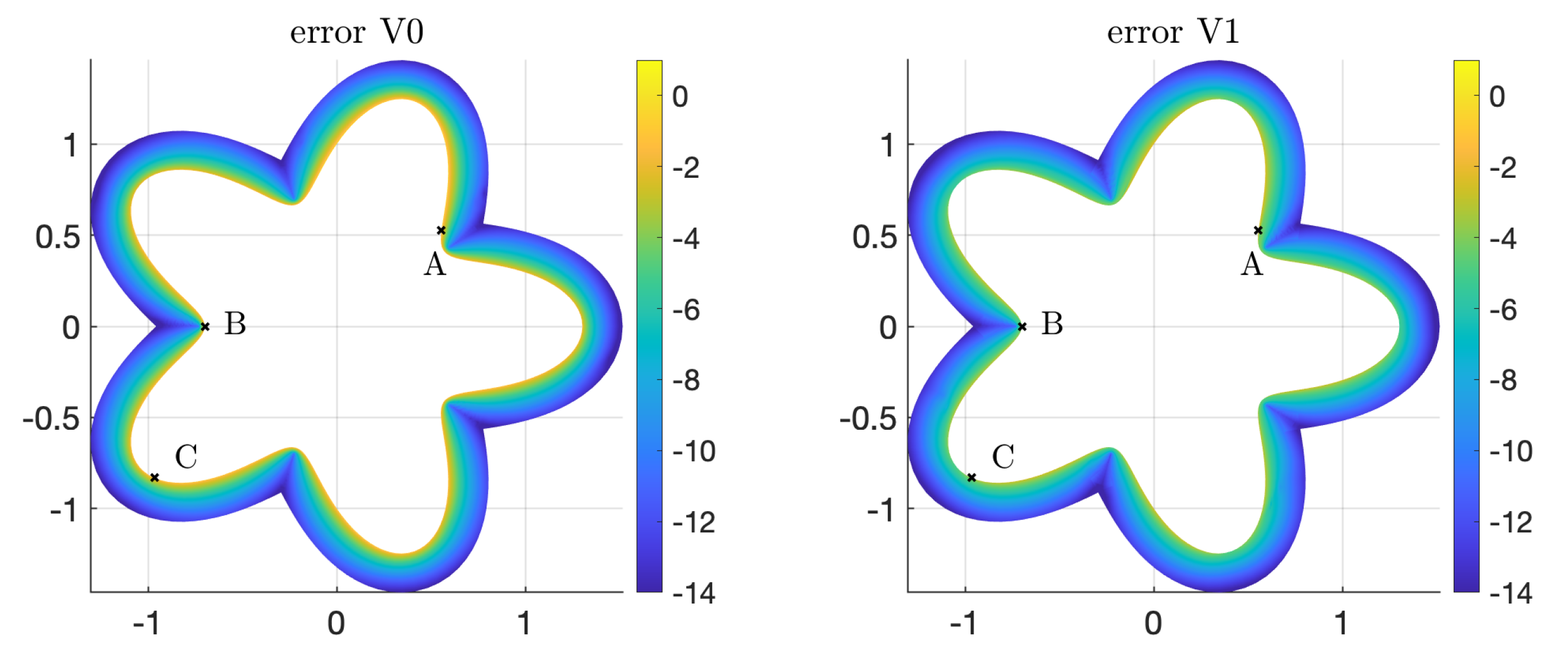
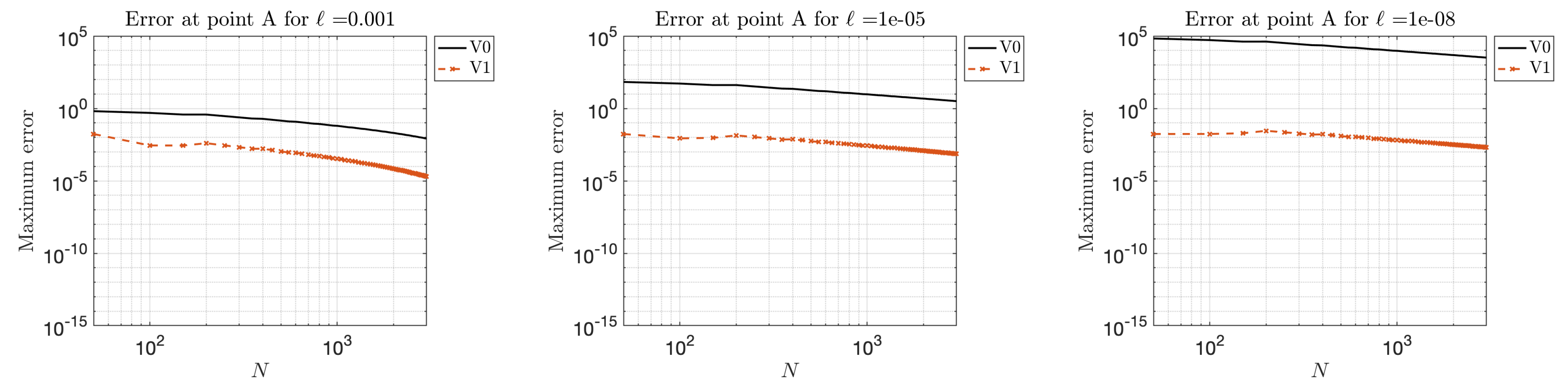
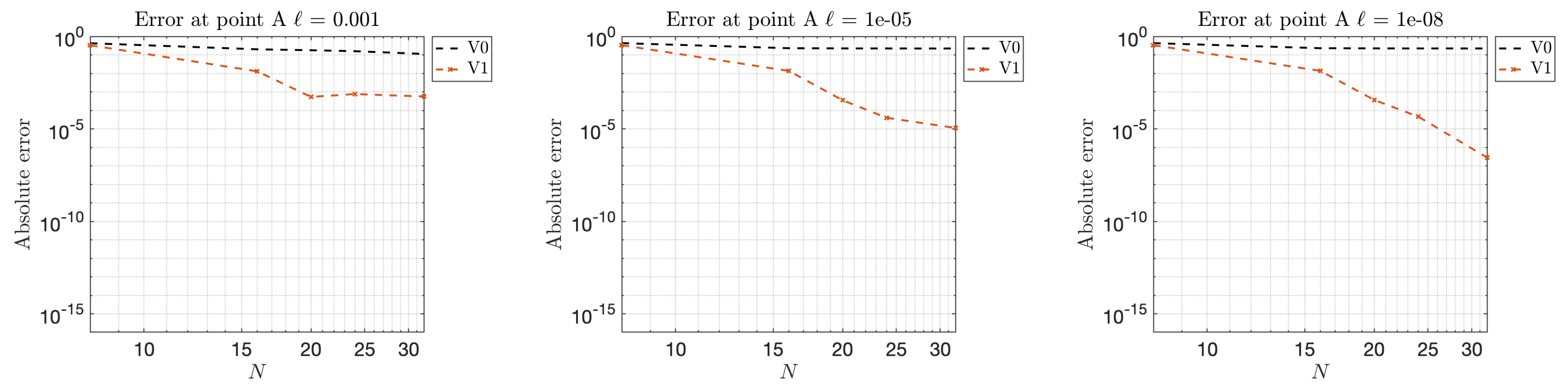
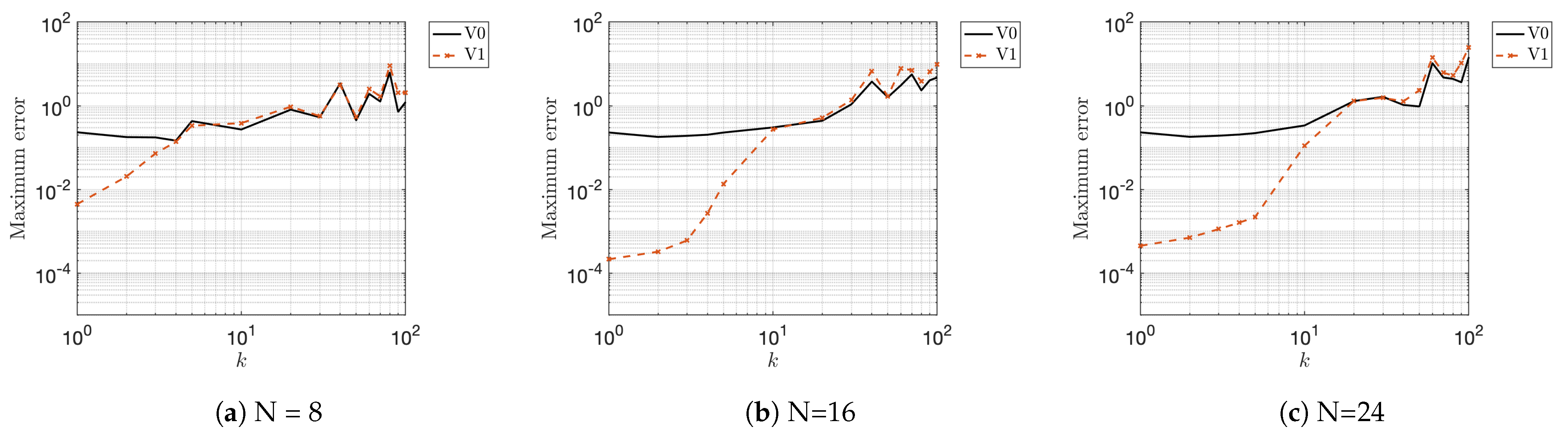
4.2.1. Example 3: Scattering in Two Dimensions
- V0: standard representation (19);
4.2.2. Example 4: Scattering in Three Dimensions
4.2.3. High Frequency Behavior
5. Modified Boundary Integral Equations
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Kress Product Quadrature
Appendix B. Galerkin Approximation
Appendix C. Proof of Modified Representations
Appendix C.1. Modified Double-Layer Potential (14)
Appendix C.2. Proof of Proposition 2
Appendix C.3. Proof of Propositions 3, 4
References
- Akselrod, G.M.; Argyropoulos, C.; Hoang, T.B.; Ciracì, C.; Fang, C.; Huang, J.; Smith, D.R.; Mikkelsen, M.H. Probing the mechanisms of large Purcell enhancement in plasmonic nanoantennas. Nat. Photonics 2014, 8, 835–840. [Google Scholar] [CrossRef]
- Barnett, A.H.; Wu, B.; Veerapaneni, S. Spectrally accurate quadratures for evaluation of layer potentials close to the boundary for the 2D Stokes and Laplace equations. SIAM J. Sci. Comput. 2015, 37, B519–B542. [Google Scholar] [CrossRef]
- Keaveny, E.E.; Shelley, M.J. Applying a second-kind boundary integral equation for surface tractions in Stokes flow. J. Comput. Phys. 2011, 230, 2141–2159. [Google Scholar] [CrossRef]
- Marple, G.R.; Barnett, A.; Gillman, A.; Veerapaneni, S. A fast algorithm for simulating multiphase flows through periodic geometries of arbitrary shape. SIAM J. Sci. Comput. 2016, 38, B740–B772. [Google Scholar] [CrossRef]
- Mayer, K.M.; Lee, S.; Liao, H.; Rostro, B.C.; Fuentes, A.; Scully, P.T.; Nehl, C.L.; Hafner, J.H. A label-free immunoassay based upon localized surface plasmon resonance of gold nanorods. ACS Nano 2008, 2, 687–692. [Google Scholar] [CrossRef]
- Novotny, L.; Van Hulst, N. Antennas for light. Nat. Photonics 2011, 5, 83–90. [Google Scholar] [CrossRef]
- Sannomiya, T.; Hafner, C.; Voros, J. In situ sensing of single binding events by localized surface plasmon resonance. Nano Lett. 2008, 8, 3450–3455. [Google Scholar] [CrossRef]
- Smith, D.J. A boundary element regularized Stokeslet method applied to cilia-and flagella-driven flow. Proc. R. Soc. Lond. A 2009, 465, 3605–3626. [Google Scholar] [CrossRef]
- Barnett, A.H. Evaluation of layer potentials close to the boundary for Laplace and Helmholtz problems on analytic planar domains. SIAM J. Sci. Comput. 2014, 36, A427–A451. [Google Scholar] [CrossRef]
- Schwab, C.; Wendland, W. On the extraction technique in boundary integral equations. Math. Comput. 1999, 68, 91–122. [Google Scholar] [CrossRef]
- Beale, J.T.; Lai, M.C. A method for computing nearly singular integrals. SIAM J. Numer. Anal. 2001, 38, 1902–1925. [Google Scholar] [CrossRef][Green Version]
- Beale, J.T.; Ying, W.; Wilson, J.R. A simple method for computing singular or nearly singular integrals on closed surfaces. Commun. Comput. Phys. 2016, 20, 733–753. [Google Scholar] [CrossRef]
- Helsing, J.; Ojala, R. On the evaluation of layer potentials close to their sources. J. Comput. Phys. 2008, 227, 2899–2921. [Google Scholar] [CrossRef]
- Af Klinteberg, L.; Tornberg, A.-K. A fast integral equation method for solid particles in viscous flow using quadrature by expansion. J. Comput. Phys. 2016, 326, 420–445. [Google Scholar] [CrossRef]
- Af Klinteberg, L.; Tornberg, A.-K. Error estimation for quadrature by expansion in layer potential evaluation. Adv. Comput. Math. 2017, 43, 195–234. [Google Scholar] [CrossRef]
- Epstein, C.L.; Greengard, L.; Klöckner, A.K. On the convergence of local expansions of layer potentials. SIAM J. Numer. Anal. 2013, 51, 2660–2679. [Google Scholar] [CrossRef][Green Version]
- Klöckner, A.; Barnett, A.; Greengard, L.; O’Neil, M. Quadrature by expansion: A new method for the evaluation of layer potentials. J. Comput. Phys. 2013, 252, 332–349. [Google Scholar] [CrossRef]
- Rachh, M.; Klöckner, A.; O’Neil, M. Fast Algorithms for Quadrature by Expansion I: Globally Valid Expansions. J. Comput. Phys. 2017, 345, 706–731. [Google Scholar] [CrossRef]
- Wala, M.; Klöckner, A. A Fast Algorithm for Quadrature by Expansion in Three Dimensions. J. Comput. Phys. 2019, 388, 655–689. [Google Scholar] [CrossRef]
- Greengard, L.; O’Neil, M.; Rachh, M.; Vico, F. Fast multipole methods for the evaluation of layer potentials with locally-corrected quadratures. J. Comput. Phys. X 2021, 10, 100092. [Google Scholar]
- Pérez-Arancibia, C. A plane-wave singularity subtraction technique for the classical Dirichlet and Neumann combined field integral equations. Appl. Numer. Math. 2018, 123, 221–240. [Google Scholar] [CrossRef]
- Pérez-Arancibia, C.; Faria, L.; Turc, C. Harmonic density interpolation methods for high-order evaluation of Laplace layer potentials in 2D and 3D. J. Comput. Phys. 2019, 376, 411–434. [Google Scholar] [CrossRef]
- Pérez-Arancibia, C.; Turc, C.; Faria, L. Planewave density interpolation methods for 3D Helmholtz boundary integral equations. SIAM J. Sci. Comput. 2019, 41, A2088–A2116. [Google Scholar] [CrossRef]
- Carvalho, C.; Khatri, S.; Kim, A.D. Asymptotic analysis for close evaluation of layer potentials. J. Comput. Phys. 2018, 355, 327–341. [Google Scholar] [CrossRef]
- Carvalho, C.; Khatri, S.; Kim, A.D. Asymptotic approximation for the close evaluation of double-layer potentials. SIAM J. Sci. Comput. 2020, 42, A504–A533. [Google Scholar] [CrossRef]
- Khatri, S.; Kim, A.D.; Cortes, R.; Carvalho, C. Close evaluation of layer potentials in three dimensions. J. Comput. Phys. 2020, 423, 109798. [Google Scholar] [CrossRef]
- Hwang, W.S. A regularized boundary integral method in potential theory. Comput. Methods Appl. Mech. Eng. 2013, 259, 9. [Google Scholar] [CrossRef]
- Liu, Y.J.; Rudolphi, T.J. New identities for fundamental solutions and their applications to non-singular boundary element formulations. Comput. Mech. 1999, 24, 286–292. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sun, Q.; Chan, D.Y. Non-singular boundary integral methods for fluid mechanics applications. J. Fluid Mech. 2012, 696, 78. [Google Scholar] [CrossRef]
- Sun, Q.; Klaseboer, E.; Khoo, B.C.; Chan, D.Y. A robust and non-singular formulation of the boundary integral method for the potential problem. Eng. Anal. Bound. Elem. 2014, 1, 117–123. [Google Scholar] [CrossRef]
- Sun, Q.; Klaseboer, E.; Khoo, B.-C.; Chan, D.Y. Boundary regularized integral equation formulation of the Helmholtz equation in acoustics. R. Soc. Open Sci. 2015, 2, 140520. [Google Scholar] [CrossRef] [PubMed]
- Faria, L.M.; Pérez-Arancibia, C.; Bonnet, M. General-purpose kernel regularization of boundary integral equations via density interpolation. Comput. Methods Appl. Mech. Eng. 2021, 378, 113703. [Google Scholar] [CrossRef]
- Kress, R. Linear Integral Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Colton, D.; Kress, R. Integral Equation Methods in Scattering Theory; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Guenther, R.B.; Lee, J.W. Partial Differential Equations of Mathematical Physics and Integral Equations; Dover Publications: New York, NY, USA, 1996. [Google Scholar]
- Atkinson, K.E. The Numerical Solution of Integral Equations of the Second Kind; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Bremer, J.; Gimbutas, Z.; Rokhlin, V. A nonlinear optimization procedure for generalized gaussian quadratures. SIAM J. Sci. Comput. 2010, 32, 1761–1788. [Google Scholar] [CrossRef]
- Bruno, O.P.; Kunyansky, L.A. A fast, high-order algorithm for the solution of surface scattering problems: Basic implementation, tests, and applications. J. Comput. Phys. 2001, 169, 80–110. [Google Scholar] [CrossRef]
- Ganesh, M.; Graham, I. A high-order algorithm for obstacle scattering in three dimensions. J. Comput. Phys. 2004, 198, 211–242. [Google Scholar] [CrossRef]
- Kress, R. Boundary integral equations in time-harmonic acoustic scattering. Math. Comput. Model. 1991, 15, 229–243. [Google Scholar] [CrossRef]
- Carvalho, C. Subtraction-Techniques Codes. Available online: https://doi.org/10.5281/zenodo.5523373 (accessed on 25 September 2021).
- Atkinson, K.E. Numerical integration on the sphere. ANZIAM J. 1982, 23, 332–347. [Google Scholar] [CrossRef][Green Version]
- Atkinson, K.E. The numerical solution Laplace’s equation in three dimensions. SIAM J. Numer. Anal. 1982, 19, 263–274. [Google Scholar] [CrossRef]
- Atkinson, K.E. Algorithm 629: An integral equation program for Laplace’s equation in three dimensions. ACM Trans. Math. Softw. 1985, 11, 85–96. [Google Scholar] [CrossRef]
- Atkinson, K.E. A survey of boundary integral equation methods for the numerical solution of Laplace’s equation in three dimensions. In Numerical Solution of Integral Equations; Springer: Boston, MA, USA, 1990; pp. 1–34. [Google Scholar]
- Ammari, H.; Millien, P.; Ruiz, M.; Zhang, H. Mathematical analysis of plasmonic nanoparticles: The scalar case. Arch. Ration. Mech. Anal. 2017, 2, 597–658. [Google Scholar] [CrossRef]
- Helsing, J.; Karlsson, A. An extended charge-current formulation of the electromagnetic transmission problem. SIAM J. Appl. Math. 2020, 80, 951–976. [Google Scholar] [CrossRef]




| Method | V0 | V1 | V2 | V3 | V4 |
|---|---|---|---|---|---|
| 0.014 | 0.044 | 0.055 | 0.045 | 0.05 | |
| 0.056 | 0.07 | 0.112 | 0.08 | 0.081 | |
| 0.12 | 0.192 | 0.263 | 0.2 | 0.19 |
| Method | V0 | V1 | V2 | V3 | V4 |
|---|---|---|---|---|---|
| N = 8 | 0.028 | 0.029 | 0.032 | 0.031 | 0.046 |
| N = 16 | 0.143 | 0.146 | 0.148 | 0.150 | 0.142 |
| N = 24 | 0.352 | 0.344 | 0.346 | 0.35 | 0.356 |
| Method | |||
|---|---|---|---|
| V0 | 0.18 | 0.27 | 0.71 |
| V1 | 0.21 | 0.33 | 0.89 |
| Method | |||
|---|---|---|---|
| V0 | 0.027 | 0.15 | 0.313 |
| V1 | 0.03 | 0.15 | 0.314 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, C. Modified Representations for the Close Evaluation Problem. Math. Comput. Appl. 2021, 26, 69. https://doi.org/10.3390/mca26040069
Carvalho C. Modified Representations for the Close Evaluation Problem. Mathematical and Computational Applications. 2021; 26(4):69. https://doi.org/10.3390/mca26040069
Chicago/Turabian StyleCarvalho, Camille. 2021. "Modified Representations for the Close Evaluation Problem" Mathematical and Computational Applications 26, no. 4: 69. https://doi.org/10.3390/mca26040069
APA StyleCarvalho, C. (2021). Modified Representations for the Close Evaluation Problem. Mathematical and Computational Applications, 26(4), 69. https://doi.org/10.3390/mca26040069





