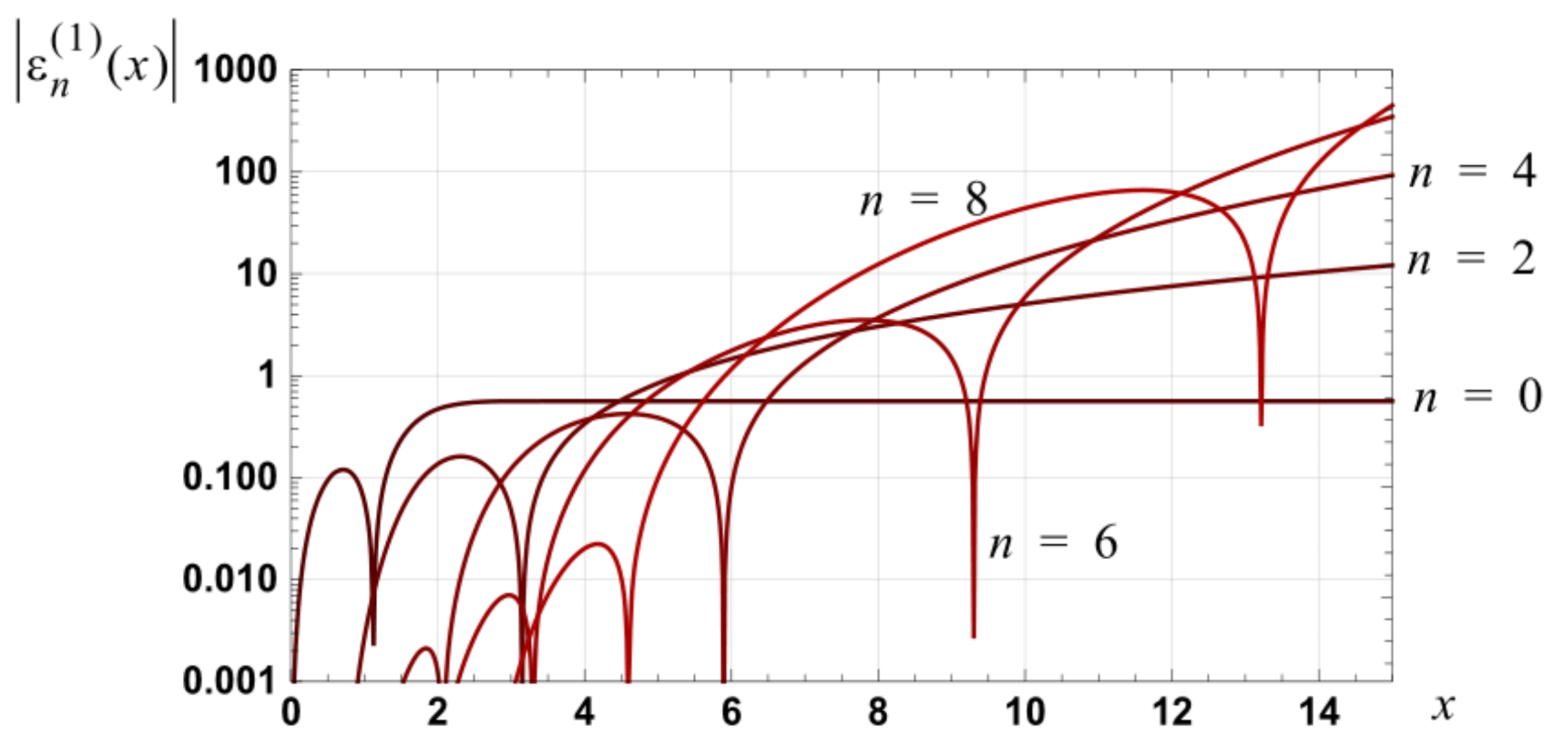
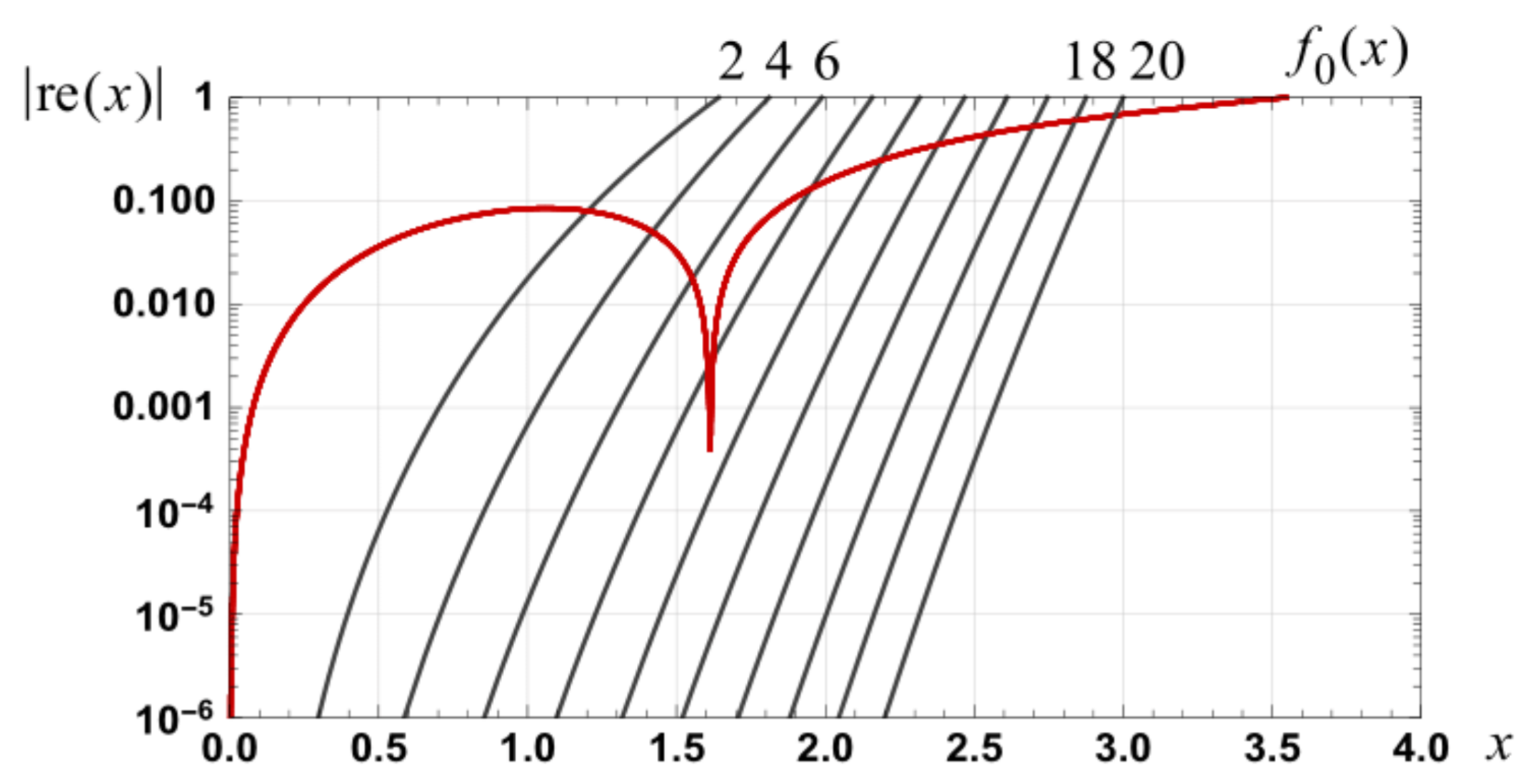
Figure 1.
Graph of the magnitude of the relative error in the approximations, detailed in
Table 1, for erf(
x).
Figure 1.
Graph of the magnitude of the relative error in the approximations, detailed in
Table 1, for erf(
x).
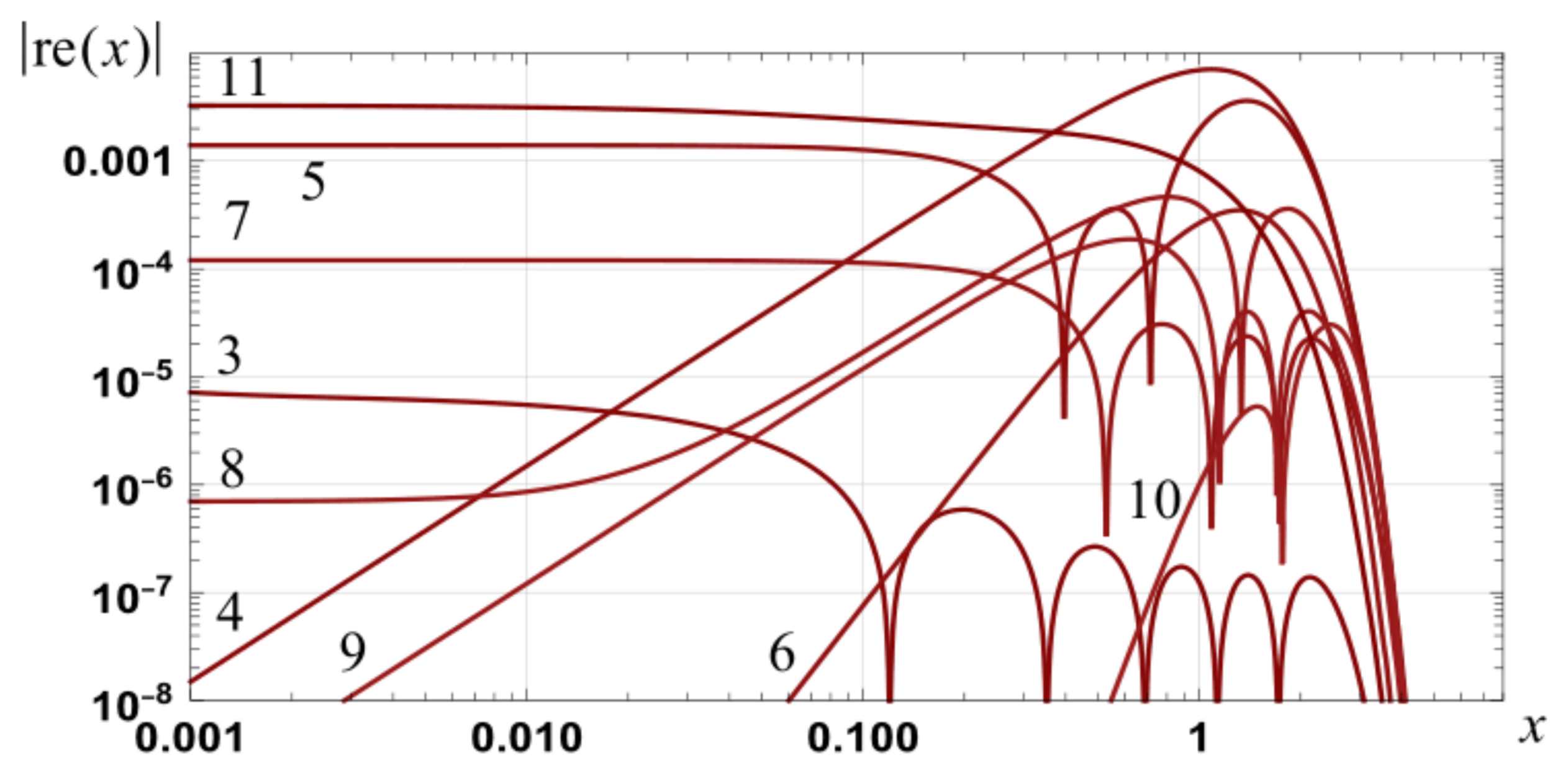
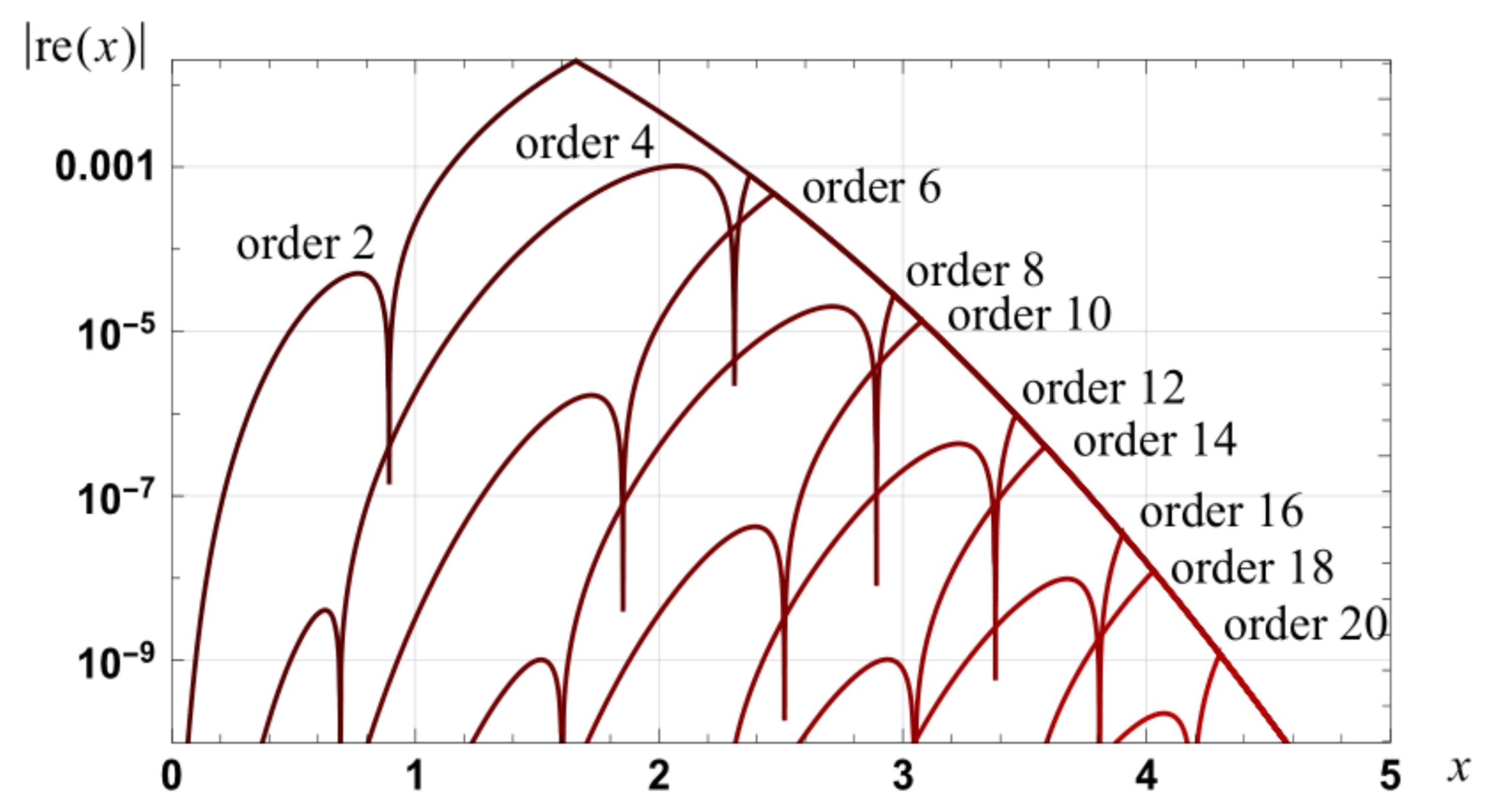
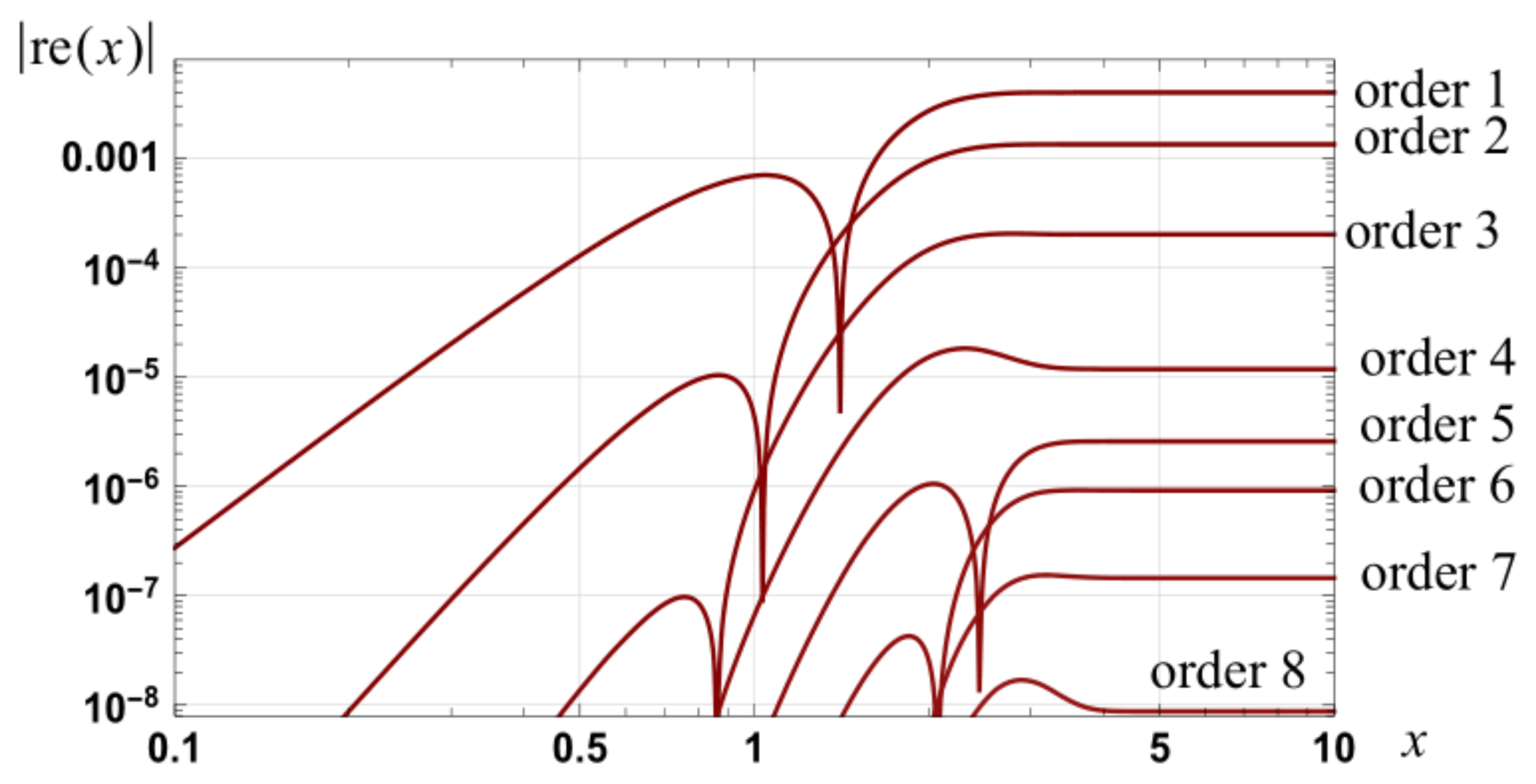
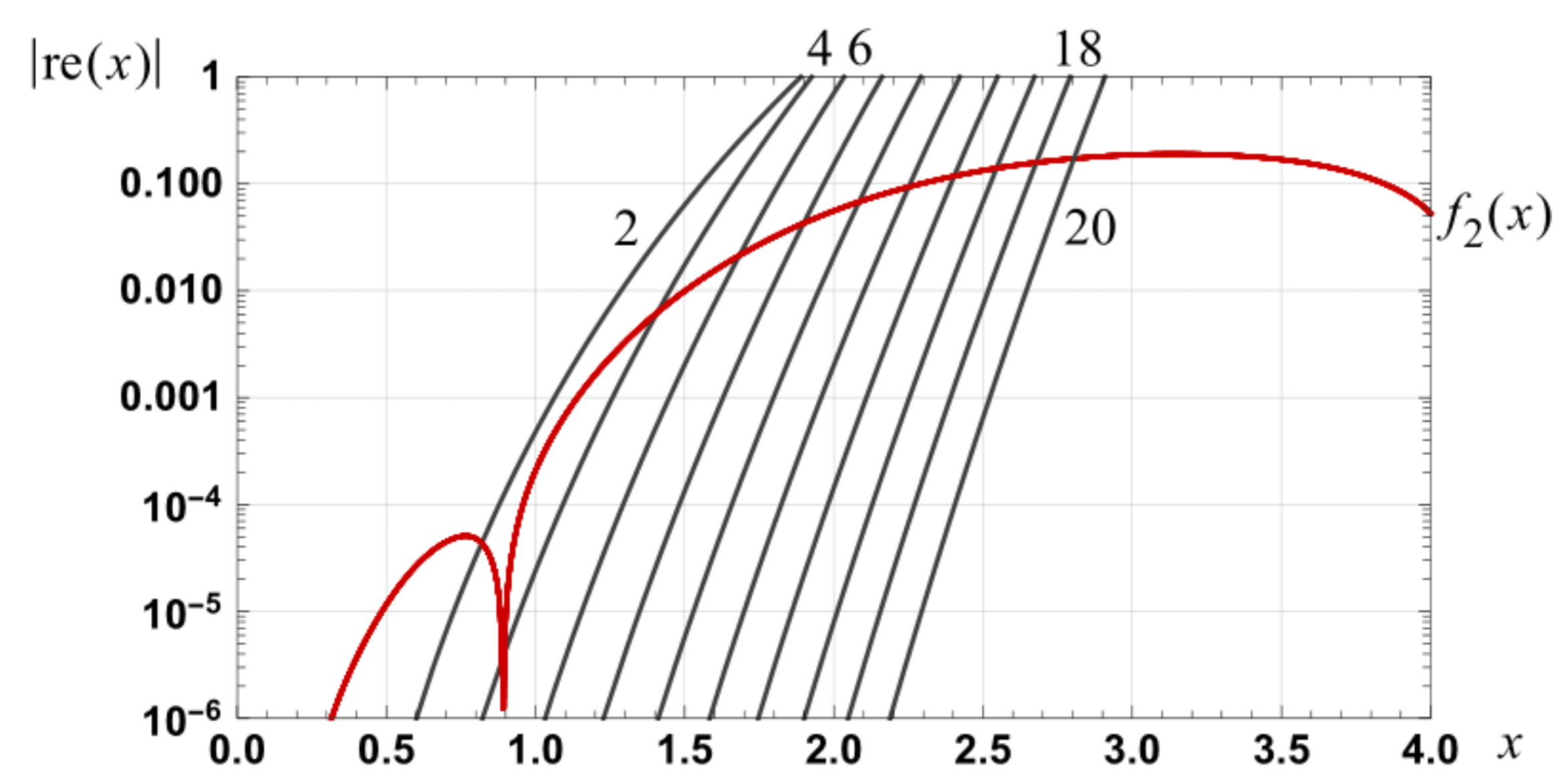
Figure 2.
Graph of the magnitude of the relative errors in approximations to erf(x): zero to tenth order integral spline based series and first, third, ..., fifteenth order Taylor series (dotted).
Figure 2.
Graph of the magnitude of the relative errors in approximations to erf(x): zero to tenth order integral spline based series and first, third, ..., fifteenth order Taylor series (dotted).
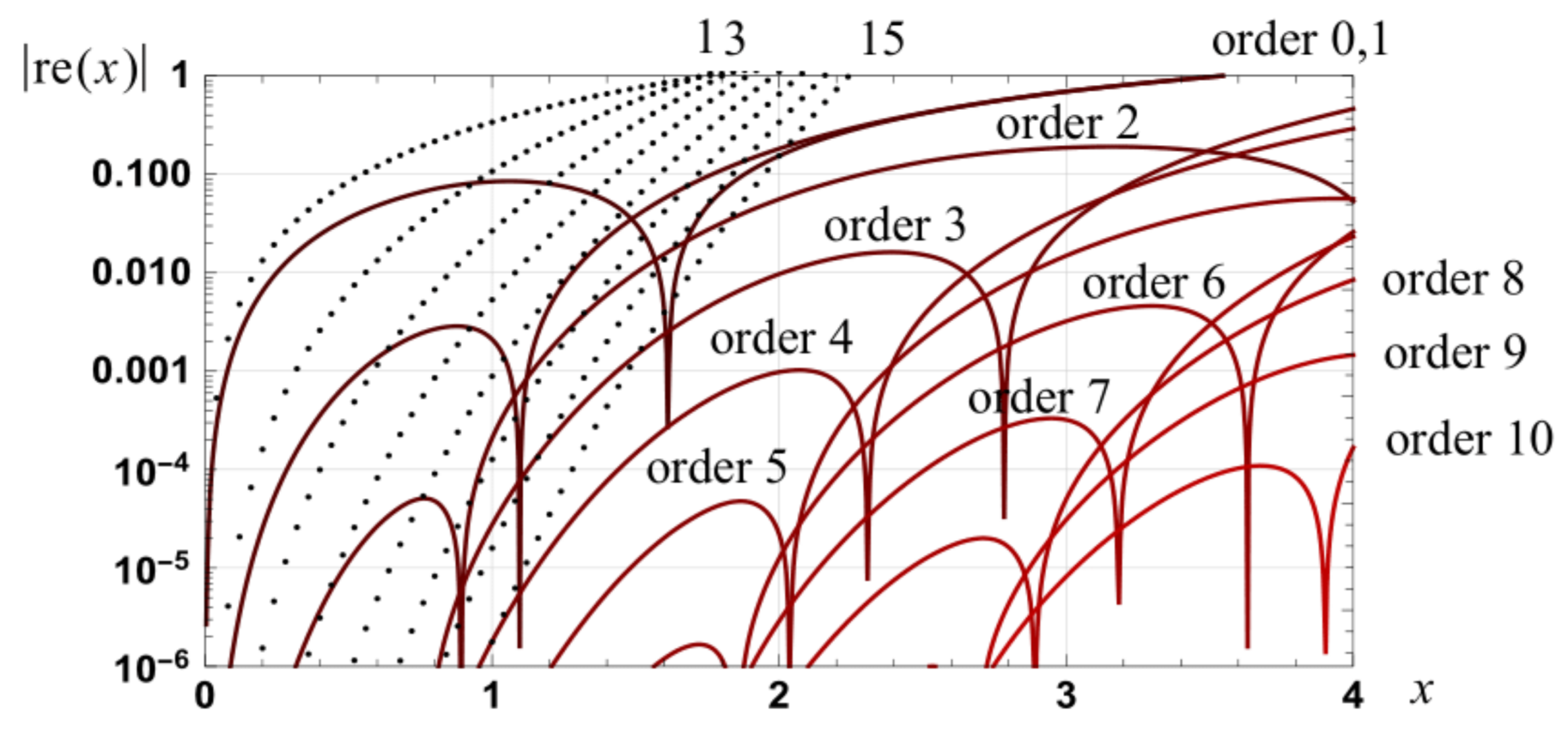
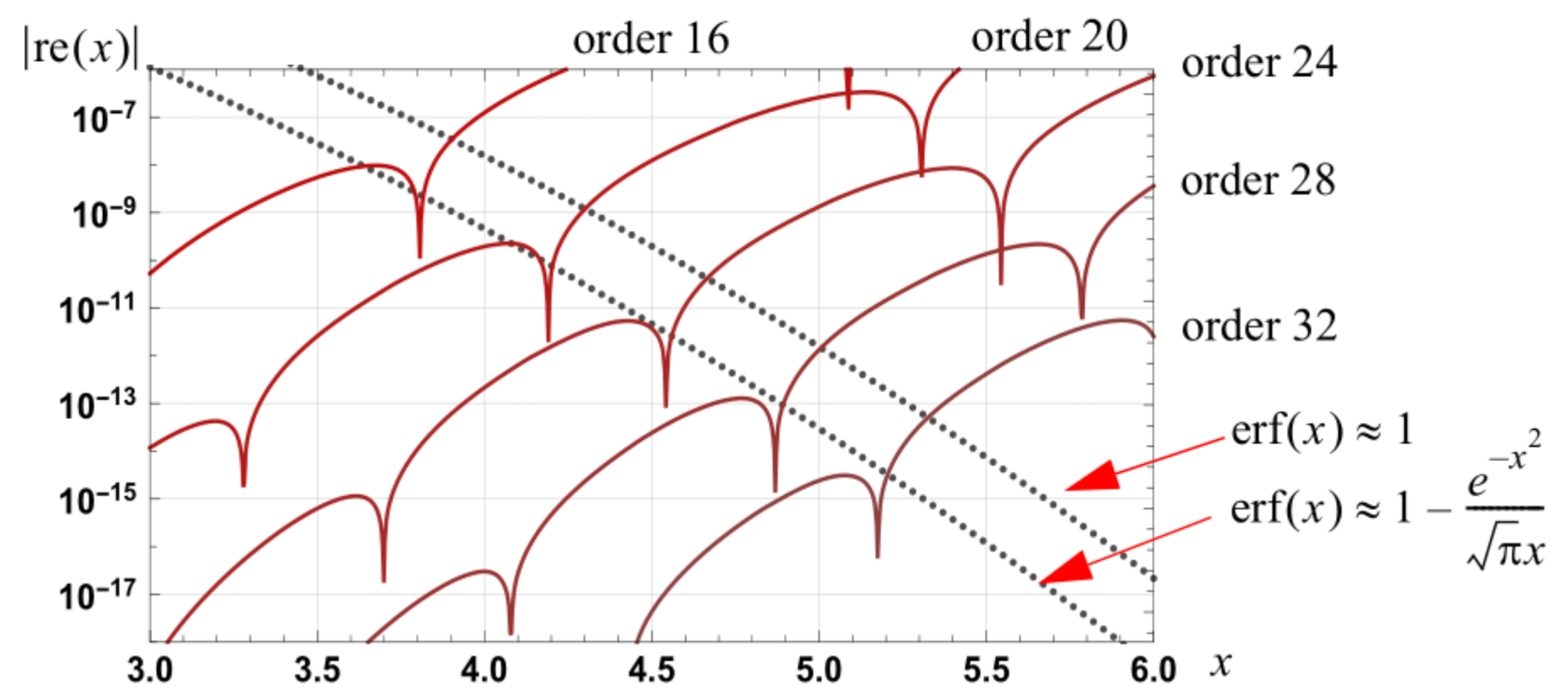
Figure 3.
Graph of the magnitude of the relative errors associated with the approximation and along with the relative error in spline approximations of orders 16, 20, 24, 28 and 32.
Figure 3.
Graph of the magnitude of the relative errors associated with the approximation and along with the relative error in spline approximations of orders 16, 20, 24, 28 and 32.
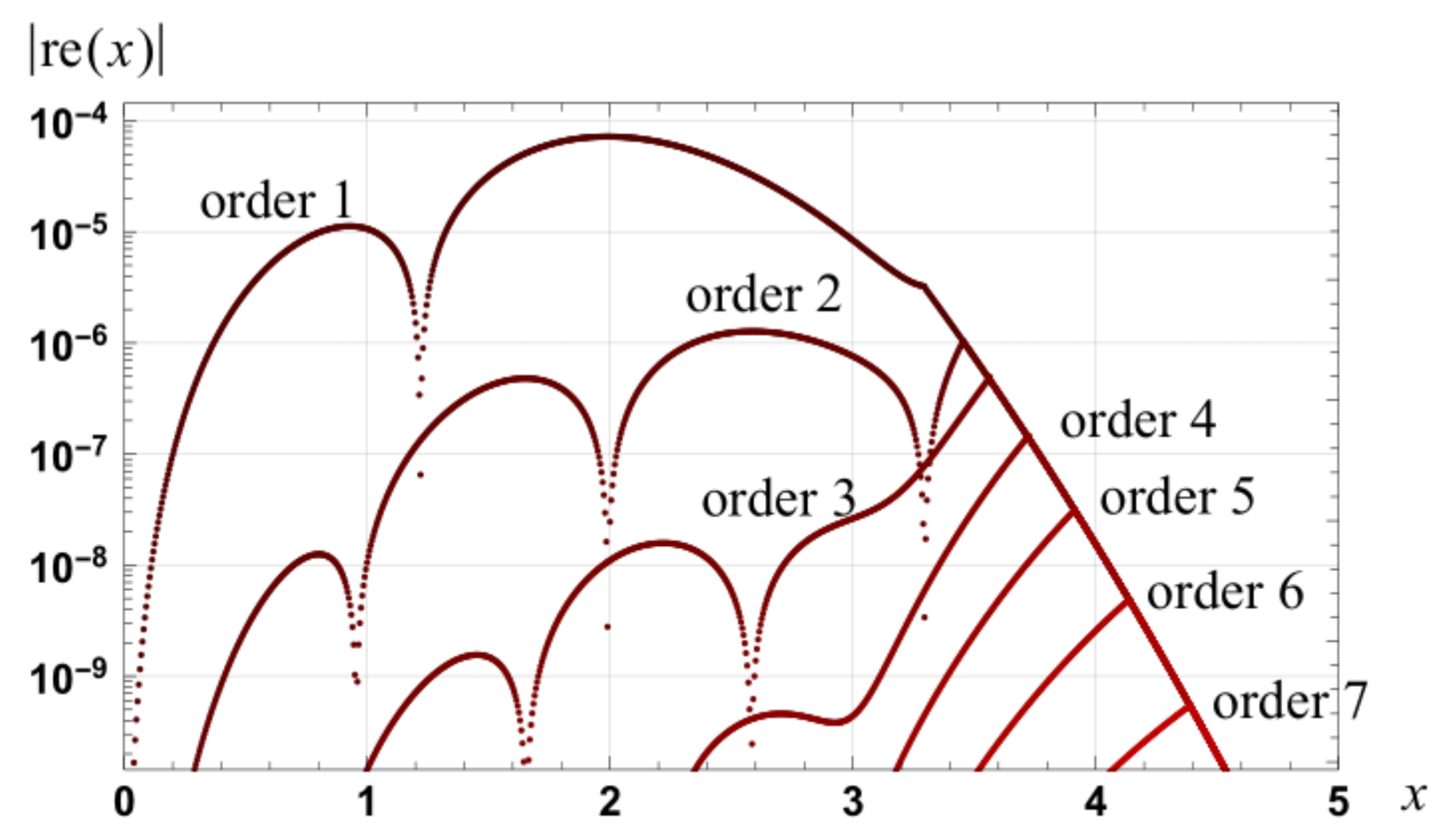
Figure 4.
Graph of the magnitude of the relative errors in the approximations to erf(x), of even orders, as specified by Equation (46). The dotted results are for the fourth order approximation specified by Theorem 1 (Equation (36)).
Figure 4.
Graph of the magnitude of the relative errors in the approximations to erf(x), of even orders, as specified by Equation (46). The dotted results are for the fourth order approximation specified by Theorem 1 (Equation (36)).
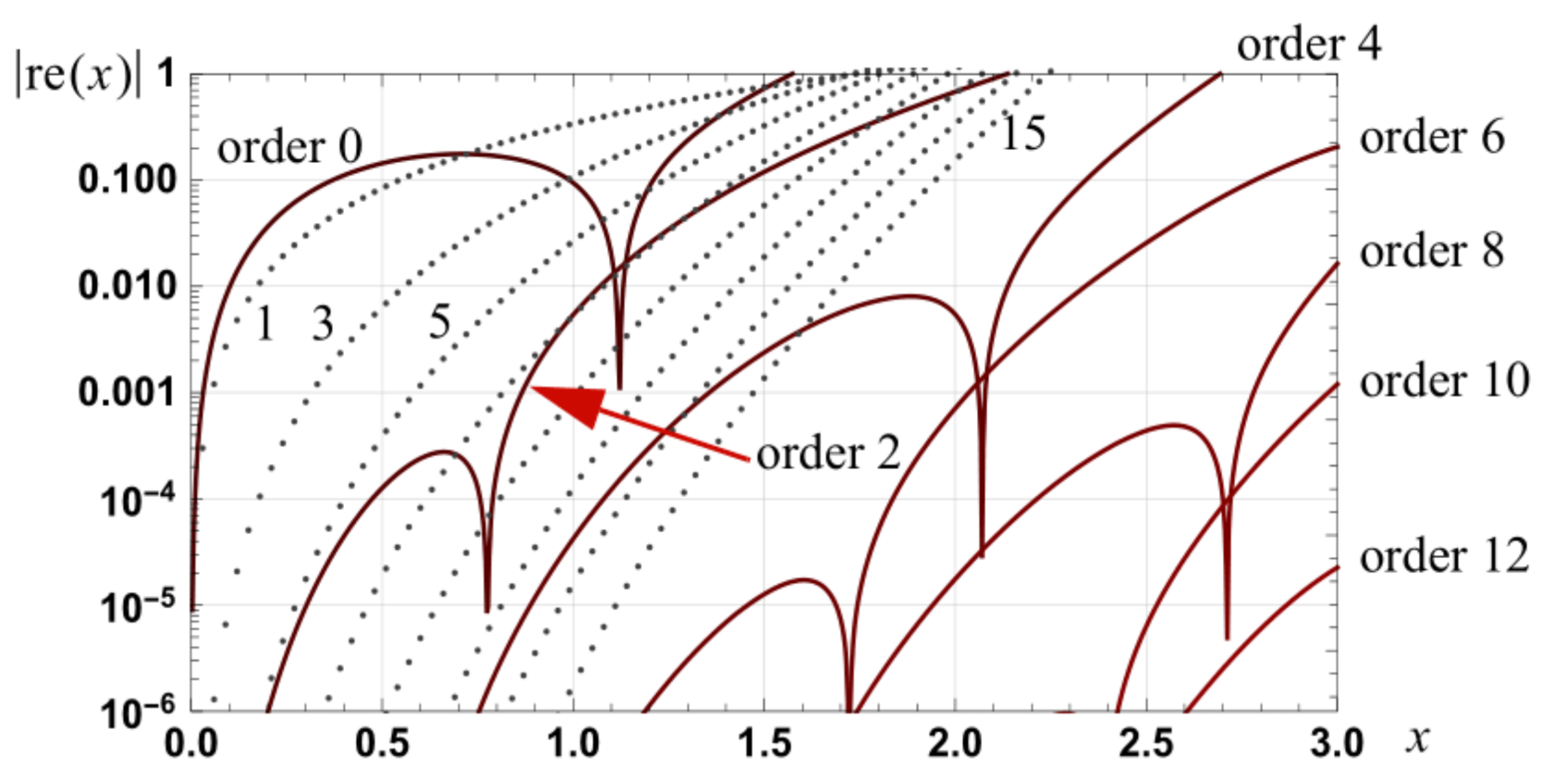
Figure 5.
Illustration of the crossover point where the magnitude of the relative error in the approximation equals the magnitude of the relative error in a set order spline approximation.
Figure 5.
Illustration of the crossover point where the magnitude of the relative error in the approximation equals the magnitude of the relative error in a set order spline approximation.
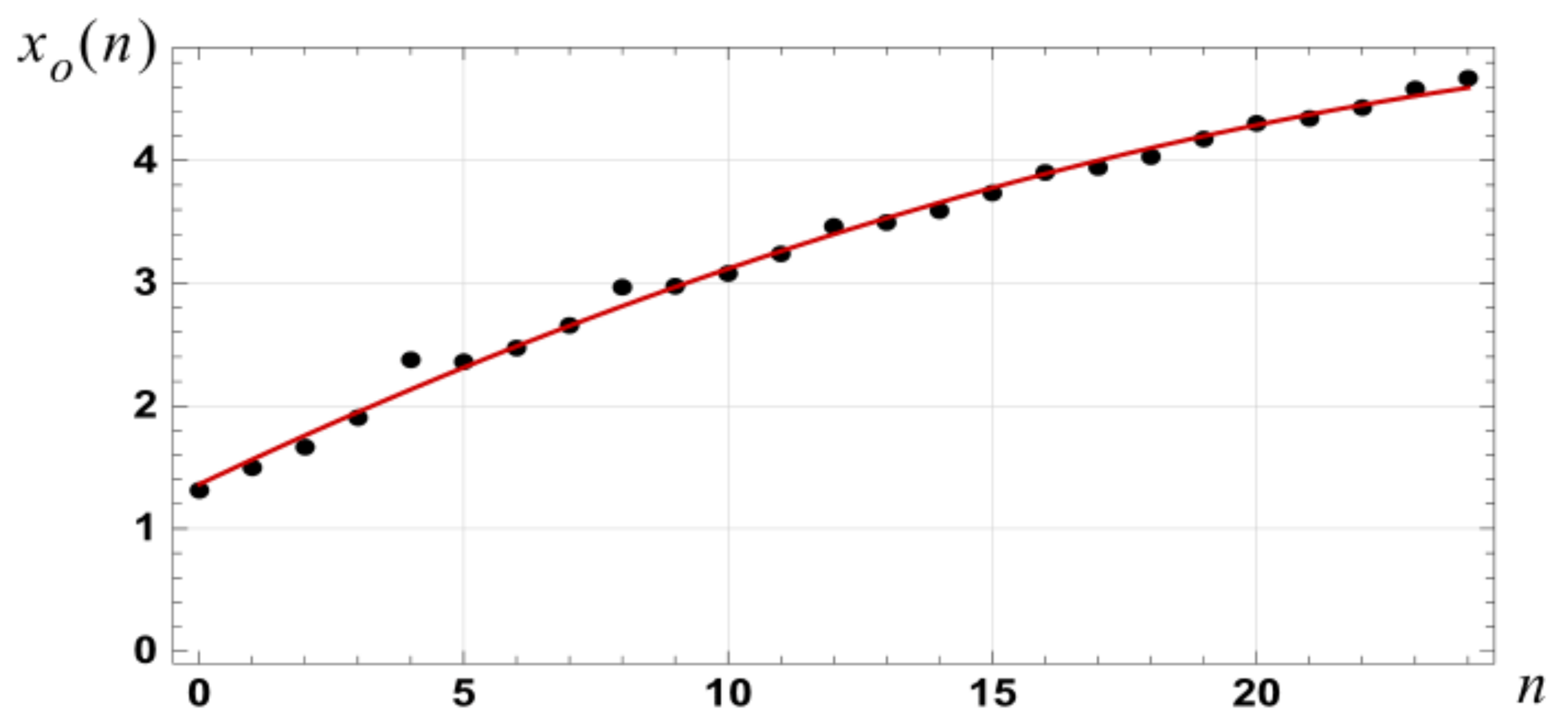
Figure 6.
Graph of the relationship between the optimum transition point , as defined by Equation (57) for the case of and the order of the spline approximation.
Figure 6.
Graph of the relationship between the optimum transition point , as defined by Equation (57) for the case of and the order of the spline approximation.
Figure 7.
Graph of the relative errors in the approximations, , to erf(x), of orders 2, 4, 6, …, 20, based on utilizing the approximation in an optimum manner.
Figure 7.
Graph of the relative errors in the approximations, , to erf(x), of orders 2, 4, 6, …, 20, based on utilizing the approximation in an optimum manner.
Figure 8.
Graph of the magnitude of the relative error in Taylor series approximations to that utilize an optimized change to the approximation .
Figure 8.
Graph of the magnitude of the relative error in Taylor series approximations to that utilize an optimized change to the approximation .
Figure 9.
Graph of the relative errors in spline approximations to , of orders one to six and based on four variable sub-intervals of equal width.
Figure 9.
Graph of the relative errors in spline approximations to , of orders one to six and based on four variable sub-intervals of equal width.
Figure 10.
Graph of the relative errors in approximations to : first to seventh order spline based series based on four sub-intervals of equal width and with utilization of the approximation at the optimum transition point.
Figure 10.
Graph of the relative errors in approximations to : first to seventh order spline based series based on four sub-intervals of equal width and with utilization of the approximation at the optimum transition point.
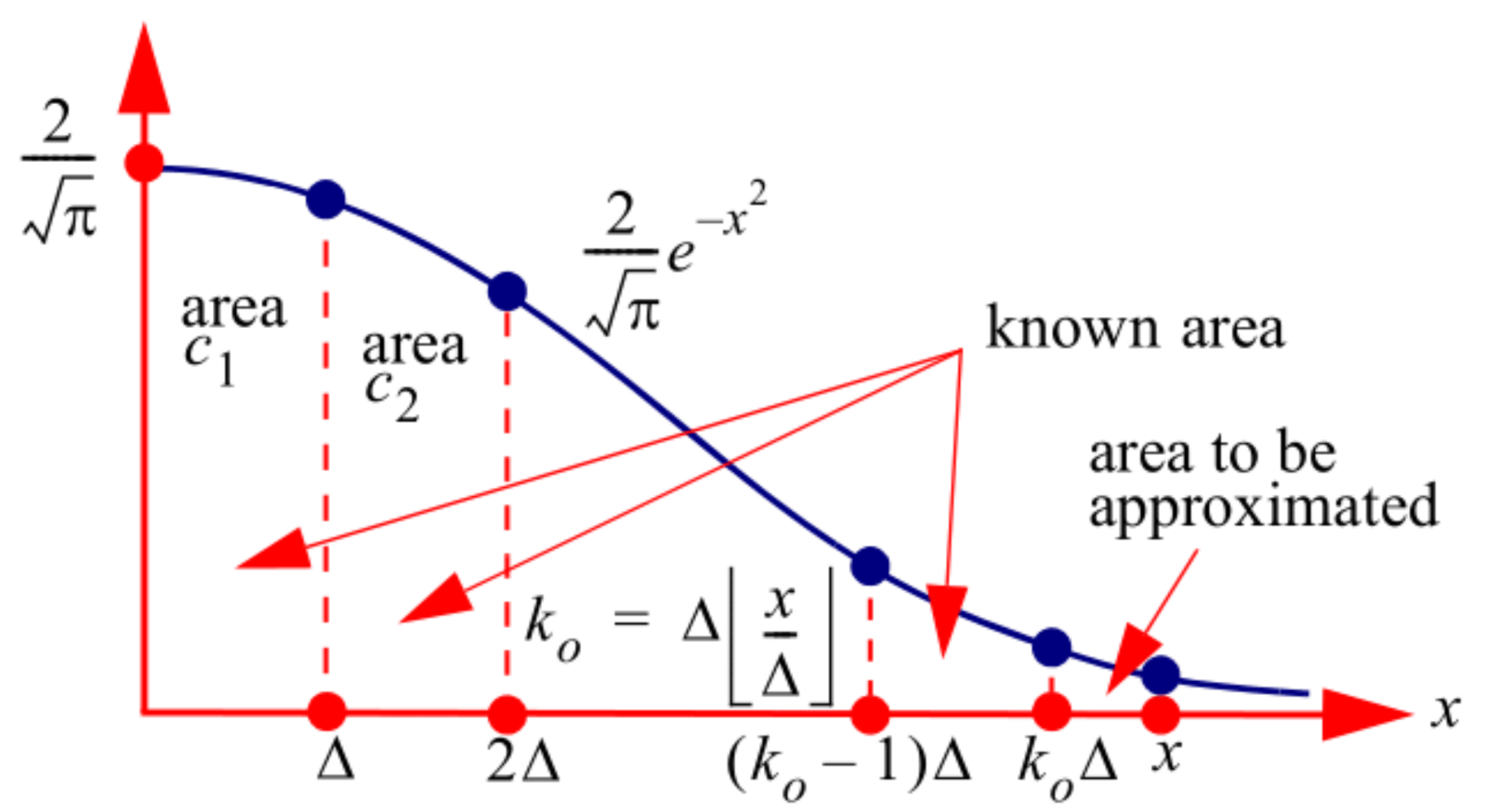
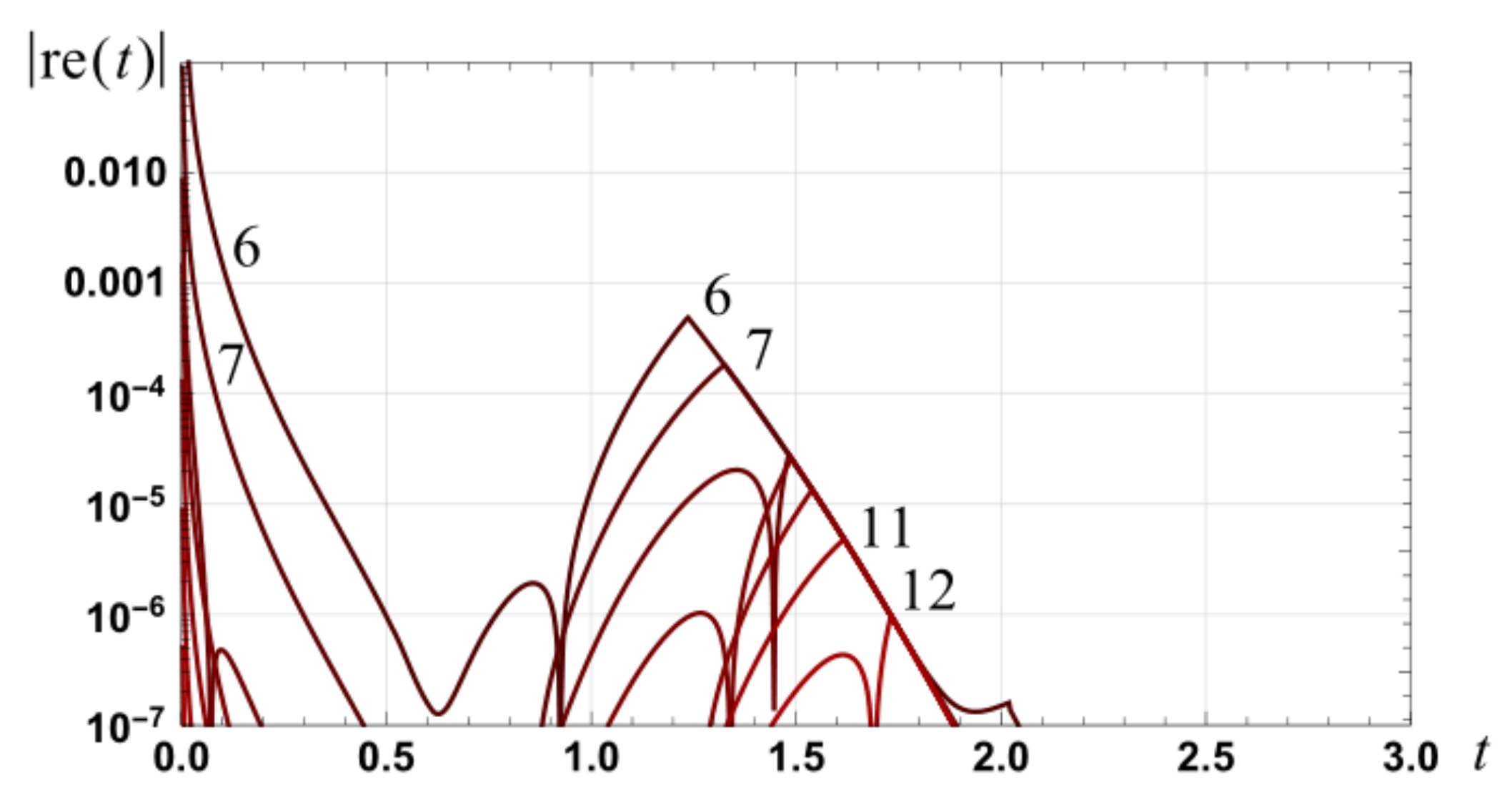
Figure 11.
Illustration of areas comprising erf(x).
Figure 11.
Illustration of areas comprising erf(x).
Figure 12.
Graph of the relative error bound, versus the order of approximation, for various set resolutions.
Figure 12.
Graph of the relative error bound, versus the order of approximation, for various set resolutions.
Figure 13.
Graph of the relative errors, based on a resolution of , in second to fourth order approximations to erf(x).
Figure 13.
Graph of the relative errors, based on a resolution of , in second to fourth order approximations to erf(x).
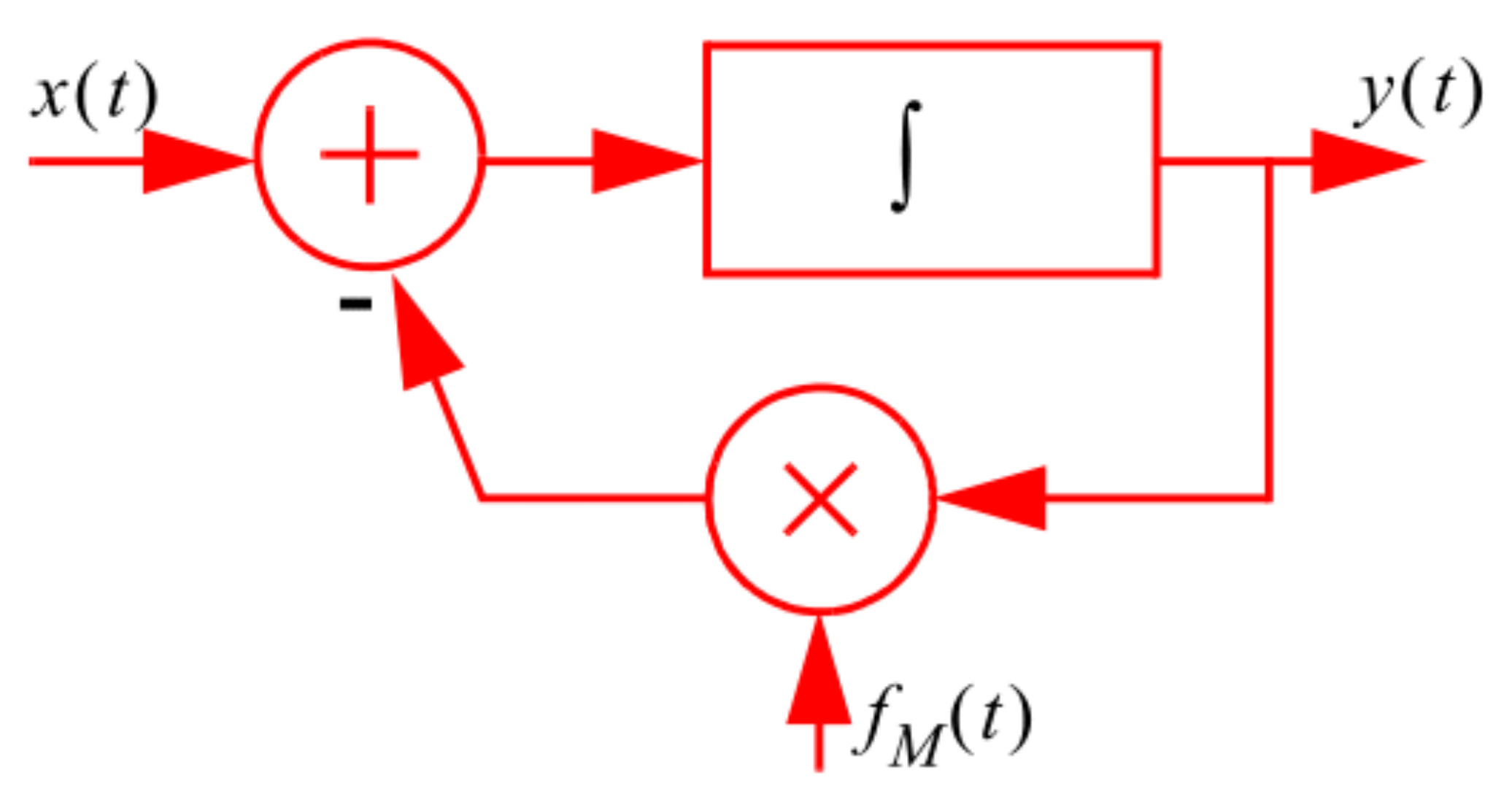
Figure 14.
Feedback system with dynamically varying (modulated) feedback.
Figure 14.
Feedback system with dynamically varying (modulated) feedback.
Figure 15.
Graph of the relative errors in approximations, of orders one to eight, to erf(x) as defined in Theorem 7.
Figure 15.
Graph of the relative errors in approximations, of orders one to eight, to erf(x) as defined in Theorem 7.
Figure 16.
Graph of the magnitude of the relative errors in approximations to exp(−x2), as defined by Equation (103), of orders 0, 2, 4, 6, 8, 10 and 12. The dotted curves are the relative errors associated with Taylor series of orders 1, 3, 5, 7, 9, 11, 13 and 15.
Figure 16.
Graph of the magnitude of the relative errors in approximations to exp(−x2), as defined by Equation (103), of orders 0, 2, 4, 6, 8, 10 and 12. The dotted curves are the relative errors associated with Taylor series of orders 1, 3, 5, 7, 9, 11, 13 and 15.
Figure 17.
Relative error in upper and lower bounds to erf(x) as, respectively, defined by Equation (110)–(112). The parameters p = 1 and q = π/4 have been used for the bounds defined by Equation (110).
Figure 17.
Relative error in upper and lower bounds to erf(x) as, respectively, defined by Equation (110)–(112). The parameters p = 1 and q = π/4 have been used for the bounds defined by Equation (110).
Figure 18.
Relative error in the approximations and to erf(x) where the residual function is approximated by the stated order.
Figure 18.
Relative error in the approximations and to erf(x) where the residual function is approximated by the stated order.
Figure 19.
Relative error in the approximations and to erf(x) where the residual function is approximated by the stated order.
Figure 19.
Relative error in the approximations and to erf(x) where the residual function is approximated by the stated order.
Figure 20.
Graph of the signals and erf(x)2.
Figure 20.
Graph of the signals and erf(x)2.
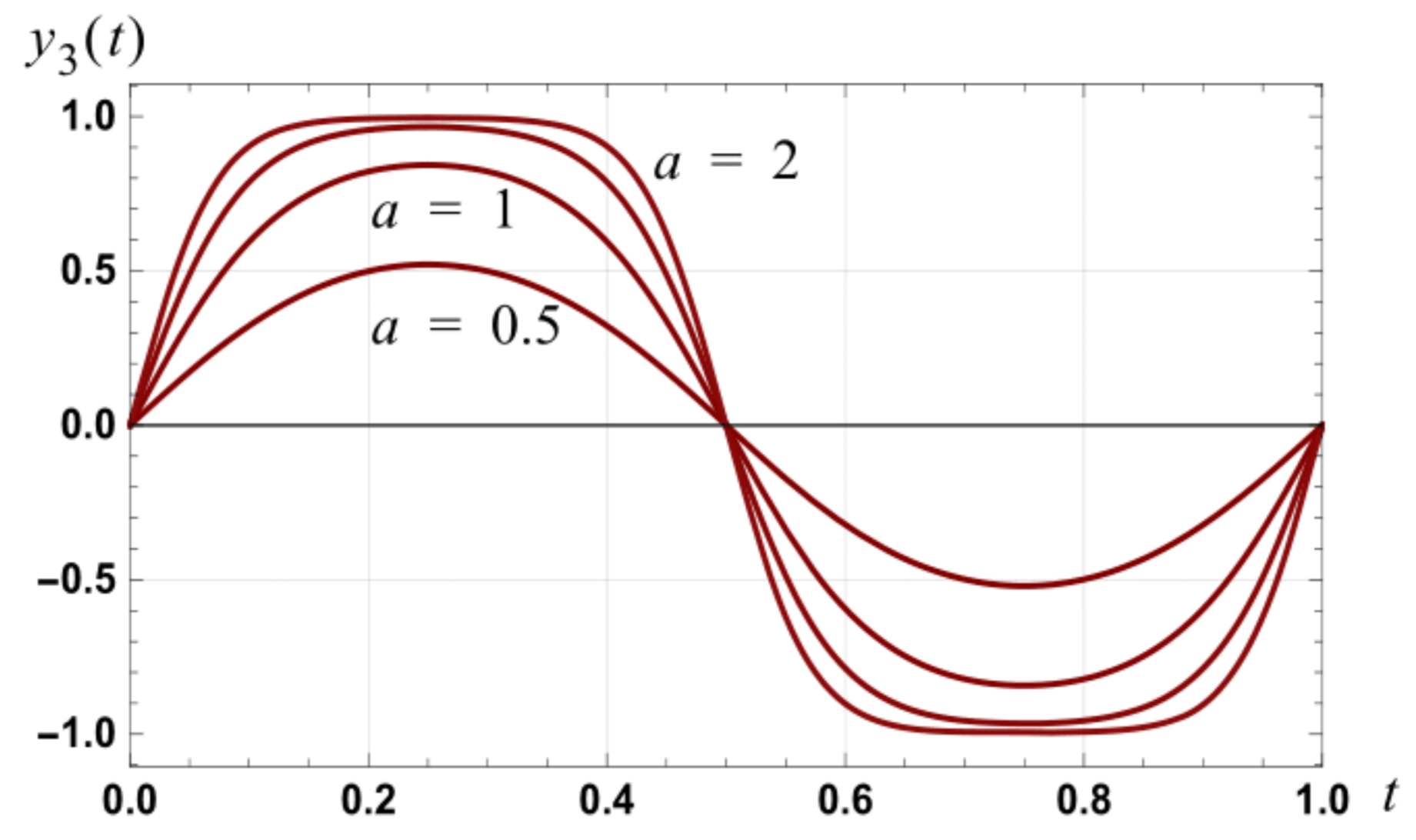
Figure 21.
Graph of for the case of and for amplitudes of a = 0.5, a = 1, a = 1.5 and a = 2.
Figure 21.
Graph of for the case of and for amplitudes of a = 0.5, a = 1, a = 1.5 and a = 2.
Figure 22.
Graph of the input power, output power and ratio of output power to input power as the amplitude of the input signal varies.
Figure 22.
Graph of the input power, output power and ratio of output power to input power as the amplitude of the input signal varies.
Figure 23.
Graph of the variation of harmonic distortion with amplitude.
Figure 23.
Graph of the variation of harmonic distortion with amplitude.
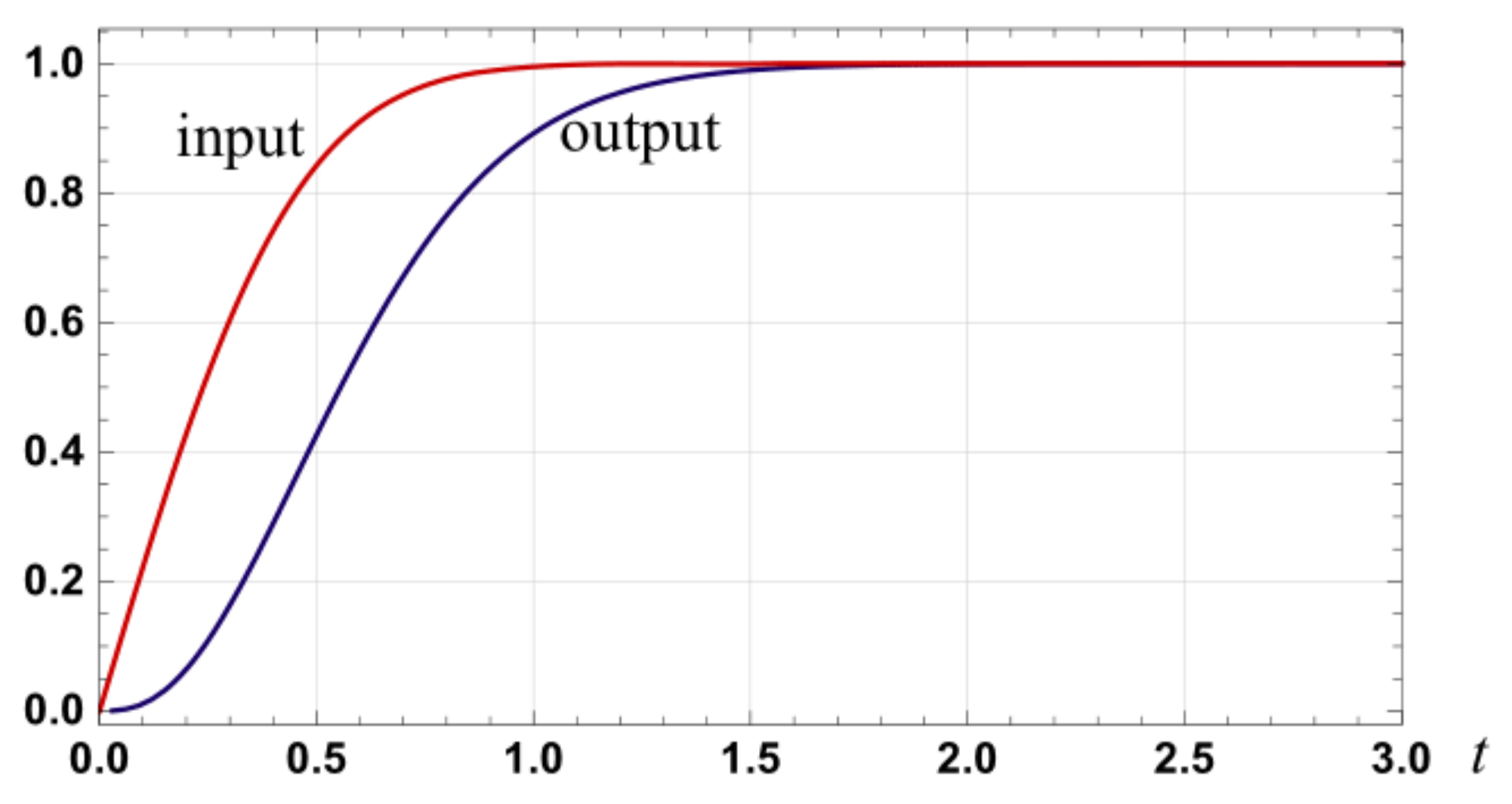
Figure 24.
Graph of the input signal , and the corresponding approximation to the output of a second order linear filter with , .
Figure 24.
Graph of the input signal , and the corresponding approximation to the output of a second order linear filter with , .
Figure 25.
Graph of the relative errors associated with the output signal, shown in
Figure 24, for approximations to the error function (Equation (56)) of orders six to twelve which utilize optimum transition points.
Figure 25.
Graph of the relative errors associated with the output signal, shown in
Figure 24, for approximations to the error function (Equation (56)) of orders six to twelve which utilize optimum transition points.
Table 1.
Examples of published approximations for , . For the third and second last approximations, the coefficient definitions are detailed in the associated reference. The stated relative error bounds arise from sampling the interval [0, 5] with 10,000 uniformly spaced points.
Table 1.
Examples of published approximations for , . For the third and second last approximations, the coefficient definitions are detailed in the associated reference. The stated relative error bounds arise from sampling the interval [0, 5] with 10,000 uniformly spaced points.
| # | Reference | Approximation | Relative Error Bound |
| 1 | Taylor series | | |
| 2 | Abramowitz [21], p. 297, Equation (7.1.6) | | |
| 3 | Abramowitz [21], p. 299, Equation (7.1.26) | | 8.09 × 10−6 |
| 4 | Menzel [14] and Nadagopal [22] | | 7.07 × 10−3 |
| 5 | Bürmann series [23], Equation (33) | | 3.61 × 10−3 |
| 6 | Winitzki [24], Equation (3) | | 3.50 × 10−4 |
| 7 | Soranzo [25], Equation (1) | | 1.20 × 10−4 |
| 8 | Vedder [26], Equation (5) | | 4.65 × 10−3 |
| 9 | Vazquez-Leal [27], Equation (3.1) | | 1.88 × 10−4 |
| 10 | Sandoval-Hernandez [13], Equation (23) | | 3.05 × 10−5 |
| 11 | Abrarov [28], Equation (16) | | 3.27 × 10−3
(N = 6) |
Table 2.
Residual functions associated with approximations for , .
Table 2.
Residual functions associated with approximations for , .
| # | Error Function | Residual Function |
| 1 | | |
| 2 | | |
| 3 | | |
Table 3.
The transition points, , and the resulting relative error bounds for the spline-based approximations specified by Equation (56). The transition points are based on sampling the interval [0, 5] with 10,000 points.
Table 3.
The transition points, , and the resulting relative error bounds for the spline-based approximations specified by Equation (56). The transition points are based on sampling the interval [0, 5] with 10,000 points.
| Approx. Order: n | Transition Point for | Relative Error Bound for | Transition Point for | Relative Error Bound for |
| 0 | 1.3085 | 0.0851 | 1.465 | 0.0400 |
| 1 | 1.492 | 0.0362 | 1.769 | 0.0126 |
| 2 | 1.658 | 1.95 × 10−2 | 1.929 | 6.42 × 10−3 |
| 3 | 1.8975 | 7.36 × 10−3 | 2.1725 | 2.13 × 10−3 |
| 4 | 2.3715 | 1.03 × 10−3 | 2.6305 | 2.28 × 10−4 |
| 6 | 2.4715 | 4.75 × 10−4 | 2.73 | 1.13 × 10−4 |
| 8 | 2.963 | 2.79 × 10−5 | 3.1855 | 6.69 × 10−6 |
| 10 | 3.0785 | 1.35 × 10−5 | 3.324 | 2.59 × 10−6 |
| 12 | 3.4625 | 9.78 × 10−7 | 3.67 | 2.12 × 10−7 |
| 14 | 3.5845 | 4.00 × 10−7 | 3.8205 | 6.57 × 10−8 |
| 16 | 3.9025 | 3.44 × 10−8 | 4.101 | 6.66 × 10−9 |
| 18 | 4.0285 | 1.22 × 10−8 | 4.257 | 1.75 × 10−9 |
| 20 | 4.300 | 1.20 × 10−9 | 4.493 | 2.11 × 10−10 |
| 22 | 4.429 | 3.76 × 10−10 | 4.652 | 4.75 × 10−11 |
| 24 | 4.6655 | 4.18 × 10−11 | 4.854 | 6.70 × 10−12 |
Table 4.
The transition points, and resulting relative error bounds, for Taylor series approximations specified by Equation (59). The transition points are based on sampling the interval [0, 4] with 10,000 points.
Table 4.
The transition points, and resulting relative error bounds, for Taylor series approximations specified by Equation (59). The transition points are based on sampling the interval [0, 4] with 10,000 points.
| Order:
| | |
| 1 | 0.8864 | 0.266 |
| 3 | 1.078 | 0.146 |
| 5 | 1.222 | 0.0917 |
| 7 | 1.344 | 0.0609 |
| 9 | 1.4532 | 0.0416 |
| 13 | 1.6452 | 0.0204 |
| 17 | 1.8144 | 0.0105 |
| 21 | 1.9672 | 5.44 × 10−3 |
| 25 | 2.1084 | 2.89 × 10−3 |
| 29 | 2.24 | 1.55 × 10−3 |
| 37 | 2.4812 | 4.53 × 10−4 |
| 45 | 2.70 | 1.35 × 10−4 |
| 53 | 2.902 | 4.09 × 10−5 |
| 61 | 3.09 | 1.24 × 10−5 |
Table 5.
Transition point and relative error bound for the four equal subintervals case. The transition points are based on sampling the interval [0, 8] with 10,000 points.
Table 5.
Transition point and relative error bound for the four equal subintervals case. The transition points are based on sampling the interval [0, 8] with 10,000 points.
| Spline Order | Transition Point | Relative Error Bound |
|---|
| 0 | 2.7016 | 5.32 × 10−3 |
| 1 | 3.292 | 7.21 × 10−5 |
| 2 | 3.4544 | 1.27 × 10−6 |
| 4 | 3.7208 | 1.43 × 10−7 |
| 8 | 4.6616 | 4.34 × 10−11 |
| 12 | 5.6784 | 9.75 × 10−16 |
| 16 | 6.3736 | 2.01 × 10−19 |
| 20 | 7.1544 | 4.62 × 10−24 |
| 24 | 7.7136 | 1.06 × 10−27 |
Table 6.
Transition point and relative error bound for the 16 equal subintervals case. The transition points are based on sampling the interval [0, 12] with 10,000 points.
Table 6.
Transition point and relative error bound for the 16 equal subintervals case. The transition points are based on sampling the interval [0, 12] with 10,000 points.
| Spline Order | Transition Point | Relative Error Bound |
|---|
| 0 | 5.5008 | 3.32 × 10−4 |
| 1 | 6.8796 | 2.82 × 10−7 |
| 2 | 7.0224 | 3.14 × 10−10 |
| 4 | 7.1544 | 4.82 × 10−16 |
| 8 | 7.5996 | 6.22 × 10−27 |
| 12 | 8.2032 | 4.16 × 10−31 |
| 16 | 8.9244 | 1.66 × 10−36 |
| 20 | 9.7284 | 4.68 × 10−43 |
| 24 | 10.584 | 1.21 × 10−50 |
Table 7.
Coefficient values for the case of .
Table 7.
Coefficient values for the case of .
| k | Definition for | |
| 1 | | 5.204998778 × 10−1 |
| 2 | | 3.222009151 × 10−1 |
| 3 | | 1.234043535 × 10−1 |
| 4 | | 2.921711854 × 10−2 |
| 5 | | 4.270782964 × 10−3 |
| 6 | | 3.848615204 × 10−4 |
| 7 | | 2.134739863 × 10−5 |
| 8 | | 7.276811144 × 10−7 |
| 9 | | 1.522064186 × 10−8 |
| 10 | | 1.950785844 × 10−10 |
| 11 | | 1.530101947 × 10−12 |
| 12 | | 7.336328181 × 10−15 |
Table 8.
Relative error bounds, over the interval , for approximations to as defined in Theorem 7.
Table 8.
Relative error bounds, over the interval , for approximations to as defined in Theorem 7.
| Order of Approx. | Relative Error Bound: Original Series—Optimum Transition Point (Table 3) | Relative Error Bound: Approx. Defined by Equation (83) |
| 0 | 0.0851 | 2.68 × 10−2 |
| 1 | 0.0362 | 3.98 × 10−3 |
| 2 | 1.95 × 10−2 | 1.34 × 10−3 |
| 3 | 7.36 × 10−3 | 2.03 × 10−4 |
| 4 | 1.03 × 10−3 | 1.82 × 10−5 |
| 6 | 4.75 × 10−4 | 9.20 × 10−7 |
| 8 | 2.79 × 10−5 | 1.69 × 10−8 |
| 10 | 1.35 × 10−5 | 7.43 × 10−10 |
| 12 | 9.78 × 10−7 | 1.67 × 10−11 |
| 14 | 4.00 × 10−7 | 6.47 × 10−13 |
| 16 | 3.44 × 10−8 | 1.68 × 10−14 |
| 18 | 1.22 × 10−8 | 5.90 × 10−16 |
| 20 | 1.20 × 10−9 | 1.73 × 10−17 |
| 22 | 3.76 × 10−10 | 5.56 × 10−19 |
| 24 | 4.18 × 10−11 | 1.79 × 10−20 |
Table 9.
Approximations that are consistent with a set relative error bound. The actual relative error bound is specified by .
Table 9.
Approximations that are consistent with a set relative error bound. The actual relative error bound is specified by .
| Relative Error Bound | Spline Approx: Theorem 4 | Variable Interval Approx: Theorem 5 | Dynamic Constant Plus Spline Approx: Theorem 6 | Iterative Approx: Theorem 7 |
| 10−6 | | | | |
| 10−10 | | | | |
| 10−16 | | | | |
Table 10.
Relative error bounds for approximations over the interval .
Table 10.
Relative error bounds for approximations over the interval .
| Order of Approx. | Relative Error Bound: Equation (103) | Relative Error Bound: Equation (77) of [19] |
| 0 | 8.00 | 35.6 |
| 1 | 3.74 | 6.98 |
| 2 | 0.957 | 0.767 |
| 3 | 1.25 × 10−1 | 5.25 × 10−2 |
| 4 | 8.04 × 10−3 | 2.42 × 10−3 |
| 5 | 7.71 × 10−3 | 7.98 × 10−5 |
| 6 | 2.09 × 10−3 | 1.97 × 10−6 |
| 7 | 3.72 × 10−4 | 3.75 × 10−8 |
| 8 | 5.02 × 10−5 | 5.69 × 10−10 |
| 10 | 4.54 × 10−7 | 7.22 × 10−14 |
| 12 | 1.09 × 10−9 | 4.62 × 10−18 |