Abstract
Thermal simulations are an important part of the design process in many engineering disciplines. In simulation-based design approaches, a considerable amount of time is spent by repeated simulations. An alternative, fast simulation tool would be a welcome addition to any automatized and simulation-based optimisation workflow. In this work, we present a proof-of-concept study of the application of convolutional neural networks to accelerate thermal simulations. We focus on the thermal aspect of electronic systems. The goal of such a tool is to provide accurate approximations of a full solution, in order to quickly select promising designs for more detailed investigations. Based on a training set of randomly generated circuits with corresponding finite element solutions, the full 3D steady-state temperature field is estimated using a fully convolutional neural network. A custom network architecture is proposed which captures the long-range correlations present in heat conduction problems. We test the network on a separate dataset and find that the mean relative error is around 2% and the typical evaluation time is 35 ms per sample (2 ms for evaluation, 33 ms for data transfer). The benefit of this neural-network-based approach is that, once training is completed, the network can be applied to any system within the design space spanned by the randomized training dataset (which includes different components, material properties, different positioning of components on a PCB, etc.).
1. Introduction
Physics simulations are becoming an essential aspect in the design of electronic systems. For an optimally designed electronic system, the interplay of many different physical domains has to be taken into account. For instance, electronic and thermal co-simulations for the design of an efficient power converter have been studied in [1]. Such coupled simulations lead, however, to large computational requirements. Often, the long simulation time render automatic optimizations of designs impossible.
Machine learning (ML) techniques are possible candidates to increase the computational speed. The application of ML techniques to the design of electronic systems focuses mainly on two aspects [2]. The first aims at reducing the number of required design iterations [3,4]. For example, a genetic algorithms required around 1000–10,000 FEM simulations to find the optimal placement of a chip in a system [5], which takes a considerable amount of computation time. Alternatively, ML is used to accelerate the evaluation of individual designs, i.e., replace the time consuming simulations by neural networks [6,7,8,9].
In addition to thermal simulations, NNs are successfully applied to perform many types of physics simulations. For instance, NNs have been explored for fluid dynamics problems [10,11,12], for electro-convection [13], transport problems [14,15], magnetic field estimation [16], classical mechanics [17] and in replicating multi-particle evolutions by learning the pair-wise interaction function [18].
Recent works aim at embedding prior physics knowledge in machine learning: For physics-informed NNs (PINNs) the physics knowledge is used to guide the convergence of the NN towards physics conforming solutions [19]. Typically, the auto-gradient feature of the NN is used to construct a loss term based on the underlying differential equation. PINNs led to promising results in many areas of computational science [20,21,22,23,24,25,26]. A review on the application of PINNs to heat transfer problems can be found here [27]. In this work we follow an alternative way to include some physics knowledge: The NN architecture is chosen such that it forces the output to satisfy physical constraints [19]. For instance, purely convolutional networks automatically preserve translational invariance [28].
Although realistic systems are three-dimensional, ML-based physics simulations have mostly focused on lower-dimensional approximations. Especially, the representation of three-dimensional full-field solutions for complex geometries remains a challenge. One technical difficulty when going from 2D to 3D systems is the limited memory of the GPUs [29]. A way to ensure a low memory requirement could be to use a more suitable representation of the geometry instead of a stack of images [30]. Although some alternatives, like point clouds based on CAD geometries [31,32,33] or octrees were proposed [34], most available NN architectures are still developed for images.
The main contribution of this paper is to explore, for the first time, the approximation of the 3D temperature distribution in an electronic system with complex geometry using NNs. Note that in [35] the thermal problem on a 3D chip was studied but in a much more simplified setting than we consider in this work. In addition to the difficulties discussed above related to memory limitations, another major obstacle when studying 3D systems is the generation of enough high quality training data. We have developed an automatized workflow that creates 3D CAD geometries representing electronic circuits and performs meshing and FEM simulations on them. The workflow generates data in a form suitable for ML requiring no human intervention. In this first proof-of-concept study, we focus on FEM solutions for the steady-state, equilibrium thermal configuration of the systems.
The paper is organized as follows. In Section 2.1, we describe our workflow for the data generation and discuss how the postprocessing of CAD geometries and FEM results into ML training data is performed. The chosen NN architecture and the objective function is discussed in Section 2.2. We present our results and conclusions in Section 3 and Section 4, respectively. Details on the generation of the training and evaluation datasets are given in Appendix A. For completeness, the general aspects of NNs most relevant for the understanding of this work are discussed in the Appendix B.
2. Materials and Methods
2.1. Dataset Generation
In this work a fully-convolutional neural network (FCN) was trained to approximate, on 3D electronic systems, the FEM solution of the time-independent heat equation
where is the density, k the heat conductivity and h a heat source. We use supervized learning, which requires a large dataset of random systems with corresponding FEM solutions. The dataset needs to be representative of the design space. This entails that all properties that one wants to change during the design process (component type/number/placement, material properties, heat sink specifications, external temperature), were randomized in the dataset. In total, 464 unique systems were generated using an automatized workflow in python (see Figure 1 for a graphical summary) consisting of the following steps:
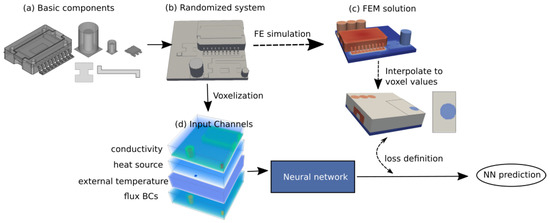
Figure 1.
Illustration of the automatized workflow: Randomized systems are generated by randomly choosing and placing basic components. After assigning randomized material properties and BC values, the system is voxelized to create a stack of four 3D-images as input for the NN. Solutions for the supervized training procedure are created using FE simulations.
- (1)
- System generation: For each system the number and type of basic components were randomly chosen and they were placed at random locations on a PCB. Material parameters were assigned to the different parts of each component.
- (2)
- Generation of FEM solutions: A constant temperature was set at the bottom of the PCB . A heat sink on top of the large IC was mimicked by a heat flux boundary condition. All other outer surfaces were modelled as heat flux boundaries to air. For each of the created systems, an external temperature and heat transfer coefficient to air and for the sink were randomly chosen. Heat sources (i.e., electric losses) with random magnitude were assigned to some of the components. The systems were meshed. FEM simulations were performed to obtain the temperature solutions.
- (3)
- Voxelization: During postprocessing the systems and the FEM solutions were converted to a set of 3D images per system as input for the NN. Four 3D-images were created per system, one for the distribution of a material property, the external temperature, the heat sources and the heat transfer coefficient.
Detailed information on the individual steps for generating the systems can be found in Appendix A.
2.2. NN Architecture
A 3D fully-convolutional NN is used. The input of the NN consists of 4-channel 3D images and the output is a single-channel 3D temperature image.
As discussed in Section 1, a major constraint for designing an appropriate NN architecture comes from the limited GPU memory. A batch of the input images requires already a significant amount of the available memory. Thus, a network with a relatively small number of parameters is required to be trainable. Therefore, instead of applying a general-purpose network, the NN architecture must be chosen to match the physical problem.
An initial rough design of the architecture was based on physical arguments and some manual exploration, that we discuss next. Once the rough design was fixed, an automatic exploration of the remaining free parameters was performed (e.g., kernel size, type of activation, number of skip connections, etc.). The impact of this fine-tuning was not very large (of the order of a percent in the relative loss, see below).
2.2.1. Properties of Heat Propagation
During the design of the architecture, we found it instructive to explore exact analytical solutions of the heat equation, even though they apply in very idealized situations only. For example, the 1D heat kernel solution of the (time-dependent) heat equation reads
Inspecting the heat kernel solution, it is possible to anticipate (1) the presence of exponentials as a general feature of solutions of the heat equation, and (2) the fact that the contributions from different spatial points are aggregated via an integral. These two features are reflected in the NN architecture by means of the choice of activation functions and what we refer to as fusion blocks, as described next.
2.2.2. Long-Range Correlations. Fusion Blocks
One of the most important aspects, that the NN must capture in order to successfully approximate the steady-state temperature distribution is the presence of long-range effects. Most of the convolutional NNs (CNNs) available in the literature have been developed for the classification of images (in the case of 2D CNNs) or of video sequences (in the case of 3D CNNs). The performance of several of the standard low-resource 3D CNNs (e.g., SqueezeNet [36]) on the dataset described in Section 2.1 was analyzed but the temperature fields obtained with such networks were very sharp, not resembling a realistic situation where around a hot spot a temperature gradient is to be expected. Moreover, heat propagation from a heat source to a distant but thermally connected point in the system was absent.
To recover the long-range effects in the system, convolutional layers with large dilations were applied. Dilations have been used previously, for example in [16], to capture long-range correlations without increasing the convolutional kernel size. The maximum dilations in the Fusions were chosen such that the receptive field of the NN spans the whole system size (see Figure 2). This is required since in the steady-state case the temperature at a point can depend on any (arbitrarily) far away point in the system. The kernel sizes were chosen small ( or 4) since the NN parameters and the size of the backpropagation tree, and, thus, the required GPU memory for training, increase quickly with the kernel sizes.
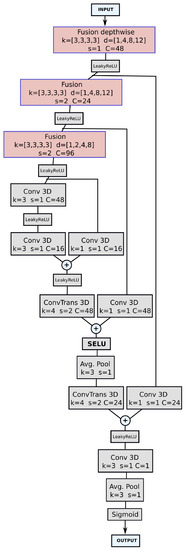
Figure 2.
Architecture used in this work. In each block, k refers to the kernels size, s to the stride, d to the dilations and C to the output channels of each layer (the same for all dimensions). See Section 2.2 for further details.
Moreover, as stressed in Section 2.2.1, the solution is an aggregation of long-range effects (via an integration in the case of the heat kernel solution). To enable these aggregations in the network we defined “Fusion blocks”: Each fusion block is composed of N 3D convolutional layers with different dilations . The result of those convolutions is concatenated along the channel dimension. An illustration of a simple (2D) fusion block is shown in Figure 3.
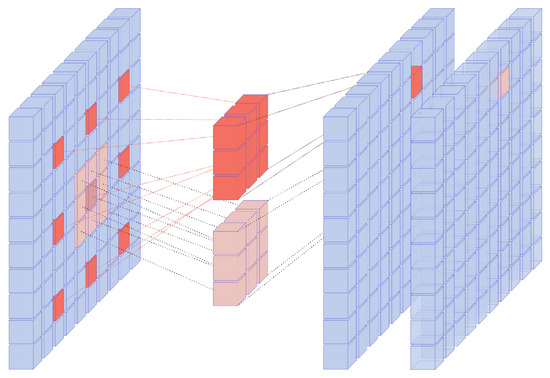
Figure 3.
Schematic representation of the action of a 2D fusion block consisting of two convolutional layers with 3 × 3 kernels and dilations 3 and 1.
The fusion block turned out to be the decisive element to obtain realistic and accurate enough predictions from the network.
2.2.3. Choice of Activation Functions
From the heat kernel solution, it can be seen that general solutions contain exponential functions. To approximate that feature, whilst keeping the network small, it is convenient to use non-linearities (activation functions) that contain an exponential. Using too many of them, however, turns out to be damaging for the performance of the network. The reason is that, several consecutive layers containing an exponential function lead to a -type functions acting on the input. After some exploration, a SELU activation function [37] was chosen for one of the layers only (see Figure 2). For the rest of the layers a LeakyReLU [38] was used.
The impact of using a SELU was not large and it mostly helped in achieving the desired accuracy with less training epochs.
2.2.4. Input to the Network
The input of NNs is typically rescaled to be in the range since that makes the training of the networks more stable numerically. In this work, a more physically meaningful rescaling scheme was chosen. Characteristic values were introduced for each of the relevant dimensional quantities: the maximum heat power , the maximum temperature , and a length scale . Note, that the maximum values defined here do not represent a hard limit at which the network will fail to work since the network does not strictly require all values to be smaller than one.
The dimensionless channels are then defined as:
where is the total volume of the sub-part where the heat density is applied (e.g., the die volume of an IC), and is the total surface area over which the heat transfer is specified (e.g., the surface area of the heat sink). The Dirichlet boundary condition is not fed to the network as an input channel, but softly imposed via the loss (see Section 2.2.6).
2.2.5. Network Architecture
We performed a fairly thorough (manual and automatic) exploration of possible network architectures containing the features discussed so far. We assessed manually the impact of using Fusion layers or not. Furthermore, after several numerical experiments we concluded that:
- Too many downsampling layers had a damaging effect on the accuracy of the output. Downsampling in CNNs is used to extract useful features from images. In our case, the most relevant features are already part of the input, as discussed above. The main reasons for downsampling in our case are to aggregate long-range effects in addition to the dilation in the fusion blocks, and to reduce the memory requirements. Thus, only two downsampling layers were used.
- As is well known in FCNs, skip connections help avoid the usual checkerboard artifacts in the output. In this work we found that using three additive skip connections led to the best results. We had skip connections from the output of the fusion blocks to the input of the two upsampling layers (transpose convolutions) and the final convolutional layer, respectively.
- An initial depthwise fusion block (depthwise means that channels are not mixed) provides the necessary additional preprocessing of the input data.
This fixed the rough architecture. The optimal size of the kernels, dilation values and the type of activations (except for the SELU unit) were found using an automatic optimisation.
As a result, we propose the architecture shown in Figure 2. In the figure, k refers to the kernels size, s to the stride, d to the dilations and C to the output channels of each layer (the same for all dimensions). This network has only ∼370 K trainable parameters, which is a tiny number compared to standard architectures. For comparison, the 3D version of SqueezeNet [36,39], which was designed to be a small network, has 2.15 M parameters).
2.2.6. Objective Function and Training Process
For the loss function a mean relative loss term, , was combined with a penalty term for the Dirichlet boundary condition at the bottom layer of the PCB (). Here, and are the temperature distributions predicted by the NN and obtained from the FEM simulation, respectively. The air region was excluded from the loss evaluation because no FEM solution is available there. A physics-informed loss as proposed by [12] did not improve the solutions. In fact, it drove the system to a uniform temperature distribution since in all parts of the system where no heat source is present, the differential heat equation error can be minimized by minimizing the temperature gradient. This is somewhat unexpected and further exploration on physics-informed losses for the present problem will be the subject of future work.
We trained the network using the RMSProp optimiser [40] with a batch size of 7. The network is trained in several steps. First a warm-up period of ∼10 epochs, with a learning rate of . After that only the Fusion layers are trained (with all other layers frozen) for 10 more epochs at a learning rate of . Next the Fusions are frozen and everything else is trained for 10 epochs at a learning rate of . Finally the network is trained for 100–200 epochs, with a decreasing learning rate from down to . Each epoch takes approximately 10 min.
3. Results
The size of the dataset was increased by four without further computational effort via three 90 degree in-plane rotations of each system, so that the total dataset consisted of 1856 systems. of the generated dataset was used as training set and the remaining as test set. It is the accuracy in reproducing the latter that truly measures the quality of the network solution. Thus, all results reported in this section are taken from the test set.
The mean relative error per system is at the percent level, with values below in most systems in the test set: This can be seen in Figure 4, where a histogram of all systems of the test set binned according to their corresponding error is shown. Additionally, the Dirichlet BC at the bottom of the PCB was fulfilled by the network with an average relative error of . The present work was intended as a proof-of-principle for an NN-based tool to evaluate the viability of potential system designs from a thermal point of view. The obtained accuracies are judged good enough for that goal.
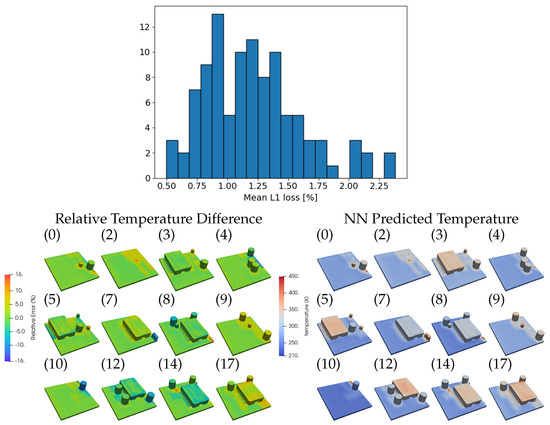
Figure 4.
Histogram of the average relative error per test system (top). Below the temperature distributions estimated by the NN (right) and the relative temperature difference (left) for selected systems of the test dataset (the corresponding error bin of the histogram is indicated in brackets, from 0 indicating the lowest mean error to 19 for the worst mean error). The average relative error (top) is the mean of the absolute values of the relative temperature differences (bottom left) per sample.
The mean value of the relative error, however, does not fully represent the (in-)accuracy of the NN results, as large but very localized error values can be smeared out when averaging over the large number of voxels in a system. More insightful is thus to compare FEM and NN solutions directly in their 3D representations. In Figure 4, a representative collection of 3D solutions and 3D maps of the relative temperature differences is shown, picking one sample from most of the bins in the histogram discussed above, as indicated in the figure. For the majority of systems the NN solution reproduces the FEM solution reasonably well. The main discrepancies appear in relation with the small chip and on the surfaces of the components and the PCB.
Further details are shown in Figure 5, where a section of a selected system is presented. There, on the surface of the PCB and also around the small chip, the error is somewhat larger. Furthermore, in the inner part of the large chip some localized discrepancies can be seen, which are a reminiscence of the checkerboard artefacts of FCNs. However, these are clearly localized and do not affect the overall temperature of the chip.

Figure 5.
FE solution (left), NN prediction (center), and relative error of the temperature distribution (right) on a horizontal cut of a selected system. High predictive errors are mostly found on the surface of the system while the internal temperature distribution is well represented.
The second aspect to consider when judging whether the presented NN approach is a valuable tool in the design workflow of electronic systems is the evaluation speed. In Table 1, a comparison of the evaluation speeds between the NN and the FEM solutions is shown. The NN was run on an NVIDIA Titan RTX GPU whilst the FEM solver was run on a single thread of an Intel Xeon W-2145 CPU. This implies that the FEM evaluation time in Table 1 does not correspond to the time a fully optimized and parallelized FEM simulation would require. Nevertheless, we see that the NN provides a solution in ∼35 ms (with most of the time, in fact, used in transferring the 3D system to the GPU memory), which is certainly a significant speed-up over any conceivable full-field 3D FEM simulation.

Table 1.
Average evaluation time for a NN solution and a FEM solution (note that, the time for the FEM simulation is not taken from a performance-optimized solver).
This high evaluation speed comes at the cost of creating a training data set and training the network. The time to create one system of the training/testing data set was about 17 min. The systems were created fully automatized, creating 8 systems in parallel, so that in one day the full data set was created without requiring any manual intervention. Note, that the workflow was not optimized for performance, 90% of the time was used for the system creation in FreeCAD and preprocessing the system (meshing, identifying surfaces to apply the BCs, etc.). The voxelization of the system took only fractions of a second. Thus, approximating FEM simulations with NNs is clearly not the right approach if only the result of one specific system is of interest. However, possible application scenarios could lie in design applications, where the impact of design variations could be studied in real time using pre-trained NNs.
It is worth discussing now some of the limitations of the FCN architecture suggested in this work. The first limitation stems from the fact that the architecture sets the maximum effective receptive field on the input images, which is determined by the combination of maximum dilation and number of downsamplings. Thus, even though the architecture is fully convolutional—which implies that it can immediately process larger systems than those it has been trained on—it will not be able to capture any heat transfer effects over larger distances than those covered in the original receptive field. We have not tested what the implications of this limitation are. A second limitation arises from the typical length scales in the system. A minimum length scale is implicitly set by choosing the voxel resolution and, in principle, if a different voxel resolution has to be chosen the network would have to be retrained. The voxelized representation of the systems has, however, the advantage that no tedious and time consuming meshing and preprocessing is required for the evaluation of the NN on a system.
The main advantage of the approach presented here is that, once the network has been trained, it can approximate the temperature field of any system within the design space spanned by the randomized training dataset. This means that the network can be applied to systems with different number of components, different placement of those components, different material properties and different BCs than those it has been trained on. Therefore, the simulation time spent in generating the dataset is compensated by the gain in future simulations, as long as many of them are needed for a certain design task.
Confidence Estimation
Finally, we would like to discuss a possible confidence estimator for the NN solutions. The goal of a confidence estimator in this context is to assess the quality of the NN approximation when no FE result exists to compare with, as would be the case in any realistic use of our tool.
Our suggested confidence estimator is based on an integral form of the steady-state heat equation
where Gauss’ theorem was used to transform the integral over the system volume V to a surface integral in the first term. Since the NN prediction is available at each voxel, the equation is discretized to obtain an approximation per voxel e
For the temperature gradient , the finite difference of the temperature (as predicted by the NN) of the voxel under consideration and its adjacent voxel (in the direction of the normal ) is inserted. If the two voxels have differing k values a piece-wise linear interpolation of the temperature was used. The bottom of the PCB is kept at a fixed temperature. On all other outer surfaces the flux boundary condition is included by evaluating the first term with:
This heat equation error should measure the local violation of the steady-state heat equation. If the net heat flux of a voxel is non-zero this implies that the temperature obtained from the NN does not represent a steady state.
The local loss values are compared with the local heat equation error for a particular sample (Figure 6) for different sections of the system in the z-direction. The proposed estimator appears to qualitatively identify many of the regions where the error of the NN estimation of the temperature map is high compared to the FEM solution. It is also apparent, however, that not all voxels with high error values are identified.
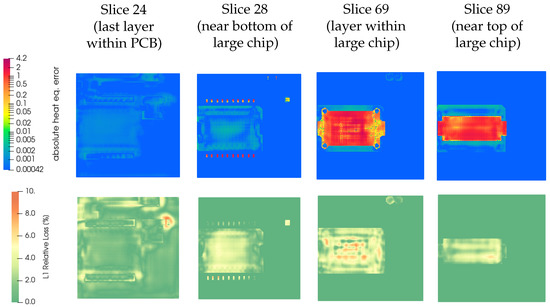
Figure 6.
Comparison of the heat equation error (top row), which can be used as error predictor if no FE solution is available, and the error (bottom row) on selected slices from bottom to top (left to right). The heat equation error is able to indicate most of the regions with high error. It illustrates the checkerboard pattern expected from purely convolutional networks. Since the heat equation error is defined via the local imbalance of heat fluxes and sources, the detected errors can be slightly more localized compared to the actual error (e.g., orange points in slice 69, top compared to bottom).
Moreover, the estimator does not provide a clear quantitative measure of the error. The absolute values of the heat equation error are much larger in regions with high k than in regions with lower k. This could indicate that the piece-wise linear interpolation used for the approximation of the temperature is not a good estimation of the actual temperature distribution. However, at the current state, it is not possible to use higher order approximations since they would require more voxels per uniform-k region, which in turn conflicts with the limited RAM available on the GPU.
More research in the direction of finding a confidence estimator is clearly needed.
4. Conclusions
An approach to quickly approximate the full-field temperature distribution of 3D electronic system using neural networks was proposed. The range of validity of the developed network spans a realistically wide range of material parameters and heat sources. Additionally, the network was trained to work with systems built with any number of the basic components at any position in the system.
The network proposed is able to provide a simulation result in an evaluation time of the order of milliseconds. The relative error achieved, when compared to a standard FEM simulation, is around averaged over the whole system, with larger errors localized mostly on the surfaces of the components.
Finally we motivated a possible criterion for estimating the confidence of a prediction based on an integral version of the heat equation. Even though the criterion proposed does not allow for a quantitative estimate of the error of a given prediction, it may be used to identify regions with large estimation errors.
Author Contributions
Both authors contributed substantially to the conceptualization, methodology, and writing—original draft preparation, review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by Silicon Austria Labs GmbH (SAL), owned by the Republic of Austria, the Styrian Business Promotion Agency (SFG), the federal state of Carinthia, the Upper Austrian Research (UAR), and the Austrian Association for the Electric and Electronics Industry (FEEI).
Acknowledgments
We thank L. Ratschbacher for a critical reading of an early version of the manuscript and C. Mentin for support.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. System Generation Details
Appendix A.1. System Generation
The main challenge we faced in generating systems was to obtain sufficiently diverse 3D geometries, and achieve enough variation of material properties and heat sources while ensuring that the resulting temperature fields stay within a physically plausible range. To simplify this task, we built the systems based on six different components. The components were designed manually (once) using FreeCAD (one large and one small IC, one large and one small capacitor, and copper layers of different shapes and sizes, see Figure 1a).
To generate a system, the components were randomly placed on a fixed-size PCB of dimensions (Figure 1b). Such a random placing procedure does not produce functional electronic circuits. However, as long as the training dataset captures the impact that different component placements have on the heat transfer, the NN is expected to generalise also to (unseen) functional electronic circuits.
Most components (e.g., the ICs) have an internal structure (e.g., legs, die). Each of these sub-parts was assigned a typical material (e.g., copper for the legs). To account for variations in the material properties, a physically plausible range was specified for each material type as the average value given in Table A1 . For each system, the material properties of each part were chosen from a uniform distribution within those ranges.

Table A1.
Average material properties: the actual values are chosen randomly from a range of [0.75 Avg, 1.25 Avg].
Table A1.
Average material properties: the actual values are chosen randomly from a range of [0.75 Avg, 1.25 Avg].
| Property Unit | Avg. k (W/(m K)) | Avg. (J/(kg K)) | Avg. (kg/m3) |
|---|---|---|---|
| Silicon | 148 | 705 | 2330 |
| Copper | 384 | 385 | 8930 |
| Epoxy | 0.881 | 952 | 1682 |
| FR4 | 0.25 | 1200 | 1900 |
| Al2O3 | 35 | 880 | 3890 |
| Aluminum | 148 | 128 | 1930 |
Appendix A.2. Finite Element Simulations
Once the systems were generated, the correct temperature distributions were obtained from FE simulations. Note, however, that instead of FE simulations any adequate simulation methods could have been used. In this proof-of-concept study we focused on the steady-state equation. Assuming that the material properties in the system do not change with temperature, the thermal behavior of the system is determined by the heat equation
where is the density, k the heat conductivity and h a heat source. , k and h are assumed to be constant over time, i.e., independent of the current temperature. Three types of boundary conditions (BCs) were imposed on the systems for the Finite Element (FE) simulations: (1) a Dirichlet-type BC at the bottom of the PCB, which was set to a constant external temperature . The value of was assigned randomly to each of the systems we generated, from the range . (2) a Neumann-type BC represented by a heat sink on the top of the large IC, modelled via a heat transfer coefficient (see Equation (9)). For each system, was randomly chosen from the range 2538.72 W/(Km2) ± 25%. (3) on all other outer exposed surfaces a heat transfer coefficient was prescribed, taken randomly from the range 14 W/(Km2) ± 25%. Electronic losses were modelled as constant heat sources. The magnitudes of the volumetric heat sources, located at the silicon die of the ICs and at the core of the capacitors, were chosen randomly from the ranges specified in Table A2.
The material properties and k depend on the position x, although in the generated systems they are constant over the different sub-parts of each component. and h do not appear separately in Equation (A1), but rather as the product . This implies that any solution of the equation will depend on this product only and, thus, it is sensible to use the product as input to the NN as explained below.
Next in the automatic workflow, a conformal mesh was generated using gmsh [41], which consisted on average of 3 million elements. Steady-state solutions were obtained with the open-source FEM solver ElmerSolver [42,43]. The main advantage of ElmerSolver is that a scriptable interface between FreeCAD (for automatic geometry generation), to ElmerGrid/gmsh (for automatic tetrahedral mesh generation) and ElmerSolver exists which enables an automatized workflow for the system generation.

Table A2.
Range of applied heat sources for the different components of the systems (in W).
Table A2.
Range of applied heat sources for the different components of the systems (in W).
| Component | Min | Max |
|---|---|---|
| Center of large capacitor | 0.1 | 0.3 |
| Silicon die of large chip | 10 | 19 |
| Silicon die of small chip | 0.1 | 0.5 |
Appendix A.3. Voxelization
For the NN, the 3D-systems were represented as a stack of 3D-images. This enabled us to adapt NN methods previously developed for vision tasks to our problem (Figure 1d). During postprocessing, each system was converted to four 3D-images. One 3D-image for each of the physical properties (k, , , ).
To create these 3D-images, the geometries of the basic components were voxelized once using a custom FreeCAD-python script. The voxel size was so that a batch of ten images fits in the GPU memory for training, while the voxel size still resolves sufficient structural detail. The smaller resolution in z-direction was chosen in order to resolve the thin copper layers. During the system generation workflow, each component in the original system was then simply replaced by the previously voxelized representation. To create the four different images, the voxelized geometry was replaced part-by-part by the corresponding material parameter used in the FEM simulation. For our systems, this procedure led to images with voxels. The four 3D-images were then stacked to create a four channel input for the network.
As labels for the supervized learning procedure the temperature solution obtained by the FEM solver was used. The 3D temperature field was directly voxelized during post-processing by Elmer. The FEM solution is only available and of interest within the geometry (where a mesh is available). The outer image regions (we call them “air” regions) were excluded in the loss definition (see Section 2.2.6).
Appendix B. Introduction to ANNs
In this section, we give an overview of neural networks, highlighting the aspects that are most relevant to understand the rest of the paper; see, e.g., [44] for a detailed treatment. In this work, NNs are used as highly versatile and non-linear function approximators. Generally speaking, a neural network can be visualized as a stack of layers, each of them computing a set of linear operations on their input data, subsequently applying a fixed non-linear operation and passing the result to the next layer. The input to the network in this work is a voxelized representation of a 3D electronic system (i.e., a 3D image), where the different properties of the system are passed as different channels (in analogy to the RGB channels of a standard 2D image). Convolutional neural networks (CNNs), consisting of a special type of layer called convolutional layer, are used for processing images.
The most important feature in a convolutional layer of a CNN is that not every pixel in the input image of a layer is connected to every pixel in the output, but rather each output pixel is determined by a small set of input pixels (the receptive field), the number of them is given by the size of the so-called convolutional kernel (or filter). To be specific, the equation defining the action of a 3D convolutional layer is:
with
where represents the value of the voxel at position of the output 3D image, C labels the channel (or feature map) of the output image, , and are natural numbers called strides and , and are naturals called dilations (their meaning is explained in Section 2.2), , and are the height, width and depth of the 3D convolutional kernels applied to the input image x, with channels, is a bias parameter for each feature map C and w are the weight parameters.
The next ideas to be presented are downsampling and upsampling. It is not necessarily the case that the size of the output and input images of a convolutional layer coincide. It can be inferred from Equation (A3), the output image size can be reduced by tuning the values of the stride parameters. For example, choosing , the size of the output image will be halved. One refers to this process as downsampling. In image processing, the purpose of downsampling is to force the CNN to extract relevant features from an image (e.g., edges)but, in this work, extracting features is not so relevant since they are, to some extent, manually implemented. Nevertheless, some degree of downsampling is necessary to reduce the memory requirements of the network. The inverse action to downsampling is upsampling. One can think of it as an interpolation procedure, where from one input pixel a higher number of pixels are generated as output. In practice, this is achieved by an operation called transposed convolution, which is mathematically very similar to the standard convolution in Equation (A2), with different weights and biases to be learned. Upsampling is necessary if downsampling is used in some of the layers of the network but the output of a CNN must be another image of the same size of the input image, as is our case. CNNs of this type are called fully-convolutional neural networks (FCNs).
Finally there is a different type of layer called pooling layer. They are parameter-free layers (non-learnable) that apply a fixed operation on their receptive field. Typical pooling layers include max-pooling and average-pooling layers, which give as output the maximum or the average value, respectively, of the pixel (resp. voxel) values in their receptive field.
The training of a CNN consists of finding the optimal values of the parameters w and b of each of the layers. This is achieved by minimising a certain objective function (loss) on a labelled dataset. For this work, as discuss in the main text, the dataset consists of a collection of simplified 3D circuits, each labelled by the result of a standard thermal simulation. The training is performed on a subset of the whole dataset (training set), whilst the rest are used to test the network (test set).
References
- Langbauer, T.; Mentin, C.; Rindler, M.; Vollmaier, F.; Connaughton, A.; Krischan, K. Closing the Loop between Circuit and Thermal Simulation: A System Level Co-Simulation for Loss Related Electro-Thermal Interactions. In Proceedings of the 2019 25th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Lecco, Italy, 25–27 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An Overview of Artificial Intelligence Applications for Power Electronics. Trans. Power Electron. 2015, 30, 6791–6803. [Google Scholar] [CrossRef]
- Wu, T.; Wang, Z.; Ozpineci, B.; Chinthavali, M.; Campbell, S. Automated heatsink optimization for air-cooled power semiconductor modules. IEEE Trans. Power Electron. 2018, 34, 5027–5031. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Z.; Wang, H.; Blaabjerg, F. Artificial Intelligence-Aided Thermal Model Considering Cross-Coupling Effects. IEEE Trans. Power Electron. 2020, 35, 9998–10002. [Google Scholar] [CrossRef]
- Delaram, H.; Dastfan, A.; Norouzi, M. Optimal Thermal Placement and Loss Estimation for Power Electronic Modules. IEEE Trans. Componen. Packag. Manuf. Technol. 2018, 8, 236–243. [Google Scholar] [CrossRef]
- Guillod, T.; Papamanolis, P.; Kolar, J.W. Artificial Neural Network (ANN) Based Fast and Accurate Inductor Modeling and Design. IEEE Open J. Power Electron. 2020, 1, 284–299. [Google Scholar] [CrossRef]
- Chiozzi, D.; Bernardoni, M.; Delmonte, N.; Cova, P. A Neural Network Based Approach to Simulate Electrothermal Device Interaction in SPICE Environment. IEEE Trans. Power Electron. 2019, 34, 4703–4710. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, Y.; Wang, X.; Tao, X.; Xu, Q. Surrogate Thermal Model for Power Electronic Modules using Artificial Neural Network. In Proceedings of the 45th Annual Conference of the IEEE Industrial Electronics Society (IECON 2019), Lisbon, Portugal, 14–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3160–3165. [Google Scholar] [CrossRef]
- Marie-Francoise, J.N.; Gualous, H.; Berthon, A. Supercapacitor thermal- and electrical-behaviour modelling using ANN. IEEE Proc. Electr. Power Appl. 2006, 153, 255. [Google Scholar] [CrossRef]
- Kim, J.; Lee, C. Prediction of turbulent heat transfer using convolutional neural networks. J. Fluid Mech. 2020, 882, A18. [Google Scholar] [CrossRef]
- Swischuk, R.; Mainini, L.; Peherstorfer, B.; Willcox, K. Projection-based model reduction: Formulations for physics-based machine learning. Comput. Fluids 2019, 179, 704–717. [Google Scholar] [CrossRef]
- Gao, H.; Sun, L.; Wang, J.X. PhyGeoNet: Physics-Informed Geometry-Adaptive Convolutional Neural Networks for Solving Parametric PDEs on Irregular Domain. arXiv 2020, arXiv:2004.13145. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Lu, L.; Zaki, T.A.; Karniadakis, G.E. DeepM&Mnet: Inferring the electroconvection multiphysics fields based on operator approximation by neural networks. arXiv 2020, arXiv:2009.12935. [Google Scholar]
- He, Q.Z.; Barajas-Solano, D.; Tartakovsky, G.; Tartakovsky, A.M. Physics-informed neural networks for multiphysics data assimilation with application to subsurface transport. Adv. Water Resour. 2020, 141, 103610. [Google Scholar] [CrossRef]
- Kadeethum, T.; Jørgensen, T.M.; Nick, H.M. Physics-informed neural networks for solving nonlinear diffusivity and Biot’s equations. PLoS ONE 2020, 15, e0232683. [Google Scholar] [CrossRef]
- Khan, A.; Ghorbanian, V.; Lowther, D. Deep learning for magnetic field estimation. IEEE Trans. Magn. 2019, 55, 7202304. [Google Scholar] [CrossRef]
- Breen, P.G.; Foley, C.N.; Boekholt, T.; Zwart, S.P. Newton vs. the machine: Solving the chaotic three-body problem using deep neural networks. Mon. Not. R. Astron. Soc. 2019, 494, 2465–2470. [Google Scholar] [CrossRef]
- Sanchez-Gonzalez, A.; Godwin, J.; Pfaff, T.; Ying, R.; Leskovec, J.; Battaglia, P.W. Learning to Simulate Complex Physics with Graph Networks. In Proceedings of the 37th International Conference on Machine Learning, ICML, Virtual Event, 13–18 July 2020; pp. 8459–8468. [Google Scholar]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics-informed Neural Networks (PINNs) for Wave Propagation and Full Waveform Inversions. arXiv 2021, arXiv:2108.12035. [Google Scholar]
- Goswami, S.; Yin, M.; Yu, Y.; Karniadakis, G. A physics-informed variational DeepONet for predicting the crack path in brittle materials. arXiv 2021, arXiv:2108.06905. [Google Scholar]
- Lin, C.; Maxey, M.; Li, Z.; Karniadakis, G.E. A seamless multiscale operator neural network for inferring bubble dynamics. J. Fluid Mech. 2021, 929, A18. [Google Scholar] [CrossRef]
- Kovacs, A.; Exl, L.; Kornell, A.; Fischbacher, J.; Hovorka, M.; Gusenbauer, M.; Breth, L.; Oezelt, H.; Praetorius, D.; Suess, D.; et al. Magnetostatics and micromagnetics with physics informed neural networks. J. Magn. Magn. Mater. 2022, 548, 168951. [Google Scholar] [CrossRef]
- Jiang, J.; Zhao, J.; Pang, S.; Meraghni, F.; Siadat, A.; Chen, Q. Physics-informed deep neural network enabled discovery of size-dependent deformation mechanisms in nanostructures. Int. J. Solids Struct. 2022, 236–237, 111320. [Google Scholar] [CrossRef]
- Di Leoni, P.C.; Lu, L.; Meneveau, C.; Karniadakis, G.; Zaki, T.A. DeepONet prediction of linear instability waves in high-speed boundary layers. arXiv 2021, arXiv:2105.08697. [Google Scholar]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks for heat transfer problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Blumberg, S.B.; Tanno, R.; Kokkinos, I.; Alexander, D.C. Deeper image quality transfer: Training low-memory neural networks for 3D images. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11070, pp. 118–125. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, E.; Saint, A.; Shabayek, A.E.R.; Cherenkova, K.; Das, R.; Gusev, G.; Aouada, D.; Ottersten, B. A survey on Deep Learning Advances on Different 3D Data Representations. arXiv 2018, arXiv:1808.01462. [Google Scholar]
- Liu, W.; Sun, J.; Li, W.; Hu, T.; Wang, P. Deep Learning on Point Clouds and Its Application: A Survey. Sensors 2019, 19, 4188. [Google Scholar] [CrossRef] [Green Version]
- Bello, S.A.; Yu, S.; Wang, C. Review: Deep learning on 3D point clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Rios, T.; Wollstadt, P.; Stein, B.V.; Back, T.; Xu, Z.; Sendhoff, B.; Menzel, S. Scalability of Learning Tasks on 3D CAE Models Using Point Cloud Autoencoders. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1367–1374. [Google Scholar] [CrossRef]
- Riegler, G.; Ulusoy, A.O.; Geiger, A. OctNet: Learning Deep 3D Representations at High Resolutions. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 6620–6629. [Google Scholar]
- He, H.; Pathak, J. An unsupervised learning approach to solving heat equations on chip based on auto encoder and image gradient. arXiv 2020, arXiv:2007.09684. [Google Scholar]
- Köpüklü, O.; Kose, N.; Gunduz, A.; Rigoll, G. Resource efficient 3d convolutional neural networks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Korea, 27–28 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1910–1919. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 971–980. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models; Citeseer: Princeton, NJ, USA, 2013. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Hinton, G.; Tieleman, T. Neural Networks for Machine Learning. Available online: http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (accessed on 21 October 2021).
- Geuzaine, C.; Remacle, J.F. Gmsh: A three-dimensional finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Malinen, M.; Råback, P. Elmer finite element solver for multiphysics and multiscale problems. Multiscale Model. Methods Appl. Mater. Sci. 2013, 19, 101–113. [Google Scholar]
- Råback, P.; Malinen, M.; Ruokolainen, J.; Pursula, A.; Zwinger, T. Elmer Models Manual; Technical Report; CSC—IT Center for Science: Espoo, Finland, 2020. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).