A Sequential Approach for Aerodynamic Shape Optimization with Topology Optimization of Airfoils †
Abstract
1. Introduction
2. Background
2.1. Aerodynamic Shape Optimization
2.1.1. Flow Governing Equations
2.1.2. Adjoint-Based Gradient Computation
2.1.3. Parametrization Technique: Free-Form Deformation
2.2. Topology Optimization
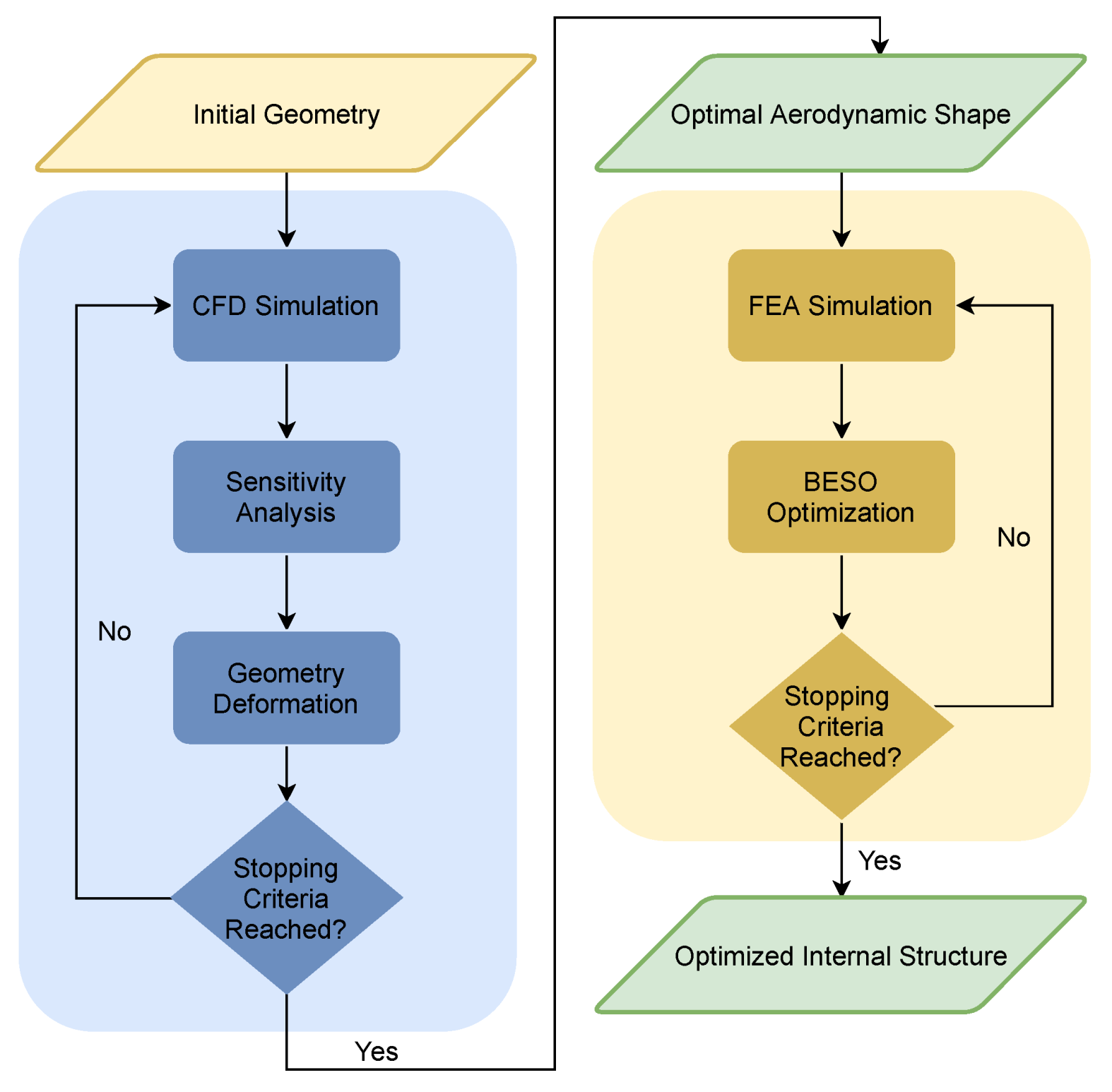
3. Methodology
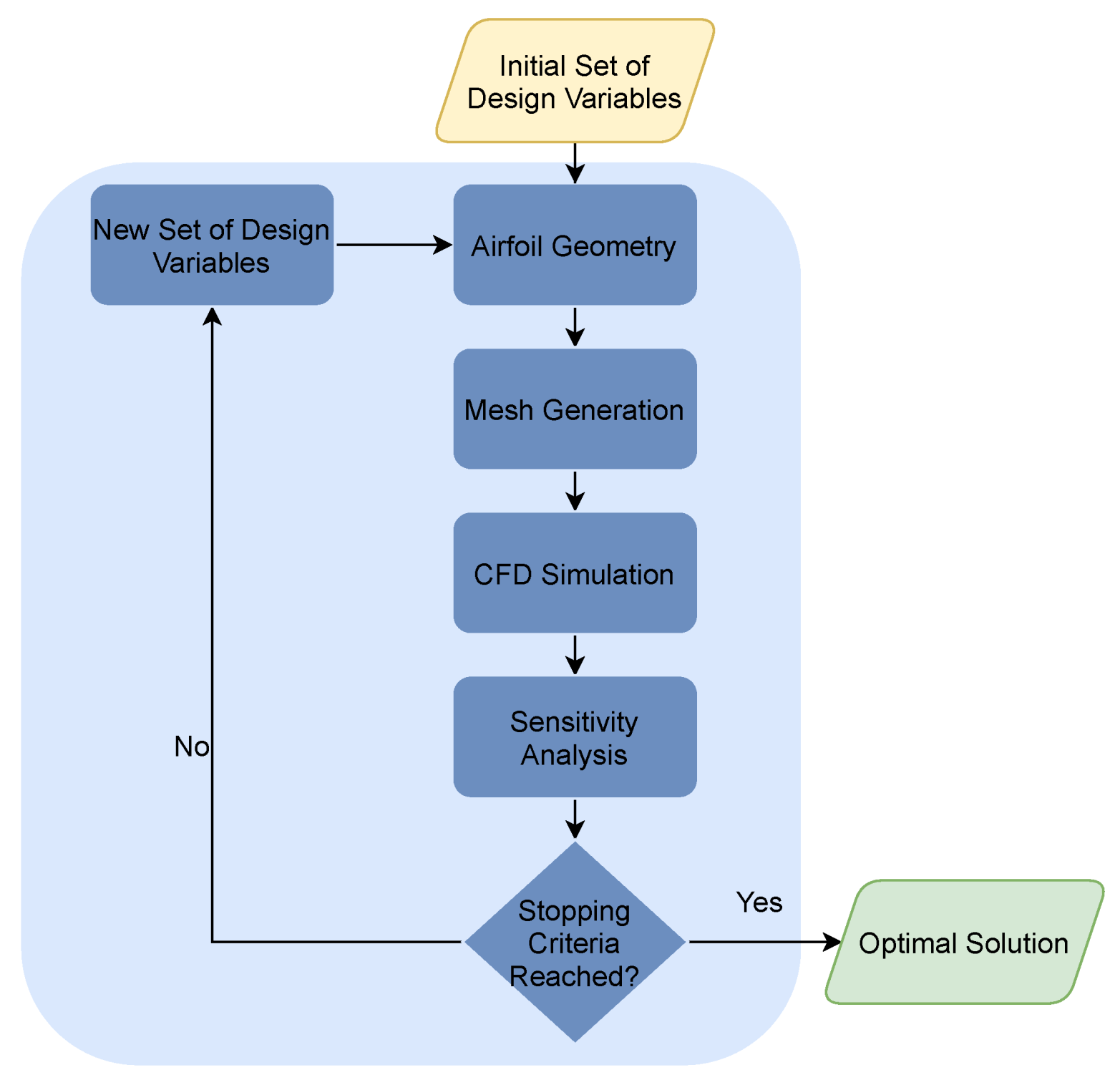
3.1. Aerodynamic Shape Optimization
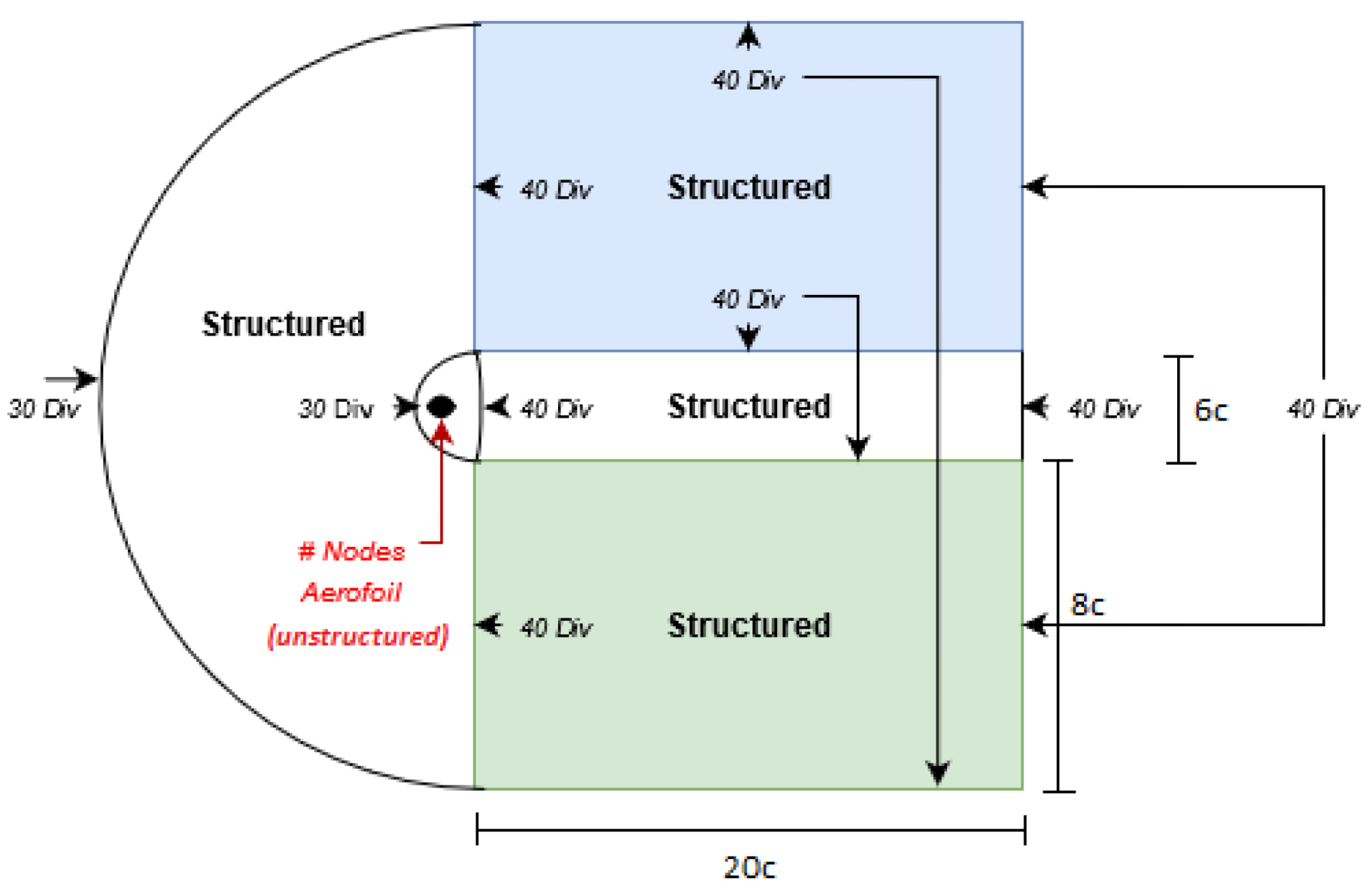
3.1.1. Mesh Definition
3.1.2. Optimization Problem
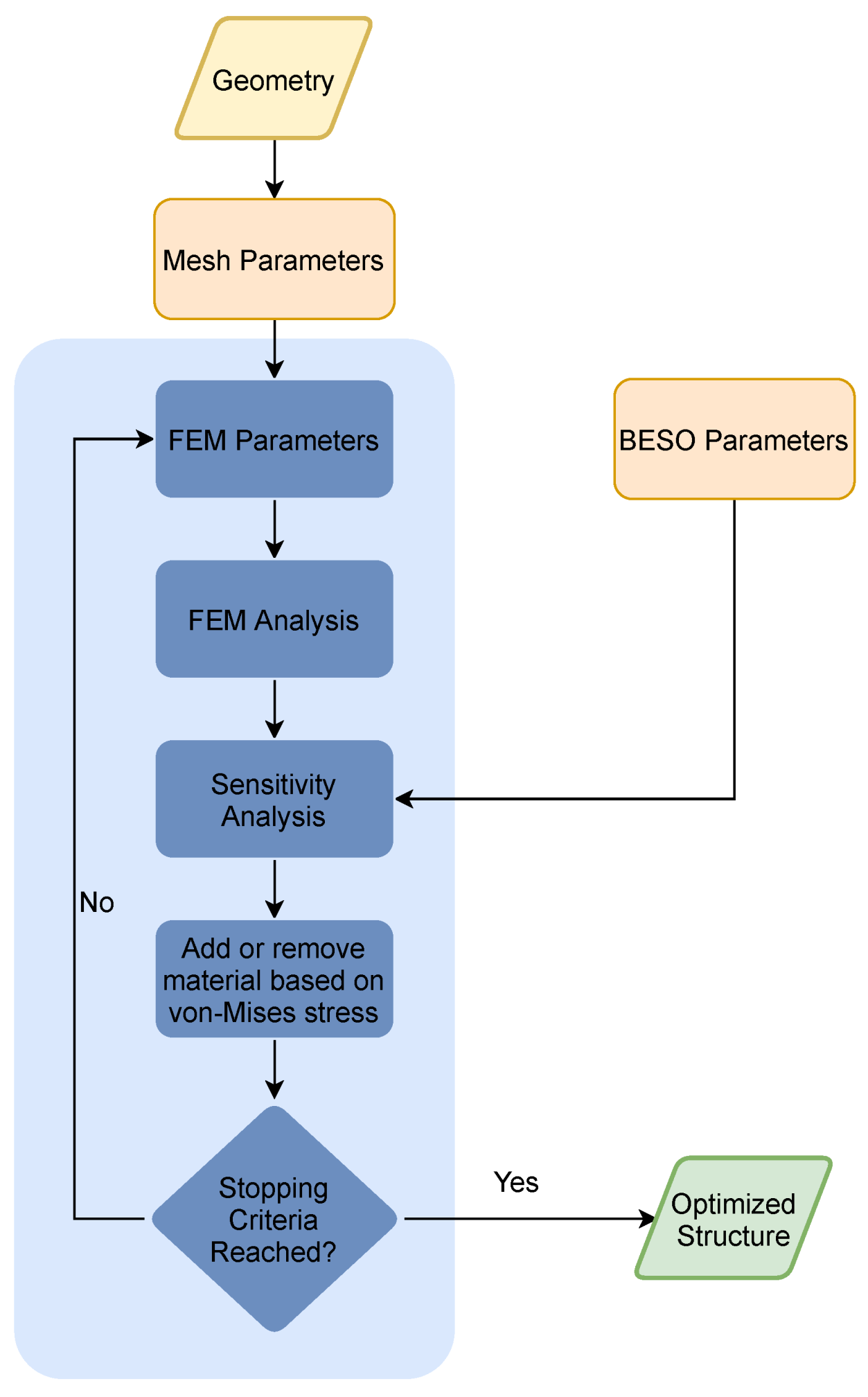
3.2. Topology Optimization
3.2.1. Finite Element Model Definition
3.2.2. Optimization Problem Definition
4. Results
4.1. Aerodynamic Optimization
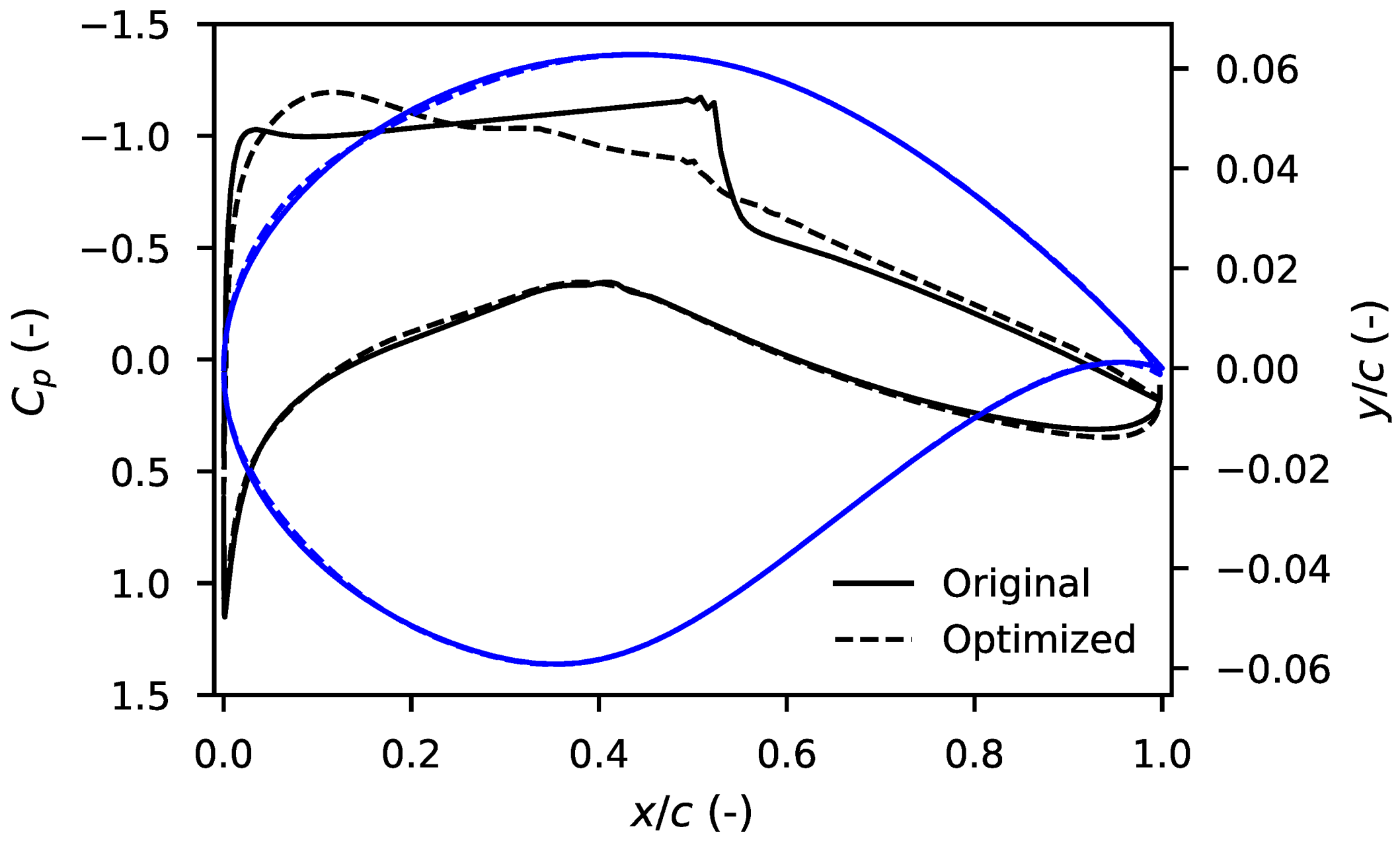
4.1.1. Case 1
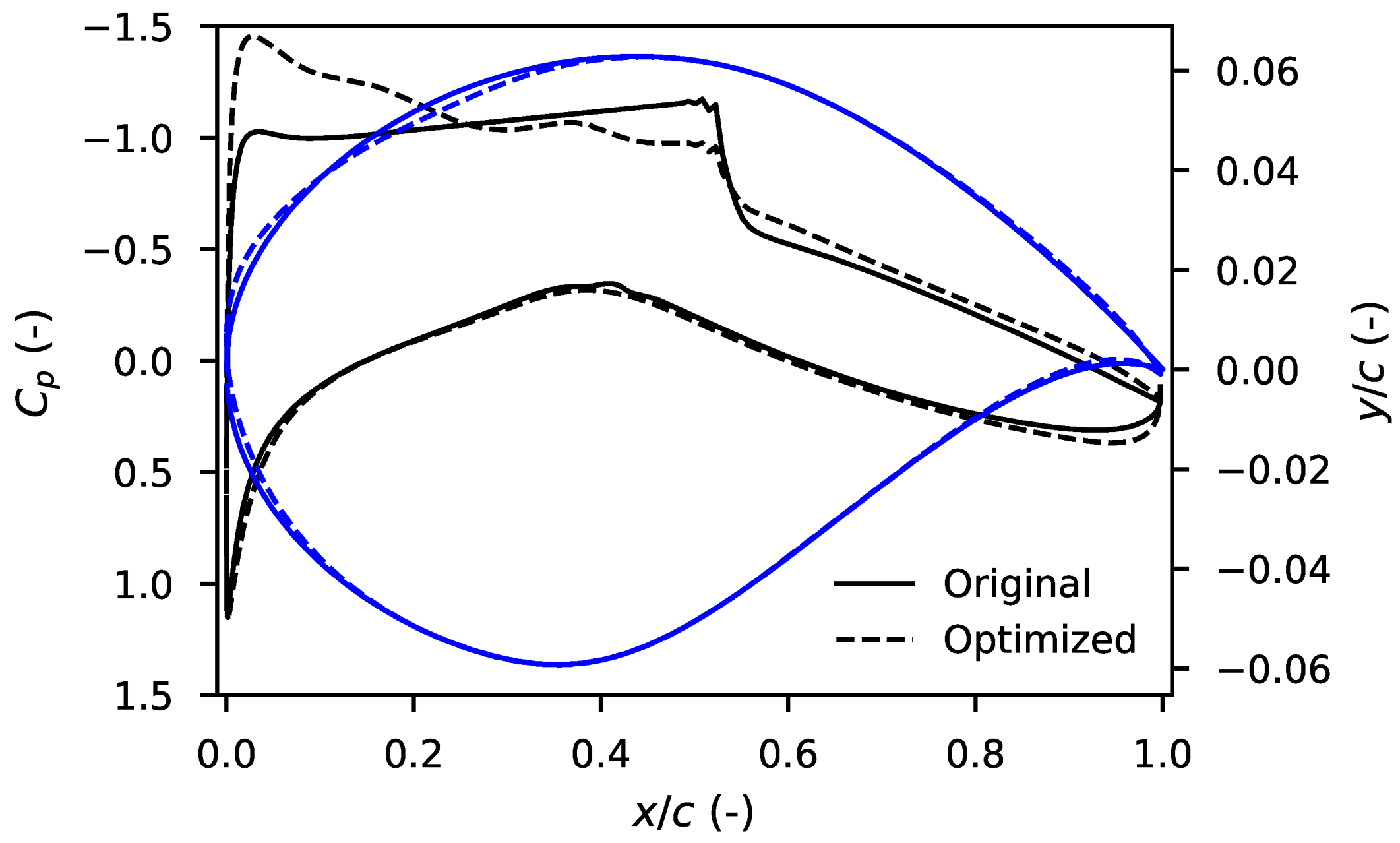
4.1.2. Case 2
4.2. Structural Results
4.3. Aerodynamic and Structural Optimizations
4.3.1. Case 1
4.3.2. Case 2
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Skinner, S.; Zare-Behtash, H. State-of-the-art in aerodynamic shape optimisation methods. Appl. Soft Comput. 2018, 62, 933–962. [Google Scholar] [CrossRef]
- Zhu, J.H.; Zhang, W.H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar] [CrossRef]
- Maute, K.; Allen, M. Conceptual design of aeroelastic structures by topology optimization. Struct. Multidiscip. Optim. 2004, 27, 27–42. [Google Scholar] [CrossRef]
- Krog, L.; Tucker, A.; Kemp, M.; Boyd, R. Topology optimisation of aircraft wing box ribs. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004. [Google Scholar] [CrossRef]
- Gomes, A.; Suleman, A. Topology Optimization of a Reinforced Wing Box for Enhanced Roll Maneuvers. AIAA J. 2008, 46, 548–556. [Google Scholar] [CrossRef]
- Stanford, B.; Ifju, P. Aeroelastic topology optimization of membrane structures for micro air vehicles. Struct. Multidiscip. Optim. 2009, 38, 301–316. [Google Scholar] [CrossRef]
- James, K.; Martins, J. An isoparametric approach to level set topology optimization using a body-fitted finite-element mesh. Comput. Struct. 2012, 90–91, 97–106. [Google Scholar] [CrossRef]
- Oktay, E.; Akay, H.; Sehitoglu, O. Three-dimensional structural topology optimization of aerial vehicles under aerodynamic loads. Comput. Fluids 2014, 92, 225–232. [Google Scholar] [CrossRef]
- Dunning, P.; Stanford, B.; Kim, H. Coupled aerostructural topology optimization using a level set method for 3D aircraft wings. Struct. Multidiscip. Optim. 2015, 51, 1113–1132. [Google Scholar] [CrossRef]
- Félix, L.; Gomes, A.; Suleman, A. Topology optimization of the internal structure of an aircraft wing subjected to self-weight load. Eng. Optim. 2020, 52, 1119–1135. [Google Scholar] [CrossRef]
- Capasso, G.; Morlier, J.; Charlotte, M.; Coniglio, S. Stress-based topologyoptimization of compliant mechanisms using nonlinear mechanics. Mech. Ind. 2020, 21, 1–17. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Martins, J.; Ning, A. Engineering Design Optimization; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Nemec, M.; Zingg, D.; Pulliam, T. Multipoint and Multi-Objective Aerodynamic Shape Optimization. AIAA J. 2004, 42, 1057–1065. [Google Scholar] [CrossRef]
- Zingg, D.; Nemec, M.; Pulliam, T. A comparative evaluation of genetic and gradient-based algorithms applied to aerodynamic optimization. Eur. J. Comput. Mech. 2008, 17, 103–126. [Google Scholar] [CrossRef]
- Chen, S.; Lyu, Z.; Kenway, G.; Martins, J. Aerodynamic Shape Optimization of the Common Research Model Wing-Body-Tail Configuration. J. Aircr. 2016, 53, 276–293. [Google Scholar] [CrossRef]
- Burdette, D.; Martins, J. Design of a Transonic Wing with an Adaptive Morphing Trailing Edge via Aerostructural Optimization. Aerosp. Sci. Technol. 2018, 81, 192–203. [Google Scholar] [CrossRef]
- Lyu, Z.; Martins, J. Aerodynamic Design Optimization Studies of a Blended-Wing-Body Aircraft. J. Aircr. 2014, 51, 1604–1617. [Google Scholar] [CrossRef]
- Secco, N.; Martins, J. RANS-based Aerodynamic Shape Optimization of a Strut-braced Wing with Overset Meshes. J. Aircr. 2019, 56, 217–227. [Google Scholar] [CrossRef]
- Masters, D.; Taylor, N.; Rendall, C.; Poole, D. Geometric Comparison of Aerofoil Shape Parameterization Methods. AIAA J. 2017, 55, 1575–1589. [Google Scholar] [CrossRef]
- De Gaspari, A.; Ricci, S. A Two-Level Approach for the Optimal Design of Morphing Wings Based On Compliant Structures. J. Intell. Mater. Syst. Struct. 2011, 22, 1091–1111. [Google Scholar] [CrossRef]
- Antunes, A.; Azevedo, J. Studies in Aerodynamic Optimization Based on Genetic Algorithms. J. Aircr. 2014, 51, 1002–1012. [Google Scholar] [CrossRef]
- Tao, J.; Sun, G. Application of deep learning based multi-fidelity surrogate model to robust aerodynamic design optimization. Aerosp. Sci. Technol. 2019, 92, 722–737. [Google Scholar] [CrossRef]
- Renganathan, S.A.; Maulik, R.; Ahuja, J. Enhanced data efficiency using deep neural networks and Gaussian processes for aerodynamic design optimization. Aerosp. Sci. Technol. 2021, 111, 106522. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; He, S.; Martins, J.R.R.A. Scalable gradient-enhanced artificial neural networks for airfoil shape design in the subsonic and transonic regimes. Struct. Multidiscip. Optim. 2020, 61, 1363–1376. [Google Scholar] [CrossRef]
- Maute, K.; Reich, G. Integrated multidisciplinary topology optimization approach to adaptive wing design. J. Aircr. 2006, 43, 253–263. [Google Scholar] [CrossRef]
- James, K.; Kennedy, G.; Martins, J. Concurrent aerostructural topology optimization of a wing box. Comput. Struct. 2014, 134, 1–17. [Google Scholar] [CrossRef]
- Gomes, P.; Palacios, R. Aerodynamic-driven topology optimization of compliant airfoils. Struct. Multidiscip. Optim. 2020, 62, 2117–2130. [Google Scholar] [CrossRef]
- Bendsøe, M. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem. Anal. Des. 2007, 43, 1039–1049. [Google Scholar] [CrossRef]
- Xia, L.; Xia, Q.; Huang, X.; Xie, Y. Bi-directional Evolutionary Structural Optimization on Advanced Structures and Materials: A Comprehensive Review. Arch. Comput. Methods Eng. 2018, 25, 437–478. [Google Scholar] [CrossRef]
- Munk, D.; Verstraete, D.; Vio, G. Effect of fluid-thermal–structural interactions on the topology optimization of a hypersonic transport aircraft wing. J. Fluids Struct. 2017, 75, 45–76. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Economon, T.; Palacios, F.; Copeland, S.; Lukaczyk, T.; Alonso, J. SU2: An open-source suite for multiphysics simulation and design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- Sederberg, T.; Parry, S. Free-form deformation of solid geometric models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 18–22 August 1986. [Google Scholar] [CrossRef]
- North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development. Experimental Data Base for Computer Program Assessment; Technical Editing and Reproduction Ltd: London, UK, 1979. [Google Scholar]
- Allmaras, S.; Venkatakrishnan, V.; Johnson, F. Farfield Boundary Conditions for 2-D Airfoils. In Proceedings of the 17th AIAA Computational Fluid Dynamics Conference, Toronto, ON, Canada, 6–9 June 2005. [Google Scholar] [CrossRef]
- Löffelmann, F. Failure Index Based Topology Optimization for Multiple Properties. In Proceedings of the 23rd International Conference on Engineering Mechanics, Svratka, Czech Republic, 15–18 May 2017. [Google Scholar]
- Löffelmann, F. Python Code for Topology Optimization Using CalculiX FEM Solver. Available online: https://github.com/fandaL/beso (accessed on 20 April 2021).
- Díaz, A.; Sigmund, O. Checkerboard patterns in layout optimization. Struct. Optim. 1995, 10, 30–45. [Google Scholar] [CrossRef]

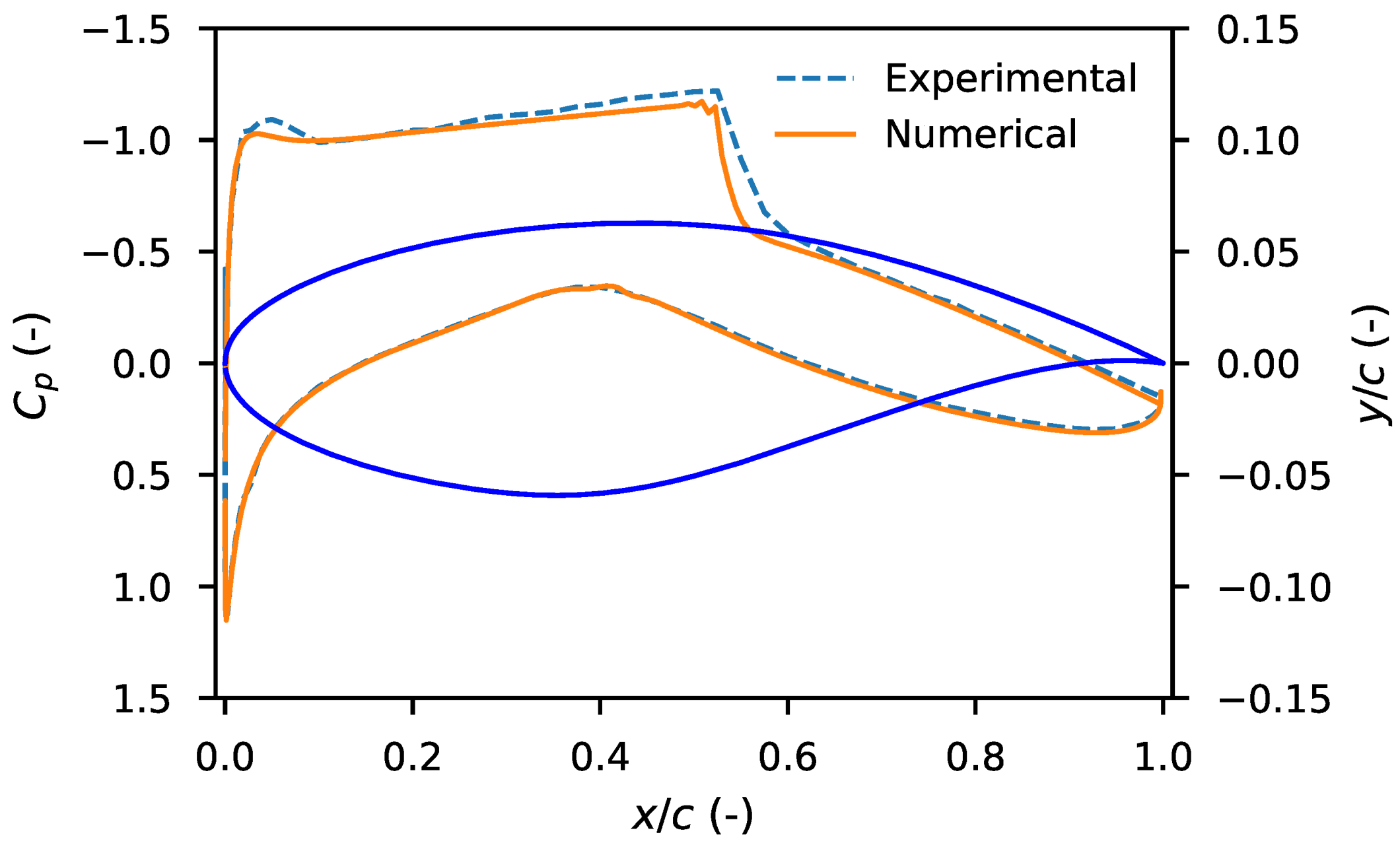
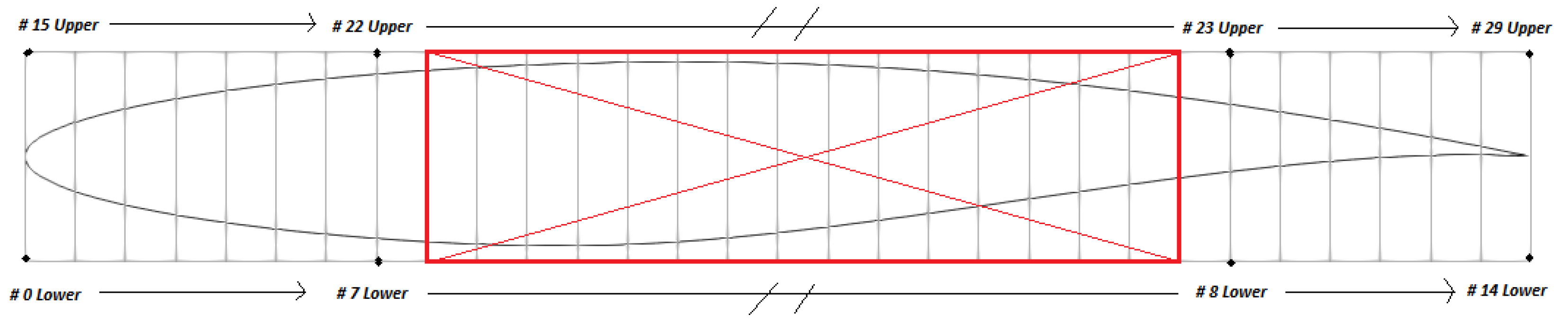

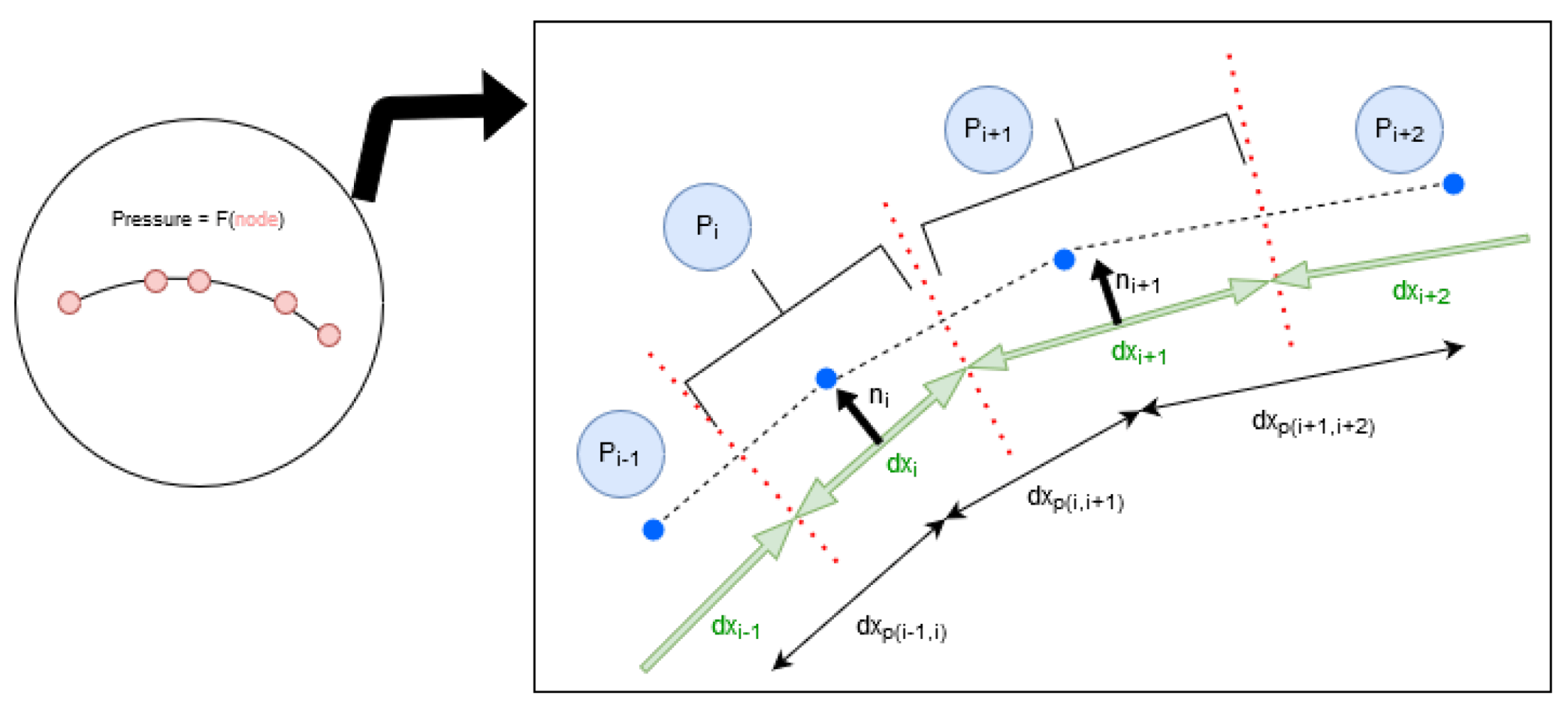
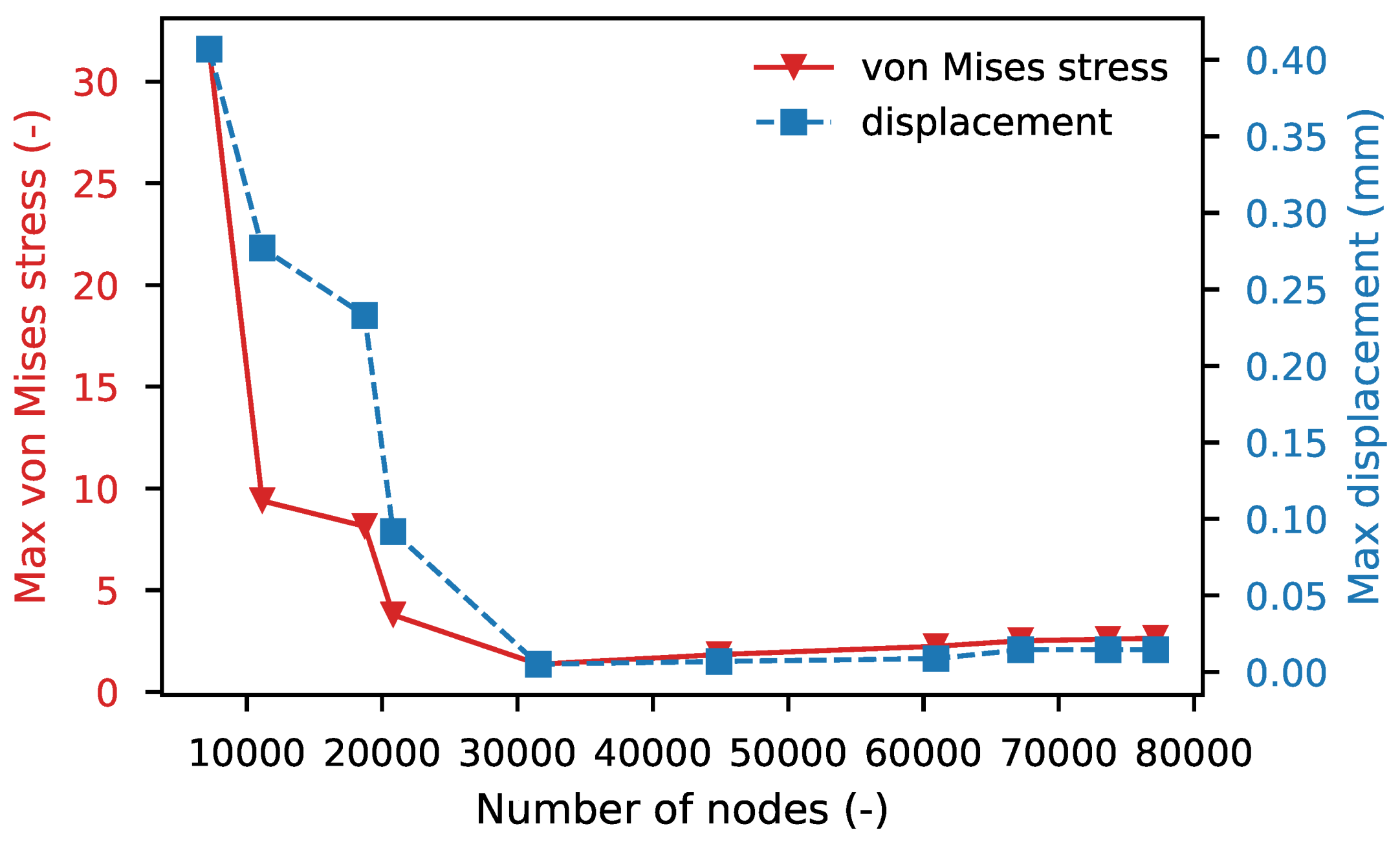





| Number of Elements (-) | Cl (-) | Cd (Drag Counts) | |
|---|---|---|---|
| Coarse | 43,322 | 0.6737 | 138.8 |
| Medium | 53,492 | 0.7164 | 137.4 |
| Fine | 75,130 | 0.7205 | 130.2 |
| Refined | 85,098 | 0.7215 | 130.5 |
| Cl (-) | Cd (Drag Counts) | |
|---|---|---|
| Present Work | 0.7164 | 137.4 |
| Experimental Work [36] | 0.7436 | 127.0 |
| Case | Initial (-) | Initial (Drag Counts) |
|---|---|---|
| 1 | 0.7164 | 137.4 |
| 2 | 0.8030 | 183.6 |
| Shape | Cl (-) | Cd (Drag Counts) |
|---|---|---|
| Original | 0.7164 | 137.40 |
| Optimized | 0.7164 | 118.23 |
| Shape | Cl (-) | Cd (Drag Counts) |
|---|---|---|
| Original | 0.803 | 183.62 |
| Optimized | 0.803 | 130.29 |
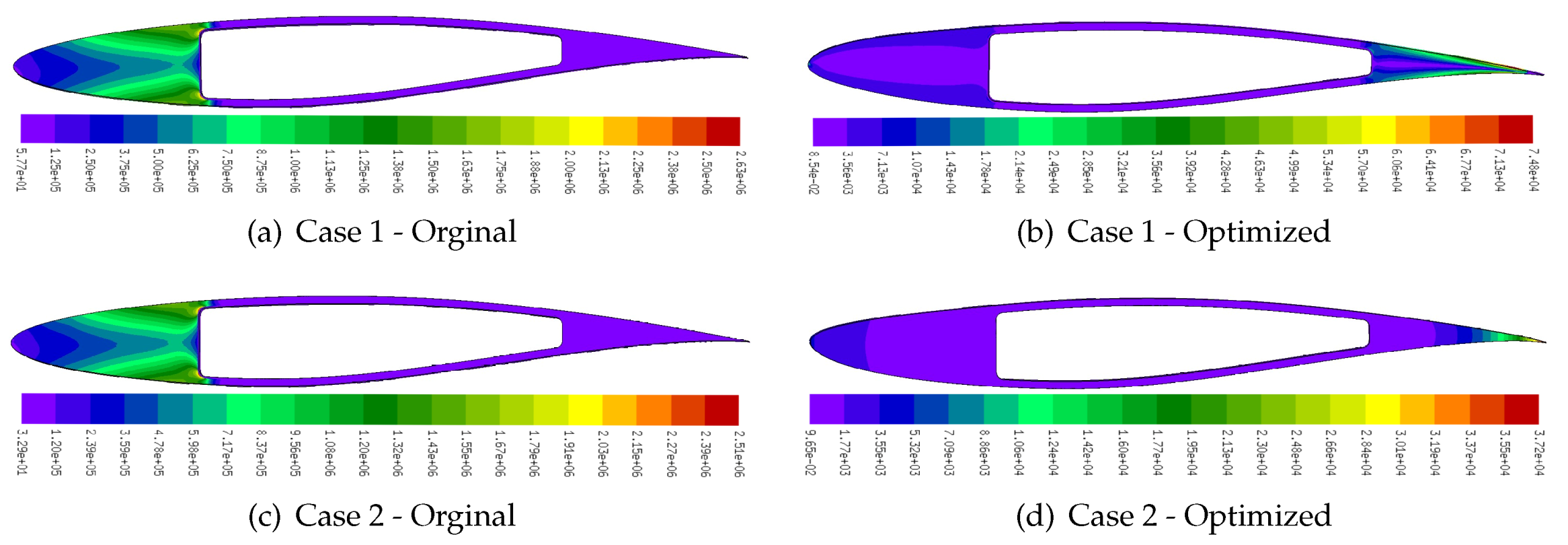
| Case | Geometry | [Pa] | [c] |
|---|---|---|---|
| 1 | Original | ||
| Optimized | |||
| 2 | Original | ||
| Optimized |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gibert Martínez, I.; Afonso, F.; Rodrigues, S.; Lau, F. A Sequential Approach for Aerodynamic Shape Optimization with Topology Optimization of Airfoils. Math. Comput. Appl. 2021, 26, 34. https://doi.org/10.3390/mca26020034
Gibert Martínez I, Afonso F, Rodrigues S, Lau F. A Sequential Approach for Aerodynamic Shape Optimization with Topology Optimization of Airfoils. Mathematical and Computational Applications. 2021; 26(2):34. https://doi.org/10.3390/mca26020034
Chicago/Turabian StyleGibert Martínez, Isaac, Frederico Afonso, Simão Rodrigues, and Fernando Lau. 2021. "A Sequential Approach for Aerodynamic Shape Optimization with Topology Optimization of Airfoils" Mathematical and Computational Applications 26, no. 2: 34. https://doi.org/10.3390/mca26020034
APA StyleGibert Martínez, I., Afonso, F., Rodrigues, S., & Lau, F. (2021). A Sequential Approach for Aerodynamic Shape Optimization with Topology Optimization of Airfoils. Mathematical and Computational Applications, 26(2), 34. https://doi.org/10.3390/mca26020034







