Operational Risk Reverse Stress Testing: Optimal Solutions
Abstract
1. Introduction
1.1. The Context: Operational Risk and Stress Testing
- 140: ex gratia payment;
- 18,000: damage to a bank branch caused during a robbery;
- 187,000: computer hacking fraud;
- 42,000,000: provision for mis-selling.
1.2. Contribution of this Paper
- To provide a clear methodological basis for RST in the context of OpRisk.
- To compare existing and new methodologies for RST in the context of OpRisk, with a view toward determining an optimal method.
- To provide guidance for practitioners, pointing out how to apply the proposed methodology in an efficient way, with a balance between accuracy and time required to complete the testing.
1.3. Acronyms and Abbreviations
- RST: Reverse Stress Testing
- OpRisk: Operational Risk
- VaR: Value-at-Risk
- Capital: cash retained by banks annually for use as a buffer against unforeseen expenditure, the details of which are specified by national regulatory bodies
- BoE Bank of England
- FCA Financial Conduct Authority, the U.K. regulator
- ECB European Central Bank, the EU regulator
- Fed Federal Reserve Board, the U.S. regulator
- BO: Bayesian Optimization (acquisition functions are listed below)
- GP: Gaussian Process
- POI: the Probability Of Improvement acquisition function
- CB: the Confidence Bound acquisition function; there are two versions: Upper (UCB) and Lower (LCB)
- EI: the Expectation Improvement acquisition function
2. Reverse Stress Testing
2.1. Problem Formulation
2.1.1. Issues in Optimization in the Context of OpRisk
2.1.2. Problem Formulation Details
2.2. Motivation and Strategies
3. Literature Review
3.1. Acquisition Function Development
3.2. Recent Advances in Reverse Stress Testing
3.3. The Financial Regulatory Environment
4. Proposed Solutions
4.1. Optimization Framework
4.2. Gaussian Processes’ Acquisition Functions
The Zero Acquisition Functions
4.3. Zero Acquisition: Properties
- is myopic, since it is defined in terms of the maximum of a point wise utility function (namely Equation (5)). Wilson showed that the implication is that the iterative strategy in a GP always selects the largest immediate reward. Usually, optimizing a myopic function is straightforward, but in our case, optimization was complicated by the stochastic nature of our function f (Equation (2)).
- is very responsive for the low-dimensional case that we considered.
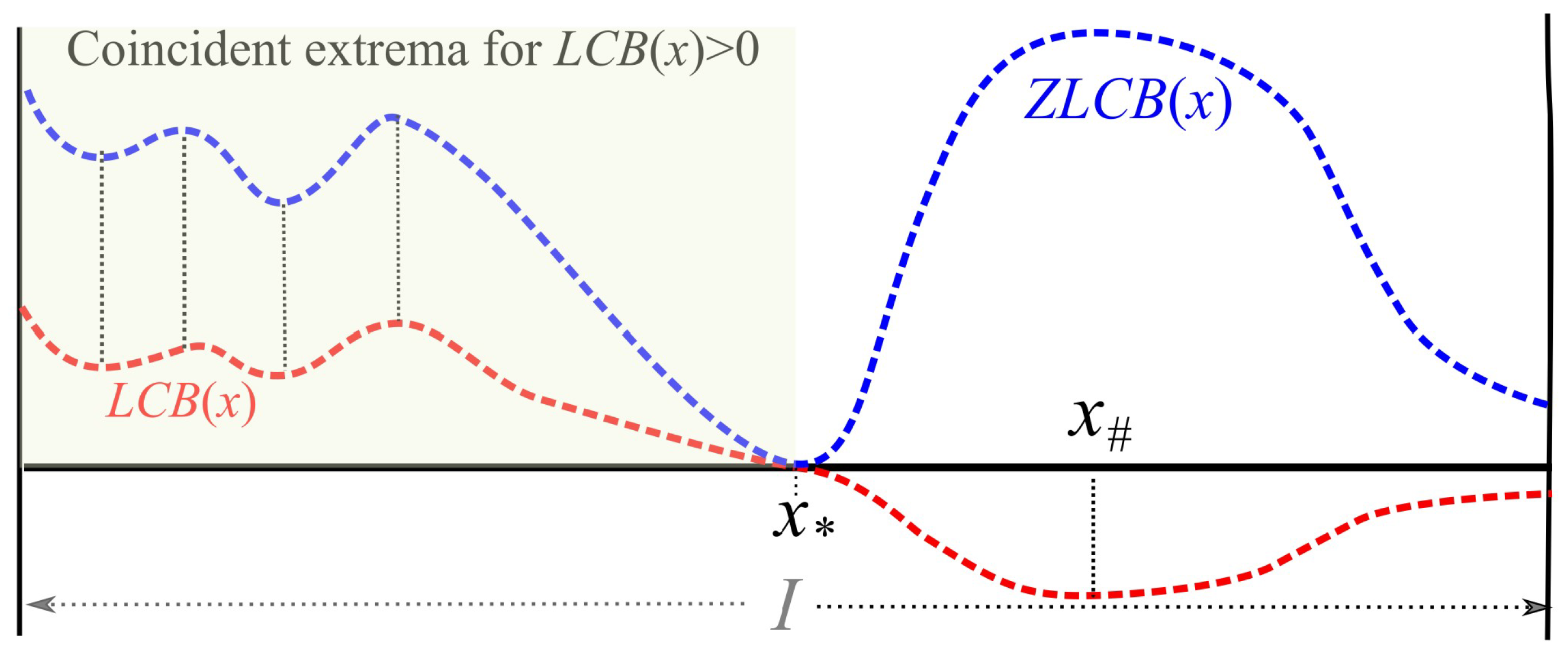
- is non-convex, as may be demonstrated by examining the value of for a set of values . Figure 1 is a typical instance.
4.4. Quantitative Analysis of Zero Acquisition
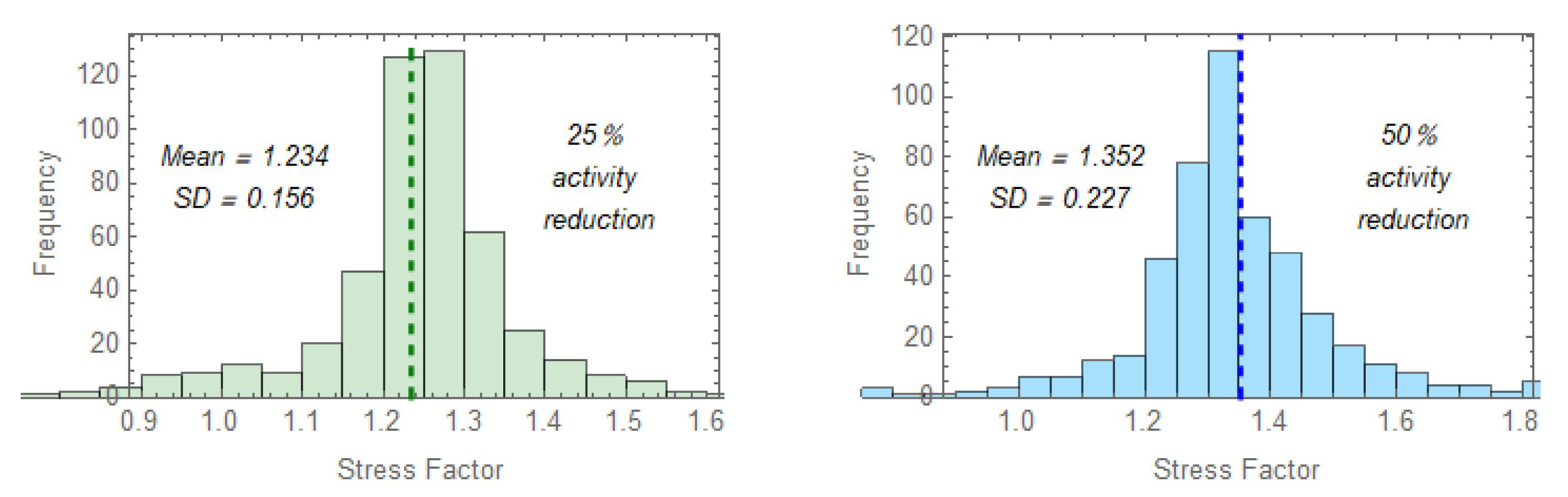
4.5. Risk Reduction
4.6. Other Acquisition Functions
4.7. Non-BO Optimizations
4.8. Run Number
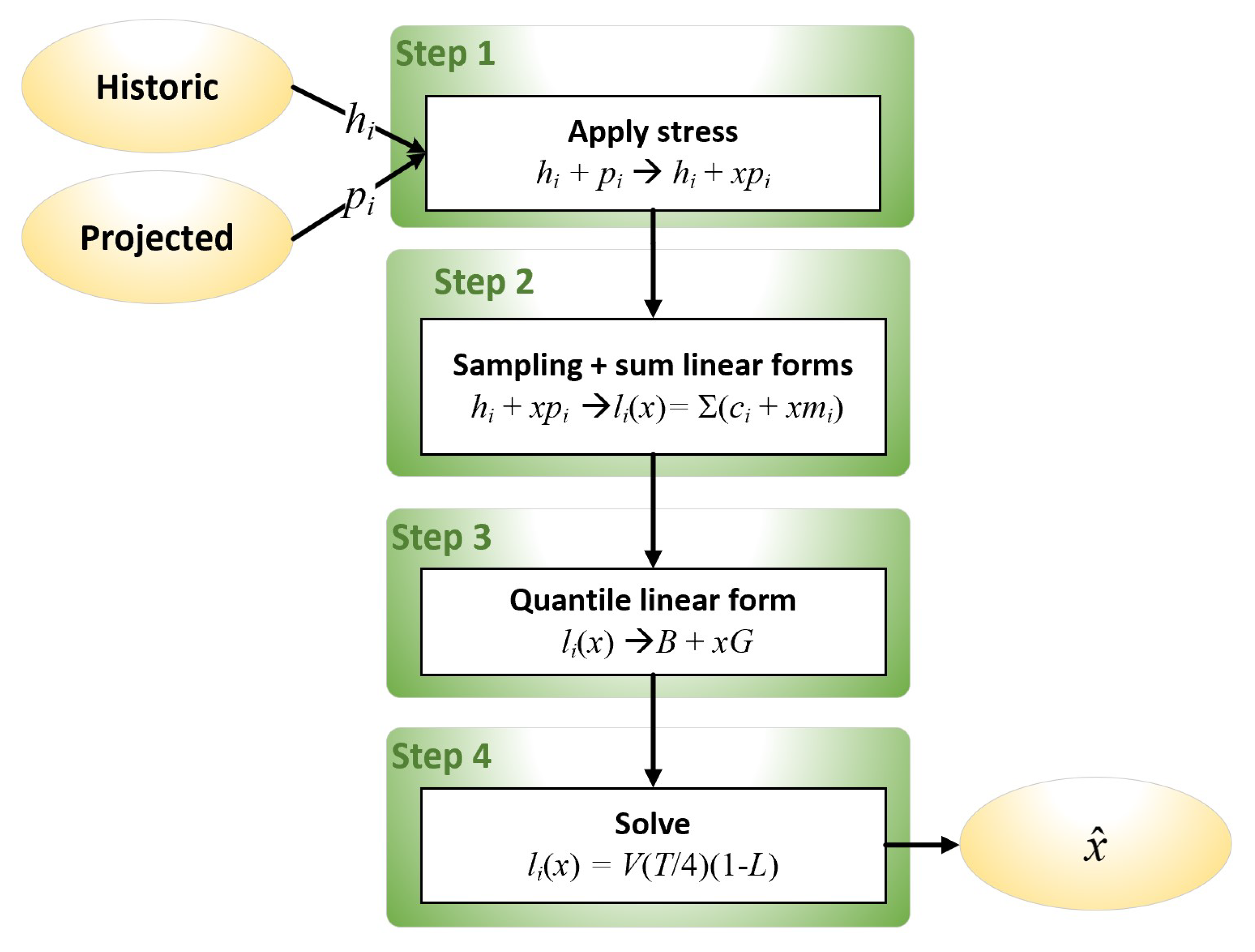
5. Approximate Analytical Method
- Apply stress
- (a)
- Stress projected losses
- (b)
- Calculate distributions and parameters for historic and projected losses
- Derive linear forms
- (a)
- Sample linear forms from the set
- (b)
- Sum linear forms:
- Derive a quantile linear form
- (a)
- Calculate the 99.9 quantiles, and of the linear forms when and . The difference measures the effect of including unstressed data. This stage establishes a base value for calculating stress.
- (b)
- Calculate the gradients, , of each linear form , and extract the 99.9 quantile, G, from the set of (**)
- (c)
- Assert that the line should be the required quantile linear form. This line measures the linear deviation from the base value as x increases.
- Solve for x
- (a)
- Solve the (linear) equation for a 1 quarter prediction. V and L are the same as in Equation (2), and T is an annual inflation factor for VaR, such as 0.5 for 50% annual inflation. For projection 1 year ahead, would be used instead. The solution, , represents a marginal stress factor, representing the amount of the inflated VaR.
- (b)
- The overall stress factor, referred to the original capital, V, is returned as .
6. Results
6.1. Data and Implementation
6.2. Previous Results
- For one million Monte Carlo trials using Block 1 (“traditional”) methods: 15.64 [11.90]
- For three million Monte Carlo trials using Block 1 (“traditional”) methods: 12.49 [9.24]
- For five million Monte Carlo trials using Block 1 (“traditional”) methods: 13.35 [10.25]
- For one million Monte Carlo trials using Block 4 (“random”) methods: 12.42 [12.56]
- For three million Monte Carlo trials using Block 4 (“random”) methods: 16.12 [12.01]
- For five million Monte Carlo trials using Block 4 (“random”) methods: 10.84 [10.88]
- For one million Monte Carlo trials using Block 2 (zero) methods: 7.25 [5.42]
- For three million Monte Carlo trials using Block 2 (zero) methods: 5.43 [3.52]
- For five million Monte Carlo trials using Block 2 (zero) methods: 5.44 [3.41]
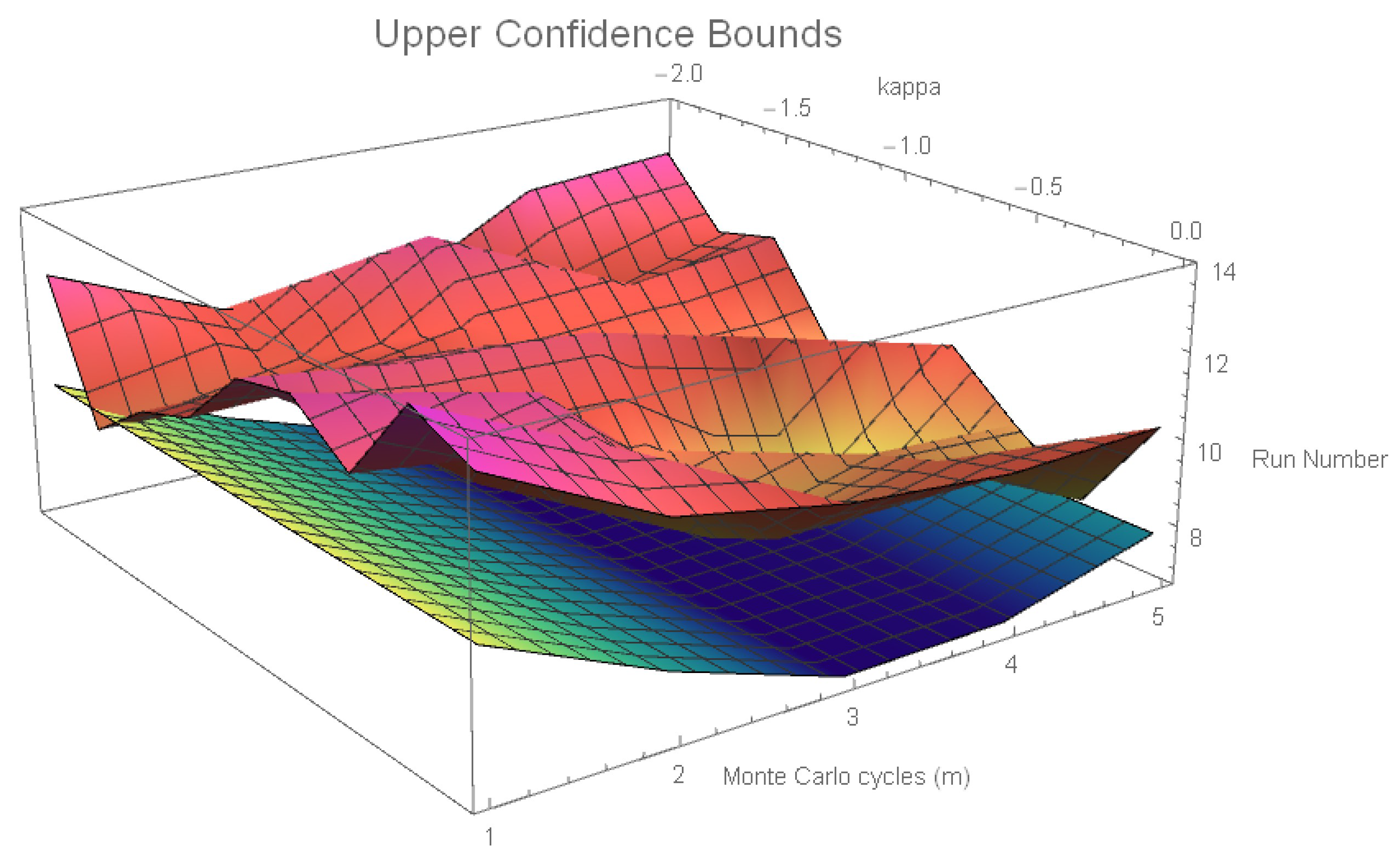
6.3. Run Number Expected Value Results
6.4. Standard Deviation Results
6.5. Results from a Few Monte Carlo Trials
6.6. Run Number 95% Confidence Interval
6.7. Optimal Value Consistency Results
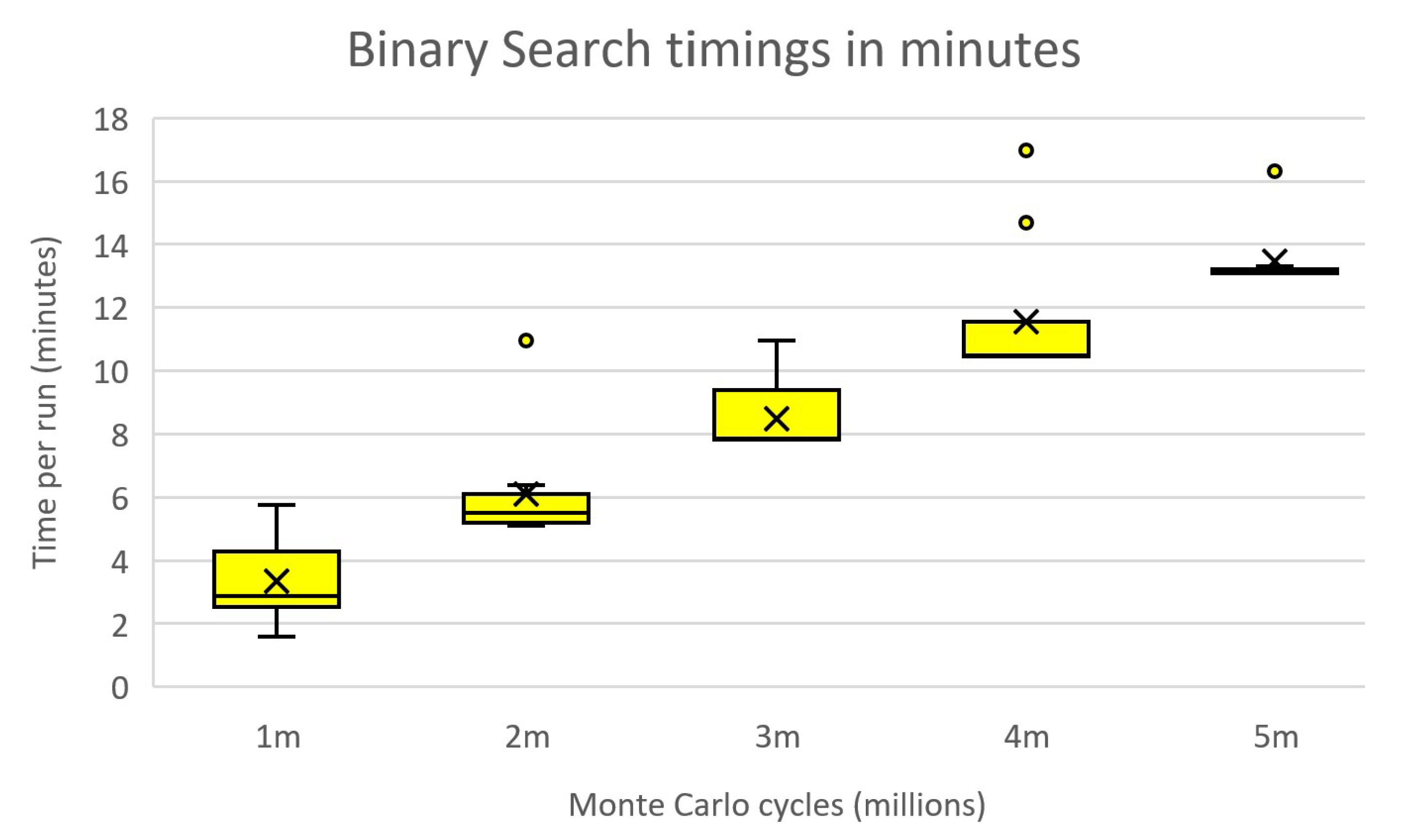
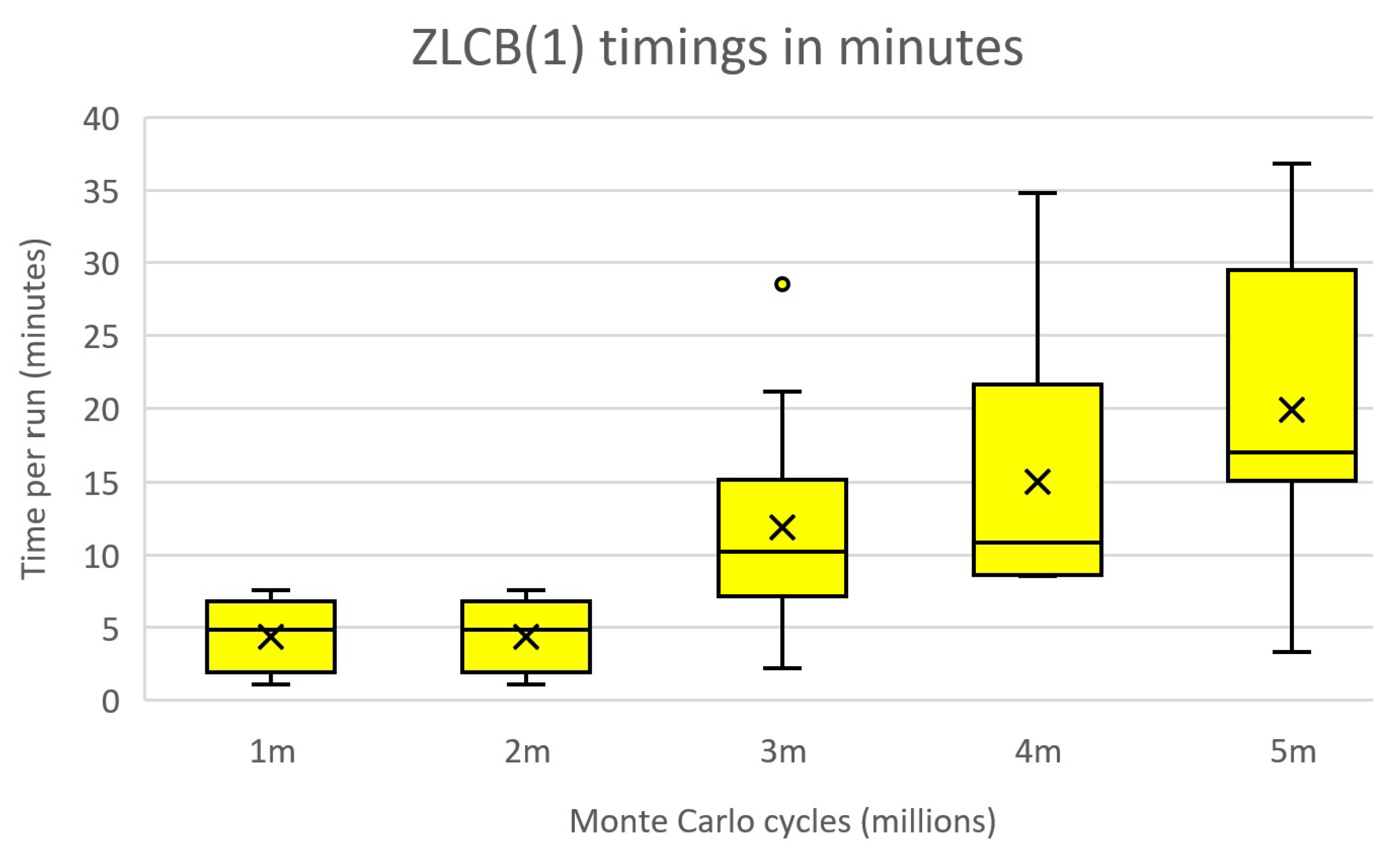
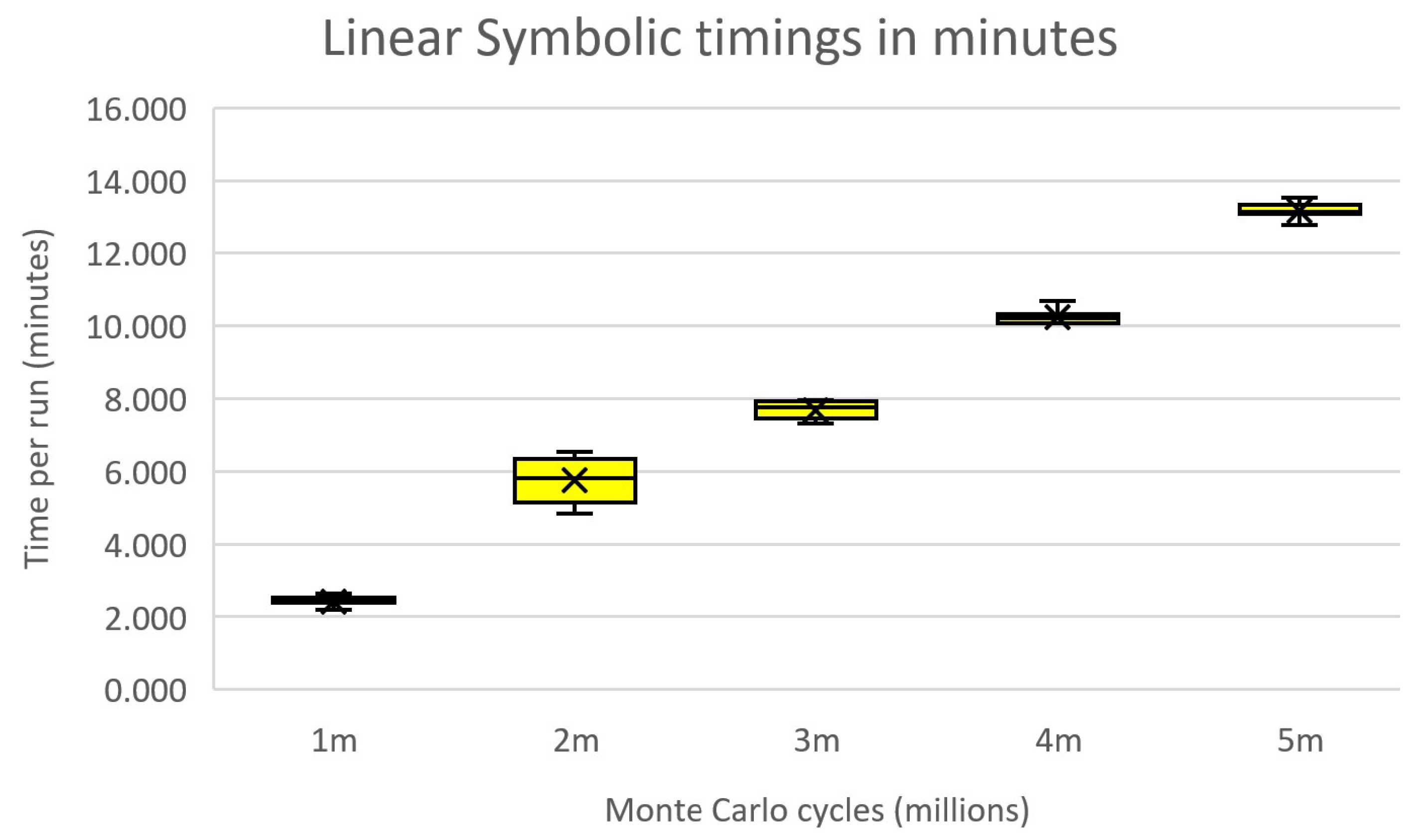
6.8. Timings
6.9. The Effect of COVID-19
7. Discussion
7.1. Implications for Practitioners
7.2. Contribution to the Literature
- This work is the first application of RST in the context of OpRisk. It is both simple conceptually and easy to apply in practice.
- The U.K. regulatory authority has hitherto avoided discussion of how stress testing (reverse or not) should be done. We provided a first solution.
- The use of “traditional” acquisition functions in Bayesian optimization has been shown to be ineffective in the context of OpRisk. A simple solution, the ZERO acquisition function, was defined and found to be performant.
- Two performant optimization methods, zero and binary, were identified as optimally performant in the context of OpRisk.
8. Conclusions
Further Work
Funding
Conflicts of Interest
Appendix A. The LDA Algorithm
- Calculate the annual loss frequency,
- Repeat m times
- (a)
- Obtain a frequency sample size by drawing a random sample of size 1 from a Poisson (f) distribution (*) (**)
- (b)
- Draw a sample of size , , from the severity distribution, F (**)
- (c)
- Sum the losses in to obtain , the annual loss estimate, and add to a vector of annual loss estimates (**)
- Calculate VaR: the th percentile of the vector of annual loss estimates.
- data: a vector of numbers n1, n2, ....
- params: the log normal parameters fitted to data
- years: the number of years covered by the data
- m: the number of Monte Carlo iterations
- threshold: the minimum datum for modelling purposes.
Appendix B. Mathematica Code Implementing Algorithm Symbolic Linear
References
- Mitic, P. A Framework for Analysis and Prediction of Operational Risk Stress. Math. Comput. Appl. 2021, 26, 19. [Google Scholar]
- Basel Committee on Banking Supervision. International Convergence of Capital Measurement and Capital Standards, Clause 644. 2006. Available online: https://www.bis.org/publ/bcbs128.pdf (accessed on 8 February 2021).
- Frachot, A.; Georges, P.; Roncalli, T. Loss Distribution Approach for Operational Risk; Working paper; Groupe de Recherche Operationnelle, Credit Lyonnais: Paris, France, 2001; Available online: http://ssrn.com/abstract=1032523 (accessed on 16 December 2020).
- Basel Committee on Banking Supervision. BCBS196: Supervisory Guidelines for the Advanced Measurement Approaches. 2011. Available online: https://www.bis.org/publ/bcbs196.pdf (accessed on 17 March 2021).
- Grundke, P. Reverse stress tests with bottom-up approaches. J. Risk Model Valid. 2011, 5, 71–90. [Google Scholar] [CrossRef]
- Bank of England. Stress Testing the UK Banking System: Key Elements of the 2021 Stress Test. 2021. Available online: https://www.bankofengland.co.uk/stress-testing/2021/key-elements-of-the-2021-stress-test (accessed on 12 March 2021).
- Mockus, J. On Bayesian methods for seeking the extremum, In Optimization Techniques IFIP Technical Conference; Springer: Berlin/Heidelberg, Germany, 1974; pp. 400–404. Available online: http://dl.acm.org/citation.cfm?id=646296.687872 (accessed on 9 March 2021).
- Cox, D.D.; John, S. A statistical method for global optimization. In Proceedings of the 1992 IEEE International Conference on Systems, Man, and Cybernetics, Chicago, IL, USA, 18–21 October 1992. [Google Scholar]
- Kushner, H.J. Stochastic model of an unknown function. J. Math. Anal. Appl. 1962, 5, 150–167. [Google Scholar] [CrossRef]
- Mockus, J.; Tiesis, V.; Zilinskas, A. The application of Bayesian methods for seeking the extremum. Towards Glob. Optim. 1978, 2, 2. [Google Scholar]
- Picheny, V.; Wagner, T.; Ginsbourger, D. A Benchmark of Kriging-Based Infill Criteria for Noisy Optimization. Struct. Multidiscip. Optim. 2013, 48, 607–626. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Boston, MA, USA, 2006. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective, Chapter 15; MIT Press: Boston, MA, USA, 2012. [Google Scholar]
- Gardner, J.R.; Kusner, M.J.; Xu, Z.; Weinberger, K.Q.; Cunningham, J.P. Bayesian Optimization with Inequality Constraints. In Proceedings of the 31st International Conference on International Conference on Machine Learning (ICML’14), Beijing, China, 22–24 June 2014; Volume 32, pp. II-937–II-945. Available online: https://dl.acm.org/doi/10.5555/3044805.3044997 (accessed on 18 March 2021).
- Gramacy, R.B.; Gray, G.A.; Le Digabel, S.; Lee, H.K.H.; Ranjan, P.; Wells, G. Modeling an Augmented Lagrangian for Blackbox Constrained Optimization. Technometrics 2016, 58, 1–11. [Google Scholar] [CrossRef]
- Wang, H.; Stein, B.; Emmerich, M.; Back, T. A new acquisition function for Bayesian optimization based on the moment-generating function. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 507–512. [Google Scholar]
- de Freitas, N.; Smola, A.; Zoghi, M. Exponential regret bounds for Gaussian Process bandits with deterministic observations. In Proceedings of the 29th International Conference on International Conference on Machine Learning (ICML’12), Edinburgh, Scotland, UK, 26 June–1 July 2012; pp. 955–962. Available online: https://dl.acm.org/doi/10.5555/3042573.3042697 (accessed on 18 March 2021).
- Merrill, E.; Fern, A.; Fern, X.; Dolatnia, N. An Empirical Study of Bayesian Optimization: Acquisition Versus Partition. J. Mach. Learn. Res. 2021, 22, 1–25. Available online: https://www.jmlr.org/papers/volume22/18-220/18-220.pdf (accessed on 18 March 2021).
- Hennig, P.; Schuler, C.J. Entropy search for information-efficient global optimization. J. Mach. Learn. Res. 2012, 13, 1809–1837. [Google Scholar]
- Frazier, P.I.; Powell, W.B.; Dayanik, S. The Knowledge-Gradient Policy for Correlated Normal Beliefs. Informs J. Comput. 2009, 21, 599–613. [Google Scholar] [CrossRef]
- Williams, L.F. A modification to the half-interval search (binary search) method. In Proceedings of the 14th Annual Southeast Regional Conference (ACM-SE 14), Birmingham, AL, USA, 22–24 April 1976; pp. 95–101. Available online: https://doi.org/10.1145/503561.503582 (accessed on 8 February 2021).
- Powell, W.B.; Ryzhov, I.O. Optimal Learning Chapter 5; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Letham, B.; Karrer, B.; Ottoni, G.; Bakshy, E. Constrained Bayesian Optimization with Noisy Experiments. Bayesian Anal. 2019, 14, 495–519. Available online: https://projecteuclid.org/journals/bayesian-analysis/volume-14/issue-2/Constrained-Bayesian-Optimization-with-Noisy-Experiments/10.1214/18-BA1110.full (accessed on 14 March 2021). [CrossRef]
- Baes, M.; Schaanning, E. Reverse Stress Testing: Scenario Design for Macroprudential Stress Tests. Available online: http://dx.doi.org/10.2139/ssrn.3670916 (accessed on 12 April 2021).
- Montesi, G.; Papiro, G.; Fazzini, M.; Ronga, A. Stochastic Optimization System for Bank Reverse Stress Testing. J. Risk Financ. Manag. 2020, 13, 174. [Google Scholar] [CrossRef]
- Grigat, D.; Caccioli, F. Reverse stress testing interbank networks. Sci. Rep. 2017, 7, 15616. [Google Scholar] [CrossRef]
- Eichhorn, M.; Mangold, P. Reverse Stress Testing for Banks: A Process-Orientated Generic Framework. J. Int. Bank. Law Regul. 2016, 4. Available online: https://www.cefpro.com/wp-content/uploads/2019/07/Eichhorn_Mangold_2016_JIBLR_Issue_4_Proof_3.pdf (accessed on 13 April 2021).
- Albanese, C.; Crepey, S.; Stefano, I. Reverse Stress Testing. 2020. Available online: http://dx.doi.org/10.2139/ssrn.3544866 (accessed on 12 April 2021).
- Grundke, P.; Pliszka, K. A macroeconomic reverse stress test. Rev. Quant. Financ. Account. 2018, 50, 1093–1130. [Google Scholar] [CrossRef]
- Bank of England. Stress Testing. Available online: https://www.bankofengland.co.uk/stress-testing (accessed on 16 December 2020).
- Financial Conduct Authority. FCA Handbook April SYSC 2021; Chapter 20. Available online: https://www.handbook.fca.org.uk/handbook/SYSC/20/ (accessed on 13 April 2021).
- European Central Bank. 2020 EU-Wide Stress Test—Methodological Note. Available online: https://www.eba.europa.eu/sites/default/documents/files/document_library/2020%20EU-wide%20stress%20test%20-%20Methodological%20Note_0.pdf (accessed on 16 December 2020).
- European Systemic Risk Board. Macro-Financial Scenario for the 2021 EU-Wide Banking Sector Stress Test. 2021. Available online: https://www.esrb.europa.eu/mppa/stress/shared/pdf/esrb.stress_test210120 0879635930.en.pdf ?a0c454e009cf7fe306d52d4f35714b9f (accessed on 13 April 2021).
- US Federal Reserve Bank. Stress Tests and Capital Planning: Comprehensive Capital Analysis and Review. 2020. Available online: https://www.federalreserve.gov/supervisionreg/ccar.htm (accessed on 18 December 2020).
- Mitic, P. Bayesian Optimization for Reverse Stress Testing. In Advances in Intelligent Systems and Computing; Vasant, P., Zelinka, I., Gerhard-Weber, G.M., Eds.; Springer: Cham, Switzerland, 2021; Chapter 17. [Google Scholar] [CrossRef]
- Mitic, P. Improved Gaussian Process Acquisition for Targeted Bayesian Optimization. Int. J. Model. Optim. 2021, 11, 12–18. [Google Scholar] [CrossRef]
- Wilson, J.T.; Hutter, F.; Deisenroth, M.P. Maximizing acquisition functions for Bayesian optimization. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS’18), Montréal, QC, Canada, 3–8 December 2018; Available online: https://dl.acm.org/doi/10.5555/3327546.3327655 (accessed on 13 April 2021).
- Srinivas, N.; Krause, A.; Kakade, S.; Seeger, M. Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design. In Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML’10), Haifa, Israel, 21–24 June 2010; pp. 1015–1022. Available online: http://dl.acm.org/citation.cfm?id=3104322.3104451 (accessed on 8 February 2021).
| Step | Operation | Comment |
|---|---|---|
| 1 | Historic VaR, no inflation | |
| 2 | Inflated VaR by p% | |
| 3 | Formulate expression for the VaR of scaled data | |
| 4 | Formulate expression for the relative change in VaR | |
| 5 | Solve for x (Equation (2)) |
| MC Iterations (m) | ||||||
|---|---|---|---|---|---|---|
| Block | Method | 1 | 2 | 3 | 4 | 5 |
| 1 | UCB () | 8.64 | 14.12 | 12.16 | 14.24 | 14.92 |
| 1 | UCB () | 13.44 | 11.88 | 14.12 | 13.08 | 12.16 |
| 1 | LCB () * | 13.60 | 11.84 | 11.00 | 10.88 | 14.24 |
| 1 | LCB () | 17.56 | 13.72 | 13.92 | 11.84 | 9.85 |
| 1 | LCB () | 15.24 | 13.76 | 9.32 | 11.56 | 16.20 |
| 1 | EI | 18.08 | 16.44 | 14.48 | 15.16 | 11.45 |
| 1 | POI | 22.92 | 16.52 | 12.44 | 15.00 | 14.60 |
| 2 | ZUCB () | 5.56 | 5.44 | 6.20 | 5.20 | 4.72 |
| 2 | ZUCB () | 6.64 | 4.36 | 5.32 | 4.84 | 4.28 |
| 2 | ZLCB () * | 5.58 | 5.60 | 5.28 | 4.68 | 5.20 |
| 2 | ZLCB () | 5.96 | 6.02 | 5.88 | 5.00 | 4.72 |
| 2 | ZLCB () | 6.19 | 5.52 | 4.96 | 4.88 | 5.08 |
| 3 | SE | 11.52 | 13.08 | 10.36 | 7.32 | 7.40 |
| 3 | KG-GP | 9.90 | 11.00 | 10.45 | 12.45 | 13.70 |
| 4 | KG | 6.50 | 5.50 | 6.25 | 5.45 | 5.40 |
| 4 | BS | 6.08 | 5.44 | 5.40 | 5.36 | 5.36 |
| 4 | LI | 6.84 | 5.60 | 6.44 | 6.60 | 6.04 |
| 4 | RS | 12.42 | 17.32 | 16.12 | 13.00 | 10.84 |
| MC Iterations (m) | ||||||
|---|---|---|---|---|---|---|
| Block | Method | 1 | 2 | 3 | 4 | 5 |
| 1 | UCB () | 7.05 | 8.85 | 9.27 | 9.57 | 9.20 |
| 1 | UCB () | 10.14 | 8.48 | 9.95 | 9.05 | 9.88 |
| 1 | LCB () * | 9.69 | 9.94 | 7.98 | 9.35 | 8.62 |
| 1 | LCB () | 15.7 | 10.98 | 10.91 | 9.72 | 7.72 |
| 1 | LCB () | 12.67 | 9.45 | 7.71 | 10.77 | 11.51 |
| 1 | EI | 12.15 | 11.53 | 9.24 | 11.47 | 10.43 |
| 1 | POI | 15.87 | 11.04 | 9.64 | 9.58 | 14.41 |
| 2 | ZUCB () | 2.75 | 2.58 | 2.75 | 2.63 | 2.53 |
| 2 | ZUCB () | 3.46 | 2.64 | 3.39 | 2.1 | 1.79 |
| 2 | ZLCB () * | 3.89 | 2.90 | 2.69 | 2.81 | 2.60 |
| 2 | ZLCB () | 3.32 | 3.03 | 3.00 | 2.97 | 1.79 |
| 2 | ZLCB () | 3.20 | 2.71 | 2.72 | 3.81 | 3.87 |
| 3 | SE | 10.31 | 10.77 | 7.34 | 5.53 | 5.86 |
| 3 | KG-GP | 6.17 | 5.21 | 5.53 | 4.24 | 4.14 |
| 4 | KG | 1.93 | 2.01 | 2.55 | 1.43 | 1.35 |
| 4 | BS | 1.91 | 1.36 | 0.71 | 0.76 | 1.25 |
| 4 | LI | 2.81 | 1.38 | 2.35 | 2.33 | 1.72 |
| 4 | RS | 12.56 | 18.12 | 12.01 | 13.79 | 10.88 |
| Method | Mean | SD | Time (Minutes) |
|---|---|---|---|
| ZUCB () | 18.0 | 17.1 | 21.0 |
| ZLCB () | 17.6 | 14.5 | 18.5 |
| BS | 22.5 | 22.1 | 14.7 |
| RS | 21.0 | 22.2 | 14.4 |
| Method | Mean | SD |
|---|---|---|
| BS | 1.0928 | 0.0054 |
| LI | 1.0882 | 0.0117 |
| KG | 1.0946 | 0.0091 |
| ZUCB () | 1.0929 | 0.0097 |
| ZLCB () | 1.0918 | 0.0101 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitic, P. Operational Risk Reverse Stress Testing: Optimal Solutions. Math. Comput. Appl. 2021, 26, 38. https://doi.org/10.3390/mca26020038
Mitic P. Operational Risk Reverse Stress Testing: Optimal Solutions. Mathematical and Computational Applications. 2021; 26(2):38. https://doi.org/10.3390/mca26020038
Chicago/Turabian StyleMitic, Peter. 2021. "Operational Risk Reverse Stress Testing: Optimal Solutions" Mathematical and Computational Applications 26, no. 2: 38. https://doi.org/10.3390/mca26020038
APA StyleMitic, P. (2021). Operational Risk Reverse Stress Testing: Optimal Solutions. Mathematical and Computational Applications, 26(2), 38. https://doi.org/10.3390/mca26020038






