Nonlinear and Stability Analysis of a Ship with General Roll-Damping Using an Asymptotic Perturbation Method
Abstract
1. Introduction
2. Mathematical Model and Asymptotic Perturbation Method
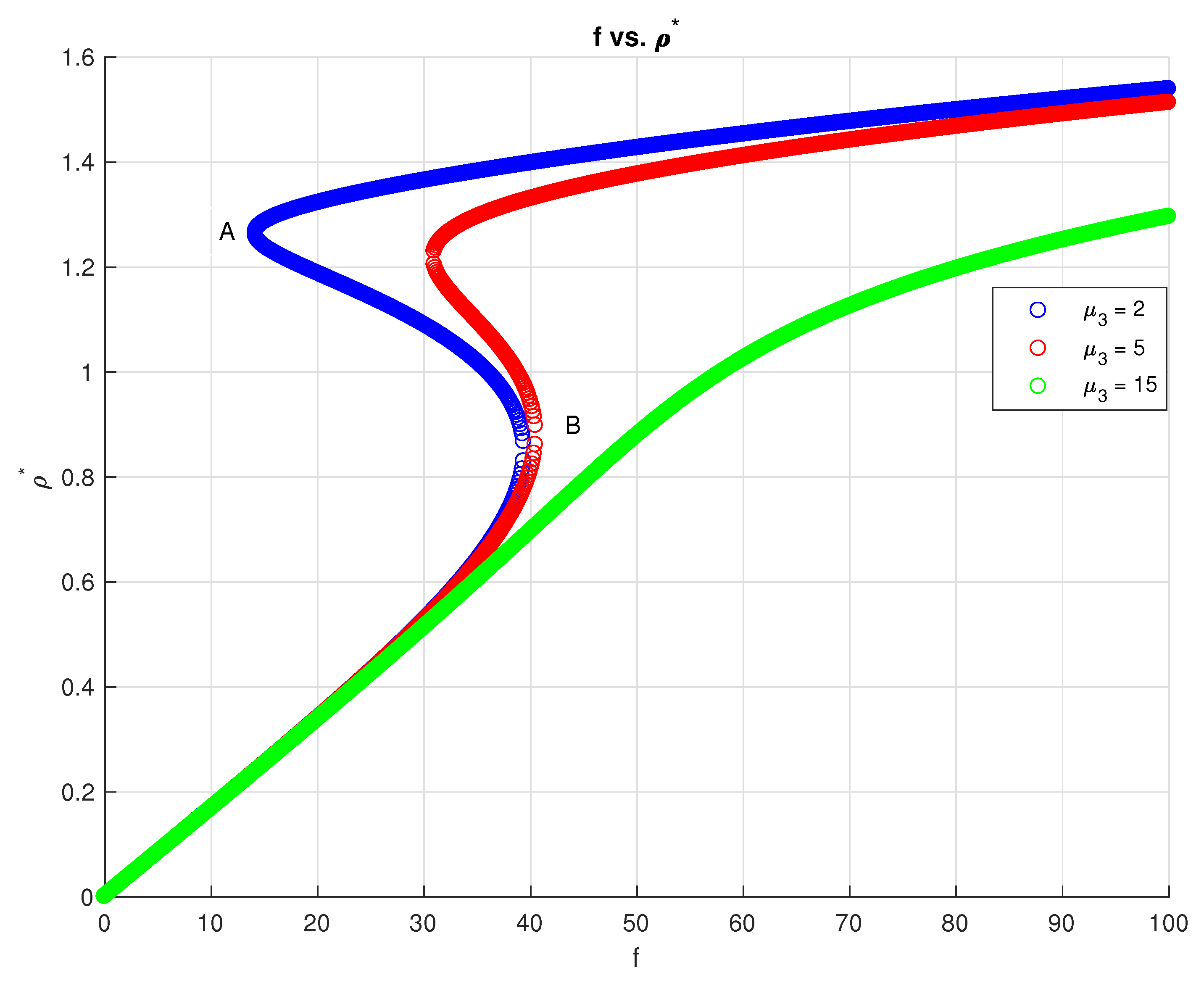
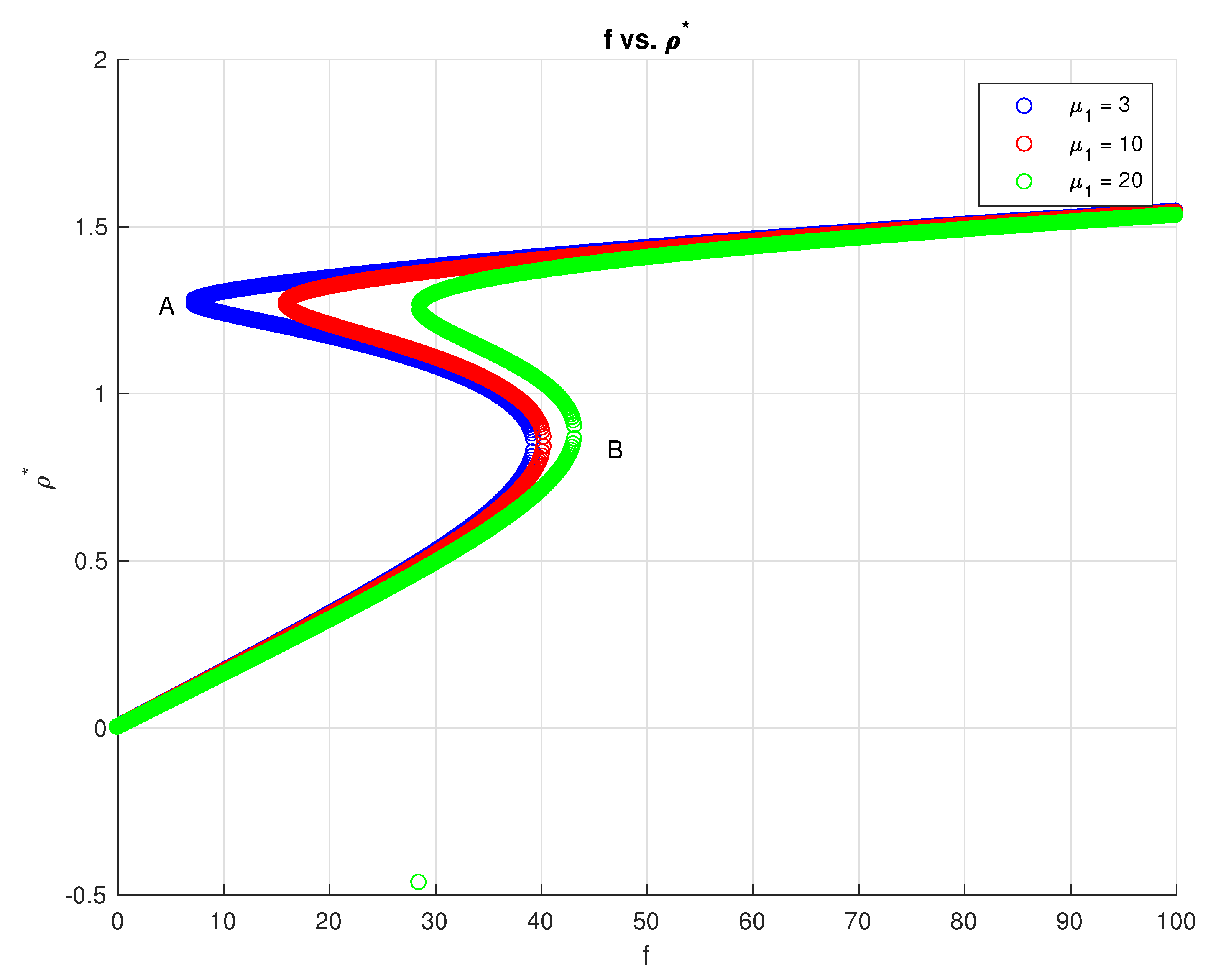
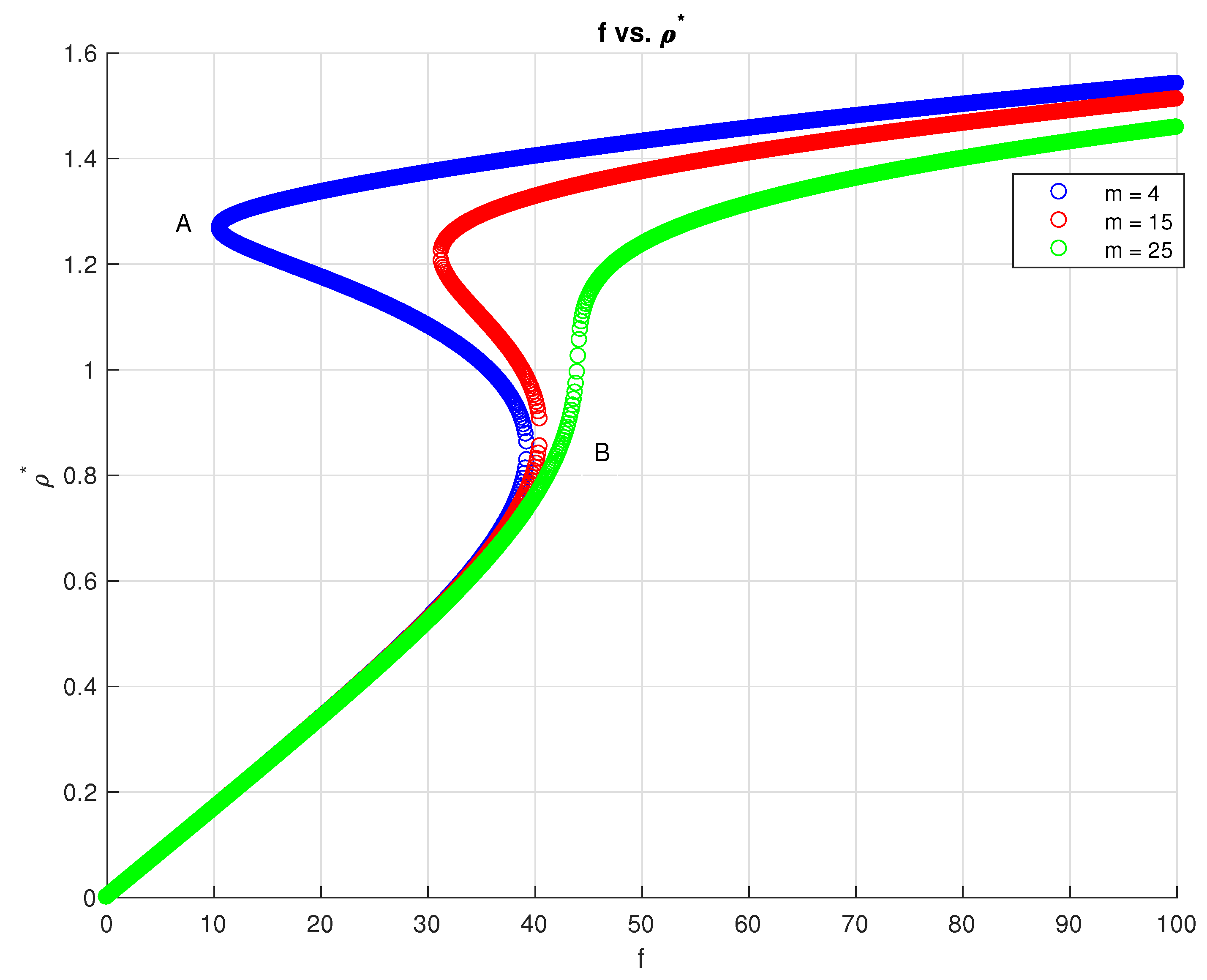
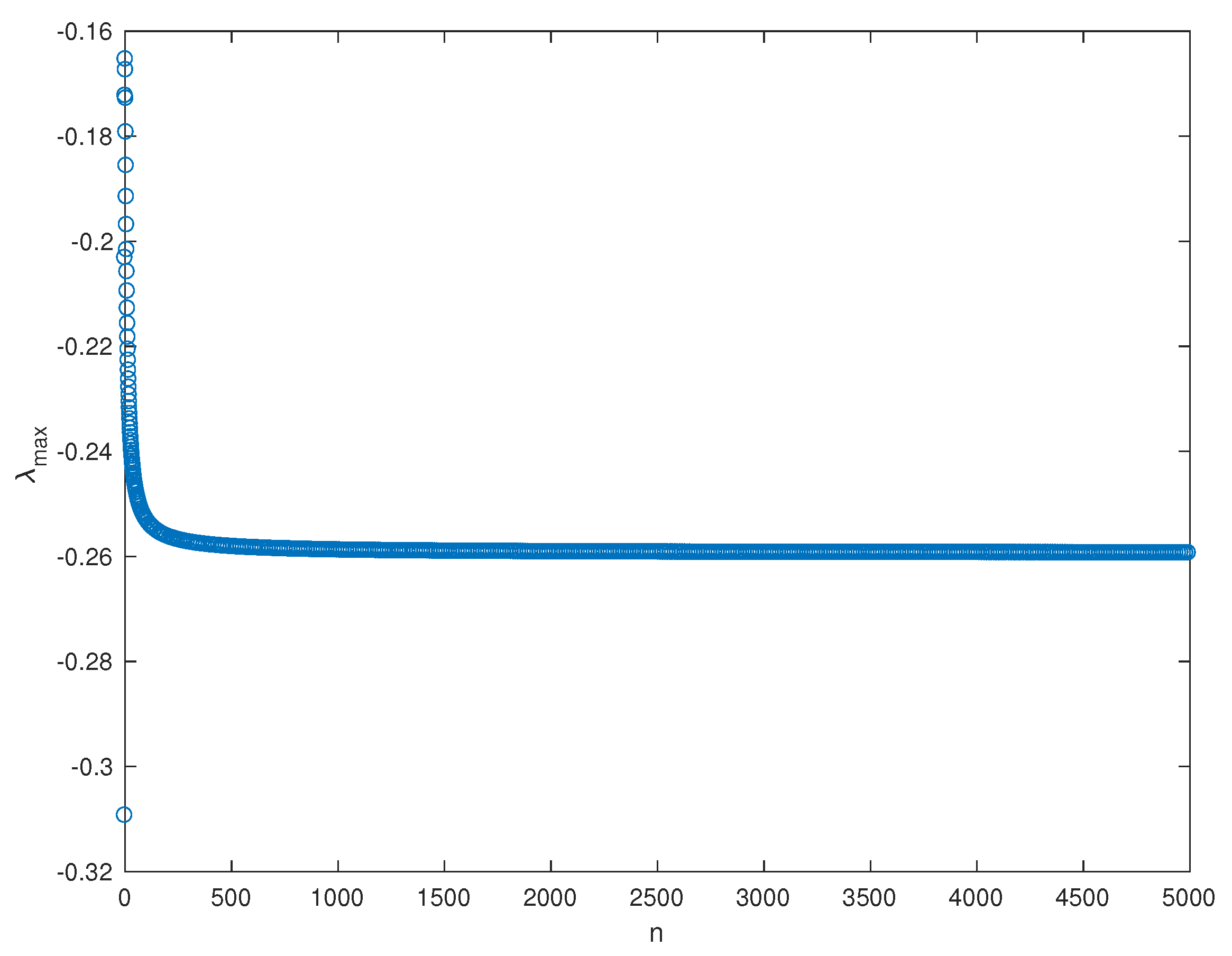
3. Stability of Steady State Solutions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jimoh, I.A.; Kucukdemiral, I.B.; Bevan, G. Fin control for ship roll motion stabilisation based on observer enhanced MPC with disturbance rate compensation. Ocean Eng. 2021, 224, 108706. [Google Scholar] [CrossRef]
- Acanfora, M.; Balsamo, F. The smart detection of ship severe roll motion and decision making for evasive actions. J. Mar. Sci. Technol. 2020, 8, 415. [Google Scholar] [CrossRef]
- The Papers of William Froude; The Institution of Naval Architects: London, UK, 1955.
- Nayfeh, A.H.; Mook, D.T.; Marshall, L.R. Nonlinear Coupling of Pitch and Roll Modes in Ship Motions. J. Hydronaut. 1973, 7, 145–152. [Google Scholar] [CrossRef]
- Zeeman, E.C. Catastrophe Theory; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Odabashi, A.Y. Methods of Analyzing Nonlinear Ship Oscillations and Stability; University of Strathclyde, Department of Shipbuilding and Naval Architecture: Strathclyde, UK, 1973. [Google Scholar]
- Odabashi, A.Y. Ultimate stability of ships. Trans. RINA 1977, 119, 237–263. [Google Scholar]
- Odabashi, A.Y. Conceptual understanding of the stability theory of ships. Schiffstechnik 1978, 25, 1–18. [Google Scholar]
- Odabashi, A.Y. A morphology of mathematical stability theory and its application to intact ship stability assessment. In Proceedings of the 2nd International Conference on Stability of Ships and Ocean Vehicles; Society of Naval Architects of Japan: Tokyo, Japan, 1982; pp. 47–64. [Google Scholar]
- Wellicome, J.F. An Analytical Study of the Mechanism of Capsizing. In Proceedings of the 1st International Conference on Stability of Ships and Ocean Vehicles; University of Strathclyde: Glasgow, Scotland, 1975. [Google Scholar]
- Wright, J.H.G.; Marshfield, W.B. Ship roll response and capsize behaviour in beam seas. Trans. RINA 1980, 122, 129–148. [Google Scholar]
- Jiang, T. Autonomous oscillations and bifurcations of a tug-tanker tow. Ship Technol. Res. Schiffstechnik 1997, 44, 4–12. [Google Scholar]
- Jiang, T.; Schellin, T.E.; Sharma, S.D. Manoeuvring simulation of a tanker moored in steady current including hydrodynamics memory effects and stability analysis. In Proceedings of the International Conference on Ship Manoeuvrability—Prediction and Achievement, London, UK, 29 April–1 May 1987. [Google Scholar]
- Kreuzer, E.; Wendt, M. Nonlinear dynamics of ship oscillations. In Proceedings of the 2000 2nd International Conference on Control of Oscillations and Chaos (Cat. No.00TH8521), St. Petersburg, Russia, 5–7 July 2000; Volume 2, pp. 315–320. [Google Scholar]
- Spyrou, K.J.; Thompson, J.M.T. The nonlinear dynamics of ship motions: A field overview and some recent developments. Philos. Trans. R. Soc. Lond. A 2000, 358, 1735–1760. [Google Scholar] [CrossRef]
- Bulian, G.; Francescutto, A. Experimental results and numerical simulations on strongly non-linear rolling of multihulls in moderate beam seas. Proc. Inst. Mech. Eng. Part M. J. Eng. Maritime Environ. 2009, 223, 189–210. [Google Scholar] [CrossRef]
- Dalzell, J.F. A note on the form of a ship roll damping. J. Ship Res. 1978, 22, 178–185. [Google Scholar] [CrossRef]
- Mathisen, J.B.; Price, W.G. Naval Architects. Trans. R. Inst. 1984, 127, 295. [Google Scholar]
- Nayfeh, A.H.; Khdeir, A.A. Nonlinear rolling of ships in regular beam seas. Int. Shipbuild. Prog. 1986, 33, 40–49. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Sanchez, N.E. Chaos and Dynamic Instability in the Rolling Motion of Ships. In Proceedings of the Symposium on Naval Hydrodynamics, Hague, The Netherlands, 29 August–2 September 1988. [Google Scholar]
- El-Bassiouny, A.F. Internal resonance of a nonlinear vibration absorber. Phys. Scr. 2005, 72, 203–211. [Google Scholar] [CrossRef]
- El-Bassiouny, A.F. Coexistance of stable solutions in the nonlinear ship motion. Phys. Scr. 2005, 71, 561–571. [Google Scholar] [CrossRef]
- El-Bassiouny, A.F. Vibration and chaos control of nonlinear torsional vibrating systems. Phys. A 2006, 366, 167–186. [Google Scholar] [CrossRef]
- El-Bassiouny, A.F. Nonlinear analysis for a ship with a general roll-damping model. Phys. Scr. 2007, 75, 691–701. [Google Scholar] [CrossRef]
- El-Bassiouny, A.F. Three-to-one Internal Resonance in The Non Linear Oscillation of Shallow Arch. Phys. Scr. 2005, 72, 439. [Google Scholar] [CrossRef]
- Henrard, J.; Meyer, K.R. Averaging and bifurcations in symmetric systems. SIAM J. Appl. Math. 1977, 32, 133–145. [Google Scholar] [CrossRef]
- King, A.C.; Billingham, J.; Otto, S.R. Differential Equations, Linear, Nonlinear, Ordinary, Partial; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Nayfeh, A.H. Introduction to Perturbation Techniques; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley-Interscience: New York, NY, USA, 1979. [Google Scholar]
- Nayfeh, A.H. Introduction to Perturbation Techniques; Wiley-Interscience: New York, NY, USA, 1981. [Google Scholar]
- Nayfeh, A.H. Problems in Perturbation; Wiley-Interscience: New York, NY, USA, 1985. [Google Scholar]
- Sidorov, N.A.; Trufanov, A.V. Nonlinear operator equations with a functional perturbation of the argument of neutral type. Diff. Equat. 2009, 45, 1840–1844. [Google Scholar] [CrossRef]
- Maccari, A. The nonlocal oscillator. Il Nuovo Cimento B 1996, 111, 917–930. [Google Scholar] [CrossRef]
- Maccari, A. The dissipative nonlocal oscillator in resonance with a periodic excitation. Il Nuovo Cimento B 1996, 111, 1173–1186. [Google Scholar] [CrossRef]
- Maccari, A. Dissipative bi-dimensional systems and resonant excitations. Int. J. Nonlinear Mech. 1998, 33, 713–726. [Google Scholar] [CrossRef]
- Maccari, A. Approximate solution of a class of nonlinear oscillators in resonance with a periodic excitation. Nonlinear Dyn. 1998, 15, 329–343. [Google Scholar] [CrossRef]
- Maccari, A. Bifurcation control in the Burgers–KdV equation. Phys. Scr. 2008, 77, 035003. [Google Scholar] [CrossRef]
- Eloe, P.W.; Usman, M. Bifurcations in Steady State Solutions of a Class of Nonlinear Dispersive Wave Equation. Int. J. Nonlinear Stud. 2012, 19, 215–224. [Google Scholar]
- Cahalan, R.F.; North, G.R. A stability theorem for energy-balance climate models. J. Atm. Sci. Vol. 1979, 36, 1178–1188. [Google Scholar] [CrossRef]
- Shen, S.; North, G. A Simple proof of the slope stability theorem for energy balance climate models. Can. Appl. Math. Q. 1999, 7, 2. [Google Scholar]

| n | Axis | Direction of Motion | Symbol |
|---|---|---|---|
| 1 | translation along x | surge | x |
| 2 | translation along y | sway | y |
| 3 | translation along z | heave | z |
| 4 | rotation along x | roll | |
| 5 | rotation along y | pitch | |
| 6 | rotation along z | yaw |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usman, M.; Abdallah, S.; Imran, M. Nonlinear and Stability Analysis of a Ship with General Roll-Damping Using an Asymptotic Perturbation Method. Math. Comput. Appl. 2021, 26, 33. https://doi.org/10.3390/mca26020033
Usman M, Abdallah S, Imran M. Nonlinear and Stability Analysis of a Ship with General Roll-Damping Using an Asymptotic Perturbation Method. Mathematical and Computational Applications. 2021; 26(2):33. https://doi.org/10.3390/mca26020033
Chicago/Turabian StyleUsman, Muhammad, Shaaban Abdallah, and Mudassar Imran. 2021. "Nonlinear and Stability Analysis of a Ship with General Roll-Damping Using an Asymptotic Perturbation Method" Mathematical and Computational Applications 26, no. 2: 33. https://doi.org/10.3390/mca26020033
APA StyleUsman, M., Abdallah, S., & Imran, M. (2021). Nonlinear and Stability Analysis of a Ship with General Roll-Damping Using an Asymptotic Perturbation Method. Mathematical and Computational Applications, 26(2), 33. https://doi.org/10.3390/mca26020033






