Abstract
In nuclear engineering, the -modes associated with the neutron diffusion equation are applied to study the criticality of reactors and to develop modal methods for the transient analysis. The differential eigenvalue problem that needs to be solved is discretized using a finite element method, obtaining a generalized algebraic eigenvalue problem whose associated matrices are large and sparse. Then, efficient methods are needed to solve this problem. In this work, we used a block generalized Newton method implemented with a matrix-free technique that does not store all matrices explicitly. This technique reduces mainly the computational memory and, in some cases, when the assembly of the matrices is an expensive task, the computational time. The main problem is that the block Newton method requires solving linear systems, which need to be preconditioned. The construction of preconditioners such as ILU or ICC based on a fully-assembled matrix is not efficient in terms of the memory with the matrix-free implementation. As an alternative, several block preconditioners are studied that only save a few block matrices in comparison with the full problem. To test the performance of these methodologies, different reactor problems are studied.
1. Introduction
The neutron transport equation is a balance equation that describes the behavior of the neutrons inside the reactor core. This equation for three-dimensional problems is an equation defined in a phase space of dimension seven, and this makes the problem very difficult to solve. Thus, some approximations are considered such as the multigroup neutron diffusion equation by relying on the assumption that the neutron current is proportional to the gradient of the neutron flux by means of a diffusion coefficient.
Given a configuration of a nuclear reactor core, its criticality can be forced by dividing the production operator in the neutron diffusion equation by a positive number, , obtaining a neutron balance equation: the -modes problem. For the two energy groups approximation and without considering up-scattering, this equation can be written as [1]:
where and denote the fast and thermal flux, respectively. The macroscopic cross-sections , , and , with , and , are values that depend on the position.
The largest eigenvalue in magnitude, called the k-effective (or multiplication factor), indicates a measure of the criticality of the reactor, and its corresponding eigenfunction describes the steady-state neutron distribution in the reactor core. Next, dominant eigenvalues and their corresponding eigenfunctions are useful to develop modal methods for the transient analysis.
To make a spatial discretization of Problem (1), a high order continuous Galerkin finite element method is used, leading to a generalized algebraic eigenvalue problem of the form:
where the matrix elements are given by:
where is the prescribed shape function for the ith node. The vector is the algebraic vector of the finite weights corresponding to the neutron flux in terms of the shape functions. The shape functions used in this work are Lagrange polynomials. The subdomains () denote the cells in which the reactor domain is divided and where the cross-sections are assumed to be constant. Similarly, is the corresponding subdomain surface, which is part of the reactor boundary. More details on the finite element discretization can be found in [2]. For the implementation of the finite element method, the open source finite elements library Deal.II [3] has been used.
In this work, a matrix-free strategy for the blocks of the matrix M and for the non-diagonal blocks of L is developed. In this way, matrix-vector products are computed on the fly in a cell-based interface. For instance, we can consider that a finite element Galerkin approximation that leads to the matrix takes a vector u as input and computes the integrals of the operator multiplied by trial functions, and the output vector is v. The operation can be expressed as a sum of cell-based operations,
where denotes the matrix that defines the location of cell-related degrees of freedom in the global vector and denotes the submatrix of on finite element e. This sum is optimized through sum-factorization. Details about the implementation are explained in [4]. This strategy greatly reduces the memory used by the matrix elements.
Calculation of the dominant lambda mode has traditionally utilized the classical power iteration method, which although robust, converges slowly for dominance ratios near one, as occurs in some practical problems. Thus, acceleration techniques are needed to improve the convergence of the power iteration method. Some approaches in diffusion theory are, for instance, Chebyshev iteration [5] and Wielandt shift [6]. Alternative approaches to the power iteration method have been studied in an attempt to improve upon the performance of accelerated power iteration methods [7,8]. The subspace iteration method [9], the Implicit Restarted Arnoldi method (IRAM) [10], the Jacobi–Davidson [11], and the Krylov–Schur method [2] implemented in the SLEPclibrary [12] have been used to compute the largest or several dominant eigenvalues for the neutron diffusion equation and their corresponding eigenfunctions. More recently, other Krylov methods have been used to compute these modes for other approximations of the neutron transport equation [7,13]. Usually, applying these kinds of methods requires either transforming the generalized problem (2) into an ordinary eigenvalue problem or applying a shift and invert technique. In both cases, in the solution process, it is necessary to solve numerous linear systems. These systems are not well-conditioned, and they need to be preconditioned. Thus, the time and computational memory needed to compute several eigenvalues become very high.
One alternative is to use a method that does not require solving any linear system, such as the generalized Davidson, used for neutron transport calculations in [14]. Other methods are the block Newton methods that have been shown to be very efficient in the computation of several eigenvalues in neutron diffusion theory. These methods either do not need to solve as many linear systems as the Krylov methods or avoid solving any linear system with some hybridization. One of these Newton methods is the modified block Newton method, which has been considered for the ordinary eigenvalue problem associated with Problem (2) [15] or directly for the generalized eigenproblem (2) [16]. One advantage of these block methods is that several eigenvectors can be approximated simultaneously, and as a consequence, the convergence behavior improves. The convergence of the eigensolvers usually depends on the eigenvalue separation, and if there are clustered or multiple eigenvalues, the methods may have problems finding all the eigenvalues. In practical situations of reactor analysis, the dominance ratio corresponding to the dominant eigenvalues is often near unity, resulting in a slow convergence. In the block methods, this convergence only depends on the separation of the group of target eigenvalues from the rest of the spectrum. Another advantage is that these methods do not require solving as many linear systems as the previous methods. However, these linear systems still need to be preconditioned. Another of this kind of Newton method is the Jacobian-free Newton–Krylov methods that have been studied with traditional methods such as the power iteration used as the preconditioner [17,18] or with a more sophisticated Schwarz preconditioner [19]. In this work, we use the Modified Generalized Block Newton Method (MGBNM) presented in [16], and we propose several ways to precondition the linear systems that need to be solved in this method in an efficient way.
The structure of the rest of the paper is as follows. In Section 2, the modified generalized block Newton method is described. In Section 3, the different preconditioners for the MGBNM are presented. The performance of the preconditioners is presented in Section 4 for two different benchmark problems. Finally, Section 5 synthesizes the main conclusions of this work.
2. The Modified Generalized Block Newton Method
This method was presented by Lösche in 1998 [20] for ordinary eigenvalue problems, and an extension to generalized eigenvalue problems was studied in [16]. Given the partial generalized eigenvalue problem (2) written as:
where is a matrix with q eigenvectors and is a diagonal matrix with the q eigenvalues associated, we suppose that the eigenvectors can be factorized as where Z is an orthogonal matrix. Moreover, the biorthogonality condition is introduced, where W is a fixed matrix. Thus, if we denote , the problem (4) can be rewritten as:
We construct this projection to ensure that the method converges to independent eigenvectors.
Then, the solution of Problem (4) is obtained by solving the non-linear problem:
By applying Newton’s method, a new iterated solution arises as:
where and are solutions of the system obtained when the equations (6) are substituted into the equations (5), and these are truncated at the first order terms.
The matrix is not necessarily a diagonal matrix, and as a result, the system is coupled. To avoid this problem, the modified generalized block Newton method (MGBNM) needs to apply the previous two steps. Firstly, the modified Gram–Schmidt process is used to orthonormalize the matrix . Then, the Rayleigh–Ritz projection method for the generalized eigenvalue problem [21] is applied. Thus, , where and where are obtained from the solutions of the linear systems:
The solution of these systems is computed by using the Generalized Minimal Residual method (GMRES) computing the matrix vector products with block matrix multiplications. However, these systems need to be preconditioned (in each iteration and for each eigenvalue) to reduce the condition number of the matrix.
3. Preconditioning
The first choice for a preconditioner is assembling the matrix:
and constructing the full preconditioner associated with the matrix. We use the ILUT(0) preconditioner since A is a non-symmetric matrix. There are no significant differences if the preconditioner obtained for the matrix associated with the first eigenvalue is used for all eigenvalues in the same iteration because in the matrix, A only changes the value of , and usually, the eigenvalues in reactor problems are clustered. This preconditioner is denoted by P.
To devise an alternative preconditioner without the necessity of assembling the matrix A, we write the explicit inverse of A, by using its block structure,
where:
We desire a preconditioner for A by suitably approximating . Let us call a preconditioner for J. For instance, , where are the incomplete L and U factors of J. Thus, we can define, after setting , the preconditioner of A as:
The previous preconditioner does not need to assemble the entire matrix A, but it needs to assemble the matrix J to build its ILUpreconditioner. Therefore, the next alternative that we propose is using a preconditioner of instead of . This preconditioner works well because in the discretization process, the L matrix comes from the discretization of the differential matrix that has the gradient operators and the diffusion terms. In addition, in nuclear calculations, is near . Thus, we can build a preconditioner of instead of the matrix J. We denote by the preconditioner where the preconditioner of is used to precondition the block J.
Finally, the last alternative is avoiding assembling the matrix L taking advantage of its block structure. For that purpose, we carry out a similar process as the one used for matrix A. We write the explicit form of the inverse of L as:
and substitute the inverses of the blocks by preconditioners. Thus, the preconditioner of L has the following structure:
where , denote a preconditioner of and , respectively. The block matrices , are symmetric and positive definite. Then, we can use as preconditioner the Incomplete Cholesky decomposition (IC(0)). However, the main advantage of this preconditioner is that it permits using a matrix-free implementation that does not require allocating all matrices. We only need to assemble the blocks and to construct the associated IC(0) preconditioners. The application of with to precondition J is called .
4. Numerical Results
In this section, the performance of the proposed preconditioners has been tested on two different problems: a version of the 3D NEACRPreactor [22] and a configuration of the Ringhals reactor [23]. The neutron diffusion equation in both problems has been discretized using the finite element method presented in Section 1 using Lagrange polynomials of degree three because it is shown in previous works that this degree is necessary to obtain accurate results in similar reactor problems [2]. The number of eigenvalues computed was four for each reactor.
The incomplete lower-upper preconditioner with Level 0 of fill (ILU) has been provided by the PETScpackage [24].
As the modified generalized block Newton method needs an initial approximation of a set of eigenvectors, a multilevel initialization with two meshes was used to obtain this approximation (for more details, see [25]).
The stopping criteria for all solvers has been set equal to in the global residual error,
where is the eigenvalue and its associated eigenvector such that .
The modified block Newton method has been implemented using a dynamic tolerance in the residual error of the solution in the linear systems. The tolerance values have been set to .
The methods have been implemented in C++ based on the data structures provided by the library Deal.ii [3] and PETSc [24]. The computer used for the computations was an Intel® Core™-4790 @3.60 GHz with 32 Gb of RAM running on Ubuntu GNU/Linux 16.04 LTS.
4.1. NEACRP Reactor
The NEACRP benchmark in a near-critical configuration [22] is chosen to compare the proposed methodology. The reactor core has a radial dimension of cm × cm per assembly. Axially, the reactor, with a total height of cm, is divided into 18 layers with height (from bottom to top): cm, cm, cm, cm, cm (10 layers), cm (two layers), cm, and cm. Figure 1 shows the reactor geometry and the distribution of the different materials. The cross-sections of materials are displayed in Table 1. The total number of cells of the reactor domain is 3978. Zero flux boundary conditions were set. The spatial discretization of the neutron diffusion equation, by using polynomials of degree three, gave a number of 230,120 degrees of freedom. The mesh built to obtain an initial guess had 1308 cells, and the computational time needed to obtain this approximation was 24 s. The four dominant eigenvalues computed are collected in Table 2. This table shows that the spectrum associated with the problem is clustered with two degenerated eigenvalues. A representation of the fast flux distribution for each mode is displayed in Figure 2.
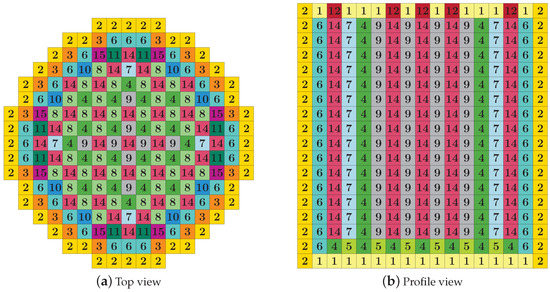
Figure 1.
Geometry and distribution of the materials of the NEACRPreactor.

Table 1.
Macroscopic cross-section of the NEACRP reactor.

Table 2.
Eigenvalues for the NEACRP reactor.
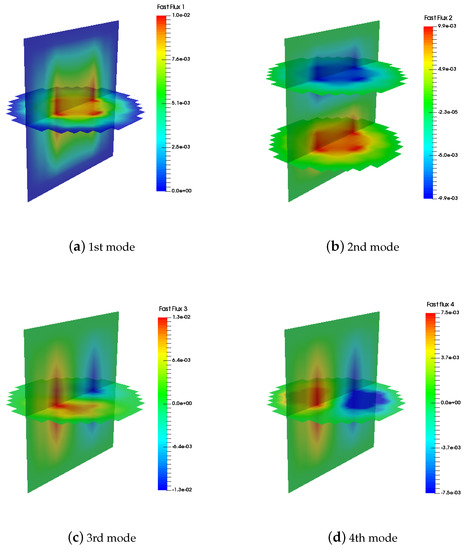
Figure 2.
Fast fluxes’ distribution of the NEACRP reactor corresponding to the first four modes.
First, we show the convergence history of the MGBNM to obtain the solution of the eigenvalue problem. Figure 3 shows the number of iterations against the residual error for the NEACRP reactor. It is observed that the MGBNM only needed four iterations to reach a residual error equal to .

Figure 3.
Convergence history of the Modified Generalized Block Newton Method (MGBNM) for the NEACRP reactor.
Table 3 collects the average number of iterations obtained by directly applying the ILU preconditioner of A and the total time that the GMRES method needs to reach the residual error in the linear systems given in Tol(). The time spent to assemble the matrices and to build the preconditioner (setup time (s)) is also displayed. These data are presented for each iteration and in a total sum. This table shows that the number of iterations is not very high, but the time spent to assemble the matrix and to construct the preconditioner increases the total CPU time considerably. It is necessary to build in each iteration a new preconditioner for A because the columns related to the block Z change considerably in each updating.

Table 3.
Data for the preconditioner P for the NEACRP reactor. GMRES, Generalized Minimal Residual.
Table 4 displays these data related to the block preconditioner proposed that uses the ILU preconditioner for approximating the inverse of . It is observed that we only needed to assemble the matrix once in the first iteration to build the preconditioner. This is because we only needed a preconditioner of , and the value of was very similar for all iterations. The mean of the number of iterations of the GMRES preconditioned with was larger than in the previous case, but the total CPU time of using this block preconditioner was reduced by 26 s with respect to the full preconditioner.

Table 4.
Data for the preconditioner with ILUfor the NEACRP reactor.
Table 5 shows the data related to the block preconditioner , but in this case, we have used the Geometric Multigrid (GMG) preconditioner to approximate the inverse of . The results show, in comparison with the results of Table 4, that in spite of the total number of iterations and the setup time being much lower for the GMG, the total computational time is much higher. This is due to the application of the GMG preconditioner being more expensive than the application of the ILU preconditioner.

Table 5.
Data for the preconditioner with the Geometric Multigrid (GMG) for the NEACRP reactor.
The next results were obtained by using the block preconditioner, , but in these cases, approximating the by the ILU preconditioner of () and by a block preconditioner of (). The most relevant data to compare the preconditioners considered in this work are exposed in Table 6. They were the total iterations of the GMRES, the total setup time, the total time to compute the solution, and the maximum computational memory spent by the matrices. We observe that the number of iterations increased when worse approximations of the inverse of A were considered, but the setup time that each preconditioner needs became smaller. Moreover, the maximum CPU memory was also reduced significantly. In the total CPU times, we observed that the block preconditioner (), in all of its versions, improved the times obtained by applying the ILU preconditioner of A directly. Between the possibilities for obtaining a preconditioner of , there were no big differences in the computational times, but there was an important savings of the computational memory. The best results were obtained by if the computational memory consumption was taken into account.

Table 6.
Data obtained by using different preconditioners for the NEACRP reactor.
Table 7 shows the timings and the memory spent in the matrix allocation by using the matrix-free technique or without using this strategy. The results show that not only the matrix memory consumption and the time to assemble were reduced, but also the time spent to compute the matrix-vector products. That implies that the matrix-free strategy reduced the total CPU time by about 30%.

Table 7.
Data obtained using different matrix implementations for the NEACRP reactor.
Finally, we compared the MGBNM with this methodology against other eigenvalue solvers commonly used in the neutron diffusion computations (Table 8). We show the results by using a different number of computed eigenvalues (No. eigs). In particular, we have chosen for this comparison the generalized Davidson preconditioned with the block Gauss–Seidel preconditioner and the Krylov–Schur method by previously reducing the generalized eigenvalue problem to an ordinary eigenvalue problem as in [2]. To use both methods, the library SLEPc has been used [12]. From the computational times, we can deduce that the MGBNM was twice as fast as the rest of solvers for the computation of one and two eigenvalues, and it was very competitive at computing four eigenvalues.

Table 8.
Computational times for the MGBNM with , the generalized Davidson method, and the Krylov–Schur method for the NEACRP reactor. eigs, eigenvalues.
4.2. Ringhals Reactor
For a practical application of the preconditioners in a real reactor, we have chosen the configuration of the Ringhals rector. Particularly, we have chosen the C9 point of the BWRreactor Ringhals I stability benchmark, which corresponds to a point of operation that degenerated in an out-of-phase oscillation [23]. It is composed of 27 planes with 728 cells in each plane. A representation with more detail of its geometry can be observed in Figure 4. The spatial discretization using finite elements of degree three gave 1,106,180 degrees of freedom. The coarse mesh considered to obtain an initial guess for the MGBNM had 6709 cells and the problem associated with this mesh a size of 386,768 degrees of freedom. The computed dominant eigenvalues were , , , and . The corresponding fast fluxes are represented in Figure 5.

Figure 4.
Geometry of the Ringhals reactor.
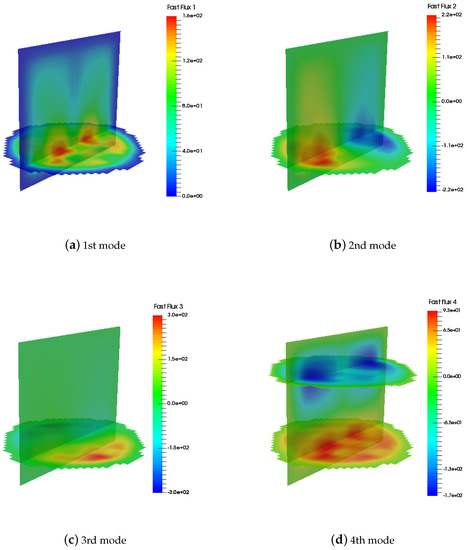
Figure 5.
Fast fluxes’ distribution of the Ringhals reactor corresponding to the first four modes.
The convergence history of the MGBNM associated with the Ringhals reactor is represented in Figure 6. For this reactor, the number of iterations needed to reach the tolerance () was also equal to four.

Figure 6.
Convergence history of the MGBNM for the Ringhals reactor.
Table 9 collects the average number of iterations for the GMRES method for each iteration of MGBNM, the time to assemble the matrices and build the preconditioners, the total time of the MGBNM to reach the tolerance, and the maximum computational memory requested to assemble the matrices. From this table, similar conclusions as the ones obtained for the previous reactor are deduced. The number of iterations was not reduced, but the total CPU time and the maximum memory decreased considerably. For the Ringhals reactor, the most efficient option, in terms of computational memory, was also to apply the block preconditioner . However, as the size of this reactor is much larger, the differences between the preconditioners for computational memory were much higher.

Table 9.
Data obtained using different preconditioners for the Ringhals reactor.
Finally, in Table 10, we compare the MGBNM with the generalized Davidson method and the Krylov–Schur method from the SLEPc library as in the previous reactor. The results show that the MGBNM was more efficient in terms of the computational time to compute one or a set of the lambda modes than the generalized Davidson and the Krylov–Schur methods.

Table 10.
Computational times for the MGBNM with , the generalized Davidson method, and the Krylov–Schur method for the Ringhals reactor.
5. Conclusions
The modified generalized block Newton method (MGBNM) is an efficient eigenvalue solver that has been used to compute the dominant -modes associated with the neutron diffusion equation. This problem has been previously discretized by using a high order finite element method. This method requires solving many linear systems that need to be previously preconditioned. Different block preconditioners have been studied as an alternative to assemble the full matrix and to construct a preconditioner in each iteration. The different preconditioners have been tested in a benchmark reactor problem (NEACRP) and in a realistic reactor problem (Ringhals). The preconditioners proposed in this work break down the setup cost at the price of a slight increase of the number of iterations. The result is a significant reduction of the total CPU time needed to reach convergence and the memory occupancy. Among the implementations studied, it is shown that the best option is the one that uses the block structure of the L matrix. Moreover, this implementation permits implementing the MGBNM with a matrix-free technique, thus greatly reducing the memory consumption. The differences increase when the size of the problem is larger. In comparison with other eigenvalue solvers, such as the generalized Davidson and the Krylov–Schur methods, the numerical results conclude that the MGBNM with this strategy of preconditioning is more efficient in some cases and very competitive in the rest. In future works, the MGBNM with these strategies for the preconditioning will be applied to other approximations of the neutron transport equations as the SPN equations.
Author Contributions
A.C., L.B., and A.M. developed and investigated the methodology; A.C. and A.V.-F. implemented and validated the methods; D.G. and G.V. supervised the work. All authors discussed the results and contributed to the final manuscript.
Acknowledgments
This work has been partially supported by the Spanish Ministerio de Economía y Competitividad under Projects ENE2014-59442-P, MTM2014-58159-P, and BES-2015-072901.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stacey, W.M. Nuclear Reactor Physics; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Vidal-Ferrandiz, A.; Fayez, R.; Ginestar, D.; Verdú, G. Solution of the Lambda modes problem of a nuclear power reactor using an h–p finite element method. Ann. Nucl. Energy 2014, 72, 338–349. [Google Scholar] [CrossRef]
- Bangerth, W.; Hartmann, R.; Kanschat, G. deal.II—A general-purpose object-oriented finite element library. ACM Trans. Math. Softw. 2007, 33, 24. [Google Scholar] [CrossRef]
- Kronbichler, M.; Kormann, K. A generic interface for parallel cell-based finite element operator application. Comput. Fluids 2012, 63, 135–147. [Google Scholar] [CrossRef]
- Hageman, L.A.; Young, D.M. Applied Iterative Methods; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Sutton, T.M. Wielandt Iteration as Applied to the Nodal Expansion Method. Nucl. Sci. Eng. 1988, 98, 169–173. [Google Scholar] [CrossRef]
- Warsa, J.S.; Wareing, T.A.; Morel, J.E.; McGhee, J.M.; Lehoucq, R.B. Krylov subspace iterations for deterministic k-eigenvalue calculations. Nucl. Sci. Eng. 2004, 147, 26–42. [Google Scholar] [CrossRef]
- Allen, E.; Berry, R. The inverse power method for calculation of multiplication factors. Ann. Nucl. Energy 2002, 29, 929–935. [Google Scholar] [CrossRef]
- Verdú, G.; Ginestar, D.; Vidal, V.; Muñoz-Cobo, J. 3D λ-modes of the neutron-diffusion equation. Ann. Nucl. Energy 1994, 21, 405–421. [Google Scholar] [CrossRef]
- Verdú, G.; Miró, R.; Ginestar, D.; Vidal, V. The implicit restarted Arnoldi method, an efficient alternative to solve the neutron diffusion equation. Ann. Nucl. Energy 1999, 26, 579–593. [Google Scholar] [CrossRef]
- Verdú, G.; Ginestar, D.; Miró, R.; Vidal, V. Using the Jacobi–Davidson method to obtain the dominant Lambda modes of a nuclear power reactor. Ann. Nucl. Energy 2005, 32, 1274–1296. [Google Scholar] [CrossRef]
- Hernandez, V.; Roman, J.E.; Vidal, V. SLEPc: A scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 2005, 31, 351–362. [Google Scholar] [CrossRef]
- Evans, T.M.; Stafford, A.S.; Slaybaugh, R.N.; Clarno, K.T. Denovo: A new three-dimensional parallel discrete ordinates code in SCALE. Nucl. Technol. 2010, 171, 171–200. [Google Scholar] [CrossRef]
- Hamilton, S.P.; Evans, T.M. Efficient solution of the simplified PN equations. J. Comput. Phys. 2015, 284, 155–170. [Google Scholar] [CrossRef]
- González-Pintor, S.; Ginestar, D.; Verdú, G. Updating the Lambda Modes of a nuclear power reactor. Math. Comput. Model. 2011, 54, 1796–1801. [Google Scholar] [CrossRef]
- Carreño, A.; Vidal-Ferràndiz, A.; Ginestar, D.; Verdú, G. Spatial modes for the neutron diffusion equation and their computation. Ann. Nucl. Energy 2017, 110, 1010–1022. [Google Scholar] [CrossRef]
- Gill, D.; Azmy, Y. Newton’s method for solving k-eigenvalue problems in neutron diffusion theory. Nucl. Sci. Eng. 2011, 167, 141–153. [Google Scholar] [CrossRef]
- Knoll, D.; Park, H.; Newman, C. Acceleration of k-eigenvalue/criticality calculations using the Jacobian-free Newton-Krylov method. Nucl. Sci. Eng. 2011, 167, 133–140. [Google Scholar] [CrossRef]
- Kong, F.; Wang, Y.; Schunert, S.; Peterson, J.W.; Permann, C.J.; Andrš, D.; Martineau, R.C. A fully coupled two-level Schwarz preconditioner based on smoothed aggregation for the transient multigroup neutron diffusion equations. Numer. Linear Algebra Appl. 2018, 25, e2162. [Google Scholar] [CrossRef]
- Lösche, R.; Schwetlick, H.; Timmermann, G. A modified block Newton iteration for approximating an invariant subspace of a symmetric matrix. Linear Algebra Appl. 1998, 275, 381–400. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Finnemann, H.; Galati, A. NEACRP 3-D LWR Core Transient Benchmark: Final Specifications. Available online: https://www.oecd-nea.org/science/docs/1991/neacrp-l-1991-335.pdf (accessed on 13 January 2019).
- Lefvert, T. OECD/NEA Ringhals 1 Stability Benchmark. Available online: http://www.nea.fr/science/docs/1996/nsc-doc96-22.pdf (accessed on 13 January 2019).
- Balay, S.; Abhyankar, S.; Adams, M.; Brune, P.; Buschelman, K.; Dalcin, L.; Gropp, W.; Smith, B.; Karpeyev, D.; Kaushik, D.; et al. PETSc Users Manual Revision 3.7; Technical Report for Argonne National Lab: Argonne, IL, USA, 2016. [Google Scholar]
- Carreño, A.; Vidal-Ferràndiz, A.; Ginestar, D.; Verdú, G. Block hybrid multilevel method to compute the dominant λ-modes of the neutron diffusion equation. Ann. Nucl. Energy 2018, 121, 513–524. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).