Mathematical Modeling and Characterization of the Spread of Chikungunya in Colombia
Abstract
1. Introduction
2. Mathematical Model
- The total population of humans is divided into five subpopulations: humans who may become infected (susceptible ), humans exposed, but still not infected due to the existence of an incubation period of the virus (latent ), humans infected by the Chikungunya virus and that develop the disease (infected ), humans who have recovered from the Chikungunya infection (recovered ), and humans who have the disease chronically (chronic ).
- The parameter is the birth rate of humans. The birth rate is assumed equal to natural death .
- The mortality rate increase due to the disease is a real fact. However, since this rate is small in comparison with other rates and is not going to affect the dynamics, we assume that .
- The total population of mosquitoes is divided into three subpopulations: mosquitoes who may become infected (susceptible ), mosquitoes in a latent stage (latent ), and mosquitoes currently infected or spreading the Chikungunya virus (infected ).
- The parameter is the birth rate of the mosquitoes, and it is assumed equal to the death rate .
- A susceptible human can transit to the latent subpopulation because of an effective transmission due to a bite of an infected mosquito at a rate of .
- A susceptible mosquito can be infected if there exists an effective transmission when it bites an infected human, at a rate .
- A fraction of the latent humans passes to infected by the virus.
- A fraction of the infected humans recovers, i.e., they do not have the disease anymore.
- A fraction of the recovered humans moves to the chronic class.
- A fraction of the latent mosquitoes goes through to infected mosquitoes.
- Homogeneous mixing is assumed, i.e., all susceptible humans have the same probability of being infected and all susceptible mosquitoes have the same probability of being infected.
3. Analysis of the Model
3.1. Equilibrium Points and Local Stability of the Chikungunya Mathematical Model
3.2. Endemic Equilibria
3.3. Global Stability Analysis
4. Numerical Simulation
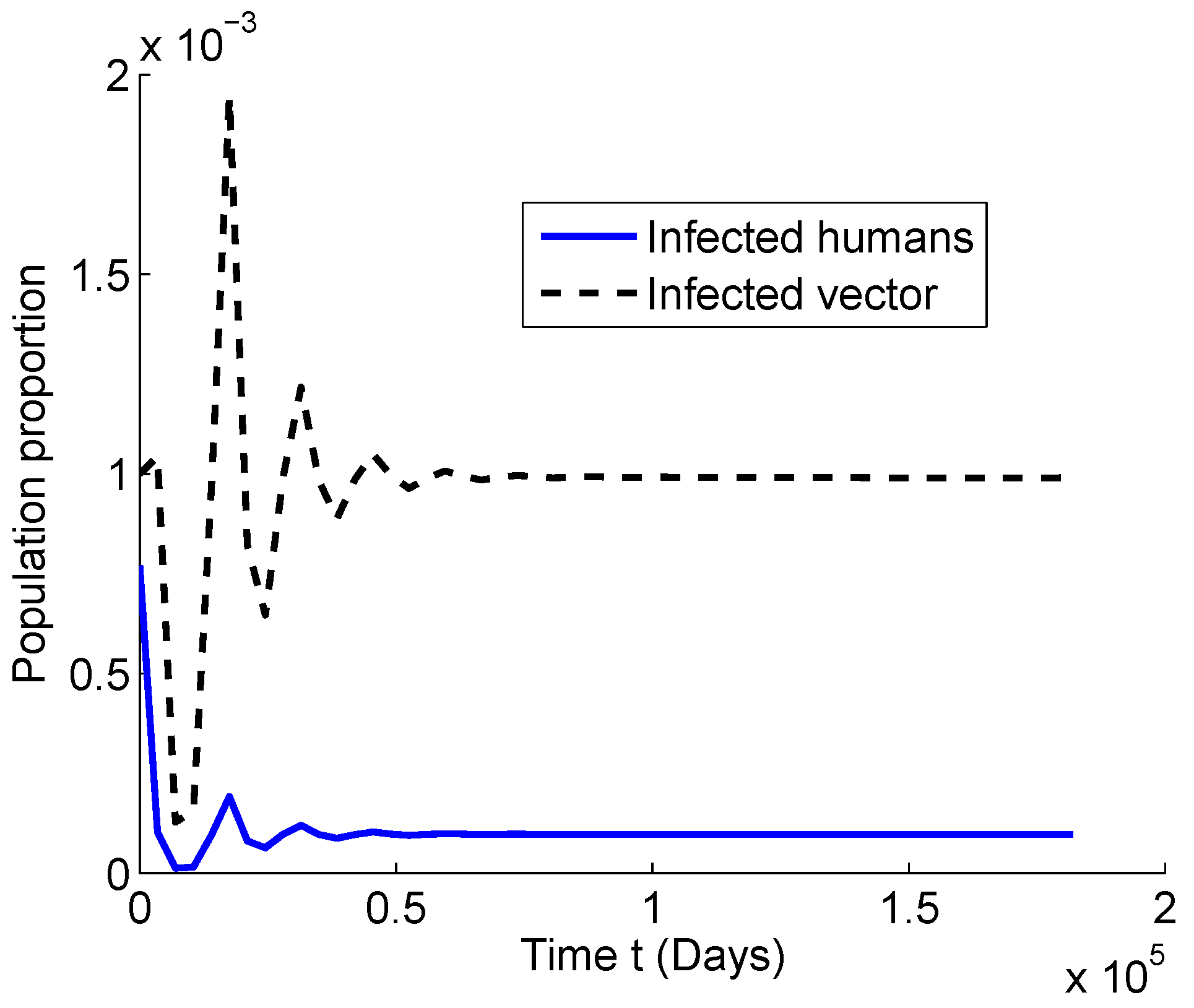
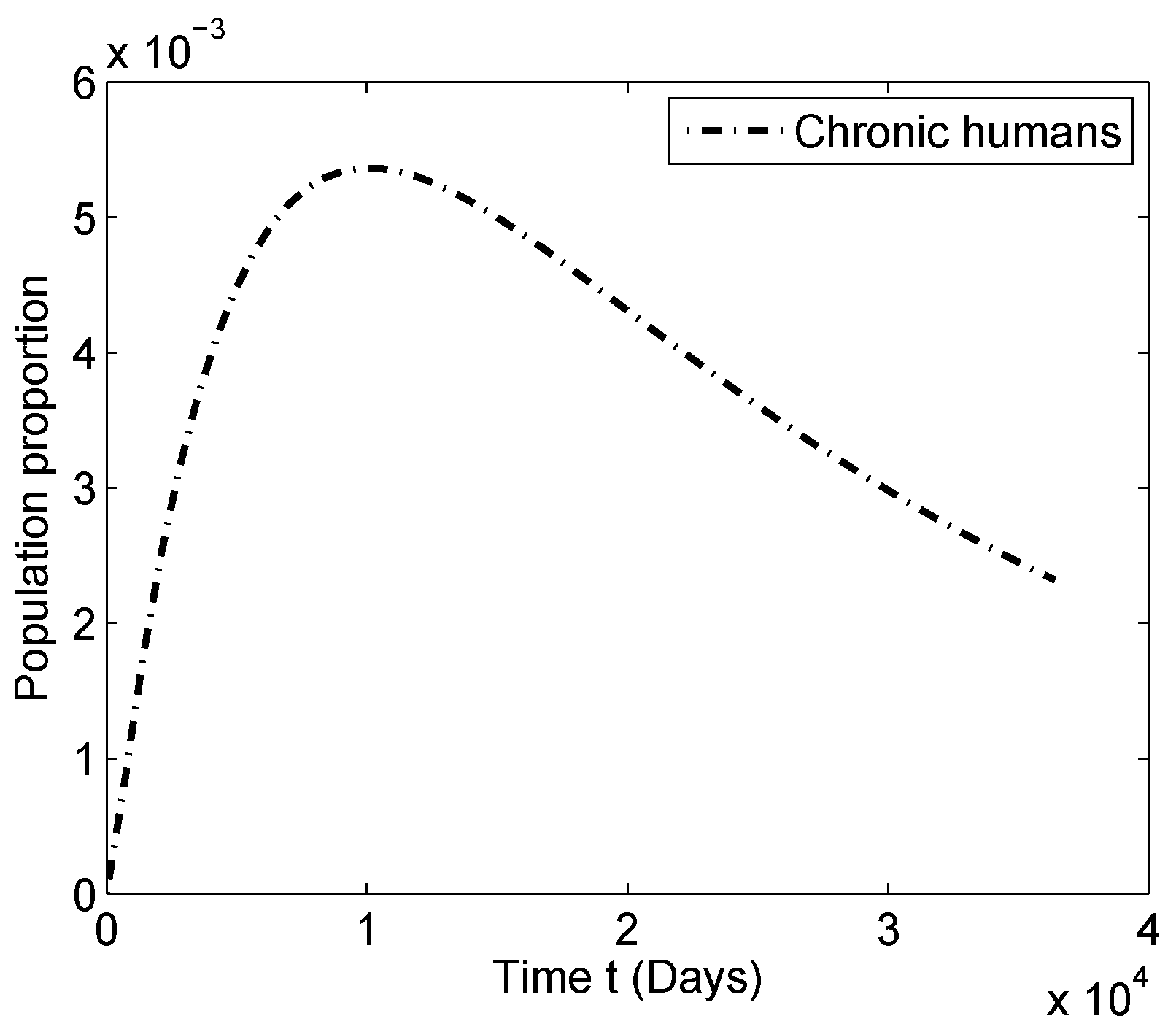
4.1. Numerical Simulations for
4.2. Numerical Simulations for
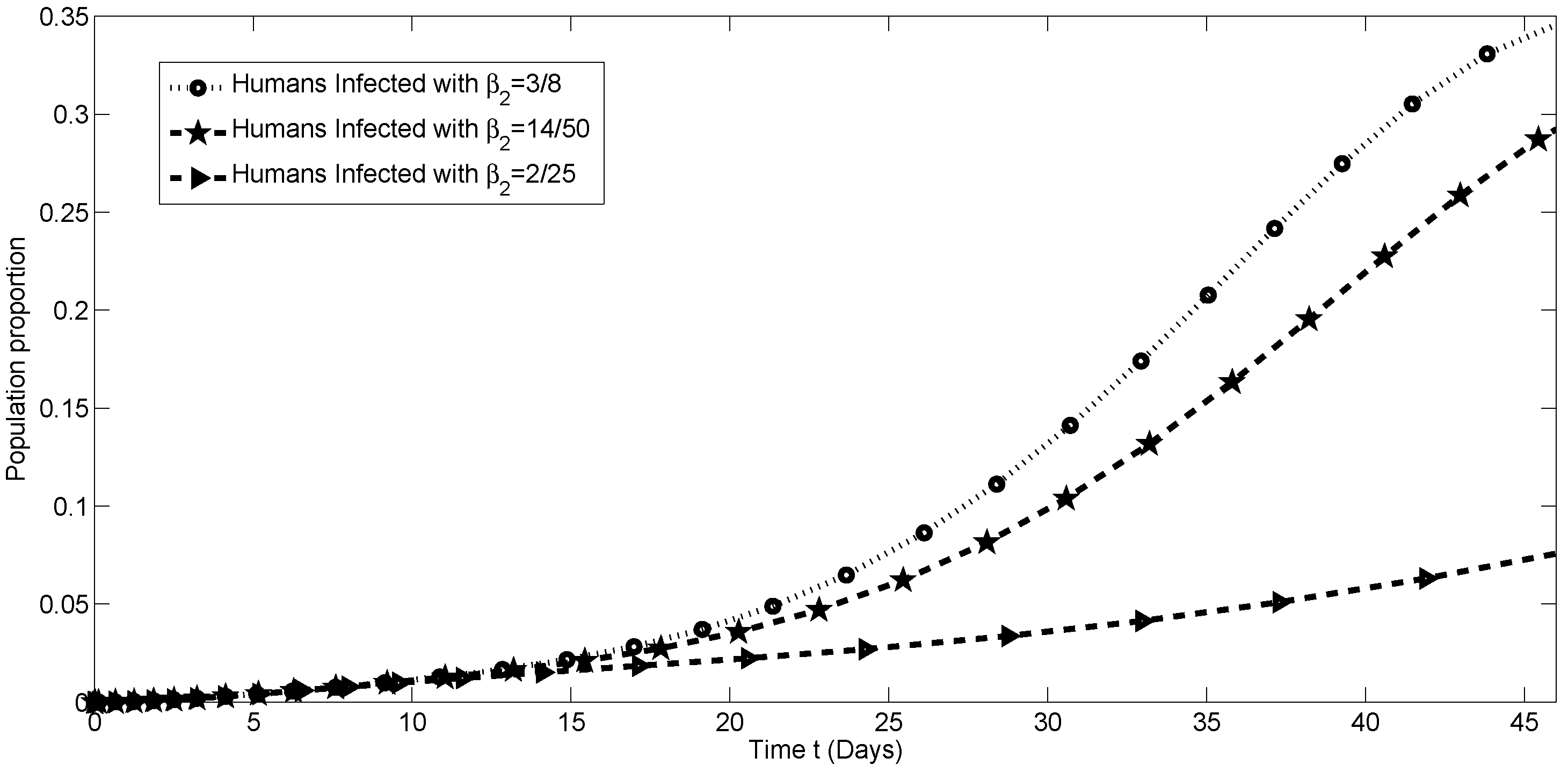
4.3. Sensitivity Analysis of the Transmission Parameters
5. Estimation of Parameters for the Colombian Scenario
5.1. Fitting Algorithm
- For a given , numerically solve the system of differential Equation (2) and obtain a solution , which is an approximation of the real data solution .
- Set (the fitting process starts at Week 0), and for , corresponding to weeks where data are available, evaluate the computed numerical solution for subpopulation ; i.e., , , , …, .
- Compute the sum of square of the difference between , , , …, , and infectious data in Table 1. This function returns the sum of squared errors (), where for the Colombia data are given by:
- Find a global minimum for the the sum of squared errors () using genetic, trust-region-reflective, and interior point algorithms.
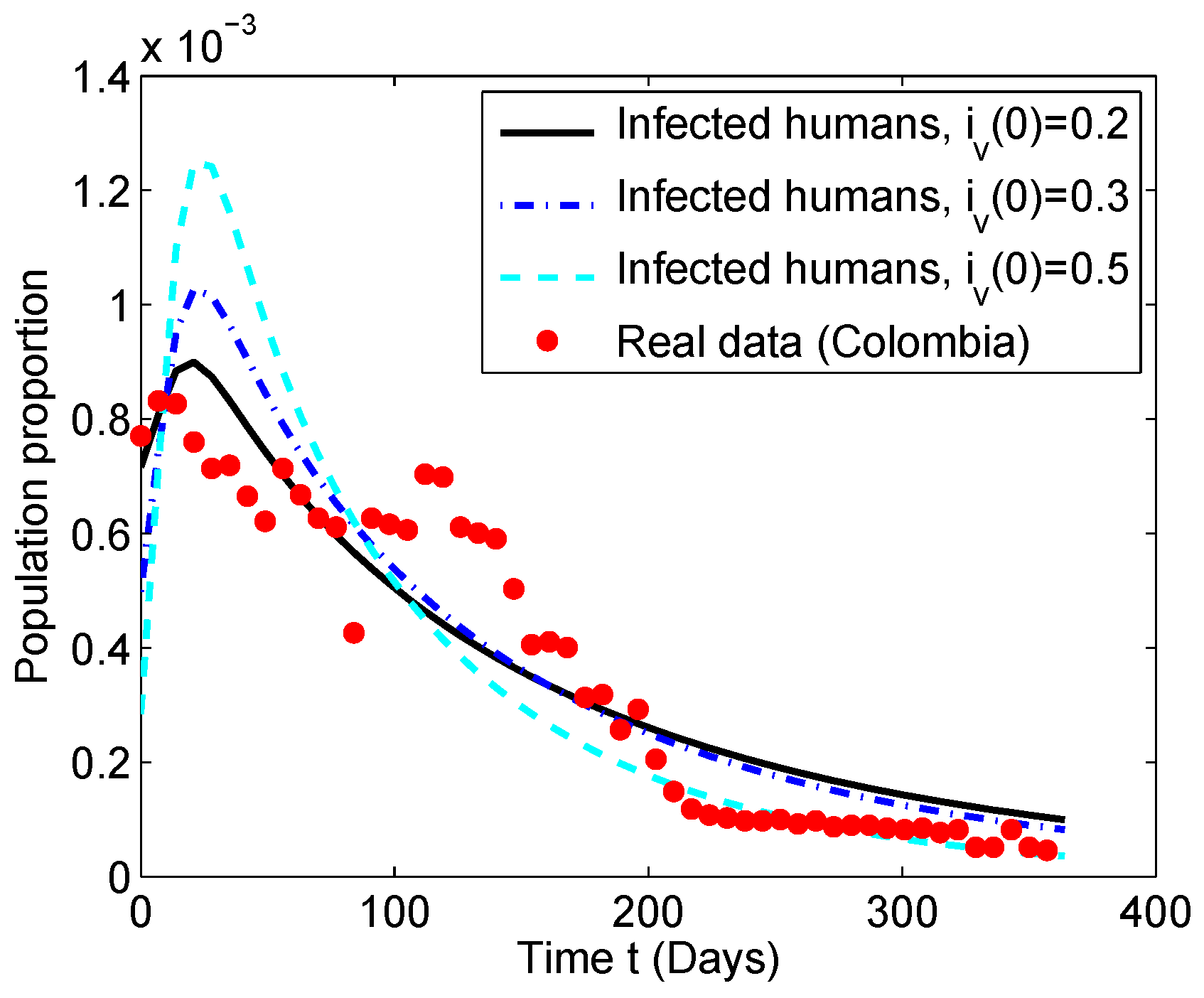
5.2. Numerical Simulation of the Chikungunya Mathematical Model
5.3. Identifiability of the Parameters
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zárate, M.L. Arbovirus y Arbovirosis en México. Instituto de Salubridad y Enfermedades Tropicales. Available online: www.fmvz.unam.mx/fmvz/cienciavet/revistas-/CVvol2/CVv2c6.pdf (accessed on 2 January 2019).
- Jupp, P.; McIntosh, B. Chikungunya virus disease. In The Arboviruses: Epidemiology and Ecology; CRC Press: Boca Raton, FL, USA, 1988; Volume 2, pp. 137–157. [Google Scholar]
- Pérez Sánchez, G.; Ramírez Alvarez, G.; Pérez Gijón, Y.; Canela Lluch, C. Fiebre de Chikungunya: Enfermedad infrecuente como emergencia médica en Cuba. Medisan 2014, 18, 848–856. [Google Scholar]
- Cook, G.C.; Zumla, A. Manson’s Tropical Diseases, 13th ed.; Elsevier Health Sciences: Philadelfia, PA, USA, 2008. [Google Scholar]
- Benedict, M.; Levine, R.; Hawley, W.; Lounibos, P. Spread of the tiger: Global risk of invasion by the mosquito Aedes albopictus. Vector Borne Zoonotic Dis. 2007, 7, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Robinson, M.; Conan, A.; Duong, V.; Ly, S.; Ngan, C.; Buchy, P.; Tarantola, A.; Rodo, X. A model for a chikungunya outbreak in a rural Cambodian setting: Implications for disease control in uninfected areas. PLoS Negl. Trop. Dis. 2014, 8, e3120. [Google Scholar] [CrossRef] [PubMed]
- Charrel, R.N.; De Lamballerie, X.; Raoult, D. Seasonality of mosquitoes and chikungunya in Italy. Lancet Infect. Dis. 2008, 8, 5–6. [Google Scholar] [CrossRef]
- Halstead, S.B. Reappearance of chikungunya, formerly called dengue, in the Americas. Emerg. Infect. Dis. 2015, 21, 557–561. [Google Scholar] [CrossRef]
- Teng, T.S.; Kam, Y.W.; Lee, B.; Hapuarachchi, H.C.; Wimal, A.; Ng, L.C.; Ng, L.F. A systematic meta-analysis of immune signatures in patients with acute chikungunya virus infection. J. Infect. Dis. 2015, 211, 1925–1935. [Google Scholar] [CrossRef] [PubMed]
- Sissoko, D.; Malvy, D.; Ezzedine, K.; Renault, P.; Moscetti, F.; Ledrans, M.; Pierre, V. Post-epidemic Chikungunya disease on Reunion Island: Course of rheumatic manifestations and associated factors over a 15-month period. PLoS Negl. Trop. Dis. 2009, 3, e389. [Google Scholar] [CrossRef]
- Montero, A. Chikungunya fever—A new global threat. Med. Clín. (Eng. Ed.) 2015, 145, 118–123. [Google Scholar] [CrossRef]
- Poo, Y.S.; Rudd, P.A.; Gardner, J.; Wilson, J.A.; Larcher, T.; Colle, M.A.; Le, T.T.; Nakaya, H.I.; Warrilow, D.; Allcock, R.; et al. Multiple immune factors are involved in controlling acute and chronic chikungunya virus infection. PLoS Negl. Trop. Dis. 2014, 8, e3354. [Google Scholar] [CrossRef]
- Taubitz, W.; Cramer, J.P.; Kapaun, A.; Pfeffer, M.; Drosten, C.; Dobler, G.; Burchard, G.D.; Löscher, T. Chikungunya fever in travelers: Clinical presentation and course. Clin. Infect. Dis. 2007, 45, e1–e4. [Google Scholar] [CrossRef]
- García, G.; Santana, E.; Martínez, J.R.; Álvarez, A.; Rodríguez, R.; Guzmán, M.G. Detección de respuesta linfoproliferativa en monos inoculados con virus dengue 4. Rev. Cubana Med. Trop. 2003, 55, 27–29. [Google Scholar] [PubMed]
- Manore, C.A.; Ostfeld, R.S.; Agusto, F.B.; Gaff, H.; LaDeau, S.L. Defining the risk of Zika and chikungunya virus transmission in human population centers of the eastern United States. PLoS Negl. Trop. Dis. 2017, 11, e0005255. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D. Mathematical Biology I: An Introduction, Vol. 17 of Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2002. [Google Scholar]
- Castillo-Chavez, C.; Brauer, F. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012. [Google Scholar]
- Hethcote, H.W. Mathematics of infectious diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.J.; Aranda, D.F.; Segovia, L. Modeling the epidemic waves of AH1N1/09 influenza around the world. Spat. Spatio-Temporal Epidemiol. 2011, 2, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Lashari, A.A.; Hattaf, K.; Zaman, G. A delay differential equation model of a vector borne disease with direct transmission. Int. J. Ecol. Econ. Stat. 2012, 27, 25–35. [Google Scholar]
- Lashari, A.A.; Hattaf, K.; Zaman, G.; Li, X.Z. Backward bifurcation and optimal control of a vector borne disease. Appl. Math. Inf. Sci. 2013, 7, 301–309. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.A.; Farooq, M. A fractional model for the dynamics of TB virus. Chaos Solitons Fractals 2018, 116, 63–71. [Google Scholar] [CrossRef]
- Sardar, T.; Rana, S.; Bhattacharya, S.; Al-Khaled, K.; Chattopadhyay, J. A generic model for a single strain mosquito-transmitted disease with memory on the host and the vector. Math. Biosci. 2015, 263, 18–36. [Google Scholar] [CrossRef]
- Wojtak, W.; Silva, C.J.; Torres, D.F. Uniform asymptotic stability of a fractional tuberculosis model. Math. Model. Nat. Phenom. 2018, 13, 9. [Google Scholar] [CrossRef]
- Yakob, L.; Clements, A.C. A mathematical model of chikungunya dynamics and control: The major epidemic on Réunion Island. PLoS ONE 2013, 8, e57448. [Google Scholar] [CrossRef]
- Agusto, F.B.; Easley, S.; Freeman, K.; Thomas, M. Mathematical Model of Three Age-Structured Transmission Dynamics of Chikungunya Virus. Comput. Math. Methods Med. 2016, 2016, 4320514. [Google Scholar] [CrossRef]
- Lashari, A.A.; Zaman, G. Global dynamics of vector-borne diseases with horizontal transmission in host population. Comput. Math. Appl. 2011, 61, 745–754. [Google Scholar] [CrossRef]
- Dumont, Y.; Chiroleu, F.; Domerg, C. On a temporal model for the Chikungunya disease: Modeling, theory and numerics. Math. Biosci. 2008, 213, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Moulay, D.; Aziz-Alaoui, M.; Cadivel, M. The chikungunya disease: Modeling, vector and transmission global dynamics. Math. Biosci. 2011, 229, 50–63. [Google Scholar] [CrossRef] [PubMed]
- Sawabe, K.; Isawa, H.; Hoshino, K.; Sasaki, T.; Roychoudhury, S.; Higa, Y.; Kasai, S.; Tsuda, Y.; Nishiumi, I.; Hisai, N.; et al. Host-feeding habits of Culex pipiens and Aedes albopictus (Diptera: Culicidae) collected at the urban and suburban residential areas of Japan. J. Med. Entomol. 2010, 47, 442–450. [Google Scholar] [CrossRef]
- Vourc’h, G.; Halos, L.; Desvars, A.; Boué, F.; Pascal, M.; Lecollinet, S.; Zientara, S.; Duval, T.; Nzonza, A.; Brémont, M. Chikungunya antibodies detected in non-human primates and rats in three Indian Ocean islands after the 2006 ChikV outbreak. Vet. Res. 2014, 45, 52. [Google Scholar] [CrossRef] [PubMed]
- Ligon, B.L. Reemergence of an unusual disease: The chikungunya epidemic. Semin. Pediatr. Infect. Dis. 2006, 17, 99–104. [Google Scholar] [CrossRef] [PubMed]
- Diallo, M.; Thonnon, J.; Traore-Lamizana, M.; Fontenille, D. Vectors of Chikungunya virus in Senegal: Current data and transmission cycles. Am. J. Trop. Med. Hyg. 1999, 60, 281–286. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- MacKay, D.J.; Mac Kay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Tulu, T.W.; Tian, B.; Wu, Z. Mathematical modeling, analysis and Markov Chain Monte Carlo simulation of Ebola epidemics. Res. Phys. 2017, 7, 962–968. [Google Scholar] [CrossRef]
- Dhamala, J.; Arevalo, H.J.; Sapp, J.; Horácek, B.M.; Wu, K.C.; Trayanova, N.A.; Wang, L. Quantifying the uncertainty in model parameters using Gaussian process-based Markov chain Monte Carlo in cardiac electrophysiology. Med. Image Anal. 2018, 48, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Bretó, C. Modeling and inference for infectious disease dynamics: A likelihood-based approach. Stat. Sci. 2018, 33, 57–69. [Google Scholar]
- Ortiz, G.A.; Alvarez, D.A.; Bedoya-Ruíz, D. Identification of Bouc–Wen type models using the transitional Markov chain Monte Carlo method. Comput. Struct. 2015, 146, 252–269. [Google Scholar] [CrossRef]
- Weber, C. Characterization of the Chikungunya Virus Entry Process and The Development of Novel Antiviral Strategies. Ph.D. Thesis, Univ.-Bibliothek Frankfurt am Main, Frankfurt, Germany, 2015. [Google Scholar]
- Arenas, A.J.; González-Parra, G.; Moraño, J.A. Stochastic modeling of the transmission of respiratory syncytial virus (RSV) in the region of Valencia, Spain. Biosystems 2009, 96, 206–212. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Guerrero, F.; González-Parra, G.; Arenas, A.J. A nonstandard finite difference numerical scheme applied to a mathematical model of the prevalence of smoking in Spain: A case study. Comput. Appl. Math. 2014, 33, 13–25. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Further notes on the basic reproduction number. In Mathematical Epidemiology; Springer: New York, NY, USA, 2008; pp. 159–178. [Google Scholar]
- Korobeinikov, A.; Maini, P.K. A Lyapunov function and global properties for SIR and SEIR epidemiological models with nonlinear incidence. Math. Biosci. Eng. 2004, 1, 57–60. [Google Scholar]
- Shuai, Z.; van den Driessche, P. Global stability of infectious disease models using Lyapunov functions. SIAM J. Appl. Math. 2013, 73, 1513–1532. [Google Scholar] [CrossRef]
- Kincaid, D.R.; Cheney, E.W. Numerical Analysis: Mathematics of Scientific Computing; American Mathematical Soc.: Providence, RI, USA, 2002; Volume 2. [Google Scholar]
- Duque, J.E.; Navarro-Silva, M.A. Simulating management of Aedes aegypti (Diptera: Culicidae) and its effects in a dengue epidemic. Revista Colombiana de Entomología 2009, 35, 66–72. [Google Scholar]
- Cardona-Ospina, J.A.; Henao-SanMartin, V.; Paniz-Mondolfi, A.E.; Rodríguez-Morales, A.J. Mortality and fatality due to Chikungunya virus infection in Colombia. J. Clin. Virol. 2015, 70, 14–15. [Google Scholar] [CrossRef] [PubMed]
- Vazeille, M.; Moutailler, S.; Coudrier, D.; Rousseaux, C.; Khun, H.; Huerre, M.; Thiria, J.; Dehecq, J.S.; Fontenille, D.; Schuffenecker, I.; et al. Two Chikungunya isolates from the outbreak of La Reunion (Indian Ocean) exhibit different patterns of infection in the mosquito, Aedes albopictus. PLoS ONE 2007, 2, e1168. [Google Scholar] [CrossRef] [PubMed]
- Chikaki, E.; Ishikawa, H. A dengue transmission model in Thailand considering sequential infections with all four serotypes. J. Infect. Dev. Countries 2009, 3, 711–722. [Google Scholar] [CrossRef]
- Gutierrez, M.F. Personal Communication. 2017. [Google Scholar]
- Plan Nacional de Respuesta Frente a la Introducción del Virus de Chikungunya en Colombia. Available online: https://www.minsalud.gov.co (accessed on 2 January 2019).
- Chou, I.C.; Voit, E.O. Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 2009, 219, 57–83. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Pacheco, G.; Esteva, L.; Vargas, C. Control measures for Chagas disease. Math. Biosci. 2012, 237, 49–60. [Google Scholar] [CrossRef] [PubMed]
- Censo Colombia 2005. Available online: https://www.dane.gov.co/files/censos/libroCenso2005nacional.pdf (accessed on 2 January 2019).
- Golberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addion Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Coleman, T.F.; Li, Y. An Interior Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Kucharski, A.J.; Funk, S.; Eggo, R.M.; Mallet, H.P.; Edmunds, W.J.; Nilles, E.J. Transmission dynamics of Zika virus in island populations: A modelling analysis of the 2013–14 French Polynesia outbreak. PLoS Negl. Trop. Dis. 2016, 10, e0004726. [Google Scholar] [CrossRef]
- González-Parra, G.; Villanueva, R.J.; Ruiz-Baragaño, J.; Moraño, J.A. Modelling influenza A(H1N1) 2009 epidemics using a random network in a distributed computing environment. Acta Trop. 2015, 143, 29–35. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997; Volume 1. [Google Scholar]
- Goodman, J.; Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Kao, Y.H.; Eisenberg, M.C. Practical unidentifiability of a simple vector-borne disease model: Implications for parameter estimation and intervention assessment. Epidemics 2018, 25, 89–100. [Google Scholar] [CrossRef] [PubMed]



| Parameter | SSR | ||||
| Value | 0.012 | 2.186 × 10−4 | 4.701 × 10−7 | 0.77 |

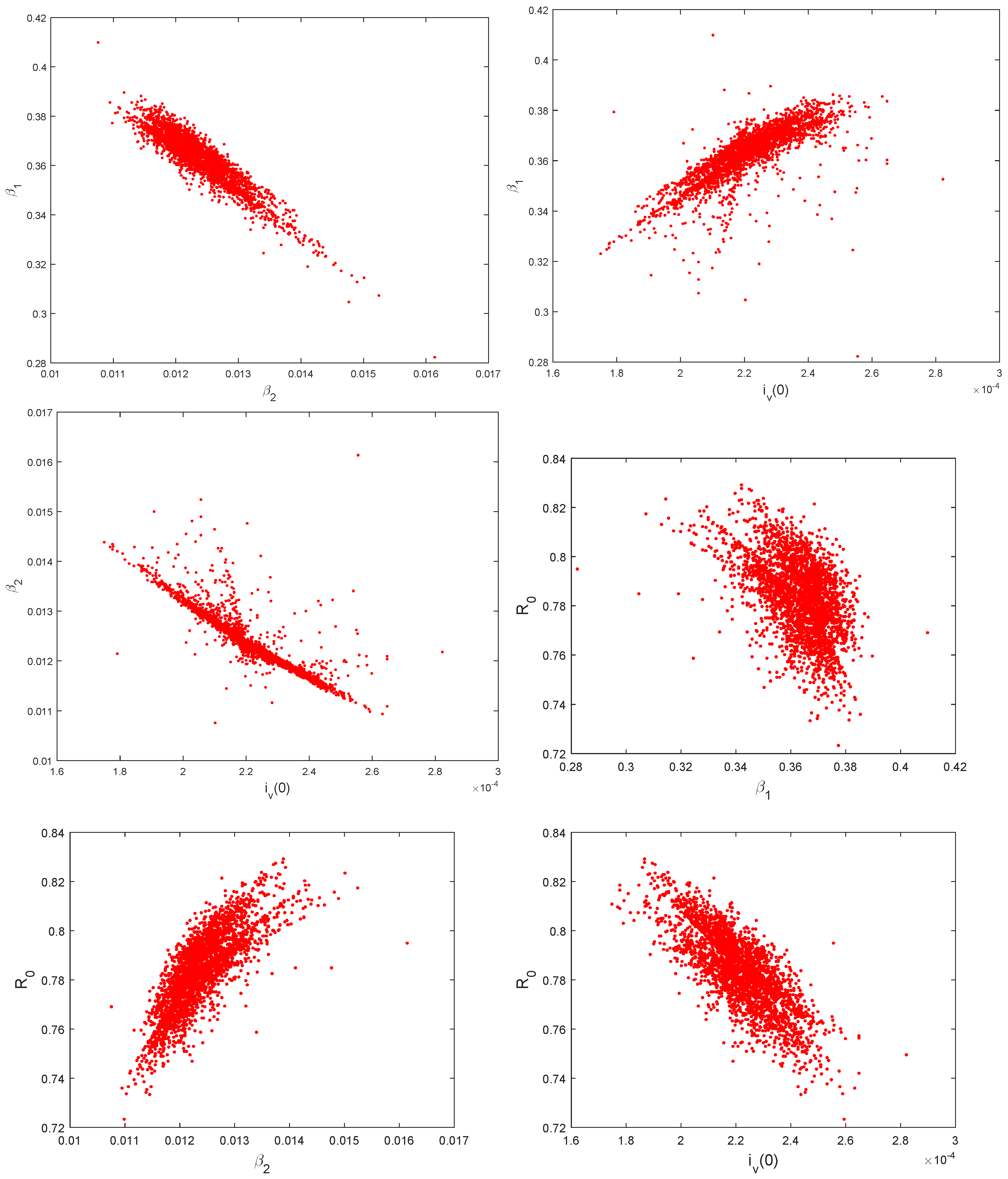
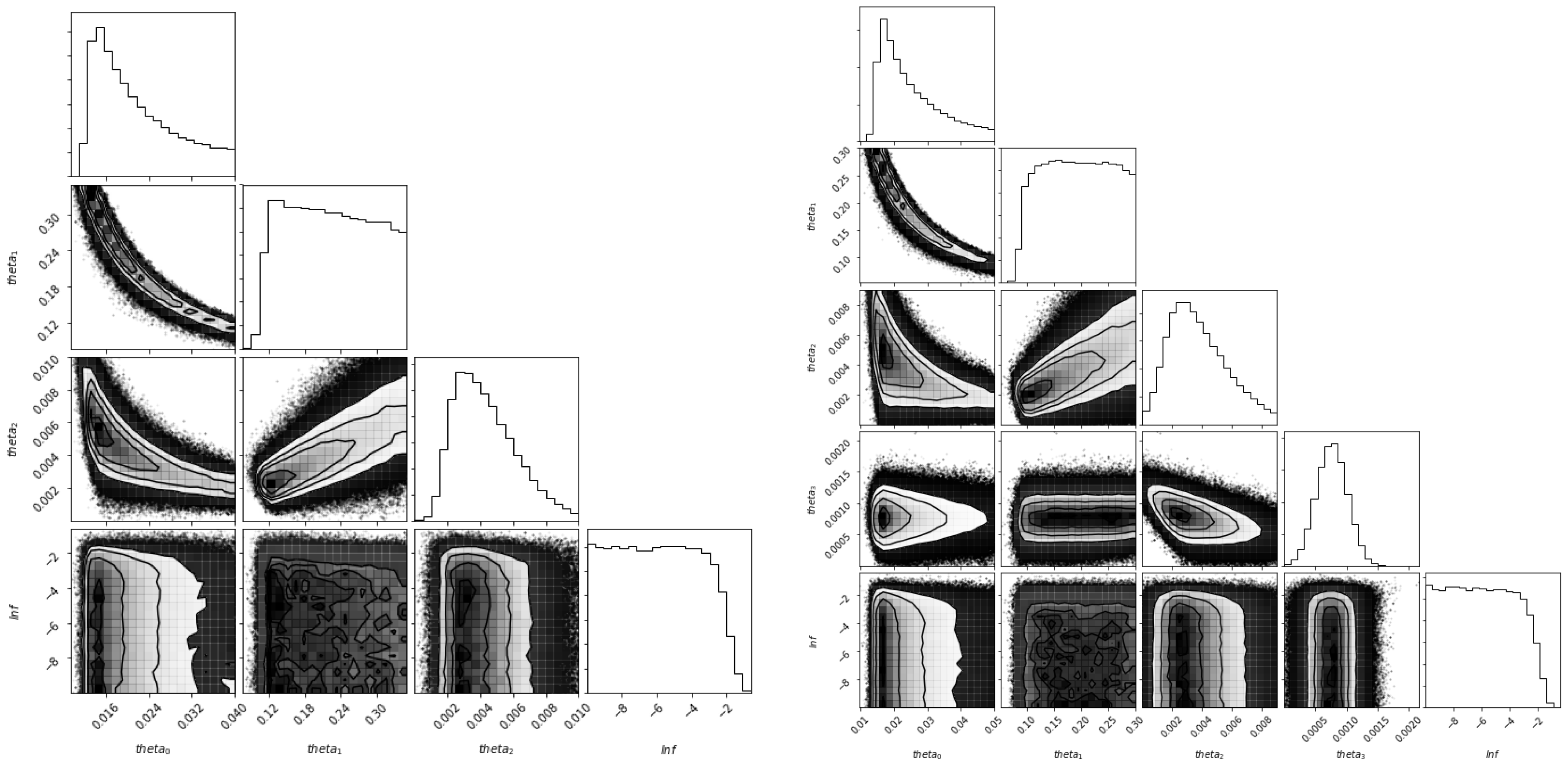
| Parameter | Symbol | Values | Rate |
|---|---|---|---|
| Average life-span of the human host [50] | 25.000 Days | ||
| Average life-span of the vector [51] | 14 Days | ||
| Average incubation time of the virus (latency in the humans) [52] | 5–12 Days | ||
| Average incubation time of the virus (latency in the vector) [28,53] | 3 Days | ||
| Average infection time (infection in humans) [51] | 5–15 Days | ||
| Chronic time [54,55] | 300 Days |
| Value | |||
|---|---|---|---|
| Value of | |||
| Value of Infected Population | million | million | million |
| Week | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Cases | 15,000 | 16,200 | 16,100 | 14,800 | 13,900 | 14,000 | 12,950 | 12,100 |
| Week | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Cases | 13,900 | 13,000 | 12,200 | 11,900 | 8300 | 12,200 | 12,000 | 11,800 |
| Week | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Cases | 13,700 | 13,600 | 11,900 | 11,700 | 11,500 | 9800 | 7900 | 8000 |
| Week | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| Cases | 7800 | 6100 | 6200 | 5000 | 5700 | 4000 | 2900 | 2300 |
| Week | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| Cases | 2100 | 2000 | 1900 | 1900 | 1950 | 1800 | 1900 | 1700 |
| Week | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| Cases | 1750 | 1750 | 1650 | 1600 | 1650 | 1500 | 1600 | 1000 |
| Week | 49 | 50 | 51 | 52 | ||||
| Cases | 1000 | 1600 | 1000 | 900 |
| Parameters | ||
|---|---|---|
| Values | 0.78 (0.74–0.84) | 2.18 (1.95 –2.45 |
| Parameters | ||
| Values | 0.36 (0.34–0.38) | 0.012 (0.011–0.13) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Parra, G.C.; Aranda, D.F.; Chen-Charpentier, B.; Díaz-Rodríguez, M.; Castellanos, J.E. Mathematical Modeling and Characterization of the Spread of Chikungunya in Colombia. Math. Comput. Appl. 2019, 24, 6. https://doi.org/10.3390/mca24010006
González-Parra GC, Aranda DF, Chen-Charpentier B, Díaz-Rodríguez M, Castellanos JE. Mathematical Modeling and Characterization of the Spread of Chikungunya in Colombia. Mathematical and Computational Applications. 2019; 24(1):6. https://doi.org/10.3390/mca24010006
Chicago/Turabian StyleGonzález-Parra, Gilberto C., Diego F. Aranda, Benito Chen-Charpentier, Miguel Díaz-Rodríguez, and Jaime E. Castellanos. 2019. "Mathematical Modeling and Characterization of the Spread of Chikungunya in Colombia" Mathematical and Computational Applications 24, no. 1: 6. https://doi.org/10.3390/mca24010006
APA StyleGonzález-Parra, G. C., Aranda, D. F., Chen-Charpentier, B., Díaz-Rodríguez, M., & Castellanos, J. E. (2019). Mathematical Modeling and Characterization of the Spread of Chikungunya in Colombia. Mathematical and Computational Applications, 24(1), 6. https://doi.org/10.3390/mca24010006








