An Approach for Integrating Uncertainty When Selecting an Anti-Torpedo Decoy in Brand New Warships

Abstract

The Spanish Navy has planned that the F-80 frigates will be replaced by the brand new F-110 frigates in 2022. The F-110 program is in the conceptual design phase and one of the objectives is to provide the new F-110 frigate with a salient anti-submarine capability. Therefore, it is necessary to choose what anti-torpedo decoy should be installed in the warship. The Joint Chiefs of Navy Staff (EMA) established some guidelines and, considering the Navy guidance’s, the Analytic Hierarchy Process (AHP) method was applied. After applying the AHP method, none of the decoys obtained a better score to the other one to make a decision. This paper addresses the problem of the selection of the best anti-torpedo decoy to be installed in the new frigates. This allowed implementing a new approach, the Graphic Method of Measurement of Uncertainty Beyond Objectivity (GMUBO). This approach considers different scenarios from the AHP, quantifies the uncertainty, and evaluates which is the best alternative. The method integrates the uncertainty in the AHP and allows measuring the robustness of the selected alternative, also providing a useful graphical tool. Furthermore, GMUBO has a great ease of use and it is helpful to make decisions under uncertainty conditions.

1. Introduction

Currently, the Spanish Navy has two types of frigates in service, the F-80 class and the F-100 one. F-80 frigates will be replaced in 2022, after 35 years of service, due to obsolescence. It is planned that F-80 units will be replaced by brand new F-110 frigates. At present, the F-110 program is in the definition and decision phase, specifically in the determination stage of obtaining alternatives [1]. This stage will end when the feasibility document (DDV) is signed. DDV establishes that a certain technical proposal, with known costs and deadlines, is feasible and can be hired. It is necessary that Spain’s government take the necessary steps to guarantee a financing of the program that makes the hiring possible [2].

The new F-110 frigates will be complex vessels properly equipped so that the Spanish Navy carries out operational and strategic missions for the defense and security of Spain and its allies. The F-110 frigates must be designed to be balanced ships in all areas of naval warfare, but with a remarkable anti-submarine warfare (ASW) capability. In warfare, there are two categories of protection in order to defeat the threat: destruction of the threat (hard kill) and distraction of the threat (soft kill). Hard kill includes both kinetic and directed energy weapons. Soft kill is the prevention of a successful attack by the threat after the attack has commenced. Distraction could be accomplished through decoys, chaff, jammers, flares, signature management, and electronic, infrared, or acoustic countermeasures [3]. ASW is one of the most complex concerns in a surface warship. The concept of uncertainty is deeply linked to ASW due to the lack of dominance of warships over the underwater environment.

The presence of an enemy submarine close to the operations area of a surface warship is a dangerous threat against the ship. Furthermore, the presence of submarines not only represents a direct threat against the physical integrity of a ship. Gathering intelligence data is considered one of the main objectives of a submarine, and a major threat to the national defense of the warship’s country. Therefore, one of the important decisions that must be taken is the choice of the best anti-torpedo decoy that will be implemented in the F-110.

The ASW capability possessed by some surface warships poses an important threat to submarines. These warships can use ASW countermeasures to prevent submarines from accessing certain areas due to the risk of detection and to avoid torpedo damage [4]. When a submarine fires a torpedo, it goes straight to the target because it is fitted with an electronic device that enables it to find and hit the target. An anti-torpedo decoy is an acoustic device used as a countermeasure to avoid the attack of torpedoes. A decoy works by transmitting the emulated ship’s signature to confuse the torpedo [5].

Both the conception and design of a warship are part of the process of developing a product of great complexity, i.e., the warship. This process is essentially a continuous decision-making process for which a number of techniques and methods could be used to help decision-making. This implies the consideration of multiple criteria and the possibility of conflict between these criteria. Therefore, the use of methods multiple-criteria decision-making (MCDM) methods is required to solve the decision-making problem. It can be said that all techniques and methods have two important objectives for these techniques to be successful and applicable in the industry: ease of use and exactness of results. However, both objectives can easily conflict. Exactness and uncertainty are closely related since uncertainty affects the variables involved in the decisions. A method that does not consider uncertainty will not provide correct results. Thus, the lower the uncertainty when applying the method, the greater the exactness of the results and, therefore, the greater the utility and applicability of the method. Methods that do not model uncertainty will fail in the exactness of their results. However, many methods that model uncertainty are not easy to apply.

One of the most used methods is the well-known Analytic Hierarchy Process (AHP), which is able to obtain a hierarchical classification of the different alternatives by comparing pairs of alternatives and criteria. A disadvantage of AHP is that it does not model uncertainty. Therefore, it is useful to have methods that consider the uncertainty inherent in MCDM problems. In recent years, MCDM methods have been developed to help decision-making in different fields [6,7,8,9,10,11,12,13,14].

Using MCDM methods to solve problems implies a complex analysis due to the number of factors that must be considered. Technical, political, institutional, standards, and economic factors take part of the problem [15]. Some methods that we want to mention in this work are Weighted Sum Method (WSM), ELimination Et Choix Traduisent la REalité (ELECTRE), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), Multi-Attribute Utility Theory (MAUT), Preference Ranking Organization Method For Enrichment Evaluation (PROMETHEE), and AHP. However, WSM and AHP stand out for their simplicity of calculation and their adaptability to multiple situations.

This work seeks to provide an approach that helps the EMA to decide on the best anti-torpedo decoy for the F-110 frigates. Two criteria, (1) logistics, and (2) operational capabilities were the monitored and chosen criteria by the EMA. Keeping in mind the Navy guidelines, two possible decoy alternatives were chosen: towed device (N) and expendable device (L) [16]. The towed device can send acoustic signals to deceive the torpedo away from the ship. This device is a passive and electro-acoustic system that provides deceptive countermeasures, by simulating a variety of machinery noises. The expendable device is a system to deceive torpedoes as the towed device does. The difference (Figure 1) lies in that the expendable device is launched into the sea from the warship and the towed device is dragged. A group of experts from the Navy established the criteria weights and the AHP method [17] was applied to determine the best anti-torpedo decoy. The AHP result is not enough to make a clear decision since sensitivity analysis identified that the result depends on criteria weights. Consequently, none of the decoys obtained a better score to make a correct decision. This brought uncertainty due to the criteria weights could come from subjective evaluations. However, by integrating uncertainty in the AHP, through the medium of the Graphic Method of Measurement of Uncertainty Beyond Objectivity (GMUBO) [18], it is possible to help the EMA to make a decision. GMUBO considers different scenarios and results of the AHP, which is the starting point. Moreover, it allows measuring the robustness of the selected alternative by means of a mathematical and graphical tool.

The capability of managing the uncertainty is one advantage of GMUBO, just as it enables alternatives to be assessed graphically and determine the best one. An additional benefit of GMUBO is that it considers changes in the process conditions themselves, when assessing and selecting alternatives. A case study is presented to demonstrate the approach by comparing AHP (initial method) with GMUBO. Managing the selection of alternatives, under uncertainty, in a graphic way, and considering the susceptibility of the selection to changes, are the novelties of the approach.

2. Methodology

A frigate is a surface warship and the new F-110 frigates should be balanced ships in all areas or scenarios of naval warfare. Keeping in mind that one of the main threats to surface ships is the presence of submarines, the F-110 should have a great capability of survival against possible attacks. This is the reason why one of the objectives is to provide the new frigate F-110 with an important anti-submarine capability [19]. Considering the aforementioned statements, the EMA decided to preselect two possible decoy alternatives: towed device (N) and expendable device (L), as indicated in the previous section. In the same way, the EMA established two criteria: logistics issues and operational capacities. The meaning of the criteria is detailed below.

• Logistics issues. This allows evaluating different aspects: storage of decoys, volume they occupy, existence of available means to train personnel in the use of the type of decoy.
• Operational capacities or effectiveness issues. This is an essential criterion to make an adequate decision to the tactical and strategic demands of a surface ship in the field of ASW.

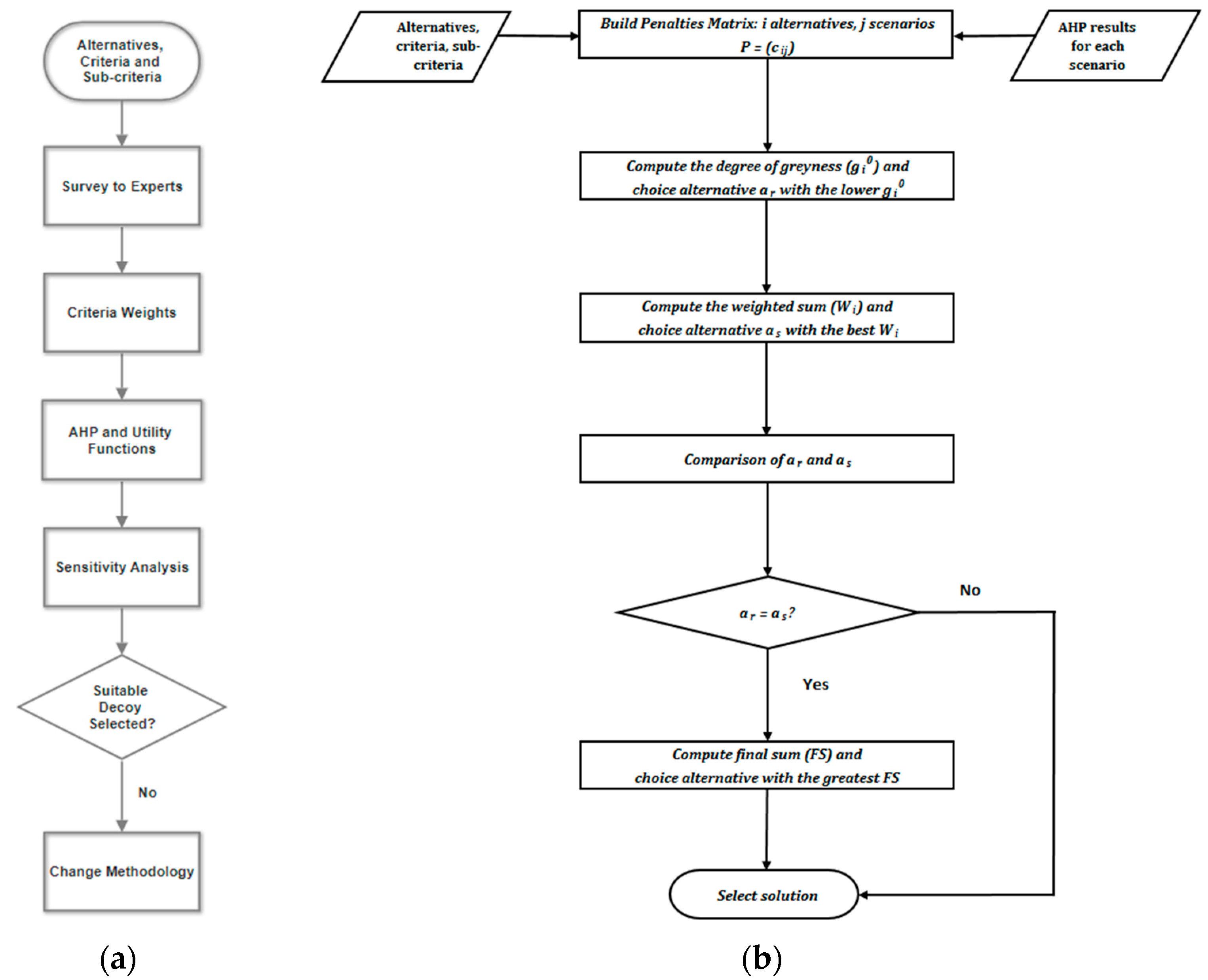
Initially, the methodology that was followed is provided on the left of the Figure 2. According to the Navy guidelines, alternatives, criteria, and sub-criteria are the starting point to manage the problem. Next, a survey was conducted by expert officers of the Navy to determine the weights of the criteria. After applying the AHP, a sensitivity analysis was carried out by varying the weights assigned to the criteria. Since none of the alternative decoys could be selected in a suitable way, it was necessary to change the methodology. Hence, the GMUBO methodology was implemented, which allows integrating uncertainty into the AHP results.

GMUBO methodology is applied considering two data sets: (1) alternatives, criteria and sub-criteria and, (2) AHP results from different scenarios. The application of GMUBO is shown on the right of the Figure 2.

Since the initial methodology was modified, it must be indicated that it was improved by integrating the uncertainty. Therefore, GMUBO starts from the data provided by the EMA, that is, decoy alternatives, criteria, and sub-criteria. Likewise, the data of the survey made by the experts were used, obtaining the weightings of criteria and sub-criteria. From here, the scenarios are defined and the AHP method is applied. Therefore, the EMA guidelines and the AHP results allow starting GMUBO. The following paragraphs give a breakdown of the whole process.

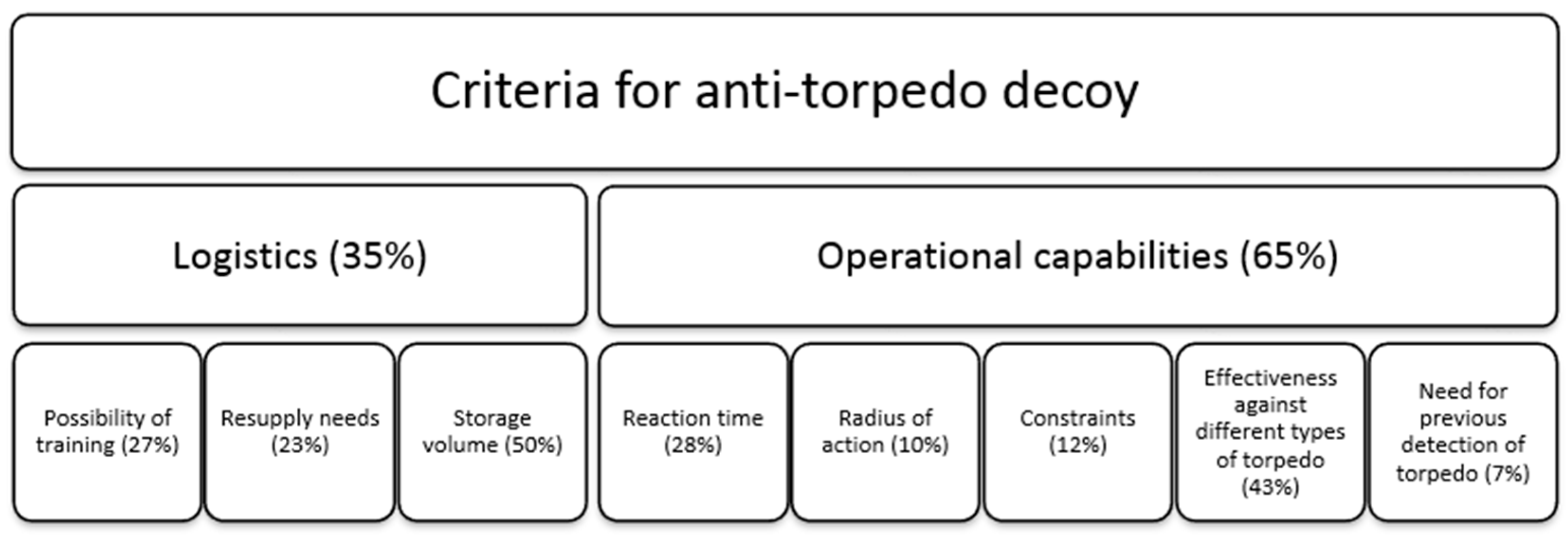
First, the chosen criteria were monitored by the EMA and the sub-criteria that emanate from each of the two criteria are provided in Figure 3. All values are fictitious due to real ones being classified information.

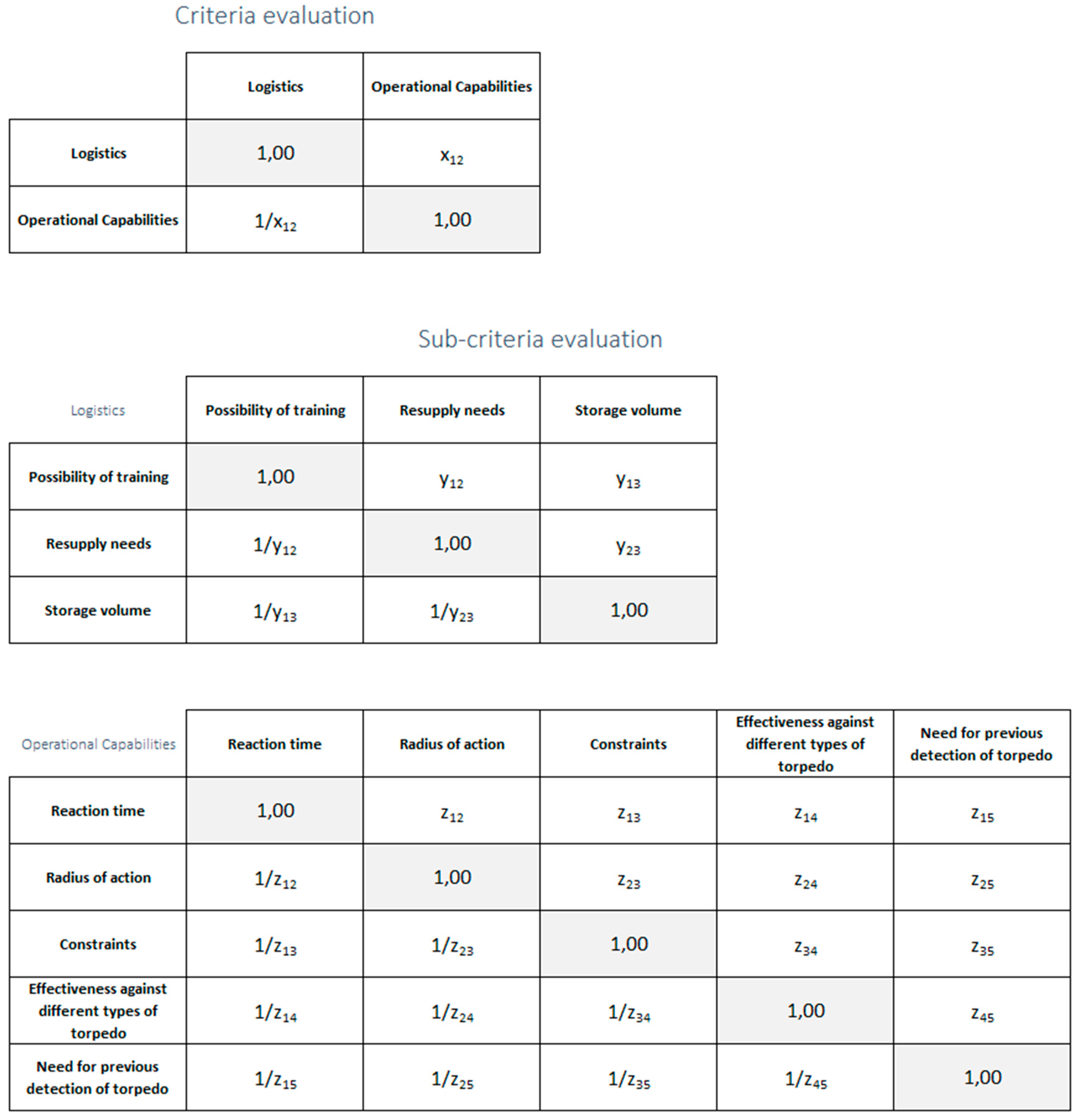
Second, the survey was conducted as follows (Figure 4): A scale of numbers proposed by Saaty indicates how many times more important one element is over another element, considering the criterion with respect to which they are compared [20]. Let x_ij denote the intensity of importance of the criteria being compared, that is, logistics, and operational capabilities. Let y_ij denote the intensity of importance of the sub-criteria belonging logistics criterion. Finally, z_ij denotes the intensity of importance given to the sub-criteria related to operational capabilities criterion. Pairwise comparison matrices for criteria and sub-criteria were given to experts of the Navy in order to fill in the x_ij, y_ij, and z_ij values. The numerical values to denote the intensity of the importance of criteria and sub-criteria are the integers from 1 to 9. The results were treated statistically to obtain the weights of the criteria, which were used in the AHP method.

Next, the AHP method was applied to determine the best anti-torpedo decoy. The decision process based on the AHP considers a finite number of alternatives x_i, for i from 1 to n. A score is assigned to each alternative (w_i is the score of alternative x_i), providing a weight vector. A square matrix of pairwise comparison is used to solve the multi-criteria decision-making (MCDM). Let A be the pairwise comparison matrix:

A = (a_ij)

(1)

where a_ij = 1/a_ji and a_ii = 1 for all i and j from 1 to n [17]. Saaty proposed a consistency index (CI) to evaluate the consistency of the pairwise comparison matrix:

CI = (λ_max − n)/(n − 1)

(2)

To deduce the weight vector, is used the eigenvector theory. The method consists of finding the Perron-Frobenius eigenvector [21], which corresponds to the maximum eigenvalue of the pairwise comparison matrix, that is:

A · w = λ_max · w

(3)

The AHP decomposes a problem into a hierarchy of smaller sub-problems, which can more easily be evaluated. Thus, the AHP provides a hierarchy of goal, criteria (c_i), sub-criteria (sc_ij), and alternatives (a_i), as shown in

Table 1. Hierarchy of the AHP.

Goal
c1	c2	…	cn
sc11…	sc21…	…	scn1…
a1	a2	…	am

.

Two sub-criteria needed to be analyzed differently from the rest. For the logistics sub-criteria “storage volume” (SV), a utility function was used. This allows adding objective data of the real volume occupied by each decoy in a warship. Similarly, a utility function is used to evaluate the sub-criteria “reaction time” (RT). This adds objectivity since the real values of the time it takes to make effective use of the decoy of each of the alternatives are known [22]. Thus, the linear utility functions shown in Equations (4) and (6) were considered:

y_SV = C₁ · x_SV + C₂

(4)

where x_SV = 5 m³ if y_SV = 0 and x_SV = 1 m³ if y_SV = 1

(5)

y_RT = C₃ · x_RT + C₄

(6)

where x_RT = 30 s if y_RT = 0 and x_RT = 0 s if y_RT = 1

(7)

For a volume of 5 m³ the minimum utility y_SV is assigned, i.e., a value of 0%, given that this volume is too large because it reduces space to other logistic needs of the vessel. Then, for a volume of 1 m³ the maximum utility y_SV is assigned, i.e., a value of 100%, since it is not possible to store decoys in a smaller space.

In a like manner, the minimum utility y_RT (0%) happens when x_RT is 30 s. Half a minute is considered as the maximum time established to make effective use of decoy capabilities. That is, once that time has passed, it is considered that the vessel is no longer able to make effective use of any of the decoys. Likewise, the maximum utility y_RT (100%) happens when the reaction time is 0 s. That is to say, the optimal value of the reaction time is a null value, which would represent the ideal situation. However, it is only a reference, because in practice reaction time can never be zero. Hence, the utility functions are:

y_SV = −25 · x_SV + 125 and y_RT = −(10/3) · x_RT + 100

(8)

Next, the GMUBO method considers the uncertainty of the process. In order to achieve a robustness in the results, the uncertainty in the process must be integrated. To do this, different scenarios were considered. These scenarios are changes to the weightings of the objective. Then, uncertainty of the alternatives, considered as grey numbers [23,24], was calculated. Subsequently, the best alternative was determined, taking into account that the scenarios are not controllable by the decision-maker.

In the AHP method, a criteria comparison matrix is multiplied by a priority vector and an overall priority vector (OPV) is obtained. The OPV determines a hierarchy on the selection of alternatives and provides a first selection that does not consider uncertainty. A decision maker does not know which scenario is going to arise. Then, it is necessary to repeat the process considering a number of scenarios. Each scenario allows to obtain a corresponding OPV. Keeping this in mind a Penalties Matrix (m × n) is built:

P = (c_ij)

(9)

Consider S_A the set of alternatives and S_S the set of scenarios. Then:

S_A = {a_i} for i = 1 to m

(10)

S_S = {s_j} for j = 1 to n

(11)

In P matrix, each c_ij is the penalty obtained after choosing the alternative a_i when the given scenario is s_j.

To choose the best alternative two calculations are performed. On the one hand, a measure of the uncertainty is needed. On the other hand, weighted sums calculation is carried out. The best alternative should have the highest value of weighted sum and the lowest value for uncertainty.

Since the penalties are considered as grey numbers, the following expression is a measure of the uncertainty for each alternative [18]:

g_i⁰ = (c_ik − c_im)/(1 · c_im + Σµ_ij · c_ij + 0 · c_ik)

(12)

where:

c_ik = max c_ij and c_im = min c_ij with µ_ij ϵ [0,1]

(13)

Now the weighted sum is calculated for each alternative i:

W_i = λ_i1 · p_i1 + … + λ_nn · p_nn

(14)

Finally, the best alternative should have the highest value of weighted sum and the lowest value for uncertainty. If both values lead to more than one alternative, then the alternative with the greatest final sum FS must be selected [18].

FS = W_i + (max g_i⁰ − g_i⁰) + 1/Σc_ij

(15)

3. Results and Discussion

The GMUBO methodology is fed from the results of applying the AHP method for different scenarios. The scenarios represent the way in which uncertainty is modeled since the decision-maker does not know what scenario will occur in the future. The changes in the scenario produce variations in the comparison matrices, all of which allows the implementation of GMUBO. One advantage of GMUBO is that it takes into account the imprecision that may be present in the minds of the experts when making the pairwise comparison.

The AHP method has wide applicability and allows dealing with complex problems by synthesizing them. Moreover, it establishes a ratio scale that makes easy the measurement [25]. The AHP has an axiomatic foundation and uses a clearly defined mathematical structure [26].

The AHP is a MCDM method that uses a hierarchy to represent a decision problem. The AHP assumes the hypothesis that each element in the hierarchy is independent. An advantage of the AHP is that it enables to include intangible qualitative criteria along with tangible quantitative criteria [27].

Although the criteria, sub-criteria and their weights were provided by a survey conducted with EMA experts, a utility functions had to be used for two of the sub-criteria. Specifically, the sub-criteria of SV and RT, since the real values of the storage volume and the reaction times were available. This was possible because the technical features of the different alternatives were available, all of which allowed the process to be more objective.

Table 2. Final decision matrix after applying the AHP.

Alternatives	Logistics (35%)	Operational Capabilities (65%)
N (49.5%)	84%	41%
L (50.5%)	16%	59%

provide the final decision matrix after applying the AHP. Then, as is shown in column 1, there is no clear preference for one of the alternatives. As shown in Table 2, the results are clearly different if only one of the criteria is taken into account. Specifically, alternative N acquires a clear advantage over alternative L if only the “logistics” criterion is considered in the evaluation. Similarly, if only the criterion “operational capabilities” is taken into account, it is observed that alternative L is better than alternative N.

It follows that, once the AHP method is applied, practically equal results are obtained for both N and L alternatives. To be exact, it is obtained that the alternative L is slightly preferable to the alternative N, but with only a 1% difference between L and N. Since this difference is very small, it can be concluded that, given the available information, it is not advisable to establish which alternative is better.

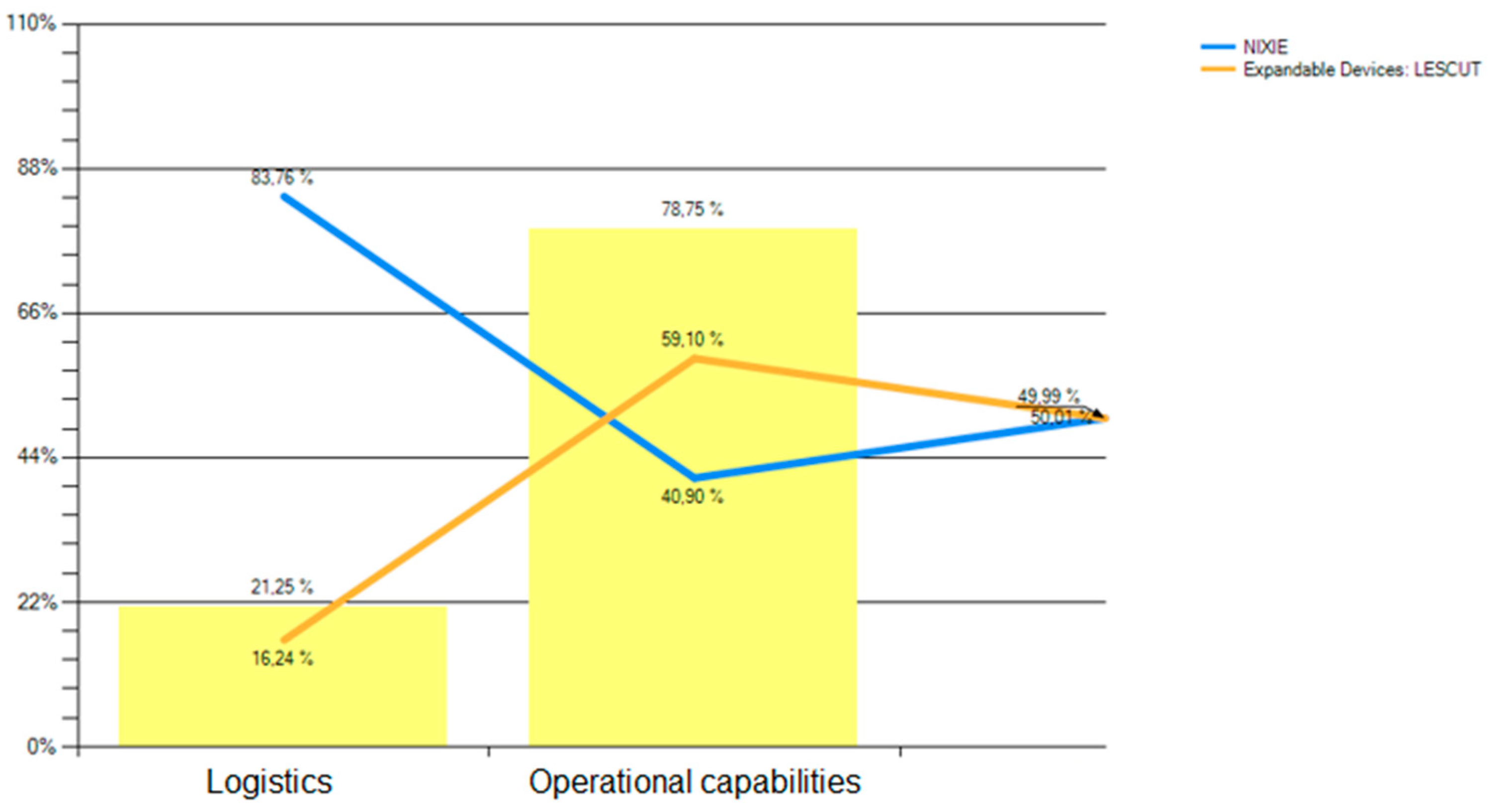
Figure 5 and Figure 6 show a sensitivity analysis obtained by varying the weights assigned to the criteria. The sensitivity analysis allows observing that a small variation in the weights assigned to the criteria produces that the chosen alternative changes. Therefore, the result obtained in the problem is very sensitive to variations in the influence or weight of the two criteria “logistics” and “operational capabilities”.

This means that, according to this result, it is not advisable to choose any of the two alternative solutions if you want to be certain of success. This is because the method does not clearly decide which alternative is preferable to the other. This is one source of uncertainty in the decision-making process. The AHP is a method that does not handle uncertainty although it is a good starting point to implement a better solution.

Different options were evaluated: re-evaluation and addition of more criteria, the use of complementary calculations, simulations or sophisticated software, and the integration of uncertainty in the AHP method. These options are discussed below.

Initially, by adding new criteria to the hierarchy to proceed to a re-evaluation, applying again the AHP. This option was discarded because it required more time and did not take into account the uncertainty inherent in the process. It should also be noted that this solution would imply that the experts would not have done their job correctly. However, the EMA took special care to define the most important criteria for decision-making. Moreover, the experts assigned the scores according to their experience and current environment.

Then, some mathematical techniques were considered as the theory of probability and fuzzy logic, among others, which do consider uncertainty. The implementation of these techniques involved complex calculations, simulations and sophisticated software. Actually, decision-makers do not have time to develop techniques that require excessive amounts of knowledge. Hence, ease of use and exactness are basic features to encourage decision-makers in using of useful techniques.

Next, let us see an example of application of the GMUBO approach. With the proposed new approach, it is assumed that the result obtained through the application of the AHP is due to the consideration of a deterministic situation, that is, without uncertainty. This situation is called Scenario S₀. Therefore, to apply GMUBO, three additional scenarios are going to be assumed in order to show how this new approach works.

Then, scenarios S₁, S₂, and S₃ are considered, taking into account that these scenarios present different conditions that will modify the valuations given by the experts of the Navy. In the following points the characteristics and implications of each scenario are explained.

• Scenario S₀. This is the initial scenario, due to a deterministic and known situation, where AHP is applied. The final decision matrix was given in Table 2 above. In addition, in Figure 3 of Section 2, the assessments of the criteria and sub-criteria were provided.
• Scenario S₁. In this new scenario, the implementation of important logistical improvements in the Navy is assumed. This has produced a change in the valuations of the criteria and sub-criteria, which is presented in

  Table 3. Final decision matrix for S₁ after applying the AHP.

  Alternatives	Logistics (40%)	Operational Capabilities (60%)
  N (55.4%)	73.9%	43.1%
  L (44.6%)	26.1%	56.9%

  . The values given for “possibility of training” and “resupply needs” have changed.
• Scenario S₂. The existence of this scenario is based on the subjectivity of the values given to two of the sub-criteria of the operational capabilities criterion. This means that the sub-criteria “radius of action” and “constraints” are very variable. Therefore, the assessments given to them have been reviewed. The values are presented in

  Table 4. Final decision matrix for S₂ after applying the AHP.

  Alternatives	Logistics (30%)	Operational Capabilities (70%)
  N (59.6%)	83.5%	49.3%
  L (40.4%)	16.5%	50.7%

  .
• Scenario S₃. In this case, it is simply assumed that the weight of the logistics criterion is reduced by up to 15% and the operational capabilities criterion increases up to 85% (

  Table 5. Final decision matrix for S₃ after applying the AHP.

  Alternatives	Logistics (15%)	Operational Capabilities (85%)
  N (42.0%)	68.6%	37.9%
  L (58.0%)	31.4%	62.1%

  ).

Now, following the steps explained in Section 2, the penalties matrix (P) is constructed from the OPV vector, obtained by applying the AHP to each scenario. Then, the matrix P is constructed from the matrix of the following OPV, given by the AHP:

$$\left[\begin{array}{cccc}0.495& 0.554& 0.596& 0.420\\ 0.505& 0.446& 0.404& 0.580\end{array}\right]$$

Once normalized, the matrix of penalties is obtained, where each c_ij represents the penalty incurred when choosing an alternative a_i when a scenario s_j has been given. Therefore, P becomes:

$$\left[\begin{array}{cccc}0.101& 0.042& 0.021& 0.176\\ 0.091& 0.150& 0.192& 0.016\end{array}\right]$$

Applying Equation (12) of Section 2, a measure of the uncertainty of each alternative is determined, from which it follows that:

g₁⁰ = 1.4598

(16)

g₂⁰ = 1.6920

(17)

The value 0 is assigned to the greatest c_ij in each column and 1 to the smallest. The other values are assigned from the linear interpolation between 0 and 1. Since it has the smallest uncertainty, alternative 1 should be chosen. However, according to the methodology exposed in Section 2, it is necessary to calculate the weighted sum to avoid high penalties. Then, calculating W_i for each alternative:

W₁ = 0.0630

(18)

W₂ = 0.1070

(19)

According to the methodology used, the best alternative is the one with the highest W_i, which would be alternative 2. Because both uncertainty (g_i⁰) and weighted sum (W_i) led to more than one alternative, then the alternative with the highest final sum FS must be selected:

FS₁ = W₁ + (max g_i⁰ − g₁⁰) + 1/Σc_1j = 3.2364

(20)

FS₂ = W₂ + (max g_i⁰ − g₂⁰) + 1/Σc_2j = 2.3342

(21)

Eventually, the alternative with the highest FS turns out to be 1.

Finally, uncertainty was implemented using the GMUBO method, which is easy to use and useful to help decision-making under uncertainty, as well as providing a very useful graphical tool (Figure 7) [18]. GMUBO provides two vectors that are combined subsequently. On the one hand, a measure of the uncertainty given by the degree of greyness of each alternative [24]. On the other hand, for a given alternative, the inverse of the sum of its penalties is measured. Both vectors can provide a clear and singular alternative. However, there are situations where each vector leads to a different alternative. In these cases, the final sum (FS) would resolve the discrepancy.

FS measures the suitability of an alternative considering all the scenarios that can arise. FS controls and minimize the effect of a very small uncertainty that could modify the choice of the best alternative. It is considered that for a given alternative, the inverse of the sum of its penalties should be as large as possible to avoid alternatives with both high penalty values and a very small uncertainty.

GMUBO considers uncertainty and allows to measure the robustness of the selected alternative. Furthermore, it is a helpful method for decision-makers since it has a great ease of use.

4. Managerial Implications

The design and construction of a warship is characterized by fundamental managerial implications for the EMA. One of the most important implications is the need of decision-making under uncertainty and unforeseen events. Thus, decisions about the capabilities of a warship involve not only engineering, but also a managerial level of analysis.

GMUBO manages the uncertainty combining it with the AHP and a weighted sum method. Weighted sum methods have advantages for multi-criteria decision-making: they are easier for understanding and to be handled by a decision-maker than complex calculations or simulations.

The approach proposed in the work would allow to managing uncertainty and risks to the decision-makers of the EMA. Hence, the findings of this work would be useful for enhancing the decision-making performance of the Spanish Navy.

When managing a MCDM problem, it is very important to know how sensitive or decisive each criterion is. In this way, managers can improve the decisions they must make. The sensitivity analysis show how sensitive the actual alternative is to changes on the current weights of the decision criteria. To learn more about the sensitivity analysis, the works [28,29,30] are available in the literature on the topic. In this work, a preliminary sensitivity analysis was done to assess the performance of the AHP. In Figure 5 and Figure 6 of Section 3 this analysis could be used to demonstrate the convenience of improving the performance obtained with the AHP. Once the GMUBO method was applied, using a computer tool, it was possible to verify how this new approach allows the robustness of the selected alternative to be measured (some data and information have not been provided due to the confidentiality of the possible implementation of the method in the Navy).

5. Conclusions

Due to the inherent complexity of the ASW, the Spanish Navy has established that the new frigates of the F-110 class must possess a remarkable ASW capability. To get it, the F-110 frigates should be equipped with a soft kill protection based on anti-torpedo decoys that allows the distraction of the underwater threat. This work seeks to provide an approach that can help the EMA to decide on the best anti-torpedo decoy for the F-110.

The methodology initially used was based on the AHP method, which does not consider uncertainty. However, the uncertainty arises in the scenarios where a frigate develops its missions. Hence, the solution obtained with the AHP method does not provide sufficient robustness. Moreover, the problem of selecting the best anti-torpedo decoy is a complex decision and another approach is required. However, AHP is a good starting point to implement a better solution, even though it does not handle uncertainty. Since AHP does not manage uncertainty, it is interesting to look for an approach that allows it to be managed. To consider uncertainty is fundamental in decision-making processes. Some of the existing MCDM methods take uncertainty into account, but require additional knowledge to be used. In general, decision-makers usually do not have a strong theoretical foundation of mathematical knowledge. In a general way, ELECTRE, TOPSIS, MAUT, and PROMETHEE are less adapted for changing easily from one to another of various situations or fields. Moreover, a good knowledge of these methods may be difficult to achieve for an inexperienced user.

GMUBO are based in the AHP, which is capable of many applications and has a wide use. A great advantage of the AHP is that it decomposes a decision problem in parts and builds hierarchies. The above-mentioned methods do not provide this structuring capability. The integration of uncertainty in an intuitive and visual way, as well as simplicity, are some of the advantages of the proposed approach.

GMUBO provides a simple method for managing uncertainty, considering different scenarios that decision-makers do not control. GMUBO allows graphically visualizing the solution. The graphic tool that provides the method not only allows a better visualization of the problem, but also helps the decision-making process.