Accurate Approximate Solution of Ambartsumian Delay Differential Equation via Decomposition Method
Abstract
1. Introduction
2. Application of the ADM
2.1. Power Series Solution
2.2. Approximate Solution in Terms of Exponential Functions
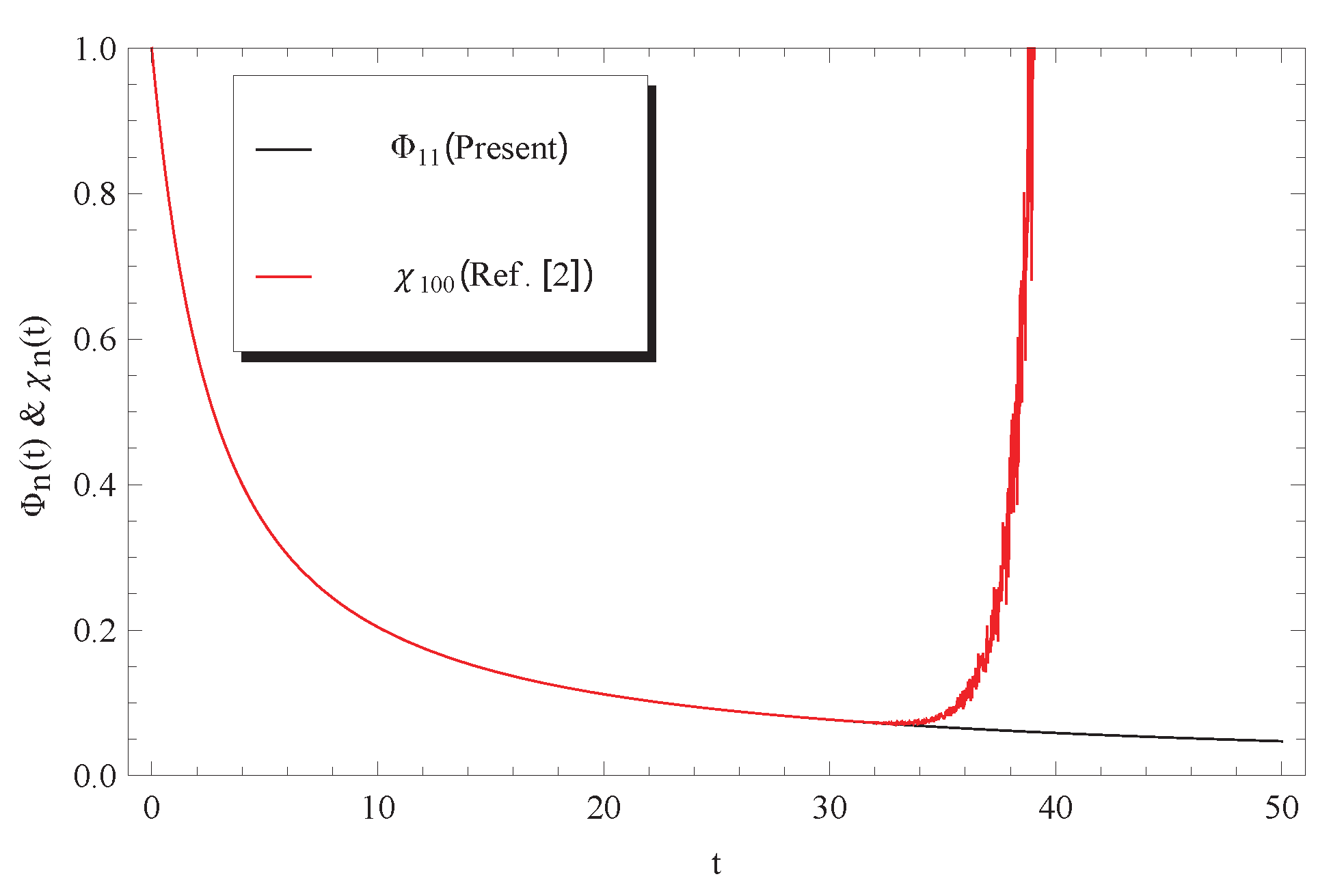
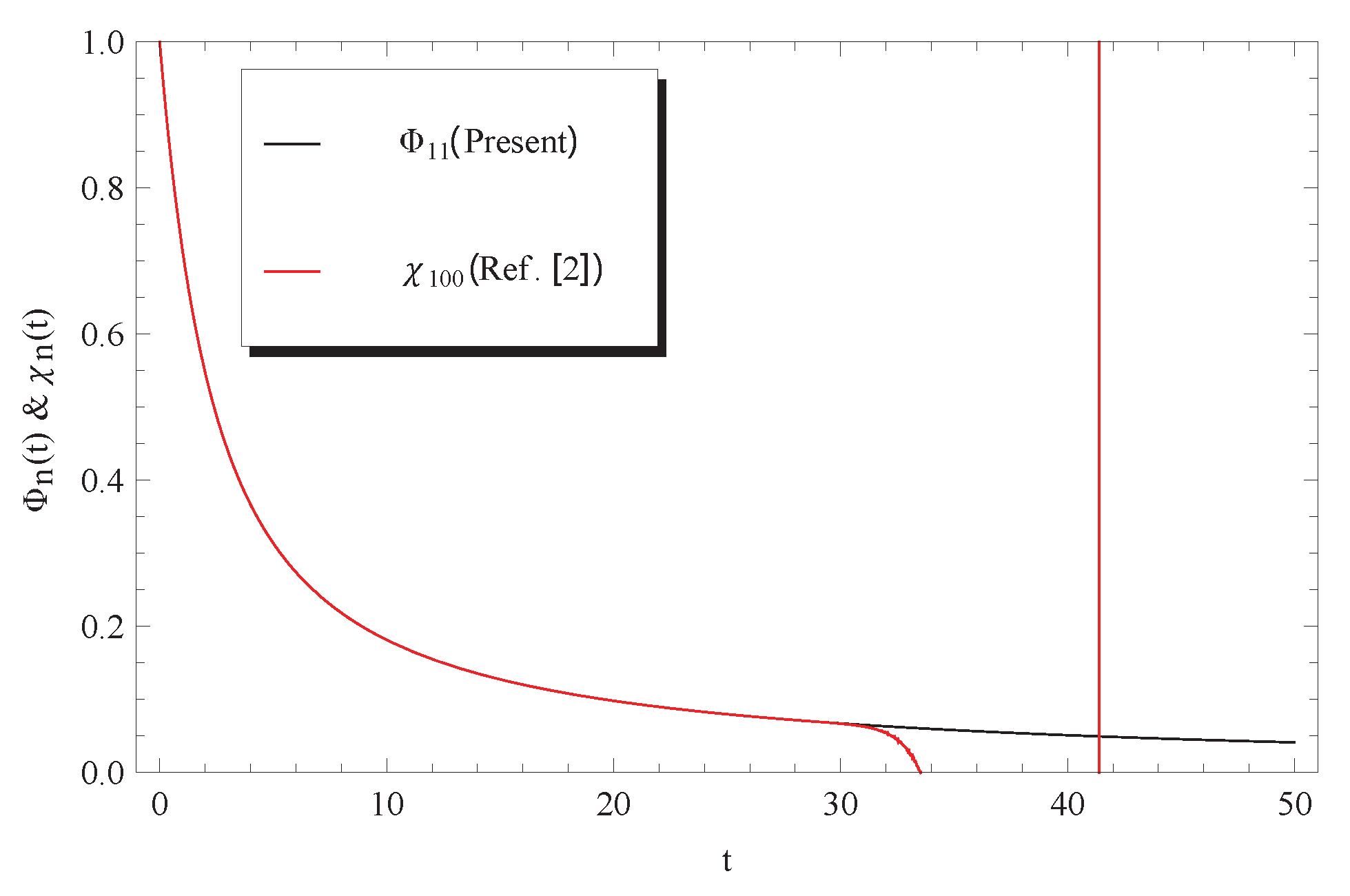
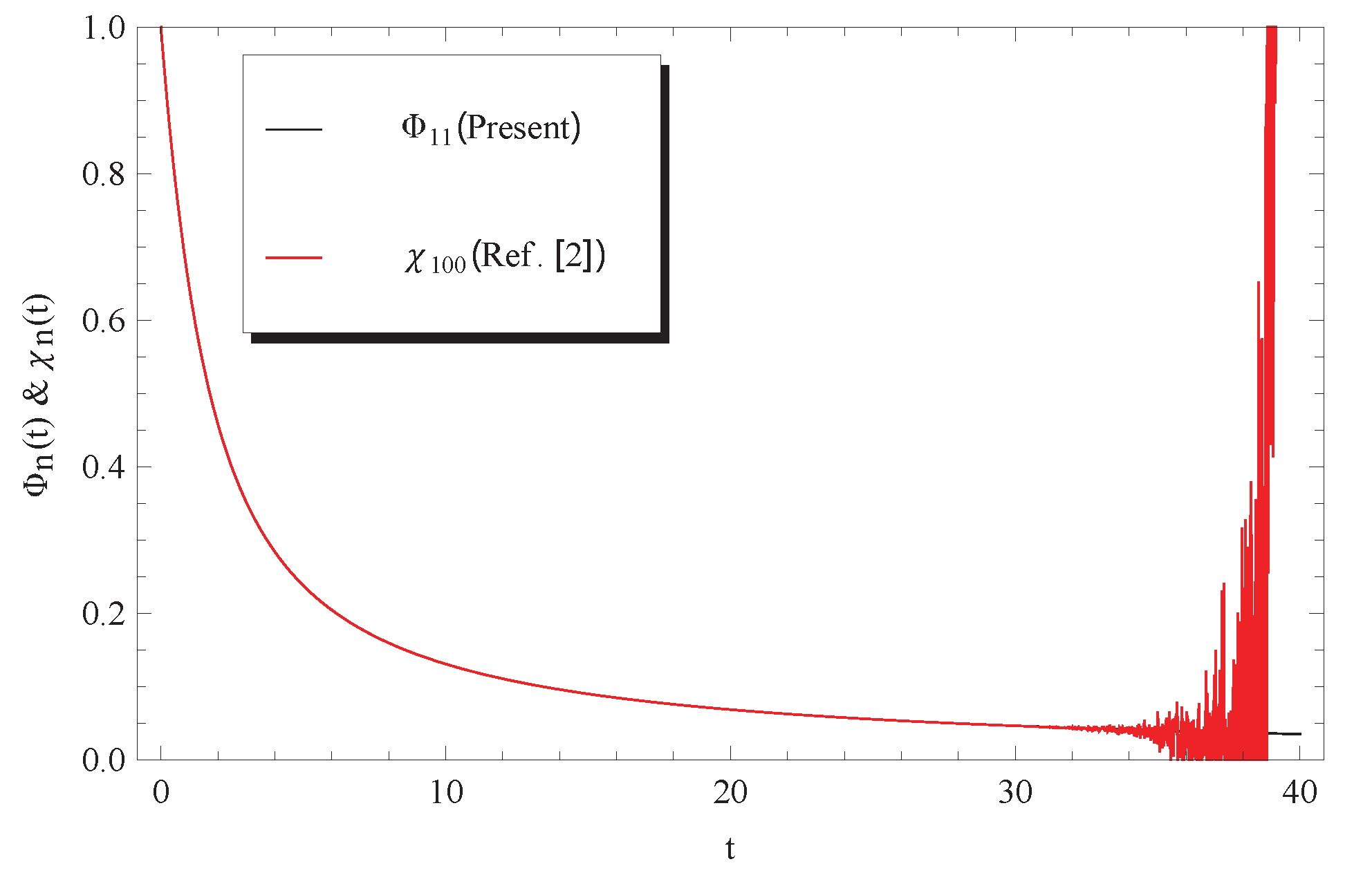
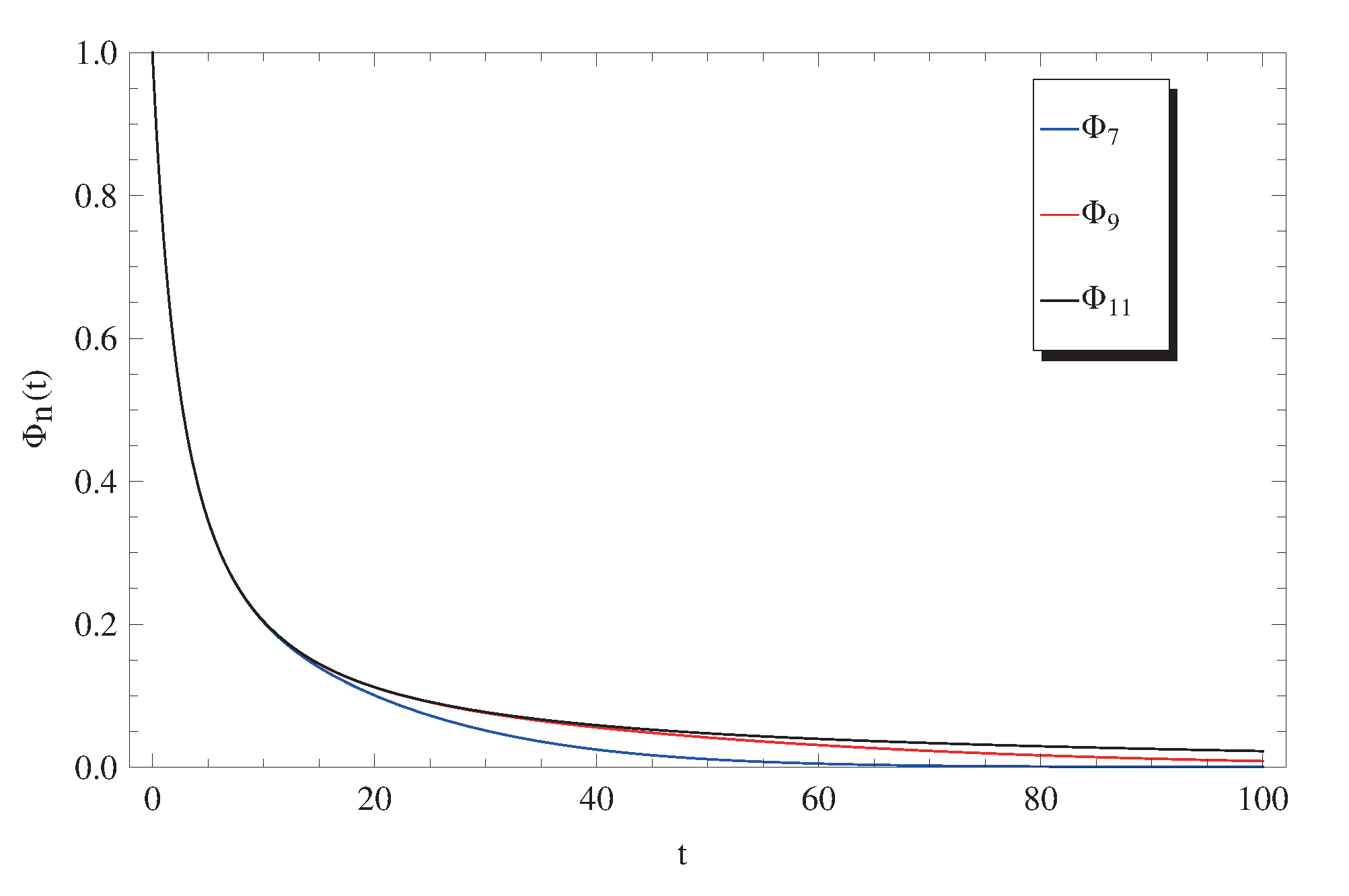
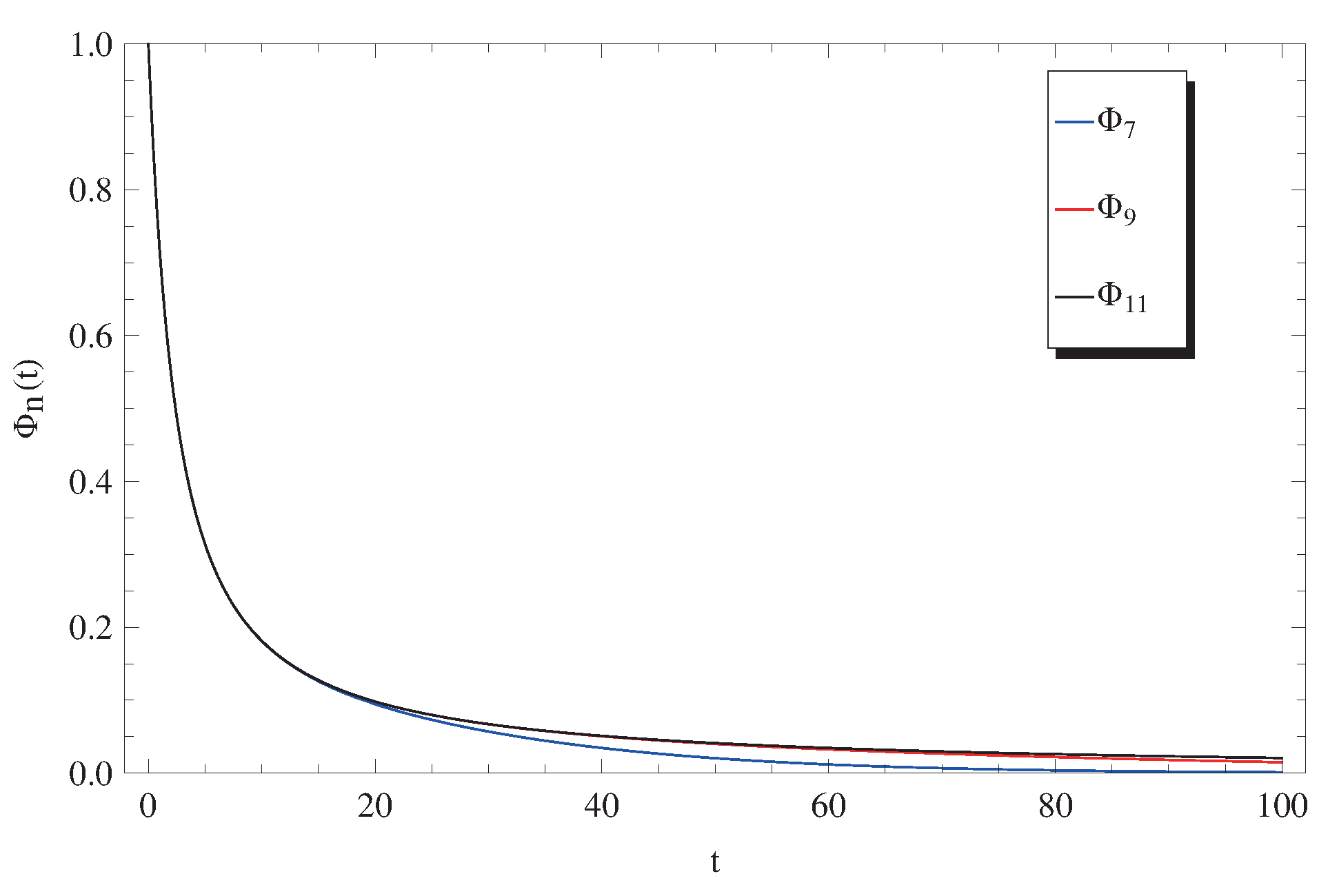
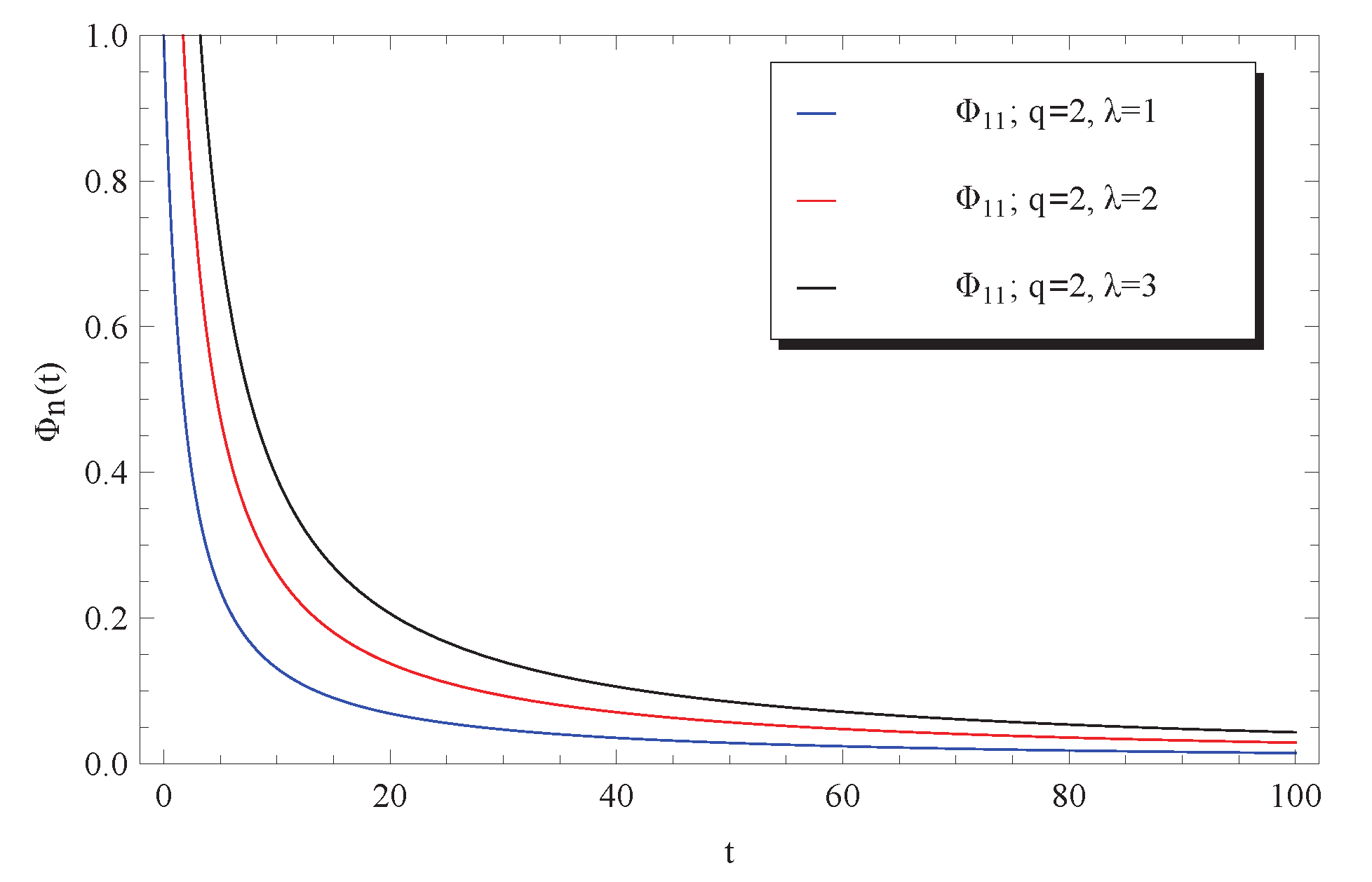
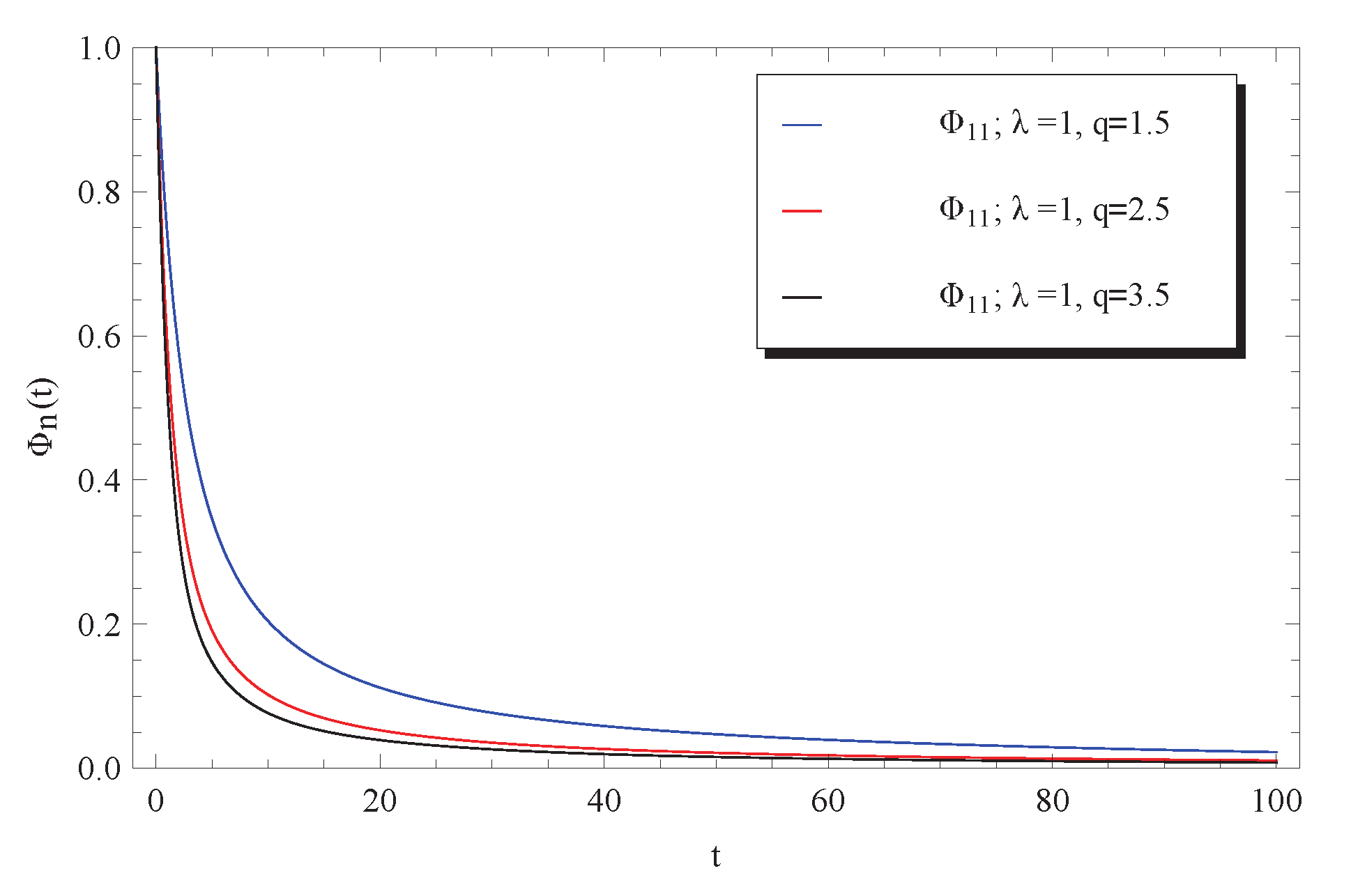
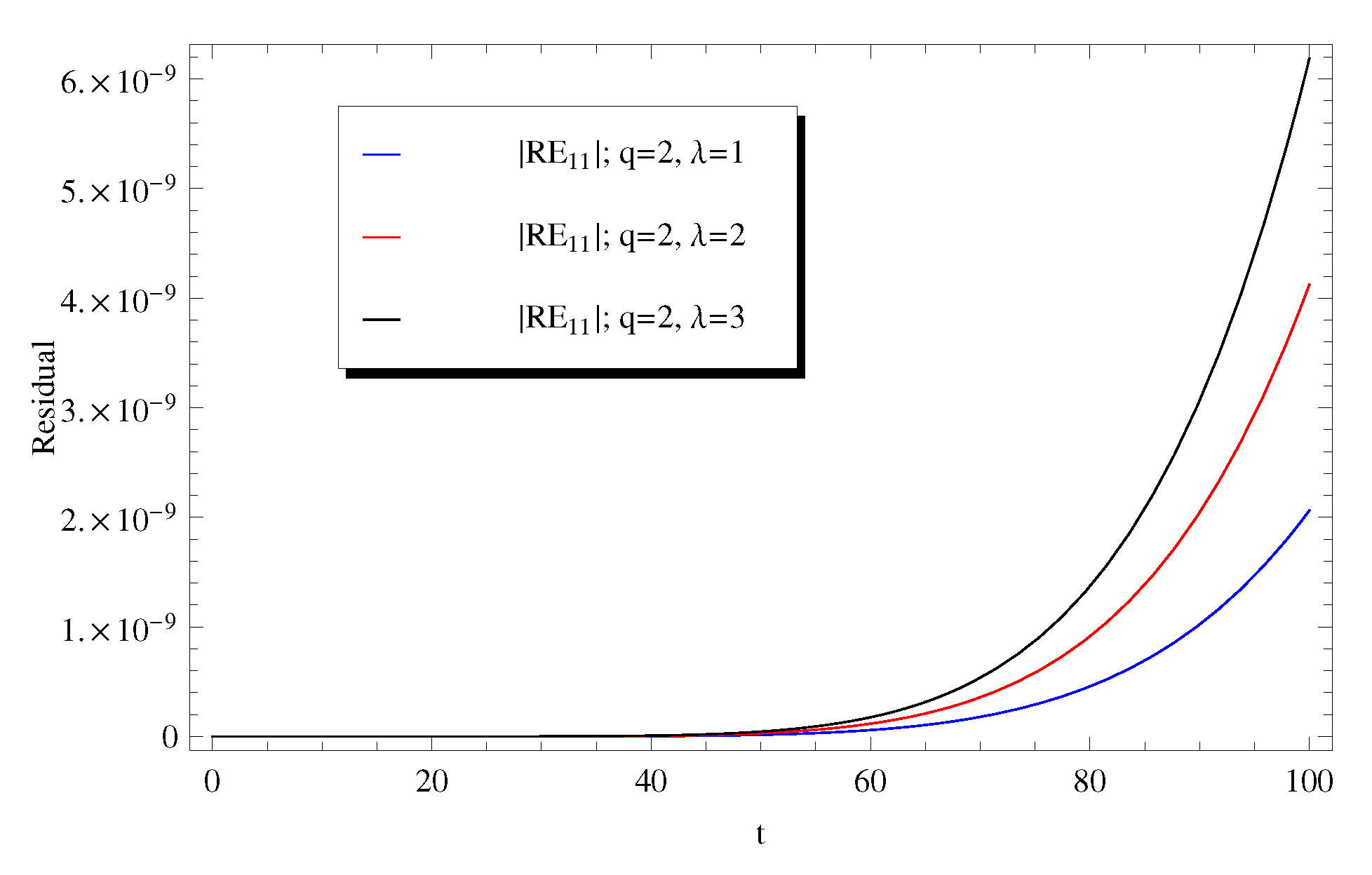
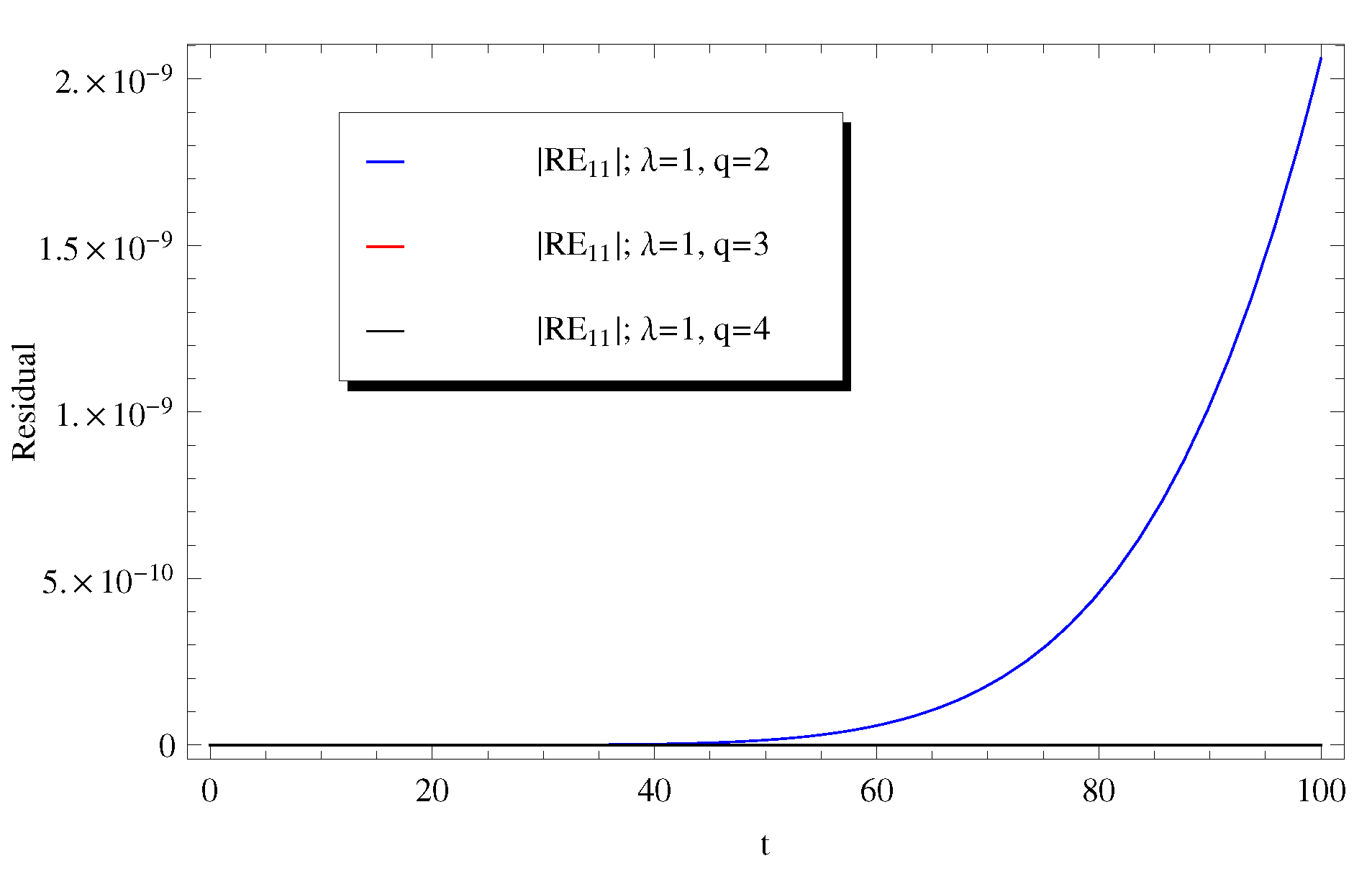
3. Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Ambartsumian, V.A. On the fluctuation of the brightness of the milky way. Doklady Akad Nauk USSR 1994, 44, 223–226. [Google Scholar]
- Patade, J.; Bhalekar, S. On Analytical Solution of Ambartsumian Equation. Natl. Acad. Sci. Lett. 2017. [Google Scholar] [CrossRef]
- Kato, T.; McLeod, J.B. The functional-differential equation y′(x) = ay(λx) + by(x). Bull. Am. Math. Soc. 1971, 77, 891–935. [Google Scholar]
- Daftardar-Gejji, V.; Bhalekar, S. Solving fractional diffusion- wave equations using the new iterative method. Fract. Calc. Appl. Anal. 2008, 11, 193–202. [Google Scholar]
- Adomian, G.; Rach, R. On the solution of algebraic equations by the decomposition method. J. Math. Anal. Appl. 1985, 105, 141–166. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Algebraic equations with exponential terms. J. Math. Anal. Appl. 1985, 112, 136–140. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Algebraic computation and the decomposition method. Kybernetes 1986, 15, 33–37. [Google Scholar] [CrossRef]
- Fatoorehchi, H.; Abolghasemi, H. Finding all real roots of a polynomial by matrix algebra and the Adomian decomposition method. J. Egypt. Math. Soc. 2014, 22, 524–528. [Google Scholar] [CrossRef]
- Alshaery, A.; Ebaid, A. Accurate analytical periodic solution of the elliptical Kepler equation using the Adomian decomposition method. Acta Astronaut. 2017, 140, 27–33. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Acad: Boston, MA, USA, 1994. [Google Scholar]
- Wazwaz, A.M. Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput. 2005, 166, 652–663. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The combined Laplace transform-Adomian decomposition method for handling nonlinear Volterra integro-differential equations. Appl. Math. Comput. 2010, 216, 1304–1309. [Google Scholar] [CrossRef]
- Ebaid, A. Approximate analytical solution of a nonlinear boundary value problem and its application in fluid mechanics. Z. Naturforschung A. 2011, 66, 423–426. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Ebaid, A. A new analytical and numerical treatment for singular two-point boundary value problems via the Adomian decomposition method. J. Comput. Appl. Math. 2011, 235, 1914–1924. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Rach, R.; Duan, J.S. Adomian decomposition method for solving the Volterra integral form of the Lane-Emden equations with initial values and boundary conditions. Appl. Math. Comput. 2013, 219, 5004–5019. [Google Scholar] [CrossRef]
- Ali, E.H.; Ebaid, A.; Rach, R. Advances in the Adomian decomposition method for solving two-point nonlinear boundary value problems with Neumann boundary conditions. Comput. Math. Appl. 2012, 63, 1056–1065. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Ashorynejad, H.R. Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol. 2013, 239, 259–265. [Google Scholar] [CrossRef]
- Chun, C.; Ebaid, A.; Lee, M.; Aly, E.H. An approach for solving singular two point boundary value problems: analytical and numerical treatment. ANZIAM J. 2012, 53, 21–43. [Google Scholar] [CrossRef]
- Kashkari, B.S.; Bakodah, H.O. New Modification Of Laplace Decomposition Method for Seventh Order KdV Equation. Appl. Math. Inf. Sci. 2015, 9, 2507–2512. [Google Scholar]
- Ebaid, A.; Aljoufi, M.D.; Wazwaz, A.-M. An advanced study on the solution of nanofluid flow problems via Adomian’s method. Appl. Math. Lett. 2015, 46, 117–122. [Google Scholar] [CrossRef]
- Bhalekar, S.; Patade, J. An analytical solution of fishers equation using decomposition method. Am. J. Comput. Appl. Math. 2016, 6, 123–127. [Google Scholar]
- Bakodah, H.O.; Al-Zaid, N.A.; Mirzazadeh, M.; Zhou, Q. Decomposition method for Solving Burgers’ Equation with Dirichlet and Neumann boundary conditions. Optik 2017, 130, 1339–1346. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. The Adomian decomposition method for the slip flowand heat transfer of nanofluids over astretching/shrinking sheet. Rom. Rep. Phys. 2018, in press. [Google Scholar]
- Diblík, J.; Kúdelcíková, M. Two classes of asymptotically different positive solutions of the equation (t) = −f(t,yt). Nonlinear Anal. 2009, 70, 3702–3714. [Google Scholar] [CrossRef]
- Diblík, J.; Kúdelcíková, M. Two classes of positive solutions of first order functional differential equations of delayed type. Nonlinear Anal. 2012, 75, 4807–4820. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. Convergence of Adomian’s method applied to nonlinear equations. Math. Comput. Model. 1994, 20, 69–73. [Google Scholar] [CrossRef]
- Cherruault, Y.; Adomian, G. Decompostion Methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Rach, R. A bibliography of the theory and applications of the Adomian decomposition method, 1961–2011. Kybernetes 2012, 41, 1087–1148. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebaid, A.; Al-Enazi, A.; Albalawi, B.Z.; Aljoufi, M.D. Accurate Approximate Solution of Ambartsumian Delay Differential Equation via Decomposition Method. Math. Comput. Appl. 2019, 24, 7. https://doi.org/10.3390/mca24010007
Ebaid A, Al-Enazi A, Albalawi BZ, Aljoufi MD. Accurate Approximate Solution of Ambartsumian Delay Differential Equation via Decomposition Method. Mathematical and Computational Applications. 2019; 24(1):7. https://doi.org/10.3390/mca24010007
Chicago/Turabian StyleEbaid, Abdelhalim, Asmaa Al-Enazi, Bassam Z. Albalawi, and Mona D. Aljoufi. 2019. "Accurate Approximate Solution of Ambartsumian Delay Differential Equation via Decomposition Method" Mathematical and Computational Applications 24, no. 1: 7. https://doi.org/10.3390/mca24010007
APA StyleEbaid, A., Al-Enazi, A., Albalawi, B. Z., & Aljoufi, M. D. (2019). Accurate Approximate Solution of Ambartsumian Delay Differential Equation via Decomposition Method. Mathematical and Computational Applications, 24(1), 7. https://doi.org/10.3390/mca24010007