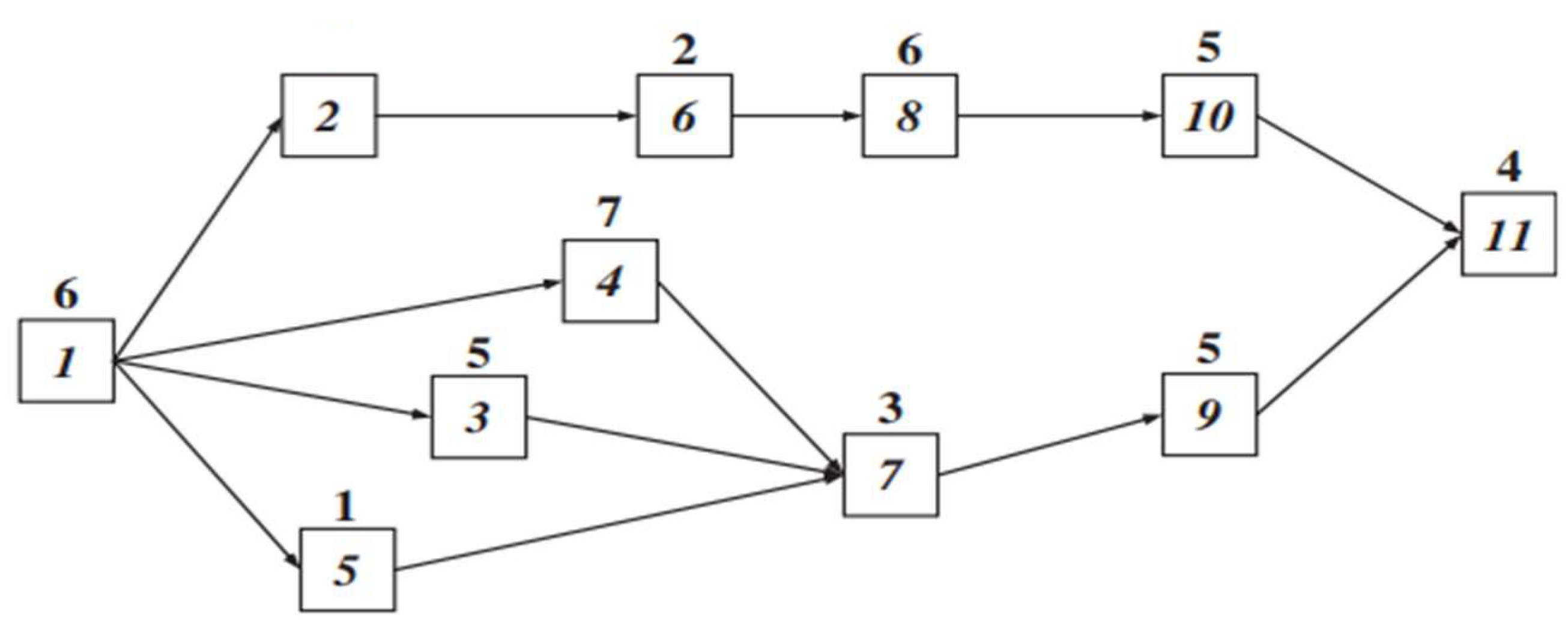
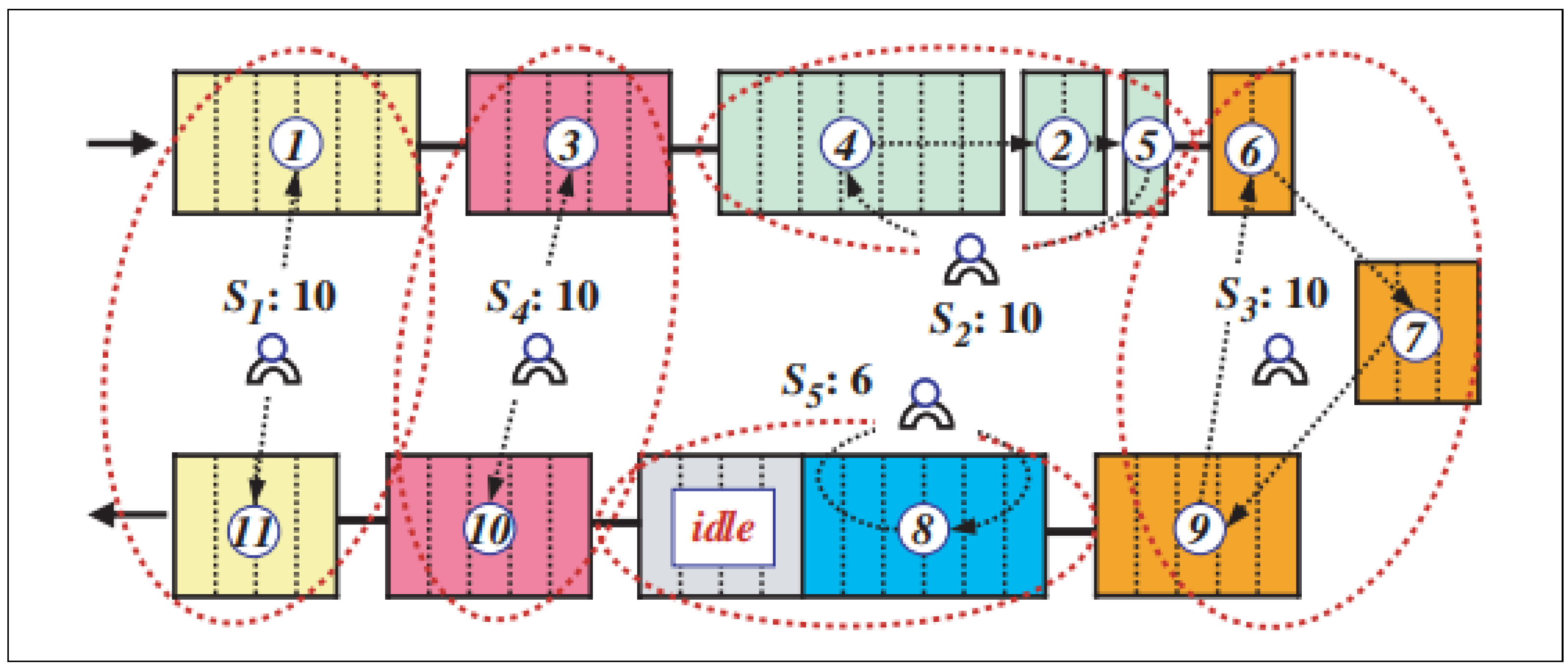
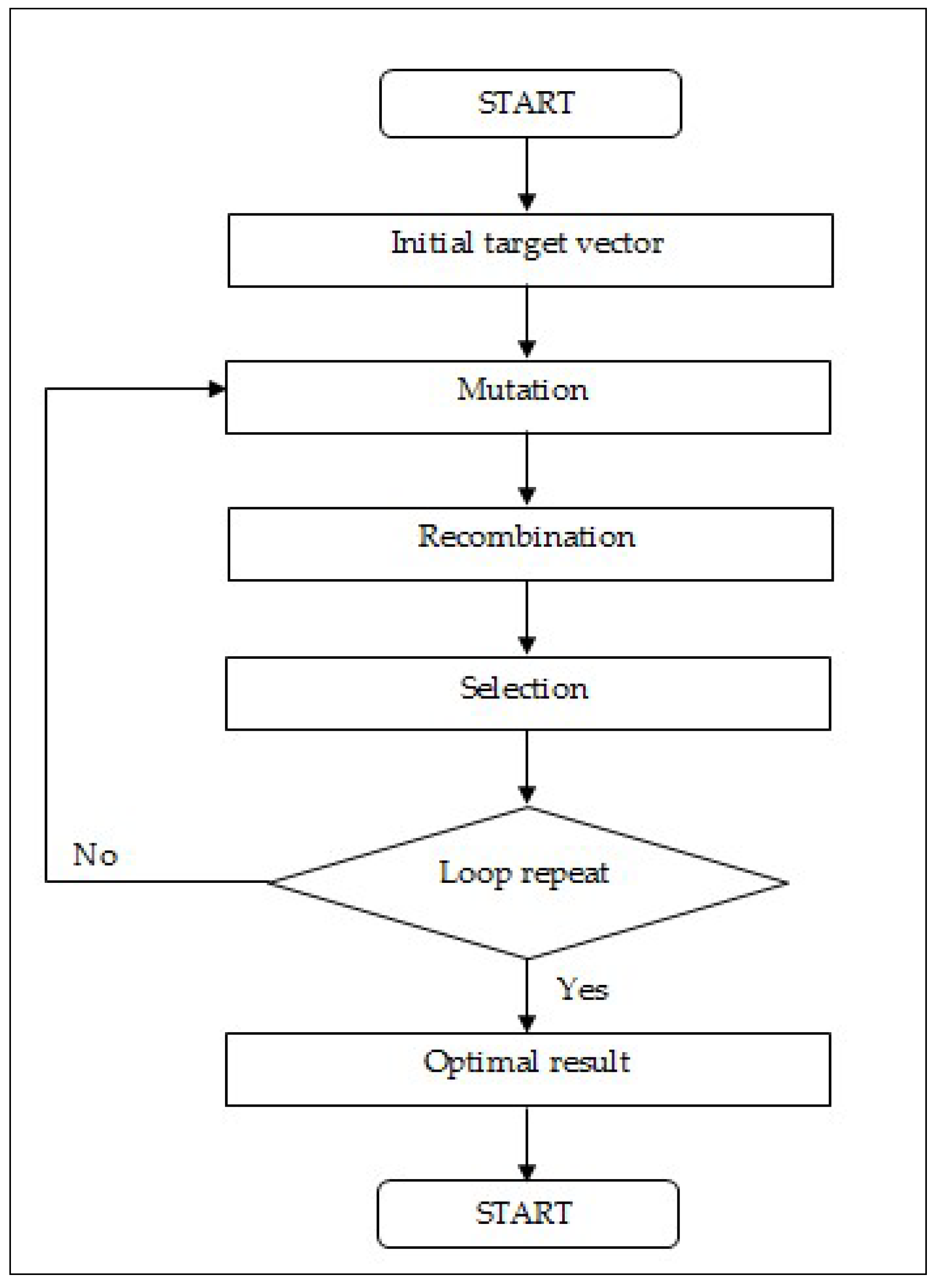
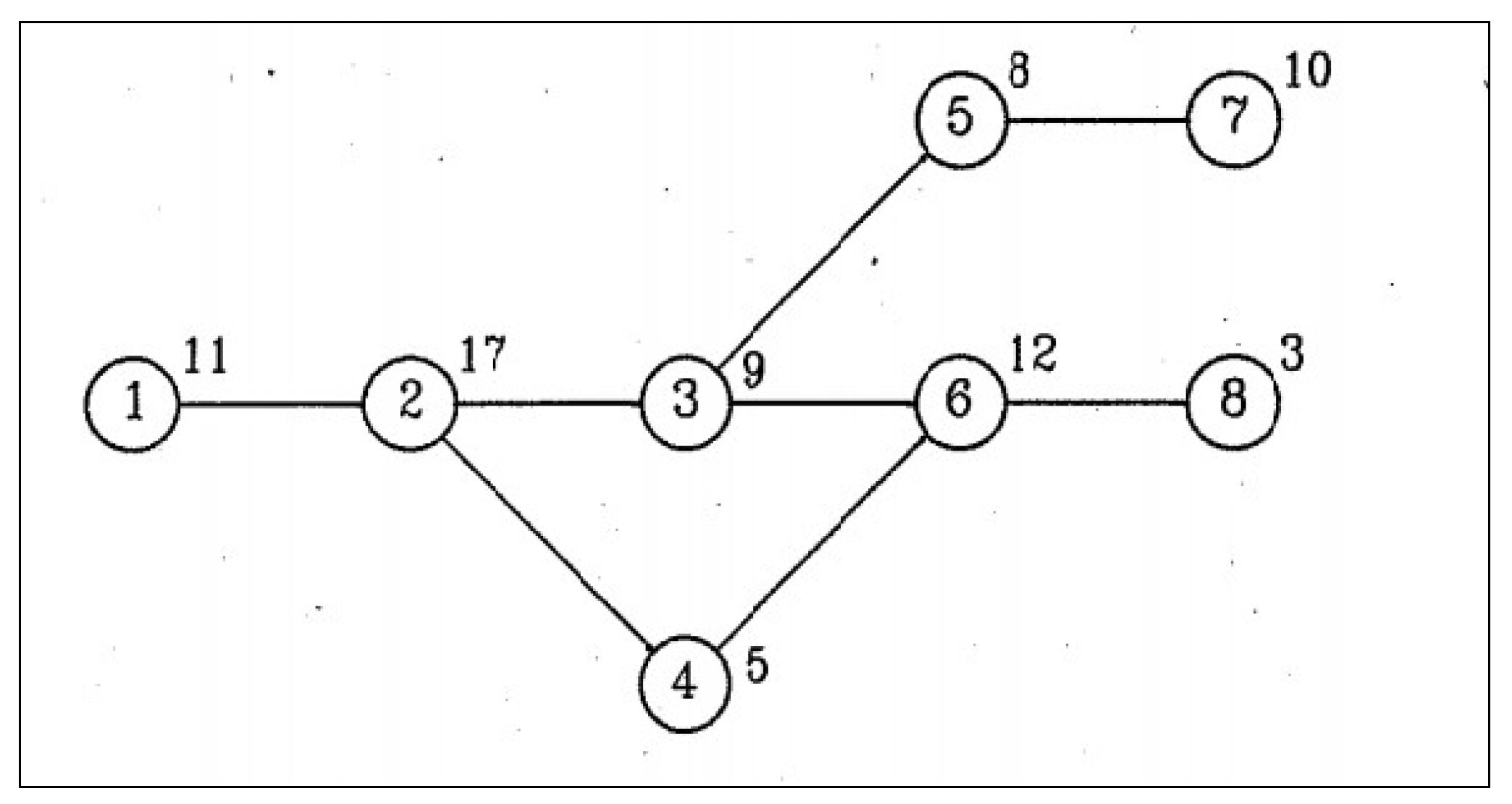
2.1. U-Shape Assembly Line Balancing by Using Other Metaheuristic Methods
The previous studies on the UALBP were reviewed and are summarized in this section. The first UALBP study in the literature was conducted in 1994 by [
10]. In their study entitled “The U-line Line Balancing Problem”, the mathematical formulation of the problem established by using dynamic programming for the single-model U-line to minimize the number of stations, and the RPWT (ranked positional weight technique) for solving a large-sized UALBP (111 tasks), which contained problems derived from previous research studies. These problems were more complicated than traditional problems because the tasks could be placed from forward to backward, from backward to forward, or from both directions simultaneously according to a sequential flowchart. A year later, [
11] developed three mathematical exact algorithms to solve the UALBP. The dynamic programming (DP) formulation was used in the first algorithm, and the other two were breadth-first and depth-first branch and bound (B&B) algorithms. The results of the calculation revealed that B&B was more effective than the DP-based algorithm, and breadth-first spent less time on calculation than depth-first, but depth-first could find the optimal solutions faster. Later, [
12] conducted research entitled “The Mixed-Model U-line Balancing Problem” and developed a heuristic method for solving the mixed-model UALBP with a precedence graph of each batch size with 25 tasks. In the same year, [
13] presented a formulation for Integer Programming (IP) for finding the optimal balance to solve the UALBP. This formulation solved the large-scale problems better than the traditional ones. Later, [
14] proposed a DP formulation for solving problems of numerous U-lines with a maximum of 22 tasks. The objective was to assign the tasks to workstations in various ways, aiming to minimize the number of workstations and time wasting [
15,
16]. This integrated model was solved with a black hole optimization based algorithm. The quality of the heuristic solution was checked with special data sets. A year later, proposed a black hole optimization (BHO) based algorithm dealing with a multi objective supply chain model is presented. The sensitivity of the enhanced algorithm is tested with benchmark functions. Numerical results with different datasets demonstrate the efficiency of the proposed model and validate the usage of Industry 4.0 inventions in first mile and last mile (FMLM) delivery.
The principles proposed could be effective methods for ALB and Rebalancing the UALBP. Later, [
17] developed a heuristic method for solving the UALBP with nine U-lines, where there were 18 tasks in each U-line with the same cycle time. The time between work and the time between U-lines were used in the consideration. A year later, [
18] produced a thesis called “Incorporating Ergonomics Criteria into Assembly Line Balancing” and developed three heuristic methods: (1) multiple ranking heuristic, (2) combinatorial genetic algorithm (GA), and (3) problem-space GA. These methods were developed by employing the criteria for ergonomic designs (such as a reduction in cycle time and the loss of grip strength due to fatigue at workstations) for the consideration of solutions of the I-shaped and U-shaped line ALB in order to obtain the lowest values. Consequently, many industrial factories benefited from the results of the study in terms of both production and ergonomics. Later, [
19] carried out a study entitled “ULINO: Optimally balancing U-shaped JIT assembly lines” by implementing a B&B method that was developed from the simple assembly line balancing optimization method (SALOME). The SALOME method, which had been previously used for solving straight-line problems, was used for solving U-line problems with 297 tasks. This new method was called ULINO (U-line optimizer). The method was based on depth-first branch and bound and dominance rules. The purpose was to minimize the number of workstations, cycle time, or both. In 2003, a method for obtaining the optimal solution of UALB with parallel stations was developed by using multiple lower bounding and a new heuristic method for finding the upper bounding. The results from the two developed methods were improved over the traditional methods.
A year later, [
20] applied the genetic algorithm (GA), which had been used for solving the SALBP, for solving the UALBP-1. Then, the optimal solutions from previous studies were compared. The results from the study showed that the GA could generate the optimal solutions or nearest solutions in the very first rounds of the experiment. Later, [
21] published “A Shortest Route Formulation of Simple U-Type Assembly Line Balancing Problem”, which applied the theory of the shortest route formulation. The theory was proposed by [
22] for solving the SALBP. However, the principles of the theory were further developed to solve the UALBP. In addition, some examples of the calculations of this method were published in many research articles and, In the same year, [
23] achieved the goal of developing an equation formulation for the UALBP that was based on the integer linear programming formulation developed for the UALBP, as well as an equation formulation for the SALBP. The principles were flexible, helping in decision making in the UALBP for cases with many conditions. In the same year, [
24] carried out research called “The Stochastic U-line Balancing Problem: A Heuristic Procedure”. The authors explained the reason why the U-lines were popular: it was because the JIT (just-in-time) production system played a major role in production. Therefore, U-shaped assembly lines were replacing the traditional straight assembly lines. The issue that was emphasized as needing consideration in the UALBP was the unreliability of the task time due to workers and other factors with unpredictable timing.
The developed heuristic approach was divided into two parts: finding basic solutions and improving basic feasible solutions. The results of the calculation revealed the effectiveness of the method used. In another study, conducted by [
25], simulated annealing (SA) was developed for solving the UALBP. This method is widely used at present. The aim of this method is to minimize the number of workstations (Type-I). The effectiveness of the principles was evaluated by a solution search for large-scale problems and by comparing the results with ULINO (U-Line optimizer), which was B&B based on the heuristic procedure. In addition, [
26] the authors proposed recommendations for further research studies as follows: (1) SA methods should be used for more difficult problems, such as mixed-/multi-model lines, stochastic task time, and U-line with other characteristics; (2) the principles of other metaheuristic methods should be utilized for solving the UALBP; (3) exact methods for solving U-line problems at a large scale should be developed; (4) the principles of other metaheuristic methods should be used for solving problems of Type-II (min. c, given m). Since the study, many researchers have explored methods for solving the UALBP by developing GA metaheuristic methods. In [
27], a GA was presented for solving the UALBP by using the Just-In-Time (JIT) approach for solving the UALBP. The results were better than those of the traditional approaches that were employed for solving the UALBP. Therefore, the GA was used for solving UALBP. The results from the verification showed that greater effectiveness was achieved. The criteria used for consideration were the number of workstations of assembly lines and the variation of the workloads. The results from the experiment showed that the proposed method was effective because the workstations were well grouped and the workload formats were improved.
Moreover, many researchers used metaheuristic methods for solving the UALBP. They proposed the ant colony system (ACS) algorithm for finding solutions and proposed four heuristic methods: the method of Kilbridge and Wester (K&W), ranked positional weight (RPW), maximum task time (Max. T. T.), and total maximum number of following tasks (Max. N.F.). The four methods were then compared to the metaheuristic method of ACS for finding solutions, and it was found that the ACS method generated better solutions than the four heuristic methods. Later, other researchers studying methods for solving the UALBP developed a heuristic method and metaheuristic method by using the max-min ant system (MMAS) of max. task time and min. task time, together with a local search method for solving the SALBP and UALBP. For the SALBP, a large-scale benchmark problem set with 45–111 tasks and the large-scale benchmark problem set of Lapierre’s Tabu Search (TS) with 297 tasks were tested. For solving the UALBP, experiments were conducted on the benchmark problem set using Max. RPW and the medium-sized UALBP with 21–45 tasks, and the benchmark problem set with some given information consisted of a large-scale problem with 75–297 tasks. From the results of the study, it was concluded that the developed Max-Min Ant system was the most efficient method when compared to the heuristic method and Max. RPW method. From the experiments, Min. task time generated the worst solution. When compared to other methods, and when there was a change that increased cycle time, the results showed that there was no effect on the capacity of the Max-Min Ant system for finding the solution. Therefore, it was concluded that the developed method was highly efficient. After that, other methods for solving the UALBP were researched by other researchers.
2.3. Differential Evolution Algorithm for Solving Other Problems
Differential evolution (DE) algorithms have been used for solving other research problems which aim to generate solutions as follows. The mutation DE algorithm was used in [
24] and involved the positions of the optimal vectors in the population of each batch and employed the crossover or recombination of positions which were exchanged between vectors through the comparison of the crossover rate (CR) with random positions. This method was found to be effective and, in 2011, [
30] developed the DE algorithm for solving assignment problems by improving two main crucial parameters in the DE process: the weighting factor (F) and crossover rate (CR). The improved differential evolution (IDE) was used for allowing an adjustable F, and the CR changed in terms of taxonomy steps. The sample problems were compared with the solutions of opposition-based differential evolution (ODE) and adaptive differential evolution (JADE). The results revealed that the developed IDE generated better solutions than the other two methods in terms of cost reduction and increased performance in the system. A year later, [
31] developed the Pareto Utility Discrete Differential Evolution (PUDDE) algorithm for handling operator allocation problems (OAP) in order to allocate jobs appropriately for the balance control of assembly lines when multiobjective functions and conditions were formulated, and a decision based on only a single objective cannot be made. The procedure, which included the discrete event simulation DES model, was used in the general simulation, and PUDDE was employed for solving OAPs by improving the operator condition in two ways: decreasing the number of operators or increasing the number of operators. The results from the experiment concluded that PUDDE could find the solutions effectively. However, this method was suitable for decreasing the number of operators. When compared to the traditional DE, the PUDDE algorithm had a much better performance when finding objectives of multi-assembly lines in the same problem.
From the literature and related research studies above, it can be concluded that the DE algorithm was the method able to find the optimal solutions for large-scale complicated problems within the possible solution area by using a short search time when compared to the other metaheuristic methods. It was reported by [
32] that DE algorithms with an evolution algorithm procedure were a new technique for increasing the efficiency of and capacity for handling problems with nondifferentiable, nonlinear, and multimodal objective functions, particularly large-scale complicated problems. It was found that the speed of the solution search of DE was better than that of other methods. Therefore, the DE method can be used for solving the ALBP and increasing the efficiency of the solution search for the ALBP. Hence, DE was chosen for solving the UALBP-1 in the current study.