Pool-Based Genetic Programming Using Evospace, Local Search and Bloat Control
Abstract
1. Introduction
2. Background
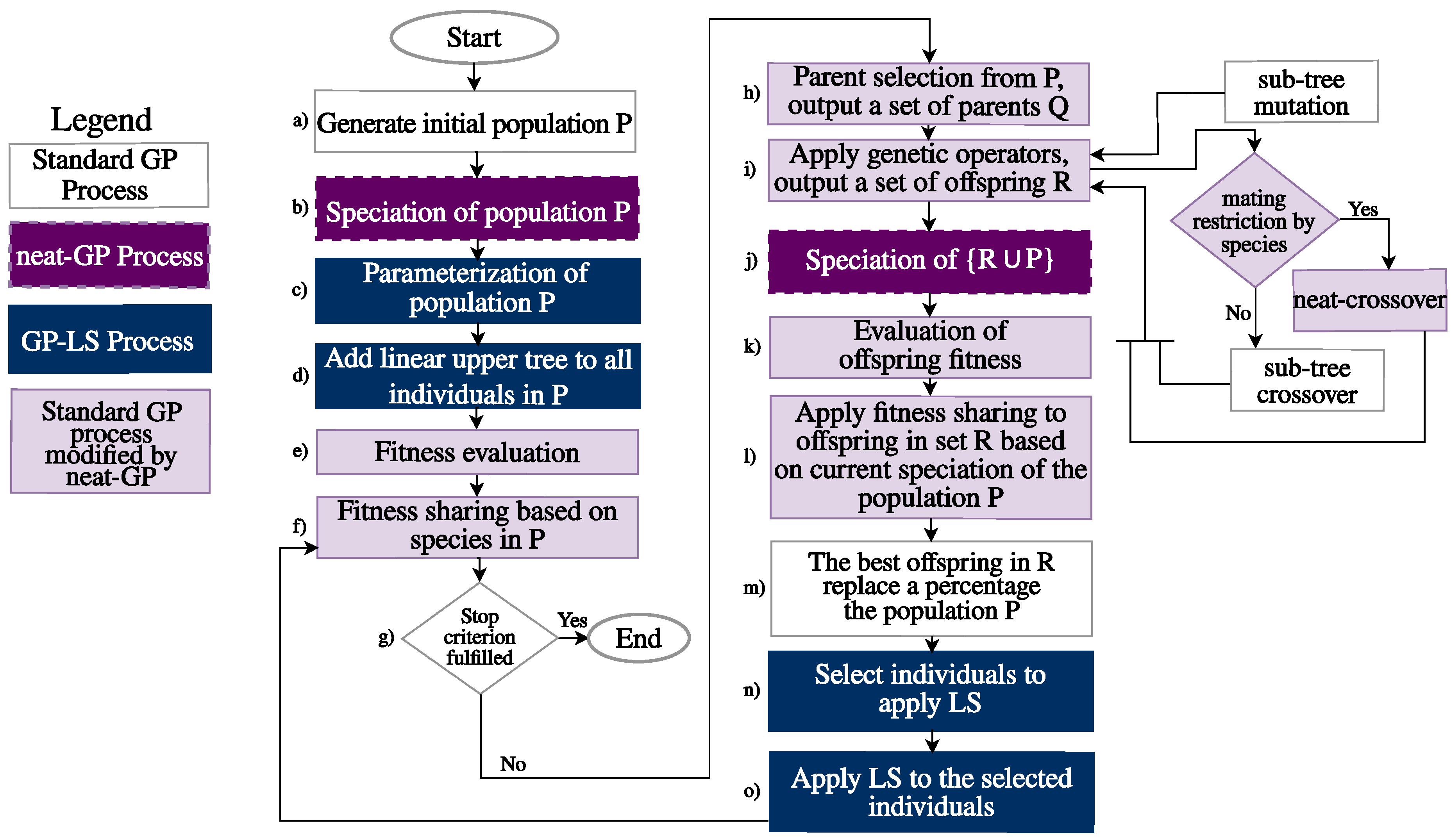
2.1. neat-GP
2.2. Local Search in Genetic Programming
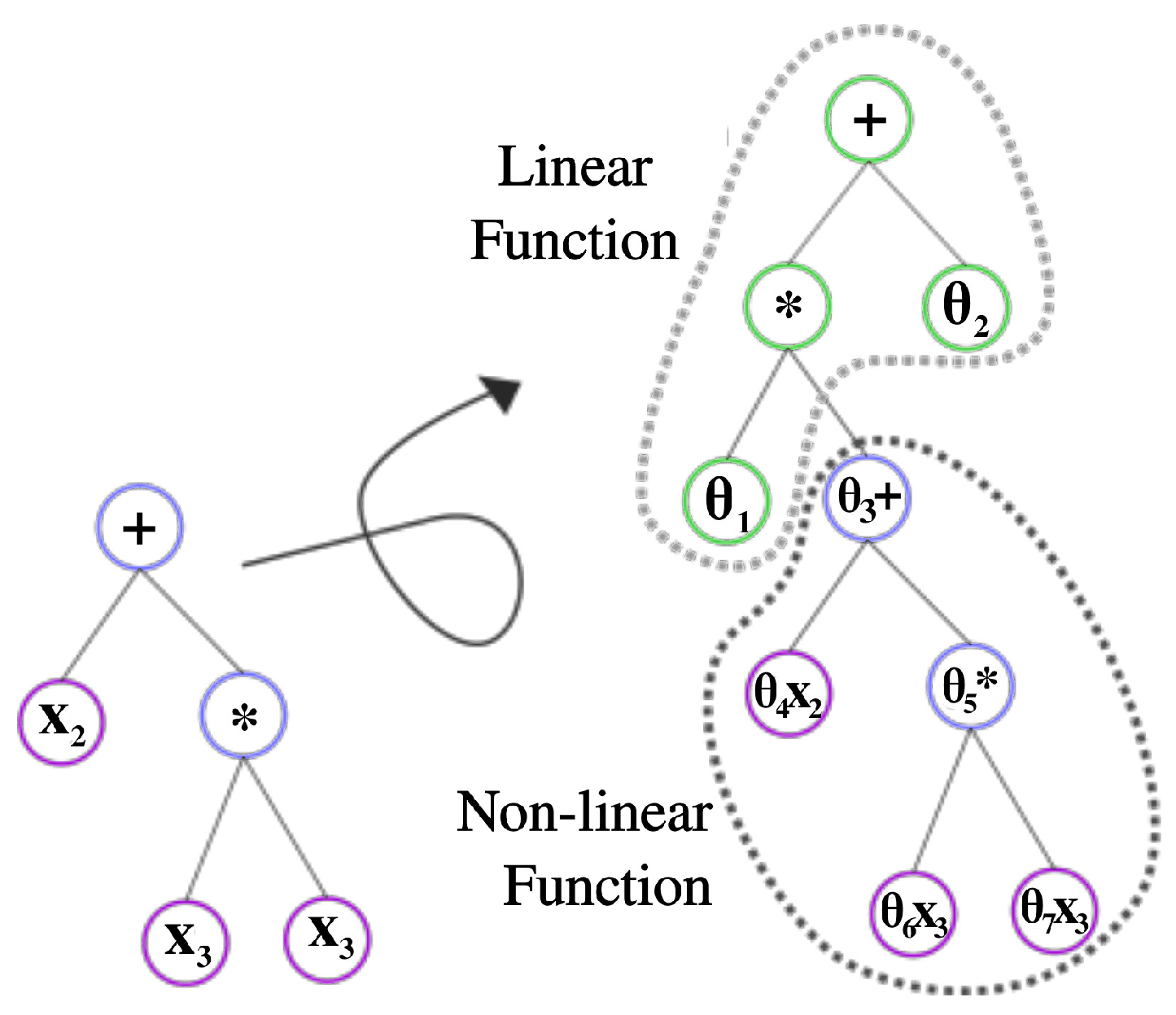
2.3. Integration LS into neat-GP
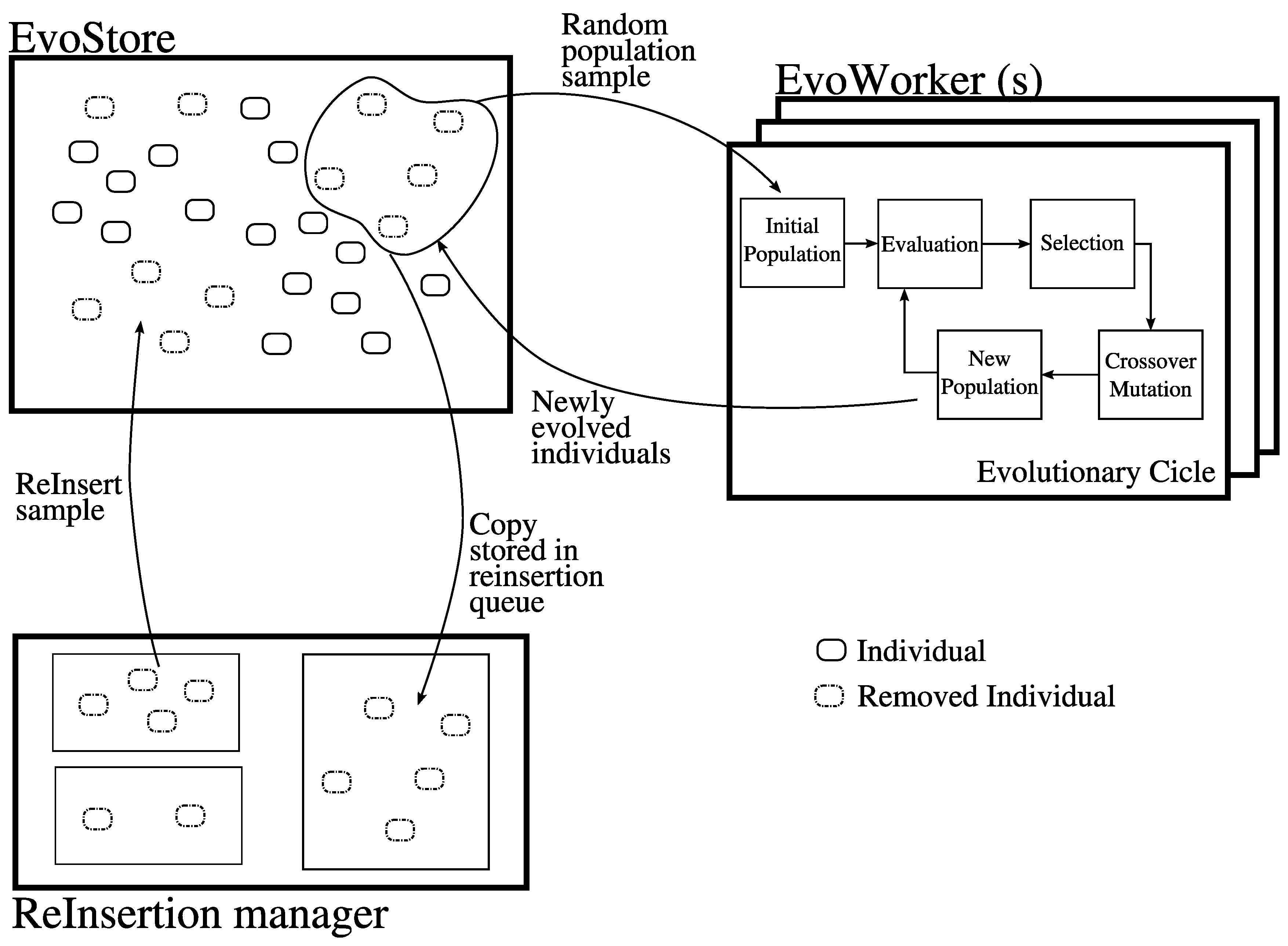
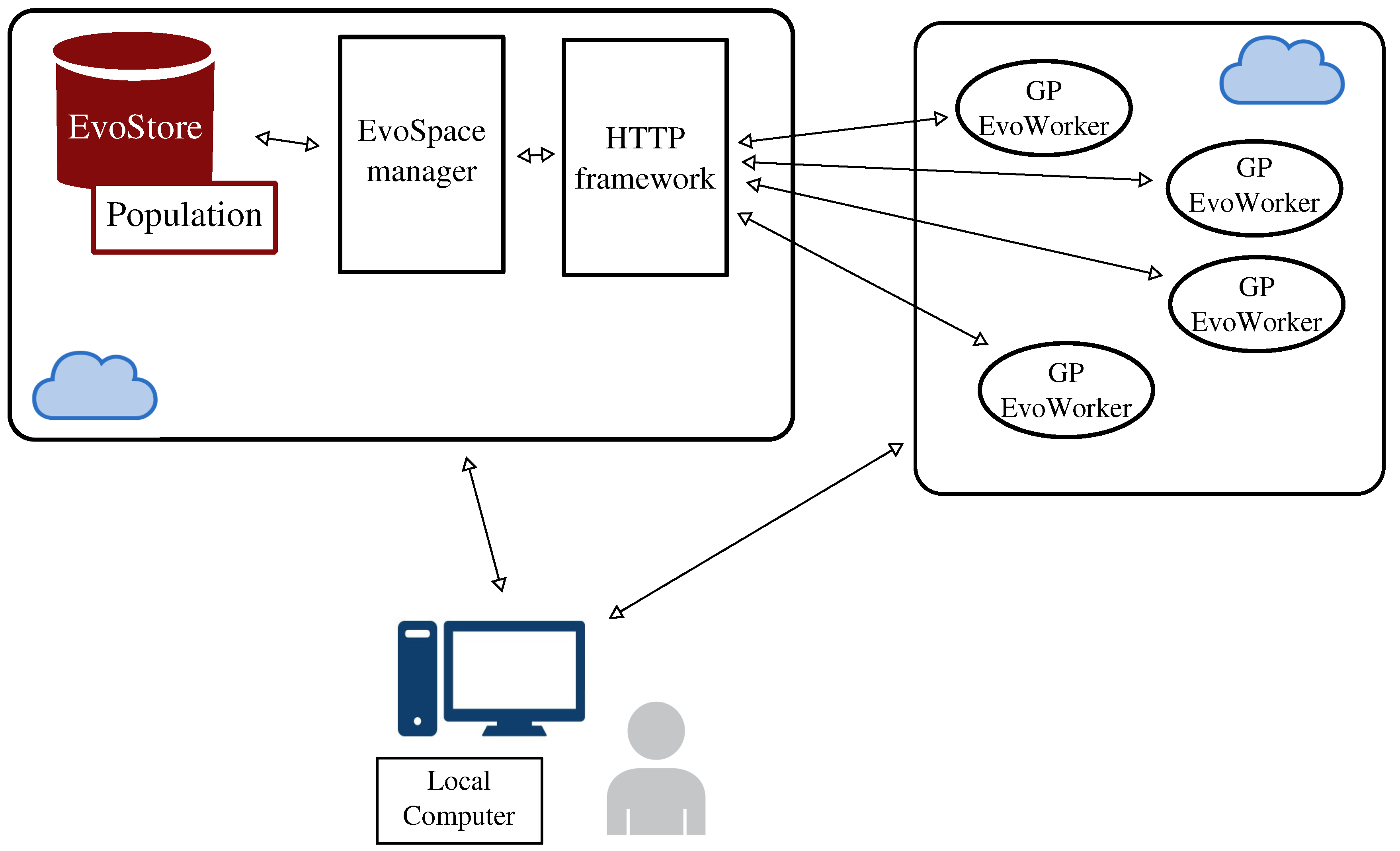
2.4. EvoSpace
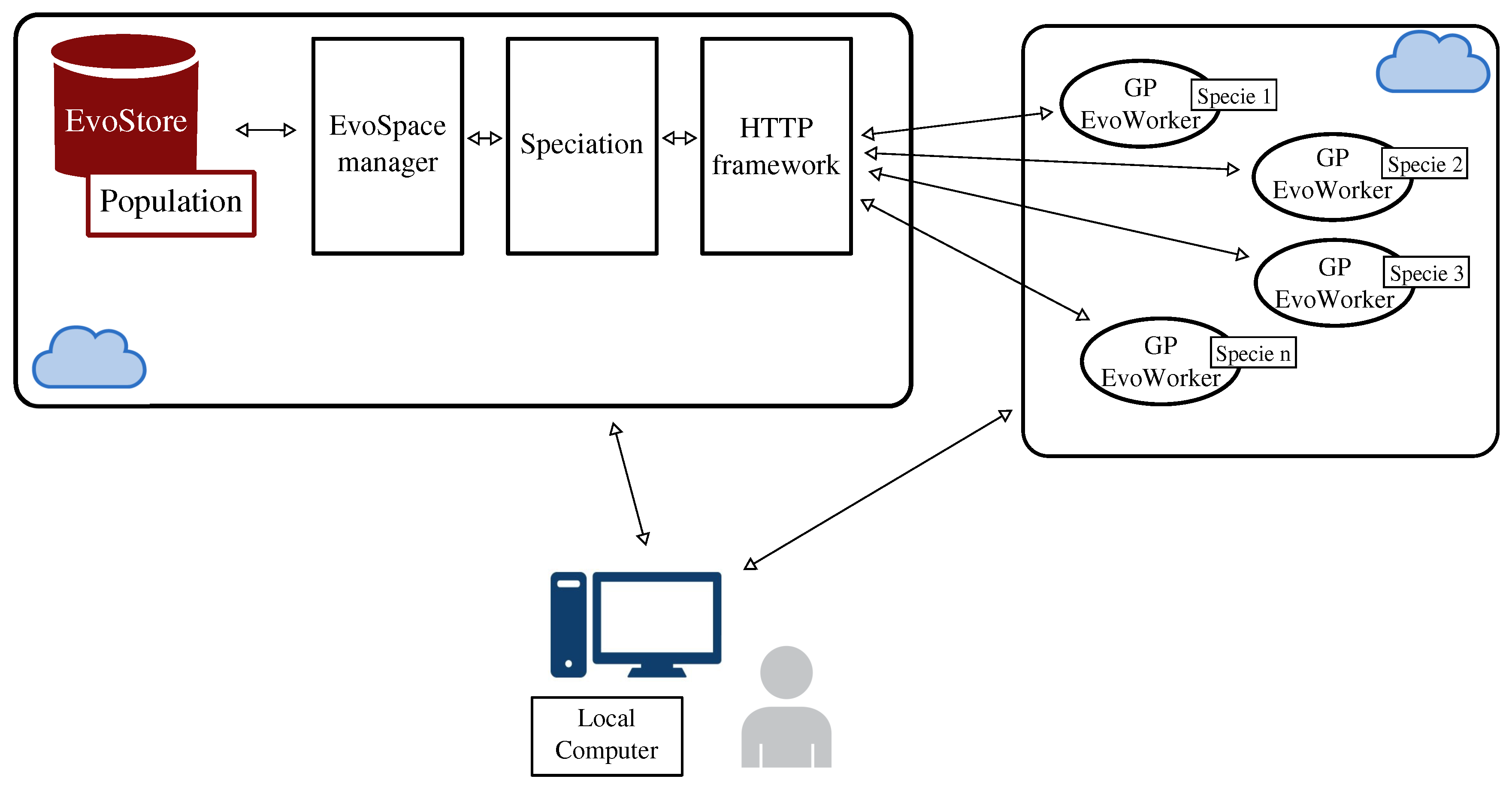
3. Distributing neat-GP-LS into the EvoSpace Model
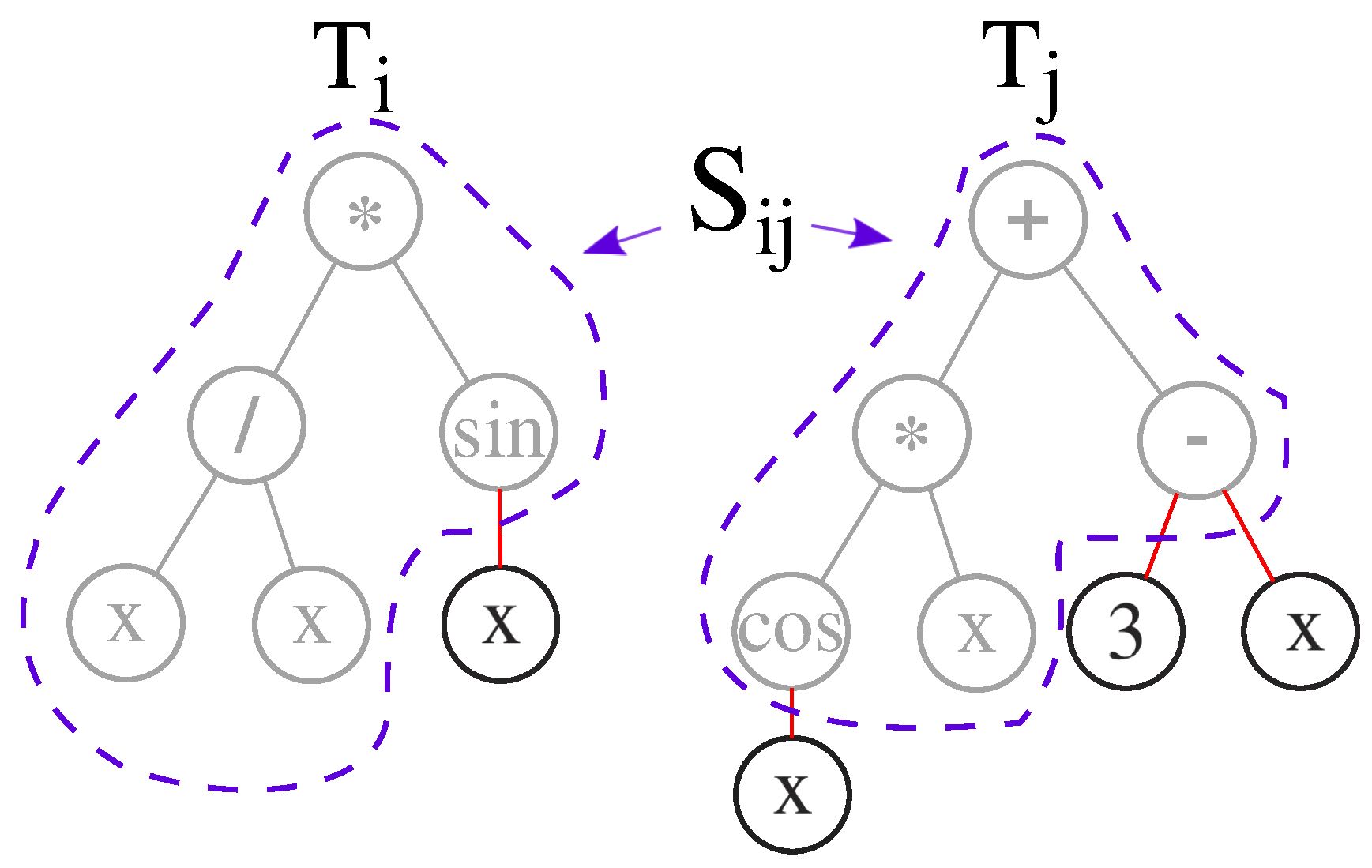
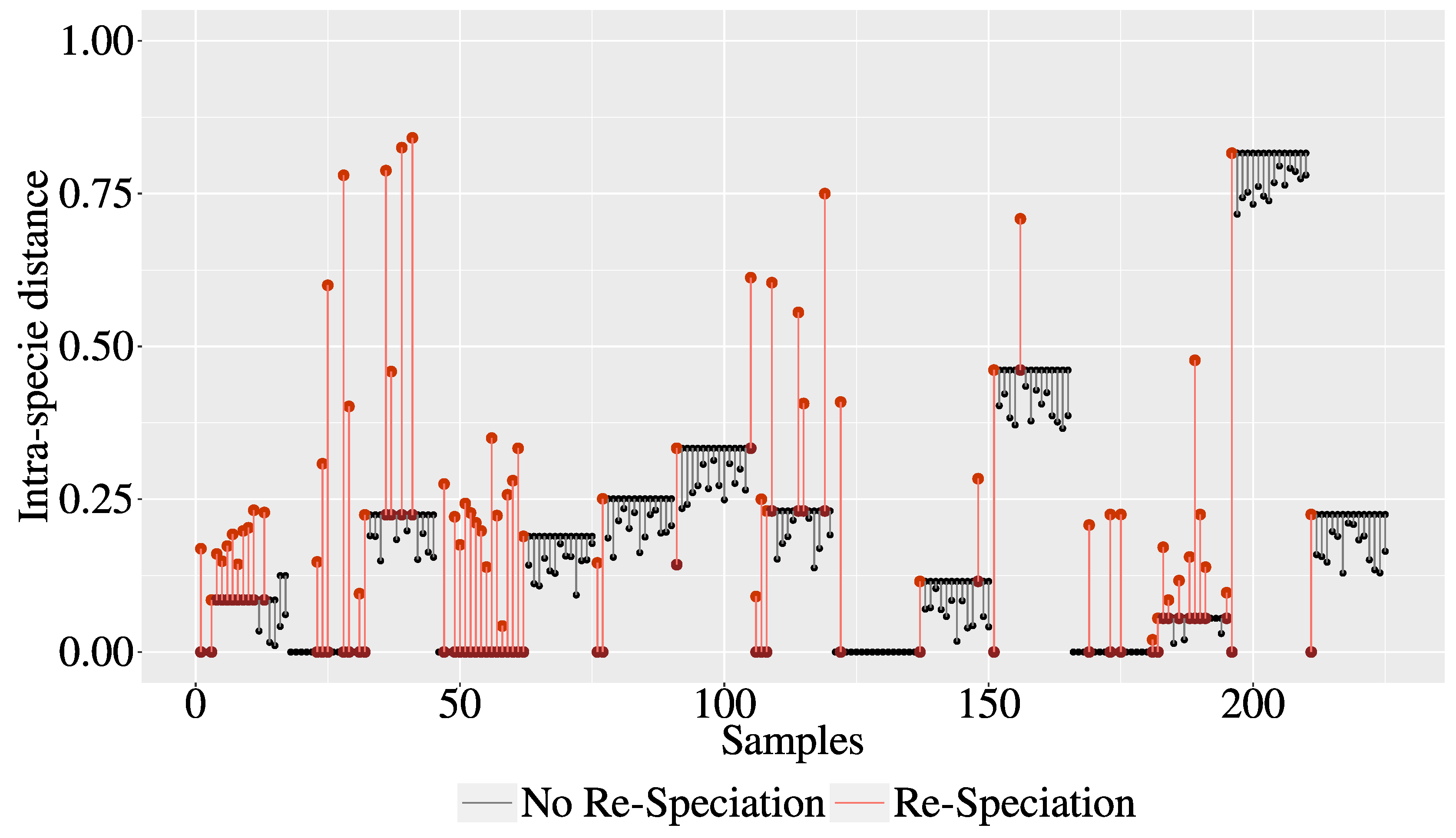
3.1. The Intra-Species Distance and Re-Speciation
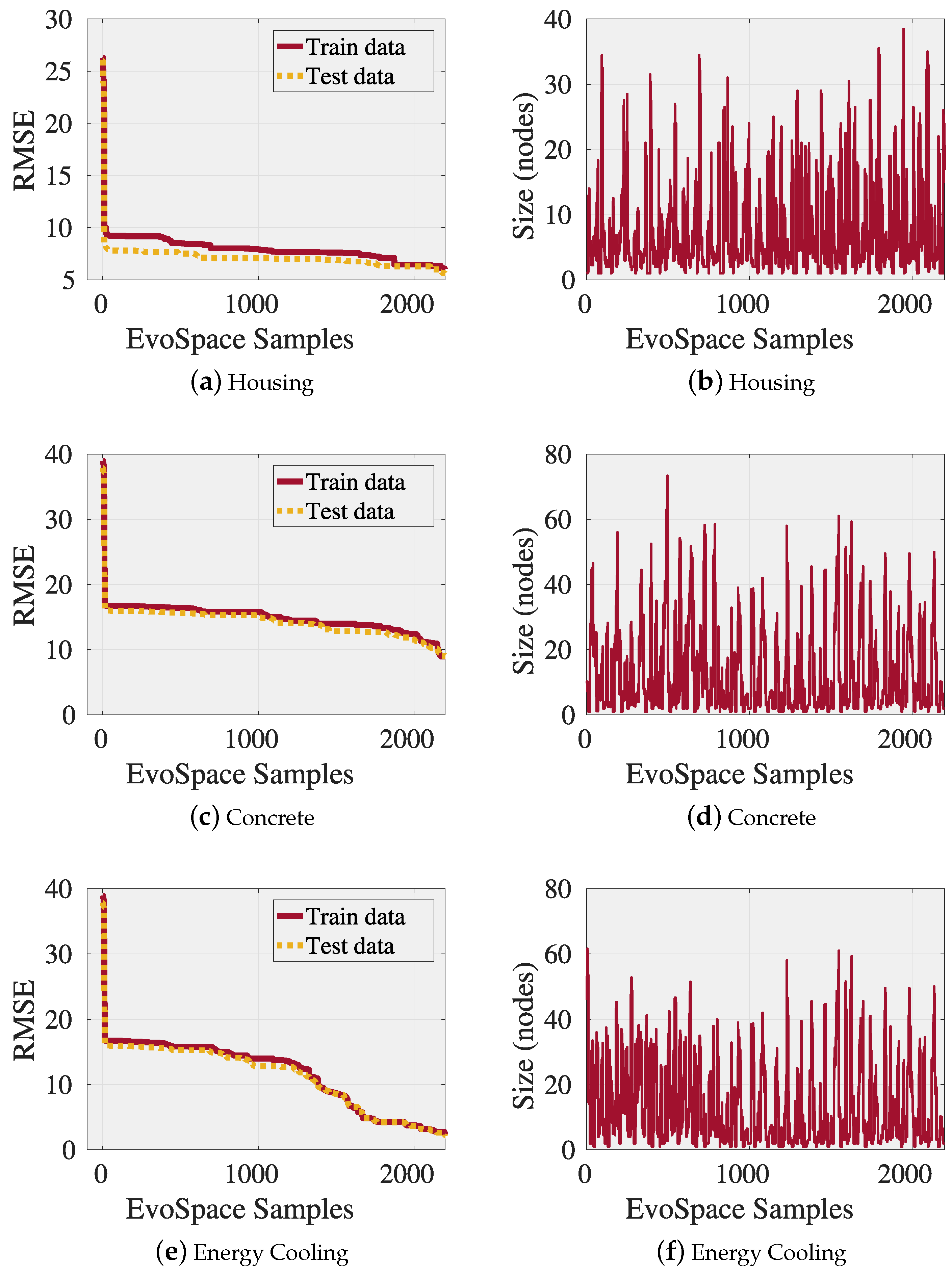
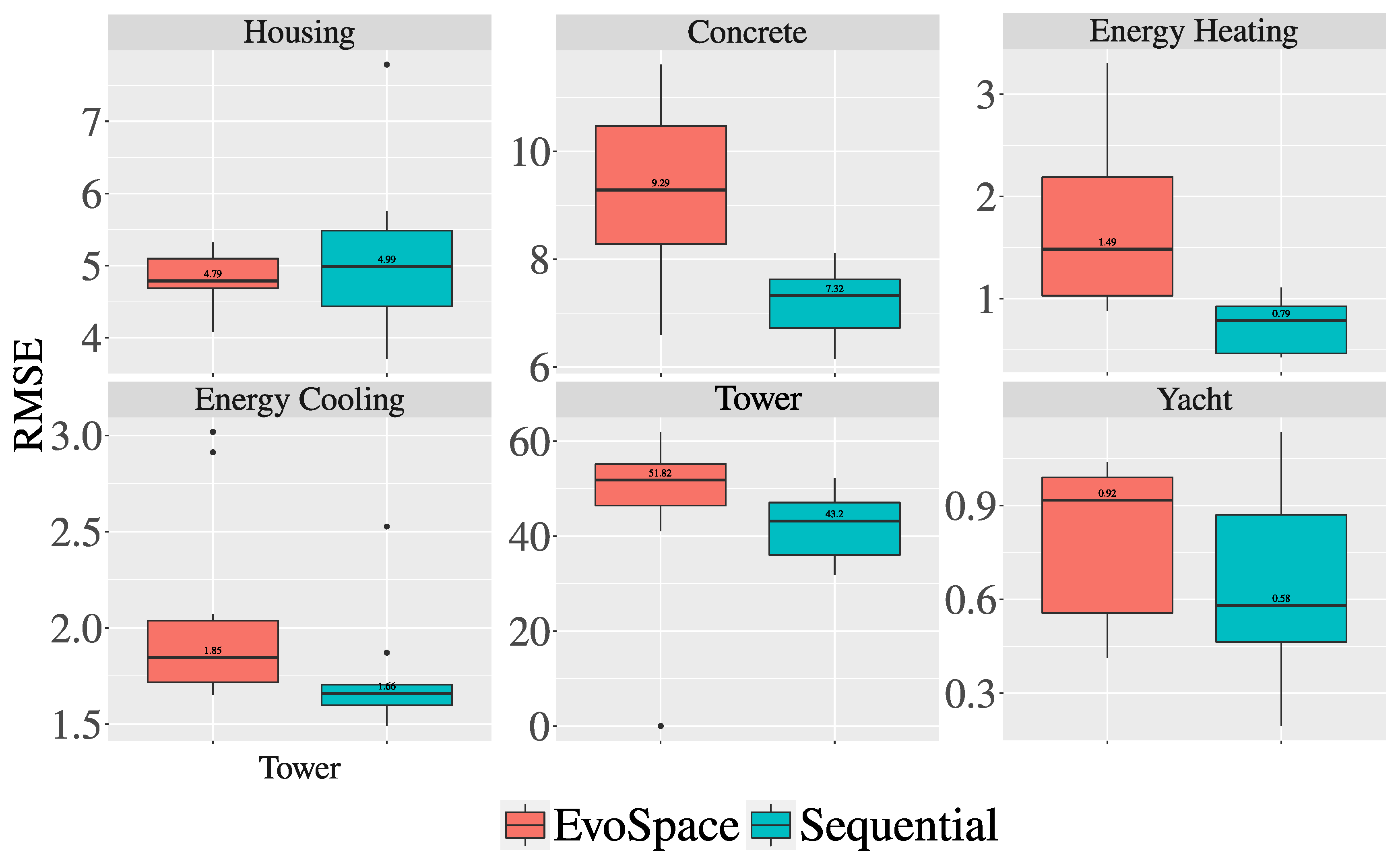
3.2. Experiments and Results
4. Conclusions and Future Work
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Juárez-Smith, P.; Trujillo, L.; García-Valdez, M.; Fernández de Vega, F.; Chávez, F. Local search in speciation-based bloat control for genetic programming. Genet. Program. Evolvable Mach. 2019. [Google Scholar] [CrossRef]
- Langdon, W.B. A Many Threaded CUDA Interpreter for Genetic Programming. In Proceedings of the 13th European Conference on Genetic Programming (EuroGP 2010), Istanbul, Turkey, 7–9 April 2010; pp. 146–158. [Google Scholar]
- Gong, Y.J.; Chen, W.N.; Zhan, Z.H.; Zhang, J.; Li, Y.; Zhang, Q.; Li, J.J. Distributed Evolutionary Algorithms and Their Models. Appl. Soft Comput. 2015, 34, 286–300. [Google Scholar] [CrossRef]
- Kshemkalyani, A.; Singhal, M. Distributed Computing: Principles, Algorithms, and Systems, 1st ed.; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Gebali, F. Algorithms and Parallel Computing, 1st ed.; Wiley Publishing: Hoboken, NJ, USA, 2011. [Google Scholar]
- Goribar-Jimenez, C.; Maldonado, Y.; Trujillo, L.; Castelli, M.; Gonçalves, I.; Vanneschi, L. Towards the development of a complete GP system on an FPGA using geometric semantic operators. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; pp. 1932–1939. [Google Scholar]
- García-Valdez, M.; Trujillo, L.; Fernández de Vega, F.; Merelo Guervós, J.J.; Olague, G. EvoSpace: A Distributed Evolutionary Platform Based on the Tuple Space Model. In Proceedings of the 16th European Conference on Applications of Evolutionary Computation, Vienna, Austria, 3–5 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 499–508. [Google Scholar]
- García-Valdez, M.; Trujillo, L.; Merelo, J.J.; Fernández de Vega, F.; Olague, G. The EvoSpace Model for Pool-Based Evolutionary Algorithms. J. Grid Comput. 2015, 13, 329–349. [Google Scholar] [CrossRef]
- García-Valdez, M.; Mancilla, A.; Trujillo, L.; Merelo, J.J.; de Vega, F.F. Is there a free lunch for cloud-based evolutionary algorithms? In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1255–1262. [Google Scholar]
- Trujillo, L.; García-Valdez, M.; de Vega, F.F.; Merelo, J.J. Fireworks: Evolutionary art project based on EvoSpace-interactive. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2871–2878. [Google Scholar]
- Trujillo, L.; Muñoz, L.; Galván-López, E.; Silva, S. neat Genetic Programming: Controlling bloat naturally. Inf. Sci. 2016, 333, 21–43. [Google Scholar] [CrossRef]
- Z-Flores, E.; Trujillo, L.; Schütze, O.; Legrand, P. Evaluating the Effects of Local Search in Genetic Programming. In EVOLVE—A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation V; Springer International Publishing: Cham, Switzerland, 2014; pp. 213–228. [Google Scholar]
- Z-Flores, E.; Trujillo, L.; Schütze, O.; Legrand, P. A Local Search Approach to Genetic Programming for Binary Classification. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation (GECCO ’15), Madrid, Spain, 11–15 July 2015; pp. 1151–1158. [Google Scholar]
- Sorensen, D. Newton’s Method with a Model Trust Region Modification. SIAM J. Numer. Anal. 1982, 16. [Google Scholar] [CrossRef]
- Z-Flores, E.; Abatal, M.; Bassam, A.; Trujillo, L.; Juárez-Smith, P.; Hamzaoui, Y.E. Modeling the adsorption of phenols and nitrophenols by activated carbon using genetic programming. J. Clean. Prod. 2017, 161, 860–870. [Google Scholar] [CrossRef]
- Enríquez-Zárate, J.; Trujillo, L.; de Lara, S.; Castelli, M.; Z-Flores, E.; Muñoz, L.; Popovič, A. Automatic modeling of a gas turbine using genetic programming: An experimental study. Appl. Soft Comput. 2017, 50, 212–222. [Google Scholar] [CrossRef]
- Dignum, S.; Poli, R. Operator Equalisation and Bloat Free GP. In Proceedings of the 11th European Conference on Genetic Programming (EuroGP 2008), Naples, Italy, 26–28 March 2008; pp. 110–121. [Google Scholar]
- Silva, S. Reassembling Operator Equalisation: A Secret Revealed. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation (GECCO ’11), Dublin, Ireland, 12–16 July 2011; pp. 1395–1402. [Google Scholar]
- Stanley, K.O.; Miikkulainen, R. Evolving Neural Networks Through Augmenting Topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
- Kommenda, M.; Kronberger, G.; Winkler, S.M.; Affenzeller, M.; Wagner, S. Effects of constant optimization by nonlinear least squares minimization in symbolic regression. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ’13), Amsterdam, The Netherlands, 6–10 July 2013; pp. 1121–1128. [Google Scholar]
- Byrd, R.H.; Schnabel, R.B.; Shultz, G.A. A trust region algorithm for nonlinearly constrained optimization. SIAM J. Numer. Anal. 1987, 24, 1152–1170. [Google Scholar] [CrossRef]
- Quinlan, J.R. Combining Instance-Based and Model-Based Learning. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 June 1993; pp. 236–243. [Google Scholar]
- Yeh, I.C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Vladislavleva, E.J.; Smits, G.F.; den Hertog, D. Order of nonlinearity as a complexity measure for models generated by symbolic regression via pareto genetic programming. IEEE Trans. Evol. Comput. 2009, 13, 333–349. [Google Scholar] [CrossRef]
- Ortigosa, I.; Lopez, R.; Garcia, J. A neural networks approach to residuary resistance of sailing yachts prediction. Proc. Int. Conf. Mar. Eng. 2007, 2007, 250. [Google Scholar]

| Problems | No. Instances | No. Features | Description |
|---|---|---|---|
| Housing [23] | 506 | 14 | Concerns housing values in suburbs of Boston. |
| Concrete [24] | 1030 | 9 | The concrete compressive strength is a highly nonlinear function of age and ingredients. |
| Energy Heating [25] | 768 | 9 | This study looked into assessing the heating load requirements of buildings as a function of building parameters. |
| Energy Cooling [25] | 768 | 9 | This study looked into assessing the cooling load requirements of buildings as a function of building parameters. |
| Tower [26] | 5000 | 26 | An industrial data set of a gas chromatography measurement of the composition of a distillation tower. |
| Yacht [27] | 308 | 7 | Delft data set, used to predict the hydodynamic performance of sailing yachts from dimensions and velocity. |
| Parameter | neat-GP-LS |
|---|---|
| Runs | 30 |
| Population | 100 |
| Generations | 10 |
| Training set | 70% |
| Testing set | 30% |
| Operators Crossover (), Mutation () | =0.9, =0.1 |
| Tree initialization | Ramped Half-and-Half, maximum depth 6. |
| Function set | +,-,x,sin,cos,log,sqrt,tan,tanh, constants |
| Terminal set | Input variables and constants as indicated in each real-world problem. |
| Selection for reproduction | Eliminate the worst individuals of each species. |
| Elitism | Do not penalize the best individual of each species. |
| Species threshold value | with |
| Local optimization probability |
| test | size | |
| Problem | p-value | |
| Housing | 0.2733 | 0.0114 |
| Concrete | 0.0010 | 0.0010 |
| Energy Cooling | 0.0578 | 0.0285 |
| Energy Heating | 0.0114 | 1.000 |
| Tower | 0.0285 | 0.0114 |
| Yacht | 0.2059 | 0.0114 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juárez-Smith, P.; Trujillo, L.; García-Valdez, M.; Fernández de Vega, F.; Chávez, F. Pool-Based Genetic Programming Using Evospace, Local Search and Bloat Control. Math. Comput. Appl. 2019, 24, 78. https://doi.org/10.3390/mca24030078
Juárez-Smith P, Trujillo L, García-Valdez M, Fernández de Vega F, Chávez F. Pool-Based Genetic Programming Using Evospace, Local Search and Bloat Control. Mathematical and Computational Applications. 2019; 24(3):78. https://doi.org/10.3390/mca24030078
Chicago/Turabian StyleJuárez-Smith, Perla, Leonardo Trujillo, Mario García-Valdez, Francisco Fernández de Vega, and Francisco Chávez. 2019. "Pool-Based Genetic Programming Using Evospace, Local Search and Bloat Control" Mathematical and Computational Applications 24, no. 3: 78. https://doi.org/10.3390/mca24030078
APA StyleJuárez-Smith, P., Trujillo, L., García-Valdez, M., Fernández de Vega, F., & Chávez, F. (2019). Pool-Based Genetic Programming Using Evospace, Local Search and Bloat Control. Mathematical and Computational Applications, 24(3), 78. https://doi.org/10.3390/mca24030078






