Abstract
The objective of this research is to develop metaheuristic methods by using the differential evolution (DE) algorithm for solving the U-shaped assembly line balancing problem Type 1 (UALBP-1). The proposed DE algorithm is applied for balancing the lines (manufacturing a single product within a fixed given cycle time), where the aim is to minimize the number of workstations. After establishing the method, the results from previous research studies were compared with the results from this study. For the UALBP, two groups of benchmark problems were used for the experiments: (1) For the medium-sized UALBP (21–45 tasks), it was found that the DE algorithm DE/best/2 to Exponential Crossover 1 produced better solutions when compared to the other metaheuristic methods: it could generate 25 optimal solutions from a total of 25 instances, and the average time used for the calculation was 0.10 seconds/instance; (2) for the large-scale UALBP (75–297 tasks), it was found that the basic DE algorithm and improved differential evolution algorithm generated better solutions, and DE/best/2 to Exponential Crossover 1 generated the optimal solutions and achieved the minimum solution search time when compared to the other metaheuristic methods: it could generate 36 optimal solutions from a total of 62 instances, and the average time used for the calculation was 4.88 seconds/instance. From the comparison of the DE algorithms, it was found that the improved differential evolution algorithm generated optimal solutions with a better solution search time than the search time of the basic differential evolution algorithm. The basic and improved DE algorithm are the effective methods for balancing UALBP-1 when compared to the other metaheuristic methods.
1. Introduction
Nowadays, the degree of competition in many industries is very high. Therefore, organizations that respond quickly to changes in their customers’ needs, require less effort to control the storage of their inventory, and spend less time in production will certainly achieve business advantages over their competitors. Moreover, organizations need to show continuous improvement and development of their products’ values in order to respond to the needs of their customers by reducing costs and improving product quality during the production process. This has resulted in changes to the production system, such as the change from the push system to the pull system, which has reduced the volume of each batch size produced. The changes also include replacing the traditional production layout of straight lines with U-shaped production lines or U-lines. When compared to the traditional production layout of straight lines, it was found that using U-lines was more advantageous in terms of balanced production lines, improved worker visibility, better communications, fewer workstations, higher flexibility, shorter operation travel, and easier material handling, among other benefits. Relevant research studies on simple assembly line balancing using a single model and mixed model were first published in 1955, and the subject has been researched intensively since then. Meanwhile, research studies on U-shaped assembly line balancing have not received much interest from researchers, with few studies conducted. Therefore, there are many interesting areas under the topic of U-shaped assembly line balancing that require further research studies [1].
The assembly line balancing problem (ALBP) is considered a problem of the NP-hard class of combinatorial optimization problems [2], which are complicated to solve. If using mathematics with exact methods for finding optimal solutions, a lot of time will be spent on calculations and expenses, especially of large-scale problems with more variables and limitations. Hence, many heuristic methods for obtaining good solutions have been developed [3]. In the last 10 years, the development of the heuristic methods known as metaheuristic methods has been of great interest to many researchers because the methods were used to obtain results for the general assembly line balancing problem (GALBP) and simple assembly line balancing problem (SALBP) [4]. The assembly line balancing problem (ALBP) has come to be considered a classic problem that interests many researchers and research studies on this problem have been carried out since 1955. Many researchers have developed mathematics methods (exact methods) and heuristic methods, including metaheuristic methods. [5] A new hybrid GSA-GA algorithm is presented for the constraint nonlinear optimization problems with mixed variables. In it, firstly the solution of the algorithm is tuned up with the gravitational search algorithm and then each solution is upgraded with the genetic operators such as selection, crossover, and mutation [6]. The main objective of this paper is to present a hybrid technique named as a PSO-GA for solving the constrained optimization problems. In this algorithm, particle swarm optimization (PSO) operates in the direction of improving the vector while the genetic algorithm (GA) has been used for modifying the decision vectors using genetic operators. However, only a small number of metaheuristic methods have been developed for solving the problems discussed in this study. Therefore, it is of interest to develop metaheuristic methods for solving the ALBP and thus increase the chance of finding an effective solution of this problem [7]. The objective of this paper is to solve the reliability redundancy allocation problems of series parallel system under the various nonlinear resource constraints using the penalty guided based biogeography based optimization. In the same year, [8] The main goal of the present paper is to present a penalty based cuckoo search (CS) algorithm to get the optimal solution of reliability e redundancy allocation problems (RRAP) with nonlinear resource constraints.
Hence, this research is a study on U-shaped assembly line balancing for the manufacture of a single product with a given fixed cycle time (c), where the aim is to minimize the number of workstations (m). The U-line assembly line balancing problem type 1 (UALBP-1) was studied, and a new metaheuristic method was developed for finding the solution by using the differential evolution algorithm (DE) [9]. The aim of this new method is to generate good solutions or the optimal solutions to this classic problem.
The main contribution of this work includes: (1) background; (2) the assembly line balancing problem; and (3) objective of the work.
2. Literature Review
2.1. U-Shape Assembly Line Balancing by Using Other Metaheuristic Methods
The previous studies on the UALBP were reviewed and are summarized in this section. The first UALBP study in the literature was conducted in 1994 by [10]. In their study entitled “The U-line Line Balancing Problem”, the mathematical formulation of the problem established by using dynamic programming for the single-model U-line to minimize the number of stations, and the RPWT (ranked positional weight technique) for solving a large-sized UALBP (111 tasks), which contained problems derived from previous research studies. These problems were more complicated than traditional problems because the tasks could be placed from forward to backward, from backward to forward, or from both directions simultaneously according to a sequential flowchart. A year later, [11] developed three mathematical exact algorithms to solve the UALBP. The dynamic programming (DP) formulation was used in the first algorithm, and the other two were breadth-first and depth-first branch and bound (B&B) algorithms. The results of the calculation revealed that B&B was more effective than the DP-based algorithm, and breadth-first spent less time on calculation than depth-first, but depth-first could find the optimal solutions faster. Later, [12] conducted research entitled “The Mixed-Model U-line Balancing Problem” and developed a heuristic method for solving the mixed-model UALBP with a precedence graph of each batch size with 25 tasks. In the same year, [13] presented a formulation for Integer Programming (IP) for finding the optimal balance to solve the UALBP. This formulation solved the large-scale problems better than the traditional ones. Later, [14] proposed a DP formulation for solving problems of numerous U-lines with a maximum of 22 tasks. The objective was to assign the tasks to workstations in various ways, aiming to minimize the number of workstations and time wasting [15,16]. This integrated model was solved with a black hole optimization based algorithm. The quality of the heuristic solution was checked with special data sets. A year later, proposed a black hole optimization (BHO) based algorithm dealing with a multi objective supply chain model is presented. The sensitivity of the enhanced algorithm is tested with benchmark functions. Numerical results with different datasets demonstrate the efficiency of the proposed model and validate the usage of Industry 4.0 inventions in first mile and last mile (FMLM) delivery.
The principles proposed could be effective methods for ALB and Rebalancing the UALBP. Later, [17] developed a heuristic method for solving the UALBP with nine U-lines, where there were 18 tasks in each U-line with the same cycle time. The time between work and the time between U-lines were used in the consideration. A year later, [18] produced a thesis called “Incorporating Ergonomics Criteria into Assembly Line Balancing” and developed three heuristic methods: (1) multiple ranking heuristic, (2) combinatorial genetic algorithm (GA), and (3) problem-space GA. These methods were developed by employing the criteria for ergonomic designs (such as a reduction in cycle time and the loss of grip strength due to fatigue at workstations) for the consideration of solutions of the I-shaped and U-shaped line ALB in order to obtain the lowest values. Consequently, many industrial factories benefited from the results of the study in terms of both production and ergonomics. Later, [19] carried out a study entitled “ULINO: Optimally balancing U-shaped JIT assembly lines” by implementing a B&B method that was developed from the simple assembly line balancing optimization method (SALOME). The SALOME method, which had been previously used for solving straight-line problems, was used for solving U-line problems with 297 tasks. This new method was called ULINO (U-line optimizer). The method was based on depth-first branch and bound and dominance rules. The purpose was to minimize the number of workstations, cycle time, or both. In 2003, a method for obtaining the optimal solution of UALB with parallel stations was developed by using multiple lower bounding and a new heuristic method for finding the upper bounding. The results from the two developed methods were improved over the traditional methods.
A year later, [20] applied the genetic algorithm (GA), which had been used for solving the SALBP, for solving the UALBP-1. Then, the optimal solutions from previous studies were compared. The results from the study showed that the GA could generate the optimal solutions or nearest solutions in the very first rounds of the experiment. Later, [21] published “A Shortest Route Formulation of Simple U-Type Assembly Line Balancing Problem”, which applied the theory of the shortest route formulation. The theory was proposed by [22] for solving the SALBP. However, the principles of the theory were further developed to solve the UALBP. In addition, some examples of the calculations of this method were published in many research articles and, In the same year, [23] achieved the goal of developing an equation formulation for the UALBP that was based on the integer linear programming formulation developed for the UALBP, as well as an equation formulation for the SALBP. The principles were flexible, helping in decision making in the UALBP for cases with many conditions. In the same year, [24] carried out research called “The Stochastic U-line Balancing Problem: A Heuristic Procedure”. The authors explained the reason why the U-lines were popular: it was because the JIT (just-in-time) production system played a major role in production. Therefore, U-shaped assembly lines were replacing the traditional straight assembly lines. The issue that was emphasized as needing consideration in the UALBP was the unreliability of the task time due to workers and other factors with unpredictable timing.
The developed heuristic approach was divided into two parts: finding basic solutions and improving basic feasible solutions. The results of the calculation revealed the effectiveness of the method used. In another study, conducted by [25], simulated annealing (SA) was developed for solving the UALBP. This method is widely used at present. The aim of this method is to minimize the number of workstations (Type-I). The effectiveness of the principles was evaluated by a solution search for large-scale problems and by comparing the results with ULINO (U-Line optimizer), which was B&B based on the heuristic procedure. In addition, [26] the authors proposed recommendations for further research studies as follows: (1) SA methods should be used for more difficult problems, such as mixed-/multi-model lines, stochastic task time, and U-line with other characteristics; (2) the principles of other metaheuristic methods should be utilized for solving the UALBP; (3) exact methods for solving U-line problems at a large scale should be developed; (4) the principles of other metaheuristic methods should be used for solving problems of Type-II (min. c, given m). Since the study, many researchers have explored methods for solving the UALBP by developing GA metaheuristic methods. In [27], a GA was presented for solving the UALBP by using the Just-In-Time (JIT) approach for solving the UALBP. The results were better than those of the traditional approaches that were employed for solving the UALBP. Therefore, the GA was used for solving UALBP. The results from the verification showed that greater effectiveness was achieved. The criteria used for consideration were the number of workstations of assembly lines and the variation of the workloads. The results from the experiment showed that the proposed method was effective because the workstations were well grouped and the workload formats were improved.
Moreover, many researchers used metaheuristic methods for solving the UALBP. They proposed the ant colony system (ACS) algorithm for finding solutions and proposed four heuristic methods: the method of Kilbridge and Wester (K&W), ranked positional weight (RPW), maximum task time (Max. T. T.), and total maximum number of following tasks (Max. N.F.). The four methods were then compared to the metaheuristic method of ACS for finding solutions, and it was found that the ACS method generated better solutions than the four heuristic methods. Later, other researchers studying methods for solving the UALBP developed a heuristic method and metaheuristic method by using the max-min ant system (MMAS) of max. task time and min. task time, together with a local search method for solving the SALBP and UALBP. For the SALBP, a large-scale benchmark problem set with 45–111 tasks and the large-scale benchmark problem set of Lapierre’s Tabu Search (TS) with 297 tasks were tested. For solving the UALBP, experiments were conducted on the benchmark problem set using Max. RPW and the medium-sized UALBP with 21–45 tasks, and the benchmark problem set with some given information consisted of a large-scale problem with 75–297 tasks. From the results of the study, it was concluded that the developed Max-Min Ant system was the most efficient method when compared to the heuristic method and Max. RPW method. From the experiments, Min. task time generated the worst solution. When compared to other methods, and when there was a change that increased cycle time, the results showed that there was no effect on the capacity of the Max-Min Ant system for finding the solution. Therefore, it was concluded that the developed method was highly efficient. After that, other methods for solving the UALBP were researched by other researchers.
2.2. U-Shape Assembly Line Balancing by Using Differential Evolution Algorithm
Assembly line balancing (ALB) by using the differential evolution algorithm for solving the ALBP has been studied by many researchers. In [28], the differential evolution algorithm was studied and proposed for solving the SALBP from the benchmark problem (retrieved from http://www.assembly-line-balancing.de) with 7–111 tasks. The purpose was to find the minimum number of workstations with the condition that the time of each station must not exceed the production cycle time and the preceding conditions must be met. The results of the study revealed that the proposed method generated a good solution with a minimum search time. This generated an initial solution from the sampling of real numbers, and the solution was further optimized. Later, [29] carried out research by using the differential evolution (DE) algorithm for solving the SALPB-1. The proposed heuristic is composed of four main steps: (1) initialization, (2) mutation, (3) crossover, and (4) selection processes. In the study, the mutation and crossover processes were combined, and a new method was found. The computational results based on many tests using a set of standard instances showed that the proposed DE algorithm was very competitive for solving the SALPB-1.
2.3. Differential Evolution Algorithm for Solving Other Problems
Differential evolution (DE) algorithms have been used for solving other research problems which aim to generate solutions as follows. The mutation DE algorithm was used in [24] and involved the positions of the optimal vectors in the population of each batch and employed the crossover or recombination of positions which were exchanged between vectors through the comparison of the crossover rate (CR) with random positions. This method was found to be effective and, in 2011, [30] developed the DE algorithm for solving assignment problems by improving two main crucial parameters in the DE process: the weighting factor (F) and crossover rate (CR). The improved differential evolution (IDE) was used for allowing an adjustable F, and the CR changed in terms of taxonomy steps. The sample problems were compared with the solutions of opposition-based differential evolution (ODE) and adaptive differential evolution (JADE). The results revealed that the developed IDE generated better solutions than the other two methods in terms of cost reduction and increased performance in the system. A year later, [31] developed the Pareto Utility Discrete Differential Evolution (PUDDE) algorithm for handling operator allocation problems (OAP) in order to allocate jobs appropriately for the balance control of assembly lines when multiobjective functions and conditions were formulated, and a decision based on only a single objective cannot be made. The procedure, which included the discrete event simulation DES model, was used in the general simulation, and PUDDE was employed for solving OAPs by improving the operator condition in two ways: decreasing the number of operators or increasing the number of operators. The results from the experiment concluded that PUDDE could find the solutions effectively. However, this method was suitable for decreasing the number of operators. When compared to the traditional DE, the PUDDE algorithm had a much better performance when finding objectives of multi-assembly lines in the same problem.
From the literature and related research studies above, it can be concluded that the DE algorithm was the method able to find the optimal solutions for large-scale complicated problems within the possible solution area by using a short search time when compared to the other metaheuristic methods. It was reported by [32] that DE algorithms with an evolution algorithm procedure were a new technique for increasing the efficiency of and capacity for handling problems with nondifferentiable, nonlinear, and multimodal objective functions, particularly large-scale complicated problems. It was found that the speed of the solution search of DE was better than that of other methods. Therefore, the DE method can be used for solving the ALBP and increasing the efficiency of the solution search for the ALBP. Hence, DE was chosen for solving the UALBP-1 in the current study.
3. U-line Assembly Line Balancing Problem Pattern and Mathematical Model
Only the UALBP-1 was focused on in this study, and the details of the problem are as follows:
3.1. U-line Assembly Line Balancing Problem (UALBP)
The UALBP-1 can be divided into three problem versions which are similar to the divisions of the Simple Assembly Line Balancing Problem [10,19]:
- UALBP-1: Given the cycle time (c), minimize the number of stations (m);
- UALBP-2: Given the number of stations (m), minimize the cycle time (c).;
- UALBP-E: Maximize the line efficiency (E) for c and m being variable.
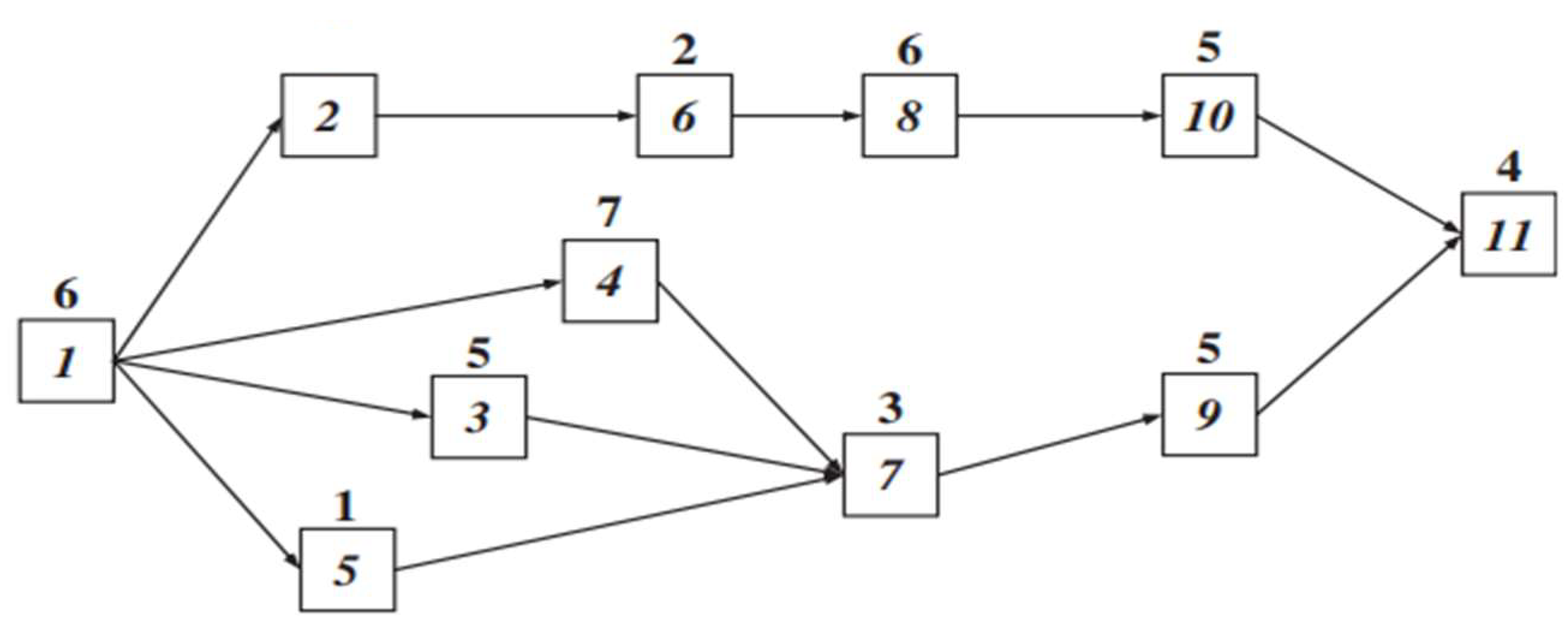
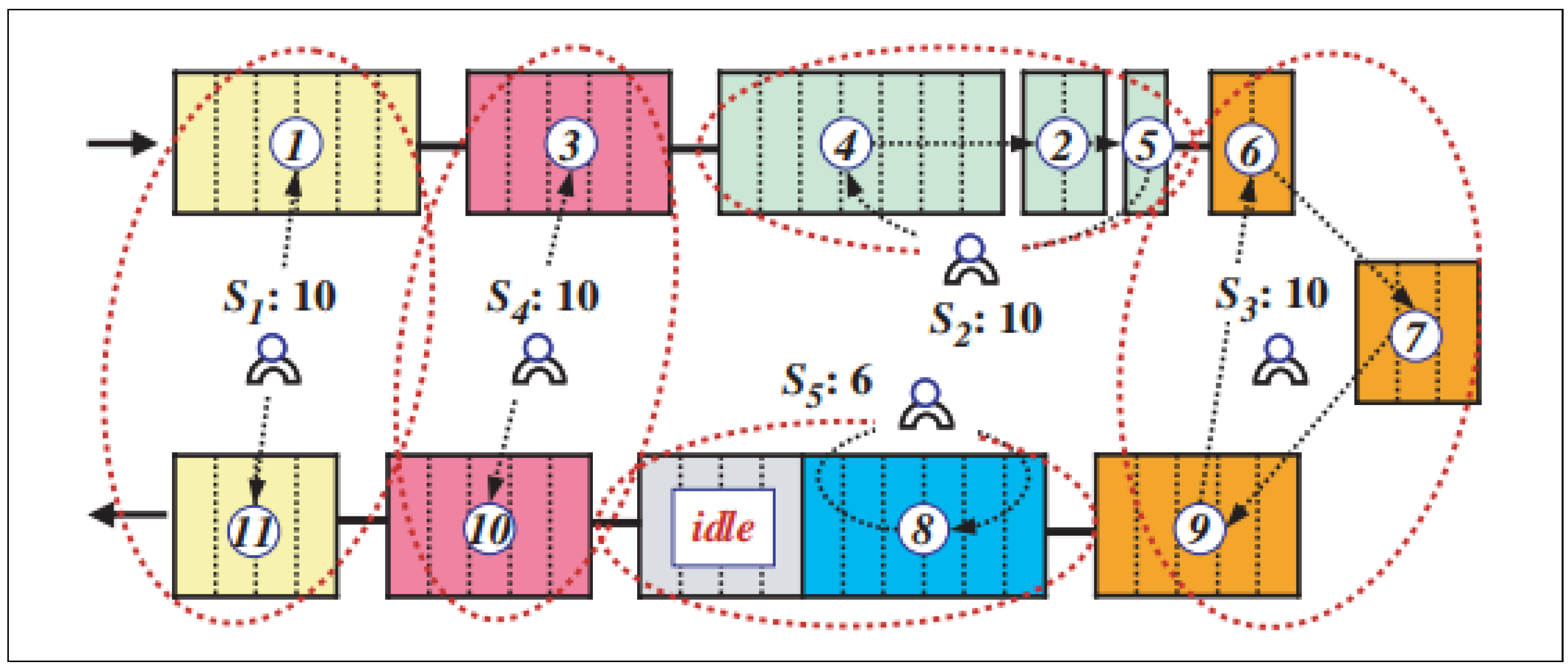
U-line Assembly Line Balancing Problem (UALBP) Pattern: The UALBP of each task can be located at only one station and is performed before its predecessor and after its successor tasks. The total time of each station cannot exceed more than the cycle time according to the conditions of the workstation assignment in the UALBP-1. The UALBP-1 can be explained using the benchmark problem called the Jackson Problem, shown in Figure 1, which is illustrated as a precedence diagram of the ALBP (11 tasks): the number inside each box represents the name of each task, and the number above each box represents the time of that task. When applying the example of Figure 1 to the UALBP, given c = 10, an optimal solution with m = 5 can be found, which is shown in Figure 2. The begging of process line balancing, the task 1 and task 11 are in station 1. It can generate a feasible line balance with a cycle time of c = 10 and with m = 5 stations given by the station loads S1 = {1, 11}, S2 = {2, 4, 5}, S3 = {6, 7, 9}, S4 = {3, 10}, and S5 = {8}. While no idle time occurs in stations 1, 2, 3, and 4, station 5 shows an idle time of 4.
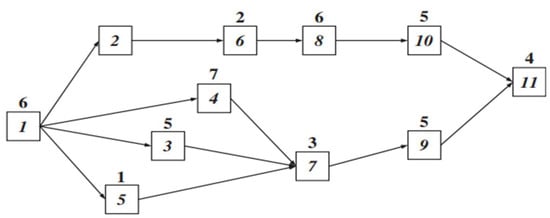
Figure 1.
Precedence diagram with assembly network [33].
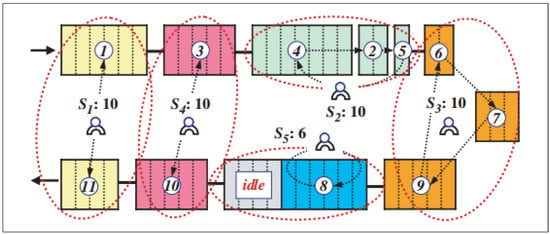
Figure 2.
Completed line assignments for the U-shaped assembly line.
3.2. Mathematical Model of the U-Shaped Assembly Line
This section presents the mathematical model for the UALBP-1, adapted from Bowman [34]. The indices, parameters, and decision variables are as defined below.
3.2.1. Indices
- n denotes the index of a task, where n = 1 …. N
- k denotes the index of workstation k, where k = 1 … M
- N denotes the total number of tasks
- M denotes the total number of workstations
3.2.2. Parameter
- Pn denotes the processing time of task n
- CT denotes the cycle time of a workstation
- Pnj denotes the relationship of task n to task j
3.2.3. Decision Variables
- Objective function:subject to
Equation (1) represents an objective function of the model to minimize the number of stations. Equation (2) guarantees that task n must be assigned to exactly one workstation. Equation (3) ensures that the precedence constraints are not violated on the U-line. Equation (4) ensures that the total processing time used by all tasks assigned to a particular workstation must not exceed a prespecified cycle time (CT). Finally, Equation (5) ensures that the station will be opened successively according to the station number.
4. General Differential Evolution Algorithm
4.1. Differential Evolution Algorithm
DE is a population-based random search method where an initial population of size N of D-dimensional vector is randomly generated, and a new population is generated through the cycles of calculations. A solution in DE algorithm is represented by D-dimensional vector, and each value in the D-dimensional space is represented as a real number. The key idea behind DE which makes the algorithm from other evolutionary algorithms (EAs) is its mechanisms for generating new solutions, called trial vectors, by mutation and crossover operation. In DE, each vector is served as a target vector which is then combined with other vectors in the population to form a new vector, called a mutant vector. Next, the mutant vector is crossover with its corresponding occurs only if the trial vector outperforms its corresponding target vector. The evolution process of DE population continues through repeated cycles of three main operator; mutation, crossover, and selection until some stopping criteria are met [30].
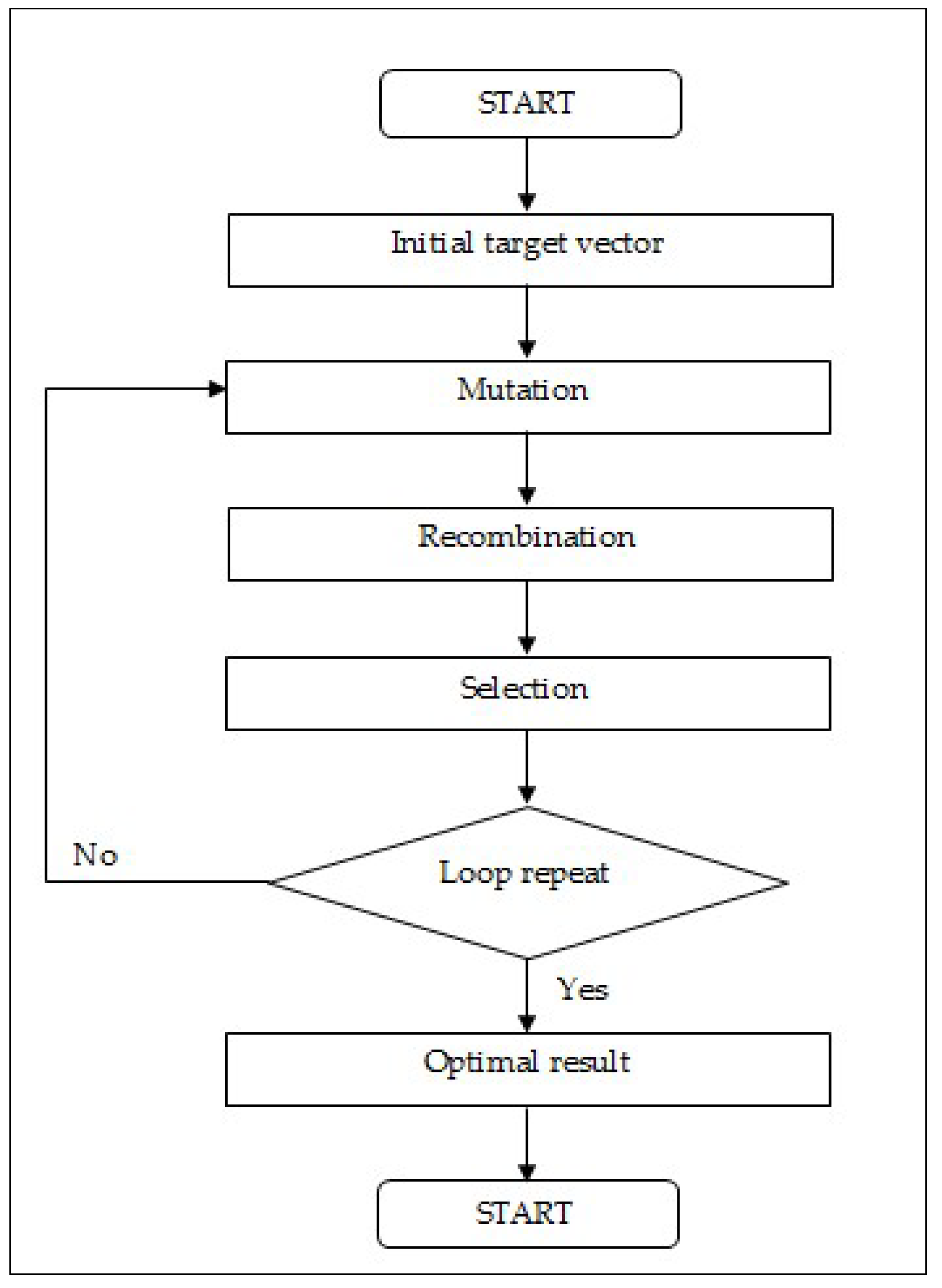
The general procedure of DE consists of several steps: (1) construct a set of initial target vectors, (2) perform a mutation process, (3) perform a recombination process, and (4) perform a selection process. The design of the procedure application is shown in Figure 3.
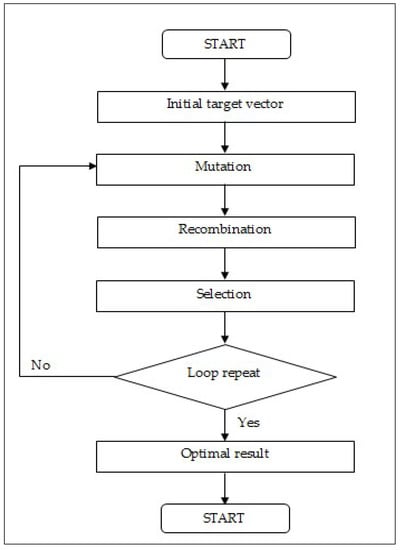
Figure 3.
General Differential Evolution Algorithm Procedure.
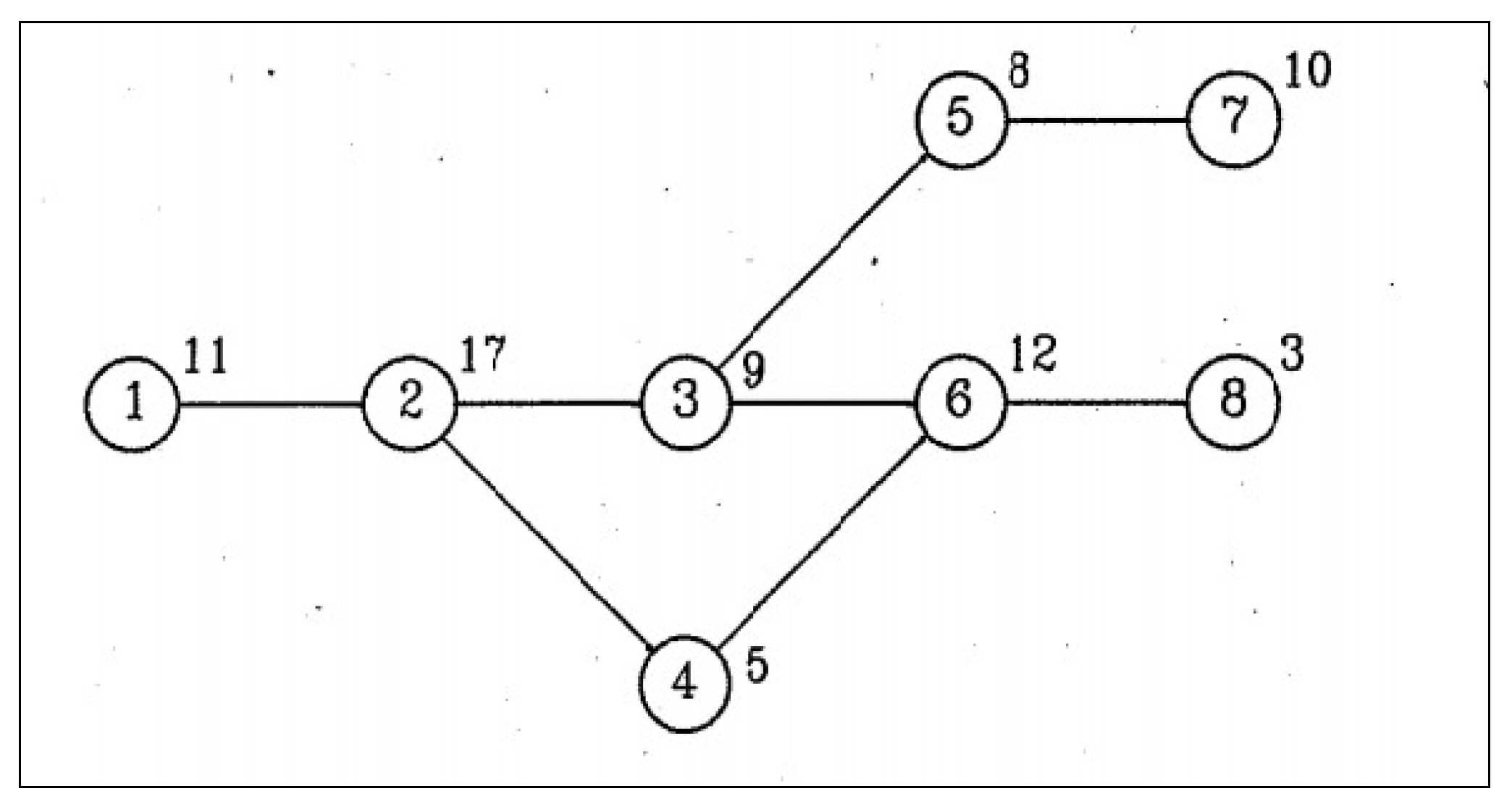
From the general differential evolution algorithm procedure in Figure 3, an initial vector is generated and the designed vector is further optimized by mutation, recombination, and selection processes. The procedure can be illustrated using the Bowman problem as an example, as shown in Figure 4.
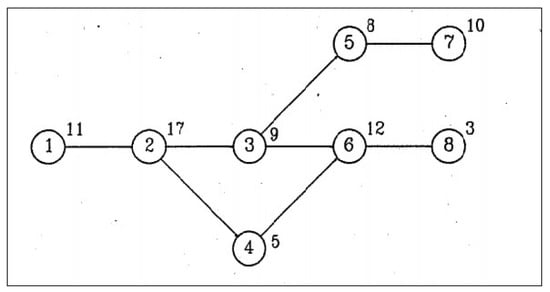
Figure 4.
Precedence Diagram of the Bowman Problem [34].
4.2. Procedure of UALB-1 by Using Differential Evolution Algorithm
The procedure of UALB-1 using the general differential evolution algorithm from the Bowman problem set in Figure 4, which presents the precedence diagram of the ALBP (8 tasks), can be interpreted as follows. The number in each circle represents the name of each task and the number above each circle represents the time of that task. Before balancing assembly lines, the values used in the calculation must be set. The variables are as follows: R = Round, NP = Numbers of tasks, F = Scaling factor, and CR = Crossover rate. In this problem’s calculation, these suitable variables were set from the experiment as R = 1, NP = 5, F = 0.8, CR = 0.8 [35], and CT (Cycle Time) = 20. The General Differential Evolution Algorithm “DE/rand/1” and binomial crossover were used in the calculation as follows.
4.2.1. Calculation Using the General Differential Evolution Algorithm DE/rand/1 and Binomial Crossover
(1) Initial population. In this step, a randomized real number between 0 and 1 for each task is obtained. This is the formulation of the target vector or initial solutions for the decision value in the workload allocation to the workstations, and the initial vector will be used further in Mutation and crossover, as shown in Table 1. In the table, the initial population calculation is presented by a randomized real number between 0 and 1 for each task. A target vector will be generated for each task in order to generate the initial solution and decision value in the workload allocation to the workstations. The workload allocation to the workstations must in line with the conditions of UALB by arranging the random numbers in ascending order for workstation allocation. From the table, NP = 5 vectors. The benchmark problem is illustrated in Figure 4, and it is described in Table 1.

Table 1.
Result of initial population NP = 5 vectors.
(2) Mutation. In this step, a position of the vector is mutated to obtain new solutions that differ from the initial population number by targeting the mutation. The calculation for the mutant vector (Vi,j,G+1) is shown in Equation (6), and an example of a mutation is illustrated in Table 2.
where:

Table 2.
Results of Mutation in Vector 1 by using DE/rand/1.
- Vi,j,G = Mutant Vector
- Xr1,j,G, Xr2,j,G, Xr3,j,G = Random vector from G round
- F = Scaling factor (random real number between 0 and 2)
The results of the mutation in Vector 1 by using “DE/rand/1” are depicted in Table 2.
Table 2 presents the results of Mutation in Vector 1 by using the DE/rand/1 method, where Xr1,j,G, Xr2,j,G, and Xr3,j,G are randomized to form Vectors 1, 2, and 3, respectively, and F = 0.8 is set so that at position 6, Xr1,j,G = 0.53, Xr2,j,G = 0.44, and Xr3,j,G = 0.62 substituted into the equation as Vi,j,G = Xr1,j,G + F(Xr2,j,G - Xr3,j,G) will be Vi,j,G = 0.53 + 0.8(0.44 − 0.62) = 0.39. Therefore, Mutant Vector 1’s position 6 is 0.39. After that, the calculation for every position is done until all eight positions are calculated.
(3) Crossover or Recombination. In this step, vector positions are exchanged. New vectors, both better and worse, are generated. The Trial Vector (Ui,j,G+1) is formulated, and the Trial Vectors are compared and exchanged as in Equation (7). The examples are presented in Table 3 and Table 4.
where:

Table 3.
Results of Binomial Crossover in Vector 1 with the DE/rand/1 Method.

Table 4.
The results of UALB by using the Trial Vector from Table 3.
- Vi,j,G = Mutant Vector
- Xi,j,G = Target Vector
- CR = Crossover Constant (real number in the range 0–1)
- rand j [0,1) = random real number between 0 and 1 in every position, j = 1, 2, 3, ..., G (G = number of position).
Table 3 shows the results of binomial crossover in Vector 1 if CR = 0.8; therefore, the value of the target vector will be used in the Trial Vector at positions 4 and 7. For other positions, the values of the mutant vector are used.
From Table 4, when employing the trial vector obtained for UALB according to the preceding conditions, the total time of each workstation must not exceed the production cycle time, which can be satisfied by considering a Trial Vector with low values before assigning the tasks to workstations. Therefore, a solution of 5 workstations is found.
(4) Selection. In this step, the next generation is selected (G + 1): only better solutions are selected by comparing the results of the Target Vector with the Trial Vector for cases in which the number of workstations of the Trial Vector is lower than/equal to that of the Target Vector. Therefore, the Trial Vector is selected as the next generation, as in Equation (8):
where:
- Ui,j,G = Trial Vector
- Xi,j,G+1 = Target Vector in the next generation, i = 1,2,...n
In sum, from the selection step for selecting the next generation, the Trial Vector of the 5 assigned workstations is found with the values higher than those of the Target Vector for 4 workstations. Therefore, the Target Vector is selected as the optimal solution, and the process is repeated for the next generation.
4.2.2. Procedure of UALB-1 by Using the Improved Differential Evolution Algorithm
(1) Improved DE. In mutation process, a mutant vector (Vi,j,G) will be calculated from one or more selected target vector (Xi,j,G). Traditionally, the mutation process of DE is performed using Equations (6) [30]. Improved DE was developed by applying the four Mutation Equations DE/best/1, DE/rand-to-best/1, DE/best/2, and DE/rand/2, as seen from Equations (9), (10), (11) and (12), respectively, as follows:
Let r1, r2, r3, r4, and r5 denote the vectors which are randomly selected from a set of target vectors j. represent the best vector found so far in the algorithm. F is a predefined integer parameter (scaling factor). In the proposed heuristics, F is set to 2; i is vector number which starts from 1 to NP, and j is position of a vector which run from 1 to D.
(2) Improved DE. The result of mutation process is a set of mutant vector Vi,j,G (i run from 1 to NP). Then a mutant vector will apply recombination equations (13) and (14) to yield trial vector (Ui,j,G) as a product of recombination processes. In traditional DE for UALBP–1, a binomial recombination Equations (7) is applied in the basic differential evolution algorithm [30]. Improved DE was developed by applying two crossover or recombination equations: Exponential Crossover 1 position and Exponential Crossover 2 position, as seen in Equations (13) and (14), as follows:
Let randbi, to be random number between 0 and 1, and CR is recombination probability which is the predefined parameters in the proposed heuristics. randbi, randbi,1 and randbi,2 are random integer numbers which are used to represent position of a vector and these random numbers ranges from 1 to D.
On the basis of the explanations in steps 1–4, the Improved Diff. is shown in Algorithm 1.
| Algorithm 1. Pseudo-code of the DE for (UALBP-1) |
| Setup initial DE parameter |
| Do while from first iteration to final iteration |
| Do while from first DE to final DE |
| Setup initial parameters: cycle time, remaining time, station number |
| Do while from first task to final task |
| Find start/following task with task time is less than or equal to |
| Remaining time, and proper precedence to data list |
| Input scaling factor, crossover rate and NP to data list |
| Select task randomly to list |
| Update remaining time/station number |
| Produce the four Mutation Equations |
| Developed by applying the two Crossover or Recombination Equations |
| Produce new target vector (selection\process) |
| End do |
| End do |
| Select best solution from all DE in the iteration |
| End do |
| Show/select best solution from all DE in all iteration |
5. Analysis of the Results from the Experiment on DE for Solving UALBP
The results obtained from the experiment on DE for solving the UALBP by using the basic DE algorithm and improved DE algorithm were analyzed. Six methods from the 15 methods for generating optimal solutions with the minimum search time were selected through the experiment. Then, the selected methods were compared. The results from the experiment were compared with other metaheuristic methods.
DE for solving the UALBP: the basic DE algorithm and improved DE algorithm consisted of six methods as follows:
- DE/rand/1 to Binomial Crossover (Basic)
- DE/rand/1 to Exponential Crossover 1 Position (improved)
- DE/rand/1 to Exponential Crossover 2 Position (improved)
- DE/ rand-to-best/1 to Binomial Crossover (improved)
- DE/Best/2 to Exponential Crossover 1 Position (improved)
- DE/Best/2 to Exponential Crossover 2 Position (improved)
The ALBP can be solved by applying the Java program (operated on a computer with Core i3, 2.3 GHz, 2 GB RAM, and the operating system Windows 7). The metaheuristic methods developed, including the Basic UALB and Improved UALB for solving the U-shaped Assembly Line Balancing Problem Type 1 (UALBP-1), used the data retrieved from http://www.assembly-line-balancing.de
The variables used in the calculation for ALB were defined as follows: R = Round, NP = Number of tasks, F = Scaling factor, and CR = Crossover rate. In this problem’s calculation, these variables were set at R = 30, NP = 30, F = 0.8, and CR = 0.8 [35]. Then, the experiment for finding the optimal solutions was conducted as follows.
1) The benchmark problems of Sawyer (30 tasks, 8 instances) and Arcus 1 (83 tasks, 16 instances) were used. The results of the experiment on the UALBP-1 by using the basic DE algorithm and improved DE algorithm are depicted in Table 5.

Table 5.
The results of the experiment on the UALBP-1 by using the basic DE algorithm and improved DE algorithm with the Sawyer and Arcus 1 problems.
From Table 5, the results from the experiment on the UALBP-1 by using the basic method and improved DE algorithm with the Sawyer and Arcus 1 problems show that all six DE algorithms generated the optimal solution of 24 instances from a total of 24 instances. The DE or DE/Best/2 Exponential Crossover 1 position was the best method to calculate the optimal solutions with the minimum average times (0.17 seconds).
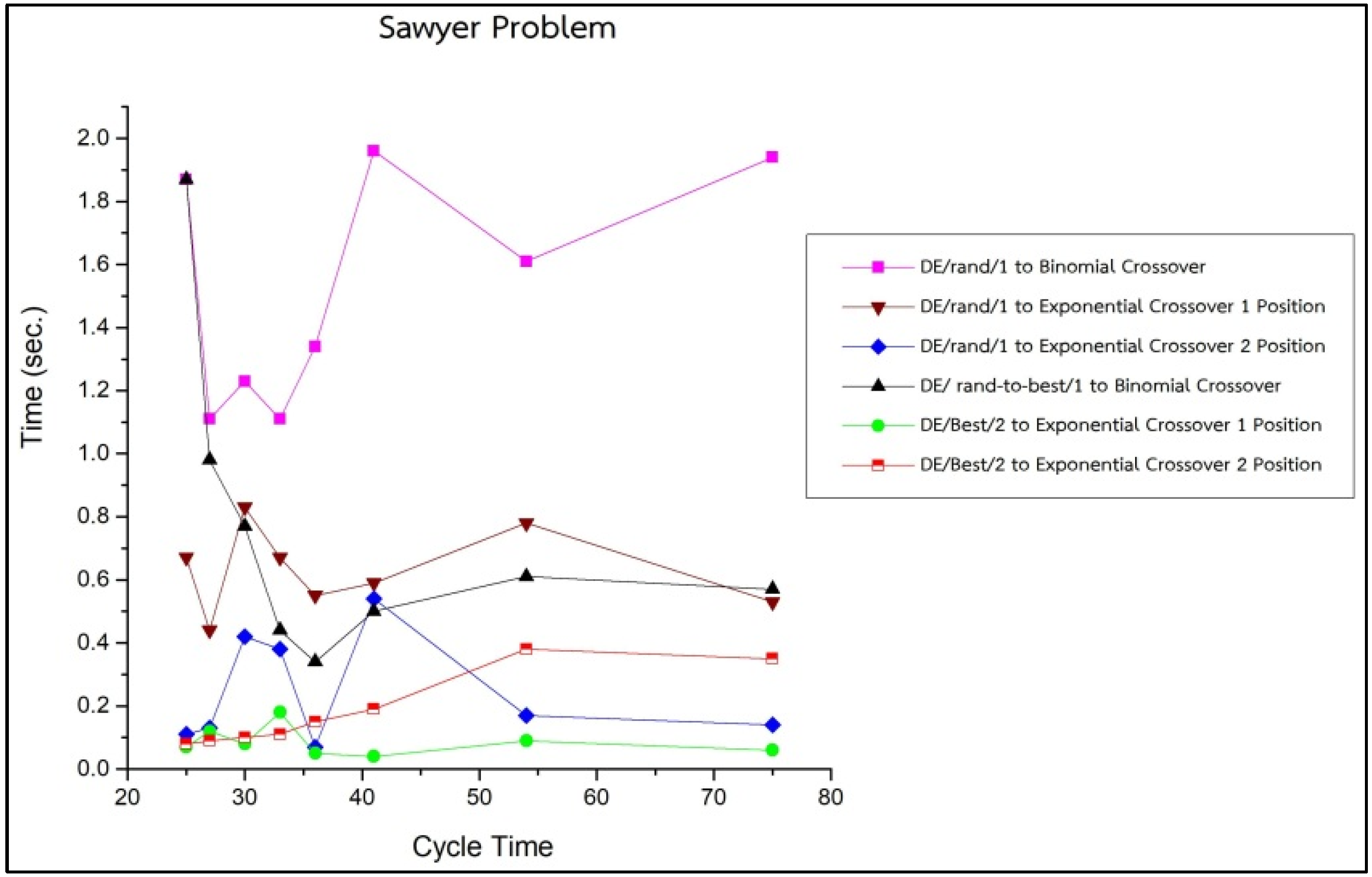
The comparison of the basic and improved DE algorithm using the optimal solution search time with the Sawyer problem (30 tasks, 8 instances) is shown in Figure 5.
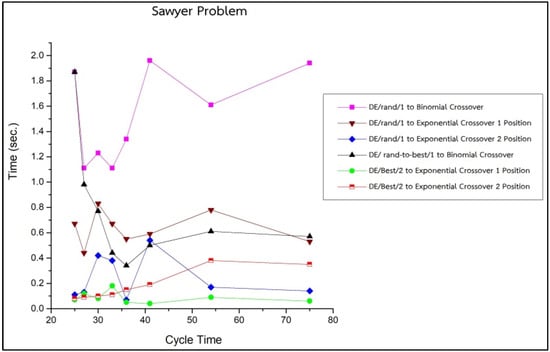
Figure 5.
Comparison of Basic and Improved DE Algorithm Using Optimal Solution Search Time with Sawyer Problem.
Figure 5 shows that the improved DE algorithm DE/Best/2 to Exponential Crossover 1 with the Sawyer problem (30 tasks, 8 instances) was the best method for generating the optimal solutions with the minimum solution search time when compared to the other DE methods, and the average optimal solution search time was 0.09 seconds. The comparison between the basic and improved DE algorithms in terms of optimal solution search time with the Arcus 1 problem (83 tasks, 16 instances) is presented in Figure 6.
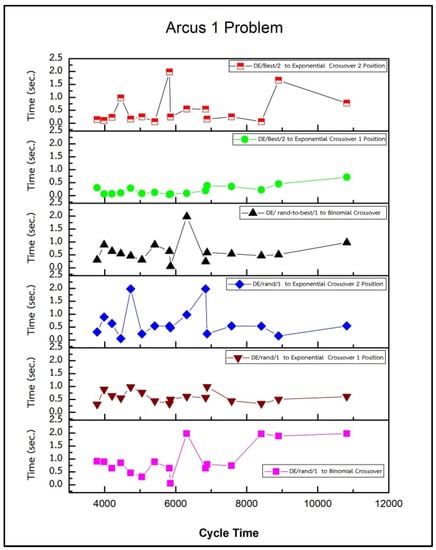
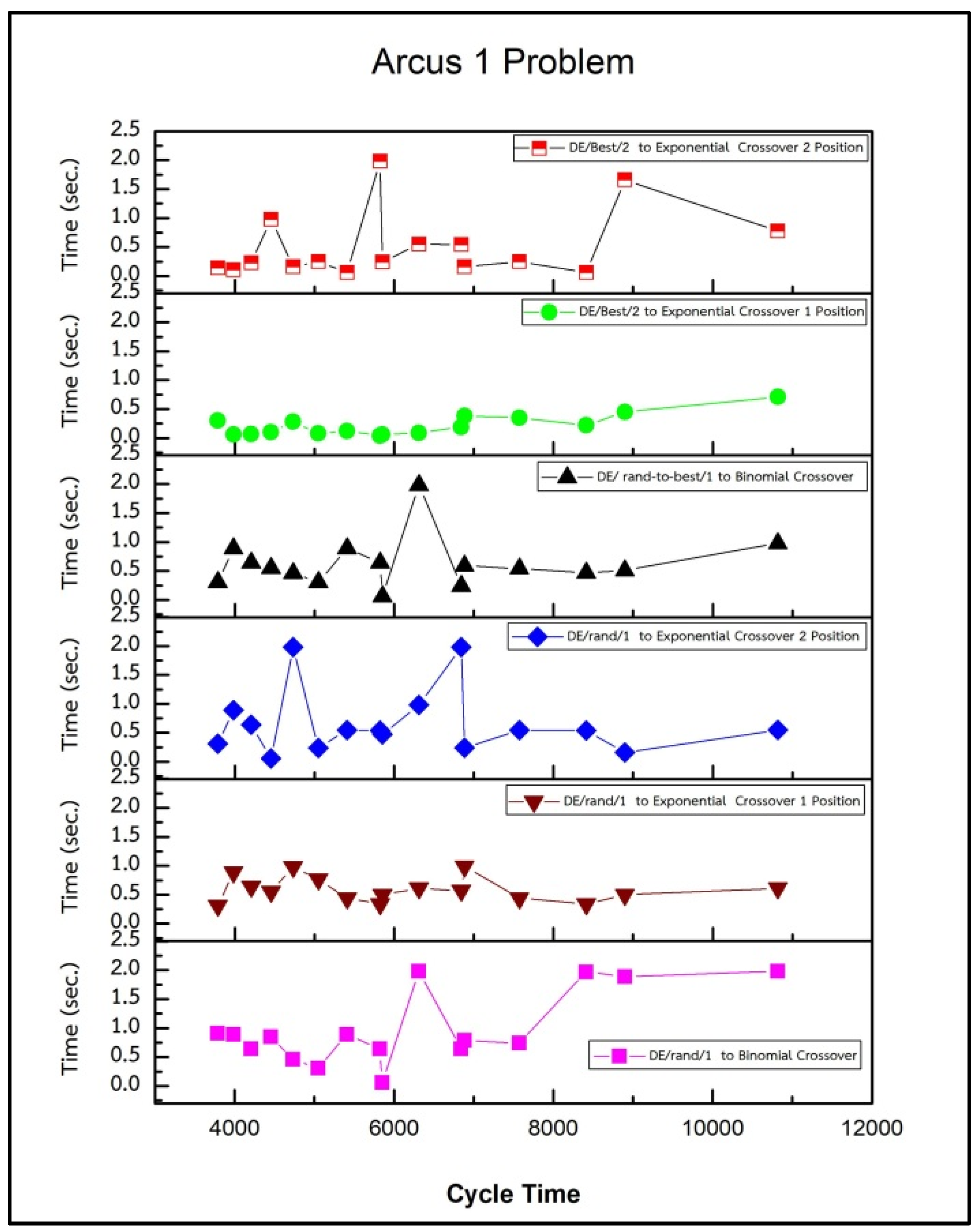
Figure 6.
Comparison of Basic and improved DE Algorithm Using Optimal Solution Search Time with Arcus 1 Problem.
From Figure 6, it is seen that the Improved DE algorithm DE/Best/2 to Exponential Crossover 1 was the best method for generating optimal solutions with the minimum solution search time when compared to the other DE methods. The average optimal solution search time was 0.22 seconds.
6. The Results from the Comparison of DE Algorithm and Other Metaheuristic Methods
From the experimental results, it can be seen that the DE algorithm DE/Best/2 to Exponential Crossover 1 was the method for the optimal solution search when finding the number of workstations and minimizing the solution search time. Therefore, the DE algorithm DE/Best/2 to Exponential Crossover 1 was compared with other metaheuristic methods in order to determine the efficiency of the optimal solution search. MMAS (no local search) was used for the comparison [36] with the benchmark problems of the medium-sized UALBP-1 (21–45 tasks), which is presented in Table 3, and of the large-scale UALBP-1 (75–297 tasks), which is presented in Table 6.

Table 6.
The Results of Using the Proposed DE Compared with Using MMAS (No Local Search) in UALBP-1 Benchmark Problems with the Medium-Sized UALBP-1 (21–45 tasks).
From Table 6, the experimental results of the ULAB benchmark problems with the medium-sized UALBP-1 (21–45 tasks) by using the DE algorithm DE/Best/2 to Exponential Crossover 1 with MMAS (no local search) (operated on a computer with Pentium 4, 3.0 GHz, 512 MB RAM, and the operating system Window XP) are presented. Four sets of the medium-sized UALBP (21–45 tasks) were tested: Mitchell’s, Heskiaoff’s, Sawyer’s, and Kilbridge and Wester’s problems, which were retrieved from http://www.assembly-line-balancing.de. Twenty-five instances resulted from calculating the minimum number of workstations, as depicted in the table. It was found that the DE algorithm DE/Best/2 to Exponential Crossover 1 can generate 25 optimal solutions from 25 instances. The method can find optimal solutions better than MMAS (no local search), which can generate 21 optimal solutions from 25 instances. The average solution search time of DE/Best/2 to Exponential Crossover 1 was 0.10 seconds, which is less than the solution search time of MMAS (no local search), which was 9.19 seconds.
Table 7 presents the experimental results of the ULAB benchmark problem with the large-scale UALBP-1 (75–297 tasks) by using the DE algorithm DE/Best/2 to Exponential Crossover 1 with MMAS (no local search) (operated on a computer with Pentium 4, 3.0 GHz, 512 MB RAM, and the operating system Window XP). Three sets of the large-scale UALBP (75–297 tasks) were used: Wee-mag’s, Arcus 1’s, and Scholl’s problems were used, and the problems were retrieved from http://www.assembly-line-balancing.de. Sixty-two instances resulted from calculating the minimum number of workstations, as presented in the Table. It was found that the DE algorithm DE/Best/2 to Exponential Crossover 1 can generate 36 optimal solutions from 62 instances. The method can find optimal solutions better than MMAS (no local search), which can generate 35 optimal solutions from 62 instances. The average solution search time of DE/Best/2 to Exponential Crossover 1 was 4.88 seconds, which is less than the solution search time of MMAS (no local search), which was 5.70 seconds.

Table 7.
The Results of Using the Proposed DE Compared to Using MMAS (No Local Search) [36] in UALBP-1 Benchmark Problems with the Large-Scale UALBP-1 (75–297 tasks).
7. Conclusions and Suggestions
Recently, the U-shaped line has been utilized in many production lines in place of the traditional straight-line configuration due to the use of the just-in-time principle. The shape of U-lines improves visibility and allows for the construction of stations containing tasks on both sides of the line. This arrangement, combined with cross-trained operators, provides greater flexibility in station construction than is available with a comparable straight production line. The UALBP and the DE algorithm of the metaheuristic for assigning tasks to stations are presented in this paper. The performance of the metaheuristic was applied to solve a large number of benchmark problems obtained from previously published research. The computational results indicate that one of the metaheuristic rules (DE algorithm) can be satisfied by the proposed algorithm, and the computational requirements are not high. This study has taken a step in the direction of finding good metaheuristic rules for solving the UALBP-1. For further research, it would be interesting to use other metaheuristics, (e.g., bee algorithm, particle swarm optimization, simulated annealing, etc.) and find more flexible solutions of the larger UALBP.
The improved DE algorithm DE/Best/2 to Exponential Crossover 1 was the most effective method with the minimum search time for finding optimal solutions, and the basic DE algorithm was the worst because it spent the maximum amount of time searching for optimal solutions when compared to the other DE methods. In the optimal solution search for the number of workstations, it was found that every method received the same answer when compared to the other DE methods.
The comparison of the method in this paper, UALBP-1 by using the DE algorithm, with other metaheuristic methods for the medium-sized UALBP (21–45 tasks) and large-scale UALBP (75–297 tasks) leads to the conclusion that the basic DE algorithm and the improved DE algorithm is better at generating optimal solutions in the search for workstations and spends less time searching for optimal solutions than MMAS (no local search).
Further studies should develop the DE algorithm methods with more difficult problems, such as the mixed-/multi-model line, stochastic task time, and U-lines with other characteristics, as well as develop other metaheuristic principles for solving the large-scale UALBP and develop the principles of other metaheuristic methods or other types of methods for solving the UALBP-2, i.e., given the number of stations (m), minimize the cycle time (Min. c, given m), and the UALBP-E, i.e., maximize the line efficiency (E) for c and m being variable (Max. E, given c, m).
In addition, the proposed DE algorithms in this study [37] can be applied to solve more realistic assembly line balancing problem in many industries; garment, automobile, electronical appliance; etc. for productivity improvement by minimizing the workstations and labor costs.
Author Contributions
P.S. designed the algorithm and validated of algorithm; N.K. and P.K. gathered data and validated of algorithm; K.C. summarized the computation and conclusion.
Acknowledgments
We would like to thank Industrial Engineering Department, Faculty of Engineering, Ubon Ratchathani University and Manufacturing Engineering Department, Faculty of Engineering, Mahasarakham University, for funding this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, S. Just-In-Time U-Shaped Assembly Line Balancing. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 2003. [Google Scholar]
- McMullen, P.; Frazier, G.V. Using Simulated Annealing to Solve a Multiobjective Assembly Line Balancing Problem with parallel workstations. Int. J. Prod. Res. 1998, 10, 2717–2741. [Google Scholar] [CrossRef]
- Suresh, G.; Sahu, S. Stochastic Assembly Line Balancing Using Simulated Annealing. Int. J. Prod. Res. 1994, 8, 1801–1810. [Google Scholar] [CrossRef]
- Kriengkorakot, N.; Pianthong, N. The Assembly Line Balancing Problem: Review Articles. KKU Eng. J. 2007, 34133–34140. [Google Scholar]
- Garg, H. A hybrid GSA-GA algorithm for constrained optimization problem. Int. Sci. 2019, 478, 499–523. [Google Scholar] [CrossRef]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problem. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Garg, H. An efficient biogeography based optimization algorithm for solving reliability optimization problems. Swarm Evolut. Comput. 2015, 24, 1–10. [Google Scholar] [CrossRef]
- Garg, H. An approach for solving constrained reliability-redundancy allocation problems using Cuckoo search algorithm. J. Appl. Sci. 2015, 4, 14–25. [Google Scholar] [CrossRef]
- Sethanan, K.; Pitakaso, R. Improved differential evolution algorithms for solving generalized assignment problem. Expert Syst. Appl. 2016, 45, 450–459. [Google Scholar] [CrossRef]
- Miltenburg, J.; Wijingaard, J. The U-line Line Balancing Problem. Memet. Sci. 1994, 40, 1378–1388. [Google Scholar] [CrossRef]
- Miltenburg, J.; Sparling, D. Optimal solution algorithms for the U-line balancing problem. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 1995. [Google Scholar]
- Sparling, D.; Miltenburg, J. The mixed-model U-line balancing problem. Int. J. Prod. Res. 1998, 36, 485–501. [Google Scholar] [CrossRef]
- Urban, T.L. Optimal Balancing of U-Shaped Assembly Lines. Memet. Sci. 1998, 44, 738–741. [Google Scholar] [CrossRef]
- Miltenburg, J. Balancing U-lines in a multiple U-line facility. Eur. J. Oper. Res. 1998, 15, 1–23. [Google Scholar] [CrossRef]
- Veres, P.; Banyai, T.; Illes, B. Optimization of In-Plant Production Supply with Black Hole Algorithm. Solid State Phenom. 2017, 261, 503–508. [Google Scholar] [CrossRef]
- Banyai, T.; Illes, B.; Banyai, A. Smart Scheduling: An Integrated First Mile and Last Mile Supply Approach. Complexity 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Nearchou, A.C. Multi-objective balancing of assembly lines by population heuristics. Int. J. Prod. Res. 2008, 46, 466–481. [Google Scholar] [CrossRef]
- Vila, M.; Pereira, J. A branch-and-bound algorithm for assembly line worker assignment and balancing problem. Comput. Oper. Res. 2013, 40, 3045–3055. [Google Scholar] [CrossRef]
- Scholl, A.; Klein, R. ULINO: optimally balancing U-Shaped JIT assembly lines. Int. J. Prod. Res. 1999, 37, 721–736. [Google Scholar] [CrossRef]
- Martinez, U.; Duff, W.S. Heuristic approaches to solve the U-shaped line balancing problem augmented by Genetic Algorithms. Inf. Eng. Des. Sym. 2004, 11, 246–259. [Google Scholar]
- Gokcen, H.; Agpak, K.; Gencer, C.; Kizilkaya, E. A shortest route formulation of simple U-type assembly line balancing problem. Appl. Math. Mode. 2005, 29, 373–380. [Google Scholar] [CrossRef]
- Gutjahr, A.L.; Nemhauser, G.L. An algorithm for the line balancing problem. Memet. Sci. 1964, 11, 308–315. [Google Scholar] [CrossRef]
- Gokcen, H.; Agpak, K. A goal programming approach to simple U-line balancing problem. Eur. J. Oper. Res. 2006, 171, 577–585. [Google Scholar] [CrossRef]
- Chiang, W.C.; Urban, T.L. The Stochastic U-line Balancing Problem: A Heuristic Procedure. Eur. J. Oper. Res. 2006, 175, 1767–1781. [Google Scholar] [CrossRef]
- Erel, E.; Sabuncuoglu, I.; Aksu, B.A. Balancing of U-type Assembly Systems Using Simulated Annealing. Int. J. Prod. Res. 2001, 39, 3003–3015. [Google Scholar] [CrossRef]
- Sotskov, Y.N.; Dolgui, A.; Portmann, M.C. Stability analysis of an optimal balance for an assembly line with fixed cycle time. Eur. J. Oper. Res. 2006, 168, 783–797. [Google Scholar] [CrossRef]
- Hwang, R.; Katayama, H.; Gen, M. U-shaped assembly line balancing problem with genetic algorithm. Eur. J. Oper. Res. 2008, 46, 4637–4649. [Google Scholar] [CrossRef]
- Andreas, C.N. A Differential Evolution Algorithm for Simple Assembly Line Balancing. IFAC. Int. Fed. Auto. Cont. 2005, 16, 1462–1467. [Google Scholar]
- Pitakaso, R. Differential evolution algorithm for simple assembly line balancing type 1 (SALBP-1). J. Ind. Prod. Eng. 2015, 32, 104–114. [Google Scholar] [CrossRef]
- Qin, A.K.; Hang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evolut. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Zou, D.; Liu, H.; Gao, L.; Li, S. An improved differential evolution algorithm for the task assignment problem. Eng. Appl. Artif. Intell. 2011, 24, 616–624. [Google Scholar] [CrossRef]
- Zeng, X.; Wong, W.; Sun Leung, S. An operator allocation optimization model for balancing control of the hybrid assembly lines using Pareto utility discrete differential evolution algorithm. Comput. Oper. Res. 2012, 39, 1145–1159. [Google Scholar] [CrossRef]
- Jackson, J.R. A computing procedure for a line balancing problem. Memet. Sci. 1956, 2, 261–271. [Google Scholar] [CrossRef]
- Bowman, E.H. Assembly Line Balancing by Linear Programming. Oper. Res. 1960, 8, 385–389. [Google Scholar] [CrossRef]
- Ronkkonen, J.; Kukkonen, S.; Price, K.V. Real-Parameter Optimization with Differential Evolution. IEEE Congr. Evolut. Comput. 2005, 8, 506–513. [Google Scholar]
- Kriengkorakot, N. Metaheuristic approach for assembly line balancing problem. Ph.D. Thesis, Ubon Ratchathani University, Ubon Ratchathani, Thailand, 2008. [Google Scholar]
- Pitakaso, R.; Sethanan, K. Modified differential evolution algorithm for simple assembly line balancing with a limit on the number of machine types. Eng. Optim. 2015, 48, 253–271. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).