Easy Computation of the Various Topologies and Modes of Liquid–Liquid Partition Chromatography by the Theory of Random Walks
Abstract
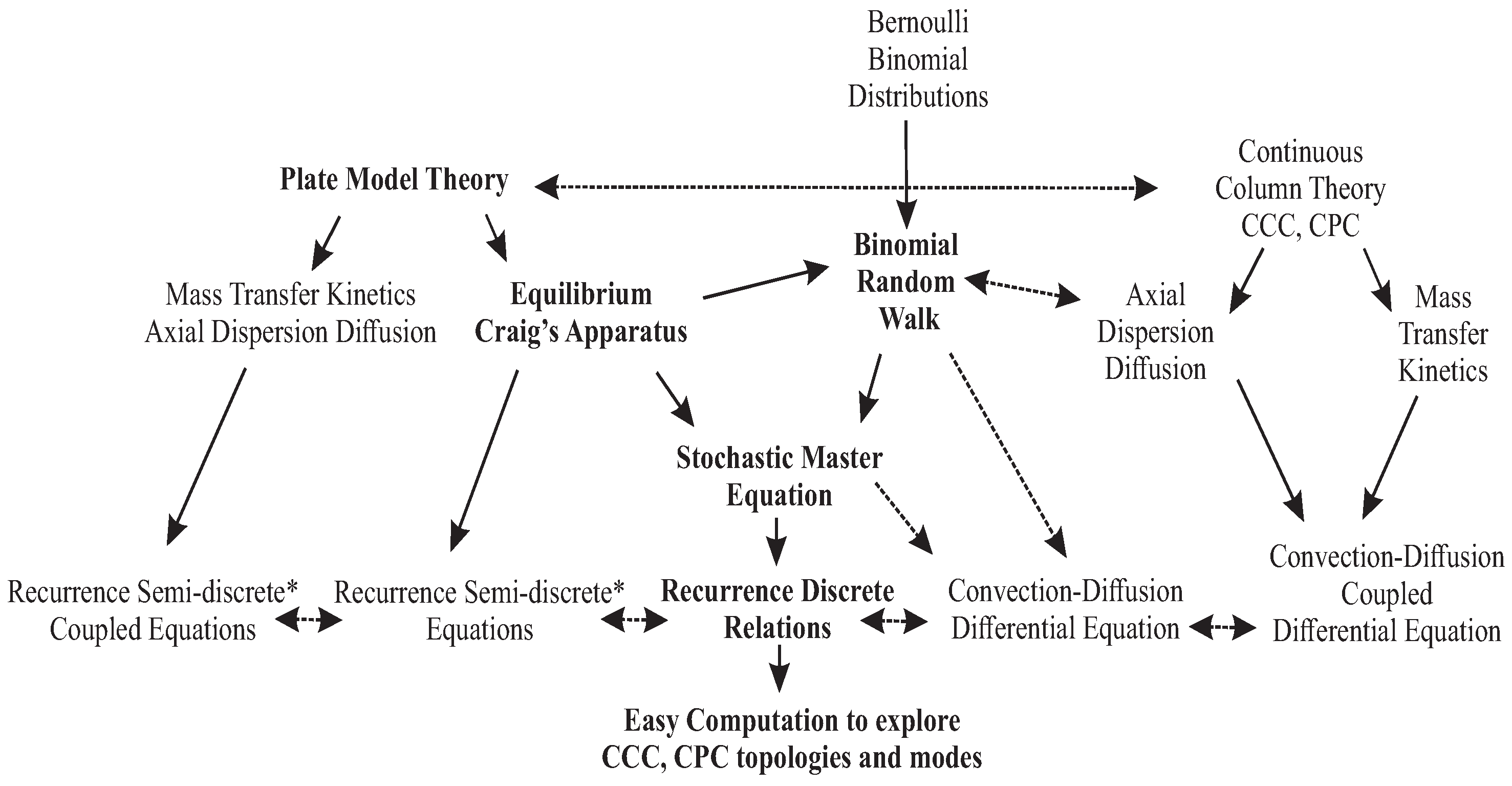
:1. Introduction
2. Materials and Methods
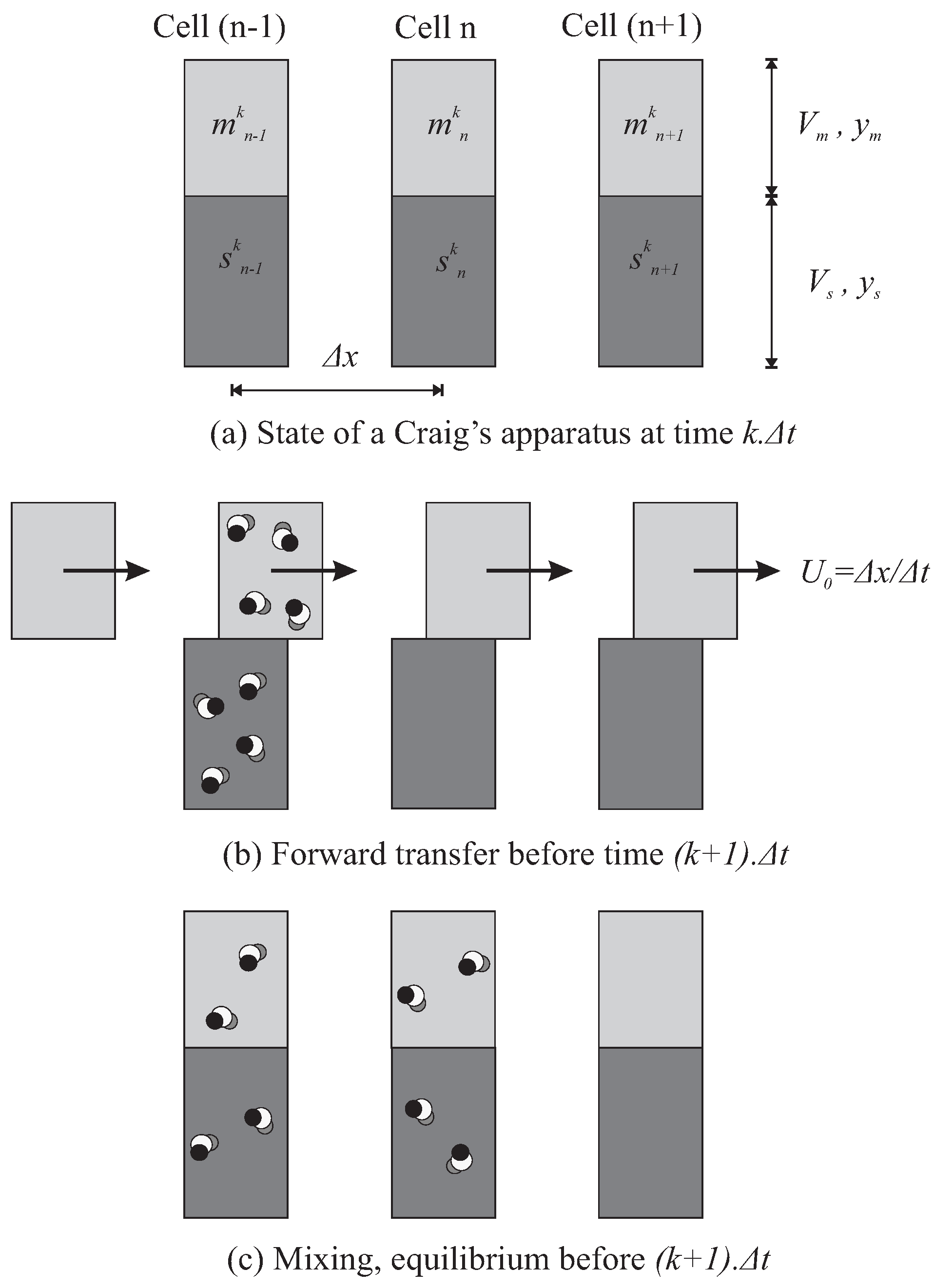
2.1. The Modeling of the Craig’s Apparatus, a Precursor in Partition Chromatography
2.1.1. The System
2.1.2. The Recurrence Phenomenological Model with Concentration
The Recurrence Relation
The Recurrence Relation Approximated by a Time Derivative
2.1.3. The Binomial Phenomenological Model in a Fraction of Injected Quantity
2.2. The Binomial Random Walk Model
2.2.1. The Statistical Moments of the Random Walk
2.2.2. Elution Speed and Diffusion Coefficient
2.3. Stochastic Master Equation and Differential Convection-Diffusion Equation
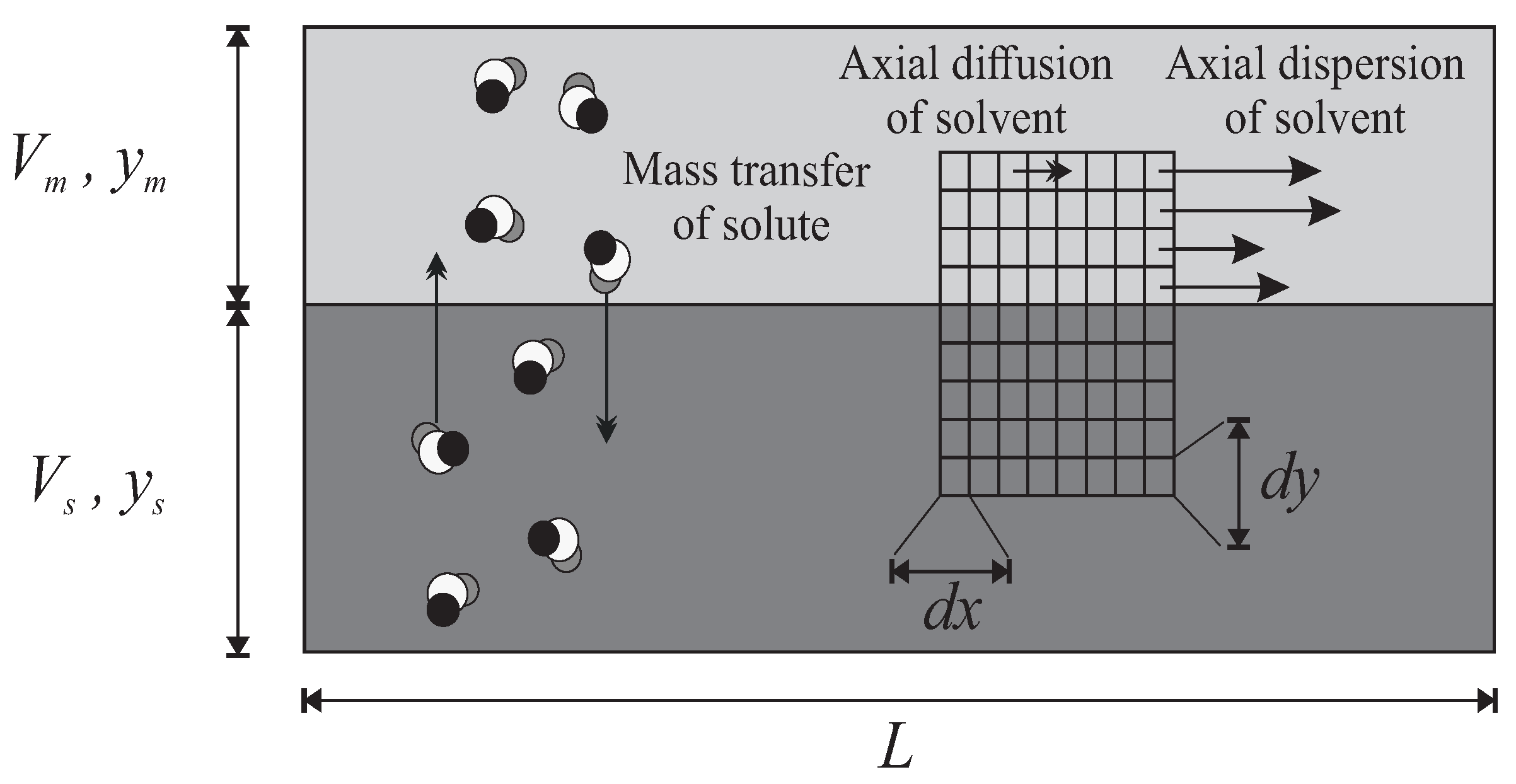
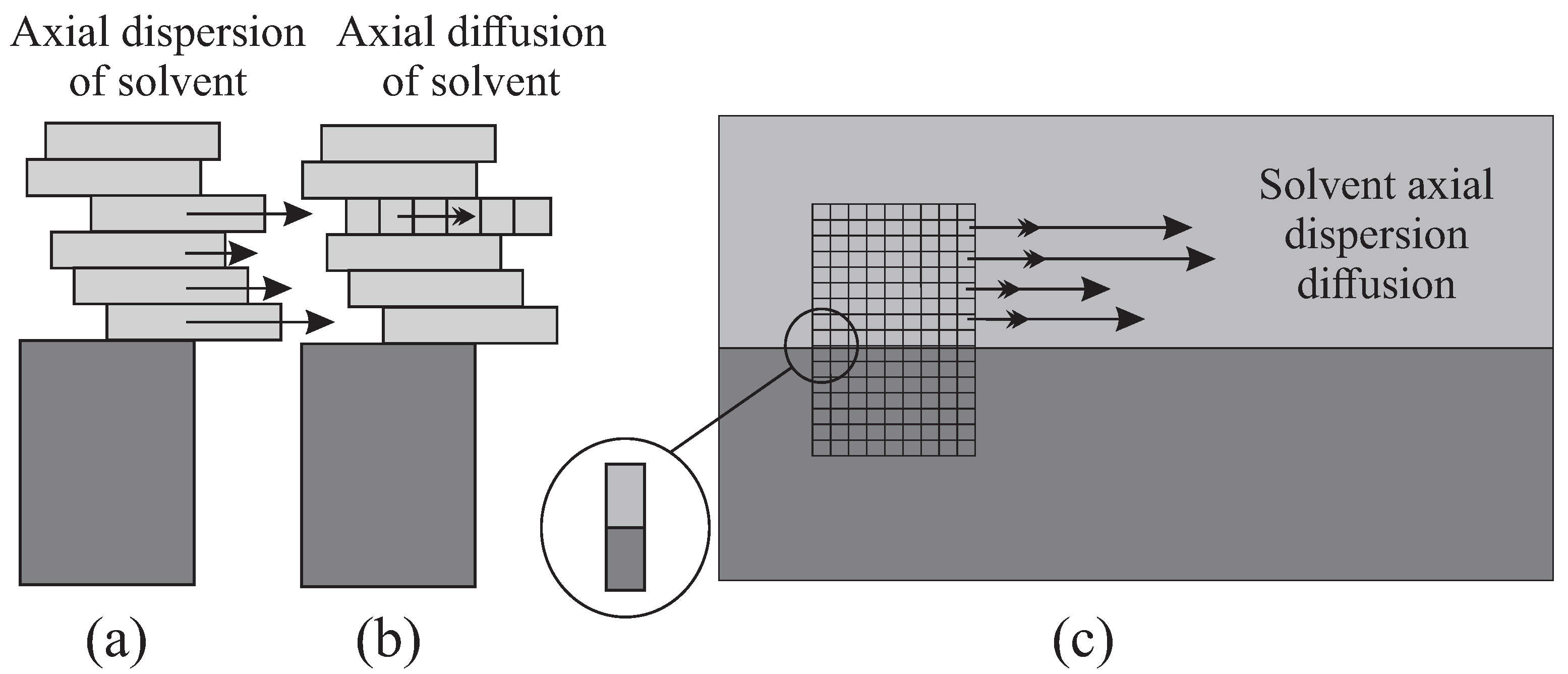
2.4. Model of the Continuous Column in a Non-Equilibrium State
2.4.1. Description of the Geometry
2.4.2. Coupled Differential Equations
2.4.3. Comparison with the Model of Craig
Limit of Null Transfer Time
2.5. Plate Model Out of Equilibrium
3. Results
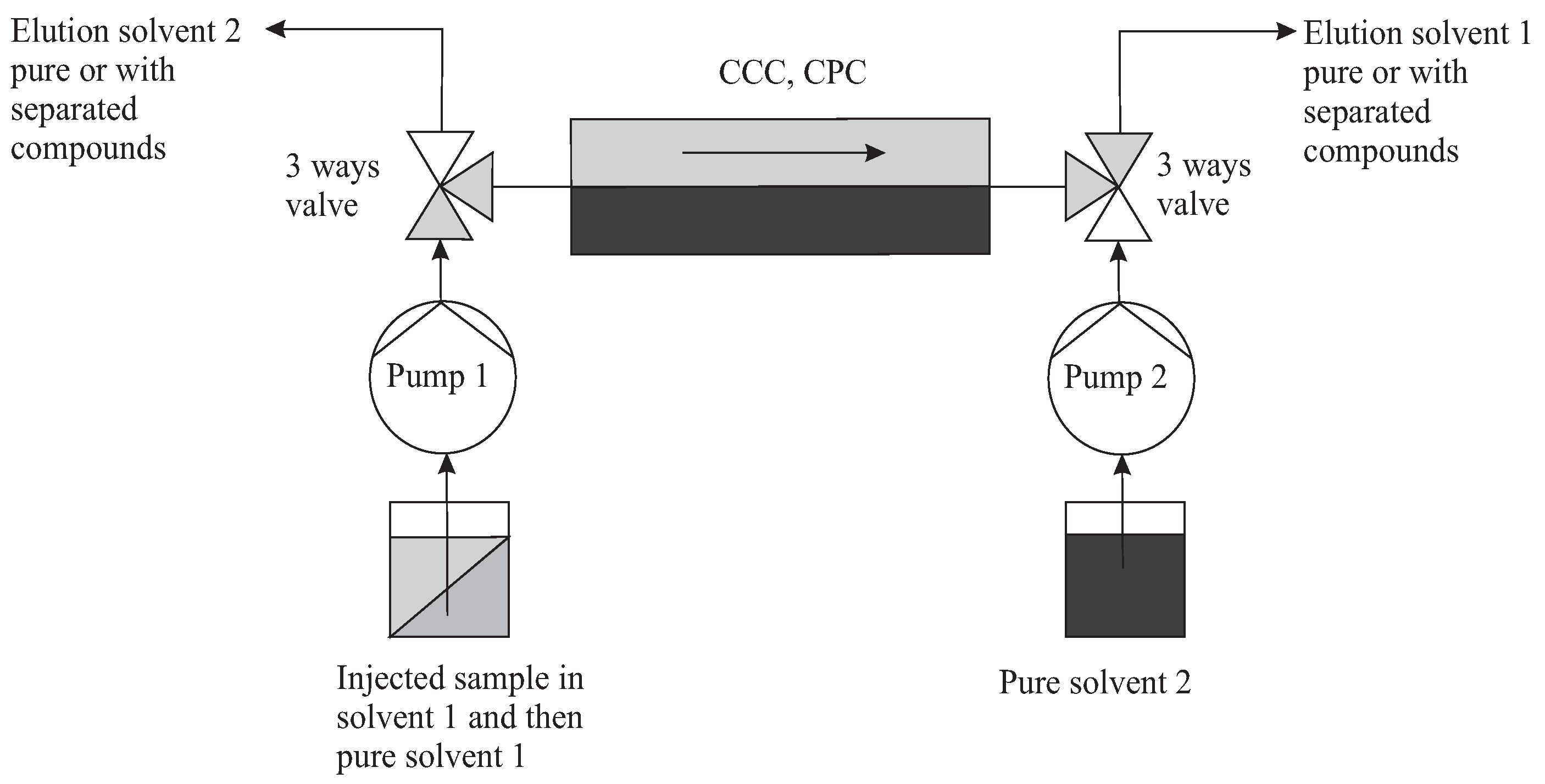
3.1. Batch Injection in Simple Elution Mode
3.1.1. Topology and Mode
3.1.2. System of Equations
Coding Injection
Coding Elution
3.1.3. Special Case
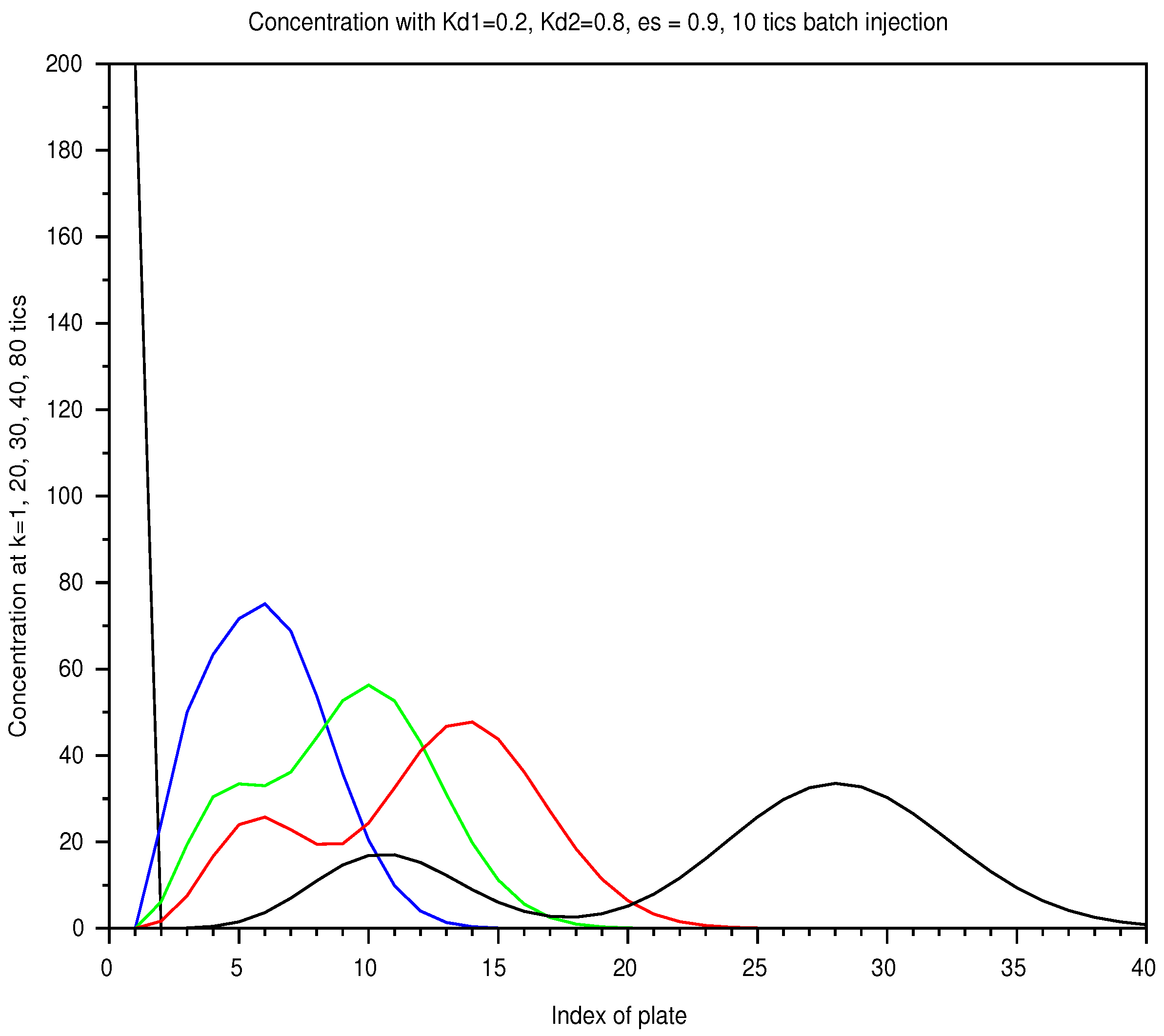
Concentration Profiles and Chromatogram for Two Solutes
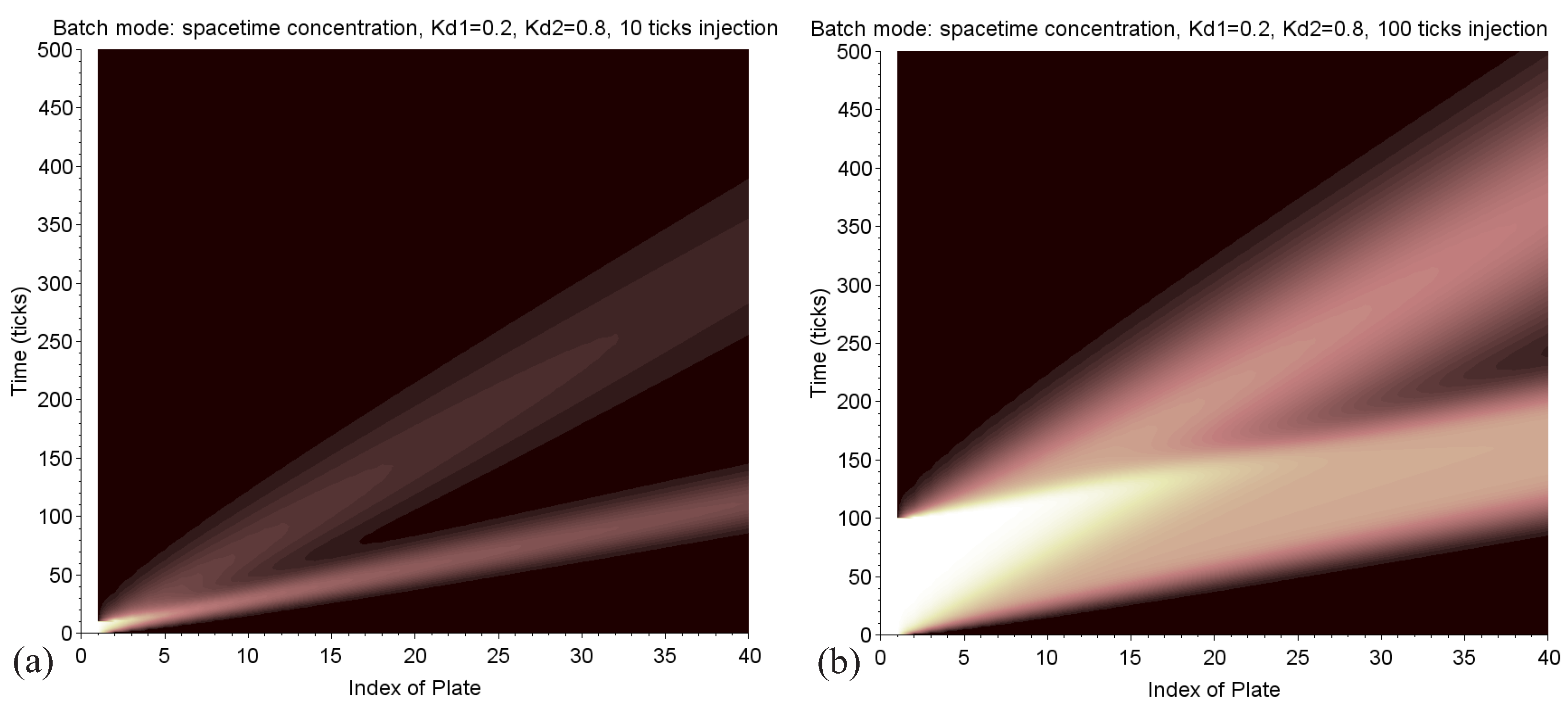
Space-Time Maps
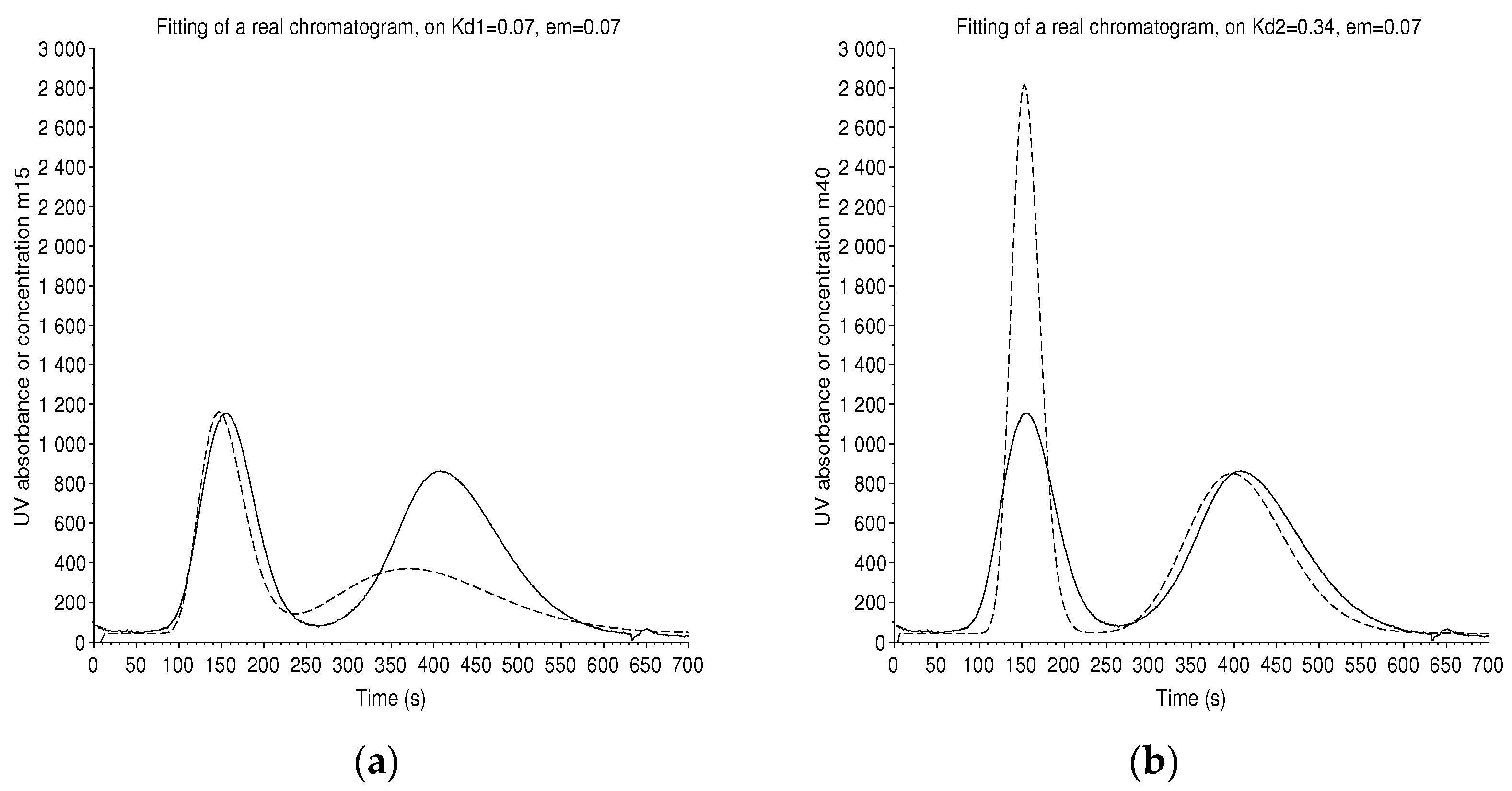
3.1.4. Correspondence with a Real Chromatogram
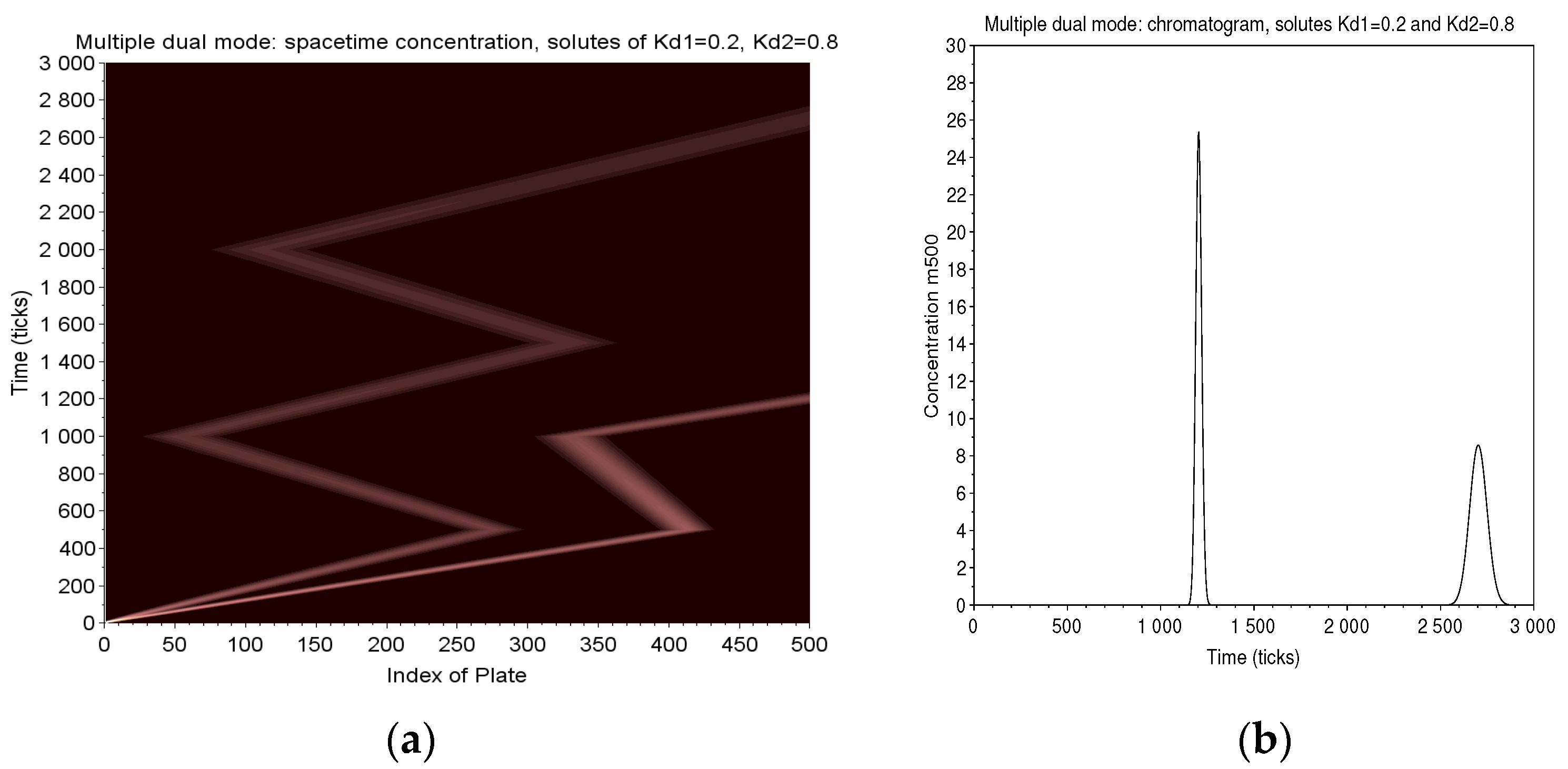
3.2. Batch Injection in Multiple Dual Mode (MDM)
3.2.1. Topology and Mode
3.2.2. System of Equations
Coding Injection
Coding the First Forward Elution
Coding the First Backward Elution
Coding J Dual Cycles
Coding a Final Forward Elution
3.2.3. A Typical Case of Amplified Separation
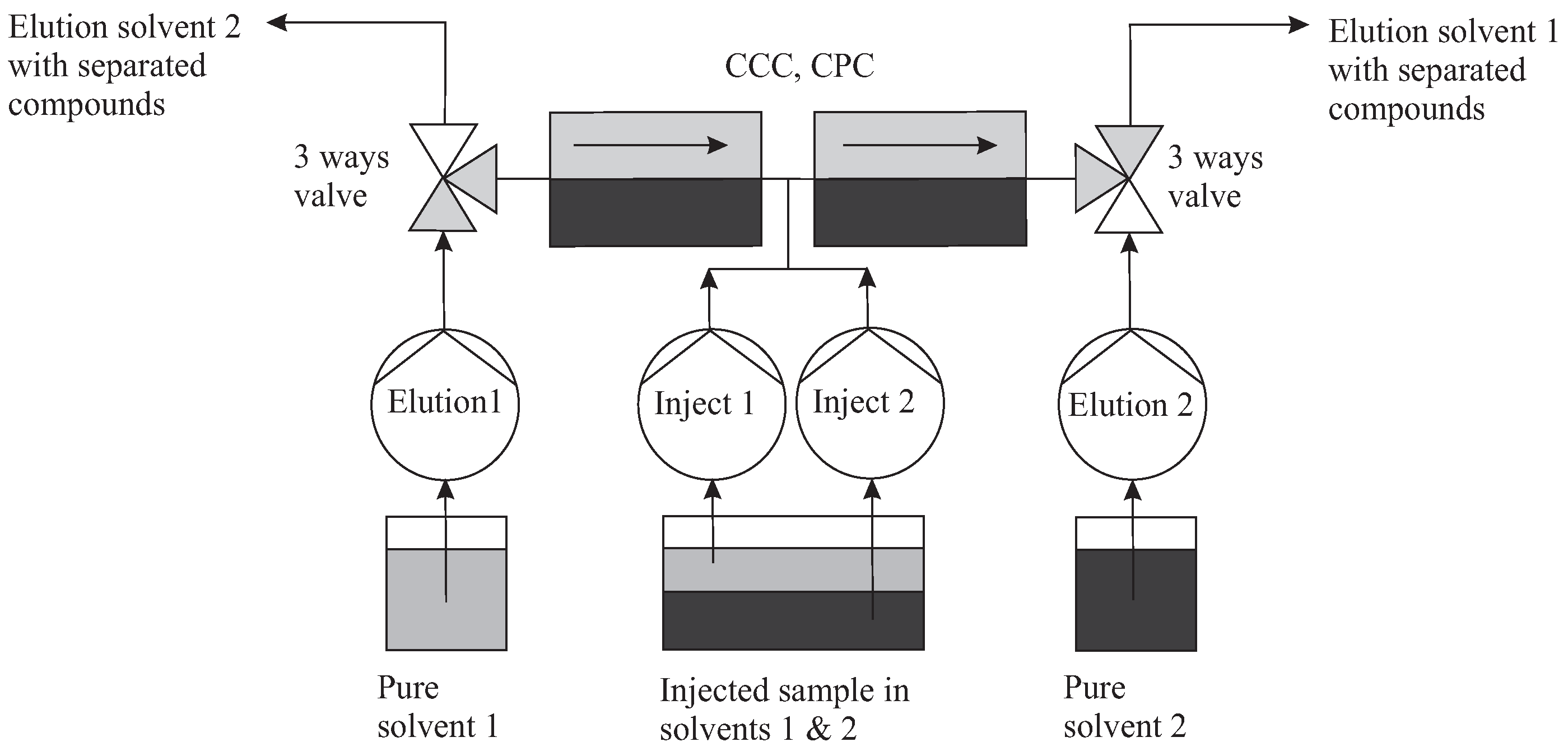
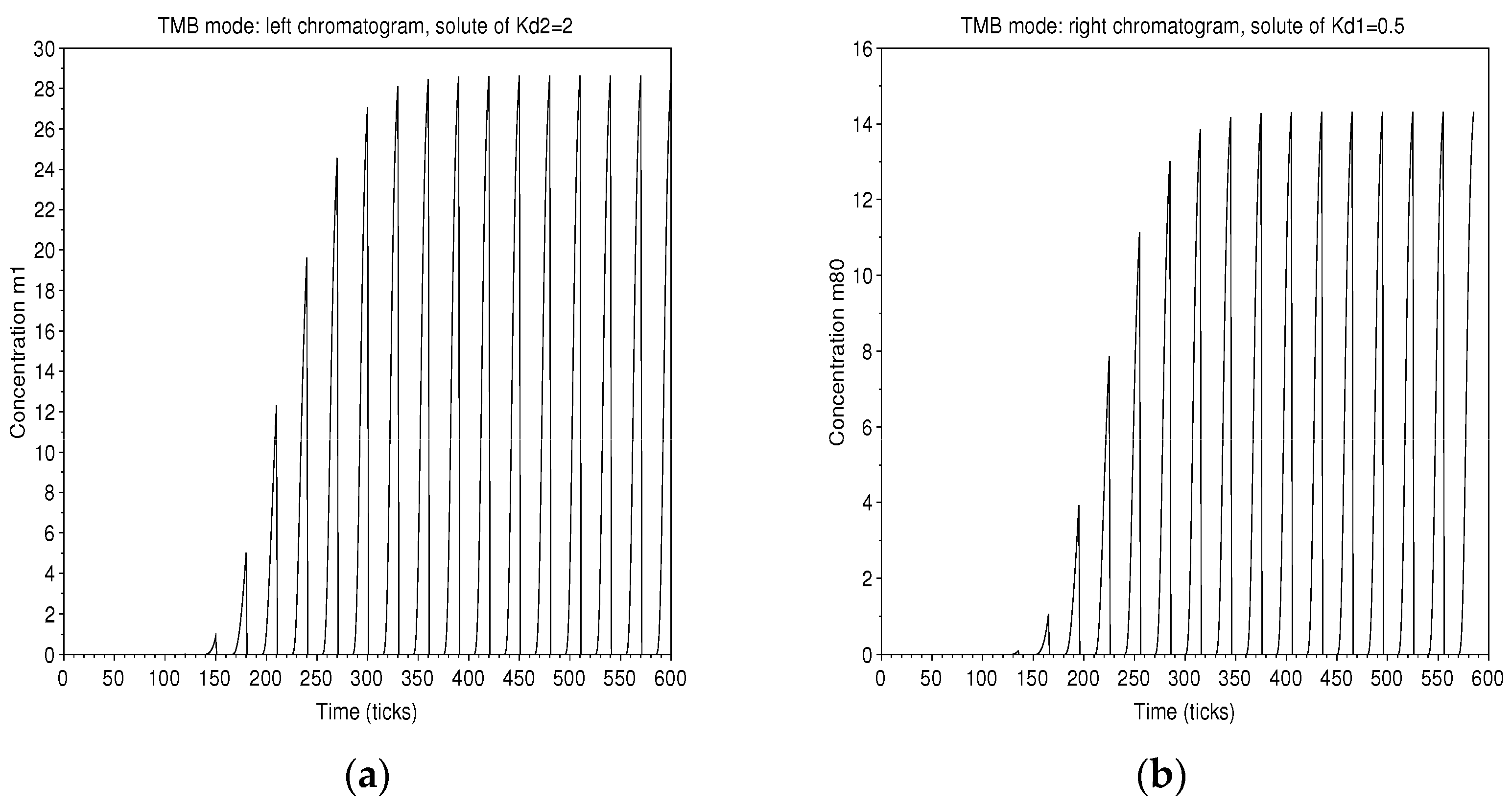
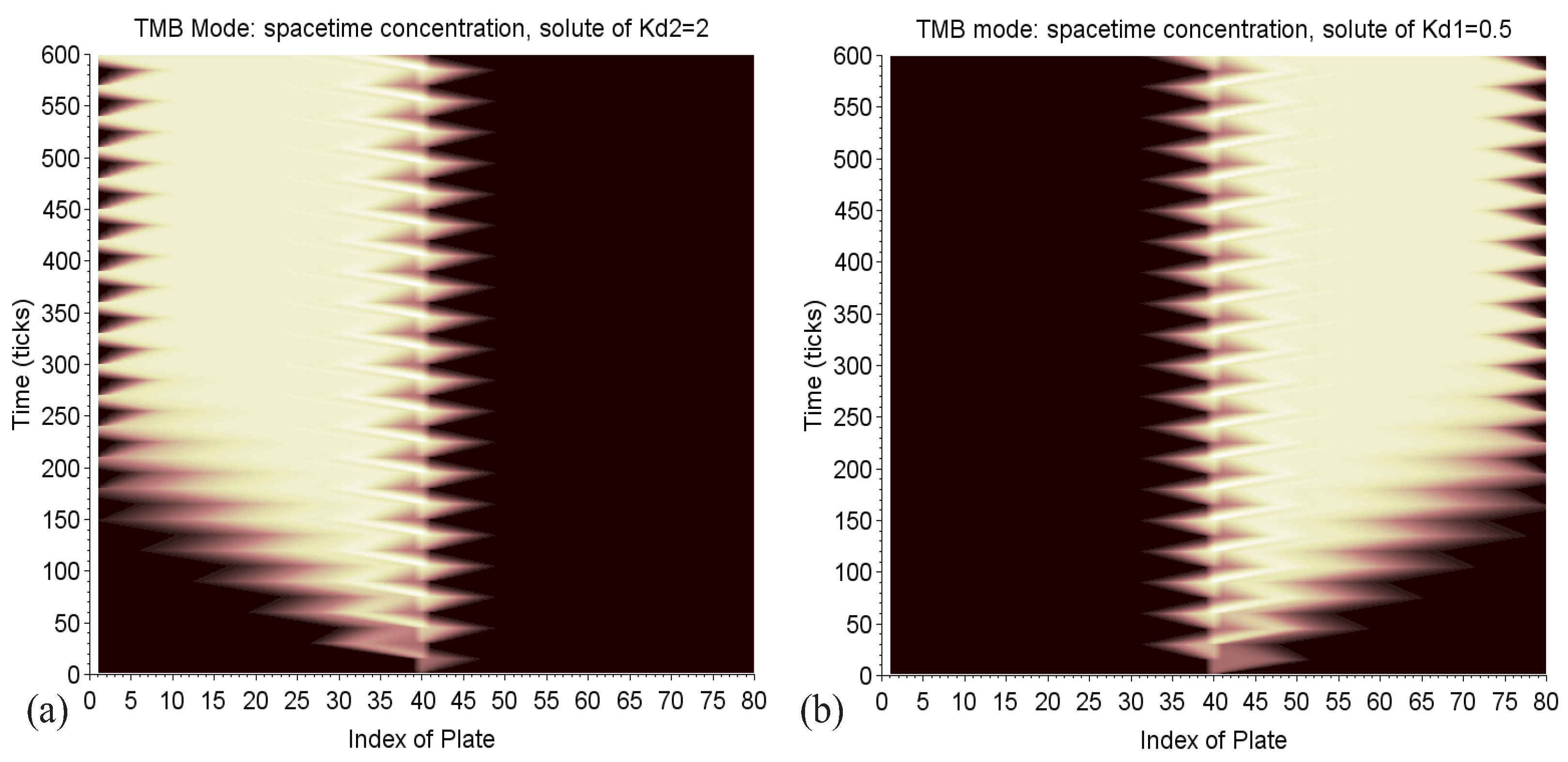
3.3. Continuous Injection in “True Moving Bed” Mode
3.3.1. Topology and Mode
3.3.2. System of Equations
3.3.3. Special Case
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| a | Specific interfacial area (per unit volume) |
| c | Celerity of solvents in dual or TMB modes or celerity of light |
| Concentration profile for a chromatogram | |
| CCC | Counter-Current Chromatography |
| CPC | Centrifugal Partition Chromatography |
| Displacement of a solute molecule after k instants | |
| D | Diffusion coefficient for the solute in the plate theory |
| Dispersion–diffusion coefficient for the mobile solvent | |
| Diffusion coefficient in mobile phase for the solute | |
| Diffusion coefficient in stationary phase for the solute | |
| Intrinsic diffusion coefficient of random walk, i.e., of mobile phase | |
| Time step for the plate model or Craig’s apparatus | |
| x | Space step for the plate model or Craig’s apparatus |
| Ratio of mobile phase | |
| Ratio of stationary phase | |
| F | Flow rate of mobile phase |
| k | Index of time |
| Retention factor of a solute | |
| Global speed of transfer of a solute | |
| Speed of transfer of a solute in the mobile phase | |
| Speed of transfer of a solute in the stationary phase | |
| Partition coefficient of a solute | |
| L | Notion of length of column |
| m | Concentration of mobile phase without index |
| Concentration of mobile phase in cell n and at instant k | |
| MDM | Multiple dual mode |
| MP | Mobile phase |
| fraction of solute in a cell or plate | |
| n | Current index of cell or plate |
| N | Total number of cells or plates |
| p | Probability for a solute molecule to be in mobile phase due to volume selection and partition |
| Probability for a solute molecule to be in mobile phase due to partition | |
| q | Probability for a solute molecule to be in stationary phase due to volume selection and partition |
| Amount of injected solute | |
| Concentration in mobile phase in the continuous case for a solute | |
| s | Concentration of stationary phase without index |
| Concentration of stationary phase in cell n and at instant k | |
| Standard deviation of the displacement of a solute molecule after k instants | |
| SP | Stationary phase |
| U | Speed of convection |
| Intrinsic speed of random walk, i.e of mobile phase | |
| T | Duration of a TMB cycle |
| TMB | True Moving Bed |
| Volume of one cell or plate | |
| Total volume of a column | |
| Volume of mobile phase of one cell or plate | |
| Volume of stationary phase of one cell or plate | |
| Total retention volume for a solute | |
| x | Horizontal space axis |
| X | Width of a cell or plate |
| y | Vertical space axis |
References
- Martin, A.J.; Synge, R.L. A new form of chromatogram employing two liquid phases: A theory of chromatography. 2. Application to the micro-determination of the higher monoamino-acids in proteins. Biochem. J. 1941, 35, 1358–1368. [Google Scholar] [CrossRef]
- Snyder, L.R.; Kirkland, J.J.; Dolan, J.W. Introduction to Modern Liquid Chromatography, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Craig, L. Identification of small amounts of organic compounds by distribution studies II. Separation by counter-current distribution. J. Biol. Chem. 1944, 155, 519–534. [Google Scholar] [CrossRef]
- Snyder, L.; Cox, G.; Antle, P. Preparative separation of peptide and protein samples by High-performance liquid chromatography with gradient elution I. The Craig model as a basis for computer simulations. J. Chromatogr. 1988, 444, 303–325. [Google Scholar] [CrossRef]
- Conway, W.; Petroski, R. Modern Countercurrent Chromatography; American Chemical Society: Washington, DC, USA, 1995. [Google Scholar]
- Van Deemter, J.; Zuiderweg, F.; Klinkenberg, A.V. Longitudinal diffusion and resistance to mass transfer as causes of nonideality in chromatography. Chem. Eng. Sci. 1956, 5, 271–289. [Google Scholar] [CrossRef]
- Felinger, A. Data Analysis and Signal Processing in Chromatography; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Nauman, E. Residence time distributions in systems governed by the dispersion equation. Chem. Eng. Sci. 1981, 36, 957–966. [Google Scholar] [CrossRef]
- Vatistas, N. Danckwerts’ degree of segregation for the axial dispersion model. Chem. Eng. Sci. 1991, 46, 307–311. [Google Scholar] [CrossRef]
- Van Buel, M.; Van der Wielen, L.; Luyben, K.C.A. Effluent concentration profiles in centrifugal partition chromatography. AIChE J. 1997, 43, 693–702. [Google Scholar] [CrossRef]
- Marchal, L. Contribution à la Théorie et au Développement de la Chromatographie de Partage Centrifuge: Etude de l’Hydrodynamique des Phases et du Transfert de Matière. Ph.D. Thesis, University of Nantes, Nantes, France, 2001. [Google Scholar]
- Marchal, L.; Legrand, J.; Foucault, A. Mass transport and flow regimes in centrifugal partition chromatography. AIChE J. 2002, 48, 1692–1704. [Google Scholar] [CrossRef]
- Adelmann, S.; Baldhoff, T.; Koepcke, B.; Schembecker, G. Selection of operating parameters on the basis of hydrodynamics in centrifugal partition chromatography for the purification of nybomycin derivatives. J. Chromatogr. A 2013, 1274, 54–64. [Google Scholar] [CrossRef]
- Kostanyan, A.E.; Belova, V.V.; Kholkin, A.I. Modeling counter-current and dual counter-current chromatography using longitudinal mixing cell and eluting counter-current distribution models. J. Chromatogr. A 2007, 1151, 142–147. [Google Scholar] [CrossRef]
- Morley, R.; Minceva, M. Trapping multiple dual mode centrifugal partition chromatography for the separation of intermediately-eluting components: Throughput maximization strategy. J. Chromatogr. A 2017, 1501, 26–38. [Google Scholar] [CrossRef] [PubMed]
- Rubio, N.; Ignatova, S.; Minguillón, C.; Sutherland, I.A. Multiple dual-mode countercurrent chromatography applied to chiral separations using a (S)-naproxen derivative as chiral selector. J. Chromatogr. A 2009, 1216, 8505–8511. [Google Scholar] [CrossRef] [PubMed]
- Mekaoui, N.; Berthod, A. Using the liquid nature of the stationary phase. VI. Theoretical study of multi-dual mode countercurrent chromatography. J. Chromatogr. A 2011, 1218, 6061–6071. [Google Scholar] [CrossRef]
- Mekaoui, N.; Berthod, A. Application du dual-mode multiple aux séparations chirales en chromatographie à contre courant. In Proceedings of the SEP 2011–9ème Congrès Francophone de l’AFSep sur les Sciences Séparatives et les Couplages, Toulouse, France, 23–25 March 2011. [Google Scholar]
- Kostanyan, A.E.; Erastov, A.A.; Shishilov, O.N. Multiple dual mode counter-current chromatography with variable duration of alternating phase elution steps. J. Chromatogr. A 2014, 1347, 87–95. [Google Scholar] [CrossRef]
- Hopmann, E.; Goll, J.; Minceva, M. Sequential centrifugal partition chromatography: A new continuous chromatographic technology. Chem. Eng. Technol. 2012, 35, 72–82. [Google Scholar] [CrossRef]
- Couillard, F.; Foucault, A.; Durand, D. Method and Device for Separating Constituents of a Liquid Charge by Means of Liquid–Liquid Centrifuge Chromatography. US Patent 7,422,685, 9 September 2008. [Google Scholar]
- Rodrigues, A. Simulated Moving Bed Technology Principles, Design and Process Applications; Elsevier: Oxford, UK, 2015. [Google Scholar]
- Giddings, J.C.; Eyring, H. A molecular dynamic theory of chromatography. J. Phys. Chem. 2002, 59, 416–421. [Google Scholar] [CrossRef]
- Kostanyan, A.E. On influence of sample loading conditions on peak shape and separation efficiency in preparative isocratic counter-current chromatography. J. Chromatogr. A 2012, 1254, 71–77. [Google Scholar] [CrossRef] [PubMed]
- Schwienheer, C.; Krause, J.; Schembecker, G.; Merz, J. Modeling centrifugal partition chromatography separation behavior to characterize influencing hydrodynamic effects on separation efficiency. J. Chromatogr. A 2017, 1492, 27–40. [Google Scholar] [CrossRef]
- Ignatova, S.; Hewitson, P.; Mathews, B.; Sutherland, I. Evaluation of dual flow counter-current chromatography and intermittent counter-current extraction. J. Chromatogr. A 2011, 1218, 6102–6106. [Google Scholar] [CrossRef] [PubMed]
- Roullier, C.; Chollet-Krugler, M.; Bernard, A.; Boustie, J. Multiple dual-mode centrifugal partition chromatography as an efficient method for the purification of a mycosporine from a crude methanolic extract of Lichina pygmaea. J. Chromatogr. B 2009, 877, 2067–2073. [Google Scholar] [CrossRef] [PubMed]
- Delannay, E.; Toribio, A.; Boudesocque, L.; Nuzillard, J.M.; Zeches-Hanrot, M.; Dardennes, E.; Le Dour, G.; Sapi, J.; Renault, J.H. Multiple dual-mode centrifugal partition chromatography, a semi-continuous development mode for routine laboratory-scale purifications. J. Chromatogr. A 2006, 1127, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Mandova, T.; Audo, G.; Michel, S.; Grougnet, R. Off-line coupling of new generation centrifugal partition chromatography device with preparative high pressure liquid chromatography-mass spectrometry triggering fraction collection applied to the recovery of secoiridoid glycosides from Centaurium erythraea Rafn. (Gentianaceae). J. Chromatogr. A 2017, 1513, 149–156. [Google Scholar] [PubMed]
- Mekaoui, N.; Chamieh, J.; Dugas, V.; Demesmay, C.; Berthod, A. Purification of Coomassie Brilliant Blue G-250 by multiple dual mode countercurrent chromatography. J. Chromatogr. A 2012, 1232, 134–141. [Google Scholar] [CrossRef]
- Hewitson, P.; Ignatova, S.; Haoyu, Y.; Chen, L.; Sutherland, I. Intermittent counter-current extraction as an alternative approach to purification of Chinese herbal medicine. J. Chromatogr. A 2009, 1216, 4187–4192. [Google Scholar] [CrossRef] [PubMed]



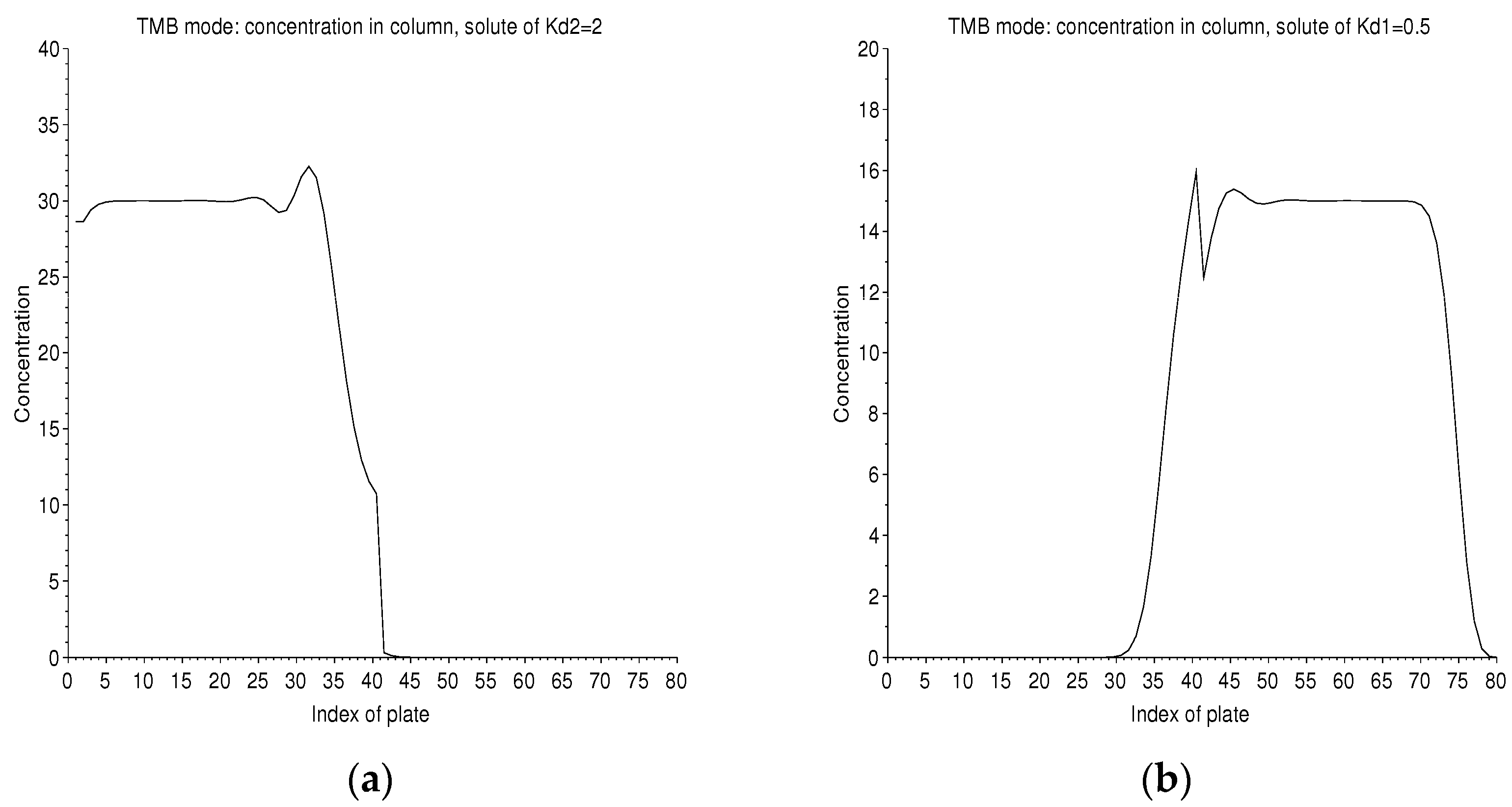
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dijoux, F.R.; Mandova, T. Easy Computation of the Various Topologies and Modes of Liquid–Liquid Partition Chromatography by the Theory of Random Walks. Separations 2021, 8, 41. https://doi.org/10.3390/separations8040041
Dijoux FR, Mandova T. Easy Computation of the Various Topologies and Modes of Liquid–Liquid Partition Chromatography by the Theory of Random Walks. Separations. 2021; 8(4):41. https://doi.org/10.3390/separations8040041
Chicago/Turabian StyleDijoux, Frédéric R., and Tsvetelina Mandova. 2021. "Easy Computation of the Various Topologies and Modes of Liquid–Liquid Partition Chromatography by the Theory of Random Walks" Separations 8, no. 4: 41. https://doi.org/10.3390/separations8040041
APA StyleDijoux, F. R., & Mandova, T. (2021). Easy Computation of the Various Topologies and Modes of Liquid–Liquid Partition Chromatography by the Theory of Random Walks. Separations, 8(4), 41. https://doi.org/10.3390/separations8040041





