Establishing SI-Traceability of Nanoparticle Size Values Measured with Line-Start Incremental Centrifugal Liquid Sedimentation
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Calibration Material
2.3. Certified Reference Materials
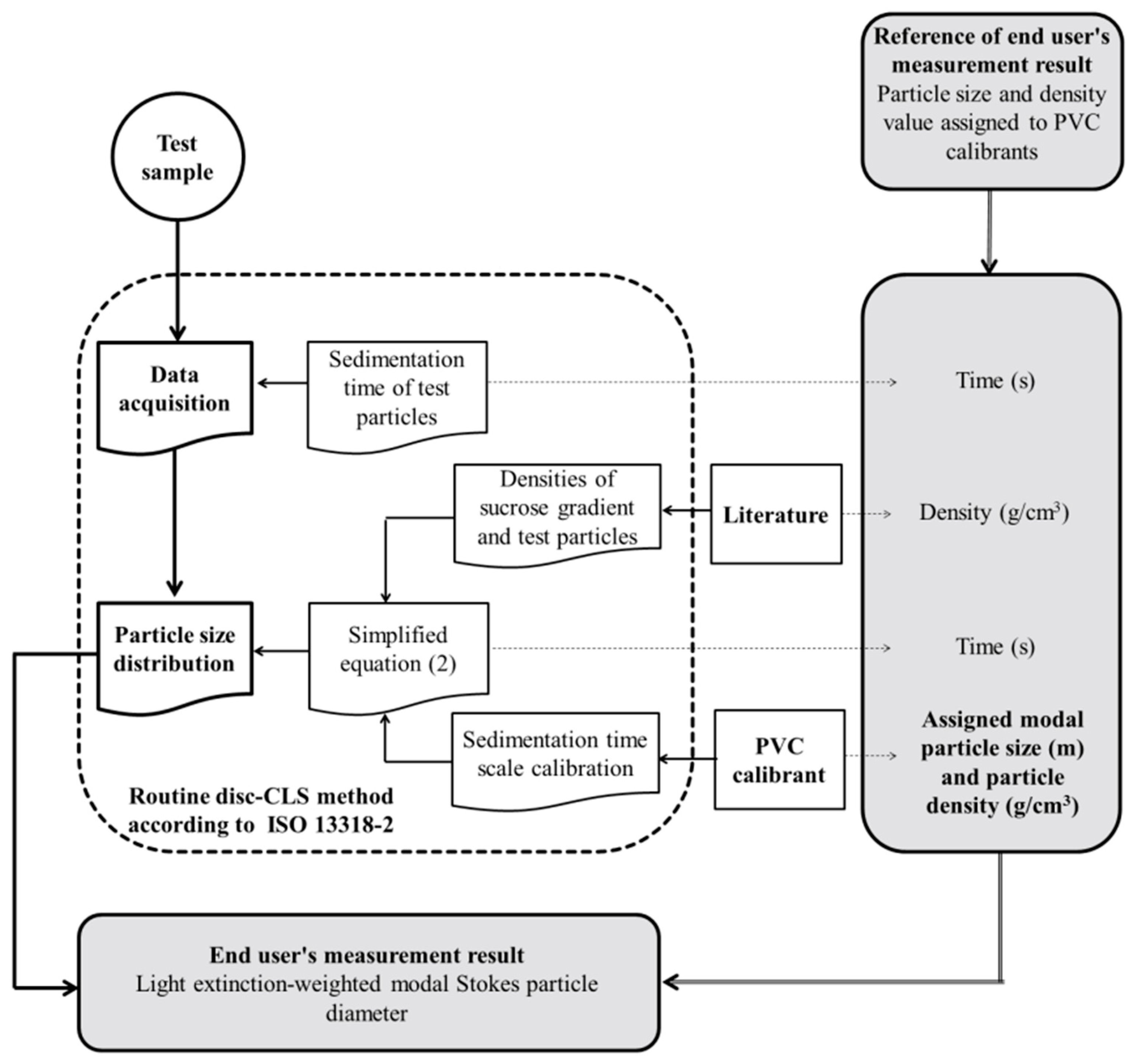
2.4. Disc-CLS Conditions and Method
3. Results and Discussion
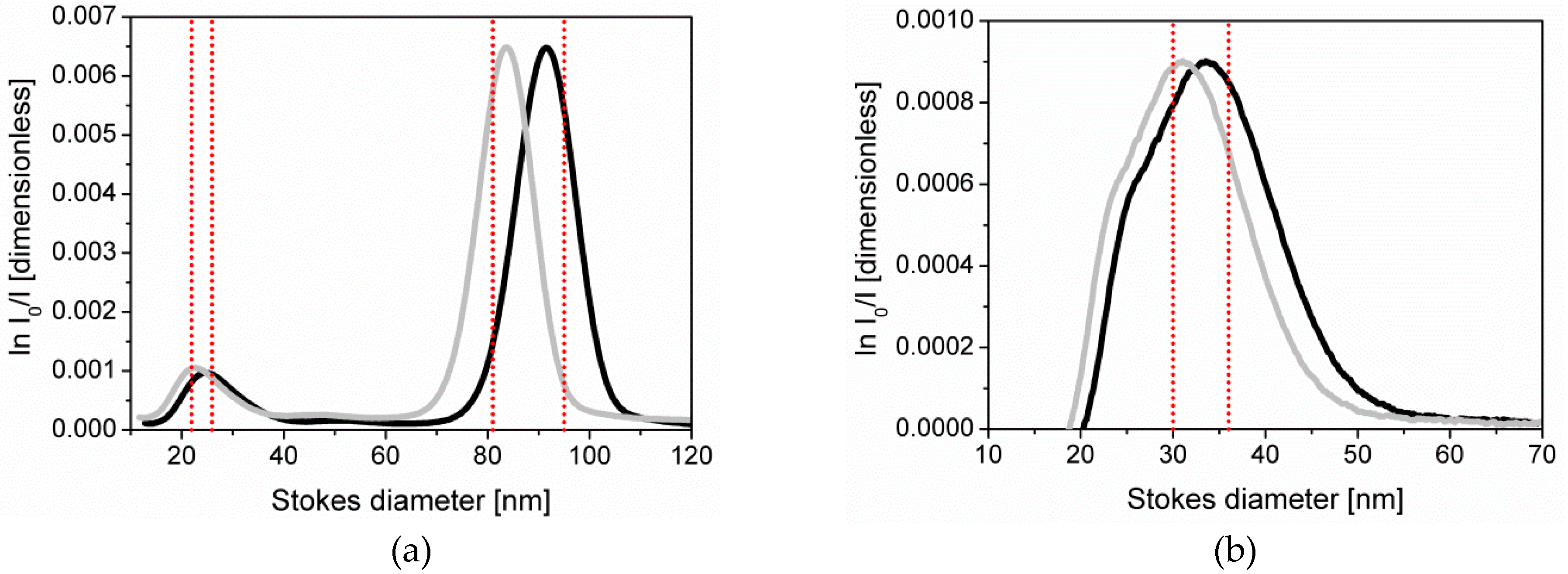
3.1. Particle Size Analysis by Disc-CLS
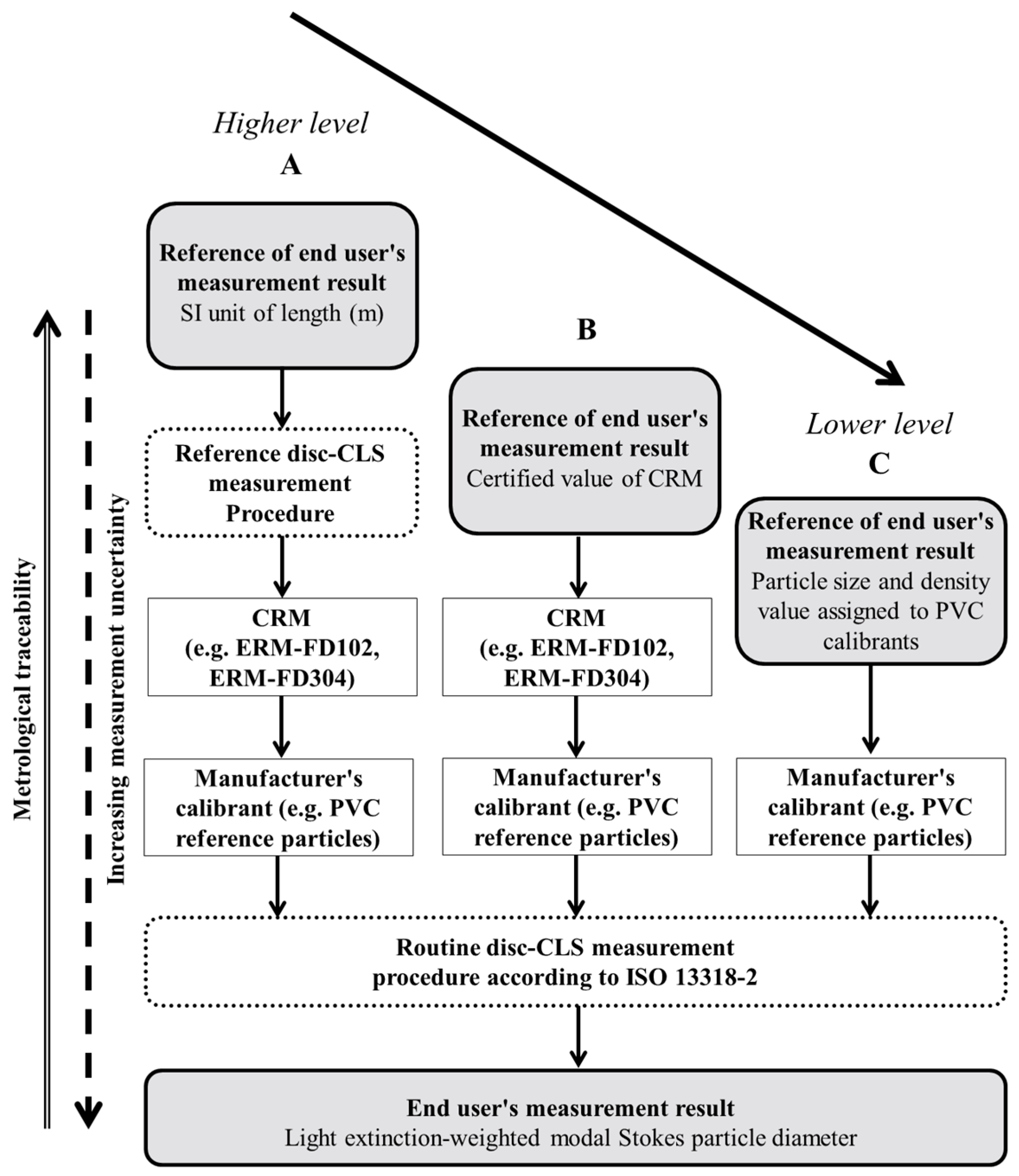
3.2. Metrological Traceability
3.2.1. Measurand Definition
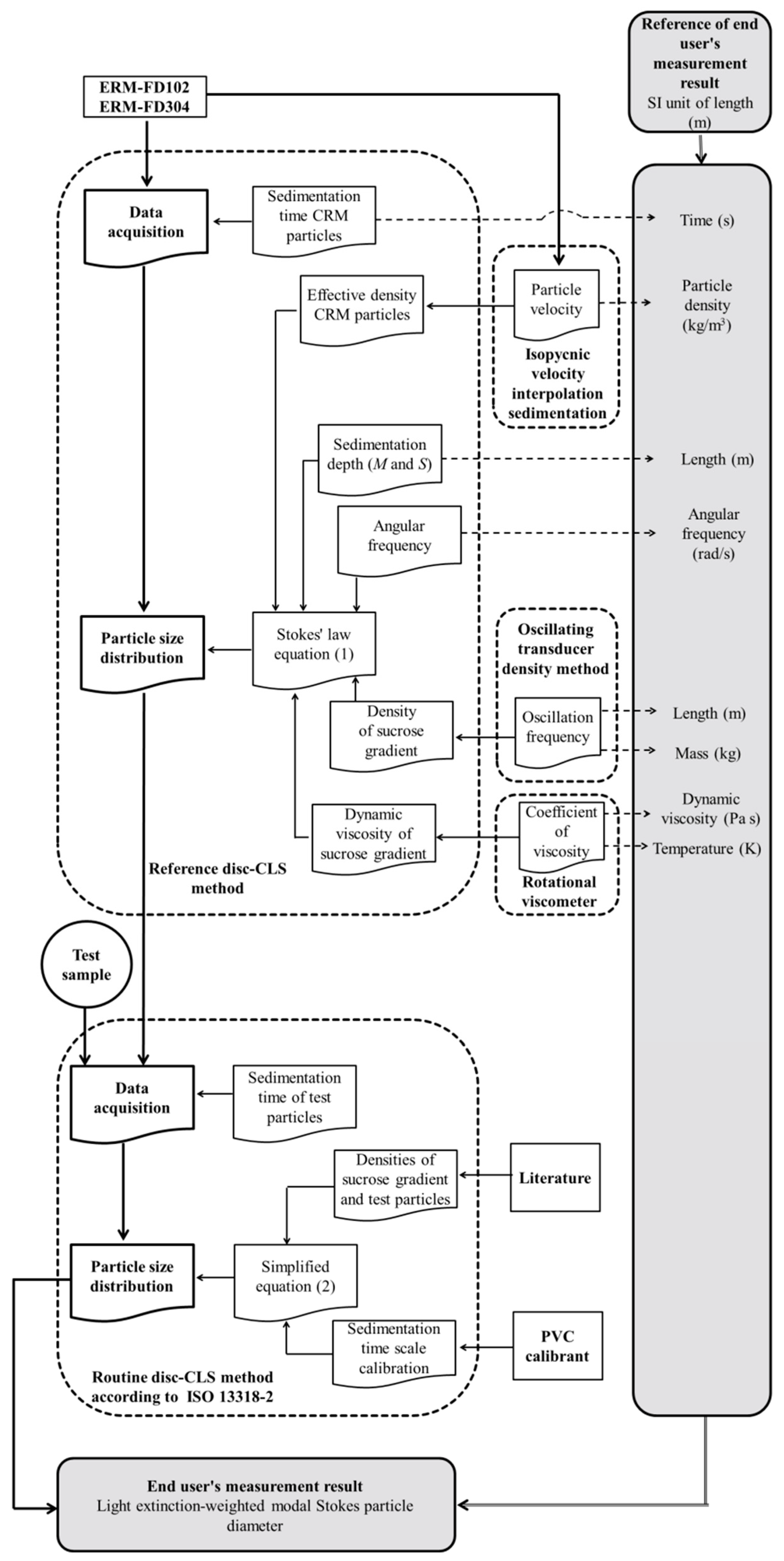
3.2.2. Traceability Network
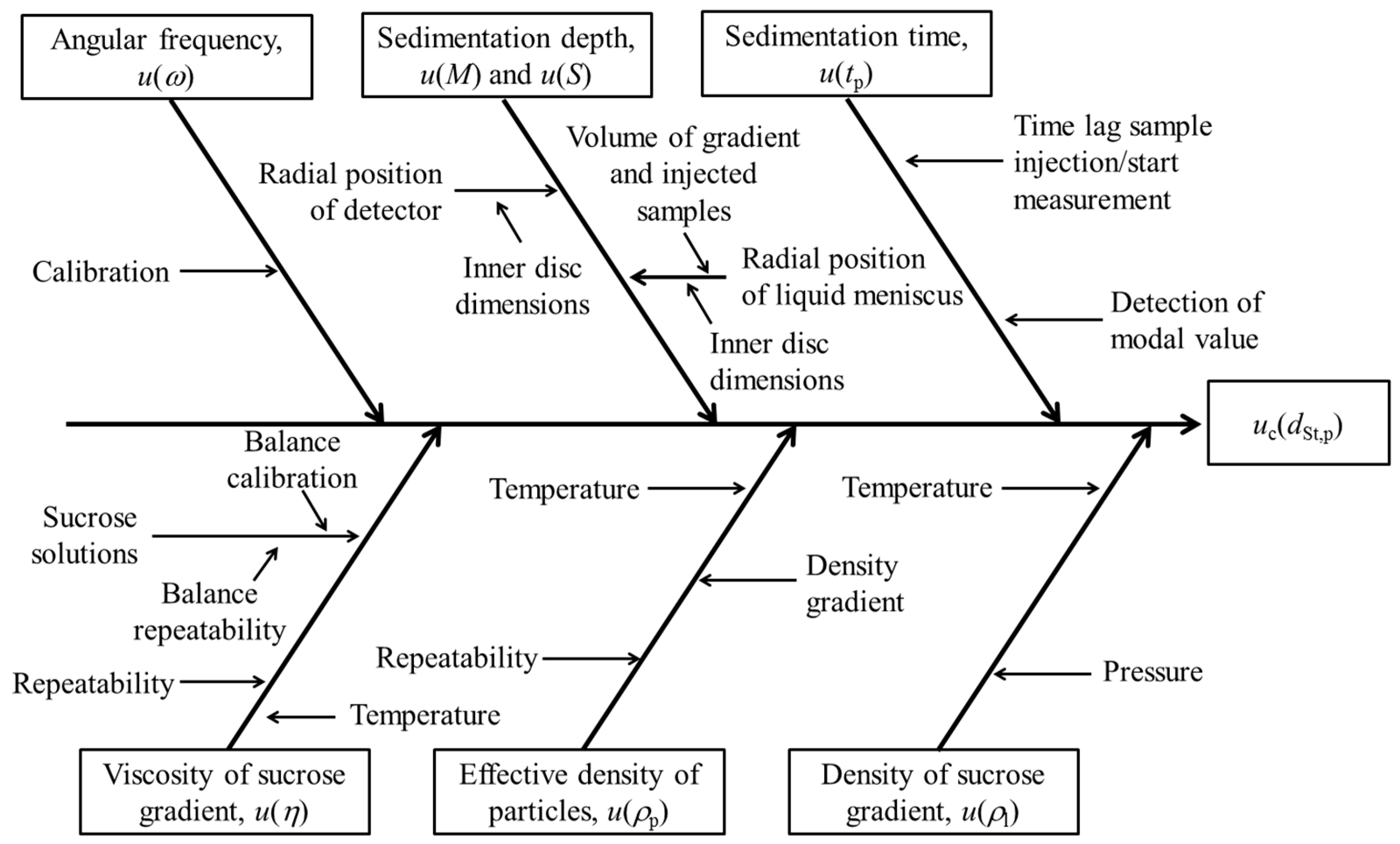
- The density of the sucrose solutions was measured using an oscillating-type density meter. The working principle of this technique is based on the well-known law of harmonic oscillation [14]. The glass U-tube is excited to vibrate at the resonance or characteristic frequency of the introduced sample, which depends on its mass. The density of the sample under investigation is calculated using cell constants previously determined by measuring resonance frequencies when the sample cell is filled with a calibrant (e.g., water, ethanol, iso-octane, toluene), which are certified for density [15]. Measurement results obtained with an oscillating-type density meter are traceable to the SI units of length and mass through calibration with suitable SI-traceable calibrants [16]. The cell constants used in the calculation of the density are temperature and pressure dependent. However, the uncertainties of the temperature and pressure calibrations are assumed to be negligible compared to the uncertainties of the input quantities of the Stokes’ equation. Hence, the traceability chains of the temperature and pressure calibrations are omitted from the disc-CLS traceability network in Figure 4.
- The average dynamic viscosity values of the density gradient (between the detector’s position M and the inner liquid surface S) were calculated from the inner disc dimensions, the viscosity results that were obtained experimentally for the individual sucrose solutions (Figure S2) and from the known volumes of each sucrose carrier fluid component used for constructing the density gradient. Viscosity results are temperature dependent, and it can be assumed that the uncertainty mainly depends on the accuracy of the temperature controller. The viscosity measurements were performed at controlled temperatures using a rotational viscometer. The temperature controller of the viscometer was SI-traceably calibrated by the manufacturer with ITS-90 fixed points [17].
- The angular frequency of the disc-CLS instrument was verified by the manufacturer using an SI-traceably calibrated tachometer.
- The radial position of the photodetector (distance M) was measured using a paper strip with integrated SI-traceable length scale that was especially designed by the manufacturer for the given purpose. The measured distance was confirmed experimentally based on the inner dimensions of the disc (personal communication CPS Instruments, Inc.) and by injecting known volumes of water until a significant change of the signal response of the detector was recorded.
- The radial positions of the inner liquid surface (distance S) were determined based on the inner dimensions of the disc, the known volume of the sucrose density gradient and the known volumes of sample (+calibrant) injected during a measurement sequence. The effective volumes were determined gravimetrically using an SI-traceably calibrated balance and using the known density of water at 20 °C.
- The effective (buoyant) density of the silica nanoparticles was determined experimentally using isopycnic velocity interpolation and multi-velocity sedimentation approaches [6,18,19]. The measurement principle is based on the creation of a density gradient in an optically transparent cell. The particles to be analyzed migrate through the density gradient until they reach the zone where the density of the gradient matches the effective density of the particles. The zone of particle accumulation is detected optically. The density gradient can be constructed in an SI-traceable manner (temperature controlled, liquids of known density); hence, the effective density of the nanoparticles can also be considered to be SI-traceable.
- The sedimentation times of the particles, which are measured using the integrated computer clock, correspond to the time intervals between the start of measurement and the detection of a particle population (e.g., modal value of a PSD). SI-traceability of these time interval measurements can be established, for example, by accessing an SI-traceable Network Time Protocol service over a data network or by using a calibrated stopwatch.
3.2.3. Measurement Uncertainties for Results of CRMs
- For similar types of disc-CLS instruments, Kamiti and co-workers have demonstrated, using a tachometer, that the rotational speed is accurate within 0.4% [21]. This value is considered to be a realistic estimate of the relative standard uncertainty for the angular frequency, u(ω).
- Among the different uncertainty sources shown in the fishbone diagram, temperature is considered to be the most important factor affecting the average viscosity of the gradient. The instrument, however, does not allow for the on-line monitoring of the gradient’s temperature during sample analysis. Instead, the temperature of the gradient can only be measured manually by immersing a temperature sensor in the carrier fluid immediately after having stopped the instrument. We conservatively consider that the measured temperature agrees with the temperature of the equilibrated gradient (during operation) within ±0.5 °C. For the given temperature variation, and using the experimental viscosity data shown in Figure S2, the average viscosity of the pristine gradient has a range of 0.018 mPa s. The experimental viscosity measurements were performed under intermediate precision conditions (different days). For both types of sucrose solutions, the standard deviation calculated from the replicate results at 30 °C was 0.043 mPa s. Considering that the effect of temperature on the viscosity follows a rectangular probability distribution (with a half-width of 0.009 mPa s), the absolute standard uncertainty for the average viscosity of the sucrose gradient, u(η), is estimated according to Equation (3),For an average viscosity of 0.907 mPa s, the relative standard uncertainty corresponds to 4.8%.
- Using the approach explained for estimating the uncertainty of the average viscosity, a standard combined uncertainty of 0.0002 g/cm3 was estimated for the average density of the sucrose gradient by combining the standard deviation (0.0001 g/cm3) of the density results at 30 °C and the half-width (0.0001 g/cm3) of the rectangular distribution when assuming a temperature fluctuation of ±0.5 °C. For an average density of the sucrose gradient of 1.0067 g/cm3, the relative standard uncertainty, u(ρf)/ρf, corresponds to 0.01%.
- The radial position of the photodetector (M) was determined to be located 4.25 cm from the center of the disc. The distance was confirmed using a paper strip specifically designed by the manufacturer for this purpose. A standard uncertainty, u(M), of 0.05 cm, or 1.18% in relative terms, is considered realistic.
- The radial position of the inner liquid surface (S) of the sucrose gradient depends on the total volume of the two sucrose solutions injected and on the injected volumes of the samples. The gradient is created by injecting nine 1.6 mL volumes of a mixture of 20 g/kg and 80 g/kg sucrose solutions and one 0.5 mL volume of n-dodecane.The sucrose solutions were injected using disposable plastic syringes with a volume scale graduated in 0.1 mL intervals. If the syringes are carefully filled with liquid, i.e., by avoiding air bubbles, then a volume accuracy of ±0.05 mL can be achieved for each injection. In this case, the effective volume of the sucrose gradient (+0.5 mL of n-dodecane) in the disc is expected to be between 14.40 mL and 15.40 mL, corresponding to S values of 3.93 cm and 3.87 cm, respectively. Based on the half-width (0.06 cm) calculated from the values for S, and assuming a triangular probability distribution, the relative standard uncertainty is about 0.6%.Sub-sampling and sample injection were performed using disposable plastic syringes with a volume scale graduated in 0.01 mL intervals. For each measurement, a nominal volume of 0.20 mL of the undiluted silica CRM was injected. Based on repeated sampling and injection experiments, the uncertainty associated with the effective sample volume has been estimated to be 3.43% or 0.01 mL. The relative standard uncertainty, u(S)/S, is estimated according to Equation (4):
- A relative standard uncertainty, u(ρp)/ρp, of 2.50% for the effective density of silica nanoparticles has been determined in a previous study [6].
- The uncertainty associated with the sedimentation time, u(tp), of the silica nanoparticles is assumed to comprise a contribution related to the actual start of the time recording (time lag between manually starting the measurement and sample injection) and a contribution related to the measurement of the time at which the modal value occurs. The time lag between sample injection and the start of the measurement is estimated to be in the range of 0.1 s to 0.5 s. Compared to the relatively long measurement time required for silica nanoparticles, this short time lag can be assumed negligible, and the uncertainty mainly depends on the repeatability of the time measurements of the modal value. Throughout a measurement sequence, the volume of the carrier fluid increases and thus also the sedimentation times. The relationship between sedimentation time and the number of injected replicates is linear. To estimate the uncertainty, u(tp), the sedimentation times are normalized using the slope of the linear relationship. Based on the half-width (0.4 s and 12.4 s for the large and small nanoparticle populations of ERM-FD102), and by considering a triangular probability distribution, the relative standard uncertainties of the sedimentation time are 0.3% and 0.7%, respectively for the large and small nanoparticle populations.
3.2.4. Implications for End Users
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Symbols
| CRM | certified reference material |
| dcal | assigned particle size of calibrant |
| dSt,p | Stokes diameter of test particles |
| Disc-CLS | disc centrifugal liquid sedimentation |
| GUM | Guide to the Expression of Uncertainty in Measurement |
| ISO | International Organization for Standardization |
| ITS-90 | International Temperature Scale of 1990 |
| JRC | Joint Research Centre of the European Commission |
| k | coverage factor |
| M | radial position of the detector |
| N | normal distribution |
| PSD | particle size distribution |
| PVC | polyvinyl chloride |
| R | rectangular distribution |
| S | radius of the inner liquid surface |
| SI | International System of Units |
| tcal | sedimentation time of the calibration particles |
| tp | sedimentation time of the test particles |
| T | triangular distribution |
| u | standard uncertainty (confidence level 68%) |
| uc | combined uncertainty (confidence level 68%) |
| U | expanded uncertainty (confidence level 95%) |
| VIM | Vocabulary of Metrology |
| xi | quantity |
| η | average dynamic viscosity between M and S |
| ρcal | assigned mean effective particle density of calibrant |
| ρf | average density of the carrier fluid between M and S |
| ρp | effective particle density |
| ω | angular frequency of the disc |
References
- International Organization for Standardization (ISO); International Electrotechnical Commission (IEC). ISO/IEC Guide 99: 2007 International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM); ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Gollwitzer, C.; Bartczak, D.; Goenaga-Infante, H.; Kestens, V.; Krumrey, M.; Minelli, C.; Pálmai, M.; Ramaye, Y.; Roebben, G.; Sikora, A.; et al. A comparison of techniques for size measurement of nanoparticles in cell culture medium. Anal. Methods 2016, 8, 5272–5282. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). ISO 13318-1 Determination of Particle Size Distribution by Centrifugal Liquid Sedimentation Methods—Part 1: General Principles and Guidelines; ISO: Geneva, Switzerland, 2001. [Google Scholar]
- EURACHEM/CITAC. Traceability in Chemical Measurement—A Guide to Achieving Comparable Results in Chemical Measurement. Available online: https://www.eurachem.org/index.php/publications/guides/trc (accessed on 5 October 2018).
- International Union of Pure and Applied Chemistry (IUPAC). Metrological traceability of measurement results in chemistry: Concepts and implementation. Pure Appl. Chem. 2011, 83, 1873–1935. [Google Scholar] [CrossRef]
- Kestens, V.; Coleman, V.A.; De Temmerman, P.-J.; Minelli, C.; Woehlecke, H.; Roebben, G. Improved metrological traceability of particle size values measured with line-start incremental centrifugal liquid sedimentation. Langmuir 2017, 33, 8213–8224. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Standardization (ISO). ISO 13318-2 Determination of Particle Size Distribution by Centrifugal Liquid Sedimentation Methods—Part 2: Photocentrifuge Method; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Kestens, V.; Roebben, G.; Herrmann, J.; Jamting, Å.K.; Coleman, V.A.; Minelli, C.; Clifford, C.A.; De Temmerman, P.-J.; Mast, J.; Junjie, L.; et al. Challenges in the size analysis of a silica nanoparticle mixture as candidate certified reference material. J. Nanopart. Res. 2016, 18, 171. [Google Scholar] [CrossRef] [PubMed]
- McDonald, S.A.; Daniels, C.A.; Davidson, J.A. Determination of the true size of poly(vinyl chloride) latices by electron microscopy using a vertical shadowing technique. J. Colloid Interface Sci. 1977, 59, 342–349. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). ISO Guide 34 General Requirements for the Competence of Reference Material Producers; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Bohren, C.F.; Huffmann, D.R. Absorption and Scattering of Light by Small Particles, 2nd ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007; ISBN 9780471293408. [Google Scholar]
- International Organization for Standardization (ISO). ISO 9276-1 Representation of Results of Particle Size Analysis—Part 1: Graphical Representation; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- Babick, F. Characterisation of colloidal suspensions. In Suspensions of Colloidal Particles and Aggregates, 1st ed.; Valverde Millán, J.M., Ed.; Springer International Publishing: Cham, Switzerland, 2016; Volume 3, pp. 8–9. ISBN 9783319306612. [Google Scholar]
- International Organization for Standardization (ISO). ISO 15212-1 Oscillation-Type Density Meters—Part 1: Laboratory Instruments; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- Fehlauer, H.; Henning, W. Density reference liquids certified by the Physikalisch-Technische Bundesanstalt. Meas. Sci. Technol. 2006, 17, 10. [Google Scholar] [CrossRef]
- McLinden, M.O.; Splett, J.D. A liquid density standard over wide ranges of temperature and pressure based on toluene. J. Res. Natl. Inst. Stand. Technol. 2008, 113, 26–67. [Google Scholar] [CrossRef]
- Preston-Thomas, H. The international temperature scale of 1990 (ITS-90). Metrologia 1990, 27, 3–10. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). ISO 18747-1 Determination of Particle Density by Sedimentation Methods—Part 1: Isopycnic Interpolation Approach; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- International Organization for Standardization (ISO). ISO/FDIS 18747-2 Determination of Particle Density by Sedimentation Methods—Part 2: Multi-Velocity Approach; ISO: Geneva, Switzerland, 2019. [Google Scholar]
- International Organization for Standardization (ISO). ISO Guide 98-3 Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995); ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Kamiti, M.; Boldridge, D.; Ndoping, L.M.; Remsen, E.E. Simultaneous absolute determination of particle size and effective density of submicron colloids by disc centrifuge photosedimentometry. Anal. Chem. 2012, 84, 10526–10530. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Standardization (ISO); International Electrotechnical Commission (IEC). ISO/IEC 17025 General Requirements for the Competence of Testing and Calibration Laboratories; ISO: Geneva, Switzerland, 2017. [Google Scholar]
| CRM | dst,p1 | 〈η〉 2 | 〈ρf〉 2 | ρp3 | M | S | ω | tp |
|---|---|---|---|---|---|---|---|---|
| [nm] | [Pa s] | [g/cm3] | [g/cm3] | [cm] | [cm] | [rad/s] | [s] | |
| ERM-FD102 | ||||||||
| Population 1 | 22.5 | 0.0091 | 1.0070 | 2.0 | 4.25 | 3.87 | 2094 | 688 |
| Population 2 | 83.7 | 0.0091 | 1.0070 | 2.0 | 4.25 | 3.87 | 2094 | 50 |
| ERM-FD304 | 31.0 | 0.0095 | 1.0079 | 2.3 | 4.25 | 3.88 | 2094 | 285 |
| CRM | Particle Size 1 [nm] | |
|---|---|---|
| Routine | Reference | |
| ERM-FD102 | ||
| Population 1 | 24.7 ± 2.5 | 23.1 ± 2.8 |
| Population 2 | 90.1 ± 9.0 | 84.2 ± 10.1 |
| ERM-FD304 | 33.3 ± 3.1 | 31.1 ± 3.6 |
| Feature | Description |
|---|---|
| Physical principle | Sedimentation rate measurement |
| Technique | Disc-CLS (line-start incremental mode) |
| Detection system | Turbidity of an ensemble of particles with the same sedimentation rate |
| Data analysis | Routine method: conversion of time to particle size through sedimentation time scale calibration Reference method: conversion of sedimentation time to particle size through Stokes’ law |
| Type of diameter | Sphere-equivalent Stokes diameter |
| Type of weighting | Light extinction |
| Type of distribution | Density distribution |
| Representative value | Mode |
| Quantity, xi [unit] | Quantity Value | Standard Uncertainty, u(xi) | Distribution Type 1 | Contribution ∂f/∂xi·u(xi) [nm] |
|---|---|---|---|---|
| Angular frequency, ω [rad/s] | 2094 | 9 | N | −0.34 |
| Average viscosity of the carrier fluid between M and S, η [Pa s] | 0.0091 | 0.0004 | N & R | 2.05 |
| Average density of the carrier fluid between M and S, ρf [g/cm3] | 1.0070 | 0.0001 | N & R | <0.01 |
| Radial position photodetector, M [cm] | 4.25 | 0.05 | N | 1.39 |
| Radial position of inner liquid surface, S [cm] | 3.87 | 0.03 | T & N | 3.76 |
| Density silica, ρp [g/cm3] | 2.0 | 0.05 | N | −2.14 |
| Sedimentation time silica, tp [s] | 48.2 | 0.2 | T | −0.15 |
| Stokes diameter, dSt,p [nm] | 83.7 | Combined measurement uncertainty, uc(dSt,p) [nm] | 5.0 | |
| Expanded (k = 2) measurement uncertainty, U [nm] | 10.0 | |||
| Input Quantity, xi [unit] | Quantity Value | Standard Uncertainty, u(xi) | Distribution Type 1 | Contribution ∂f/∂xi·u(xi) [nm] |
|---|---|---|---|---|
| Angular frequency, ω [rad/s] | 2094 | 9 | N | −0.09 |
| Average viscosity of the carrier fluid between M and S, η [Pa s] | 0.0091 | 0.0004 | N & R | 0.55 |
| Average density of the carrier fluid between M and S, ρf [g/cm3] | 1.0070 | 0.0001 | N & R | <0.01 |
| Radial position photodetector, M [cm] | 4.25 | 0.05 | N | 0.37 |
| Radial position of inner liquid surface, S [cm] | 3.87 | 0.03 | T & N | −0.84 |
| Density silica, ρp [g/cm3] | 2.0 | 0.05 | N | −0.57 |
| Sedimentation time silica, tp [s] | 675 | 5.1 | T | −0.09 |
| Stokes diameter, dSt,p [nm] | 22.5 | Combined measurement uncertainty, uc(dSt,p) [nm] | 1.3 | |
| Expanded (k = 2) measurement uncertainty, U [nm] | 2.7 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kestens, V.; A. Coleman, V.; Herrmann, J.; Minelli, C.; G. Shard, A.; Roebben, G. Establishing SI-Traceability of Nanoparticle Size Values Measured with Line-Start Incremental Centrifugal Liquid Sedimentation. Separations 2019, 6, 15. https://doi.org/10.3390/separations6010015
Kestens V, A. Coleman V, Herrmann J, Minelli C, G. Shard A, Roebben G. Establishing SI-Traceability of Nanoparticle Size Values Measured with Line-Start Incremental Centrifugal Liquid Sedimentation. Separations. 2019; 6(1):15. https://doi.org/10.3390/separations6010015
Chicago/Turabian StyleKestens, Vikram, Victoria A. Coleman, Jan Herrmann, Caterina Minelli, Alex G. Shard, and Gert Roebben. 2019. "Establishing SI-Traceability of Nanoparticle Size Values Measured with Line-Start Incremental Centrifugal Liquid Sedimentation" Separations 6, no. 1: 15. https://doi.org/10.3390/separations6010015
APA StyleKestens, V., A. Coleman, V., Herrmann, J., Minelli, C., G. Shard, A., & Roebben, G. (2019). Establishing SI-Traceability of Nanoparticle Size Values Measured with Line-Start Incremental Centrifugal Liquid Sedimentation. Separations, 6(1), 15. https://doi.org/10.3390/separations6010015





