Box–Behnken-Assisted Optimization of High-Performance Liquid Chromatography Method for Enhanced Sugar Determination in Wild Sunflower Nectar

Abstract

Sunflower (Helianthus annuus L.) is a cross-pollinated species that relies on pollinators, attracted by itsnectar composition. Nectar consists primarily of sugars (up to 70%), with sucrose, glucose, and fructose being dominant, while minor components such as mannose, arabinose, xylose, and sugar alcohols (e.g., mannitol and inositol) occur in lower concentrations and vary with biotic and abiotic factors. This study developed a robust high-performance liquid chromatography method with refractive index detection (HPLC-RID) for the simultaneous quantification of eight sugars (D-ribose, xylose, arabinose, fructose, mannose, glucose, sucrose, and maltose) and two sugar alcohols (mannitol, meso-inositol) in wild sunflower nectar. A Box–Behnken design (BBD), coupled with response surface methodology (RSM), was used to systematically optimize column temperature (20–23 °C), acetonitrile concentration (80–85%), and flow rate (0.7–1 mL/min), while achieving baseline separation of critical sugar pairs, including the previously co-eluting glucose/mannitol and glucose/mannose. Satisfactory resolution (Rs > 1 for all analytes) was achieved under optimized separation conditions comprising a column temperature of 20 °C, 82.5% acetonitrile, and a flow rate of 0.766 mL/min. The RSM efficiently evaluated factor interactions to maximize chromatographic performance, resulting in an optimized protocol that provides a cost-effective and environmentally friendly alternative to conventional sugar analysis methods. Method validation confirmed satisfactory linearity across relevant concentration ranges (50–500 mg/L for most sugars; 50–5500 mg/L for fructose and glucose), with correlation coefficients (R) between 0.985 and 0.999. The limits of detection (LOD) and quantification (LOQ) for the analyzed sugars and sugar alcohols ranged from 4.04 to 19.46 mg/L and from 13.46 to 194.61 mg/L, respectively. Glucose exhibited the highest sensitivity showing LOD of 4.04 and LOQ of 13.46 mg/L, whereas mannose was identified as the least sensitive analyte, with LOD of 19.46 mg/L and LOQ of 194.61 mg/L. The described method represents a reliable tool for sugar and sugar alcohol analysis in sunflower nectar and can be extended to other plant and food matrices with suitable sample preparation.

1. Introduction

Sugars are essential for plants, as energy sources, carbon skeletons, and signaling molecules that reflect the physiological status, developmental stage, and environmental conditions [1]. They play a key role in stress responses by supporting the synthesis of defense compounds such as flavonoids, stilbenes, and lignins, while their accumulation increases under abiotic stresses like extreme temperatures or drought [2,3,4]. Specific sugars, including sucrose, glucose, fructose, and trehalose, act as metabolic signals regulating defense gene expression [1]. Sugar composition determines nutritional value and authenticity in foods, with profiling as a reliable tool to detect adulteration and ensure quality control [5,6].

Plants also provide nectar and pollen to pollinators, where sugars and amino acids in nectar are crucial for nutrition, thereby influencing pollinator behavior, and supporting plant reproduction [7]. Nectar is a complex aqueous solution that provides essential nutritional resources to pollinators. The dominant nectar sugars—sucrose, glucose, and fructose—vary in concentration and ratio across plant species and environments, often ranging from 10% to 70% of total solutes [8,9]. In addition, minor sugars and sugar alcohols, such as maltose, mannose, arabinose, xylose, ribose, melibiose, raffinose, stachyose, melezitose, mannitol, and sorbitol, may also be found, especially under abiotic stress conditions, where they function as osmoprotectants [10,11,12,13,14,15]. Mannitol is a compatible solute that supports plant tolerance to osmotic stress and drought by modulating genes involved in osmotic adjustment, ROS signaling, and hormone regulation [16,17,18]. The detection of mannitol in nectar under drought conditions likely reflects an adaptive stress response.

Sugar composition of nectar is shaped by plant genetics, phenology, environmental factors (e.g., drought, frost, heat), and pollinator preferences [7,9,19,20,21,22]. These variations are particularly pronounced in wild sunflower species, whose ecological plasticity and nectar traits remain underexplored. Understanding nectar sugar profiles can thus provide an insight into plant adaptation and pollinator interactions, especially important in the context of climate change [7,12,14,19,20,23,24].

Traditional techniques such as thin-layer chromatography have limited sensitivity and resolution for sugar analysis [10,11,12,20,25]. In contrast, High-Performance Liquid Chromatography (HPLC) has emerged as a more powerful tool for accurate sugar quantification, providing higher sensitivity, specificity, and accuracy in sugar quantification [26,27,28]. Given the limitations of detection systems—UV detection being less suitable due to sugars weak UV absorbance, and RID lacking gradient compatibility. Various HPLC methods have been developed for sugar analysis using detectors such as refractive index detectors (RID) [29,30], evaporative light scattering detectors (ELSD) [31,32], and ultraviolet detectors UV [33]. Robust HPLC method development requires precise optimization of conditions, such as mobile phase composition, pH, column temperature, and flow rate. Besides HPLC, sugars can be analyzed by gas chromatography–mass spectrometry or capillary electrophoresis, though both require extensive sample preparation and derivatization [34,35]. Non-destructive methods such as nuclear magnetic resonance, visible/near-infrared spectroscopy, Raman spectroscopy, and hyperspectral imaging have recently gained attention due to their speed, cost efficiency, and sustainability [36,37,38,39,40,41], although they may provide less detailed qualitative information than chromatographic techniques. Traditional HPLC method development often relies on the one-variable-at-a-time approach, which overlooks interactions between factors and requires numerous experiments, increasing time and resource use. In contrast, Response Surface Methodology (RSM) enables efficient optimization by evaluating the effects and interactions of multiple factors simultaneously, while requiring fewer experiments [42,43,44]. The Box–Behnken design, as a type of RSM, efficiently identifies individual and combined effects of variables, thereby reducing experimental load and improving method efficiency [45]. It has been successfully applied in optimizing various chromatographic methods [45,46,47,48,49,50,51].

The aim of this study was to apply RSM, and a Box–Behnken design, to develop and optimize an accurate, precise, and robust HPLC method with RID for the separation and simultaneous determination of multiple sugars and sugar alcohols in wild sunflower nectar. This approach was developed in response to the limitations of previous methods, particularly to address the co-elution of glucose and mannitol, as well as the incomplete resolution of glucose and mannose, which prevented accurate quantification. The significance of this method lies not only in its ability to quantify a broad range of sugars and sugar alcohols simultaneously, but also in its successful resolution of critical sugar pairs such as glucose/mannitol and glucose/mannose. Consequently, the method is a reliable, cost-effective, and environmentally friendly tool for routine nectar analysis and broader sugar profiling applications, particularly valuable for ecological and physiological studies.

2. Materials and Methods

2.1. Chemicals and Solutions

Standard sugars and sugar alcohols, including D-ribose, xylose, arabinose, mannose, mannitol, sucrose and maltose, were obtained from Sigma-Aldrich Chemie (Steinheim, Germany), while fructose, glucose, and meso-inositol were sourced from Merck (Steinheim, Germany). Individual stock solutions of each sugar (10,000 µg/mL) were prepared by dissolving 0.02 g of the respective compound in 2 mL of HPLC-grade distilled water (Milli-Q). From these, mixed working solutions were prepared containing ten sugars (including sugar alcohols) per mixture, with final concentrations ranging from 100 to 500 µg/mL, by appropriate dilution with Milli-Q water. Each working solution contained equal concentrations of the selected sugars. HPLC-grade acetonitrile used for mobile phase preparation was purchased from J.T. Baker (Deventer, The Netherlands), and Milli-Q water was used throughout the analysis. Nectar samples were collected from tubular flowers of wild sunflower species cultivated during the summer of 2024 at the experimental fields of the Institute of Field and Vegetable Crops, Novi Sad, Serbia, at the Rimski šančevi location.

2.2. HPLC Analysis and Sample Preparation

Sugar was determined using an HPLC system LC-2050C 3D (Shimadzu, Japan) equipped with a RID-20A refractive index detector (Shimadzu, Japan). Chromatographic separation was achieved on a Nucleosil 100-5 NH₂ column (250 mm × 4.6 mm, 5 µm particle size) from Macherey-Nagel (Düren, Germany). Data were acquired, processed and stored using LabSolution software version 5.117 (Shimadzu, Kyoto, Japan). Prior to injection, samples were centrifuged using a LACE16R centrifuge (COLO Lab Experts, Novo Mesto, Slovenia) and filtered through a CHROMAFIL RC disposable syringe filter (0.45 µm pore size, 25 mm diameter) from Macherey-Nagel (Düren, Germany).

2.3. Experimental Design and Statistical Analysis

The Box–Behnken Design (BBD) was selected as the experimental design, generated using Design Expert software (trial version), while data analysis was carried out using TIBCO Statistica 13.3.0 software (Palo Alto, CA, USA; 2017) and Microsoft Excel. This article evaluated the predictive performance of three distinct models—Linear, Linear Model with Main Effects Two Ways, and Quadratic—to assess their ability to predict two dependent variables: Rgm and Rmg. Additionally, analysis of variance (ANOVA) was conducted to assess the significance of the effects and interactions within the models.

Multiple statistical metrics, including the Root Mean Square Error (RMSE), Mean Bias Error (MBE), Mean Percentage Error (MPE), Sum of Squared Errors (SSE), Average Absolute Relative Deviation (AARD), and the coefficient of determination (R²), were employed in order to verify the mathematical models.

3. Results and Discussion

3.1. Preliminary Study

Preliminary separation and quantification of a mixture containing five standard sugars (xylose, fructose, mannose, glucose, and mannitol) was initially performed using a previously established HPLC method developed for the analysis of glucose, fructose, and sucrose in nectar [52,53]. The analysis was conducted on an HPLC system equipped with RID maintained at 40 °C and a Nucleosil 100-5 NH₂ amino column held at a column oven temperature of 30 °C. The mobile phase consisted of acetonitrile and water (80:20, v/v), delivered at a constant flow rate of 1 mL/min. The effectiveness of separation was evaluated based on the resolution (Rs) between adjacent peaks, calculated using the following formula:

$$Rs={\displaystyle \frac{1.18x\left({Rt}_2-{Rt}_1\right)}{\left(w_1+w_2\right)}},$$

(1)

where w₁ and w₂ are the peak widths at 50% and Rt₁, Rt₂ are retention times.

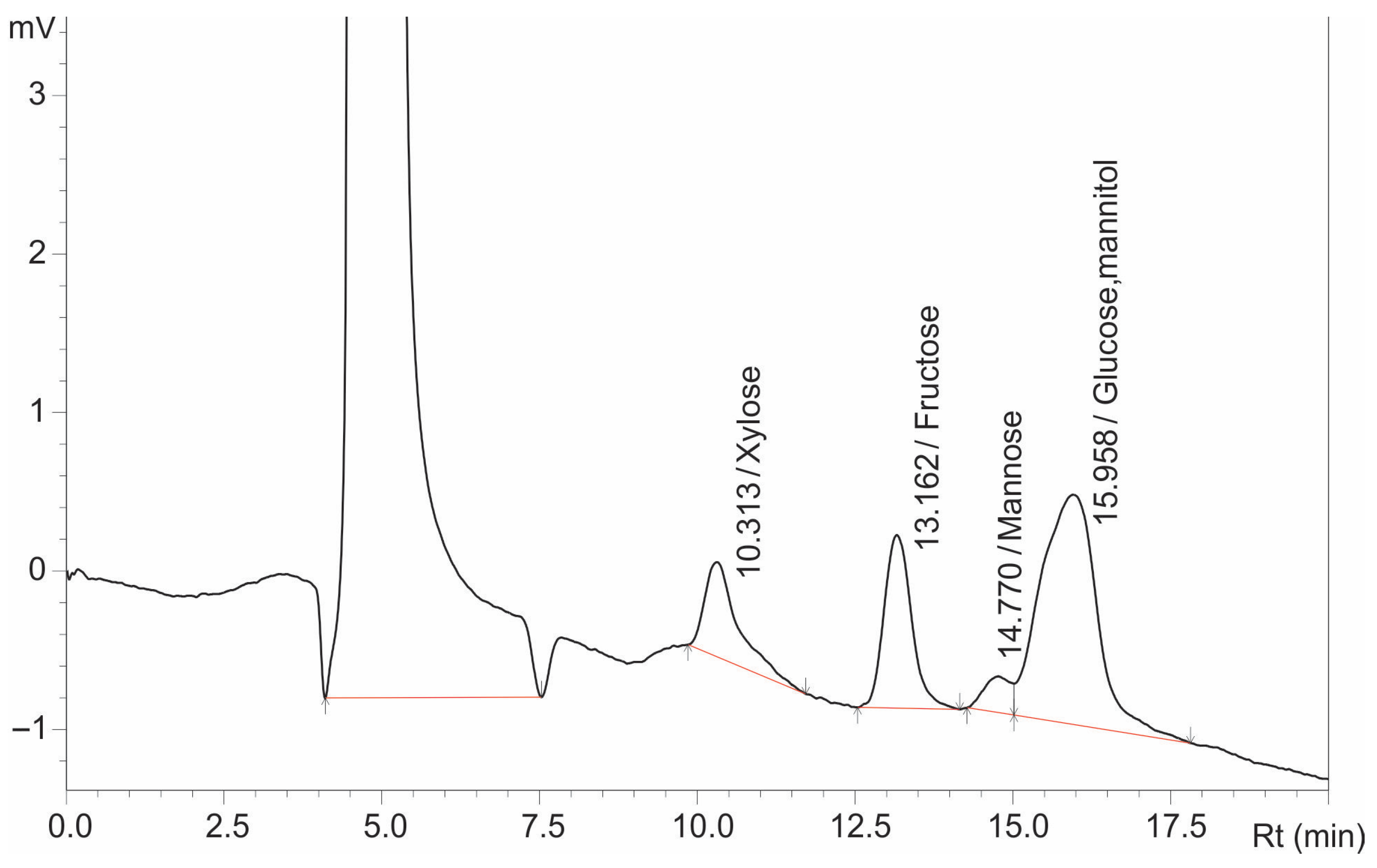
In chromatographic terms, a Rs value greater than 1.0 is generally considered acceptable, while Rs ≥ 1.5 indicates baseline (complete) separation. As shown in Figure 1, the previously applied method, as reported by Das et al., 2022 [52], failed to provide sufficient separation of some sugar components: the peaks of glucose and mannitol completely overlapped, and glucose and mannose were only partially resolved.

In contrast, xylose and fructose exhibited a resolution value above 1.5, confirming complete separation.

Experimental trials were performed to overcome the limitations of the previously published HPLC method and facilitate separation of mannose, glucose, and mannitol. These involved systematic adjustments to the key chromatographic parameters such as column temperature, mobile phase composition, flow rate, and elution mode, with the aim to improve resolution, particularly between the critical sugar pairs, and attain Rs values approaching or exceeding 1.5.

Among the investigated parameters, column temperature had a particularly significant impact on the separation efficiency of the critical sugar pairs mannose/glucose and glucose/mannitol. Column temperature is known to influence retention time, peak shape, and resolution by affecting analyte–stationary phase interactions [54,55]. For amino columns used in this study, such as the Nucleosil 100-5 NH₂, hydrogen bonding plays a key role in the retention of sugars. As the temperature increases, hydrogen bonds weaken, leading to faster elution but often at the cost of resolution. Conversely, lower temperatures strengthen hydrogen bonding, thereby improving separation and sensitivity [29]. This effect is particularly important for structurally related sugars, such as glucose and mannose, where subtle stereochemical differences in hydroxyl group orientation are discriminated more effectively at lower temperatures. Stabilization of hydrogen bonding under these conditions adds fine structural distinctions, resulting in enhanced chromatographic selectivity [56,57,58]. Temperature also affects the viscosity of the mobile phase, affecting analyte migration and overall retention. 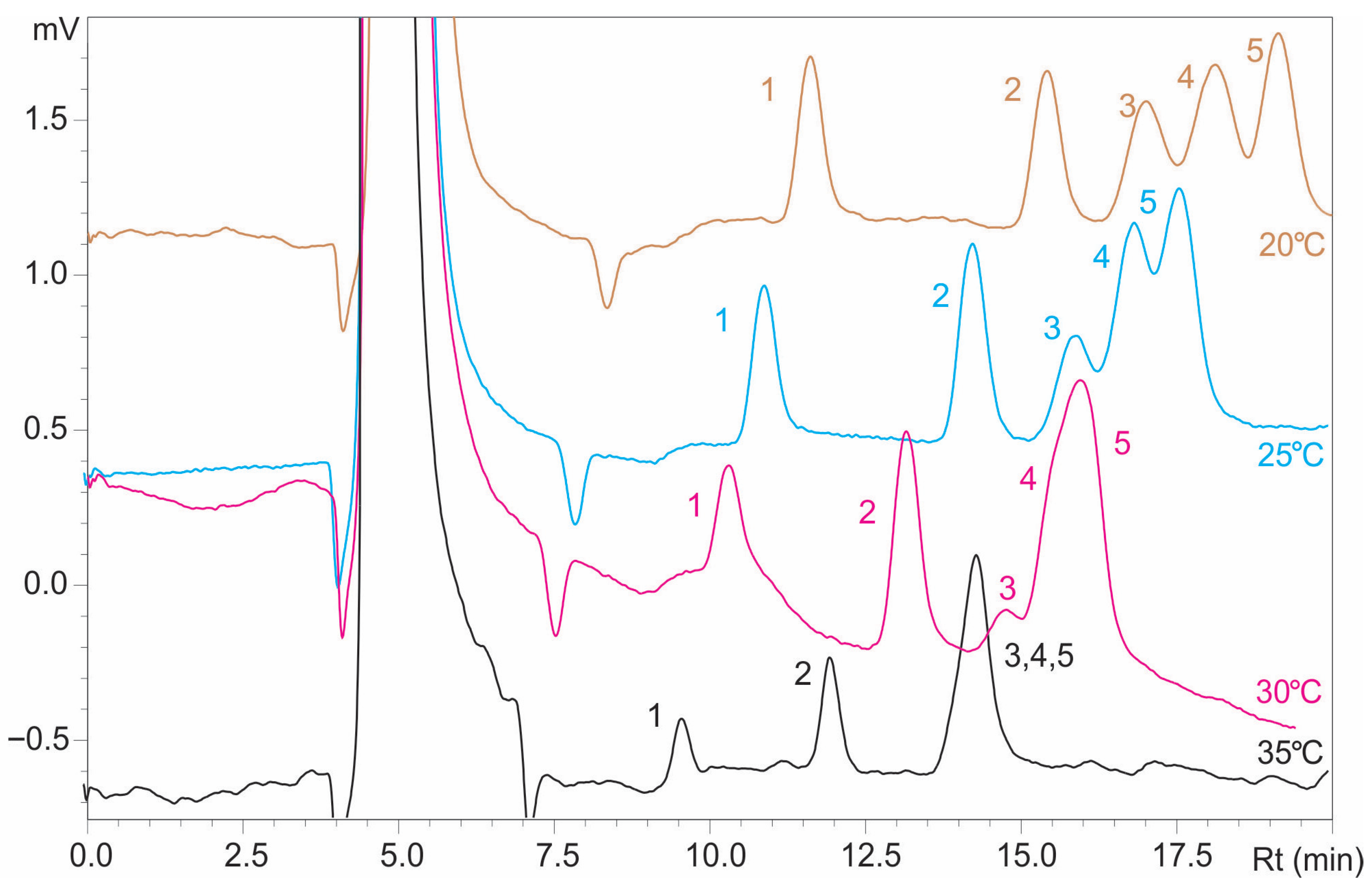Higher temperatures reduce viscosity, allowing compounds to elute more rapidly, but may result in insufficient resolution [59]. To evaluate the influence of column temperature on the separation of mannose, glucose, and mannitol, a series of experiments was conducted at 20 °C, 25 °C, 30 °C, and 35 °C, by using a mobile phase of acetonitrile:water (80:20, v/v) while keeping the flow rate constant at 1 mL/min. At higher temperatures (30 °C and 35 °C), the resolution values were below 1.0 for both sugar pairs, indicating inadequate separation. At 25 °C, an improved separation was observed, with the resolution between mannose and glucose (Rmg) reaching 1.200, which is acceptable, although the glucose and mannitol resolution (Rgm) remained insufficient at 0.916. The optimal separation was achieved at 20 °C, where Rmg was 1.160 and Rgm reached 1.066, as shown in Figure 2 and

Table 1. Effect of column temperature on the resolution of mannose/glucose (Rmg) and glucose/mannitol (Rgm) pairs under isocratic conditions (acetonitrile: water = 80:20, v/v; flow rate 1 mL/min).

Column Temperature (°C)	Rmg	Rgm
35	0	0
30	1.079	0
25	1.200	0.916
20	1.160	1.066

, highlighting that lower temperatures stabilize hydrogen bonding and enhance selectivity for structurally similar sugars, such as glucose and mannose, by effectively discriminating subtle stereochemical differences.

In addition to improving resolution, lower column temperatures enhanced detector response, which is particularly beneficial for sensitive and accurate quantification resulting in increased peak areas and improved signal quality.

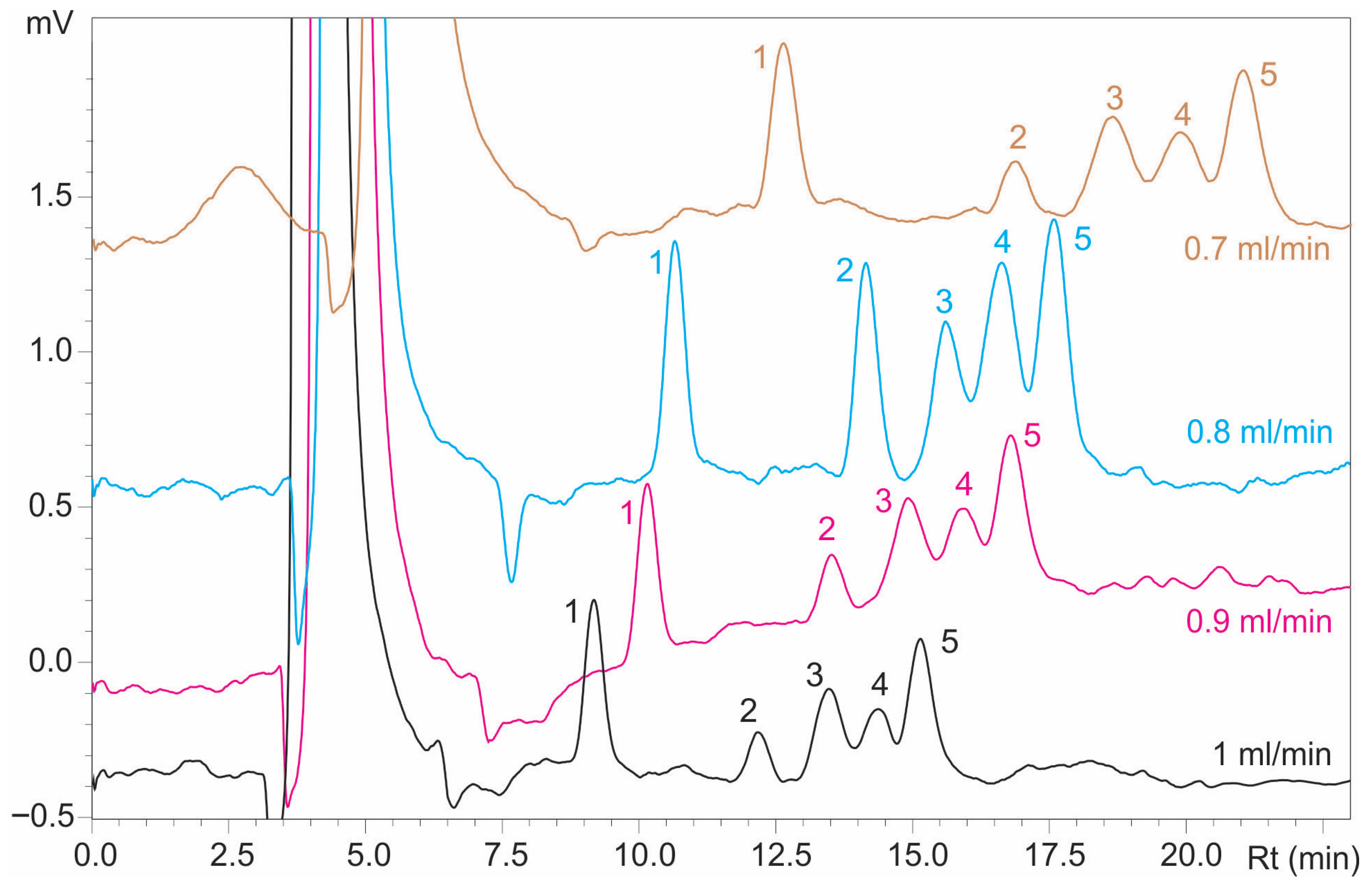
Furthermore, the effect of flow rate on sugar separation was investigated by varying it from 1 mL/min to 0.7 mL/min. A reduction in flow rate contributed to better resolution, but it also led to longer elution. As shown in Figure 3, retention times were extended at flow rates of 0.8 and 0.7 mL/min. The highest resolution factors (Rmg = 1.217 and Rgm = 1.032) were achieved at 0.9 mL/min, though the improvement over 1 mL/min was marginal, highlighting the balance between analyte–stationary phase interaction and peak broadening for optimal high-resolution separation, as summarized in

Table 2. Effect of flow rate on sugar resolution of mannose/glucose (Rmg) and glucose/mannitol (Rgm) pairs under at 20 °C using acetonitrile:water (80:20, v/v) mobile phase.

Mobile Phase Flow Rate (mL/min)	Rmg	Rgm
1	1.145	1.056
0.9	1.217	1.032
0.8	1.160	1.066
0.7	1.165	1.112

.

The mobile phase composition is a critical factor influencing separation efficiency. Given the polar nature of carbohydrates, highly polar solvents—such as water, methanol, or acetonitrile—are essential for effective resolution. A widely employed mobile phase for carbohydrate separation consists of acetonitrile and water in varying ratios [25,29,30,60,61]. The optimal acetonitrile content (typically 75–85%) depends on the column chemistry, flow rate, temperature, and the characteristics of the analyte. Increasing the water fraction accelerates elution but often compromises resolution and peak symmetry. Conversely, higher acetonitrile concentrations enhance separation selectivity at the expense of prolonged retention times and increased baseline noise [27,29,61,62,63]. In summary, higher acetonitrile content reduces analyte solvation, strengthening hydrogen bonding and dipole interactions with the stationary phase, and thereby improving retention and selectivity for structurally similar sugars. On the other hand, lower acetonitrile ratios favor solvation in the mobile phase, and reduce selectivity [57,64,65]. To systematically evaluate these effects, analyses were performed using acetonitrile compositions ranging from 75% to 85% under fixed chromatographic conditions (flow rate: 0.7 mL/min; column temperature: 20 °C).

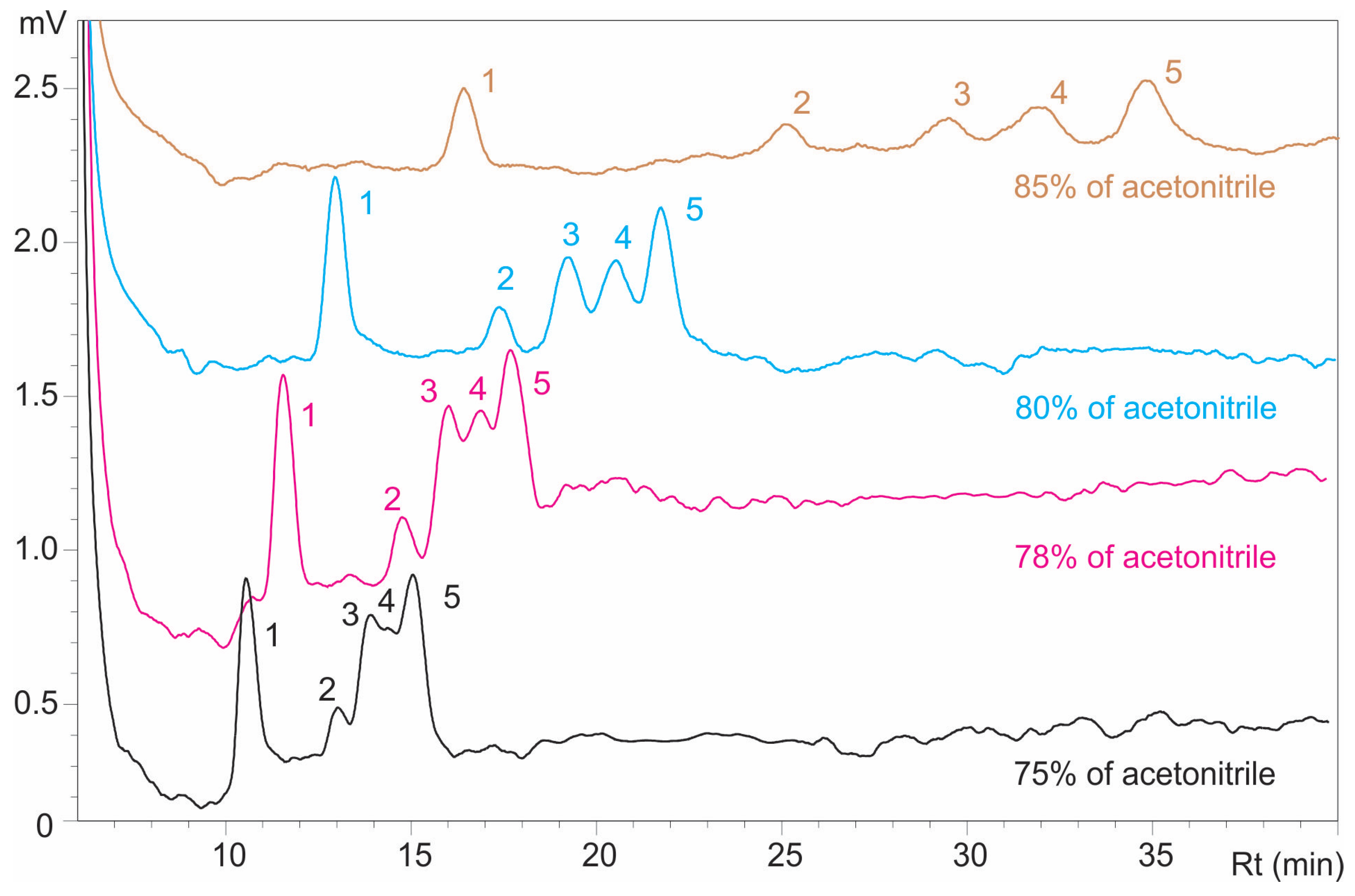
Faster elution of components was observed with mobile phases containing 75% and 78% acetonitrile (Figure 4); however, inadequate separation was achieved under these conditions. At 75% acetonitrile, resolution factors of 1.068 (Rmg) and 1.076 (Rgm) were obtained, while at 78%, resolution factors had very similar values of 1.042 (Rmg) and 1.040 (Rgm). Separation improved when acetonitrile concentration was increased to 80%, with Rmg and Rgm values rising to 1.184 and 1.106, respectively (

Table 3. Effect of acetonitrile percentage on resolution of mannose/glucose (Rmg) and glucose/mannitol (Rgm) pairs under isocratic conditions (Flow rate 0.7 mL/min; Column temperature 20 °C).

Percentage of Acetonitrile in the Mobile Phase (%)	Rmg	Rgm
75	1.068	1.076
78	1.042	1.040
80	1.184	1.106
85	1.200	1.433

), reflecting the mechanistic effect of higher acetonitrile content in reducing analyte solvation and enhancing interactions with the stationary phase for better retention and selectivity of structurally similar sugars.

In contrast, separation was satisfactory attained when using a mobile phase with 85% acetonitrile, yielding which resulted in resolution factors of 1.200 (Rmg) and 1.433 (Rgm) but also in broad peaks, prolonged elution times, and elevated baseline noise, as illustrated in Figure 4.

Mobile phase pH optimization can significantly enhance chromatographic separation. However, in aminopropyl-silica columns, pH modification induces covalent bond formation between the stationary phase amino groups and analytes, ultimately leading to column poisoning and efficiency degradation [27,60]. Given this pH sensitivity, no pH adjustments were made, and the mobile phase maintained the inherent pH of the pure solvent mixture (acetonitrile/water, 80:20 v/v) in all the experiments.

3.2. Experimental Design

Following the results of the preliminary study, a three-level, three-factor Box–Behnken experimental design was used to determine the influence of A. temperature T (°C), B. acetonitrile (%), and C. flow rate (mL/min) on the resolution between mannose and glucose (Rmg) and glucose and mannitol (Rgm). Upper and lower levels of variables were chosen based on the results of the preliminary study. The best results were achieved at column temperatures between 20 °C and 23 °C, with the percentage of acetonitrile in the mobile phase ranging from 80% to 85%, and flow rates between 0.7 and 1 mL/min. Although resolution (Rgm) was obtained at 25 °C, its relatively low value (0.91) was considered insufficient for reliable separation, and this temperature was excluded from the optimal range. Since the best result was observed at 20 °C, the authors decided to test a narrow temperature range between 20 and 23 °C for further method optimization The Design-Expert software (free trial) was used at three levels: A: 20 °C (−1), 21.5 °C (0), 23 °C (1); B: 80% (−1), 82.5% (0), 85% (+1); C: 0.7 mL/min (−1), 0.85 mL/min (0), 1 mL/min (+1) listed in

Table 4. Independent variables, ranges, and levels used in the Box–Behnken design to determine resolution between mannose, glucose, and mannitol.

Factors	Unit	Symbol	Levels
			(−1)	(0)	(+1)
Temperature	°C	A	20	21.5	23
Acetonitrile	%	B	80	82.5	85
Flow rate	mL/min	C	0.7	0.85	1

.

The Box–Behnken design matrix demonstrated consistent and reliable results (

Table 5. Box–Behnken design matrix and experimental data.

Runs	Factors			Responses
	A: T (°C)	B: Acetonitrile (%)	C: Flow Rate (mL/min)	Rmg	Rgm
1	20	82.5	1	1.017	1.155
2	21.5	80	1	1.080	1.170
3	21.5	82.5	0.85	1.258	1.036
4	21.5	82.5	0.85	1.258	1.036
5	23	80	0.85	1.130	0.999
6	21.5	80	0.7	1.130	1.050
7	20	82.5	0.7	1.191	1.064
8	23	82.5	1	1.197	1.068
9	20	85	0.85	1.320	1.330
10	23	82.5	0.70	1.236	0.986
11	23	85	0.85	1.210	1.180
12	21.5	85	1	1.160	1.180
13	20	80	0.85	1.080	1.170
14	21.5	85	0.7	1.310	1.250
15	21.5	82.5	0.85	1.170	1.220

), particularly evident from the replicated center point runs (Runs 3 and 4), which yielded identical values (Rmg = 1.258, Rgm = 1.036), and a third center point (Run 15) with a minor variation. The responses (Rmg: 1.017–1.320; Rgm: 0.986–1.330) indicated a strong influence of the experimental factors. The highest values for both responses were observed in Run 9 (T = 20 °C, Acetonitrile 85%, Flow = 0.85 mL/min), suggesting a synergistic effect of low temperature and high acetonitrile concentration. Lower flow rates (e.g., 0.7 mL/min in Run 14) also appeared to enhance Rmg, potentially due to increased residence time or improved mass transfer. The data supported a second-order model, as expected in Box–Behnken designs, showing evidence of nonlinear behavior and interaction effects between temperature, acetonitrile concentration, and flow rate. The near-identical values of Rmg and Rgm in several runs (e.g., Runs 2, 12, and 13) under different combinations of factors suggest possible factor interactions that offset each other, and stabilize the response. The center point replicates provide a good estimation of experimental error and confirm model reproducibility.

Notably, higher acetonitrile percentages (85%) generally led to improved Rgm values, likely due to enhanced solubility or better chromatographic behavior under these conditions. Flow rate also played a significant role, with lower values tending to increase Rmg, as seen in Runs 7 and 14, while excessively low flow (0.7 mL/min) sometimes diminished Rgm, possibly due to peak broadening. These trends highlight the importance of carefully balancing the three factors to achieve optimal response values, which will be further confirmed and quantified through regression analysis and response surface modeling.

3.2.1. Linear Model

A linear model with main effects can be expressed as:

$$Y={\beta }_0+{\sum }_{i=1}^3{\beta }_i·X_i+\epsilon$$

(2)

where Y represents the dependent variable, β₀ is the intercept, β₁, β₂, β₃, are the coefficients for the main effects of the variables X₁, X₂, X₃, and the term ϵ denotes the error term.

The ANOVA results for the response variable Rgm indicate that the overall regression model is statistically significant, with an R² value of 0.71579 and an adjusted R² of 0.63827. The individual factor analysis showed that temperature and acetonitrile percentage have statistically significant effects on Rgm. The flow rate, however, is not a significant factor (p > 0.05).

From the regression coefficients, temperature had a negative effect on Rgm (β₁ = −0.0536), meaning that increasing temperature tends to reduce Rgm values. Conversely, the acetonitrile percentage had a positive effect (β₂ = 0.0384), indicating that higher acetonitrile concentrations lead to increased Rgm. The flow rate showed a positive coefficient (β₃ = 0.085), but this effect is not statistically reliable due to its high standard error and non-significant p-value.

The linear model for the response variable Rmg showed a moderate fit, with an R² value of 0.61588 and an adjusted R² of 0.51112. The mean square of the residuals (0.005502) suggested acceptable variation remaining in the model.

According to the ANOVA table, acetonitrile percentage had a statistically significant positive effect on Rmg (p < 0.05), with a regression coefficient of β₂ = 0.03115, indicating that the increase in acetonitrile concentration tends to increase Rmg values. The flow rate also showed a significant negative effect (p < 0.05), with a coefficient of β₃ = −0.46167, indicating that higher flow rates are associated with a decrease in Rmg. In contrast, temperature did not have a statistically significant impact (p > 0.05), and its confidence interval included zero, suggesting its effect is not distinguishable from random error under the current model.

The linear model for Rmg suggested that acetonitrile concentration and flow rate are the key variables influencing Rmg, and their inclusion significantly improves the model’s explanatory power.

3.2.2. Linear Model with Main Effects Two Ways

A linear model with main effects and two-way interactions can be expressed as:

$$Y={\beta }_0+{\sum }_{i=1}^3{\beta }_i·X_i+{\sum }_{i=1,j=1+i}^3{\beta }_{ij}·{(X}_i·X_j)+\epsilon$$

(3)

where Y represents the dependent variable, β₀ is the intercept, β₁, β₂, β₃, are the coefficients for the main effects of the variables X₁, X₂, X₃, and β₁₂, β₁₃, β₂₃ represents the interaction between X₁, X₂, X₃. The term ϵ denotes the error term.

The linear model with main effects two ways for the response variable Rgm demonstrated a relatively good fit, with an R² of 0.74799 and an adjusted R² of 0.55898, indicating that the total variability in Rgm is explained by the model, although the adjusted R² suggests that the inclusion of several non-significant terms reduces its overall efficiency. According to the ANOVA results, temperature (p < 0.05) and acetonitrile concentration (p < 0.05) showed significant main effects, while the flow rate was not statistically significant (p > 0.05). However, in the regression coefficient output, none of the main effects showed statistical significance (all p > 0.05), likely due to high standard errors and multicollinearity caused by the inclusion of interaction terms, as reflected in the wide confidence intervals. Furthermore, none of the interaction terms (temperature×acetonitrile, temperature×flow rate, acetonitrile×flow rate) were statistically significant, with all p-values exceeding 0.05, indicating the absence of meaningful synergistic or antagonistic interactions between the examined factors. These results suggest that the variation in Rgm is primarily influenced by the linear effects of temperature and acetonitrile, as indicated by the ANOVA, while the overall model could benefit from simplification by removing non-significant interaction terms to enhance precision and interpretability.

The linear regression model for the dependent variable Rmg, based on three factors (temperature, acetonitrile, and flow rate) and their interactions, explains the total variability (R² = 0.77465), with an adjusted R² of 0.60564, indicating a moderate model fit. Among the linear terms, acetonitrile exhibits a statistically significant effect (p < 0.05), suggesting a meaningful contribution to the prediction of Rmg. The factor flow rate was also significant at the 5% level (p < 0.05), while the effect of temperature was not statistically significant (p > 0.05). None of the interaction terms reached statistical significance, although the interaction between temperature and flow rate approached the 10% significance level (p < 0.10), indicating a possible synergistic effect that may warrant further investigation. The relatively low mean square residual (MS = 0.0044381) suggests that the model captures the response variability well, though the wide confidence intervals for regression coefficients and large standard errors—particularly for flow rate and its interactions—point to a certain degree of imprecision and variability in the estimates.

The results suggested that acetonitrile was the most influential factor affecting Rmg under the conditions tested, while temperature and flow rate may have had weaker or more complex roles. The non-significant but borderline interaction between temperature and flow rate could indicate potential combined effects not fully captured by the current experimental design. The adjusted R² indicated some overfitting, as the model lost its explanatory power when accounting for the number of predictors. Further refinement through model simplification or expansion of the dataset could help improve model reliability and interpretability. Validation through replication or external data testing is recommended to ensure the generalizability of these findings.

3.2.3. Quadratic Model

A quadratic model can be expressed as:

$$Y={\beta }_0+{\sum }_{i=1}^3{\beta }_i·X_i+{\sum }_{i=1}^3{\beta }_i·{X_i}^2+{\sum }_{i=1,j=1+i}^3{\beta }_{ij}·{(X}_i·X_j)+\epsilon$$

(4)

where Y represents the dependent variable, β₀ is the intercept, β₁, β₂, β₃, are the coefficients for the main effects of the variables X₁, X₂, X₃, and β₁₂, β₁₃, β₂₃ represents the interaction between X₁, X₂, X₃. The term ϵ denotes the error term.

The quadratic regression model for the response variable Rgm explained approximately 82.82% of the total variability in the data (R² = 0.82817), indicating a good overall model fit. However, the adjusted R² was substantially lower at 0.51889, suggesting that the inclusion of additional terms (quadratic and interaction) may not substantially improve model performance relative to model complexity, particularly due to the small sample size (15 runs).

Among the linear terms, the factor acetonitrile showed a statistically significant effect (p < 0.05), indicating it plays an important role in predicting Rgm. Temperature also contributed significantly in its linear form (p < 0.05), while the linear and quadratic terms for flow rate, as well as all interaction terms, were not statistically significant. The quadratic effects of temperature and acetonitrile were not significant either, with p-values of p > 0.05, respectively, suggesting slight curvature in their relationships with Rgm.

The model’s residual mean square (MS = 0.0060742) was acceptably low, but the high standard errors and wide 95% confidence intervals for regression coefficients—especially for linear and quadratic terms of flow rate—indicated high variability and low precision of these estimates, further implying that some terms may have been overfitted the data or affected by collinearity.

The quadratic model identified acetonitrile and temperature as the most influential factors in determining Rgm, primarily through their linear effects. The overall predictive robustness of the model was limited by the small sample size, non-significant higher-order terms, and wide confidence intervals, suggesting that a simpler linear model or additional data may yield more reliable and interpretable results.

The quadratic model for the response variable Rmg, based on three factors and their linear, quadratic, and two-way interaction terms, explained 83.2% of the total variability (R² = 0.83208), though the adjusted R² dropped to 52.98%, suggesting potential overfitting or the inclusion of non-informative terms. According to the ANOVA table, only the linear effects of acetonitrile (p < 0.05) and flow rate (p = 0.0432) were statistically significant at the 0.05 level, while all quadratic and interaction terms showed no significant contribution (p > 0.05). Although linear terms of acetonitrile and flow rate appeared to be significant in the ANOVA, their corresponding regression coefficients were not statistically significant, likely due to collinearity, limited degrees of freedom, or low statistical power stemming from the small sample size (15 runs). The mean square residual was low (0.005291), indicating minimal unexplained variance, but the inconsistency between the ANOVA and regression p-values suggested that the model may benefit from simplification by removing non-significant terms to improve interpretability and model parsimony.

The effects and interactions of key process variables (temperature, acetonitrile, and flow rate) on Rmg and Rgm were visually presented using 3D surface plots, as shown in Figure 5.

The critical value analysis for the response variable Rmg indicates a saddle point solution with a predicted value of 1.213, suggesting that this point is not a clear maximum or minimum but a transitional region on the response surface where the effect of variables changes direction. The critical values identified by the model were 24.04 °C for temperature, acetonitrile = 82.25%, and flow rate = 0.92 mL/min. While the acetonitrile and flow rate values lied within the experimental range (80–85% and 0.7–1.0 mL/min, respectively), the temperature slightly exceeded the tested maximum of 23 °C, indicating that further experiments at higher temperatures may help clarify the response trend. The saddle point nature implies that small changes in these variables could lead to either an increase or decrease in Rmg, depending on the direction, highlighting the significance of interaction effects between parameters in determining Rmg.

The critical value analysis for the response variable Rgm revealed a saddle point solution with a predicted value of 0.989, indicating a transitional zone on the response surface rather than a distinct maximum or minimum. The critical values determined by the model were temperature = 23.32 °C, acetonitrile = 79.74%, and flow rate = 0.76 mL/min. All three values lied within or very close to the boundaries of the experimental range, suggesting that the saddle point occurs near the edge of the tested conditions. The slight deviation of acetonitrile below the minimum and the proximity of temperature to the upper limit indicated that minor changes in these variables may significantly influence the Rgm response.

3.3. Mathematical Verification of the Models

The verification table compares the predictive performance of three models—Linear, Linear model with main effects two ways, and Quadratic—for two dependent variables (Rgm and Rmg) using multiple statistical metrics (

Table 6. Experimental verification of mathematical models.

Model	Parametar	χ2	RMSE	MBE	MPE	SSE	AARD	R2
Linear	Rmg	0.004	0.064	0.000	3.994	0.061	15.000	0.616
	Rgm	0.004	0.058	0.000	4.733	0.050	15.000	0.716
Linear model with main effects, two-way	Rmg	0.003	0.049	0.000	3.265	0.036	15.000	0.775
	Rgm	0.003	0.054	0.000	4.715	0.045	15.000	0.748
Quadratic	Rmg	0.002	0.042	0.000	3.191	0.026	15.000	0.832
	Rgm	0.002	0.045	0.000	3.549	0.030	15.000	0.828

RMSE—Root Mean Square Error, MBE—Mean Bias Error, MPE—Mean Percentage Error, SSE—Sum of Squared Errors, AARD—Average Absolute Relative Deviation, R²—the coefficient of determination.

). Overall, the quadratic model demonstrated the best performance, followed by the linear model with interaction terms, and then the purely linear model.

For both Rgm and Rmg, the quadratic model yielded the lowest values of RMSE (0.045 and 0.042), MPE (3.549 and 3.191), and SSE (0.030 and 0.026), indicating higher accuracy and lower prediction error. The R² values were also highest in the quadratic model (0.828 for Rgm and 0.832 for Rmg), confirming that this model explains the greatest proportion of variance in the observed data. Additionally, the χ² values were lowest for the quadratic model (0.002 for both variables), further supporting its superior fit.

The mean bias error (MBE) was zero across all models and variables, indicating no systematic over- or under-prediction, and the mean percentage error (MPE) remained relatively low across all models, with the quadratic model again showing the smallest values (3.549 for Rgm and 3.191 for Rmg). The skewness and kurtosis values for the residuals were close to zero across all models, with no extreme departures from normality, although some negative kurtosis (platykurtic distribution) was observed.

The standard deviation (StDev) and variance (Var) of residuals were the lowest in the quadratic model, reflecting more consistent prediction errors.

3.4. Experimental Verification of the Models

The optimization was carried out with the objective of maximizing both Rmg and Rgm, as high resolution between these sugar pairs is critical for reliable quantification. Among the tested models, the quadratic model provided the best fit to the experimental data and allowed reliable prediction of factor–response relationships. The optimal chromatographic conditions identified (

Table 7. Validation of mathematical models through experiments.

Model	Parameters			Calculated Results		Experimental Results
	T (C°)	Acetonitrile (%)	Flow Rate (mL/min)	Rmg	Rgm	Rmg	Rgm
Linear	20	82.5	0.700	1.202	1.184	1.151	1.180
Linear model with main effects two ways	20	82.5	0.700	1.267	1.147	1.151	1.180
Quadratic	20	82.5	0.766	1.208	1.163	1.171	1.155

), which yielded the highest simultaneous values of Rmg and Rgm. To interpret the optimization results statistically, the examination of each model’s predictions for Rmg and Rgm was aligned with experimental values; for the Linear model, the optimized Rmg (1.202) was somewhat higher than the experimental (1.151), while the optimized Rgm (1.184) closely matched the experimental (1.180) (Table 7). Similarly, the Linear model with main effects two ways model showed a higher optimized Rmg (1.267) compared to the experimental (1.151) and a slightly lower optimized Rgm (1.147) than the experimental (1.180). In contrast, to these results, the Quadratic model’s optimized Rmg (1.208) was closer to its experimental counterpart (1.171), while its optimized Rgm (1.163) also closely approximated the experimental value (1.155), with the added distinction of an optimized flow rate of 0.766 mL/min compared to the fixed 0.7 mL/min for the other models (Table 7).

Based on the closeness of the optimized values to the experimental values, the Linear and Quadratic models showed promising fits for Rgm, while the Quadratic model appeared slightly better for Rmg. To statistically validate these observations, the MSE and RMSE values were calculated for each model. For the Linear model, the MSE was 0.003 for Rmg and 0.000 for Rgm, resulting in RMSE values of 0.053 and 0.004, respectively. The Linear model with main effects and the two-way model exhibited higher errors, with an MSE of 0.014 for Rmg (RMSE 0.118) and 0.0011 for Rgm (RMSE 0.033), indicating a less accurate fit. Notably, the Quadratic model demonstrated the lowest errors for Rmg, with an MSE of 0.0013 and RMSE of 0.036, and also a low MSE of 0.000 (RMSE 0.009) for Rgm. These statistical metrics confirm that the Quadratic model generally provides the best fit to the experimental data for both Rmg and Rgm, while the Linear model performs comparably well for Rgm, and the Linear model with the main effects two-way model exhibits the poorest predictive capability among the three models.

3.5. Chromatographic Separation and Sugar Composition Analysis

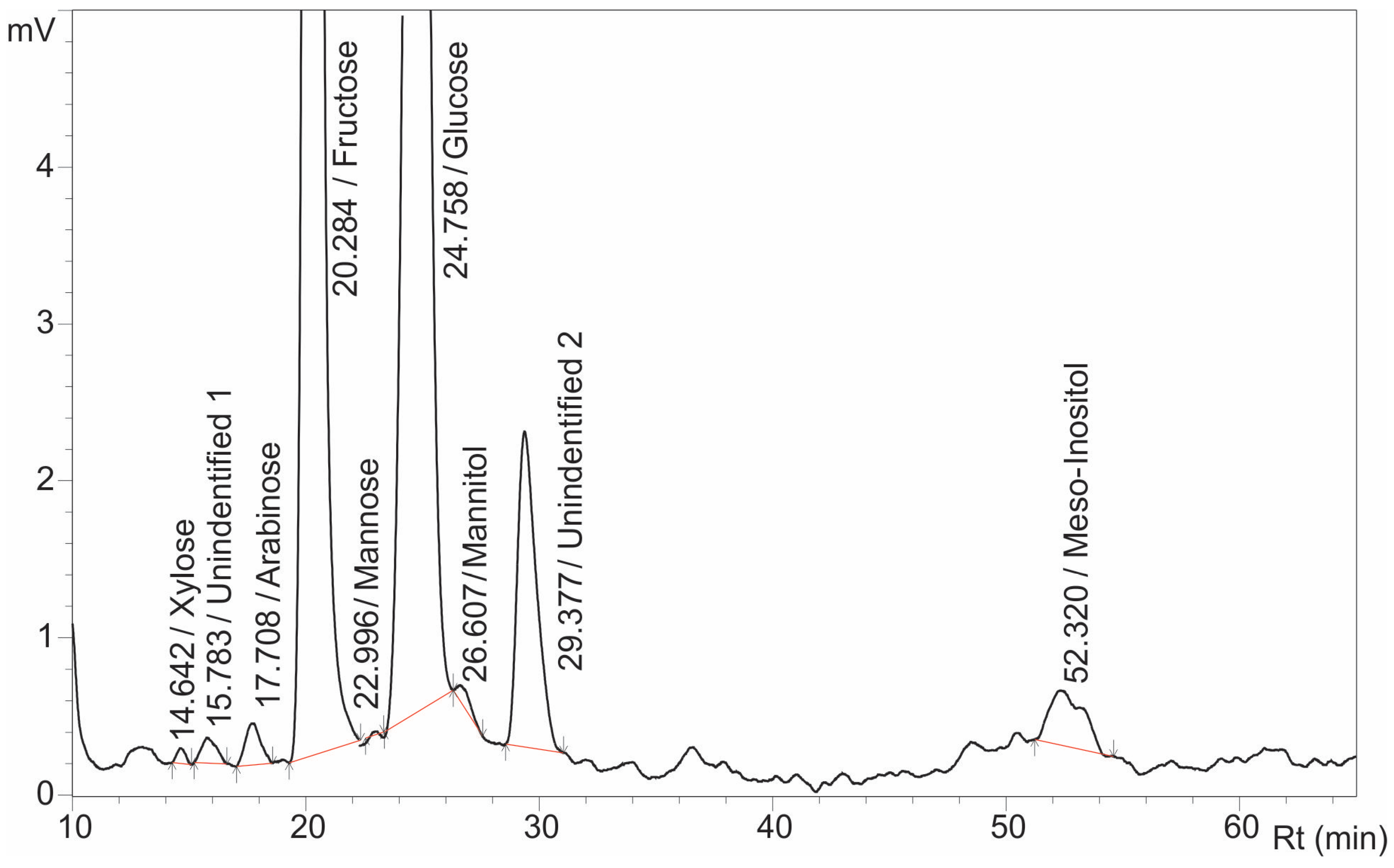
The developed method was applied to a real sample of wild sunflower (Helianthus annuus L.) nectar. The Box–Behnken linear model-optimized parameters (column temperature: 20 °C; flow rate: 0.7 mL/min; mobile phase: acetonitrile/water 82.5:17.5, v/v) yielded chromatograms with nine resolved peaks, as shown in Figure 6. Seven sugars were identified: arabinose, meso-inositol, xylose, fructose, mannose, glucose, and mannitol (two peaks remained unassigned). Resolution values for critical pairs—mannose/glucose (Rmg = 1.47) and glucose/mannitol (Rgm = 1.30)—exceeded the baseline separation threshold (Rs > 1) for all components (

Table 8. Quantitative and qualitative analysis of detected sugars: retention time (Rt), peak area, concentration (mg/L), and resolution.

Peak	Name	Rt (min)	Area	Concentration (mg/L)	Resolution
1	Xylose	14.642	2457	35.039	1.120
2	Unknown compound 1	15.783	7212	-	1.529
3	Arabinose	17.708	12,013	164.818	2.238
4	Fructose	20.284	1,050,277	4914.341	2.925
5	Mannose	22.996	1499	27.144	1.471
6	Glucose	24.758	826,625	4506.217	1.304
7	Mannitol	26.607	4485	33.677	2.028
8	Unknown compound 2	29.377	112,818	-	9.833
9	meso-Inositol	52.320	35,440	140.738	-

).

Quantitative analysis revealed a hexose-dominated profile: fructose (4914.341 mg/L) and glucose (4506.217 mg/L) constituted the primary sugars, while sucrose was undetected. Fructose accounts for 50% of the total sugars, closely followed by glucose at 48.9%, consistent with the findings of Bergonzoli et al., 2022 [22]. Trace amounts of stress-associated mannitol (33.677 mg/L) comparable to levels in non-hybrid sunflower nectar (Bergonzoli et al.), indicated the exposure to drought stress during flowering and likely reflected an adaptive plant response [7,16,17,18,66,67]. Minor sugars included arabinose (164.818 mg/L), xylose (35.039 mg/L), and mannose (27.144 mg/L)—compounds known to affect pollinator attraction and toxicity [10,21]. In addition to mannitol, a notable concentration of meso-inositol (140.738 mg/L) was detected. This cyclitol is rarely reported in nectar but is frequently found in honey [68]. The occurrence of mannitol, sorbitol, and cyclitols such as meso-inositol is often linked to extreme abiotic stress, as these compounds contribute to plant protection against water deficit, salinity, frost, and osmotic stress [69,70,71]. Further studies are needed to clarify how temperature, rainfall, and soil composition shape nectar sugar profiles.

3.6. Linearity

To determine the linearity of the HPLC method, a series of standard solutions were prepared with concentrations ranging from 50 mg/L to 500 mg/L for arabinose, xylose, mannose, mannitol, and meso-inositol, and from 50 mg/L to 5500 mg/L for fructose and glucose (

Table 9. Linearity parameters for sugar analysis: correlation coefficients (R), slope, and intercept values of calibration curves.

Sugar	Correlation Coefficients (R)	Slope	Intercept
D-ribose	0.989	79.316	3345.850
Xylose	0.996	107.589	−1313.160
Arabinose	0.998	66.629	1031.790
Fructose	0.999	215.861	−10,537.100
Mannose	0.996	36.850	498.903
Glucose	0.987	182.020	6402.23
Mannitol	0.994	122.805	348.957
Sucrose	0.986	213.942	−2237.100
meso-Inositol	0.992	264.764	−1822.310
Maltose	0.985	142.283	1238.250

). Calibration curves were constructed by plotting the peak area against the initial concentration of each sugar standard solution.

Linearity was evaluated with six-point calibrations over 50–500 mg/L for most sugars and sugar alcohols, and 50–5500 mg/L for fructose and glucose. Calibration curves exhibited strong correlation coefficients (R = 0.985–0.999), with fructose, arabinose, xylose, and mannose (R > 0.995) meeting stringent validation criteria (Table 9). Although mannitol (R = 0.994) and meso-inositol (R = 0.992) slightly deviated from the 0.995 threshold, their performance remained analytically acceptable. Maltose (R = 0.985) indicated potential matrix interference, warranting method refinement.

The LOD and LOQ values were determined to assess the method’s sensitivity, using a dilution series followed by replicate measurements at the lowest detectable concentration (

Table 10. HPLC-based quantification parameters, LOD and LOQ values for selected sugars.

	Compounds	Area	SA	KVA	c (mg/L)	SC	LOD (mg/L)	LOQ (mg/L)
1	D-ribose	7564	262.337	0.035	53.188	1.844	5.534	18.446
2	Xylose	5085	391.737	0.077	59.468	4.581	13.744	45.813
3	Arabinose	3516	340.867	0.097	37.278	3.614	10.843	36.144
4	Fructose	7820	498.984	0.064	85.042	5.426	16.279	54.262
5	Mannose	1772	318.198	0.179	36.125	6.487	19.461	194.610
6	Glucose	8455	949.076	0.112	11.987	1.345	4.037	13.456
7	Mannitol	7834	301.935	0.038	60.957	2.349	7.048	70.477
8	Sucrose	7456	373.508	0.050	45.306	2.270	6.809	22.697
9	meso-Inositol	17,280	615.002	0.036	72.148	2.568	7.703	25.678
10	Maltose	20,174	550.325	0.027	133.083	3.630	10.891	36.304

Area—mean value of five replicates in internal unit of integrator, S_A, S_c—standard deviation of area and concentration, KV_A—variation coefficient of area, c—lowest detectable concentration (mg/L), LOD—limit of detection (mg/L), LOQ—limit of quantitation (mg/L).

). Five replicate measurements at the minimum detectable concentration were used to calculate the limit of detection (LOD) and limit of quantitation (LOQ), defined as three and ten times the standard deviation, respectively [67,72]

The LOD values for the analyzed sugars and alcohols ranged from 4.037 mg/L (glucose) to 19.461 mg/L (mannose), while LOQ values varied between 13.456 mg/L and 194.610 mg/L. The detection and quantification limits were lowest in glucose, whereas mannose had the highest.

Accuracy was evaluated using six different concentrations of sugar and sugar alcohol, with each concentration injected in triplicate. Recoveries were calculated to assess the accuracy in laboratory-prepared mixtures, ranging from 90.177% to 106.906%, which is consistent with AOAC (1993) guidelines [73]. The results are presented in

Table 11. Recovery-based accuracy of sugars and sugar alcohols (%).

Compounds	Recovery (%)
	50 (mg/L)	100 (mg/L)	200 (mg/L)	300 (mg/L)	400 (mg/L)	500 (mg/L)
D-ribose	106.377	104.326	101.009	97.088	100.991	100.661
Xylose	103.430	90.891	104.119	102.777	101.142	101.810
Arabinose	100.350	94.120	95.640	104.093	100.312	102.590
Fructose	105.412	103.434	106.906	103.182	99.635	98.323
Mannose	104,423	105.526	99.769	96.675	102.187	100.972
Glucose	105,247	105.827	99.881	99.991	98.849	99.168
Mannitol	90.177	103.046	102.459	102.066	101.074	101.851
Sucrose	90.613	96.372	103.612	99.185	100.184	103.094
meso-Inositol	105.350	91.422	99.810	95.801	102.597	102.228
Maltose	n.d.	102.994	105.883	98.001	101.739	100.023

n.d.—not detected.

.

Intra-day precision was assessed using three mixtures (50, 300, and 500 mg/L) of the tested sugars and sugar alcohols, with %RSD values below 1%. Inter-day precision was evaluated over three consecutive days using the same concentrations, yielding %RSD values below 2%.

4. Conclusions

This study developed and optimized a robust HPLC-RID method for simultaneous determination of eight sugars and two sugar alcohols in wild sunflower nectar, using a Box–Behnken experimental design with response surface methodology (RSM). Optimized chromatographic conditions (20 °C column temperature, 82.5% acetonitrile, and 0.766 mL/min flow rate) enabled baseline separation of the previously unresolved critical sugar pairs, such as mannose/glucose and glucose/mannitol (Rmg = 1.171, Rgm = 1.155). The method exhibited satisfactory linearity (R = 0.985–0.999) across a broad concentration range, allowing accurate quantification of both dominant (fructose, glucose) and minor nectar components (arabinose, xylose, mannose, mannitol, meso-inositol, maltose, and sucrose). Limits of detection and quantification ranged from 4.037 to 19.461 mg/L and 13.456 to 194.610 mg/L, respectively, with glucose showing the greatest and mannose the lowest sensitivity. High precision was achieved, with intra-day and inter-day %RSD values below 1% and 2%, respectively. RSM analysis identified column temperature and acetonitrile concentration as the most influential parameters, while flow rate exhibited a secondary effect. The quadratic model provided the best fit, emphasizing the importance of nonlinear interactions in chromatographic optimization. The validated method was successfully applied to a real nectar sample, revealing a hexose-dominated composition, with fructose (4914.341 mg/L) and glucose (4506.217 mg/L) as the predominant sugars. Trace levels of stress-associated sugars and sugar alcohols such as mannitol (33.677 mg/L), arabinose (164.818 mg/L), xylose (35.039 mg/L), mannose (27.144 mg/L), and the rarely reported meso-inositol (140.738 mg/L) were also quantified, providing avaluable insight into plant physiological and ecological adaptations. Successful resolution of the challenging sugar pairs, combined with their robustness, sensitivity, and precision, makes this method a superior alternative to the existing protocols for nectar analysis. Overall, this study highlights the utility of RSM in chromatographic method development, establishing a cost-effective, environmentally friendly analytical tool for nectar analysis. Besides sunflower, the approach shows potential for a broader application in plant-pollinator studies, ecological and agricultural research, and assessments of plant responses to climate change. Future research may extend the use of this method by exploring its adaptability to other plant species and by including additional nectar components for a more comprehensive biochemical profiling. Moreover, the approach could be applied to food analysis, where sugar composition is crucial for determining nutritional value and authenticity, with profiling serving as a reliable tool to detect adulteration, ensure quality control, and support the development of safe and trustworthy food products.