Experimental Study on Spatiotemporal Evolution Mechanisms of Roll Waves and Their Impact on Particle Separation Behavior in Spiral Concentrators
Abstract
1. Introduction
2. Theoretical Model
3. Orthogonal Design and Experiments
3.1. Orthogonal Design
3.2. Measurement and Analysis of Roll Waves in Spiral Concentrators
3.2.1. Experimental Setup and Slurry Preparation
3.2.2. Evaluation Metrics for Roll Wave Intensity Characteristics
- 1
- Global Mean Fluctuation Amplitude ():
- 2
- Per-Turn Mean Fluctuation Amplitude ():
- 3
- Per-Radial-Position Mean Fluctuation Amplitude ():
4. Results and Analysis
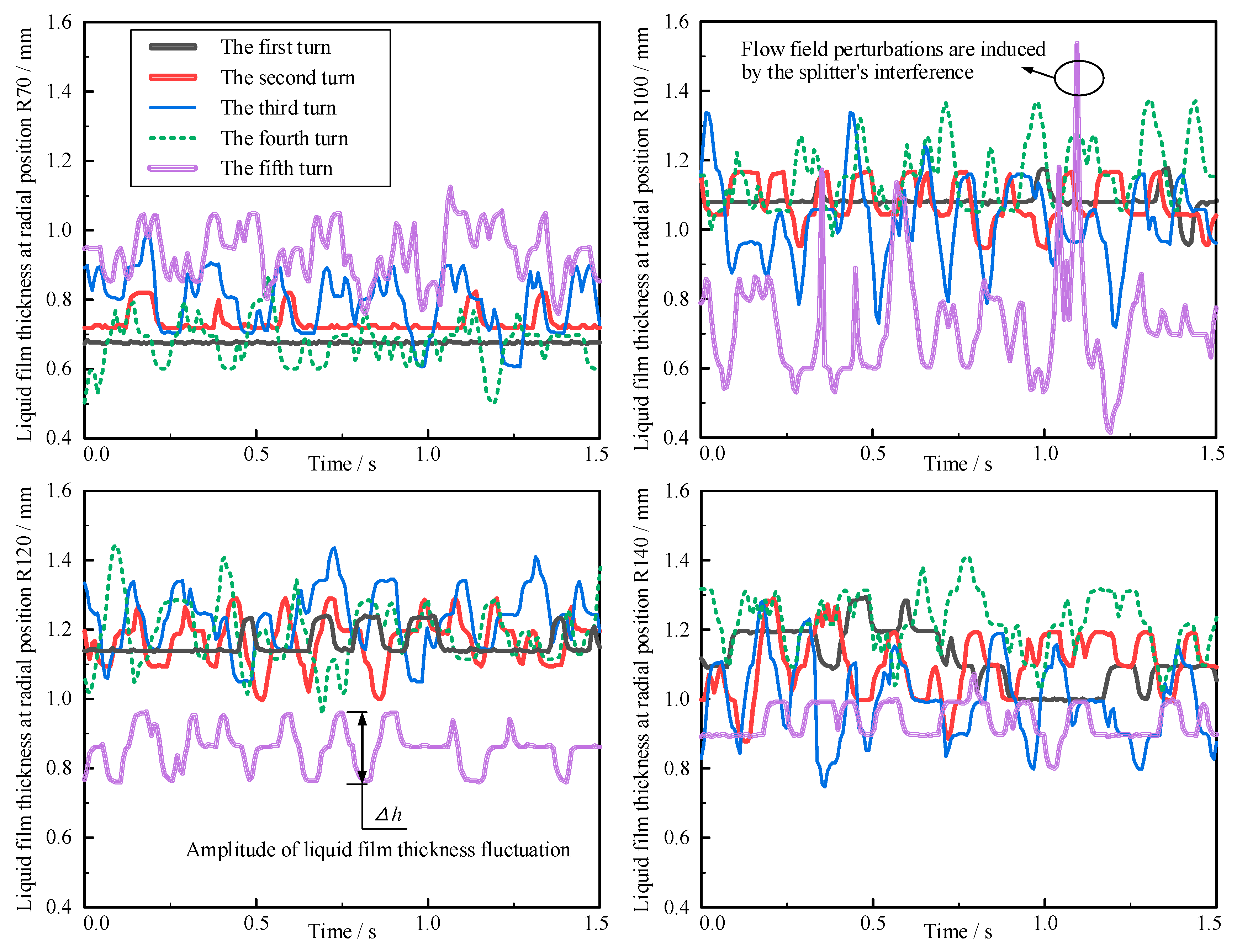
4.1. Analysis of Spatiotemporal Evolution of Roll Waves
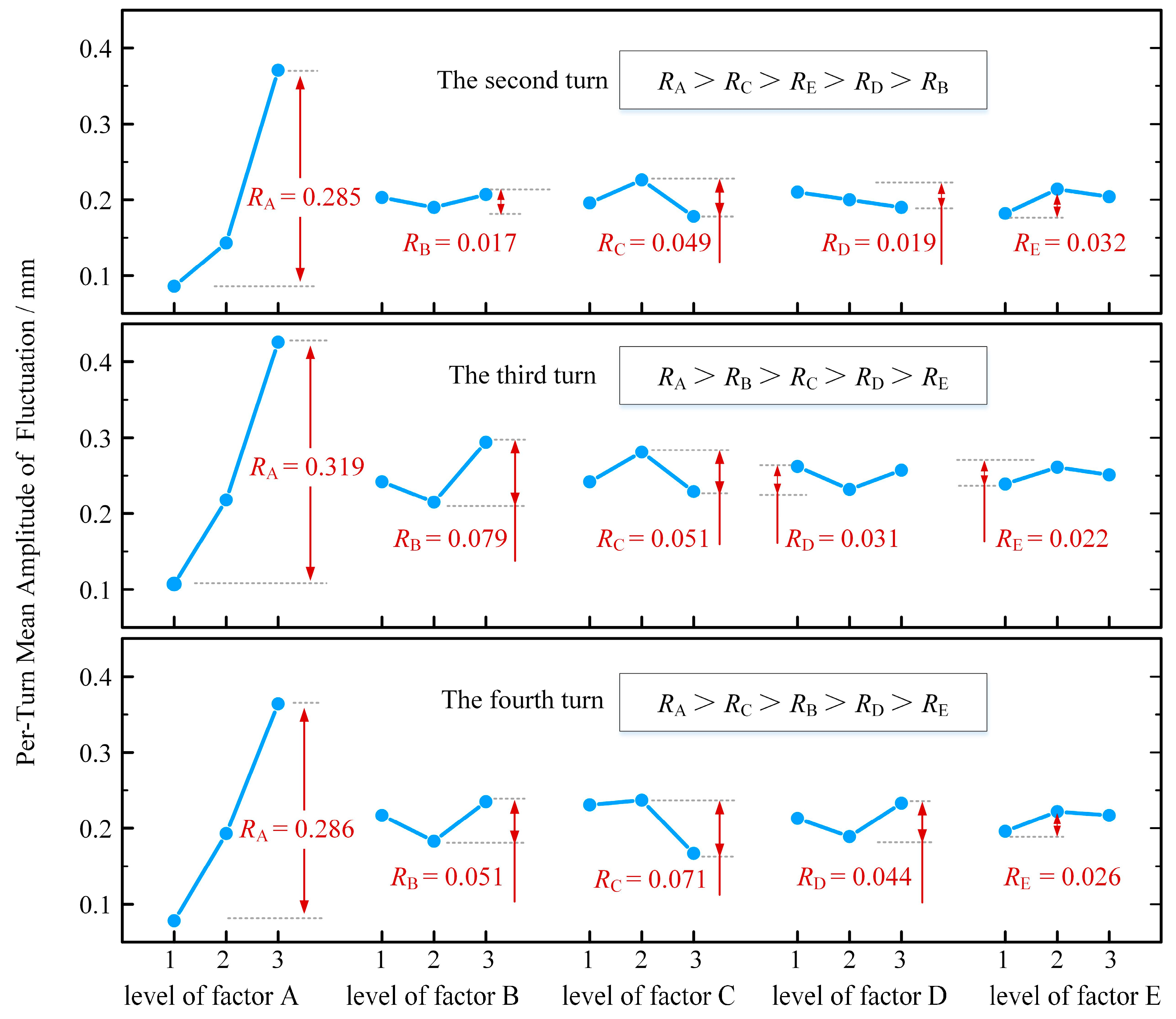
4.2. Ranking of Factors Influencing Liquid Film Thickness Variation (Range Analysis)
4.2.1. Range Analysis for Global Mean Amplitude of Fluctuation
4.2.2. Range Analysis for Per-Turn Mean Amplitude of Fluctuation
4.2.3. Range Analysis for Per-Radial-Position Mean Amplitude of Fluctuation
4.3. Significance Analysis of Factor Influence
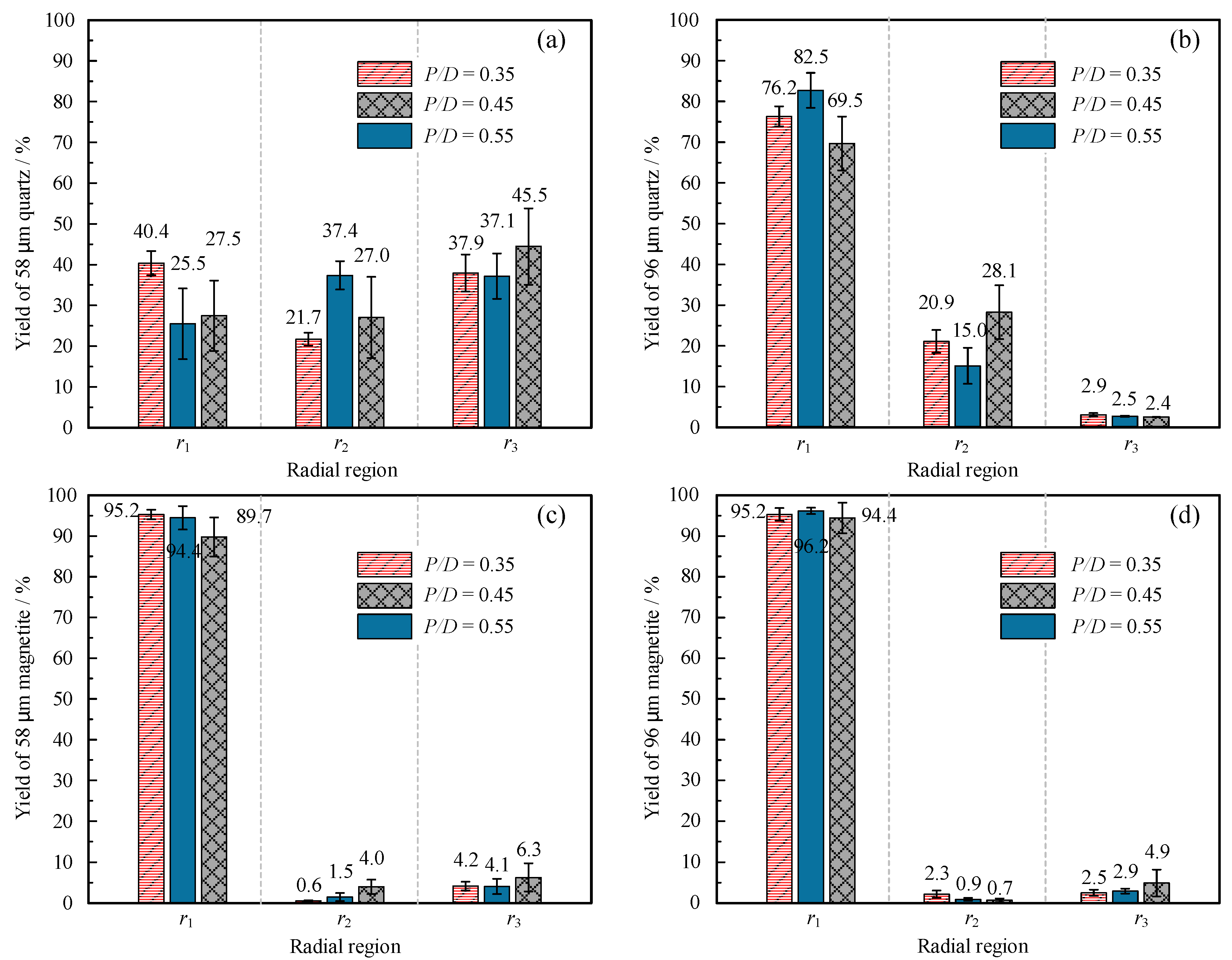
4.4. Analysis of Roll Wave Impact on Particle Migration
5. Conclusions
- 1
- Spatiotemporal Evolution of Roll Waves: Significant quasi-periodic roll waves appear on the surface of the slurry flow traversing the inner to middle groove regions. The dynamic characteristics of roll waves exhibit clear spatiotemporal evolution patterns. Spatially, roll wave intensity significantly increases from the inner towards the middle groove region, attributed to enhanced fluid shear stress due to increasing centrifugal force gradients. Temporally, roll waves follow an evolutionary sequence: “initiation in turn 2, peak in turn 3, and attenuation in turn 4”.
- 2
- Influence Mechanisms of Key Parameters: Parameter sensitivity analysis identifies the pitch-to-diameter ratio () as a highly significant controlling factor for roll wave intensity. When increases from 0.35 to 0.55, the global fluctuation amplitude increases drastically, driven by quadratic growth in centrifugal force disrupting flow field stability. Particle characteristics (density and size) exhibit generally significant influence: light minerals (e.g., quartz sand) induce roll waves more readily than heavy minerals (e.g., magnetite); medium-fine particles () exhibit the strongest disturbance effect. In contrast, the influence of inlet flow rate and slurry mass concentration did not reach statistical significance.
- 3
- Impact of Roll Waves on Separation Process: Roll waves induce stochastic particle migration by enhancing fluid disturbances, leading to an increased standard deviation of ZRR and significantly reduced separation precision. Stronger roll waves, resulting from liquid instability within the groove, correspond to more significant stochastic particle migration. Fine particles, due to their low inertia and ease of oscillation with the fluid, are far more affected by roll wave disturbances than coarse particles. Coarse particles, possessing greater inertia, exhibit relatively stable migration behavior.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richards, R.; Hunter, J.; Holland-Batt, A. Spiral concentrators for fine coal treatment. Coal Prep. 1985, 1, 207–229. [Google Scholar] [CrossRef]
- Tripathy, S.K.; Murthy, Y.R. Modeling and optimization of spiral concentrator for separation of ultrafine chromite. Powder Technol. 2012, 221, 387–394. [Google Scholar] [CrossRef]
- Routray, S.; Rao, R.B. Optimization of some parameters of rougher spiral concentrator for preconcentration of total heavy minerals from beach sand. World Metall. ERZMETALL 2013, 66, 5–12. [Google Scholar]
- Rao, G.; Rath, B.; Sharma, P.; Chaurasiya, S. Modeling and Optimisation of Spiral Concentrator for Beneficiation of Iron Ore Slimes from Kirandul, India. Trans. Indian Natl. Acad. Eng. 2020, 5, 497–508. [Google Scholar] [CrossRef]
- Jain, P.K.; Rayasam, V. An analytical approach to explain the generation of secondary circulation in spiral concentrators. Powder Technol. 2017, 308, 165–177. [Google Scholar] [CrossRef]
- Meng, L.; Gao, S.; Wei, D.; Cui, B.; Shen, Y.; Song, Z. Investigation on the evolution of flow field stability in a spiral separator. Miner. Eng. 2021, 174, 107224. [Google Scholar] [CrossRef]
- Mahran, G.M.; Doheim, M.A.; Abu-Ali, M.H.; Abdel, A.F. CFD simulation of particulate flow in a spiral concentrator. Mater. Test. 2015, 57, 811–816. [Google Scholar] [CrossRef]
- Sudikondala, P.; Mangadoddy, N.; Tripathy, S.K.; Yanamandra, R.M. CFD Modelling of the Spiral Concentrator at Moderate Feed Solids Content-Prediction of Particle Segregation. Trans. Indian Inst. Met. 2024, 77, 4193–4204. [Google Scholar] [CrossRef]
- Boucher, D.; Deng, Z.; Leadbeater, T.; Langlois, R.; Waters, K.E. Observation of iron ore beneficiation within a spiral concentrator by positron emission particle tracking of large (Ø = 1440 μm) and small (Ø = 58 μm) hematite and quartz tracers. Chem. Eng. Sci. 2016, 140, 217–232. [Google Scholar] [CrossRef]
- Sadeghi, M.; Bazin, C.; Renaud, M. Radial distribution of iron oxide and silica particles in the reject flow of a spiral concentrator. Int. J. Miner. Process. 2016, 153, 51–59. [Google Scholar] [CrossRef]
- Gao, S.; Meng, L.; Zhou, X.; Shen, Y.; Cui, B.; Song, Z. Design of partial cross-sectional geometry and prediction of separation performance in the spiral separator. Sep. Sci. Technol. 2022, 57, 2127–2144. [Google Scholar] [CrossRef]
- Stokes, Y.M.; Duffy, B.R.; Wilson, S.K.; Tronnolone, H. Thin-film flow in helically wound rectangular channels with small torsion. Phys. Fluids 2013, 25, 083103. [Google Scholar] [CrossRef]
- Jain, P. An analytical approach to explain complex flow in spiral concentrator and development of flow equations. Miner. Eng. 2021, 174, 107027. [Google Scholar] [CrossRef]
- Das, S.K.; Godiwalla, K.; Panda, L.; Bhattacharya, K.; Singh, R.; Mehrotra, S. Mathematical modeling of separation characteristics of a coal-washing spiral. Int. J. Miner. Process. 2007, 84, 118–132. [Google Scholar] [CrossRef]
- Meng, L.; Gao, S.; Wei, D.; Cui, B.; Shen, Y.; Song, Z.; Yuan, J. Effects of cross-sectional geometry on flow characteristics in spiral separators. Sep. Sci. Technol. 2021, 56, 2967–2977. [Google Scholar] [CrossRef]
- Ye, G.; Liu, Q.; Ma, L.; Dong, X. CFD-DEM investigation of fluid and particle motion behaviors in initial stage of spiral separation process at low solids concentration. Miner. Process. Extr. Metall. Rev. 2023, 44, 475–480. [Google Scholar] [CrossRef]
- Ankireddy, P.R.; Purushotham, S.; Narasimha, M. Fluid Flow Modeling and Analysis of Low-and High-Gravity Spiral Concentrators: Experimental and Analytical Approaches. Chem. Eng. Technol. 2023, 46, 1619–1629. [Google Scholar] [CrossRef]
- Romeijn, T.; Behrens, M.; Paul, G.; Wei, D. Experimental analysis of water and slurry flows in gravity-driven helical mineral separators. Powder Technol. 2022, 405, 117538. [Google Scholar] [CrossRef]
- Sudikondala, P.; Mangadoddy, N.; Kumar, M.; Tripathy, S.K.; Yanamandra, R.M. CFD Modelling of Spiral Concentrator-Prediction of Comprehensive Fluid Flow Field and Particle Segregation. Miner. Eng. 2022, 183, 107570. [Google Scholar] [CrossRef]
- Meng, L.; Gao, S.; Wei, D.; Zhao, Q.; Cui, B.; Shen, Y.; Song, Z. Particulate flow modelling in a spiral separator by using the Eulerian multi-fluid VOF approach. Int. J. Min. Sci. Technol. 2023, 33, 251–263. [Google Scholar] [CrossRef]
- Gao, S.; Zhou, X.; Meng, L.; Zhao, Q.; Liu, W. Variation of flow hydrodynamic parameters and prediction of particle separation indices in the spiral concentrator with the regulation of pitch-diameter ratio. Separations 2023, 10, 410. [Google Scholar] [CrossRef]
- Loveday, G.; Cilliers, J. Fluid flow modelling on spiral concentrators. Miner. Eng. 1994, 7, 223–237. [Google Scholar] [CrossRef]
- Dressler, R.F. Mathematical solution of the problem of roll-waves in inclined opel channels. Commun. Pure Appl. Math. 1949, 2, 149–194. [Google Scholar] [CrossRef]
- Julien, P.Y.; Hartley, D.M. Formation of roll waves in laminar sheet flow. J. Hydraul. Res. 1986, 24, 5–17. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, K.; Li, P.; Meng, Y.; Zhao, L. Hydrodynamic characteristics and evolution law of roll waves in overland flow. Catena 2021, 198, 105068. [Google Scholar] [CrossRef]
- da Cunha, E.F.; de Oliveira Ferreira, F.; de Freitas Maciel, G.; Kitano, C. Absorbance photometric technique to measure roll waves in a free surface of a non-Newtonian fluid flow. Measurement 2024, 235, 114880. [Google Scholar] [CrossRef]
- Rocho, V.d.R.; Fiorot, G.H.; Viçosa Möller, S. Influence of the Perturbation Amplitude and the Froude Number on the Establishment Length of Roll Waves. J. Eng. Mech. 2022, 148, 04022057. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Lamberti, A. Instability and surge development in debris flows. Rev. Geophys. 2007, 45, RG3006. [Google Scholar] [CrossRef]
- Thomas, H.A. The Propagation of Waves in Steep Prismatic Conduits. In Proceedings of the Hydraulics Conference, Iowa City, IA, USA, 12–15 June 1939; Thomas, H.A., Ed.; University of Iowa: Iowa City, IA, USA, 1940. [Google Scholar]
- Fiorot, G.H.; Rocho, V.d.R.; Möller, S.V.; Pereira, J.B.; da Cunha, E.F.; Maciel, G.d.F. An experimental assessment of roll waves evolution in mud-like fluids flowing down steep slopes. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 483. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Liu, Q. Numerical study of roll wave characteristics based on Navier-Stokes equations: A two-dimensional simulation. J. Eng. Mech. 2021, 147, 04020149. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Lamberti, A. Roll waves simulation using shallow water equations and weighted average flux method. J. Hydraul. Res. 2002, 40, 610–622. [Google Scholar] [CrossRef]
- Fei, J.; Jie, Y.; Wu, Z.; Zhu, M. Emerging, ripening, and attenuating stages of granular roll waves. J. Non Newton. Fluid Mech. 2021, 287, 104411. [Google Scholar] [CrossRef]
- Wang, J.-W.; Andrews, J. Numerical simulations of liquid flow on spiral concentrators. Miner. Eng. 1994, 7, 1363–1385. [Google Scholar] [CrossRef]
- Holland-Batt, A. A method for the prediction of the primary flow on large diameter spiral troughs. Miner. Eng. 2009, 22, 352–356. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J. Impact of inlet flow rate on dynamic liquid film thickness and flow stability in spiral concentrator. Powder Technol. 2025, 466, 121472. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Zhang, Z.; Taylor, S.; Chen, M.; Wang, X. Experimental investigation on thermal performance of self-service cold storage cabinet based on the orthogonal test. Appl. Therm. Eng. 2024, 242, 122315. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Shi, C.; Zhang, M.; Tao, Z.; Zhang, Y. Orthogonal Analysis for Structural Optimization of Ejector for Multiejector Air Curtain. Asia-Pac. J. Chem. Eng. 2025, 20, e70011. [Google Scholar] [CrossRef]
- Ankireddy, P.R.; Sudikondala, P.; Mangadoddy, N.; Tripathy, S.K.; Yanamandra, R.M. Comparative studies of experimental and numerical investigations of fluid flow and particle separation of high-gravity spiral concentrators. Ind. Eng. Chem. Res. 2024, 63, 12177–12198. [Google Scholar] [CrossRef]
- Peng, C.; Jin, S.; Zhang, X.; Zhang, H.; Guo, Z.; Ouyang, X. Orthogonal optimization and parameter analysis of the hydraulic combined seals for the marine crane. Appl. Ocean Res. 2025, 158, 104595. [Google Scholar] [CrossRef]
- Xu, H.; Kong, Y.; Cheng, D.; Zhao, L.; Dong, H.; Zhang, M. Optimization of bischofite pyrolysis furnace system based on orthogonal experiments and exergy analysis with assessment of its green economy. Energy 2025, 322, 135773. [Google Scholar] [CrossRef]
- Sadeghi, M. Modeling and Simulation of Spiral Concentrators. Ph.D. Thesis, Université Laval, Quebec, QC, Canada, 2021. [Google Scholar]






| Factor | Symbol | Mapping | Value Level | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| Pitch-to-diameter ratio (-) | A | 0.35 | 0.45 | 0.55 | |
| Average density of pulp particles (kg/m3) | B | 3533 | 5300 | 2650 | |
| Particle diameter (μm) | C | 22 | 58 | 96 | |
| Solid mass fraction (%) | D | 10 | 20 | 30 | |
| Inlet flow rate (L/min) | E | 5 | 8 | 11 | |
| Test No. | Factor Level | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 | 2 | 2 |
| 3 | 1 | 1 | 3 | 3 | 3 |
| 4 | 1 | 2 | 1 | 2 | 3 |
| 5 | 1 | 2 | 2 | 3 | 1 |
| 6 | 1 | 2 | 3 | 1 | 2 |
| 7 | 1 | 3 | 1 | 3 | 2 |
| 8 | 1 | 3 | 2 | 1 | 3 |
| 9 | 1 | 3 | 3 | 2 | 1 |
| 10 | 2 | 1 | 1 | 3 | 3 |
| 11 | 2 | 1 | 2 | 1 | 1 |
| 12 | 2 | 1 | 3 | 2 | 2 |
| 13 | 2 | 2 | 1 | 1 | 2 |
| 14 | 2 | 2 | 2 | 2 | 3 |
| 15 | 2 | 2 | 3 | 3 | 1 |
| 16 | 2 | 3 | 1 | 2 | 1 |
| 17 | 2 | 3 | 2 | 3 | 2 |
| 18 | 2 | 3 | 3 | 1 | 3 |
| 19 | 3 | 1 | 1 | 1 | 2 |
| 20 | 3 | 1 | 2 | 2 | 3 |
| 21 | 3 | 1 | 3 | 3 | 1 |
| 22 | 3 | 2 | 1 | 2 | 1 |
| 23 | 3 | 2 | 2 | 3 | 2 |
| 24 | 3 | 2 | 3 | 1 | 3 |
| 25 | 3 | 3 | 1 | 3 | 3 |
| 26 | 3 | 3 | 2 | 1 | 1 |
| 27 | 3 | 3 | 3 | 2 | 2 |
| Sample Label | d10 (μm) | d50 (μm) | d90 (μm) | Span |
|---|---|---|---|---|
| 1 | 18 | 22 | 40 | 1.00 |
| 2 | 49 | 58 | 84 | 0.60 |
| 3 | 81 | 96 | 124 | 0.45 |
| 4 | 17 | 23 | 43 | 1.13 |
| 5 | 49 | 58 | 84 | 0.60 |
| 6 | 78 | 97 | 128 | 0.52 |
| 7 | 18 | 22 | 42 | 1.09 |
| 8 | 47 | 59 | 86 | 0.66 |
| 9 | 81 | 95 | 126 | 0.47 |
| Test No. | /mm | /mm | /mm | |||||
|---|---|---|---|---|---|---|---|---|
| T2 | T3 | T4 | R70 | R100 | R120 | R140 | ||
| 1 | 0.125 | 0.100 | 0.150 | 0.125 | 0.000 | 0.133 | 0.233 | 0.133 |
| 2 | 0.142 | 0.125 | 0.150 | 0.150 | 0.100 | 0.133 | 0.200 | 0.133 |
| 3 | 0.017 | 0.050 | 0.000 | 0.000 | 0.033 | 0.033 | 0.000 | 0.000 |
| 4 | 0.058 | 0.075 | 0.050 | 0.050 | 0.133 | 0.033 | 0.000 | 0.067 |
| 5 | 0.042 | 0.025 | 0.075 | 0.025 | 0.100 | 0.000 | 0.000 | 0.067 |
| 6 | 0.088 | 0.075 | 0.113 | 0.075 | 0.000 | 0.117 | 0.133 | 0.100 |
| 7 | 0.146 | 0.100 | 0.175 | 0.163 | 0.117 | 0.167 | 0.167 | 0.133 |
| 8 | 0.146 | 0.150 | 0.175 | 0.113 | 0.100 | 0.133 | 0.150 | 0.200 |
| 9 | 0.050 | 0.075 | 0.075 | 0.000 | 0.100 | 0.067 | 0.000 | 0.033 |
| 10 | 0.250 | 0.138 | 0.275 | 0.338 | 0.083 | 0.317 | 0.350 | 0.250 |
| 11 | 0.204 | 0.150 | 0.250 | 0.213 | 0.167 | 0.200 | 0.217 | 0.233 |
| 12 | 0.154 | 0.138 | 0.213 | 0.113 | 0.083 | 0.167 | 0.200 | 0.167 |
| 13 | 0.158 | 0.175 | 0.150 | 0.150 | 0.100 | 0.233 | 0.200 | 0.100 |
| 14 | 0.121 | 0.100 | 0.125 | 0.138 | 0.083 | 0.067 | 0.133 | 0.200 |
| 15 | 0.125 | 0.088 | 0.138 | 0.150 | 0.133 | 0.067 | 0.200 | 0.100 |
| 16 | 0.183 | 0.150 | 0.225 | 0.175 | 0.150 | 0.250 | 0.200 | 0.133 |
| 17 | 0.292 | 0.250 | 0.313 | 0.313 | 0.167 | 0.267 | 0.400 | 0.333 |
| 18 | 0.175 | 0.100 | 0.275 | 0.150 | 0.133 | 0.233 | 0.133 | 0.200 |
| 19 | 0.321 | 0.338 | 0.313 | 0.313 | 0.183 | 0.300 | 0.367 | 0.433 |
| 20 | 0.433 | 0.463 | 0.450 | 0.388 | 0.350 | 0.350 | 0.367 | 0.667 |
| 21 | 0.338 | 0.325 | 0.375 | 0.313 | 0.383 | 0.283 | 0.350 | 0.333 |
| 22 | 0.350 | 0.350 | 0.363 | 0.338 | 0.167 | 0.267 | 0.500 | 0.467 |
| 23 | 0.421 | 0.400 | 0.488 | 0.375 | 0.367 | 0.383 | 0.500 | 0.433 |
| 24 | 0.404 | 0.425 | 0.438 | 0.350 | 0.183 | 0.433 | 0.467 | 0.533 |
| 25 | 0.413 | 0.338 | 0.475 | 0.425 | 0.317 | 0.400 | 0.433 | 0.500 |
| 26 | 0.433 | 0.375 | 0.500 | 0.425 | 0.367 | 0.417 | 0.433 | 0.517 |
| 27 | 0.371 | 0.325 | 0.438 | 0.350 | 0.183 | 0.367 | 0.417 | 0.517 |
| Item | Factor | Significance | |||
|---|---|---|---|---|---|
| Global mean fluctuation amplitude | 0.414 | 0.029 | 114.207 | *** | |
| 0.011 | 3.034 | - | |||
| 0.015 | 4.138 | * | |||
| 0.003 | 0.828 | - | |||
| 0.003 | 0.828 | - | |||
| The second turn | 0.409 | 0.031 | 105.548 | *** | |
| 0.001 | 0.258 | - | |||
| 0.011 | 2.839 | - | |||
| 0.002 | 0.516 | - | |||
| 0.005 | 1.290 | - | |||
| The third turn | 0.473 | 0.049 | 77.224 | *** | |
| 0.029 | 4.7347 | * | |||
| 0.013 | 2.1224 | - | |||
| 0.005 | 0.8163 | - | |||
| 0.002 | 0.3265 | - | |||
| The fourth turn | 0.373 | 0.045 | 66.311 | *** | |
| 0.012 | 2.1333 | - | |||
| 0.027 | 4.800 | * | |||
| 0.009 | 1.600 | - | |||
| 0.004 | 0.711 | - | |||
| R70 | 0.201 | 0.055 | 29.236 | *** | |
| 0.008 | 1.1636 | - | |||
| 0.023 | 3.3455 | - | |||
| 0.013 | 1.891 | - | |||
| 0.004 | 0.582 | - | |||
| R100 | 0.319 | 0.056 | 45.571 | *** | |
| 0.027 | 3.857 | * | |||
| 0.006 | 0.857 | - | |||
| 0.014 | 2.000 | - | |||
| 0.0119 | 1.700 | - | |||
| R120 | 0.491 | 0.116 | 33.862 | *** | |
| 0.002 | 0.138 | - | |||
| 0.021 | 1.448 | - | |||
| 0.009 | 0.621 | - | |||
| 0.0191 | 1.317 | - | |||
| R140 | 0.756 | 0.065 | 93.046 | *** | |
| 0.014 | 1.723 | - | |||
| 0.038 | 4.677 | * | |||
| 0.003 | 0.369 | - | |||
| 0.020 | 2.462 | - |
| Particle Characteristics | The Standard Deviation of ZRR | /mm | |||
|---|---|---|---|---|---|
| r1 | r2 | r3 | |||
| Medium-grained quartz | 0.35 | 2.956 | 1.594 | 4.553 | 0.122 |
| 0.45 | 8.675 | 3.470 | 5.570 | 0.291 | |
| 0.55 | 8.682 | 9.948 | 9.394 | 0.420 | |
| Coarse-grained quartz | 0.35 | 2.463 | 2.797 | 0.425 | 0.050 |
| 0.45 | 4.293 | 4.427 | 0.153 | 0.171 | |
| 0.55 | 6.612 | 6.599 | 0.083 | 0.362 | |
| Medium-grained magnetite | 0.35 | 1.206 | 0.145 | 1.062 | 0.042 |
| 0.45 | 2.871 | 0.999 | 1.881 | 0.108 | |
| 0.55 | 4.788 | 1.768 | 3.468 | 0.398 | |
| Coarse-grained magnetite | 0.35 | 1.526 | 0.913 | 0.752 | 0.091 |
| 0.45 | 0.760 | 0.344 | 0.604 | 0.112 | |
| 0.55 | 3.757 | 0.451 | 3.306 | 0.365 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, H.; Zou, Q.; Hu, J. Experimental Study on Spatiotemporal Evolution Mechanisms of Roll Waves and Their Impact on Particle Separation Behavior in Spiral Concentrators. Separations 2025, 12, 245. https://doi.org/10.3390/separations12090245
Wang J, Liu H, Zou Q, Hu J. Experimental Study on Spatiotemporal Evolution Mechanisms of Roll Waves and Their Impact on Particle Separation Behavior in Spiral Concentrators. Separations. 2025; 12(9):245. https://doi.org/10.3390/separations12090245
Chicago/Turabian StyleWang, Jian, Huizhong Liu, Qihua Zou, and Jun Hu. 2025. "Experimental Study on Spatiotemporal Evolution Mechanisms of Roll Waves and Their Impact on Particle Separation Behavior in Spiral Concentrators" Separations 12, no. 9: 245. https://doi.org/10.3390/separations12090245
APA StyleWang, J., Liu, H., Zou, Q., & Hu, J. (2025). Experimental Study on Spatiotemporal Evolution Mechanisms of Roll Waves and Their Impact on Particle Separation Behavior in Spiral Concentrators. Separations, 12(9), 245. https://doi.org/10.3390/separations12090245







