Numerical Investigation of 2D Ordered Pillar Array Columns: An Algorithm of Unit-Cell Automatic Generation and the Corresponding CFD Simulation
Abstract
1. Introduction
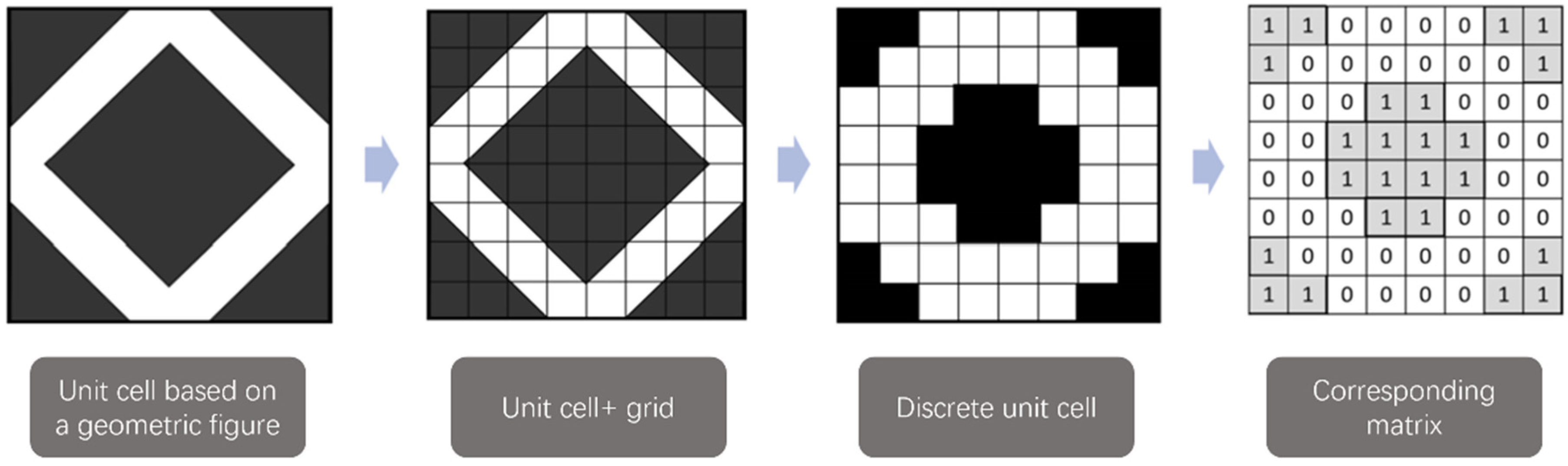
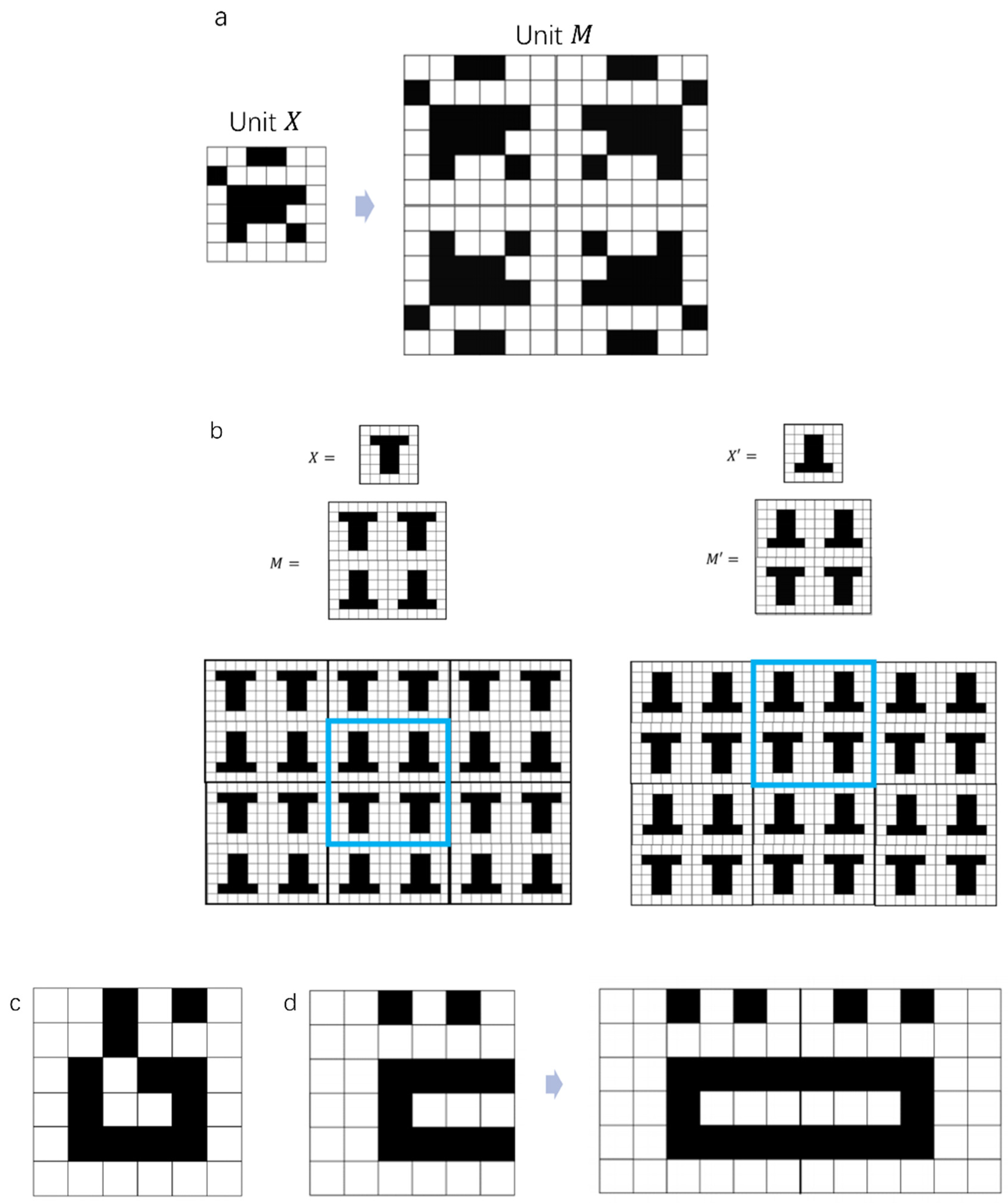
2. Numerical Algorithm for the Generation of PAC Morphologies
3. Computational Fluid Dynamics Methods
3.1. Governing Equations for CFD Models
3.2. Boundary Conditions and Tracer Inlet
3.3. Space Discretization of the CFD Model
4. Results and Discussion
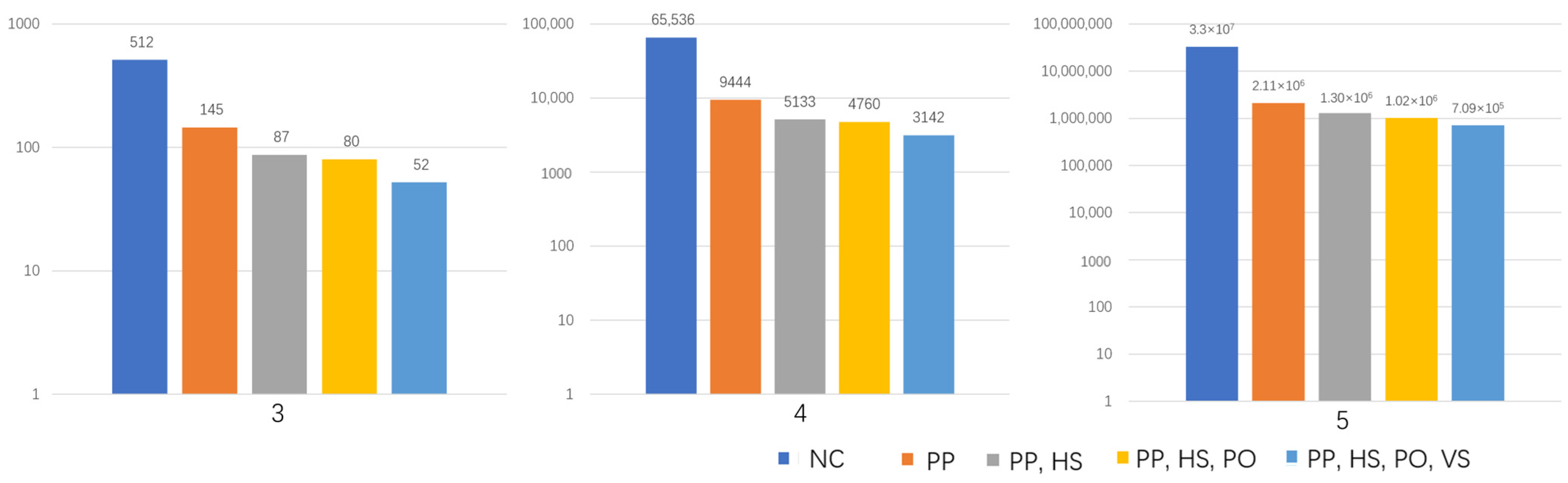
4.1. Impact of the Implementation of the Constraints on Size of Domain Space
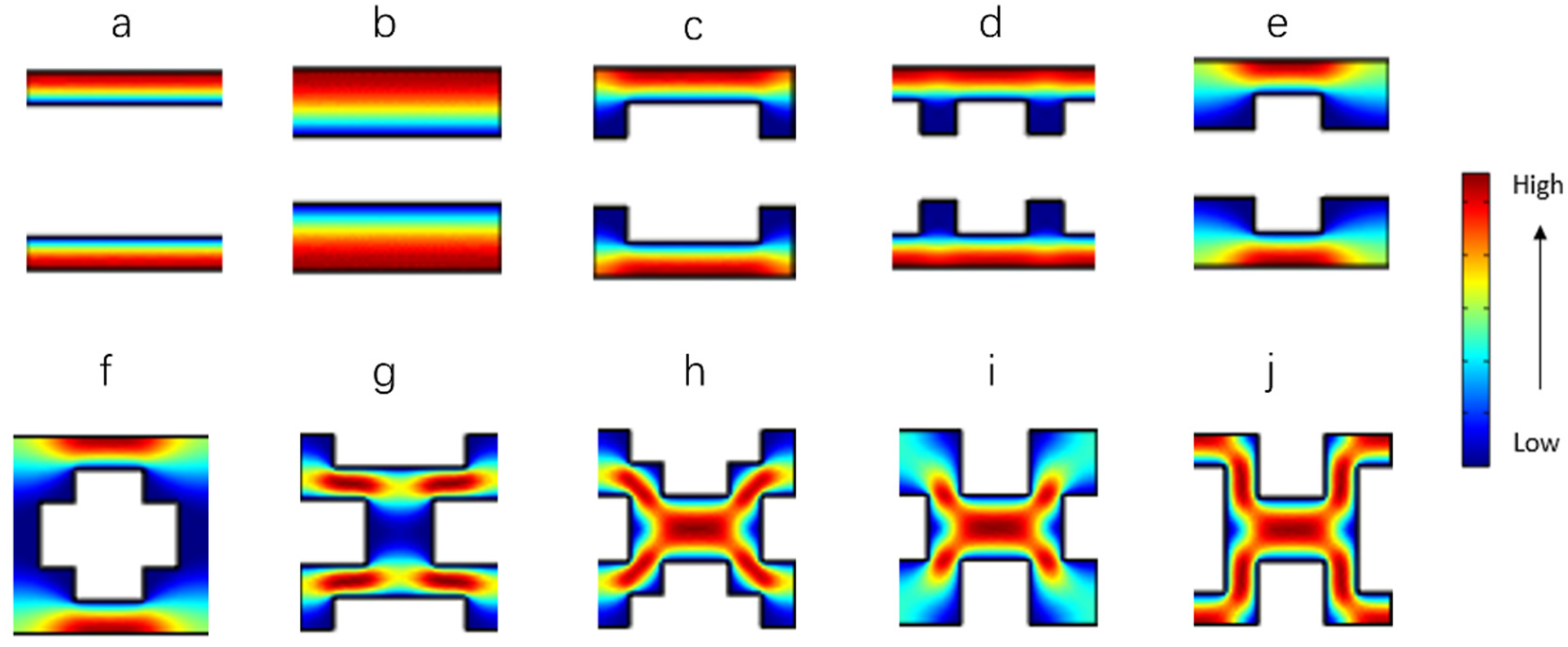
4.2. Effect of Unit-Cell Morphology on Fluid Flow and Band Broadening
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Knox, J.H. Band dispersion in chromatography—A universal expression for the contribution from the mobile zone. J. Chromatogr. A 2002, 960, 7–18. [Google Scholar] [CrossRef]
- He, B.; Tait, N.; Regnier, F. Fabrication of Nanocolumns for Liquid Chromatography. Anal. Chem. 1998, 70, 3790–3797. [Google Scholar] [CrossRef]
- Op De Beeck, J.; Callewaert, M.; Ottevaere, H.; Gardeniers, H.; Desmet, G.; De Malsche, W. On the Advantages of Radially Elongated Structures in Microchip-Based Liquid Chromatography. Anal. Chem. 2013, 85, 5207–5212. [Google Scholar] [CrossRef]
- De Smet, J.; Gzil, P.; Vervoort, N.; Verelst, H.; Baron, G.V.; Desmet, G. On the optimisation of the bed porosity and the particle shape of ordered chromatographic separation media. J. Chromatogr. A 2005, 1073, 43–51. [Google Scholar] [CrossRef]
- Gzil, P.; De Smet, J.; Vervoort, N.; Verelst, H.; Baron, G.V.; Desmet, G. Computational study of the band broadening in two-dimensional etched packed bed columns for on-chip high-performance liquid chromatography. J. Chromatogr. A 2004, 1030, 53–62. [Google Scholar] [CrossRef]
- Dolamore, F.; Dimartino, S.; Fee, C.J. Numerical Elucidation of Flow and Dispersion in Ordered Packed Beds: Nonspherical Polygons and the Effect of Particle Overlap on Chromatographic Performance. Anal. Chem. 2019, 91, 15009–15016. [Google Scholar] [CrossRef]
- Jiang, Q.; Dimartino, S. Simulation of the performance of pillar array columns using the pore-throat ratio as efficiency descriptor. J. Chromatogr. A 2025, 1743, 465704. [Google Scholar] [CrossRef]
- Dolamore, F.; Houlton, B.; Fee, C.J.; Watson, M.J.; Holland, D.J. A numerical investigation of the hydrodynamic dispersion in triply periodic chromatographic stationary phases. J. Chromatogr. A 2022, 1685, 463637. [Google Scholar] [CrossRef] [PubMed]
- Lauriola, C.; Venditti, C.; Desmet, G.; Adrover, A. Dispersion properties of triply periodic minimal surface stationary phases for LC: The case of superficial adsorption. J. Chromatogr. A 2025, 1743, 465676. [Google Scholar] [CrossRef] [PubMed]
- Moussa, A.; Adrover, A.; Desmet, G. Theoretical Prediction of the Ideal Support Shape of 3D-Ordered Liquid Chromatography Supports. Anal. Chem. 2025, 97, 10360–10368. [Google Scholar] [CrossRef] [PubMed]
- Vankeerberghen, B.; Op de Beeck, J.; Desmet, G. Column-Only Band Broadening in a Porous Shell Radially Elongated Pillar Array Column. Anal. Chem. 2024, 96, 3618–3626. [Google Scholar] [CrossRef] [PubMed]
- Schure, M.R.; Maier, R.S.; Kroll, D.M.; Ted Davis, H. Simulation of ordered packed beds in chromatography. J. Chromatogr. A 2004, 1031, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Dolamore, F.; Fee, C.; Dimartino, S. Modelling ordered packed beds of spheres: The importance of bed orientation and the influence of tortuosity on dispersion. J. Chromatogr. A 2018, 1532, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Schure, M.R.; Maier, R.S. How does column packing microstructure affect column efficiency in liquid chromatography? J. Chromatogr. A 2006, 1126, 58–69. [Google Scholar] [CrossRef]
- Daneyko, A.; Khirevich, S.; Höltzel, A.; Seidel-Morgenstern, A.; Tallarek, U. From random sphere packings to regular pillar arrays: Effect of the macroscopic confinement on hydrodynamic dispersion. J. Chromatogr. A 2011, 1218, 8231–8248. [Google Scholar] [CrossRef]
- Schure, M.R.; Maier, R.S.; Kroll, D.M.; Davis, H.T. Simulation of Packed-Bed Chromatography Utilizing High-Resolution Flow Fields: Comparison with Models. Anal. Chem. 2002, 74, 6006–6016. [Google Scholar] [CrossRef]
- Daneyko, A.; Hlushkou, D.; Khirevich, S.; Tallarek, U. From random sphere packings to regular pillar arrays: Analysis of transverse dispersion. J. Chromatogr. A 2012, 1257, 98–115. [Google Scholar] [CrossRef]
- Horváth, K.; Lukács, D.; Sepsey, A.; Felinger, A. Effect of particle size distribution on the separation efficiency in liquid chromatography. J. Chromatogr. A 2014, 1361, 203–208. [Google Scholar] [CrossRef]
- Smits, W.; Nakanishi, K.; Desmet, G. The chromatographic performance of flow-through particles: A computational fluid dynamics study. J. Chromatogr. A 2016, 1429, 166–174. [Google Scholar] [CrossRef]
- Walls, D.; Walker, J.M. Protein Chromatography; Humana Press: Totowa, NJ, USA, 2017; Volume 1485, ISBN 9781493964109. [Google Scholar]
- Hager, W.H.; Castro-Orgaz, O. William Froude and the Froude number. J. Hydraul. Eng. 2017, 143, 2516005. [Google Scholar] [CrossRef]
- Makov, G.; Payne, M.C. Periodic boundary conditions in ab initio calculations. Phys. Rev. B 1995, 51, 4014–4022. [Google Scholar] [CrossRef] [PubMed]
- Richardson, S. On the no-slip boundary condition. J. Fluid Mech. 1973, 59, 707–719. [Google Scholar] [CrossRef]
- Sahraoui, M.; Kaviany, M. Slip and no-slip velocity boundary conditions at interface of porous, plain media. Int. J. Heat Mass Transf. 1992, 35, 927–943. [Google Scholar] [CrossRef]
- Dolamore, F. In Silico Analysis of Flow and Dispersion in Ordered Porous Media; University of Canterbury: Christchurch, New Zealand, 2017. [Google Scholar] [CrossRef]
- Rimmer, C.E. Heftmann: Chromatography, 6th edition. Fundamentals and applications of chromatography and related differential migration methods. Part A: Fundamentals and techniques. Anal. Bioanal. Chem. 2005, 382, 1447–1448. [Google Scholar] [CrossRef]
- Poole, C.F. The Essence of Chromatography; Elsevier: Amsterdam, The Netherlands, 2003; ISBN 978-0-444-50198-1. [Google Scholar]
- Mesh Element Quality and Size. n.d. Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.comsol/comsol_ref_mesh.15.18.html (accessed on 2 May 2025).
- Caluin, G.J. Dynamics of Chromatography Principles and Theory; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781315275871. [Google Scholar]
- Guiochon, G.; Shirazi, D.G.; Felinger, A. Fundamentals of Preparative and Nonlinear Chromatography; Academic Press: Cambridge, MA, USA, 2006; ISBN 978-0-12-370537-2. [Google Scholar]
- van Deemter, J.J.; Zuiderweg, F.J.; Klinkenberg, A. Commentary from Current Contents ® No. 3 January 19 1981, Longitudinal diffusion and resistance to mass transfer as causes of nonideality in chromatography. Chem. Eng. Sci. 1995, 50, 3867. [Google Scholar] [CrossRef]
- Billen, J.; Gzil, P.; Vervoort, N.; Baron, G.V.; Desmet, G. Influence of the packing heterogeneity on the performance of liquid chromatography supports. J. Chromatogr. A 2005, 1073, 53–61. [Google Scholar] [CrossRef]
- Ovsianikov, A.; Chichkov, B.N. Three-dimensional microfabrication by two-photon polymerization technique. Methods Mol. Biol. 2012, 868, 311–325. [Google Scholar] [CrossRef]
- Gittard, S.D.; Nguyen, A.; Obata, K.; Koroleva, A.; Narayan, R.J.; Chichkov, B.N. Fabrication of microscale medical devices by two-photon polymerization with multiple foci via a spatial light modulator. Biomed. Opt. Express 2011, 2, 3167–3178. [Google Scholar] [CrossRef]
- Emons, M.; Obata, K.; Binhammer, T.; Ovsianikov, A.; Chichkov, B.N.; Morgner, U. Two-photon polymerization technique with sub-50 nm resolution by sub-10 fs laser pulses. Opt. Mater. Express 2012, 2, 942–947. [Google Scholar] [CrossRef]
- De Malsche, W.; Op De Beeck, J.; De Bruyne, S.; Gardeniers, H.; Desmet, G. Realization of 1 × 106 Theoretical Plates in Liquid Chromatography Using Very Long Pillar Array Columns. Anal. Chem. 2012, 84, 1214–1219. [Google Scholar] [CrossRef]
- De Malsche, W.; Eghbali, H.; Clicq, D.; Vangelooven, J.; Gardeniers, H.; Desmet, G. Pressure-Driven Reverse-Phase Liquid Chromatography Separations in Ordered Nonporous Pillar Array Columns. Anal. Chem. 2007, 79, 5915–5926. [Google Scholar] [CrossRef]
- Karcher, H. The triply periodic minimal surfaces of Alan Schoen and their constant mean curvature companions. Manuscripta Math. 1989, 64, 291–357. [Google Scholar] [CrossRef]
- Karcher, H.; Polthier, K. Construction of triply periodic minimal surfaces. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1996, 354, 2077–2104. [Google Scholar] [CrossRef]
- Meeks, W.H., III. The theory of triply periodic minimal surfaces. Indiana Univ. Math. J. 1990, 39, 877–936. [Google Scholar] [CrossRef]
- Schoen, A.H. Infinite Periodic Minimal Surfaces Without Self-Intersections; National Aeronautics and Space Administration: Washington, DC, USA, 1970; Volume 5541. [Google Scholar]
- Jung, Y.; Torquato, S. Fluid permeabilities of triply periodic minimal surfaces. Phys. Rev. 2005, 72, 056319. [Google Scholar] [CrossRef]



| Dimensional Variables | Scale Factor | Dimensionless Variables |
|---|---|---|
| Length | Characteristic length of mobile phase | & |
| Velocity | Characteristic velocity | |
| Time | Characteristic time | |
| Pressure | Pressure (in Stokes regime) | |
| Tracer concentration | Reference concentration |
| /mol/L | 0.5 | 1 | 10 | 20 | 40 |
|---|---|---|---|---|---|
| Pe = 5 | 0.729 | 0.729 | 0.722 | 0.728 | 0.732 |
| Pe = 20 | 0.310 | 0.308 | 0.309 | 0.308 | 0.309 |
| Mesh Number | a (Ref) | b | c | d | e | f |
|---|---|---|---|---|---|---|
| Total element number | 345,542 | 138,508 | 38,246 | 25,984 | 15,580 | 2418 |
| Average mesh quality | 0.851 | 0.845 | 0.827 | 0.816 | 0.792 | 0.756 |
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| Porosity, | 0.33 | 0.66 | 0.44 | 0.44 | 0.55 | 0.77 | 0.55 | 0.55 | 0.66 | 0.55 |
| Permeability, | 0.11 | 0.21 | 0.12 | 0.18 | 0.12 | 0.08 | 0.08 | 0.06 | 0.04 | 0.04 |
| Minimum height equivalent to a theoretical plate, | 0.56 | 0.55 | 1.71 | 2.05 | 1.30 | 1.77 | 1.67 | 1.13 | 0.61 | 0.33 |
| Minimum separation impedance, | 0.94 | 0.96 | 10.72 | 12.27 | 7.74 | 30.15 | 19.17 | 11.70 | 6.13 | 1.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Q.; Rocca, S.; Shaikhuzzaman, K.; Dimartino, S. Numerical Investigation of 2D Ordered Pillar Array Columns: An Algorithm of Unit-Cell Automatic Generation and the Corresponding CFD Simulation. Separations 2025, 12, 184. https://doi.org/10.3390/separations12070184
Jiang Q, Rocca S, Shaikhuzzaman K, Dimartino S. Numerical Investigation of 2D Ordered Pillar Array Columns: An Algorithm of Unit-Cell Automatic Generation and the Corresponding CFD Simulation. Separations. 2025; 12(7):184. https://doi.org/10.3390/separations12070184
Chicago/Turabian StyleJiang, Qihao, Stefano Rocca, Kareem Shaikhuzzaman, and Simone Dimartino. 2025. "Numerical Investigation of 2D Ordered Pillar Array Columns: An Algorithm of Unit-Cell Automatic Generation and the Corresponding CFD Simulation" Separations 12, no. 7: 184. https://doi.org/10.3390/separations12070184
APA StyleJiang, Q., Rocca, S., Shaikhuzzaman, K., & Dimartino, S. (2025). Numerical Investigation of 2D Ordered Pillar Array Columns: An Algorithm of Unit-Cell Automatic Generation and the Corresponding CFD Simulation. Separations, 12(7), 184. https://doi.org/10.3390/separations12070184






