A Review of Prediction and Optimization for Sequence-Driven Scheduling in Job Shop Flexible Manufacturing Systems
Abstract
:1. Introduction
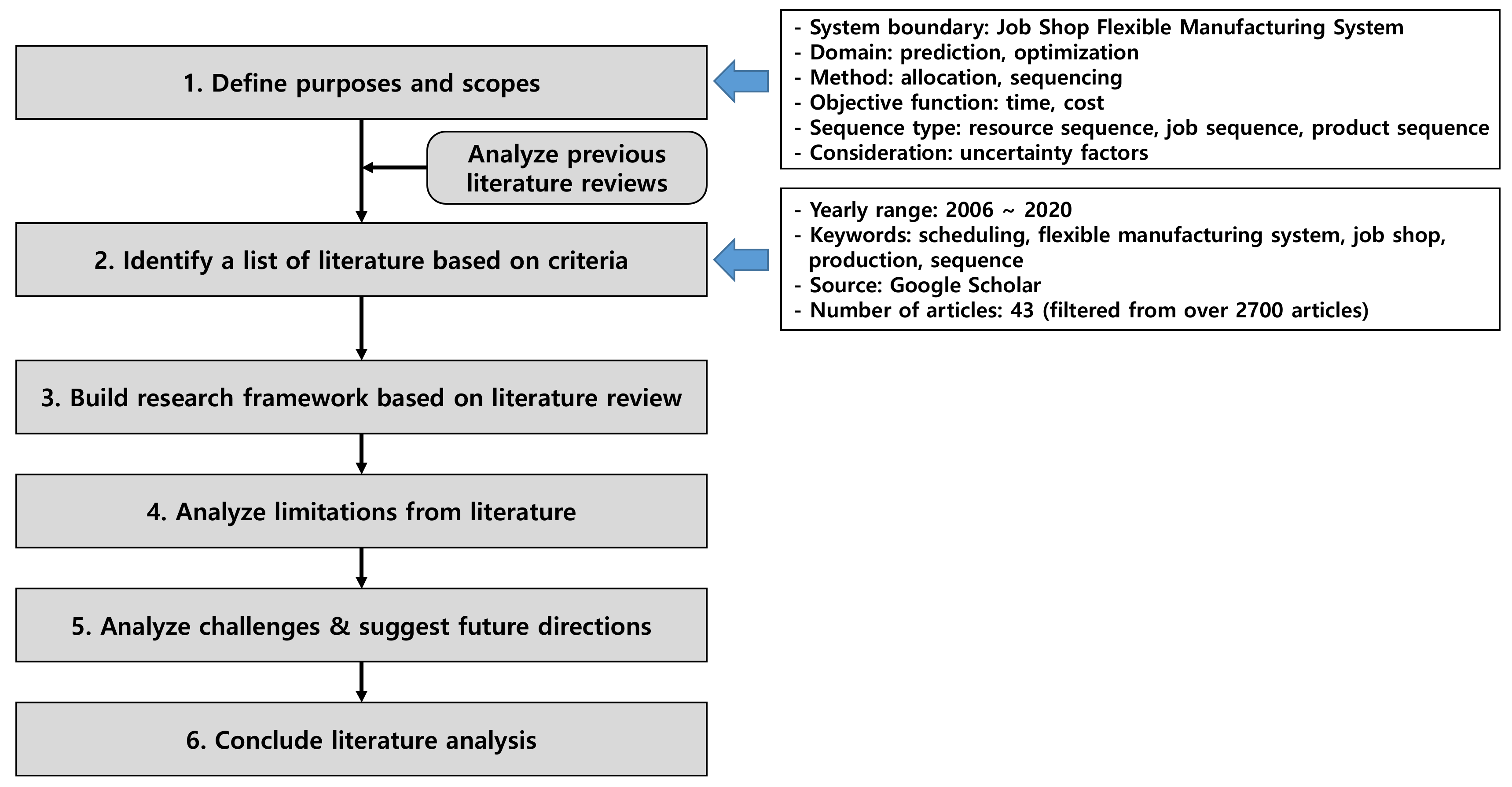
2. Scope and Method
2.1. Review of Previous Reviews
| Author | Keyword | Production Type | Findings |
|---|---|---|---|
| Zhu X and Wilhelm (2006) [11] |
|
|
|
| Demir and İşleyen (2013) [14] |
|
|
|
| Chaudhry and Khan (2016) [12] |
|
|
|
| Gao et al. (2019) [13] |
|
|
|
| Zhang et al. (2019) [15] |
|
|
|
| Xie et al. (2020) [7] |
|
|
|
2.2. Scope
- ‑
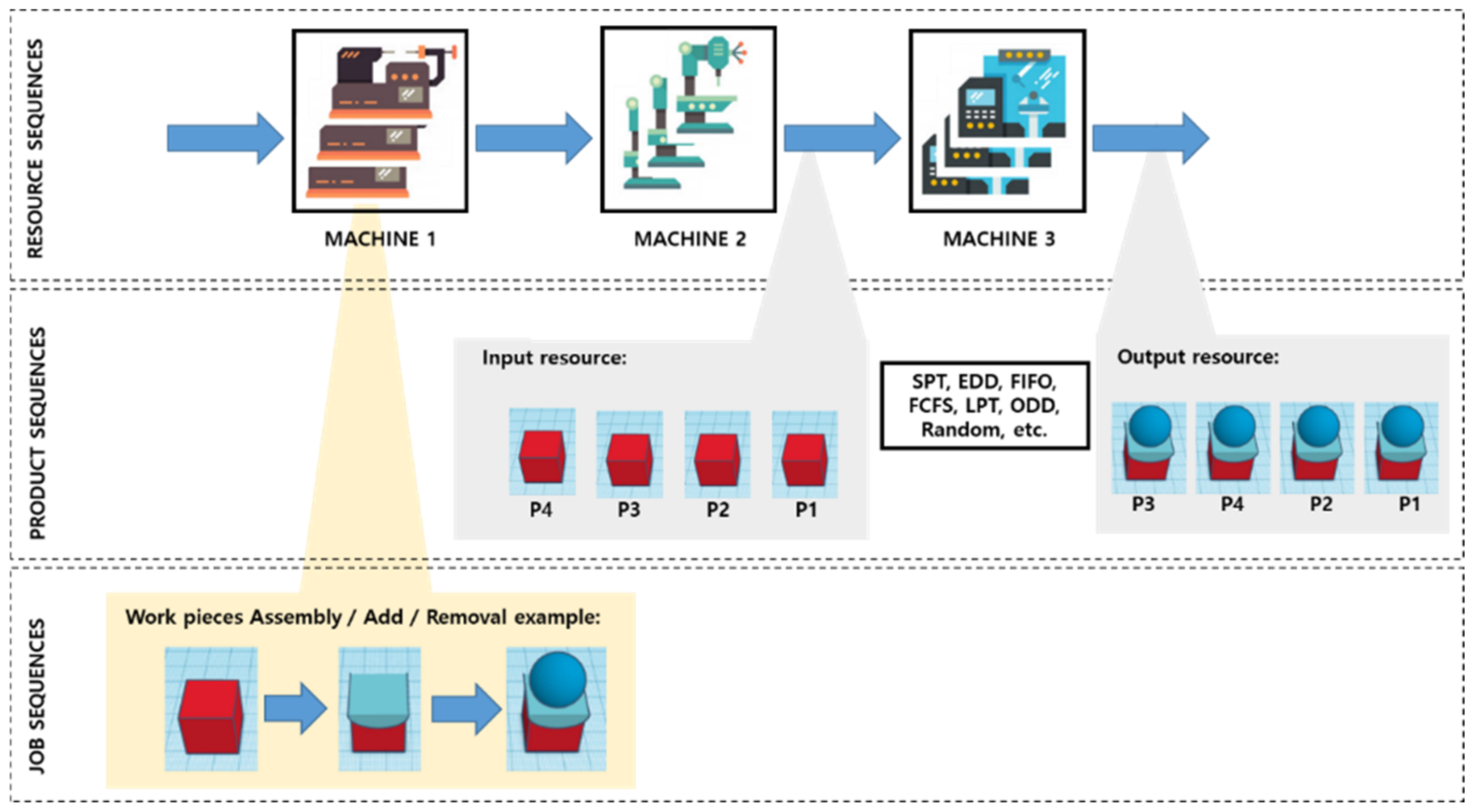
- System boundary: job shop flexible manufacturing systems (JS-FMS);
- ‑
- Domain: prediction and optimization;
- ‑
- Primary method: scheduling and sequencing;
- ‑
- Objective function: time indicators and cost indicators;
- ‑
- Sequence type: resource sequence, job sequence, and product sequence;
- ‑
- Consideration: uncertainty factors.
2.3. Methodology
3. Literature Analysis
3.1. Review Summary
| No | Authors | Optimization(O)/ Prediction(P) | Techniques | Objective | Sequence | Uncertainty | |||
|---|---|---|---|---|---|---|---|---|---|
| Resource | Job | Product | Dispatching Rule | ||||||
| 1 | Luo et al. (2008) [20] | O | ACO & LS | MS, WL | ○ | ○ | SPT | N/A | |
| 2 | Pezzella et al. (2008) [21] | O | GA | MS | ○ | ○ | MWR & MOR | PT | |
| 3 | Vinod et al. (2008) [22] | O & P | SIMULATION | MT, MFT, MST, MNS | ○ | FIFO, SPT, EDD, EMDD, CR, SSPT, SIMSET, JSPT, JEDD, JEMDD, JCR, JSSPT | ST & PT | ||
| 4 | Qiu et al. (2009) [23] | O | GA | MS | ○ | RAND | N/A | ||
| 5 | Song et al. (2010) [24] | O | GA and LS | MS | ○ | ○ | RAND | N/A | |
| 6 | Wang et al. (2010) [25] | O | FBS | MS, TWL, CMW | ○ | N/A | MA | ||
| 7 | Bagheri et.al. (2011) [26] | O | VNS | MS & MT | ○ | RAND | ST | ||
| 8 | Moslehi et al. (2011) [27] | O | PSO | MS, TWL, KT | ○ | SPT | PT | ||
| 9 | Wan et al. (2011) [28] | O | GA | MS | ○ | RAND, MWR, MOR | N/A | ||
| 10 | Xue et al. (2011) [29] | O | HDS | TC | ○ | SD | ST | ||
| 11 | Agrawal et al. (2012) [30] | O&P | GA | MS & TMT | ○ | SD | PT | ||
| 12 | Gao et al. (2012) [31] | O&P | PDHS | MS & MT | ○ | ○ | SPT, EFTRAND, MWR, MOR | N/A | |
| 13 | Özgüven et al. (2012) [32] | O | MIGP | MT, MS, WL | ○ | ○ | SD | ST & PT | |
| 14 | Xiong et al. (2012) [33] | O&P | GA | MS | ○ | RAND | MB | ||
| 15 | Xu et al. (2012) [34] | O | DAM | MS | ○ | N/A | Complex Product | ||
| 16 | Chen et al. (2013) [35] | O | WBMR | MT | ○ | FIFO, WSPT, SPRT, RRrule, WBMR | N/A | ||
| 17 | Kechadi (2013) [36] | O & P | RNN | MS | ○ | ○ | WSPT & WLPT | PT | |
| 18 | Yuan et al. (2013) [37] | O | HHS (NN & HS) | MS | ○ | MWR | N/A | ||
| 19 | Liu et al. (2014) [38] | O | GA | MS | ○ | RAND | N/A | ||
| 20 | Song et al. (2014) [39] | O | DSP | MS | ○ | SDP | N/A | ||
| 21 | Moghadam et al. (2014) [40] | O & P | GA | MS | ○ | ○ | RAND | PT & WL | |
| 22 | Rossi (2014) [41] | O | SIA | MS | ○ | SD | UE | ||
| 23 | Abdelmaguid (2015) [42] | O | TS, NSF | MS | ○ | ○ | RAND & MOD | ST & PT | |
| 24 | Palacios et al. (2015) [43] | O & P | HGA (GA & TS) | TT & MS | ○ | N/A | PT | ||
| 25 | Ham et al. (2016) [44] | O | MIP & CP | MS | ○ | SD | N/A | ||
| 26 | Torkaman et al. (2017) [45] | O | MIP | IC | ○ | SD | ST, Q, PT, NoP | ||
| 27 | Gong et al. (2018) [46] | O & P | HGA | MS, TWC, GP(+)* | ○ | ○ | N/A | N/A | |
| 28 | Jamrus et al. (2018) [47] | O | PSO & GA | CT | ○ | RAND | PT | ||
| 29 | Shen et al. (2018) [19] | O | MILP & TS | MS | ○ | SD | ST & PT | ||
| 30 | Zhang et al. (2018) [48] | O | MILP & CP | MS | ○ | ○ | ECT, JMRW, MLW | MB, MU, RO | |
| 31 | Novas (2019) [49] | O | CP | MS | ○ | SD | MC | ||
| 32 | Li et al. (2019) [50] | O | SH | MS & TSC | ○ | ○ | RAND | ST | |
| 33 | Huang et al. (2019) [51] | O & P | HGA (GA & SA) | MS | ○ | SPTT | Transfer Time | ||
| 34 | Wu et al. (2019) [52] | O | DDE, SA, CSA | MS | ○ | N/A | PT | ||
| 35 | Zhang et al. (2019) [53] | O & P | IH-PSO (PSO, GA, SA) | MS, ML, PC, BML | ○ | ○ | SD | ST | |
| 36 | Zhao et al. (2019) [54] | O | DRL | MS | ○ | N/A | N/A | ||
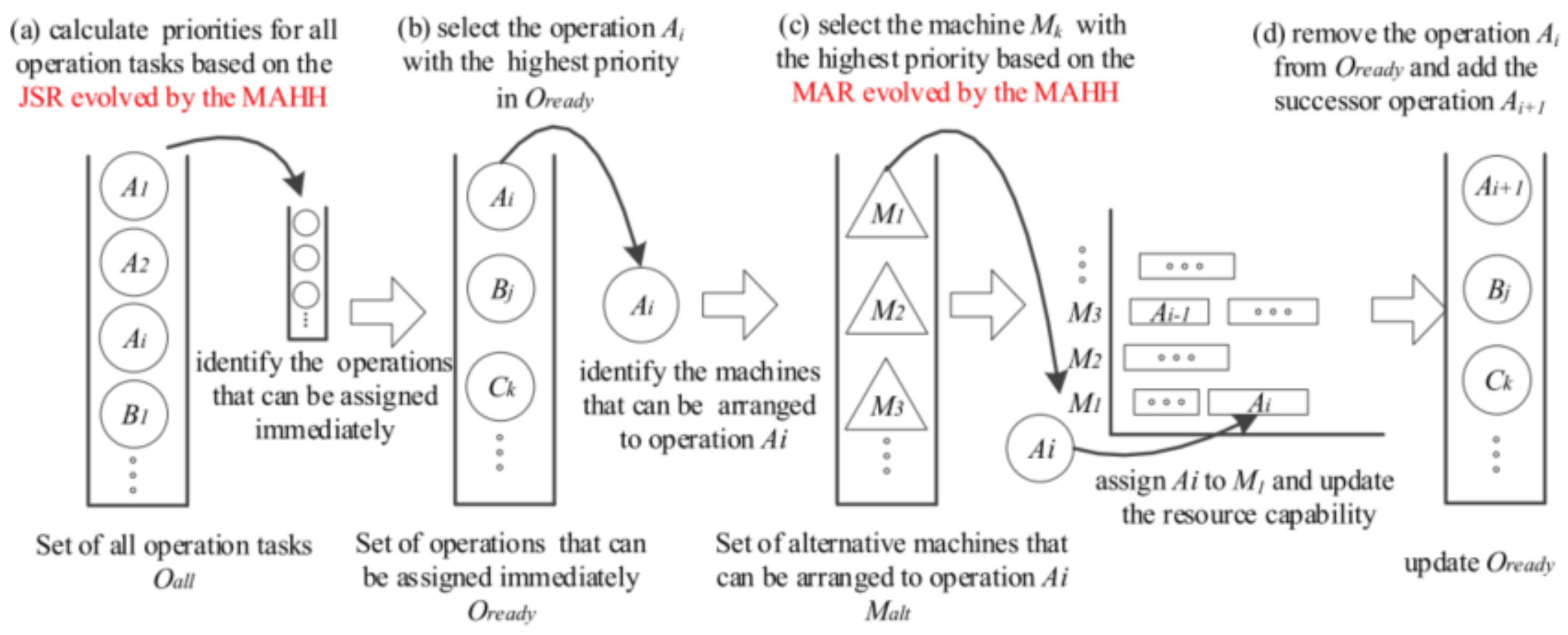
| 37 | Zhou et al. (2019) [55] | O & P | MAHH | TTO & WT | ○ | RAND | BML & EC | ||
| 38 | Abreu et al. (2020) [56] | O & P | HGA(GA, SA, VNS) | MS | ○ | ○ | SD | ST | |
| 39 | Defersha et al. (2020) [57] | O | GA | MS | ○ | ○ | SD | ST | |
| 40 | Fattahi et al. (2020) [58] | O | PSO & PVNS | MS | ○ | RAND | N/A | ||
| 41 | Gu et al. (2020) [59] | O | PSO | MS, BML, TW | ○ | ○ | RAND & GSO | PT | |
| 42 | Lin (2020) [60] | O | GA | MS | ○ | RAND | PT | ||
| 43 | Luo (2020) [61] | O | RL | TT | ○ | FIFO, EDD, MRT, SPT, LPT | New Job Insertion | ||
| 44 | Wang et al. (2020) [62] | O | ABC | MS | ○ | ○ | RAND | PT | |
| 45 | Wu et al. (2020) [63] | O | CSA | MS | ○ | FIFO | PT | ||
| 46 | Wu et al. (2021) [64] | O | Branch and Bound | TT | ○ | N/A | PT | ||
| 47 | Wu et al. (2021) [65] | O | DDE, IG, GA | MS | ○ | N/A | PT | ||
3.2. Detailed Analysis
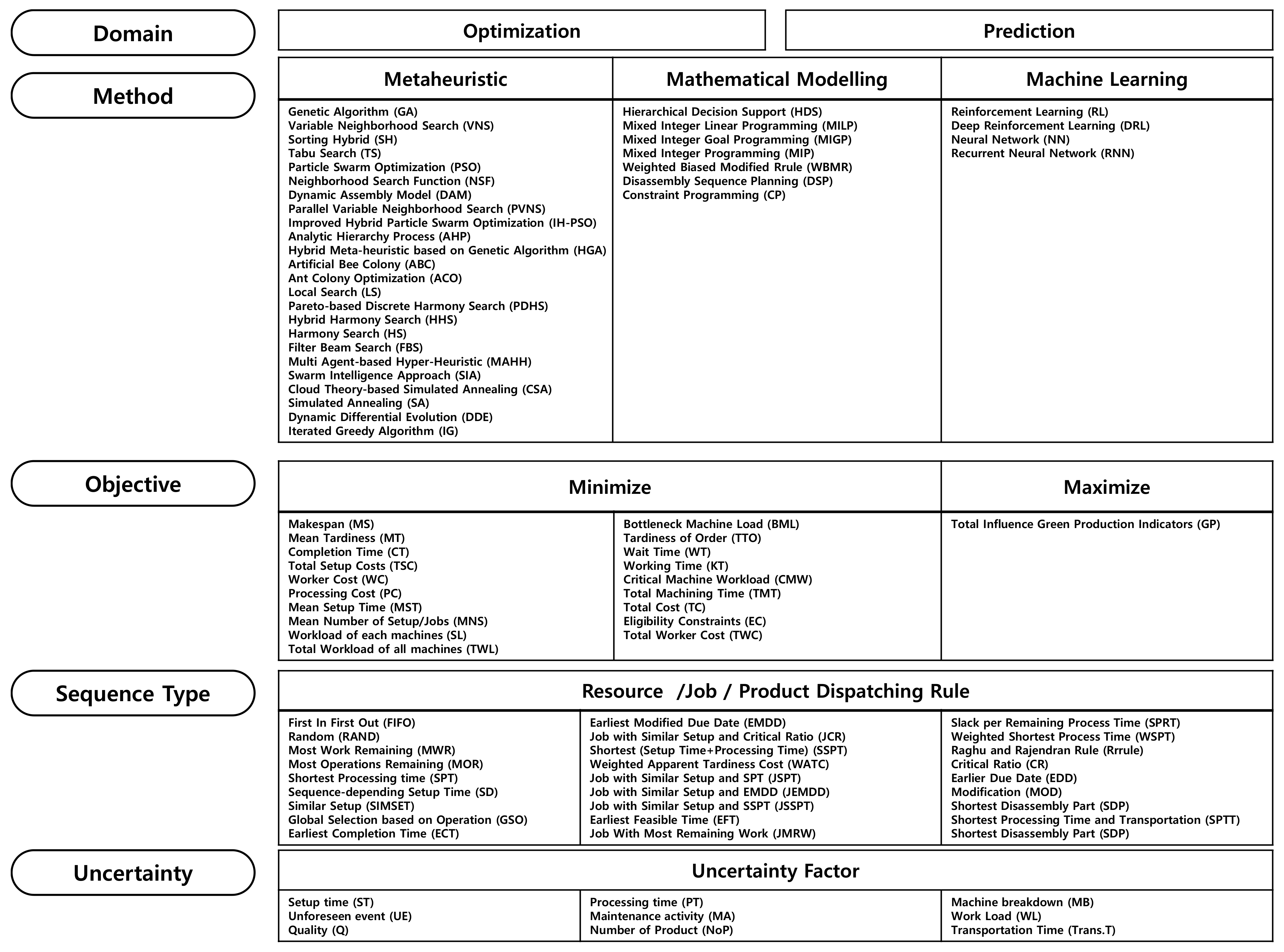
3.2.1. Domain
3.2.2. Method
3.2.3. Objective
3.2.4. Sequence Type
3.2.5. Uncertainty
4. Challenges and Future Directions
4.1. Challenges
4.2. Future Directions
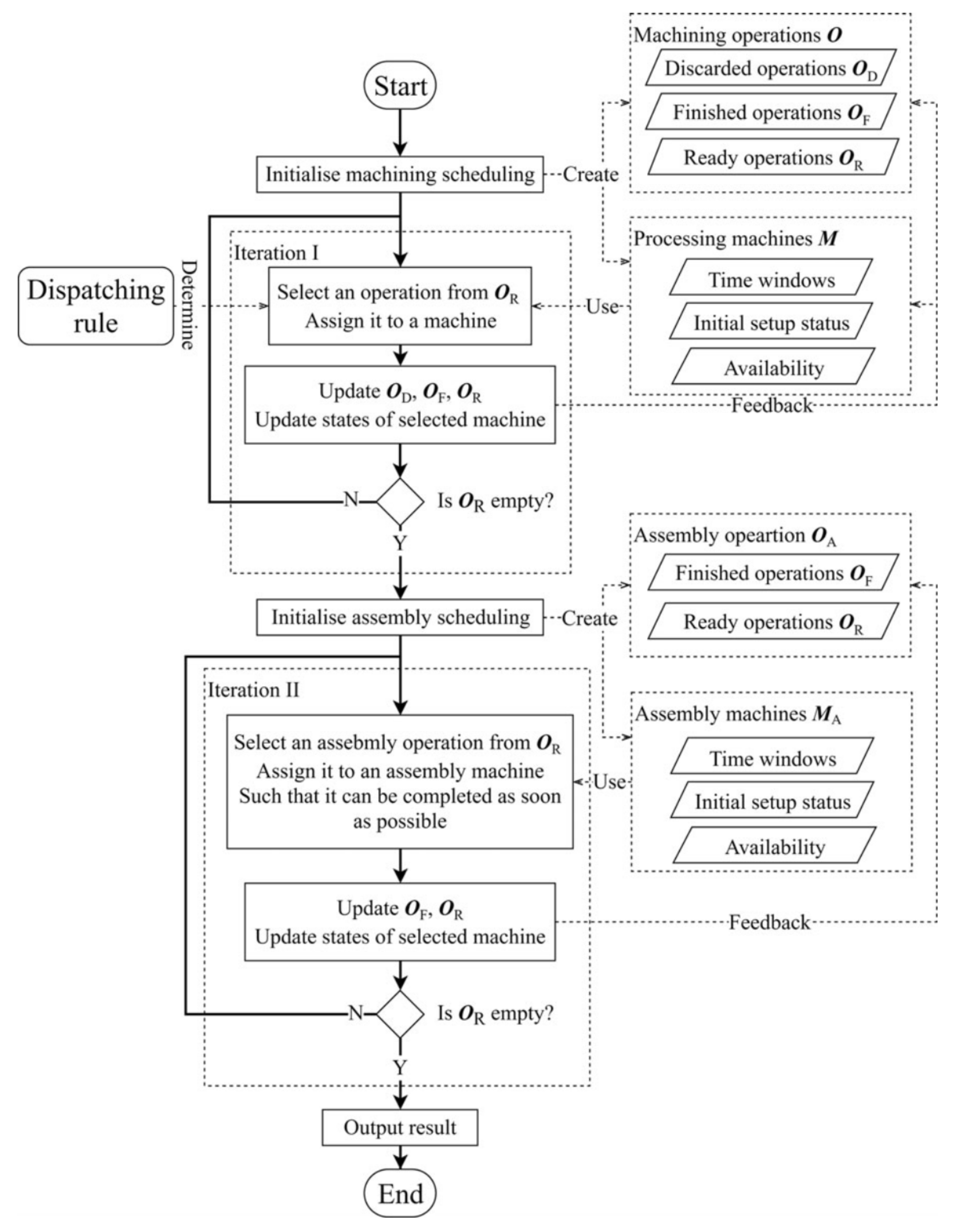
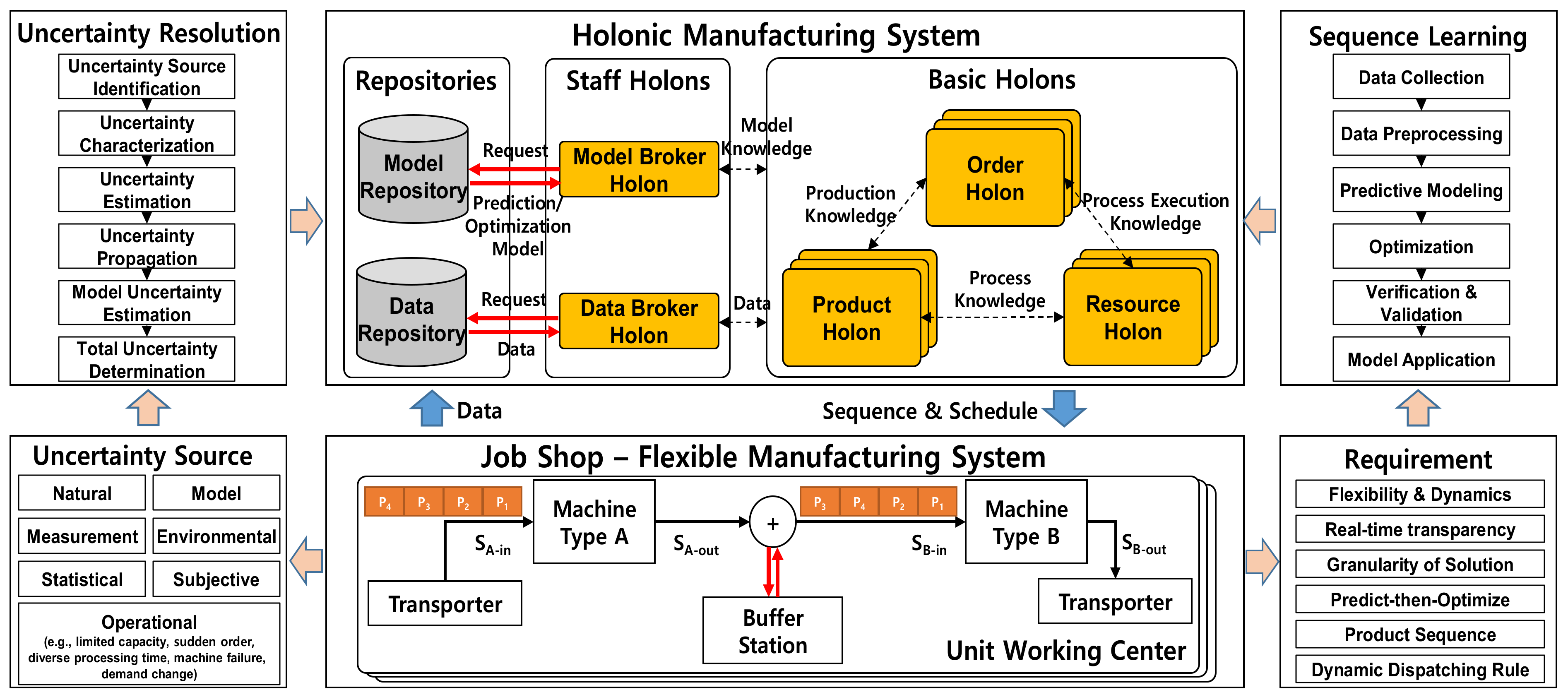
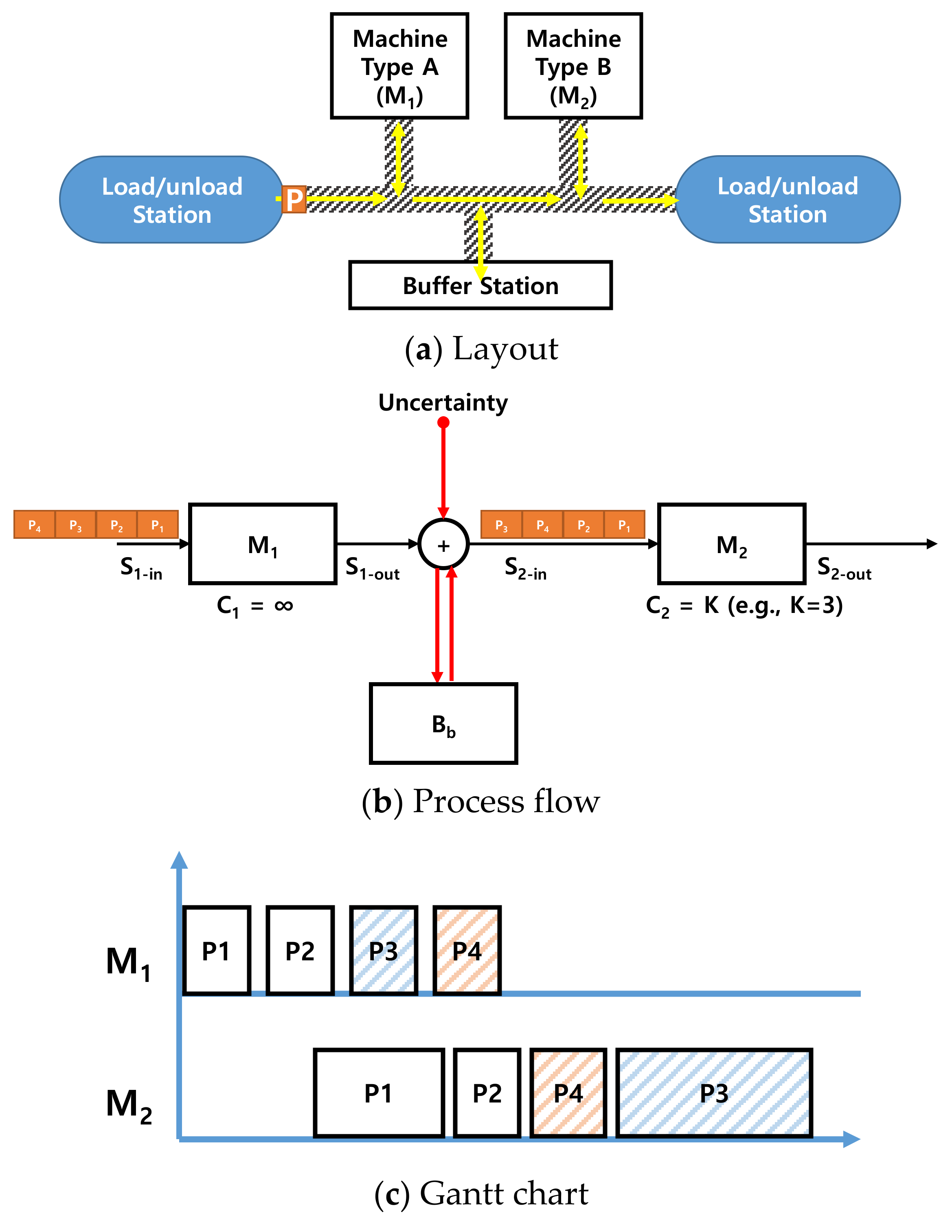
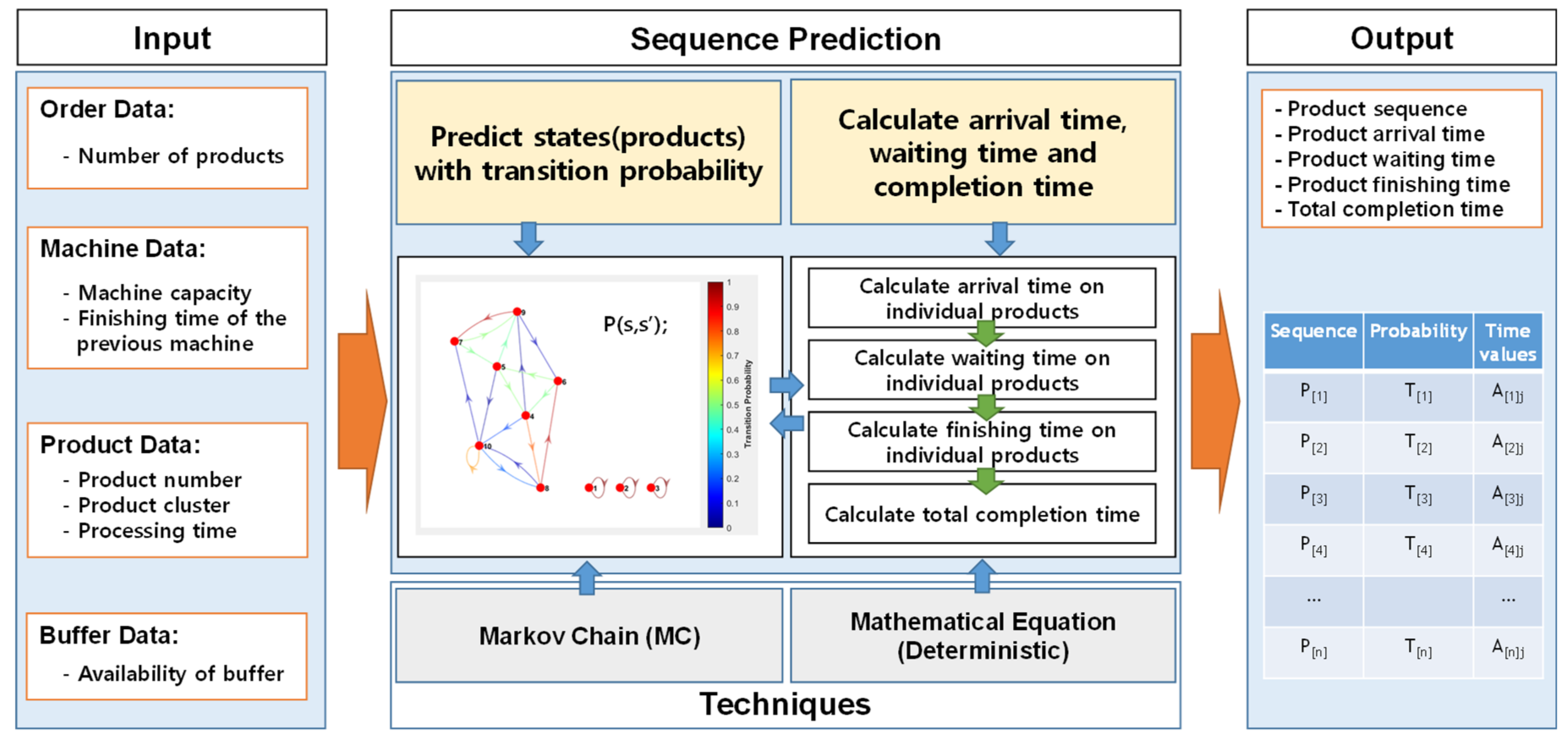
4.3. Application Case of Sequence Learning
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ElMaraghy, H.; Caggiano, A. Flexible Manufacturing System in the International Academy for Product; Laperrière, L., Reinhart, G., Eds.; CIRP Encyclopedia of Production Engineering; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Shivanand, H.K.; Benal, M.M.; Koti, V. Flexible Manufacturing System; New Age International Ltd.: New Delhi, India, 2006. [Google Scholar]
- GE Digital team. GE Digital. 2020. Available online: https://www.ge.com/ (accessed on 3 February 2021).
- Koh, S.C.L.; Saad, S. Development of a business model for diagnosing uncertainty in ERP environments. Int. J. Prod. Res. 2002, 40, 3015–3039. [Google Scholar] [CrossRef]
- Haupt, R. A survey of priority rule based scheduling. Oper. Res. Spektrum 1989, 11, 3–16. [Google Scholar] [CrossRef]
- Owen, H.A. Job Shop vs Flow Shop: Can Robots Work for Both? Robotiq. 2017. Available online: https://blog.robotiq.com/ (accessed on 10 February 2021).
- Xie, J.; Gao, L.; Peng, K.; Li, X.; Li, H. Review on Flexible Job Shop Scheduling in Effective Methods for Integrated Process Planning and Scheduling; Engineering Applications of Computational Methods; Springer: Berlin/Heidelberg, Germany, 2020; Volume 2. [Google Scholar]
- Baker, K.R.; Trietsch, D. Principles of Scheduling and Sequencing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hall, N.G.; Magazine, M. Scheduling and sequencing. In Encyclopedia of Operations Research and Management Science; Gass, S.I., Michael, C.F., Eds.; Springer: Boston, MA, USA, 2013. [Google Scholar]
- Swamidass, P.M. (Ed.) Job Sequence Rules. Encyclopedia of Production and Manufacturing Management; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Zhu, X.; Wilhelm, W.E. Scheduling and lot sizing with sequence dependent setup: A literature review. IIE Trans. 2006, 38, 987–1007. [Google Scholar] [CrossRef]
- Chaudhry, I.A.; Khan, A.A. A research survey: Review of flexible job shop scheduling techniques. Int. Trans. Oper. Res. 2016, 23, 551–591. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Demir, Y.; İşleyen, S.K. Evaluation of mathematical models for flexible job-shop scheduling problems. Appl. Math. Model. 2013, 37, 977–988. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 2019, 30, 1809–1830. [Google Scholar] [CrossRef]
- Rasheed, F.; Wahid, A. Sequence generation for learning: A transformation from past to future. Int. J. Inf. Learn. Technol. 2019, 36, 434–452. [Google Scholar] [CrossRef]
- Akbar, M.; Irohara, T. Scheduling for sustainable manufacturing: A review. J. Clean. Prod. 2018, 205, 866–883. [Google Scholar] [CrossRef]
- Shin, S.J.; Kim, Y.M.; Meilanitasari, P. A holonic-based self-learning mechanism for energy-predictive planning in machining processes. Processes 7 2019, 10, 739. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Pérès, S.D.; Neufeldd, J.N. Solving the flexible job shop scheduling problem with sequence-dependent setup times. Eur. J. Oper. Res. 2018, 265, 503–516. [Google Scholar] [CrossRef]
- Luo, D.L.; Wu, S.X.; Li, M.Q.; Yang, Z. Ant colony optimization with local search applied to the Flexible Job Shop Scheduling Problems. Int. Conf. Commun. Circuits Syst. 2008, 1015–1020. [Google Scholar]
- Pezzella, F.; Morganti, G.; Chiaschetti, G. A genetic algorithm for the flexible job-shop scheduling problem. Comput. Oper. Res. 2008, 35, 3202–3212. [Google Scholar] [CrossRef]
- Vinod, V.; Sridharan, R. Scheduling a dynamic job shop production system with sequence-dependent setups: An experimental study. Robot. Comput. Integr. Manuf. 2008, 24, 435–449. [Google Scholar] [CrossRef]
- Qiu, H.; Zhou, W.; Wang, H. A genetic algorithm-based approach to flexible job-shop scheduling problem. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjin, China, 14–16 August 2009. [Google Scholar]
- Song, L.; Xu, X. Flexible job shop scheduling problem solving based on genetic algorithm with chaotic local search. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010. [Google Scholar]
- Wang, S.; Yu, J. An effective heuristic for flexible job-shop scheduling problem with maintenance activities. Comput. Ind. Eng. 2010, 59, 436–447. [Google Scholar] [CrossRef]
- Bagheri, A.; Zandieh, M. Bi-criteria flexible job-shop scheduling with sequence-dependent setup times variable neighborhood search approach. J. Manuf. Syst. 2011, 30, 8–15. [Google Scholar] [CrossRef]
- Moslehi, G.; Mahnam, M. A pareto approach to multi-objective flexible job-shop scheduling problem using particle swarm optimization and local search. Int. J. Prod. Econ. 2011, 129, 14–22. [Google Scholar] [CrossRef]
- Wan, M.; Xu, X.; Nan, J. Flexible job-shop scheduling with integrated genetic algorithm. In Proceedings of the Fourth International Workshop on Advanced Computational Intelligence, Wuhan, China, 19–21 October 2011. [Google Scholar]
- Xue, G.; Offodile, O.F.; Zhou, H.; Troutt, M.D. Integrated production planning with sequence-dependent family setup times. Int. J. Prod. Econ. 2011, 131, 674–681. [Google Scholar] [CrossRef]
- Agrawal, R.; Pattanaik, L. Scheduling of a flexible job shop using a multi objective genetic algorithm. J. Adv. Manag. Res. 2012, 9, 178–188. [Google Scholar] [CrossRef]
- Gao, K.; Suganthan, P.; Chua, T. Pareto-based discrete harmony search algorithm for flexible job shop scheduling. In Proceedings of the 2012 12th International Conference on Intelligent Systems Design and Applications (ISDA), Kochi, India, 27–29 November 2012. [Google Scholar]
- Özgüven, C.; Yavuz, Y.; Özbakır, L. Mixed integer goal programming models for the flexible job-shop scheduling problems with separable and non-separable sequence dependent setup times. Appl. Math. Model. 2012, 36, 846–858. [Google Scholar] [CrossRef]
- Xiong, J.; Xing, L.N.; Chen, Y.W. Robust scheduling for multi-objective flexible job-shop problems with random machine breakdowns. Int. J. Prod. Econ. 2013, 141, 112–126. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.; Zhang, J.; Cheng, H.; Jiang, S.; Tang, W. A dynamic assembly model for assembly sequence planning of complex product based on polychromatic sets theory. Assem. Autom. 2012, 32, 152–162. [Google Scholar] [CrossRef]
- Chen, B.; Matis, T.I. A flexible dispatching rule for minimizing tardiness in job shop scheduling. Int. J. Prod. Econ. 2013, 141, 360–365. [Google Scholar] [CrossRef]
- Kechadi, M.T.; Low, K.S.; Goncalves, G. Recurrent neural network approach for cyclic job shop scheduling problem. J. Manuf. Syst. 2013, 32, 689–699. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Xu, H.; Yang, J. A hybrid harmony search algorithm for the flexible job shop scheduling problem. Appl. Soft Comput. 2013, 13, 3259–3272. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Y.; Chou, J. Solving distributed and flexible job-shop scheduling problems for a real-world fastener manufacturer. IEEE Access 2014, 2, 1598–1606. [Google Scholar]
- Song, X.; Zhou, W.; Pan, X.; Feng, K. Disassembly sequence planning for electro-mechanical products under a partial destructive mode. Assem. Autom. 2014, 34, 106–114. [Google Scholar] [CrossRef]
- Moghadam, A.; Wong, K.; Piroozfard, H. An efficient genetic algorithm for flexible job-shop scheduling problem. In Proceedings of the 2014 IEEE International Conference on Industrial Engineering and Engineering Management, Bandar Sunway, Malaysia, 9–12 December 2014. [Google Scholar]
- Rossi, A. Flexible job shop scheduling with sequence-dependent setup and transportation times by ant colony with reinforced pheromone relationships. Int. J. Prod. Econ. 2014, 153, 253–267. [Google Scholar] [CrossRef]
- Abdelmaguid, T.F. A neighborhood search function for flexible job shop scheduling with separable sequence-dependent setup times. Appl. Math. Comput. 2015, 260, 188–203. [Google Scholar] [CrossRef]
- Palacios, J.J.; González, M.A.; Vela, C.R.; Rodríguez, I.G.; Puente, J. Genetic tabu search for the fuzzy flexible job shop problem. Comput. Oper. Res. 2015, 54, 74–89. [Google Scholar] [CrossRef] [Green Version]
- Ham, A.M.; Cakici, E. Flexible job shop scheduling problem with parallel batch processing machines: MIP and CP approaches. Comput. Ind. Eng. 2016, 102, 160–165. [Google Scholar] [CrossRef]
- Torkaman, S.; Ghomi, S.M.T.F.; Karimi, B. Multi-stage multi-product multi-period production planning with sequence-dependent setups in closed-loop supply chain. Comput. Ind. Eng. 2017, 113, 602–613. [Google Scholar] [CrossRef]
- Gong, G.; Deng, Q.; Gong, X.; Liu, W.; Ren, Q. A new double flexible job-shop scheduling problem integrating processing time, green production, and human factor indicators. J. Clean. Prod. 2018, 174, 560–576. [Google Scholar] [CrossRef]
- Jamrus, T.; Chien, C.; Gen, M.; Sethanan, K. Hybrid particle swarm optimization combined with genetic operators for flexible job-shop scheduling under uncertain processing time for semiconductor manufacturing. IEEE Trans. Semicond. Manuf. 2018, 31, 32–41. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, S. Flexible assembly job-shop scheduling with sequence-dependent setup times and part sharing in a dynamic environment: Constraint programming model, mixed-integer programming model, and dispatching rules. IEEE Trans. Eng. Manag. 2018, 65, 487–504. [Google Scholar] [CrossRef]
- Novas, J.M. Production scheduling and lot streaming at flexible job-shops environments using constraint programming. Comput. Ind. Eng. 2019, 136, 252–264. [Google Scholar] [CrossRef]
- Li, Z.C.; Qian, B.; Hu, R.; Chang, L.L.; Yang, J.B. An elitist nondominated sorting hybrid algorithm for multi-objective flexible job-shop scheduling problem with sequence-dependent setups. Knowl. Based Syst. 2019, 173, 83–112. [Google Scholar] [CrossRef]
- Huang, X.; Yang, L. A hybrid genetic algorithm for multi-objective flexible job shop scheduling problem considering transportation time. Int. J. Intell. Comput. Cybern. 2019, 12, 154–174. [Google Scholar] [CrossRef]
- Wu, C.C.; Azzouz, A.; Chung, I.H.; Lin, W.C.; Said, L.B. A two-stage three-machine assembly scheduling problem with deterioration effect. Int. J. Prod. Res. 2019, 57, 6634–6647. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, H.; Tang, D. An improved hybrid particle swarm optimization for multi-objective flexible job-shop scheduling problem. Kybernetes 2019, 49, 2873–2892. [Google Scholar] [CrossRef]
- Zhao, M.; Guo, X.; Zhang, X.; Fang, Y.; Ou, Y. ASPW-DRL: Assembly sequence planning for work pieces via a deep reinforcement learning approach. Assem. Autom. 2019, 40, 65–75. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, J.J.; Zheng, L.Y. Multi-agent based hyper-heuristics for multi objective flexible job shop scheduling: A case study in an aero-engine blade manufacturing plant. IEEE Access 2019, 7, 21147–21176. [Google Scholar] [CrossRef]
- Abreu, L.; Prata, B. A genetic algorithm with neighborhood search procedures for unrelated parallel machine scheduling problem with sequence-dependent setup times. J. Model. Manag. 2020, 15, 809–828. [Google Scholar] [CrossRef]
- Defersha, F.M.; Rooyani, D. An efficient two-stage genetic algorithm for a flexible job-shop scheduling problem with sequence dependent attached/detached setup, machine release date and lag-time. Comput. Ind. Eng. 2020, 147, 106605. [Google Scholar] [CrossRef]
- Fattahi, P.; Bagheri Rad, N.; Daneshamooz, F.; Ahmadi, S. A new hybrid particle swarm optimization and parallel variable neighborhood search algorithm for flexible job shop scheduling with assembly process. Assem. Autom. 2020, 40, 419–432. [Google Scholar] [CrossRef]
- Gu, X.; Huang, M.; Liang, X. A discrete particle swarm optimization algorithm with adaptive inertia weight for solving multi objective flexible job-shop scheduling problem. IEEE Access 2020, 8, 33125–33136. [Google Scholar] [CrossRef]
- Lin, C.S.; Li, P.Y.; Wei, J.M.; Wu, M.C. Integration of process planning and scheduling for distributed flexible job shops. Comput. Oper. Res. 2020, 124, 105053. [Google Scholar] [CrossRef]
- Luo, S. Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning. Appl. Soft Comput. J. 2020, 91, 106208. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, N. Flexible flow shop scheduling with interval grey processing time. Grey Syst. Theory Appl. 2020, 2043–9377. [Google Scholar]
- Wu, C.C.; Gupta, J.N.D.; Cheng, S.R.; Lin, B.M.T.; Yip, S.H.; Lin, W.C. Robust scheduling for a two-stage assembly shop with scenario-dependent processing times. Int. J. Prod. Res. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Wu, C.C.; Bai, D.; Zhang, X.; Cheng, S.R.; Lin, J.C.; Wu, Z.L.; Lin, W.C. A robust customer order scheduling problem along with scenario-dependent component processing times and due dates. J. Manuf. Syst. 2021, 58, 291–305. [Google Scholar] [CrossRef]
- Wu, C.C.; Zhang, X.; Azzouz, A.; Shen, W.L.; Cheng, S.R.; Hsu, P.H.; Lin, W.C. Metaheuristics for two-stage flow-shop assembly problem with a truncation learning function. Eng. Optim. 2021, 53, 843–866. [Google Scholar] [CrossRef]
- Nouri, H.E.; Driss, O.B.; Ghédira, K. Solving the flexible job shop problem by hybrid metaheuristics-based multi agent model. J. Ind. Eng. Int. 2018, 14, 1–14. [Google Scholar] [CrossRef]
- Candan, G.; Yazgan, H.R. Genetic algorithm parameter optimization using Taguchi method for a flexible manufacturing system scheduling problem. Int. J. Prod. Res. 2015, 53, 897–915. [Google Scholar] [CrossRef]
- Udhayakumar, P.; Kumanan, S. Sequencing and scheduling of job and tool in a flexible manufacturing system using ant colony optimization algorithm. Int. J. Adv. Manuf. Technol. 2010, 50, 1075–1984. [Google Scholar] [CrossRef]
- Kantor, I.; Robineau, J.L.; Bütün, H.; Maréchal, F. A mixed integer linear programming formulation for optimizing multi scale material and energy integration. Front. Energy Res. 2020, 8, 49. [Google Scholar] [CrossRef]
- NCSS, NCSS Statistical Software: Chapter 482: Mixed Integer Linear Programming. 2021. Available online: https://www.ncss.com/software/ncss/ncss-documentation/ (accessed on 3 March 2021).
- Hurwitz, J.; Kirsch, D. Machine Learning IBM Limited Edition; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Greeff, G.; Ghoshal, R. (Eds.) Production scheduling, management and control. In Practical E-Manufacturing and Supply Chain Management; Elsevier: Amsterdam, The Netherlands, 2004; pp. 243–269. [Google Scholar]
- Pena, P.N.; Costa, T.A.; Silva, R.S.; Takahashi, R.H. Control of flexible manufacturing systems under model uncertainty using supervisory control theory and evolutionary computation schedule synthesis. Inf. Sci. 2016, 329, 491–502. [Google Scholar] [CrossRef]
- Akpan, E. Job shop sequencing problems via network scheduling technique. Int. J. Oper. Prod. Manag. 1996, 16, 76–86. [Google Scholar] [CrossRef]
- Chapter II: Sequencing and scheduling–An Overview. 2020. Available online: http://courseware.cutm.ac.in/wp-content/uploads/2020/06/sequencing-pdf.pdf (accessed on 10 February 2021).
- Elmachtoub, A.N.; Grigas, P. Smart “Predict, then Optimize”. arXiv 2020, arXiv:1710.08005. [Google Scholar]
- Wazed, M.A.; Ahmed, S.; Yusoff, N. Uncertainty factors in real manufacturing environment. Aust. J. Basic Appl. Sci. 2009, 3, 342–351. [Google Scholar]
- Roy, C.J.; Oberkampf, W.L. A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing. Comput. Methods Appl. Mech. Eng. 2011, 200, 2131–2144. [Google Scholar] [CrossRef]
- Mahadevan, S.; Liang, B. Error and uncertainty quantification and sensitivity analysis in mechanics computational models. Int. J. Uncertain. Quantif. 2011, 1, 147–161. [Google Scholar] [CrossRef]
- Nannapaneni, S.; Mahadevan, S.; Rachuri, S. Performance evaluation of a manufacturing process under uncertainty using Bayesian networks. J. Clean. Prod. 2016, 113, 947–959. [Google Scholar] [CrossRef] [Green Version]
- Monostori, L. AI and machine learning techniques for managing complexity, changes and uncertainties in manufacturing. Eng. Appl. Artif. Intell. 2003, 16, 277–291. [Google Scholar] [CrossRef]
- Brussel, V.H.; Wyns, J.; Valckenaers, P.; Bongaerts, L.; Peeters, P. Reference architecture for holonic manufacturing systems: PROSA. Comput. Ind. 1998, 37, 255–274. [Google Scholar] [CrossRef]
- Shen, W.; Hao, Q.; Yoon, H.J.; Norrie, D.H. Applications of agent-based systems in intelligent manufacturing: An updated review. Adv. Eng. Inform. 2019, 20, 415–431. [Google Scholar] [CrossRef]
- Norrie, D.H.; Walker, S.S.; Brennan, R.W. Holonic job shop scheduling using a multiagent system. IEEE Intell. Syst. 2005, 20, 50–57. [Google Scholar]
- Priore, P.; Fuente, D.D.L.; Puente, J.; Parreno, J. A comparison of machine-learning algorithms for dynamic scheduling of flexible manufacturing systems. Eng. Appl. Artif. Intell. 2006, 19, 247–255. [Google Scholar] [CrossRef]
- Sun, R. Introduction to Sequence Learning, in Sequence Learning Paradigms, Algorithms, and Applications; Springer: Berlin/Heidelberg, Germany, 2001; pp. 1–12. [Google Scholar]
| Name of Journal or Proceeding | Number of Articles |
|---|---|
| 2008 International Conference on Communications, Circuits, and Systems | 1 |
| 2009 Fifth International Conference on Natural Computation | 1 |
| 2010 Sixth International Conference on Natural Computation | 1 |
| 2012 12th International Conference on Intelligent Systems Design and Applications (ISDA) | 1 |
| 2014 IEEE International Conference on Industrial Engineering and Engineering Management | 1 |
| Applied Mathematical Modelling | 1 |
| Applied Mathematics and Computation | 1 |
| Assembly Automation | 4 |
| Computers & Industrial Engineering | 5 |
| Computers & Operations Research | 3 |
| Engineering Optimization | 1 |
| European Journal of Operational Research | 1 |
| Applied Soft Computing | 1 |
| Grey Systems: Theory and Application | 1 |
| IEEE Access | 3 |
| IEEE Transactions on Automation Science and Engineering | 1 |
| IEEE Transactions on Engineering Management | 1 |
| IEEE Transactions on Semiconductor Manufacturing | 1 |
| Industrial Robot | 1 |
| International Journal of Intelligent Computing and Cybernetics | 1 |
| International Journal of Production Economics | 5 |
| International Journal of Production Research | 2 |
| Journal of Advances in Management Research | 1 |
| Journal of Cleaner Production | 1 |
| Journal of Manufacturing Systems | 3 |
| Journal of Modelling in Management | 1 |
| Knowledge-Based Systems | 1 |
| Kybernetes | 1 |
| Robotics and Computer-Integrated Manufacturing | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meilanitasari, P.; Shin, S.-J. A Review of Prediction and Optimization for Sequence-Driven Scheduling in Job Shop Flexible Manufacturing Systems. Processes 2021, 9, 1391. https://doi.org/10.3390/pr9081391
Meilanitasari P, Shin S-J. A Review of Prediction and Optimization for Sequence-Driven Scheduling in Job Shop Flexible Manufacturing Systems. Processes. 2021; 9(8):1391. https://doi.org/10.3390/pr9081391
Chicago/Turabian StyleMeilanitasari, Prita, and Seung-Jun Shin. 2021. "A Review of Prediction and Optimization for Sequence-Driven Scheduling in Job Shop Flexible Manufacturing Systems" Processes 9, no. 8: 1391. https://doi.org/10.3390/pr9081391
APA StyleMeilanitasari, P., & Shin, S.-J. (2021). A Review of Prediction and Optimization for Sequence-Driven Scheduling in Job Shop Flexible Manufacturing Systems. Processes, 9(8), 1391. https://doi.org/10.3390/pr9081391







