Optimization of Pipeline Network Layout for Multiple Heat Sources Distributed Energy Systems Considering Reliability Evaluation †
Abstract
:1. Introduction
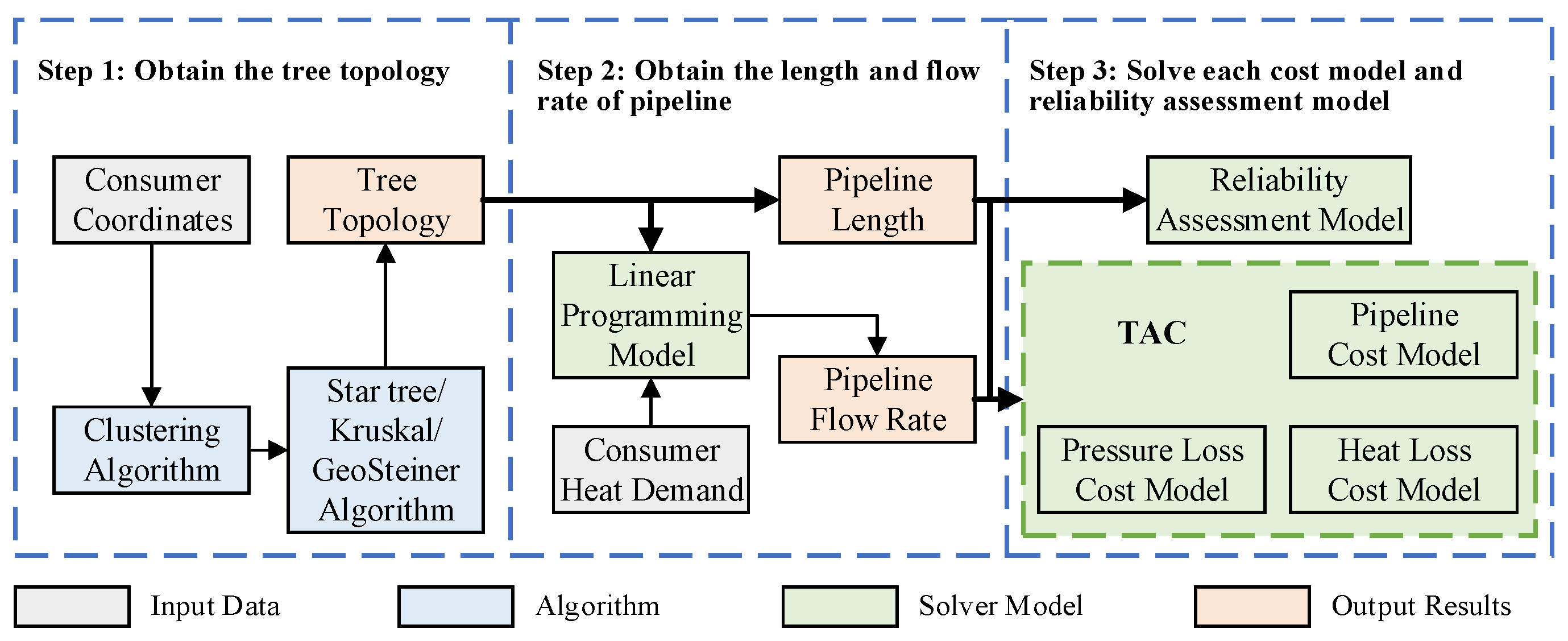
2. Methodology
2.1. Problem Statement
2.1.1. Assumption
- (1)
- The pipeline length is the distance between the two vertices that are connected.
- (2)
- The steam in the pipeline network system is an incompressible fluid.
- (3)
- The temperature of the fluid in each pipeline is constant.
- (4)
- The flow rate of the fluid in each pipeline is constant.
2.1.2. Given
- (1)
- The number of consumers and heat sources.
- (2)
- The coordinates and heat demand of consumers.
- (3)
- The coordinates and the heat supply of heat source.
2.1.3. Determine
- (1)
- The pipeline network topology of multiple heat sources DES.
- (2)
- Total annual cost and reliability of multiple heat sources DES.
2.2. Mathematical Model
2.2.1. Objective Function
2.2.2. Linear Programming Model
2.2.3. Pipeline Cost Model
2.2.4. Pressure Loss Cost Model
2.2.5. Heat Loss Cost Model
2.2.6. Reliability Assessment Model
3. Algorithm
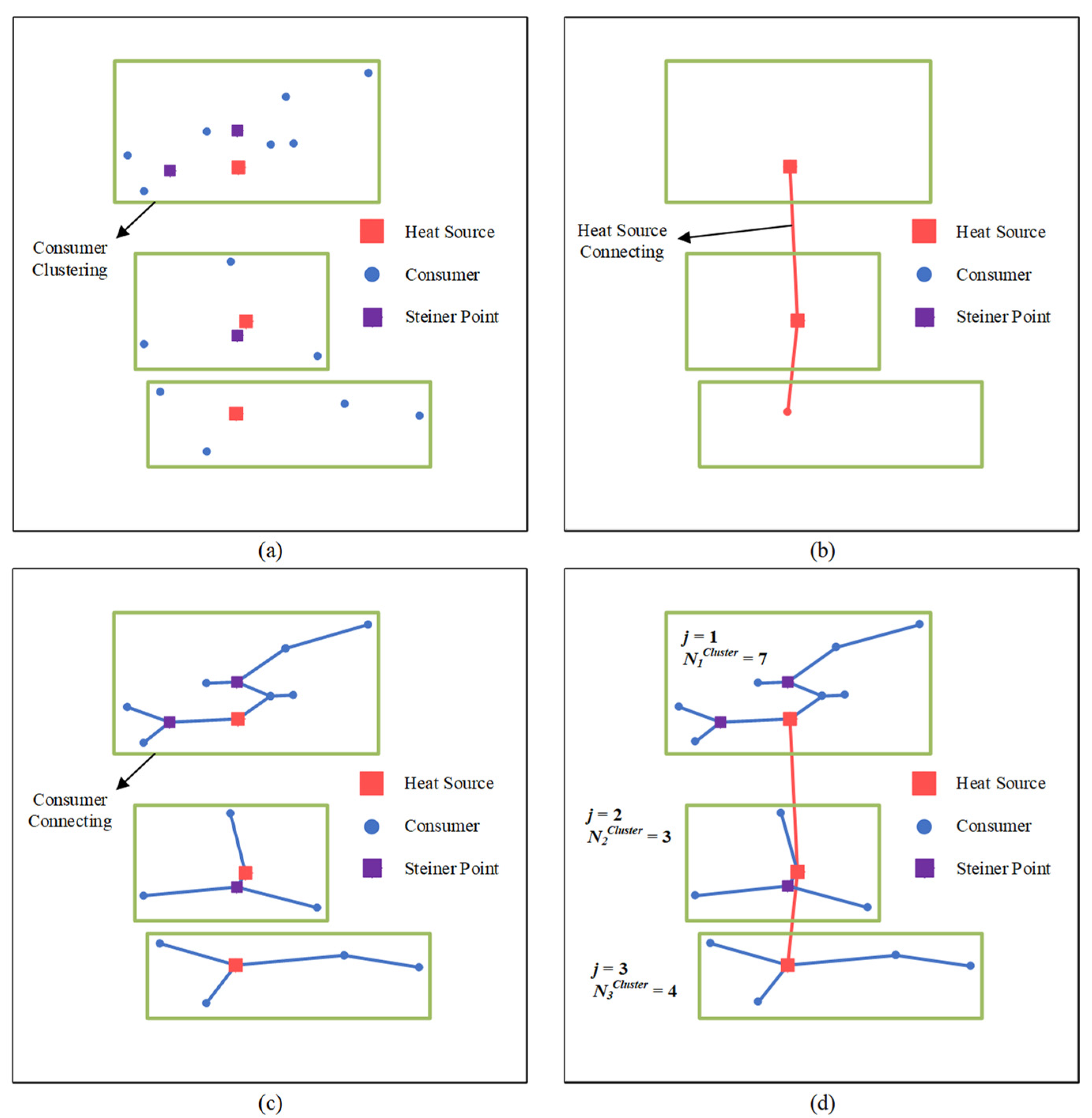
3.1. Clustering Algorithm
| Algorithm 1: Clustering Algorithm | |
| Input: The coordinates of consumers , the number of clusters , and the coordinates of heat sources . | |
| Output: A set of clusters . | |
| 1: | Let |
| 2: | for all do |
| 3: | |
| 4: | |
| 5: | |
| 6: | end for |
| 7: | return |
3.2. Star Tree Algorithm
| Algorithm 2: Star tree algorithm | |
| Input: A graph . | |
| Output: A Star tree . | |
| 1: | Let |
| 2: | choose the heat source as the center of all consumers |
| 3: | for all do |
| 4: | generate by connecting consumer i and the center straightly |
| 5: | |
| 6: | end for |
| 7: | return |
3.3. Kruskal Algorithm
| Algorithm 3: Kruskal algorithm | |
| Input: A connected graph . | |
| Output: A minimum spanning tree . | |
| 1: | Let |
| 2: | Sort the edges such that |
| 3: | for all do |
| 4: | |
| 5: | if cycle is generated in then |
| 6: | delete from the |
| 7: | else |
| 8: | maintain the unchanged |
| 9: | end if |
| 10: | if then |
| 11: | break |
| 12: | else |
| 13: | continue |
| 14: | end if |
| 15: | end for |
| 16: | return |
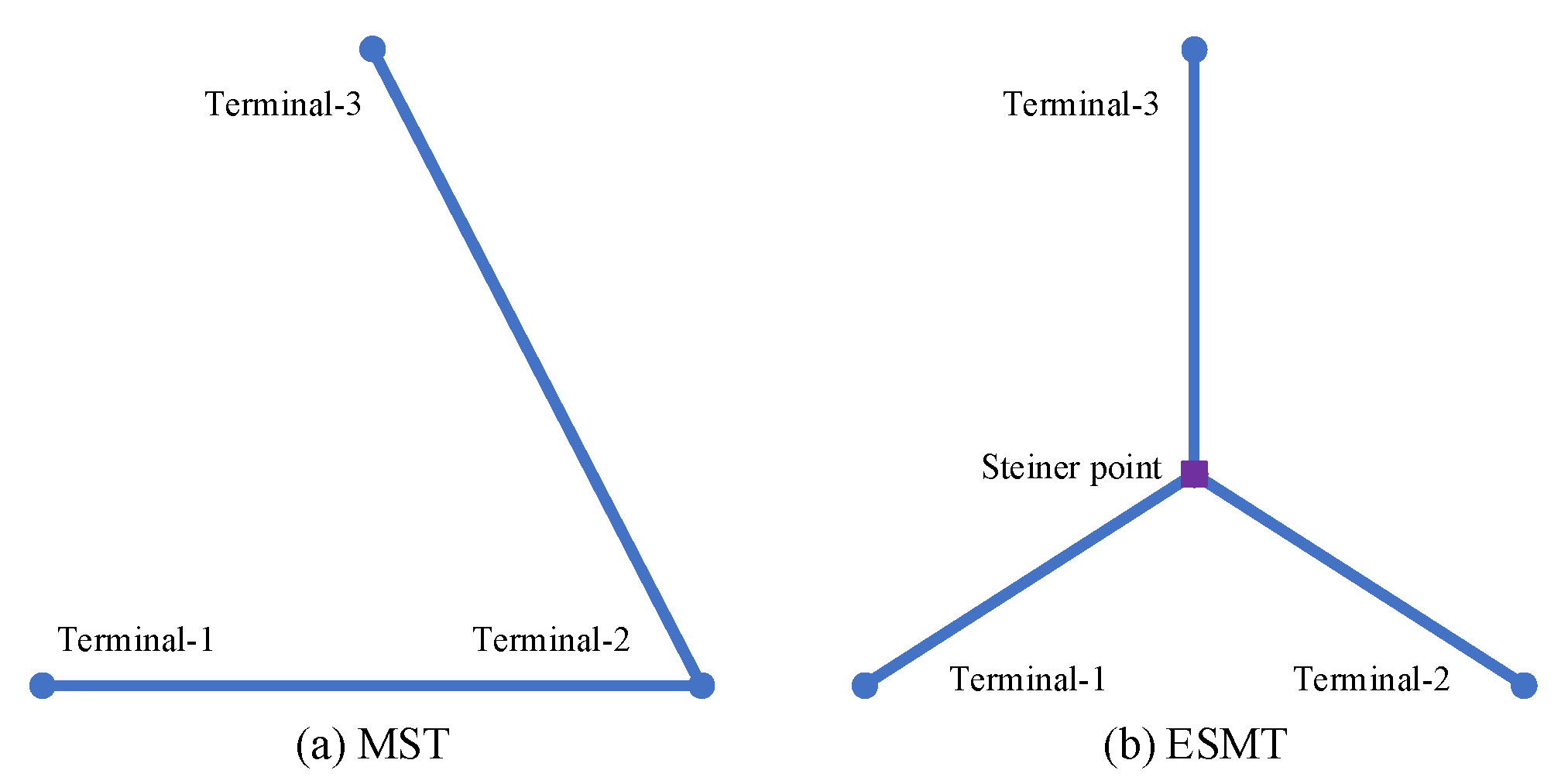
3.4. GeoSteiner Algorithm
4. Case Study
4.1. Data Acquisition
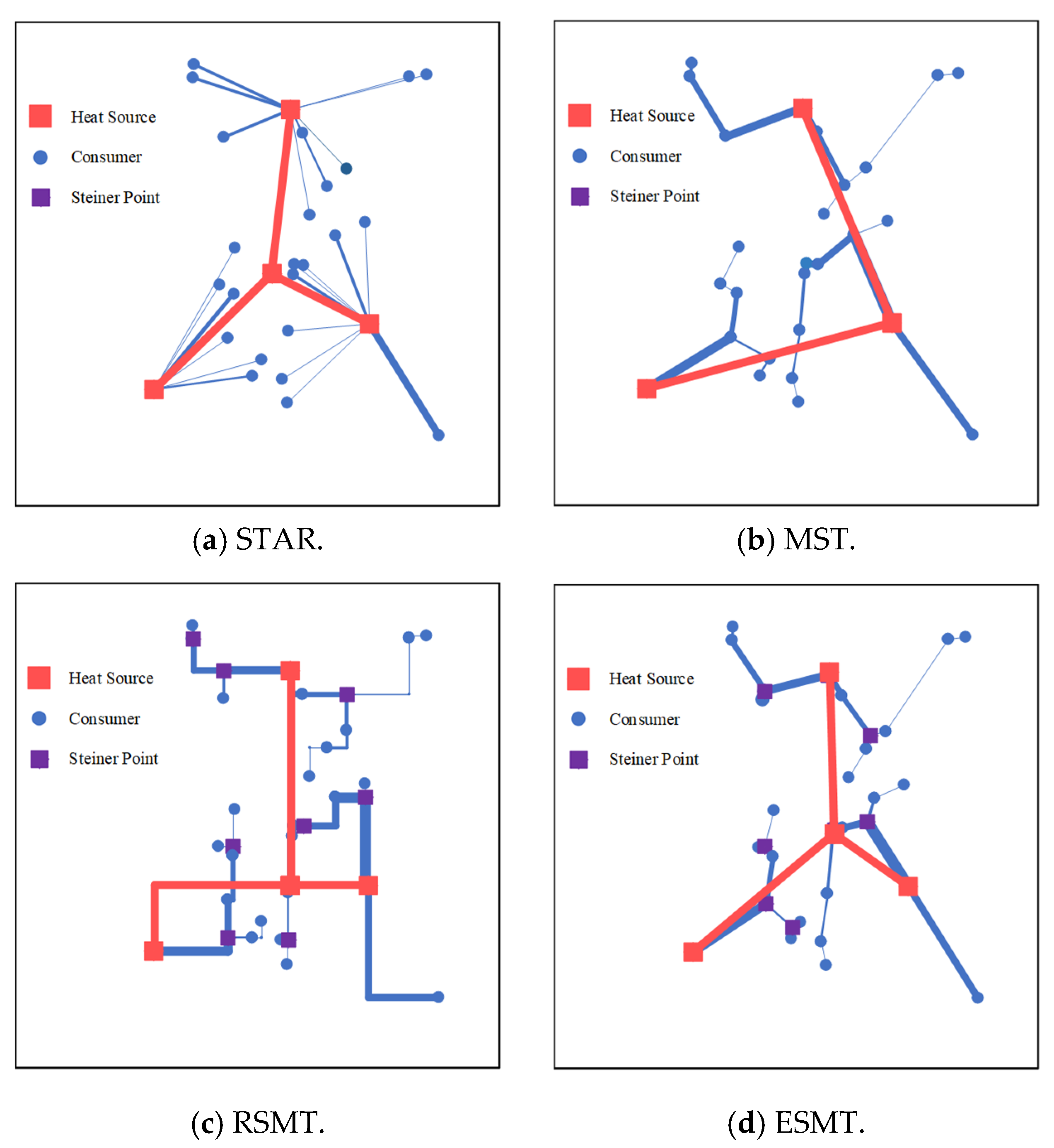
4.2. Optimal Results and Analysis
4.3. Analysis of Small-Scale DES
5. Conclusions
- Compared with the single heat source scenario, the multiple heat sources system will reduce the long-distance and high-flow pipelines in the system, so that both economy and reliability of the pipeline network system is improved.
- Compared with the traditional pipeline network obtained using MST, an ESMT pipeline network can reduce the total annual cost by 3% and increase reliability by 1%.
- When considering the actual path constraints, the RSMT pipeline network can be better adapted to the road layout.
- The geographically scale of the problem does not have a great impact on the relative performance of the four structures.
- By using the proposed method, both economic and reliability can be improved for the DES system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| DES | Distributed Energy System |
| ESMT | Euclidean Steiner Minimum Tree |
| FSTs | Full Steiner trees |
| GA | Genetic algorithm |
| LP | Linear programming |
| MILP | Mixed Integer Linear Programming |
| MIP | Mixed Integer Programming |
| MST | Minimum Spanning Tree |
| MSTHG | The MST in hypergraph |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| RSMT | Rectilinear Steiner Minimum Tree |
| SMT | Steiner Minimum Tree |
| STAR | Star tree |
| TAC | Total annual cost, Ұ·a−1 |
| Indices and Sets | |
| The set of clusters, denoted by index j | |
| An index, which is used to control the positive and negative of by | |
| An index, referring to the edge in | |
| The set of edges in a graph | |
| The set of edges in the hypergraph | |
| The set of edges in the connected tree, denoted by indices i, | |
| The set of edges in the connected tree which are connected directly to the vertex z. | |
| The graph of empty set in Star tree algorithm, or the weighted connected graph without direction in Kruskal algorithm | |
| A hypergraph | |
| The set of all vertices in a graph, denoted by indices | |
| The set of vertices in the hypergraph, denoted by indices | |
| The set of vertices in MST, denoted by indices , | |
| The set of weights of edges in a graph, denoted by indices | |
| The set of weights of edges in the connected tree, denoted by indices , | |
| Variables | |
| The electricity cost, Ұ·kW·h−1 | |
| The unit price of the th pipeline of the cluster , Ұ·m−1 | |
| The unit price of steam, Ұ·kg−1 | |
| Binary variables indicating whether the edge (, ) in the connected tree is connected directly to the vertex z. | |
| The heat loss cost of pipeline, Ұ·a−1 | |
| The heat loss cost of the th pipeline of the cluster , Ұ·a−1 | |
| The construction cost of pipeline, Ұ·a−1 | |
| The construction cost of the th pipeline of the cluster , Ұ·a−1 | |
| The pressure loss cost of pipeline, Ұ·a−1 | |
| The pressure loss cost of the th pipeline of the cluster , Ұ·a−1 | |
| The Euclidean distance between vertex and vertex | |
| The inner diameter of the insulation layer of the th pipeline of the cluster , m | |
| The inner diameter of the th pipeline of the cluster , m | |
| The outer diameter of the insulation layer of the th pipeline of the cluster , m | |
| The outer diameter of the th pipeline of the cluster , m | |
| The th edge in the hypergraph | |
| The th edge in the connected tree | |
| g | Gravitational acceleration |
| The head loss of the th pipeline of the cluster , m | |
| The annual interest rate | |
| The length of the th pipeline of the cluster , m | |
| The length of the th pipeline between consumer and the heat source in the area where this consumer is located, m | |
| The number of clusters of the pipeline network system | |
| The number of branch pipelines in cluster | |
| The number of consumers of the pipeline network system | |
| The number of vertices in the connected tree | |
| The number of vertices in the connected tree | |
| The life cycle of the pipeline network system, a | |
| The shaft power of the th pipeline of the cluster , W | |
| The effective power of the th pipeline of the cluster , W | |
| The probability of connecting the th pipeline in the path connected between the consumer and the heat source in its area | |
| The connected probability between the consumer α and the heat source of the area where this consumer is located | |
| The latent heat of steam, kJ·kg−1 | |
| The heat demand of consumer | |
| The heat loss of the th pipeline of the cluster , kJ·m−1·s−1 | |
| The reliability of the pipeline network system | |
| The head loss of the th pipeline of the cluster , m2 | |
| The outer surface temperature of the pipeline, | |
| The ambient temperature, | |
| The number of annual operating hours of the device, h | |
| The flow rate of the steam, m·s−1 | |
| The sum of the steam mass flow rate in all branch pipelines in the entire pipeline network | |
| The mass flow rate of the th pipeline of the cluster , kg·s−1 | |
| The mass flow rate of steam at vertex z, kg·s−1 | |
| A weight function of the edges in a hypergraph | |
| The weight of edge in a spanning tree in the hypergraph | |
| The sum of weights of the edges in a spanning tree in the hypergraph | |
| and | The mass flow rate within the branch pipeline connecting vertices x and when using vertex z as a reference for material accountancy, kg·s−1 |
| The weight per unit length of the th pipeline of the cluster , kg·m−1 | |
| The solution vector in the hypergraph | |
- Greek letters
| Heat transfer coefficient between the outer surface of the insulation and the atmosphere, W·m−2·K−1 | |
| The local resistance coefficient at the standard elbows (90°) | |
| The local resistance coefficient of the th pipeline of the cluster | |
| The resistance coefficient of the th pipeline of the cluster | |
| The efficiency of the conveying equipment | |
| The thermal conductivity of insulating material products at average temperature, W·m−1·K−1 | |
| The index used to determine which heat source consumer is assigned to | |
| The density of the steam, kg·m−3 | |
| The friction coefficient of the pipeline | |
| he empty set |
References
- Fichera, A.; Marrasso, E.; Sasso, M.; Volpe, R. Environmental and Economic Performance of an Urban Community Hybrid Distributed Energy System. Energy 2020, 13, 2545. [Google Scholar]
- Ren, H.; Zhou, W.; Nakagami, K.I.; Gao, W.; Wu, Q. Multi-objective optimization for the operation of distributed energy systems considering economic and environmental aspects. Appl. Energy 2010, 87, 3642–3651. [Google Scholar] [CrossRef]
- Wu, Q.; Ren, H.; Gao, W.; Ren, J. Multi-objective optimization of a distributed energy network integrated with heating interchange. Energy 2016, 109, 353–364. [Google Scholar] [CrossRef]
- Jing, R.; Zhu, X.; Zhu, Z.; Wang, W.; Meng, C.; Shah, N.; Li, N.; Zhao, Y. A multi-objective optimization and multi-criteria evaluation integrated framework for distributed energy system optimal planning. Energy Convers. Manag. 2018, 166, 445–462. [Google Scholar] [CrossRef]
- Yuan, J.; Xiao, Z.; Zhang, C.; Gang, W. A control strategy for distributed energy system considering the state of thermal energy storage. Sustain. Cities Soc. 2020, 63, 102492. [Google Scholar] [CrossRef]
- Wang, X.; Tian, H.; Yan, F.; Feng, W.; Wang, R.; Pan, J. Optimization of a distributed energy system with multiple waste heat sources and heat storage of different temperatures based on the energy quality. Appl. Therm. Eng. 2020, 181, 115975. [Google Scholar] [CrossRef]
- Buoro, D.; Casisi, M.; De Nardi, A.; Pinamonti, P.; Reini, M. Multicriteria optimization of a distributed energy supply system for an industrial area. Energy 2013, 58, 128–137. [Google Scholar] [CrossRef]
- Wang, M.; Yu, H.; Lin, X.; Jing, R.; He, F.; Li, C. Comparing stochastic programming with posteriori approach for multi-objective optimization of distributed energy systems under uncertainty. Energy 2020, 210, 118571. [Google Scholar] [CrossRef]
- Keçebaş, A.; Ali Alkan, M.; Bayhan, M. Thermo-economic analysis of pipe insulation for district heating piping systems. Appl. Therm. Eng. 2011, 31, 3929–3937. [Google Scholar] [CrossRef]
- Salem, E.A.; Farid Khalil, M.; Sanhoury, A.S. Optimization of insulation thickness and emissions rate reduction during pipeline carrying hot oil. Alex. Eng. J. 2021, 60, 3429–3443. [Google Scholar] [CrossRef]
- Li, X.-l.; Duanmu, L.; Shu, H.-w. Optimal design of district heating and cooling pipe network of seawater-source heat pump. Energy Build. 2010, 42, 100–104. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Gao, M.; Zhang, D.; Liu, Y.; Tan, Z.; Zhu, J. Cost-based siting and sizing of energy stations and pipeline networks in integrated energy system. Energy Convers. Manag. 2021, 235, 113958. [Google Scholar] [CrossRef]
- Zeng, J.; Han, J.; Zhang, G. Diameter optimization of district heating and cooling piping network based on hourly load. Appl. Therm. Eng. 2016, 107, 750–757. [Google Scholar] [CrossRef]
- Mehleri, E.D.; Sarimveis, H.; Markatos, N.C.; Papageorgiou, L.G. A mathematical programming approach for optimal design of distributed energy systems at the neighbourhood level. Energy 2012, 44, 96–104. [Google Scholar] [CrossRef]
- Khir, R.; Haouari, M. Optimization models for a single-plant District Cooling System. Eur. J. Oper. Res. 2015, 247, 648–658. [Google Scholar] [CrossRef]
- Chan, A.L.S.; Hanby, V.I.; Chow, T.T. Optimization of distribution piping network in district cooling system using genetic algorithm with local search. Energy Convers. Manag. 2007, 48, 2622–2629. [Google Scholar] [CrossRef]
- Haikarainen, C.; Pettersson, F.; Saxén, H. A model for structural and operational optimization of distributed energy systems. Appl. Therm. Eng. 2014, 70, 211–218. [Google Scholar] [CrossRef]
- Sanaye, S.; Mahmoudimehr, J. Optimal design of a natural gas transmission network layout. Chem. Eng. Res. Des. 2013, 91, 2465–2476. [Google Scholar] [CrossRef]
- Su, H.; Zio, E.; Zhang, J.; Li, X.; Chi, L.; Fan, L.; Zhang, Z. A method for the multi-objective optimization of the operation of natural gas pipeline networks considering supply reliability and operation efficiency. Comput. Chem. Eng. 2019, 131, 106584. [Google Scholar] [CrossRef]
- Sokolov, D.V.; Barakhtenko, E.A. Optimization of transmission capacity of energy water pipeline networks with a tree-shaped configuration and multiple sources. Energy 2020, 210, 118469. [Google Scholar] [CrossRef]
- Liu, X. Energy stations and pipe network collaborative planning of integrated energy system based on load complementary characteristics. Sustain. Energy Grids Netw. 2020, 23, 100374. [Google Scholar] [CrossRef]
- Rimkevicius, S.; Kaliatka, A.; Valincius, M.; Dundulis, G.; Janulionis, R.; Grybenas, A.; Zutautaite, I. Development of approach for reliability assessment of pipeline network systems. Appl. Energy 2012, 94, 22–33. [Google Scholar] [CrossRef]
- Shan, X.; Wang, P.; Lu, W. The reliability and availability evaluation of repairable district heating networks under changeable external conditions. Appl. Energy 2017, 203, 686–695. [Google Scholar] [CrossRef]
- Alsharqawi, M.; Zayed, T.; Parvizsedghy, L.; Senouci, A.; Al-Derham, H. Reliability Assessment Model for Water Distribution Networks. J. Pipeline Syst. Eng. Pract. 2020, 11, 04019059. [Google Scholar] [CrossRef]
- Chen, Q.; Zuo, L.; Wu, C.; Cao, Y.; Bu, Y.; Chen, F.; Sadiq, R. Supply reliability assessment of a gas pipeline network under stochastic demands. Reliab. Eng. Syst. Saf. 2021, 209, 107482. [Google Scholar] [CrossRef]
- Yu, W.; Huang, W.; Wen, Y.; Li, Y.; Liu, H.; Wen, K.; Gong, J.; Lu, Y. An integrated gas supply reliability evaluation method of the large-scale and complex natural gas pipeline network based on demand-side analysis. Reliab. Eng. Syst. Saf. 2021, 212, 107651. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, P.; Wang, Y.; Tong, R.; Yu, B.; Qu, Z. Assessment method for gas supply reliability of natural gas pipeline networks considering failure and repair. J. Nat. Gas Sci. Eng. 2021, 88, 103817. [Google Scholar] [CrossRef]
- Chang, C.; Chen, X.; Wang, Y.; Feng, X. An efficient optimization algorithm for waste Heat Integration using a heat recovery loop between two plants. Appl. Therm. Eng. 2016, 105, 799–806. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Z.; Liang, G.; Zhou, L.; Zhou, X. General Models for Optimal Design of Star–Star Gathering Pipeline Network. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021024. [Google Scholar] [CrossRef]
- Weiss, M.A. Data Structures and Algorithm Analysis in C++, 4th ed.; Pearson Education India: London, UK, 2014. [Google Scholar]
- Zachariasen, M. Rectilinear full Steiner tree generation. Networks 1999, 33, 125–143. [Google Scholar] [CrossRef]
- Warme, D.M. Spanning Trees in Hypergraphs with Applications to Steiner Trees. Ph.D. Thesis, University of Virginia, Charlottesville, VA, USA, 1998. [Google Scholar]
- Juhl, D.; Warme, D.M.; Winter, P.; Zachariasen, M. The GeoSteiner software package for computing Steiner trees in the plane: An updated computational study. Math. Prog. Comp. 2018, 10, 487–532. [Google Scholar] [CrossRef] [Green Version]
- Salowe, J.S.; Warme, D.M. Thirty-five-point rectilinear steiner minimal trees in a day. Networks 1995, 25, 69–87. [Google Scholar] [CrossRef]

| DN (mm) | Pipeline Surface Temperature (°C) | ||||
|---|---|---|---|---|---|
| ≤60 | ≤150 | ≤250 | ≤300 | ≤350 | |
| Insulation Layer Thickness (mm) | |||||
| 15 | 30 | 30 | 40 | 50 | 50 |
| 20 | 30 | 30 | 40 | 50 | 50 |
| 25 | 30 | 30 | 50 | 50 | 60 |
| 40 | 30 | 50 | 50 | 60 | 60 |
| 50 | 30 | 50 | 50 | 60 | 70 |
| 80 | 30 | 50 | 60 | 70 | 70 |
| 100 | 30 | 50 | 60 | 70 | 80 |
| 150 | 30 | 60 | 70 | 70 | 80 |
| 200 | 30 | 60 | 70 | 80 | 90 |
| 250 | 30 | 60 | 70 | 80 | 90 |
| 300 | 30 | 60 | 70 | 80 | 90 |
| 350 | 30 | 50 | 70 | 80 | 90 |
| 400 | 30 | 50 | 70 | 80 | 90 |
| 450 | 30 | 50 | 70 | 80 | 90 |
| 500 | 30 | 50 | 70 | 80 | 90 |
| 600 | 30 | 50 | 70 | 80 | 90 |
| 700 | 30 | 50 | 70 | 80 | 90 |
| 800 | 30 | 50 | 70 | 80 | 90 |
| 900 | 30 | 50 | 70 | 80 | 100 |
| 1000 | 30 | 50 | 70 | 80 | 100 |
| 1100 | 30 | 50 | 70 | 80 | 100 |
| 1200 | 30 | 50 | 70 | 80 | 100 |
| Name | Coordinate X (m) | Coordinate Y (m) | Heat Demand ( Steam) |
|---|---|---|---|
| Consumer-01 | 7097 | 9542 | 15.0 |
| Consumer-02 | 8800 | 4024 | 6.0 |
| Consumer-03 | 9602 | 5124 | 0.5 |
| Consumer-04 | 12,013 | 7072 | 4.0 |
| Consumer-05 | 13,392 | 11,430 | 3.0 |
| Consumer-06 | 13,949 | 14,857 | 5.0 |
| Consumer-07 | 3384 | 24,093 | 10.0 |
| Consumer-08 | 25,483 | 0 | 25.0 |
| Consumer-09 | 11,914 | 2235 | 3.0 |
| Consumer-10 | 11,369 | 3893 | 4.0 |
| Consumer-11 | 6561 | 6546 | 5.0 |
| Consumer-12 | 12,437 | 10,805 | 12.0 |
| Consumer-13 | 12,454 | 11,538 | 0.3 |
| Consumer-14 | 16,227 | 13,461 | 10.0 |
| Consumer-15 | 18,914 | 14,341 | 1.2 |
| Consumer-16 | 7171 | 12,650 | 0.3 |
| Consumer-17 | 13,255 | 20,390 | 4.0 |
| Consumer-18 | 15,489 | 16,736 | 7.0 |
| Consumer-19 | 17,153 | 17,937 | 1.0 |
| Consumer-20 | 22,789 | 24,165 | 2.0 |
| Consumer-21 | 24,416 | 24,203 | 1.2 |
| Consumer-22 | 6206 | 20,012 | 10.0 |
| Consumer-23 | 5818 | 10,120 | 4.0 |
| Consumer-24 | 3465 | 24,915 | 10.0 |
| Heat source-01 | 0 | 3144 | −45.8 |
| Heat source-02 | 12,200 | 21,944 | −45.2 |
| Heat source-03 | 19,200 | 7544 | −52.5 |
| Parameter | Number | Unit | Parameter | Number | Unit |
|---|---|---|---|---|---|
| 10 | a | 0.1945 | Ұ·kg−1 | ||
| 0.02 | 1999.9 | kJ·kg−1 | |||
| 0.60 | kg·m−3 | 3.5 | °C | ||
| 30.00 | m·s−1 | 0.06 | W·m−1·K−1 | ||
| 0.21 | Ұ·kW·h−1 | 3.50 | m·s−1 | ||
| 8760 | h | 11.63 | W·m−2·K−1 | ||
| 0.8 | 0.98 | km−1 | |||
| 0.015 |
| Topology Type of Pipeline Networks | STAR | MST | RSMT | ESMT |
|---|---|---|---|---|
| Total pipeline cost (×107 Ұ·a−1) | 2.706 (100%) | 2.035 (75.2%) | 2.152 (79.5%) | 1.962 (72.5%) |
| Pressure loss cost (×107 Ұ·a−1) | 0.668 (100%) | 0.504 (75.4%) | 0.533 (79.8%) | 0.486 (72.8%) |
| Heat loss cost (×107 Ұ·a−1) | 0.990 (100%) | 0.623 (62.9%) | 0.654 (66.0%) | 0.605 (61.1%) |
| Total annual cost (×107 Ұ·a−1) | 4.364 (100%) | 3.162 (72.5%) | 3.339 (76.5%) | 3.053 (70.0%) |
| 0.848 (100%) | 0.815 (96.1%) | 0.802 (94.6%) | 0.822 (96.9%) |
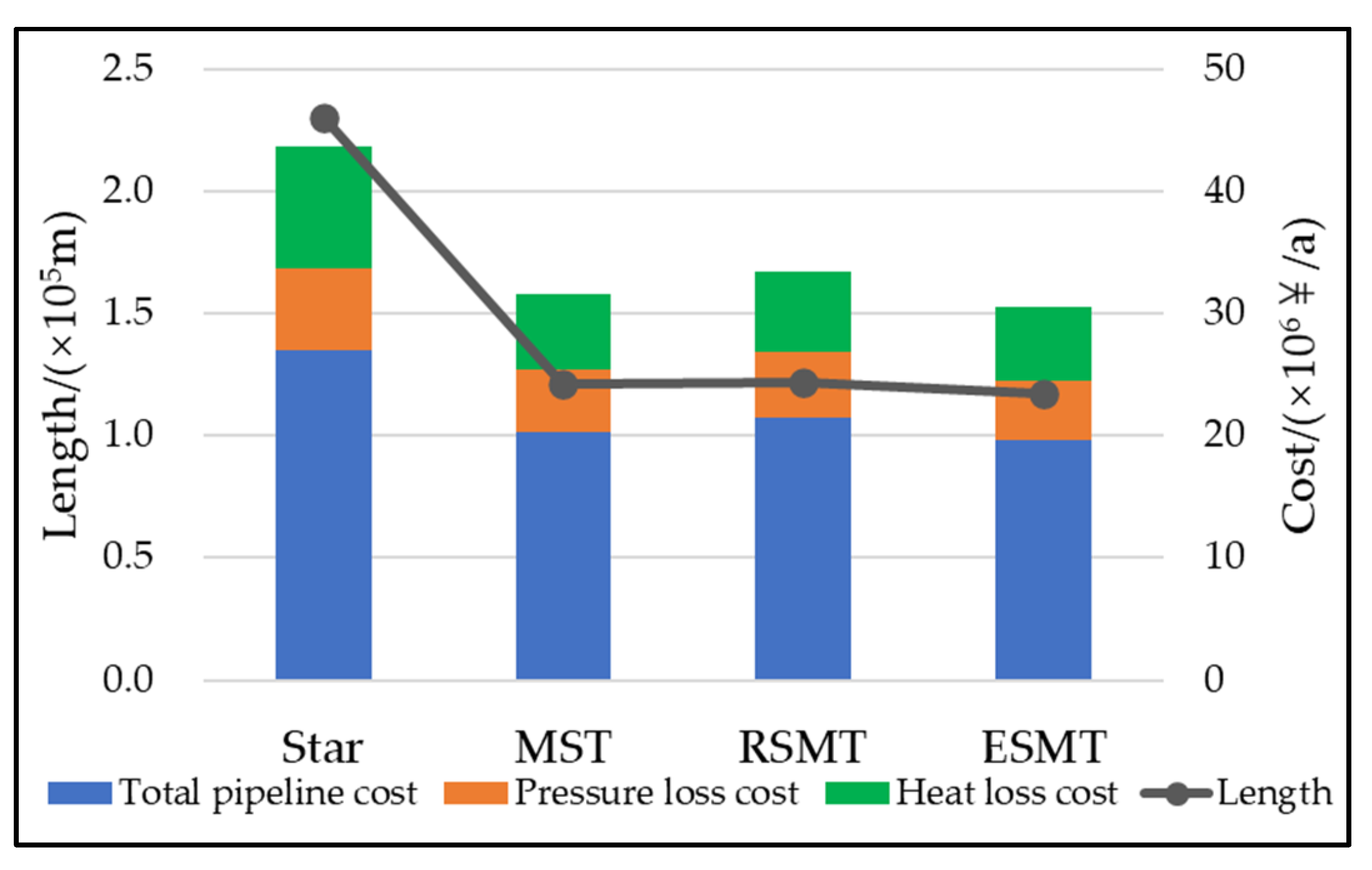
| Topology Type of Pipeline Networks | STAR | MST | RSMT | ESMT |
|---|---|---|---|---|
| Total pipeline length (×104 m) | 4.603 | 2.421 | 2.433 | 2.345 |
| Total pipeline cost (×106 Ұ·a−1) | 5.412 | 4.069 | 4.304 | 3.925 |
| Pressure loss cost (×106 Ұ·a−1) | 1.313 | 1.002 | 1.062 | 0.967 |
| Heat loss cost (×106 Ұ·a−1) | 1.313 | 1.002 | 1.062 | 0.967 |
| Total annual cost (×106 Ұ·a−1) | 6.725 | 5.072 | 5.366 | 4.892 |
| 0.967 | 0.959 | 0.956 | 0.961 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Lin, H.; Wu, Y.; Wang, Y.; Feng, X. Optimization of Pipeline Network Layout for Multiple Heat Sources Distributed Energy Systems Considering Reliability Evaluation. Processes 2021, 9, 1308. https://doi.org/10.3390/pr9081308
Cui Z, Lin H, Wu Y, Wang Y, Feng X. Optimization of Pipeline Network Layout for Multiple Heat Sources Distributed Energy Systems Considering Reliability Evaluation. Processes. 2021; 9(8):1308. https://doi.org/10.3390/pr9081308
Chicago/Turabian StyleCui, Ziyuan, Hai Lin, Yan Wu, Yufei Wang, and Xiao Feng. 2021. "Optimization of Pipeline Network Layout for Multiple Heat Sources Distributed Energy Systems Considering Reliability Evaluation" Processes 9, no. 8: 1308. https://doi.org/10.3390/pr9081308
APA StyleCui, Z., Lin, H., Wu, Y., Wang, Y., & Feng, X. (2021). Optimization of Pipeline Network Layout for Multiple Heat Sources Distributed Energy Systems Considering Reliability Evaluation. Processes, 9(8), 1308. https://doi.org/10.3390/pr9081308







