A Hybrid LSTM-Based Genetic Programming Approach for Short-Term Prediction of Global Solar Radiation Using Weather Data
Abstract
1. Introduction
2. Genetic Programming and Long Short-Term Memory Models
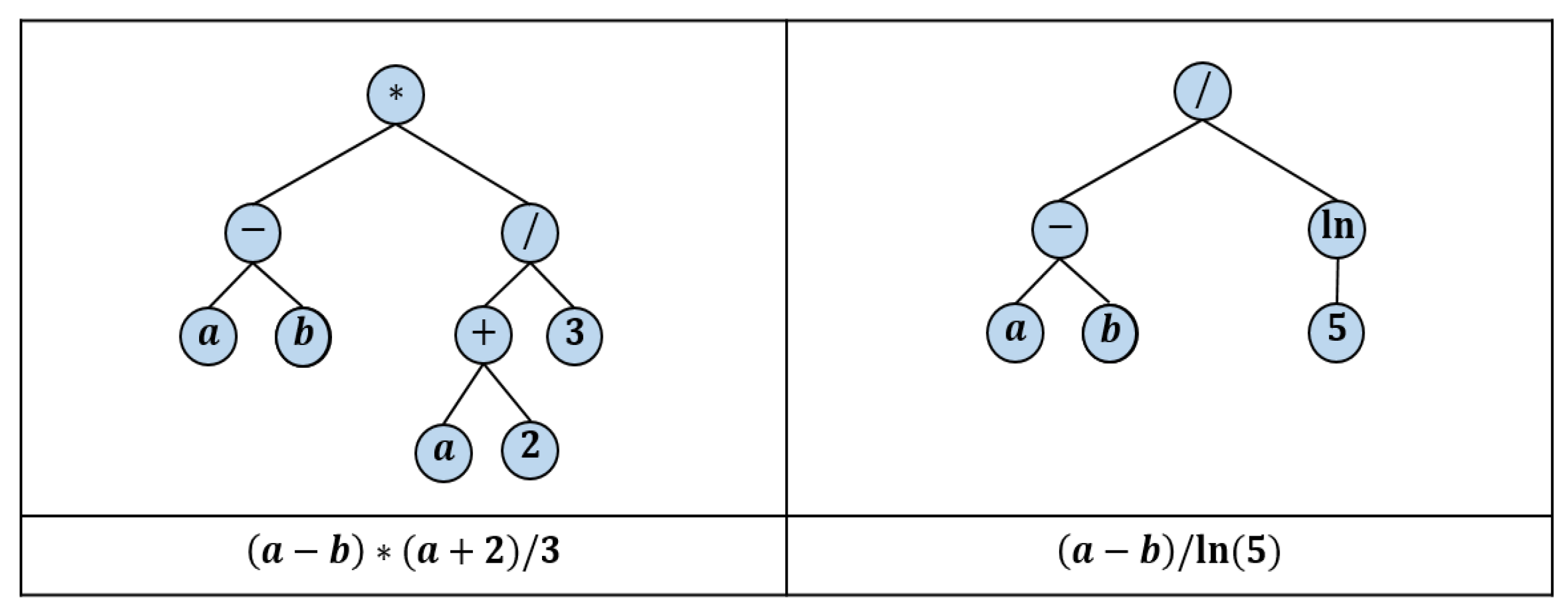
2.1. Genetic Programming
- Measure the fitness value for each individual using a predefined fitness function. This fitness value indicates how the individual function (computer program) suits the problem under consideration.
- Select a set of individuals, based on their fitness values, from the present population using a suitable selection strategy.
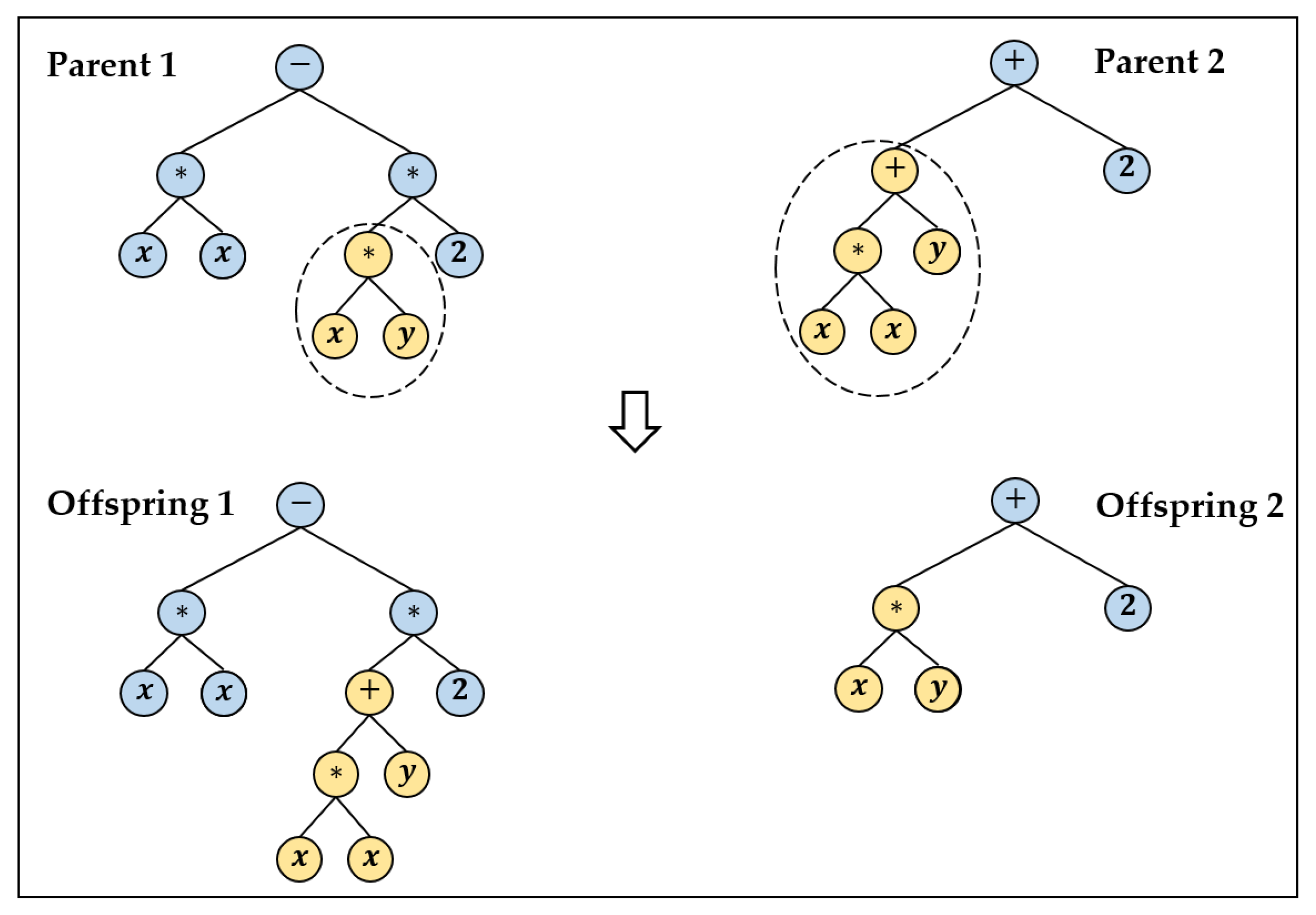
- Generate the next population by applying the crossover and mutation operators to selected individuals based on predefined crossover and mutation probabilities.
- Based on a predefined reproduction probability, the clone is based on individuals with the best fitness values to the next population.
2.1.1. GPLearn Framework
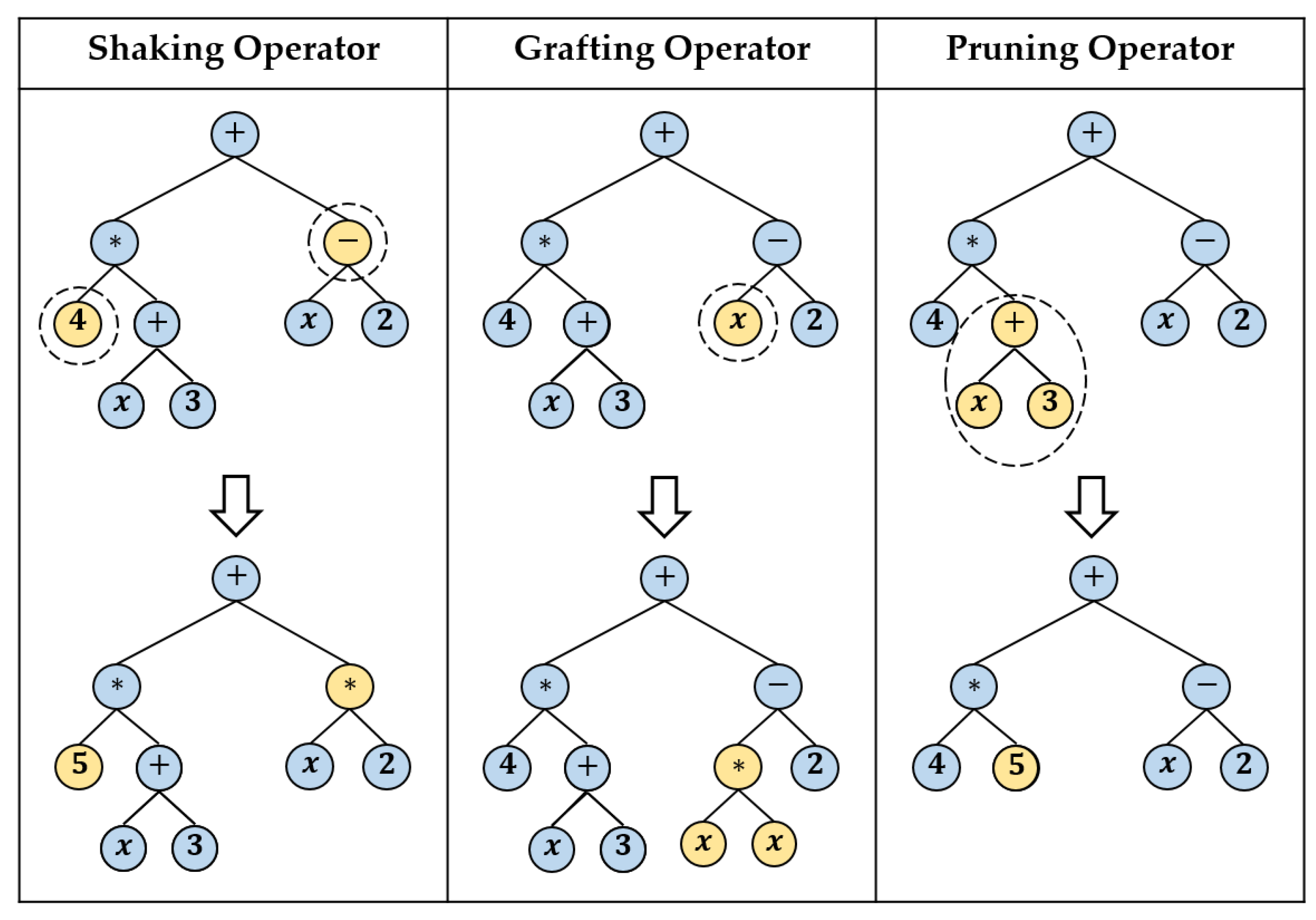
- Sub-tree mutation: it takes the winner (a tree) of a random selection and then selects a random sub-tree from it to be replaced. A donor sub-tree is generated at random, and this is inserted into the chosen winner tree to form offspring in the next generation. This type of mutation is considered one of the aggressive mutations. It allows big changes in an individual by replacing a complete sub-tree and all its descendants with totally naïve random components.
- Hoist mutation: it takes the winner of a random selection and selects a random sub-tree from it. Then, a random sub-tree of that sub-tree is selected, and this is lifted (hoisted) into the original sub-tree’s location to produce offspring in the next generation.
- Point mutation: it takes the winner of a random selection and selects random nodes from the winner to be replaced. Functions are replaced by other functions that require the same number of arguments, and other terminals replace terminals. The resulting tree forms offspring in the next generation. Figure 3 depicts the three described types of mutations.
2.1.2. Memetic Programming
2.2. Long Short-Term Memory (LSTM) Models
3. Hybrid Approach Development
3.1. Building Base Models
- AirDensity (Kg/m3): the density of the air
- AirTemp_Avg (°C): the average temperature of the air 3 m above the surface
- HeatIndex (°C): the heat index
- RelativeWindSpeed_Max (m/s): the maximum relative wind speed
- RH_ Avg (%): the relative humidity in the air
- SurfaceTemp_Avg (°C): the average temperature 10 cm close to the surface
- SolarRadiation_Avg (W/m2): the average global solar radiation
- LSTM_1 receives in each input vector the following parameters: Air Density, Max Relative Wind Speed, and Solar Radiation for the current and the previous 15-min slots.
- LSTM_2 receives in each input vector the following parameters: Air Density, Average Surface Temperature, and Solar Radiation for the current and the previous 15-min slots.
- LSTM_3 receives in each input vector the following parameters: Average Air Temperature, Heat Index, and Solar Radiation for the current and the previous 15-min slots.
- LSTM_4 receives in each input vector the following parameters: Average Air Temperature, Relative Humidity, and Solar Radiation for the current and the previous 15-min slots.
- LSTM_5 receives in each input vector the following parameters: Average Air Temperature, Average Surface Temperature, and Solar Radiation for the current and the previous 15-min slots.
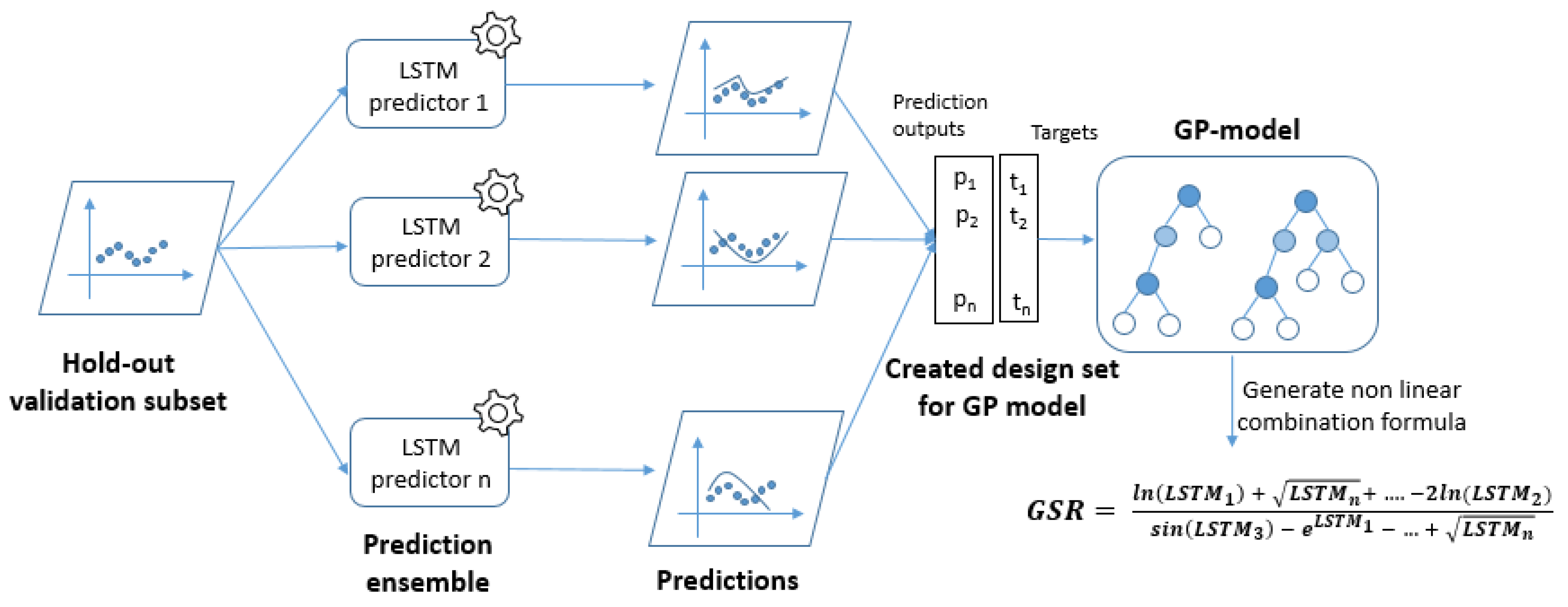
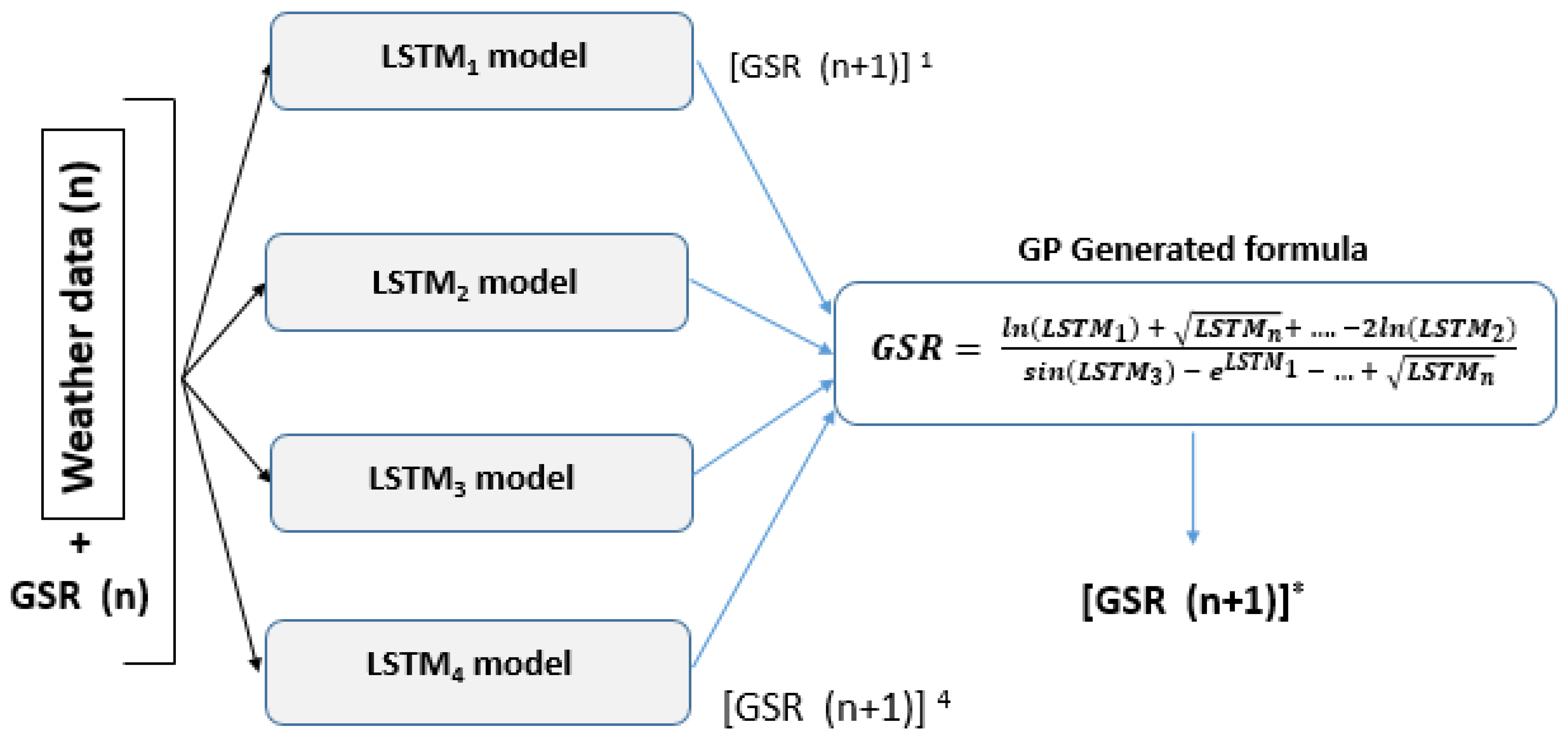
3.2. Building the Hybrid GP-LSTM Model
- A standard version consists of the primary mutation and crossover operators as is described in Section 2. The parameters of this version of GP module are setup as follows:
- ○
- The population size is set to be equal to 200 individuals. Each individual represents a nonlinear combination formula of the outputs of the base predictors.
- ○
- The set of operators that are used in the internal nodes of the trees that represent the individuals includes the four arithmetic operators: addition (+), difference (−), division (/), and multiplication (*). In addition, it includes the decimal log , the exponential function and the square root ().
- ○
- The depth of each of the trees that represent individuals is equal to eight. The maximum depth allowed for trees in each population is one of the adjustable parameters in a GP evolution process. The depth of each of the binary trees is set to be dynamic. It starts by an initial depth that can be dynamically increased until a selected maximum value is reached.
- ○
- The fitness function evaluates the efficiency of each of the individuals that represent candidate solutions (chromosomes). A fitness function related to the root mean square error (RMSE) has been used.
- ○
- The probability of applying each of the genetic operators (crossover and mutation).
- ○
- The sampling method to select individuals from the current population to participate in generating new individuals for the next generation.
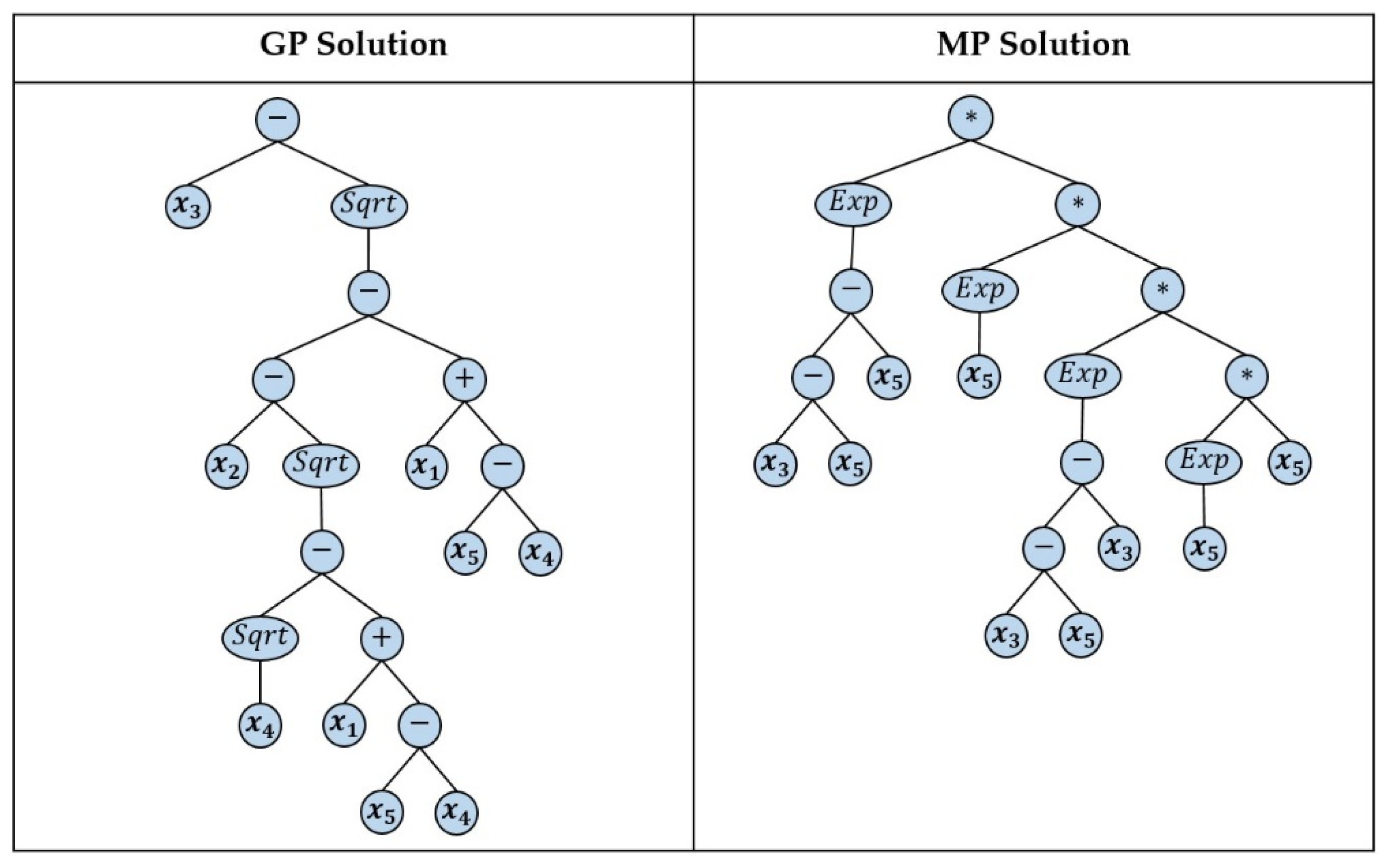
- A hybrid version of the GP algorithm, named MP, consists of a local search module that permits selecting the best breeding among possible children from two crossover parents. The parameters of this version of GP module are setup almost the same as the standard one for comparison reasons. Therefore, the exact population sizes, set of operators, maximum depth, and fitness functions, and sampling methods have been adopted for this version.
3.3. Experiments Setup
3.3.1. Training and Testing Dataset
3.3.2. Experiments
- A standard version of GP comprises the crossover operator with advanced versions of and mutation operators described in Section 2.1. This version is implemented in the GPLearn framework as described in Section 2.1.1.
3.3.3. Evaluation Metrics
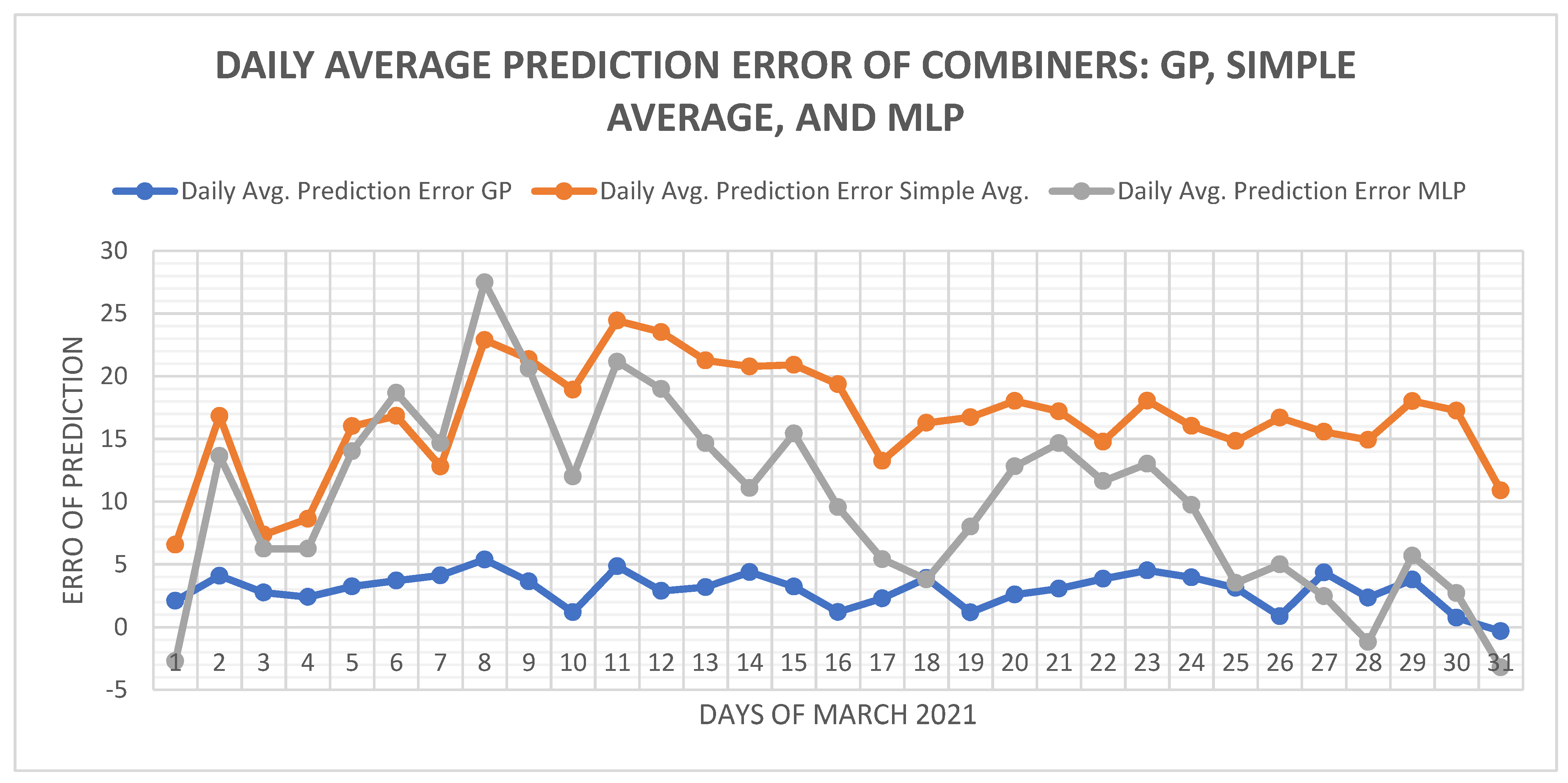
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| GSR | Global Solar Radiation |
| LSTM | Long-Short Term Memory |
| RNN | Recurrent Neural Network |
| SR | Solar Radiation |
| GP | Genetic Programming |
| ANN | Artificial Neural Network |
| SVM | Support Vector Machines |
| RF | Random Forest |
| DT | Decision Tree |
| RT | Regression Tree |
| RMSE | Root Mean Square Error |
| ARIMA | Autoregressive Integrated Moving Average |
| MLR | Multilinear Regression |
| BDT | Bagged Decision Tree |
| BDTs | Bagging Decision Techniques |
| SVR | Support Vector Regressors |
| MP | Memetic Programming |
| LGP | Linear Genetic programming |
| MGGP | Multi-Gene Genetic Programming |
| Tpanel | Panel’s Temperature |
| NOCT | Nominal Operating Cell Temperature |
| NMOT | Nominal Module Operating Temperature |
| GEP | Gene Expression Programming |
| SA | Simulated Annealing |
| BPTT | Back-Propagation Through Time |
| GA | Genetic Algorithm |
| KNN | K-Nearest Neighbors |
| MAE | Mean Absolute Error |
| MBE | Mean Bias Error |
| MAPE | Mean Absolute Percentage Error |
| r | Correlation Coefficient |
| Coefficient of Determination |
References
- Vasylieva, T.; Lyulyov, O.; Bilan, Y.; Streimikiene, D. Sustainable economic development and greenhouse gas emissions: The dynamic impact of renewable energy consumption, GDP, and corruption. Energies 2019, 12, 3289. [Google Scholar] [CrossRef]
- Islam, M.T.; Huda, N.; Abdullah, A.B.; Saidur, R. A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: Current status and research trends. Renew. Sustain. Energy Rev. 2019, 91, 987–1018. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Al-Hajj, R.; Assi, A.; Fouad, M.M. Forecasting Solar Radiation Strength Using Machine Learning Ensemble. In Proceedings of the 7th IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 184–188. [Google Scholar]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Hou, M.; Zhang, T.; Weng, F.; Ali, M.; Al-Ansari, N.; Yaseen, Z.M. Global solar radiation prediction using hybrid online sequential extreme learning machine model. Energies 2018, 11, 3415. [Google Scholar] [CrossRef]
- Al-Hajj, R.; Assi, A.; Fouad, M. Short-Term Prediction of Global Solar Radiation Energy Using Weather Data and Machine Learning Ensembles: A Comparative Study. J. Sol. Energy Eng. 2021, 8, 1–38. [Google Scholar]
- Sharma, A.; Kakkar, A. Forecasting daily global solar irradiance generation using machine learning. Renew. Sustain. Energy Rev. 2018, 82, 2254–2269. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Automatic hourly solar forecasting using machine learning models. Renew. Sustain. Energy Rev. 2019, 105, 487–498. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Zeng, W.; Wang, X.; Zou, H. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: A review and case study in China. Renew. Sustain. Energy Rev. 2019, 100, 186–212. [Google Scholar] [CrossRef]
- Li, P.; Bessafi, M.; Morel, B.; Chabriat, J.P.; Delsaut, M.; Li, Q. Daily surface solar radiation prediction mapping using artificial neural network: The case study of Reunion Island. ASME J. Sol. Energy Eng. 2020, 142, 021009. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Mohammadi, K.; Petković, D.; Sudheer, C. A support vector machine–firefly algorithm-based model for global solar radiation prediction. Sol. Energy 2015, 115, 632–644. [Google Scholar] [CrossRef]
- Shang, C.; Wei, P. Enhanced support vector regression based forecast engine to predict solar power output. Renew. Energy 2018, 127, 269–283. [Google Scholar] [CrossRef]
- Piri, J.; Shamshirband, S.; Petković, D.; Tong, C.W.; Rehman, M.H. Prediction of the solar radiation on the earth using support vector regression technique. Infrared Phys. Technol. 2015, 68, 179–185. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. Ensemble methods for wind and solar power forecasting—A state-of-the-art review. Renew. Sustain. Energy Rev. 2015, 50, 82–91. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. Review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Linares-Rodriguez, A.; Ruiz-Arias, J.A.; Pozo-Vazquez, D.; Tovar-Pescador, J. An artificial neural network ensemble model for estimating global solar radiation from Meteosat satellite images. Energy 2013, 61, 636–645. [Google Scholar] [CrossRef]
- Ahmed Mohammed, A.; Aung, Z. Ensemble learning approach for probabilistic forecasting of solar power generation. Energies 2016, 9, 1017. [Google Scholar] [CrossRef]
- Guo, J.; You, S.; Huang, C.; Liu, H.; Zhou, D.; Chai, J.; Black, C. An ensemble solar power output forecasting model through statistical learning of historical weather dataset. In Proceedings of the Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Yeboah, F.E.; Pyle, R.; Hyeng, C.B.A. Predicting solar radiation for renewable energy technologies: A random forest approach. Int. J. Mod. Eng. 2015, 16, 100–107. [Google Scholar]
- Pan, C.; Tan, J. Day-Ahead Hourly Forecasting of Solar Generation Based on Cluster Analysis and Ensemble Model. IEEE Access 2019, 7, 112921–112930. [Google Scholar] [CrossRef]
- Basaran, K.; Özçift, A.; Kılınç, D. A New Approach for Prediction of Solar Radiation with Using Ensemble Learning Algorithm. Arab. J. Sci. Eng. Springer Sci. Bus. Media BV 2019, 44, 7159–7171. [Google Scholar] [CrossRef]
- Abuella, M.; Chowdhury, B. Random forest ensemble of support vector regression models for solar power forecasting. In Proceedings of the Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Piscataway, NJ, USA, 23–26 April 2017; pp. 1–5. [Google Scholar]
- Poli, R.; Langdon, W.; McPhee, N. Genetic Programming: An Introductory Tutorial and a Survey of Techniques and Applications; Technical Report CES-475; University of Essex: Colchester, UK, 2007; ISSN 1744-8050. [Google Scholar]
- Poli, R.; Langdon, W.; McPhee, N. A Field Guide to Genetic Programming; Lulu Enterprises: Egham, UK, 2008; ISBN 1409200736. [Google Scholar]
- Riolo, R.; Vladislavleva, E.; Moore, J. Genetic Programming Theory and Practice IX; Springer Science & Business Media: Berlin, Germany, 2001; ISBN 1461417708. [Google Scholar]
- Mabrouk, E.; Hedar, A.; Fukushima, M. Memetic programming with adaptive local search using tree data structures. In Proceedings of the 5th International Conference on Soft Computing as Transdisciplinary Science and Technology, Paris, France, 28–31 October 2008; pp. 258–264. [Google Scholar]
- Mabrouk, E.; Hernández-Castro, J.C.; Fukushima, M. Prime number generation using memetic programming. Artif. Life Robot. 2010, 16, 53–56. [Google Scholar] [CrossRef][Green Version]
- Shavandi, H.; Ramyani, S.S. A linear genetic programming approach for the prediction of solar global radiation. Neural Comput. Appl. 2013, 23, 1197–1204. [Google Scholar] [CrossRef]
- Guven, A.; Aytek, A.; Yuce, M.I.; Aksoy, H. Genetic programming-based empirical model for daily reference evapotranspiration estimation. CLEAN Soil Air Water 2008, 36, 905–912. [Google Scholar] [CrossRef]
- Citakoglu, H.; Babayigit, B.; Haktanir, N.A. Solar radiation prediction using multi-gene genetic programming approach. Theor. Appl. Climatol. 2020, 142, 885–897. [Google Scholar] [CrossRef]
- Sohani, A.; Sayyaadi, H. Employing genetic programming to find the best correlation to predict temperature of solar photovoltaic panels. Energy Convers. Manag. 2020, 224, 113291. [Google Scholar] [CrossRef]
- Mostafavi, E.S.; Ramiyani, S.S.; Sarvar, R.; Moud, H.I.; Mousavi, S.M. A hybrid computational approach to estimate solar global radiation: An empirical evidence from Iran. Energy 2013, 49, 204–210. [Google Scholar] [CrossRef]
- Shiri, J.; Kim, S.; Kisi, O. Estimation of daily dew point temperature using genetic programming and neural networks approaches. Hydrol. Res. 2014, 45, 165–181. [Google Scholar] [CrossRef]
- Al-Hajj, R.; Assi, A. Estimating solar irradiance using genetic programming technique and meteorological records. AIMS Energy 2017, 5, 798–813. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Aslam, M.; Lee, J.M.; Kim, H.S.; Lee, S.J.; Hong, S. Deep Learning Models for Long-Term Solar Radiation Forecasting Considering Microgrid Installation: A Comparative Study. Energies 2020, 13, 147. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnail, L. Genetic Algorithms: A Survey; IEEE Computer: Washington, DC, USA, 1994; Volume 27. [Google Scholar]
- GPlearn. Available online: https://gplearn.readthedocs.io/en/stable/intro.html (accessed on 21 May 2021).
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson, Prentice Hall: Delhi, India, 2010. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Karamizadeh, S.; Abdullah, S.M.; Manaf, A.A.; Zamani, M.; Hooman, A. An overview of principal component analysis. J. Signal Inf. Process. 2013, 4, 173. [Google Scholar] [CrossRef]
- Devroye, L.; Gyorfi, L.; Krzyzak, A.; Lugosi, G. On the strong universal consistency of nearest neighbor regression function estimates. Ann. Stat. 1994, 22, 1371–1385. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Vanderplas, J. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Zhang, D. A coefficient of determination for generalized linear models. Am. Stat. 2017, 71, 310–316. [Google Scholar] [CrossRef]



| Authors | Base Learners | Ensemble Type | Combiner Meta-Model |
|---|---|---|---|
| Al-Hajj et al. [4] | RNNs + SVRs | Parallel stacking | MLPs |
| Linares-Rodriguez et al. [17] | ANNs | Parallel structure | Simple averaging |
| Ahmed et al. [18] | DTs + RF Regressors + Lasso Regressors | Parallel with probabilistic combination | Normal distribution methods for probabilistic forecasts |
| Guo et al. [19] | ANNs, Linear Regression + RF | Parallel structure—weighted sum | Linear weighted sum |
| Yeboah et al. [20] | DT | Bagging technique | RF |
| Pan et al. [21] | RF | Parallel staking | Weighted average with Ridge Regression |
| Basaran et al. [22] | SVR, ANN, DT | Bagging technique | Boosting–Bagging |
| Abuella et al. [23] | SVRs | Parallel structure—stacking | Random Forest RF |
| Model | RMSE | MAE | MBE | MAPE | ||
|---|---|---|---|---|---|---|
| Global model | LSTM_6 | 0.0666 | 0.0513 | −0.0352 | 123.50% | 0.9840 |
| Individual models | LSTM_1 | 0.1112 | 0.0901 | −0.0446 | 325.17% | 0.9814 |
| LSTM_2 | 0.0766 | 0.0608 | −0.0269 | 85.92% | 0.9696 | |
| LSTM_3 * | 0.0272 | 0.0201 | −0.0118 | 70.58% | 0.9977 | |
| LSTM_4 | 0.0359 | 0.0287 | −0.0159 | 58.72% | 0.9939 | |
| LSTM_5 | 0.0301 | 0.0235 | 0.0122 | 30.08% | 0.9957 |
| Model | RMSE | MAE | MBE | MAPE | ||
|---|---|---|---|---|---|---|
| Simple Averaging | LSTM_Avg | 0.0443 | 0.0349 | 0.0174 | 13.60% | 0.9942 |
| Machine Learning Stacking Models | LSTM_RF | 0.0540 | 0.0352 | 0.0069 | 11.59% | 0.9848 |
| LSTM_MLP | 0.0337 | 0.0262 | 0.0024 | 11.25% | 0.9959 | |
| LSTM_SVR | 0.0625 | 0.0540 | −0.0236 | 15.08% | 0.9914 | |
| LSTM_KNN | 0.0506 | 0.0382 | 0.0093 | 12.86% | 0.9904 | |
| GP | LSTM_GP (Standard) | 0.0238 | 0.0173 | 0.0033 | 8.41% | 0.9976 |
| LSTM_MP (GP + Local Search) | 0.0233 | 0.0177 | − 0.0018 | 30.14% | 0. 9969 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Hajj, R.; Assi, A.; Fouad, M.; Mabrouk, E. A Hybrid LSTM-Based Genetic Programming Approach for Short-Term Prediction of Global Solar Radiation Using Weather Data. Processes 2021, 9, 1187. https://doi.org/10.3390/pr9071187
Al-Hajj R, Assi A, Fouad M, Mabrouk E. A Hybrid LSTM-Based Genetic Programming Approach for Short-Term Prediction of Global Solar Radiation Using Weather Data. Processes. 2021; 9(7):1187. https://doi.org/10.3390/pr9071187
Chicago/Turabian StyleAl-Hajj, Rami, Ali Assi, Mohamad Fouad, and Emad Mabrouk. 2021. "A Hybrid LSTM-Based Genetic Programming Approach for Short-Term Prediction of Global Solar Radiation Using Weather Data" Processes 9, no. 7: 1187. https://doi.org/10.3390/pr9071187
APA StyleAl-Hajj, R., Assi, A., Fouad, M., & Mabrouk, E. (2021). A Hybrid LSTM-Based Genetic Programming Approach for Short-Term Prediction of Global Solar Radiation Using Weather Data. Processes, 9(7), 1187. https://doi.org/10.3390/pr9071187









