Stability of a Viscous Liquid Jet in a Coaxial Twisting Compressible Airflow

Abstract

Based on the linear stability analysis, a mathematical model for the stability of a viscous liquid jet in a coaxial twisting compressible airflow has been developed. It takes into account the twist and compressibility of the surrounding airflow, the viscosity of the liquid jet, and the cavitation bubbles within the liquid jet. Then, the effects of aerodynamics caused by the gas–liquid velocity difference on the jet stability are analyzed. The results show that under the airflow ejecting effect, the jet instability decreases first and then increases with the increase of the airflow axial velocity. When the gas–liquid velocity ratio A = 1, the jet is the most stable. When the gas–liquid velocity ratio A > 2, this is meaningful for the jet breakup compared with A = 0 (no air axial velocity). When the surrounding airflow swirls, the airflow rotation strength E will change the jet dominant mode. E has a stabilizing effect on the liquid jet under the axisymmetric mode, while E is conducive to jet instability under the asymmetry mode. The maximum disturbance growth rate of the liquid jet also decreases first and then increases with the increase of E. The liquid jet is the most stable when E = 0.65, and the jet starts to become more easier to breakup when E = 0.8425 compared with E = 0 (no swirling air). When the surrounding airflow twists (air moves in both axial and circumferential directions), given the axial velocity to change the circumferential velocity of the surrounding airflow, it is not conducive to the jet breakup, regardless of the axisymmetric disturbance or asymmetry disturbance.

1. Introduction

A liquid jet is a common phenomenon in various fields, including rainfall in nature, pesticide spraying in agriculture, and fuel injection of internal combustion engines in engineering, and so on. Therefore, the instability mechanism of the liquid jet has an important academic significance and engineering value.

At present, many studies have confirmed that the liquid jet in a coaxial high-speed airflow can achieve efficient mixing of the liquid jet and the surrounding gas. Compared with the liquid jet in a stationary gas, the liquid jet in the high-speed airflow is more conducive to atomization, and some research works have been obtained about the stability of a liquid jet in a coaxial airflow [1,2,3,4,5,6,7,8]. Sometimes, in the process of spraying and atomization, it is often accompanied by the swirling of the surrounding airflow [9,10]. Actually, the swirling movement of the surrounding airflow has a complex effect on the jet instability, which has gradually become a research hotspot [11,12,13,14,15,16,17,18,19,20]. Jog and Ibrahim [11] studied the swirling effect with the neglect of airflow compressibility. Lin et al. [12] studied the swirling effect with the neglect of the liquid viscosity and the airflow compressibility. Du et al. [14,15] studied the swirling effect with the neglect of the twisting motion and compressibility of the surrounding airflow. Strasser and Battaglia [16] studied the swirling effect and the compressibility of the jet based on the large-eddy simulation. Lü et al. [17,18] studied the swirling and compressibility effect of the surrounding airflow with the neglect of the liquid viscosity and the twisting motion of the surrounding airflow.

In addition, the effect of liquid viscosity on jet stability cannot be ignored [20,21,22]. Chandrasekhar [23] and Decent [24] studied the effect of fluid viscosity on the stability of liquid jet, and found that the fluid viscosity played an important role in promoting jet instability. Lin [25] mainly considered the viscosity of the liquid jet and analyzed the jet stability under different liquid viscosities. Yan [26,27] considered both the fluid viscosity and the airflow compressibility in order to analyze the jet stability. However, both of them neglected the swirling of the surrounding airflow. In addition, in the process of liquid injection, such as fuel injection in the internal combustion engines, cavitation bubbles always exist in the fuel jet leaving the nozzle [17,18]. Cavitation bubbles turn the liquid jet into a gas–liquid two-phase flow, which increases the instability of the liquid jet. Therefore, the study of the effect of cavitation bubbles on jet instability is of significance.

However, because of the complexity of all of these problems, scholars often neglect the coupling effect of the twist (movement both in axial and circumferential direction) and compressibility of the surrounding airflow, the viscosity of the liquid jet, and the cavitation bubbles within the liquid jet, which makes the research results deviate from the actual conditions.

According to current research situations and existing problems, on the premise of a comprehensive consideration of the twist and compressibility of the surrounding airflow, the viscosity of the liquid jet, and the cavitation bubbles within the liquid jet, the dispersion equation for the stability of a viscous liquid jet in a coaxial twisting compressible airflow has been developed. On this basis, the effects of airflow ejection, airflow swirling, and airflow twist on the stability of the liquid jet are discussed.

2. Mathematical Model

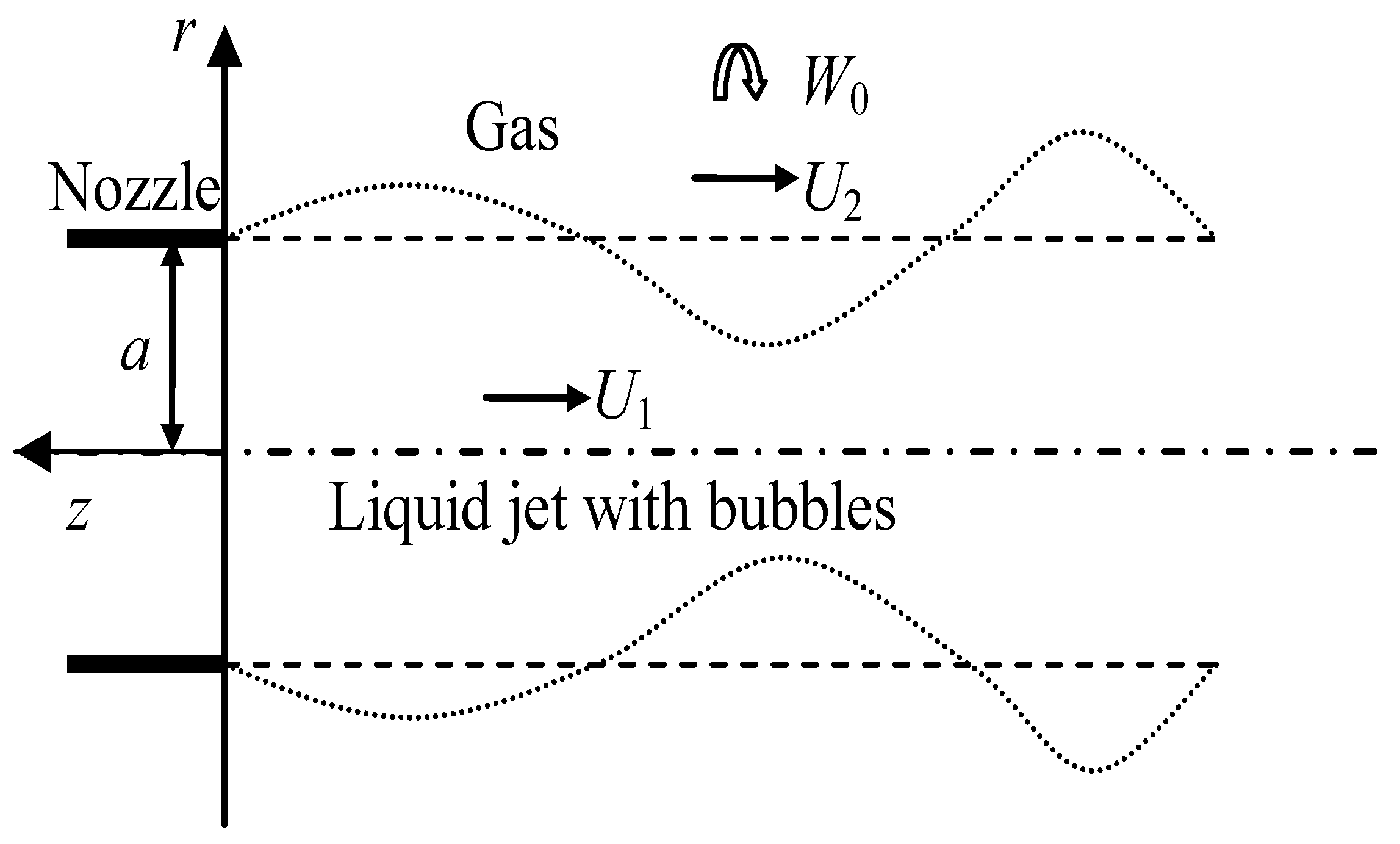
2.1. Physical Model and Initial Flow Field

A bundle of viscous liquid is injected into a coaxial twisting compressible gas medium from a cylindrical nozzle with a radius of a. The cylindrical coordinate system is established at the outlet of the nozzle, and the jet direction is opposite to the z-axis direction. The liquid jet is assumed to have a radius a and initial velocity U₀, while the surrounding gas has velocity in the z-axis direction U₂ and airflow rotation strength W₀, as shown in Figure 1.

Based on the above physical model, the following assumptions are made:

(1)

The surrounding gas is a compressible Newtonian fluid;

(2)

Ignore the influence of the viscosity, gravity, and temperature of the surrounding gas;

(3)

The liquid jet does not swirl, and the surrounding gas has a coaxial twisting velocity;

(4)

There is no slippage between the cavitation bubbles and the liquid jet, and there is no interaction between the cavitation bubbles;

(5)

The mixed phase consisting of uniformly distributed cavitation bubbles and liquid jet is a continuous medium.

In the coordinate system shown in Figure 1, the basic flow field (liquid jet velocity, the surrounding airflow velocity, the pressure difference between the liquid jet and the surrounding airflow, jet density, jet viscosity, and sound velocity in the liquid jet) is established based on the above assumptions, as follows:

$${\overline{V}}_1=\left(0,0,-U_1\right)\left(0\le r\le a\right)$$

(1)

$${\overline{V}}_2=\left(0,W_0/r,-U_2\right)\left(a<r<\infty \right)$$

(2)

$$\begin{array}{cc}{\overline{p}}_2\left(r\right)-{\overline{p}}_1=p_{\sigma }+p_{int}=-\frac{\sigma }{a}+\frac{1}{2}{\overline{\rho }}_2{W}_0^2\left(\frac{1}{a^2}-\frac{1}{r^2}\right)& \left(a<r<\infty \right)\end{array}$$

(3)

$${\overline{\rho }}_1=\alpha {\rho }_v+\left(1-\alpha \right){\rho }_l$$

(4)

$${\mu }_1=\alpha {\mu }_v+\left(1-\alpha \right){\mu }_l$$

(5)

where ${\overline{p}}_2\left(r\right)$ represent the surrounding gas pressure; ${\overline{p}}_1$ represent the liquid jet pressure; $p_{\sigma }$ is the surface tension; p_in is the gas phase inertia; σ is the surface tension factor at the interface; ${\overline{\rho }}_2$ is the gas density; ${\overline{\rho }}_1$ is the liquid jet density; W₀ is the gas rotation strength; ρ_v and ρ_l are cavitation bubble density and liquid density, respectively; μ_v and μ_l are the cavitation bubble viscosity and liquid viscosity, respectively; α is the bubble volume fraction, $\alpha =4\pi r_v^{3}N/3$; r_v is the cavity average radius; and N is the number of cavitations per unit volume.

2.2. Establishment and Solution of Mathematical Model

The equation is based on the linear stability analysis method, which is based on the establishment of the airflow and liquid fluid disturbance governing equations and the determination of the boundary conditions, using the linear small disturbance method to ignore the high-order small quantities to linearize the equation, build and solve the equations, and then carry out research.

(1) Disturbance governing equations of compressible twisting airflows

Consider the compressibility and neglect the viscosity and gravity of the surrounding airflow, the airflow satisfies the following continuity equation and Euler equation [28]:

$$\frac{\mathrm{D}{\rho }_2}{\mathrm{D}t}+{\rho }_2\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r{v}_{r2}\right)+\frac{1}{r}\frac{\partial v_{\theta 2}}{\partial \theta }+\frac{\partial v_{z2}}{\partial z}\right)=0$$

(6)

$$\{\begin{array}{l}\frac{\mathrm{D}{v}_{r2}}{\mathrm{D}t}-\frac{v_{\theta 2}^2}{r}=-\frac{1}{{\rho }_2}\frac{\partial p_2}{\partial r}\\ \frac{\mathrm{D}{v}_{\theta 2}}{\mathrm{D}t}+\frac{v_{r2}{v}_{\theta 2}}{r}=-\frac{1}{{\rho }_{2}r}\frac{\partial p_2}{\partial \theta }\\ \frac{\mathrm{D}{v}_{z2}}{\mathrm{D}t}=-\frac{1}{{\rho }_2}\frac{\partial p_2}{\partial z}\end{array}$$

(7)

where subscript 2 represents airflow parameters, and $v_r$, $v_{\theta }$, and $v_z$ are the radial, circumferential, and axial velocities, respectively.

Perturbation analysis and linearization of Equations (6) and (7), we can get the surrounding airflow disturbance governing equations as the following form:

$$\frac{\partial \left({p^{\prime }}_2/c_2^2\right)}{\partial t}+\frac{W_0}{r^2}\frac{\partial \left({p^{\prime }}_2/c_2^2\right)}{\partial \theta }-U_2\frac{\partial \left({p^{\prime }}_2/c_2^2\right)}{\partial z}+{\overline{\rho }}_2\left(\frac{{v^{\prime }}_{r2}}{r}+\frac{\partial {v^{\prime }}_{r2}}{\partial r}+\frac{1}{r}\frac{\partial {v^{\prime }}_{\theta 2}}{\partial \theta }+\frac{\partial {v^{\prime }}_{z2}}{\partial z}\right)=0$$

(8)

$$\{\begin{array}{l}{\overline{\rho }}_2\left(\frac{\partial {v^{\prime }}_{r2}}{\partial t}+\frac{W_0}{r^2}\frac{\partial {v^{\prime }}_{r2}}{\partial \theta }-U_2\frac{\partial {v^{\prime }}_{r2}}{\partial z}-\frac{2W_0{v^{\prime }}_{\theta 2}}{r^2}\right)=-\frac{\partial {p^{\prime }}_2}{\partial r}\\ {\overline{\rho }}_2\left(\frac{\partial {v^{\prime }}_{\theta 2}}{\partial t}+\frac{W_0}{r^2}\frac{\partial {v^{\prime }}_{\theta 2}}{\partial \theta }-U_2\frac{\partial {v^{\prime }}_{\theta 2}}{\partial z}\right)=-\frac{1}{r}\frac{\partial {p^{\prime }}_2}{\partial \theta }\\ {\overline{\rho }}_2\left(\frac{\partial {v^{\prime }}_{z2}}{\partial t}+\frac{W_0}{r^2}\frac{\partial {v^{\prime }}_{z2}}{\partial \theta }-U_2\frac{\partial {v^{\prime }}_{z2}}{\partial z}\right)=-\frac{\partial {p^{\prime }}_2}{\partial z}\end{array}$$

(9)

where the apostrophe indicates a small disturbance parameter.

Equations (8) and (9) include four equations, but contain five unknown parameters. In order to close the four equations, use $\partial {p^{\prime }}_2/\partial {{\rho }^{\prime }}_2=c_2^2$ to relate the disturbance density and pressure with the speed of sound. At this point, the airflow disturbance governing equations are established.

(2) Disturbance governing equations of viscous liquid jets

Consider the viscosity and neglect the compressibility and gravity of the liquid jet, the liquid jet satisfies the following continuity equation and momentum equation [28]:

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r{v}_{r1}\right)+\frac{1}{r}\frac{\partial v_{\theta 1}}{\partial \theta }+\frac{\partial v_{z1}}{\partial z}=0$$

(10)

$$\{\begin{array}{l}\frac{\mathrm{D}{v}_{r1}}{\mathrm{D}t}-\frac{v_{\theta 1}^2}{r}=-\frac{1}{{\rho }_1}\frac{\partial p_1}{\partial r}+{\nu }_1\left({\nabla }^2{v}_{r1}-\frac{v_{r1}}{r^2}-\frac{2}{r^2}\frac{\partial v_{\theta 1}}{\partial \theta }\right)\\ \frac{\mathrm{D}{v}_{\theta 1}}{\mathrm{D}t}+\frac{v_{r1}{v}_{\theta 1}}{r}=-\frac{1}{{\rho }_{1}r}\frac{\partial p_1}{\partial \theta }+{\nu }_1\left({\nabla }^2{v}_{\theta 1}+\frac{2}{r^2}\frac{\partial v_{r1}}{\partial \theta }-\frac{v_{\theta 1}}{r^2}\right)\\ \frac{\mathrm{D}{v}_{z1}}{\mathrm{D}t}=-\frac{1}{{\rho }_1}\frac{\partial p_1}{\partial z}+{\nu }_1{\nabla }^2{v}_{z1}\end{array}$$

(11)

where subscript 1 represents the liquid jet parameters and ν₁ is the liquid jet kinematic viscosity.

From the perturbation analysis and linearization of Equations (10) and (11), we can obtain the following disturbance governing equations of the liquid jet:

$$\frac{{v^{\prime }}_{r1}}{r}+\frac{\partial {v^{\prime }}_{r1}}{\partial r}+\frac{1}{r}\frac{\partial {v^{\prime }}_{\theta 1}}{\partial \theta }+\frac{\partial {v^{\prime }}_{z1}}{\partial z}=0$$

(12)

$$\frac{\partial {v^{\prime }}_{r1}}{\partial t}-U_1\frac{\partial {v^{\prime }}_{r1}}{\partial z}=-\frac{1}{{\overline{\rho }}_1}\frac{\partial {p^{\prime }}_1}{\partial r}+{\nu }_1\left({\nabla }^2{v^{\prime }}_{r1}-\frac{{v^{\prime }}_{r1}}{r^2}-\frac{2}{r^2}\frac{\partial {v^{\prime }}_{\theta 1}}{\partial \theta }\right)$$

(13)

$$\frac{\partial {v^{\prime }}_{\theta 1}}{\partial t}-U_1\frac{\partial {v^{\prime }}_{\theta 1}}{\partial z}=-\frac{1}{{\overline{\rho }}_{1}r}\frac{\partial {p^{\prime }}_1}{\partial \theta }+{\nu }_1\left({\nabla }^2{v^{\prime }}_{\theta 1}+\frac{2}{r^2}\frac{\partial {v^{\prime }}_{r1}}{\partial \theta }-\frac{{v^{\prime }}_{\theta 1}}{r^2}\right)$$

(14)

$$\frac{\partial {v^{\prime }}_{z1}}{\partial t}-U_1\frac{\partial {v^{\prime }}_{z1}}{\partial z}=-\frac{1}{{\overline{\rho }}_1}\frac{\partial {p^{\prime }}_1}{\partial z}+{\nu }_1{\nabla }^2{v^{\prime }}_{z1}$$

(15)

(3) Boundary conditions

At the interface between the liquid jet and the surrounding gas, the boundary conditions include the kinematic boundary conditions and the dynamic boundary conditions:

$$v_{ri}=\frac{\partial \eta }{\partial t}+\frac{v_{\theta i}}{r}\frac{\partial \eta }{\partial \theta }+v_{zi}\frac{\partial \eta }{\partial z}$$

(16)

$$p_1-p_2=2{\mu }_1\frac{\partial v_{r1}}{\partial r}-\sigma \left(\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{a}\right)+\frac{1}{2}{\overline{\rho }}_2{W}_0^2\left(\frac{1}{a^2}-\frac{1}{{\left(a+\eta \right)}^2}\right)$$

(17)

where η is the perturbation on the liquid jet at the interface.

Perturbation analysis and linearization of Equations (16) and (17) can obtain the following boundary conditions:

$${\overline{v}}_{ri}+{v^{\prime }}_{ri}=\frac{\partial \eta }{\partial t}+\frac{{\overline{v}}_{\theta i}}{a+\eta }\frac{\partial \eta }{\partial \theta }+{\overline{v}}_{zi}\frac{\partial \eta }{\partial z}$$

(18)

$$a^4\left({p^{\prime }}_1-{p^{\prime }}_2\right)=2a^4{\mu }_1\frac{\partial {v^{\prime }}_{r1}}{\partial r}-a^2\sigma \left(\eta +a^2\frac{{\partial }^2\eta }{\partial z^2}+\frac{{\partial }^2\eta }{\partial {\theta }^2}\right)+{\overline{\rho }}_2{W}_0^{2}a\eta$$

(19)

(4) Dispersion equation

Through the above disturbance governing Equations (8), (9), (12)–(15) and boundary conditions (18)–(19), a homogeneous linear algebraic equations is established:

$$\mathit{A}\mathit{X}=0$$

(20)

where X = [a₁₁, a₁₂, d₁₁, d₂₂, η₀]^T, and A is a 5 × 5 coefficient matrix containing k, ω, m, and other jet parameters:

$$\mathit{A}=\left[\begin{array}{ccccc}{A}_{11}& A_{12}& A_{13}& A_{14}& A_{15}\\ A_{21}& A_{22}& A_{23}& A_{24}& A_{25}\\ A_{31}& A_{32}& A_{33}& A_{34}& A_{35}\\ A_{41}& A_{42}& A_{43}& A_{44}& A_{45}\\ A_{51}& A_{52}& A_{53}& A_{54}& A_{55}\end{array}\right]$$

The expressions for each element in matrix A are shown in the Appendix A.

The condition for the existence of a non-zero solution of the Equation (20) is that the determinant of the coefficient matrix is 0:

$$\left|\mathit{A}\right|=0$$

(21)

Equation (21) is the dispersion equation describing the stability of a viscous liquid jet in a compressible twisting airflow. In view of the complexity of the dispersion equation, this paper gives the following abbreviated form:

f (k, ω, m, We, Re₁, E, A, Ma₂, Q) = 0

(22)

where $k=k_r+i{k}_i$, k_r is the wave number in the z direction, and the relationship with the wavelength λ is k_r = 2πa/λ, k_i is the disturbance spatial growth rate; ω = ω_r + iω_i, ω_r is the disturbance temporal growth rate and ω_i is the wave frequency; m is the wave number in the θ direction; We = $\sigma /\left(\alpha {\rho }_v+\left(1-\alpha \right){\rho }_l\right)U_1^{2}a$, note that We is the reciprocal of the Weber number and signifies the ratio of the surface tension to the inertial force; $R{e}_1=U_{1}a/{\nu }_1$ is the liquid jet Reynolds number, which reflects the ratio of inertial force to viscous force; E = W₀/(U₀a) is the non-dimensional rotational strength; A = U₂/U₁, is the gas–liquid axial velocity ratio; Ma₂ = U₀/c₂ is the surrounding gas Mach number; and Q = ${\overline{\rho }}_2/\left(\alpha {\rho }_v+\left(1-\alpha \right){\rho }_l\right)$ is the gas–liquid density ratio.

The effects of the liquid jet viscosity, cavitation bubbles within the liquid jet, and the twist and compressibility of the surrounding airflow are considered in the above established dispersion Equation (22). In addition, the secant method is used to solve this dispersion equation.

The mathematical modal is based on a simplified mathematical model that assumes (as valid) a modal and stability analysis. Through theoretical analysis, the mechanism of jet breakup and atomization can be explained fundamentally. However, there is a certain difference compared with the actual jet column; the next step will be studied through direct numerical simulations or experiments. Furthermore, the bubble volume fraction bubble has a certain value range. If $\alpha$ > 0.2, it will not be used as a continuum, and the dispersion equation in this paper will be inapplicable.

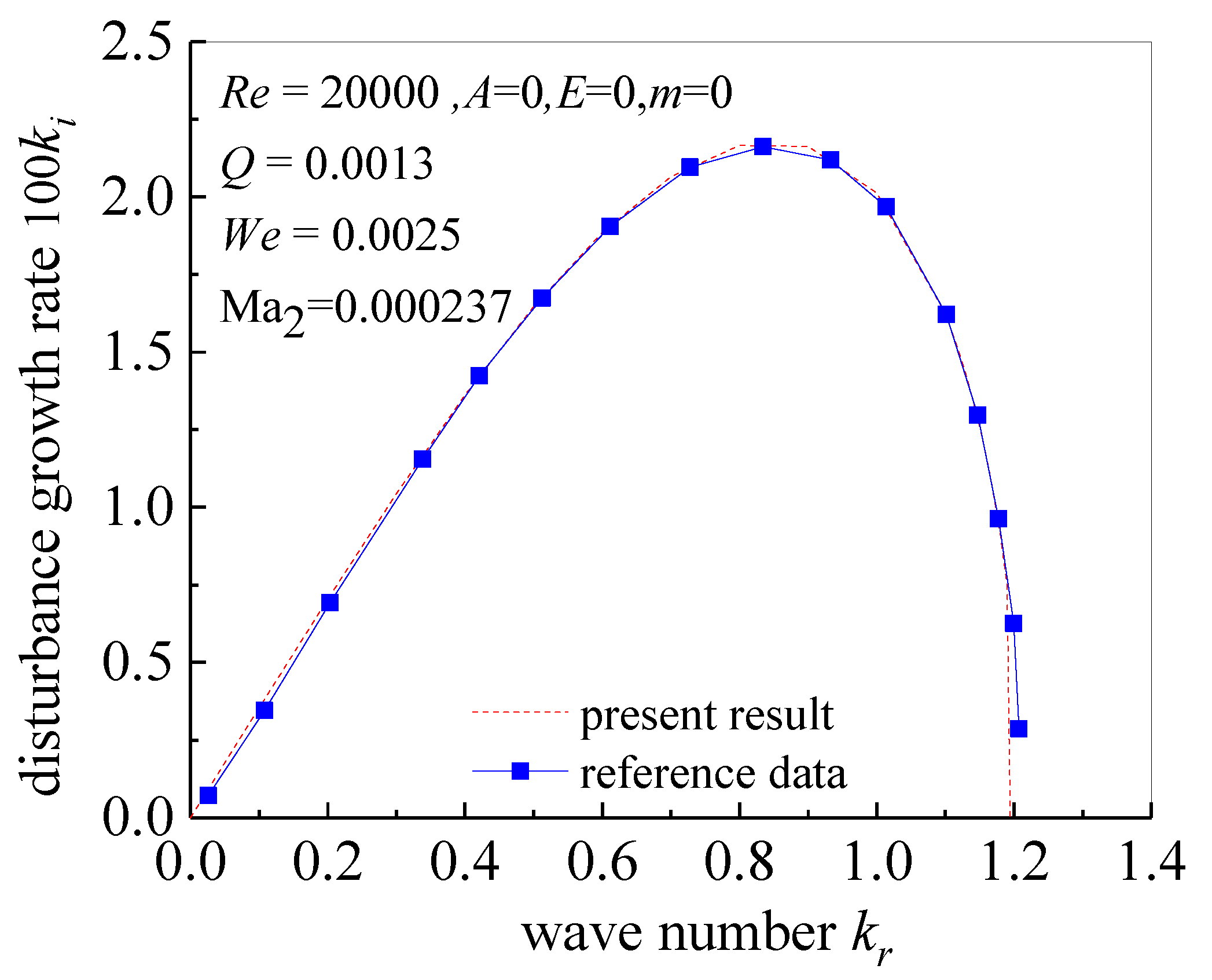
2.3. Verification and Solution

For a special case where an inviscid liquid jet without cavitation bubbles is injected into an untwisted and incompressible airflow under axisymmetric mode, m = 0, Re₁ = 0, E = 0, A = 0, Ma₂ = 0, and α = 0, then the dispersion Equation (22) is reduced to the following:

$$\frac{{\left(\omega -\mathrm{i}k\right)}^2{\mathrm{I}}_0\left(k\right)}{{\mathrm{I}}_1\left(k\right)}+\frac{Q{\omega }^2{\mathrm{K}}_0\left(k\right)}{{\mathrm{K}}_1\left(k\right)}+kWe\left(k^2-1\right)=0$$

(23)

The reduced dispersion Equation (23) is the same as the dispersion equation derived by Lin and Lian [18].

For another special case where only the compressibility of the surrounding airflow and the cavitation bubbles within the liquid jet are neglected, that is, Ma₂ = 0, α = 0, then the dispersion Equation (22) is reduced to the following:

$$a_1\left(\frac{{\mathrm{I}}_m^{\prime }\left(k\right)}{{\mathrm{I}}_m\left(k\right)}\right){\left(\frac{{\mathrm{I}}_m^{\prime }\left(\lambda \right)}{{\mathrm{I}}_m\left(\lambda \right)}\right)}^2+a_2{\left(\frac{{\mathrm{I}}_m^{\prime }\left(\lambda \right)}{{\mathrm{I}}_m\left(\lambda \right)}\right)}^2+a_3\left(\frac{{\mathrm{I}}_m^{\prime }\left(k\right){\mathrm{I}}_m^{\prime }\left(\lambda \right)}{{\mathrm{I}}_m\left(k\right){\mathrm{I}}_m\left(\lambda \right)}\right)+a_4\left(\frac{{\mathrm{I}}_m^{\prime }\left(k\right)}{{\mathrm{I}}_m\left(k\right)}\right)+a_5\left(\frac{{\mathrm{I}}_m^{\prime }\left(\lambda \right)}{{\mathrm{I}}_m\left(\lambda \right)}\right)+a_6=0$$

(24)

The reduced dispersion Equation (24) is consistent with the one derived by Lin [29], and the formal difference is due to the definition of the axial direction and wave frequency.

The comparison of the above two specific cases can prove the correctness of the dispersion equation to some extent.

In order to verify the correctness of the numerical solution method, the calculating conditions and original data from [24] are compared with the present calculation results in this paper. The comparison results are shown in Figure 2.

The authors of [24] provide an example that a viscous liquid jet is injected into the stationary gas under the axisymmetric disturbance. As shown in Figure 2, the calculation results in this paper are in good agreement with the data in the literature, which indicates that the numerical solution method of the dispersion equation is reasonable and effective.

3. Results and Discussions

In this paper, diesel was chosen as the liquid jet and air was chosen as the surrounding gas, and the relevant parameters used are shown in

Table 1. Calculating parameters.

Parameters	Units	Values
Liquid density	kg/m3	848
Surface tension	N/m	2.689 × 10−2
Gas density	kg/m3	1.193
Kinematic viscosity	m2/s	7.6658 × 10−6
Jet speed	m/s	10
Nozzle radius	m	1 × 10−4
Temperature	K	300
Sound speed in gas	m/s	348

.

The dispersion Equation (22) can reflect the effects of the liquid jet viscosity, cavitation bubbles within the liquid jet, and the twist and compressibility of the surrounding airflow on jet instability. Here, we only investigate the aerodynamic effects caused by the surrounding airflow ejection (axial speed), swirl (circumferential speed), and twist (both the axial and circumferential speed) on the stability of the liquid jet when the other parameter values are given as We = 0.0032, Re₁ = 130, Ma₂ = 0.029, and Q = 0.0014.

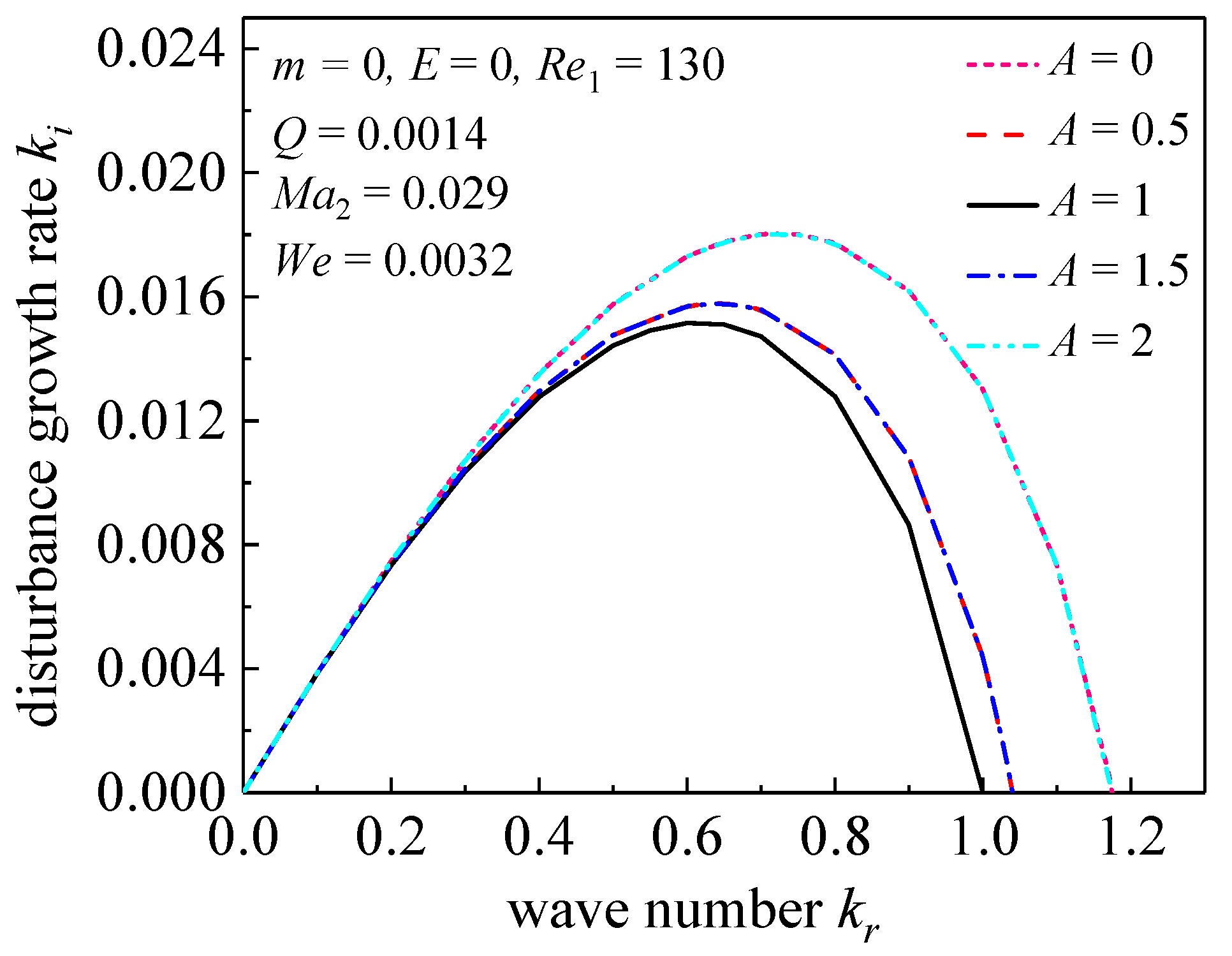
3.1. Effect of Ejecting Airflow on the Stability of Viscous Liquid Jet

This section analyzes the effect of ejecting airflow on the stability of a viscous liquid jet. A = U₂/U₁ is the gas–liquid axial velocity ratio, which can be used to characterize the ejecting airflow velocity size. A = 1 means that the axial velocity of liquid jet is equal to the axial velocity of the surrounding airflow. According to the value of the gas–liquid axial velocity ratio A, the surrounding airflow ejection is divided into strong ejection and weak ejection. When gas–liquid axial velocity ratio A ≤ 2, it is classified as a weak ejection. A > 2 is classified as the strong ejection in this paper.

Figure 3 shows that the disturbance growth rate changes with the axial wave number in the axisymmetric disturbance (m = 0) under the weak airflow ejection.

As shown in Figure 3, when the surrounding airflow ejection exists, and gas–liquid axial velocity ratio A ≤ 2, the disturbance growth rate of the liquid jet decreases first and then increases with the increase of the gas–liquid velocity ratio A (from 0 to 2). When the air axial velocity is equal to the liquid axial velocity (A = 1), the disturbance growth rate is the smallest, and the liquid jet is the most stable. When gas–liquid axial velocity ratio A = 2, the disturbance growth rate of the liquid jet is basically the same as when A = 0 (no air axial velocity); it is also observed that the disturbance growth rate curve basically coincides when A = 0.5 and A = 1.5. So, we can get that when the absolute value of (A − 1) is the same, the resulting aerodynamic effect on the liquid jet stability is basically the same. Therefore, the ejection of the surrounding airflow can suppress the breakup of the liquid jet when A ∈ [0, 2] compared with no air axial velocity.

Figure 4 shows the comparison of the disturbance growth rates versus axial wave numbers under the strong airflow ejection (A > 2) in the axisymmetric disturbance mode (m = 0) and the asymmetry disturbance mode (m = 1), respectively.

It can be seen from Figure 4a that the disturbance growth rates increase sharply with the increase of the gas–liquid velocity ratios, and the range of the unstable axial wave numbers is significantly widened. This indicates that the increase in the airflow axial velocity can increase the aerodynamic effect and then promote the instability of the liquid jet when A > 2. From the inverse proportional relationship between the axial wave number and the droplet size, it can be concluded that the increase of the airflow axial velocity will reduce the droplet size and get the stronger atomization effect under the strong airflow ejection.

A comparison of Figure 4a,b shows that the effect of airflow ejection on the jet stability in the axisymmetric and asymmetry mode is similar. In addition, the maximum disturbance growth rate of the axisymmetric mode is always bigger than that of the asymmetry mode, but the gap between the two modes is gradually narrowing with the increasing of the gas–liquid speed ratios, which suggests that the airflow ejection may change the dominant mode of the liquid jet.

3.2. Effect of Swirling Airflow on the Stability of Viscous Liquid Jet

Some research results have shown that the swirling airflow has a complex effect on the jet stability, and it is different under the axisymmetric mode and asymmetry mode [30]. This section will analyze the influence of the aerodynamic caused by the swirl of the surrounding airflow on the jet stability. E = W₀/(U₀a) represents the non-dimensional airflow rotational strength.

Figure 5 shows the effects of the swirling airflow on jet stability under the axisymmetric mode (m = 0) and asymmetry mode (m = 1). Note that the gas–liquid velocity ratio A = 0.

As shown in Figure 5a, under the axisymmetric mode, with the increase of the surrounding airflow rotation strength, the disturbance growth rates decrease obviously, and the range of the axial wave numbers decrease significantly. When the airflow rotation strength E = 1.5, the disturbance growth rate is very small, which is difficult to observe in Figure 5a. As shown in Figure 5b, under the asymmetry mode, it is found that the effect of the swirling airflow on the jet stability is completely opposite to that in Figure 5a, that is, the disturbance growth rates increases sharply with the increasing of the airflow rotation strength, which will increase the jet instability.

Comparing Figure 5a with Figure 5b, it is found that when the airflow rotation strength E = 0.5, the maximum disturbance growth rate of the axisymmetric disturbance k_{i_max} = 0.0162, while the maximum disturbance growth rate of asymmetry disturbance k_{i_max} = 0.0128, so the dominant mode is the axisymmetric mode. When the airflow rotation strength E = 1, the maximum disturbance growth rate of the axisymmetric disturbance k_{i_max} = 0.0106, while the maximum disturbance growth rate of the asymmetry disturbance k_{i_max} = 0.0198, so the asymmetry mode is dominant. It is indicated that the coaxial swirl of the surrounding airflow can change the dominant mode of the liquid jet stability, and as the rotation strength E increases, the dominant mode changes from axisymmetric mode to asymmetric mode.

Table 2. The dominant modes under different airflow rotation strengths.

E	0	0.5	1	3	5	7
m	0	0	1	2	6	10

shows the dominant modes under different airflow rotation strengths.

In order to further analyze the effects of the swirling airflow on jet stability under the dominant modes, Figure 6 gives the maximum disturbance growth rate under the dominant mode versus the different airflow rotation strength.

It can be seen from Figure 6 that the maximum disturbance growth rate is not proportional to the airflow rotation strength. Similar to the law of airflow ejection, as the airflow rotation strength increases, the maximum disturbance growth rate decreases first and then increases sharply. The maximum disturbance growth rate is the smallest when the airflow rotation strength is at point A (E = 0.65, k_{i_max} = 0.1534). At this point, the aerodynamic force is the smallest, and the liquid jet is the most stable. When point A is at its lowest, the coaxial swirl of the surrounding airflow can change the dominant mode of the liquid jet stability. Under axisymmetric disturbances, rotation strength is conducive to the stability of the jet, while under asymmetry disturbances, it is conducive to the instability and splitting of the jet. When the airflow rotation strength is at point B (E = 0.8425, k_{i_max} = 0.1802), the maximum disturbance growth rate just exceeds the case of no airflow rotation (E = 0). According to the calculation conditions of this paper, when the surrounding airflow swirls, the increase of the airflow rotation strength when E > 0.8425 is beneficial to the breakup of the liquid jet.

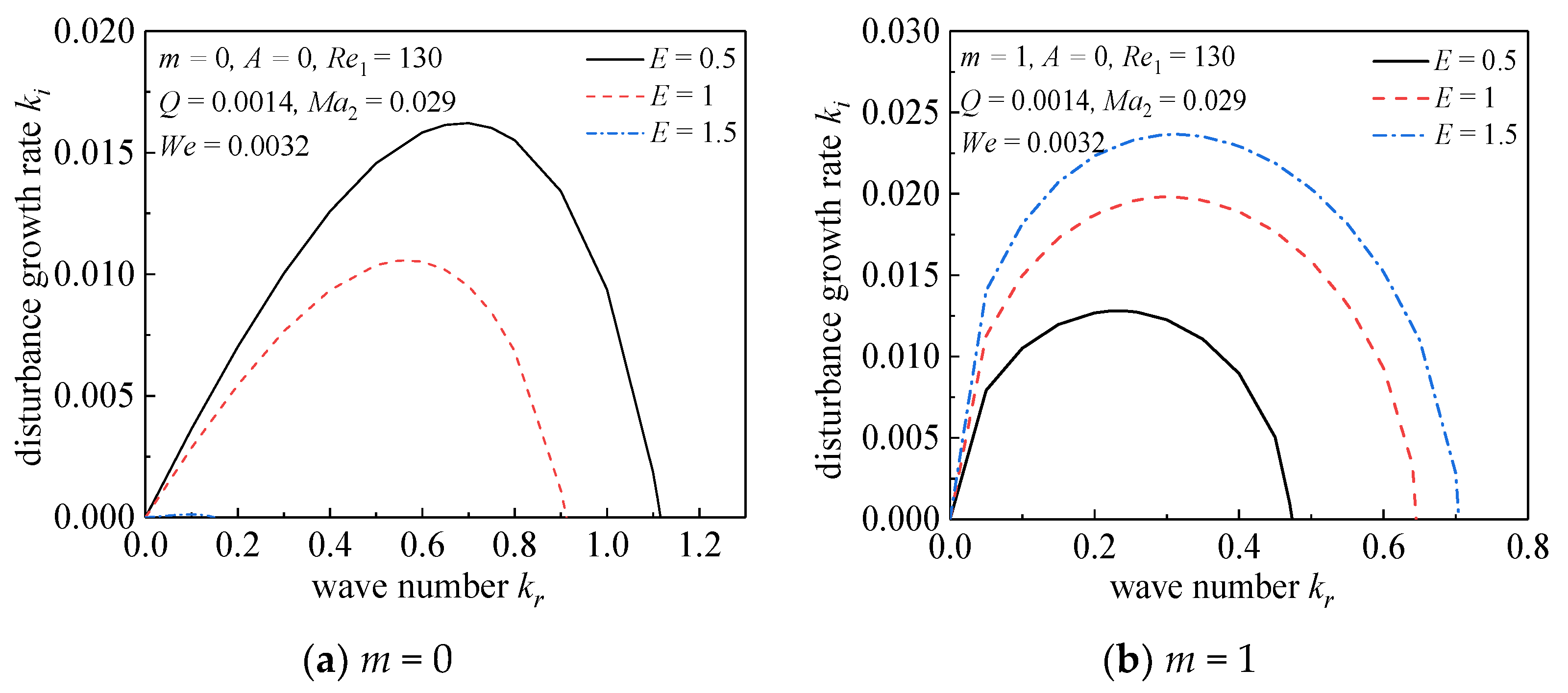
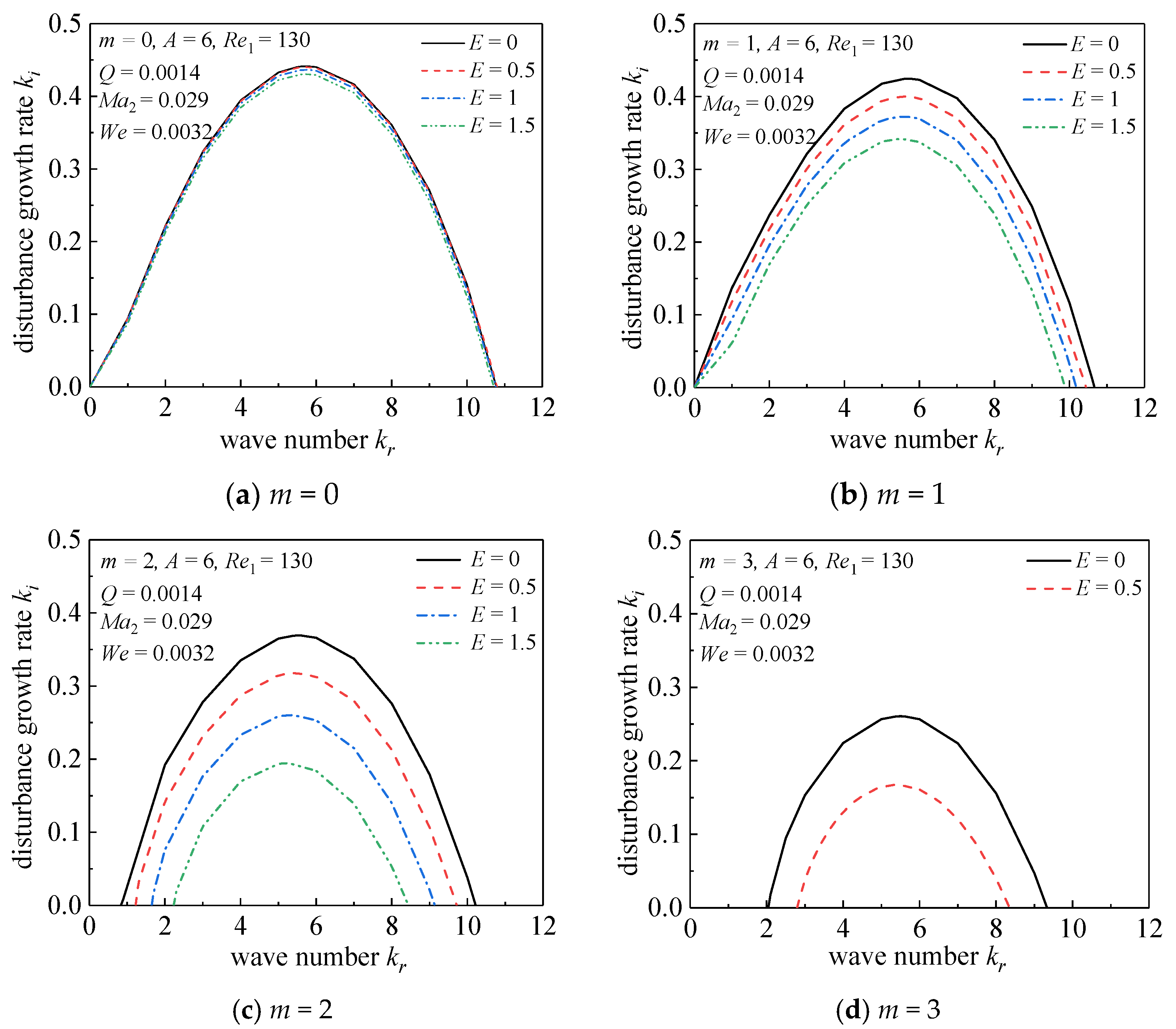
3.3. Effect of Twisting Airflow on the Stability of Viscous Liquid Jet

To our knowledge, few scholars have studied the influence of the coupling effect on the jet stability when the surrounding airflow has both an axial and circumferential velocity. This section will analyze the influence of the aerodynamic effect caused by the twist of the surrounding airflow on the stability of the liquid jet.

Figure 7 shows the comparison of the effects of the twisting airflow on jet stability under the axisymmetric mode (m = 0) and asymmetry mode (m = 1, 2, 3). Note that the surrounding airflow has an axial velocity (A = 6) and has different rotation strengths (E = 0, 0.5, 1, and 1.5).

As shown in Figure 7, when the surrounding airflow twists and the gas–liquid axial velocity ratio A is given, under the axisymmetric mode, the disturbance growth rates decrease with the increase of the airflow rotation strengths, but the effects of the airflow rotation strengths on the jet stability are relatively small. Under the asymmetry mode, it is different from the case that m = 0. When the airflow rotation strengths increase, the disturbance growth rates decrease obviously. Therefore, when the surrounding airflow twists, the stability of the liquid jet is enhanced with the increase of the airflow rotation strength both in the axisymmetric mode and in the asymmetry mode. According to the calculation conditions of this paper, the twist of the surrounding airflow is not conducive to the breakup of the liquid jet.

In addition, a comparison of Figure 5 and Figure 7 shows that the effects of the twisting airflow on jet stability are different compared with the effects of swirling airflow on jet stability, which indicates that the gas–liquid axial velocity ratio A plays an important role in jet stability.

4. Conclusions

(1)

Take into account the twist and compressibility of the surrounding airflow, the viscosity of the liquid jet and the cavitation bubbles within the liquid jet, a mathematical model for describing the stability of the liquid jet in a coaxial twisting compressible gas flow was established, the model and its solving method were verified.

(2)

The ejection of surrounding airflow is divided into weak ejection (A $\le$ 2) and strong ejection (A > 2). Under the weak ejection of the surrounding airflow, the maximum perturbation growth rate of the jet decreases first and then increases with the increase of the axial velocity of the airflow. When the gas–liquid axial velocity is the same (A = 1), the maximum perturbation growth rate of the liquid jet is the smallest. When the absolute value of (A − 1) is the same, the resulting aerodynamic effect on the liquid jet stability is basically the same. Under the strong ejection of the surrounding airflow, the maximum perturbation growth rate of the liquid jet increases sharply with the increase in the air ejection velocity. It is concluded that the greater the gas–liquid velocity, the more unstable the liquid jet becomes.

(3)

When the surrounding airflow swirls, the swirling airflow plays a stable role on the liquid jet in the axisymmetric mode, as opposed to the asymmetry mode. The dominant mode changes from axisymmetric to asymmetry as the airflow rotation strength increases. For a cylindrical liquid jet, when the airflow rotation strength is increased, the maximum growth rate of the liquid jet decreases first and then increases. The liquid jet is the most stable when E = 0.65, and the liquid jet begins to become easier to breakup when E = 0.8425 compared with E = 0 (no swirling air). The increase in the airflow rotation strength from 0.8425 is beneficial to the breakup of the liquid jet, and the airflow rotation strength has a significant effect on the stability of the liquid jet.

(4)

When the surrounding airflow twists, the stability of the liquid jet is enhanced with the increase of the airflow rotation strength, both in the axisymmetric mode and in the asymmetry mode. According to the calculation conditions of this paper, the twist of the surrounding airflow is not conducive to the breakup of the liquid jet.