Heat Generation in Irradiated Gold Nanoparticle Solutions for Hyperthermia Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Optical Predictions
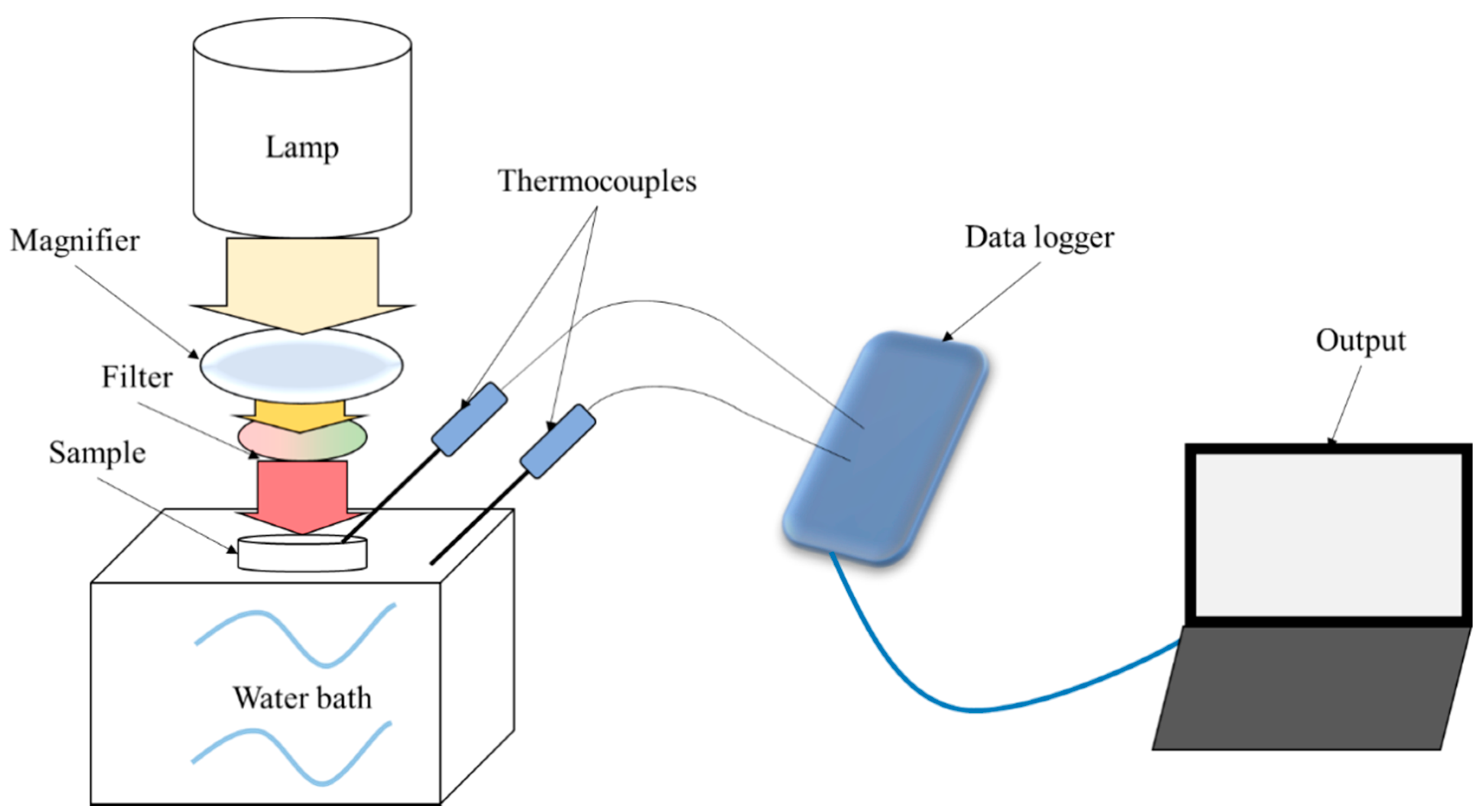
2.3. Experimental Measurement of Heat Generation
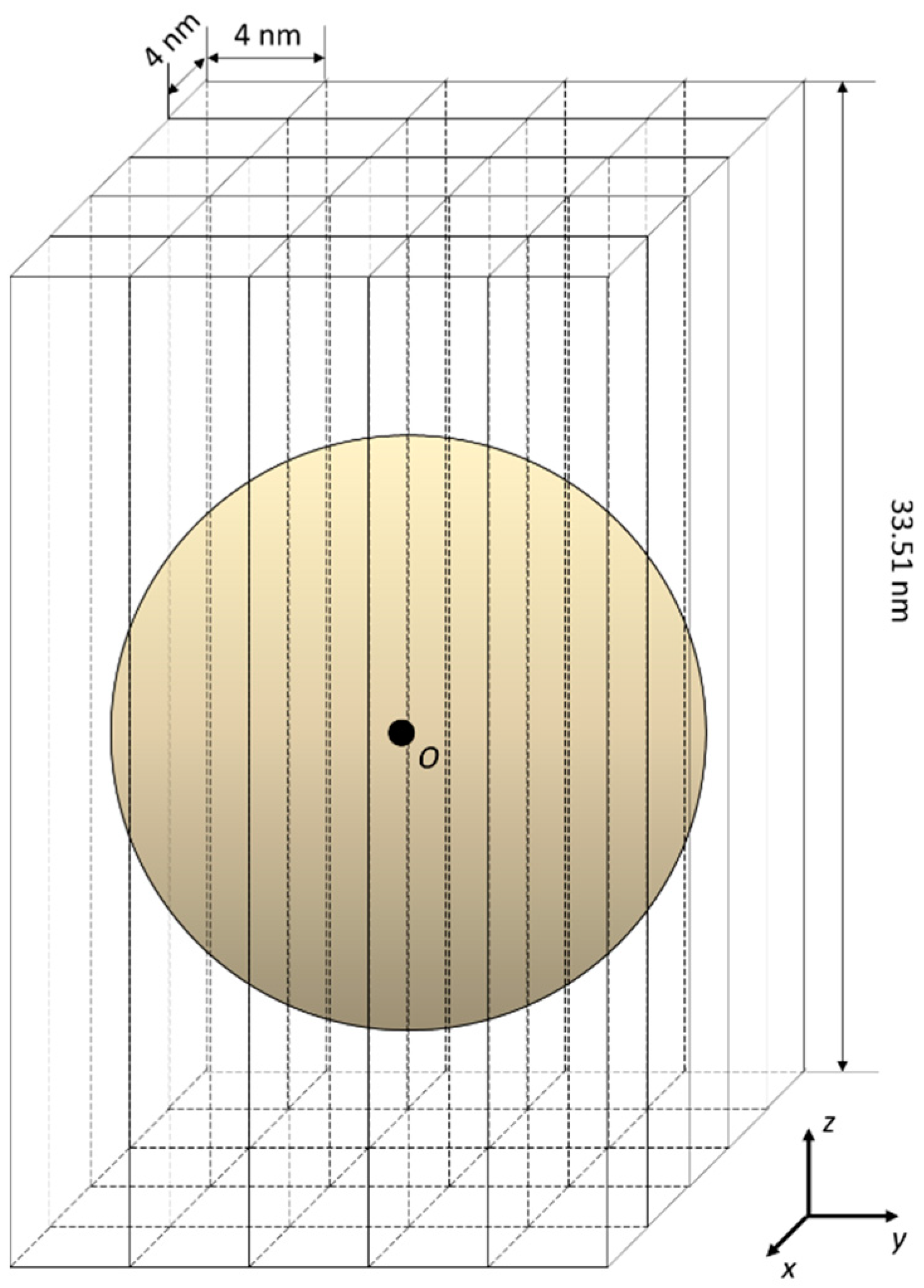
2.4. Numerical Prediction of Heat Generation
3. Results
3.1. Size Distributions
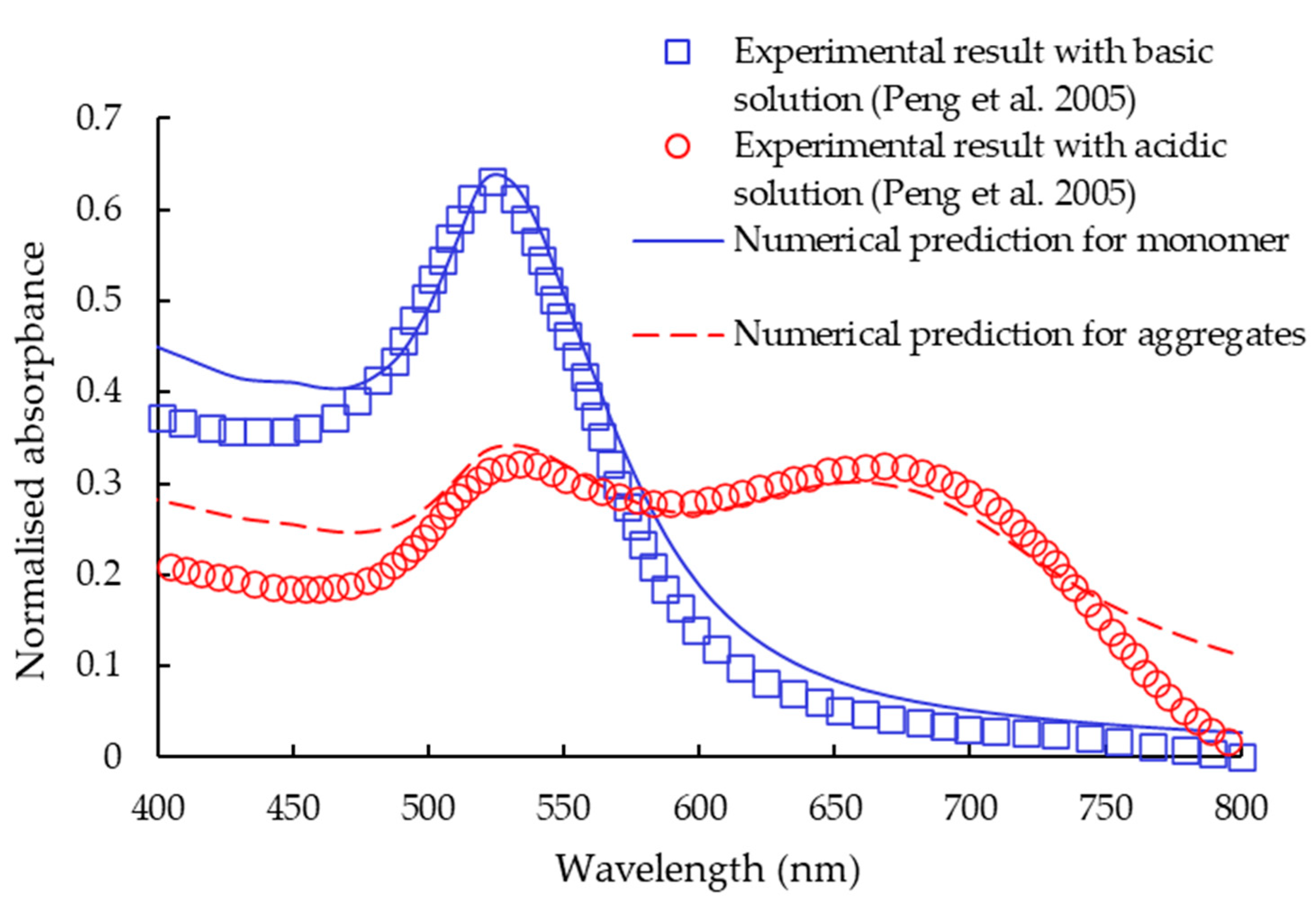
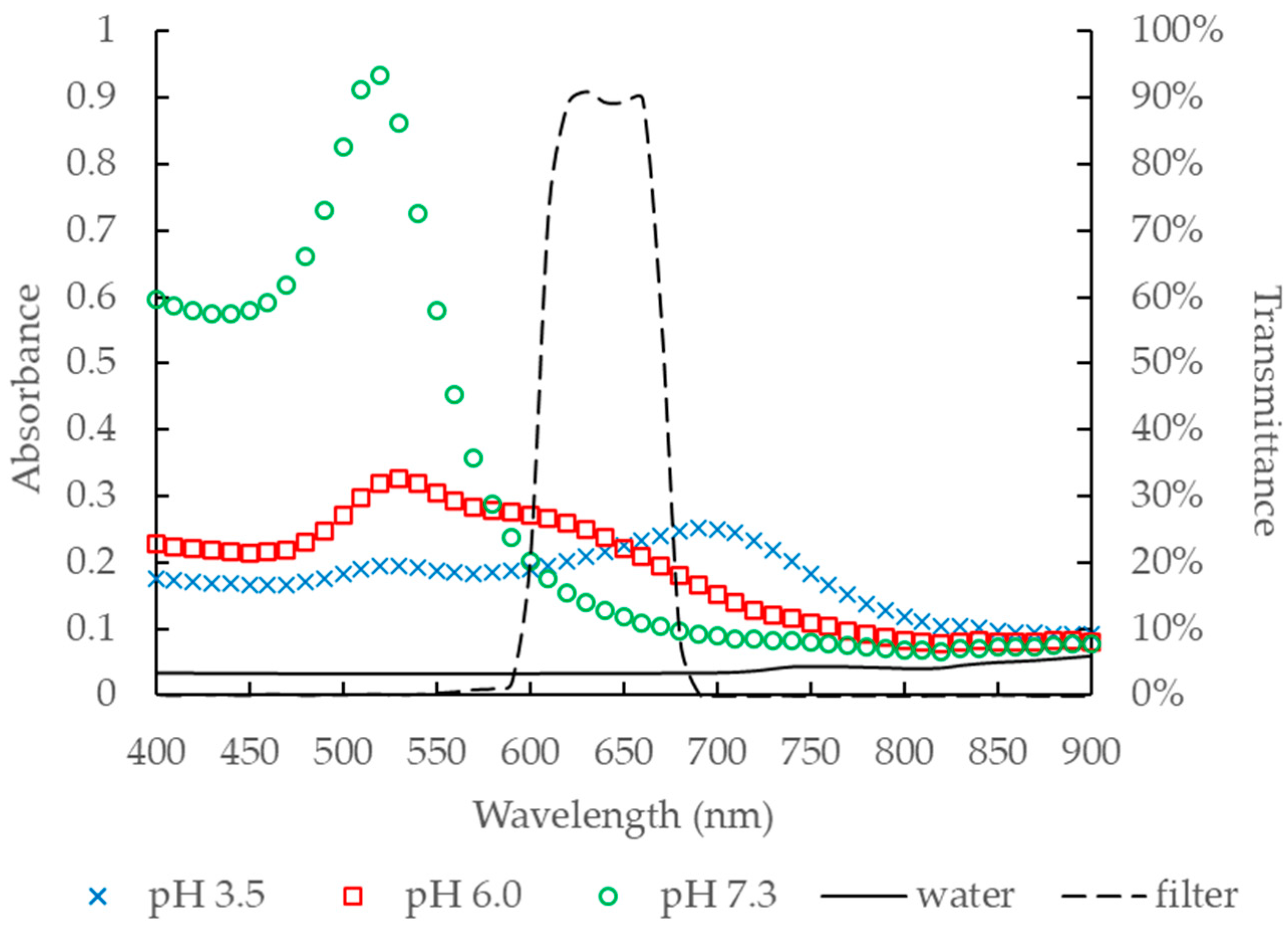
3.2. Optical Properties
3.3. Measured Temperature Change
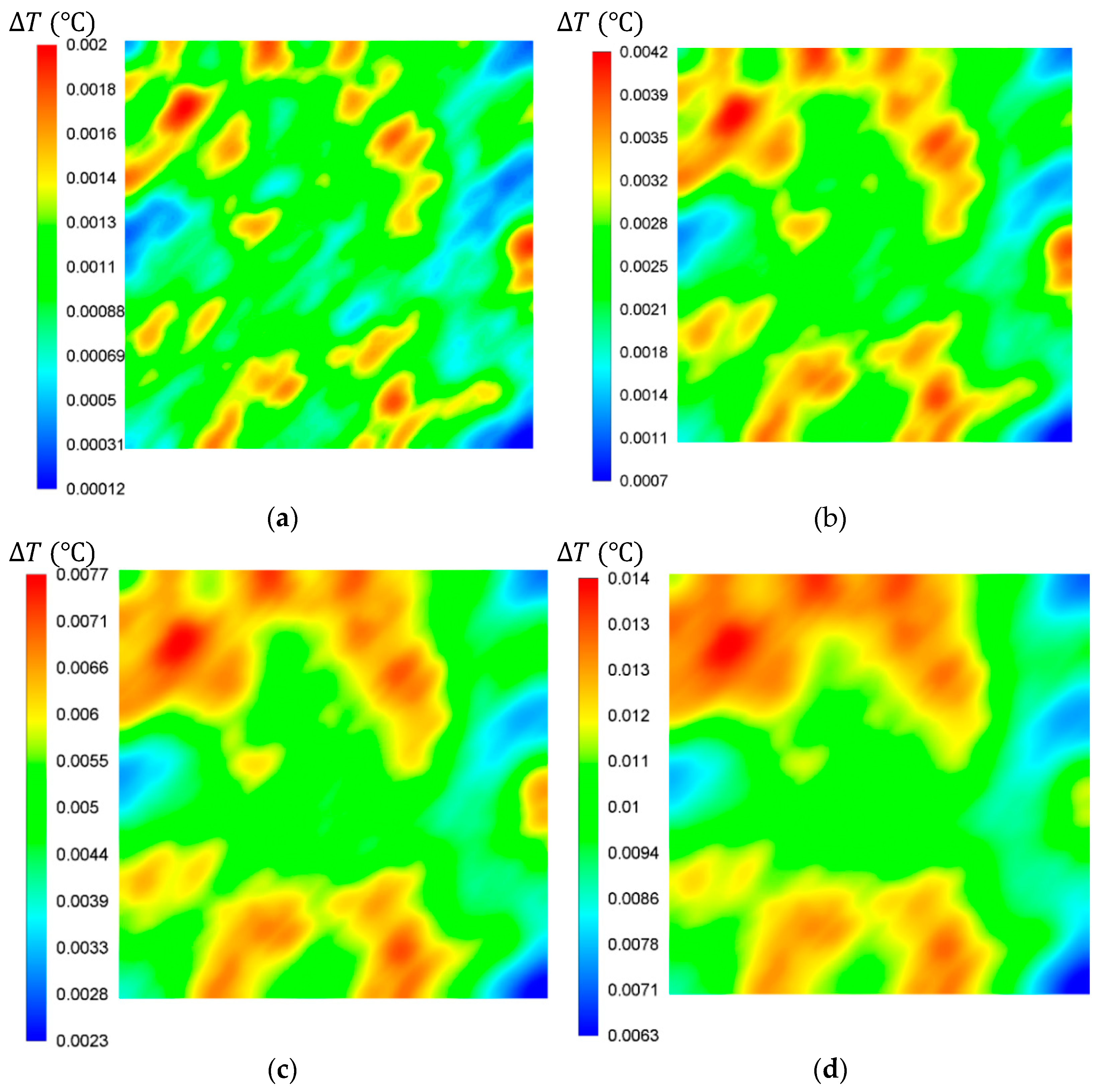
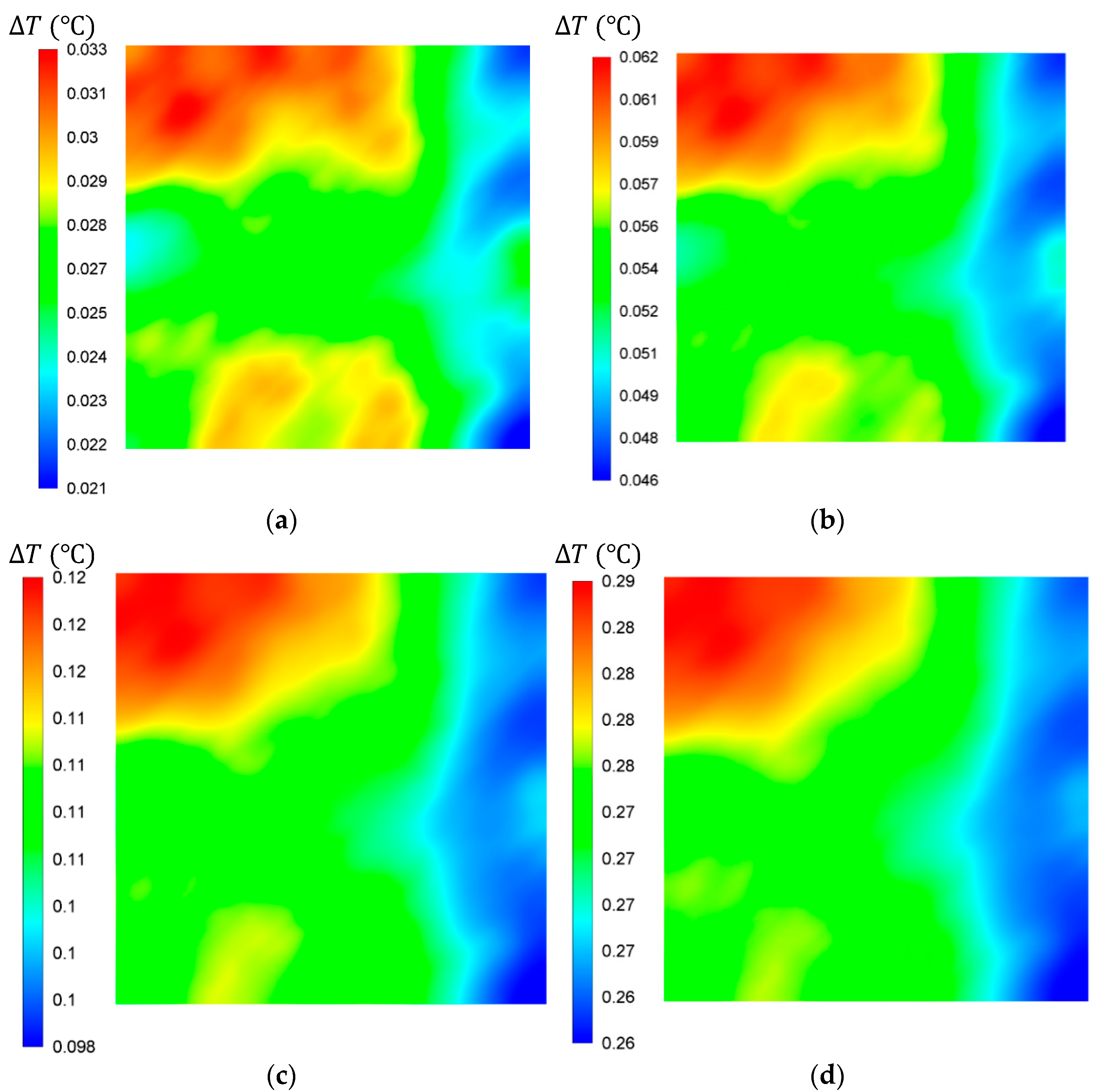
3.4. Heat Generation in an Observation Window of the Sample
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Meaning | Unit |
| absorption cross-sectional area | m2 | |
| extinction cross-sectional area | m2 | |
| projected area | m2 | |
| scattering cross-sectional area | m2 | |
| volumetric material properties of the cell | depends on the represented properties | |
| volumetric material properties of gold | ||
| volumetric material properties of water | ||
| volumetric radiation source term | W/m3 | |
| volume of the cell | m3 | |
| radiative flux | W/m2 | |
| spectral irradiance | W m−2 nm−1 | |
| effective particle radius | m | |
| scattering direction vector | / | |
| absorption efficiency | / | |
| extinction efficiency | / | |
| scattering efficiency | / | |
| scattering coefficient | m−1 | |
| particle volume fraction | / | |
| linear-anisotropic phase function coefficient | / | |
| incident radiation | W/m | |
| radiation intensity | W/m2 | |
| number of dipoles | / | |
| temperature | K | |
| transmittance | / | |
| volume | m3 | |
| specific heat capacity | J/(kg K) | |
| lattice spacing | m3 | |
| thermal conductivity | W/(m K) | |
| refractive index | / | |
| particle radius | m | |
| time | s | |
| diffraction or size parameter | / | |
| solid angle | / | |
| linear absorption coefficient | m−1 | |
| wavelength | nm | |
| density | kg/m3 | |
| Stefan–Boltzmann constant | W/(m2∙K4) | |
| phase function | / |
References
- Svaasand, L.O.; Gomer, C.J.; Morinelli, E. On the Physical Rationale of Laser Induced Hyperthermia. Lasers Med Sci. 1990, 5, 121–128. [Google Scholar] [CrossRef]
- Huang, X.; El-Sayed, M.A. Plasmonic Photo-Thermal Therapy (PPTT). Alex. J. Med. 2011, 47, 1–9. [Google Scholar] [CrossRef]
- Alves, A.F.; Mendo, S.G.; Ferreira, L.P.; Mendonça, M.H.; Ferreira, P.; Godinho, M.; Cruz, M.M.; Carvalho, M.D. Gela-Tine-Assisted Synthesis of Magnetite Nanoparticles for Magnetic Hyperthermia. J. Nanopart. Res. 2016, 18, 1–13. [Google Scholar] [CrossRef]
- Taylor, R.A.; Coulombe, S.; Otanicar, T.; Phelan, P.; Gunawan, A.; Lv, W.; Rosengarten, G.; Prasher, R.; Tyagi, H. Small Particles, Big Impacts: A Review of the Diverse Applications of Nanofluids. J. Appl. Phys. 2013, 113, 1–19. [Google Scholar] [CrossRef]
- Thovhogi, N.; Sibuyi, N.; Meyer, M.; Onani, M.; Madiehe, A. Targeted Delivery Using Peptide-Functionalised Gold Nano-Particles to White Adipose Tissues of Obese Rats. J. Nanopart. Res. 2015, 17, 112–120. [Google Scholar] [CrossRef]
- Pissuwan, D.; Valenzuela, S.M.; Miller, C.M.; Killingsworth, M.C.; Cortie, M.B. Destruction and Control OfToxoplasmagondiiTachyzoites Using Gold Nanosphere/Antibody Conjugates. Small 2009, 5, 1030–1034. [Google Scholar] [CrossRef]
- Hainfeld, J.F.; Lin, L.; Slatkin, D.N.; Dilmanian, F.A.; Vadas, T.M.; Smilowitz, H.M. Gold Nanoparticle Hyperthermia Re-Duces Radiotherapy Dose. Nanomed. Nanotechnol. Biol. Med. 2014, 10, 1609–1617. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Walther, T.; Kleinermanns, K. Influence of Intense Pulsed Laser Irradiation on Optical and Morphological Prop-Erties of Gold Nanoparticle Aggregates Produced by Surface acid− Base Reactions. Langmuir 2005, 21, 4249–4253. [Google Scholar] [CrossRef] [PubMed]
- Li, D.D.; Gu, X.; Timchenko, V.; Chan, Q.N.; Yuen, A.C.Y.; Yeoh, G.-H. Study of Morphology and Optical Properties of Gold Nanoparticle Aggregates under Different PH Conditions. Langmuir 2018, 34, 10340–10352. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.; Timchenko, V.; Yeoh, G.H.; Dombrovsky, L.A.; Taylor, R.A. Heat Generation in Gold Nanorods Solutions Due to Absorption of Near-Infrared Radiation. In Proceedings of the CHT-17 ICHMT International Symposium on Advances in Computational Heat Transfer, Napoli, Italy, 28 May–1 June 2017. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Chen, X.; Xu, H.; Liu, J. Chitosan-Capped Gold Nanoparticles for Selective and Colorimetric Sensing of Heparin. J. Nanoparticle Res. 2013, 15, 1–9. [Google Scholar] [CrossRef]
- Pamies, R.; Cifre, J.G.H.; Espín, V.F.; Collado-González, M.; Baños, F.G.D.; De La Torre, J.G. Aggregation Behaviour of Gold Nanoparticles in Saline Aqueous Media. J. Nanoparticle Res. 2014, 16, 1–11. [Google Scholar] [CrossRef]
- Jain, P.K.; El-Sayed, M.A. Surface Plasmon Coupling and Its Universal Size Scaling in Metal Nanostructures of Complex Geometry: Elongated Particle Pairs and Nanosphere Trimers. J. Phys. Chem. C 2008, 112, 4954–4960. [Google Scholar] [CrossRef]
- Gu, X.; Timchenko, V.; Yeoh, G.H.; Dombrovsky, L.; Taylor, R. The Effect of Gold Nanorods Clustering on Near-Infrared Radiation Absorption. Appl. Sci. 2018, 8, 1132. [Google Scholar] [CrossRef]
- Kattumuri, V.; Katti, K.; Bhaskaran, S.; Boote, E.J.; Casteel, S.W.; Fent, G.M.; Robertson, D.J.; Chandrasekhar, M.; Kannan, R.; Katti, K.V. Gum Arabic As a Phytochemical Construct for the Stabilization of Gold Nanoparticles: In Vivo Pharmacokinetics and X-Ray-Contrast-Imaging Studies. Small 2007, 3, 333–341. [Google Scholar] [CrossRef] [PubMed]
- DeVoe, H. Optical Properties of Molecular Aggregates. I. Classical Model of Electronic Absorption and Refraction. J. Chem. Phys. 1964, 41, 393–400. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. User Guide for the Discrete Dipole Approximation Code DDSCAT 7.3. arXiv 2013, arXiv:1305.6497. [Google Scholar]
- Jain, P.K.; Eustis, S.; El-Sayed, M.A. Plasmon Coupling in Nanorod Assemblies: Optical Absorption, Discrete Dipole Approximation Simulation, and Exciton-Coupling Model. J. Phys. Chem. B 2006, 110, 18243–18253. [Google Scholar] [CrossRef]
- Lee, K.-S.; El-Sayed, M.A. Dependence of the Enhanced Optical Scattering Efficiency Relative to That of Absorption for Gold Metal Nanorods on Aspect Ratio, Size, End-Cap Shape, and Medium Refractive Index. J. Phys. Chem. B 2005, 109, 20331–20338. [Google Scholar] [CrossRef] [PubMed]
- Dombrovsky, L.A. Radiation Heat Transfer in Disperse Systems; Begell House: New York, NY, USA, 1996. [Google Scholar]
- Dombrovsky, L.A.; Timchenko, V.; Pathak, C.; Piazena, H.; Müller, W.; Jackson, M. Radiative Heating of Superficial Human Tissues with the Use of Water-Filtered Infrared-A Radiation: A Computational Modeling. Int. J. Heat Mass Transf. 2015, 85, 311–320. [Google Scholar] [CrossRef]
- Zhang, M.; Kim, H.S.; Jin, T.; Moon, W.K. Near-Infrared Photothermal Therapy Using EGFR-Targeted Gold Nanoparticles in-Creases Autophagic Cell Death in Breast Cancer. J. Photochem. Photobiol. B Biol. 2017, 170, 58–64. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Inc. ANSYS Fluent Theory Guide v17.0; ANSYS Inc.: Park City, UT, USA, 2006. [Google Scholar]
- Dombrovsky, L.A.; Dembele, S.; Wen, J.X.; Sikic, I. Two-Step Method for Radiative Transfer Calculations in a Developing Pool Fire at the Initial Stage of Its Suppression by a Water Spray. Int. J. Heat Mass Transf. 2018, 127, 717–726. [Google Scholar] [CrossRef]
- Meyer, K.R.; Hopwood, L.E.; Gillette, E.L. The Thermal Response of Mouse Adenocarcinoma Cells at Low PH. Eur. J. Cancer 1979, 15, 1219–1222. [Google Scholar] [CrossRef]
- Pampus, F. Die Wasserstoffionenkonzentration Des Hirngewebes Bei Raumfordernden Intracraniellen Prozessen. Acta Neurochir. 1963, 11, 305–318. [Google Scholar] [CrossRef] [PubMed]
- Wike-Hooley, J.; Haveman, J.; Reinhold, H. The Relevance of Tumour PH to the Treatment of Malignant Disease. Radiother. Oncol. 1984, 2, 343–366. [Google Scholar] [CrossRef]







| Particle Cluster Identifier | Particle Structure | ηabs | ηsca |
|---|---|---|---|
| Monomer |  | 0.18 | 2.14 × 10−3 |
| Dimer |  | 0.91 | 1.22 × 10−2 |
| Trimer 3-0 |  | 1.05 | 1.63 × 10−2 |
| Trimer 3-1 |  | 1.45 | 2.64 × 10−2 |
| Tetramer 4-1 |  | 1.57 | 3.67 × 10−2 |
| Tetramer 4-2 |  | 1.60 | 3.15 × 10−2 |
| Tetramer 4-3 |  | 1.29 | 2.20 × 10−2 |
| Tetramer 4-4 |  | 1.48 | 2.64 × 10−2 |
| Sample | pH | Absorbance at λ = 640 nm | Maximum Temperature Increase (°C) | Error of Temperature Measurement (°C) |
|---|---|---|---|---|
| Water | N/A | 0.03 | 13.41 | +0.013 |
| GNP solutions | 3.5 | 0.22 | 23.58 | −0.010 |
| 6.0 | 0.24 | 23.96 | +0.008 | |
| 7.3 | 0.13 | 16.22 | +0.021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, X.; Li, D.D.; Yeoh, G.H.; Taylor, R.A.; Timchenko, V. Heat Generation in Irradiated Gold Nanoparticle Solutions for Hyperthermia Applications. Processes 2021, 9, 368. https://doi.org/10.3390/pr9020368
Gu X, Li DD, Yeoh GH, Taylor RA, Timchenko V. Heat Generation in Irradiated Gold Nanoparticle Solutions for Hyperthermia Applications. Processes. 2021; 9(2):368. https://doi.org/10.3390/pr9020368
Chicago/Turabian StyleGu, Xi, Darson D. Li, Guan H. Yeoh, Robert A. Taylor, and Victoria Timchenko. 2021. "Heat Generation in Irradiated Gold Nanoparticle Solutions for Hyperthermia Applications" Processes 9, no. 2: 368. https://doi.org/10.3390/pr9020368
APA StyleGu, X., Li, D. D., Yeoh, G. H., Taylor, R. A., & Timchenko, V. (2021). Heat Generation in Irradiated Gold Nanoparticle Solutions for Hyperthermia Applications. Processes, 9(2), 368. https://doi.org/10.3390/pr9020368








