Optimal Design and Operation of Multi-Period Water Supply Network with Multiple Water Sources
Abstract
1. Introduction
2. Methodology
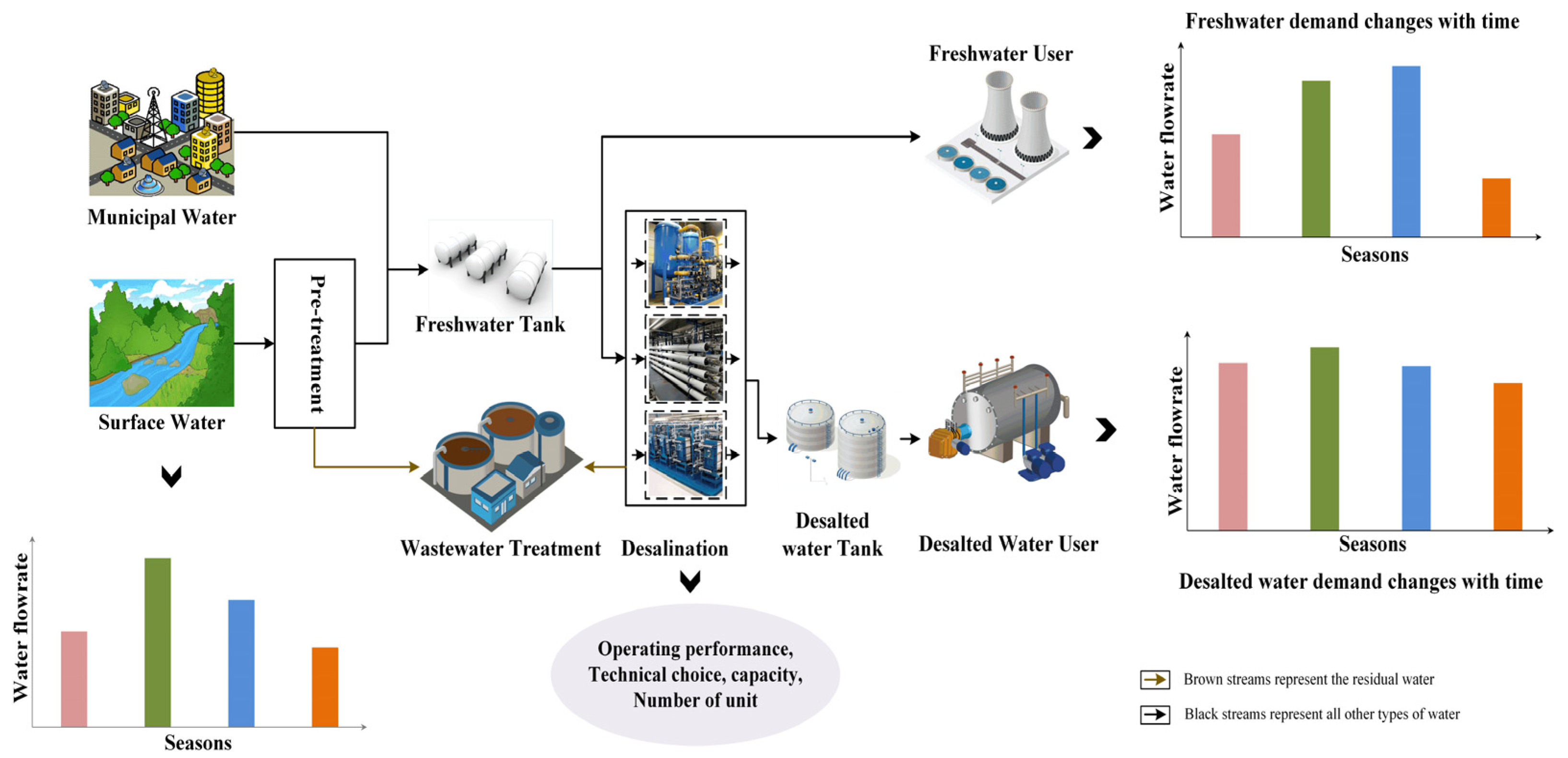
2.1. Problem Statement
2.2. Mathematical Model
2.3. Constraints
2.4. Objective Function
2.5. Model Summary
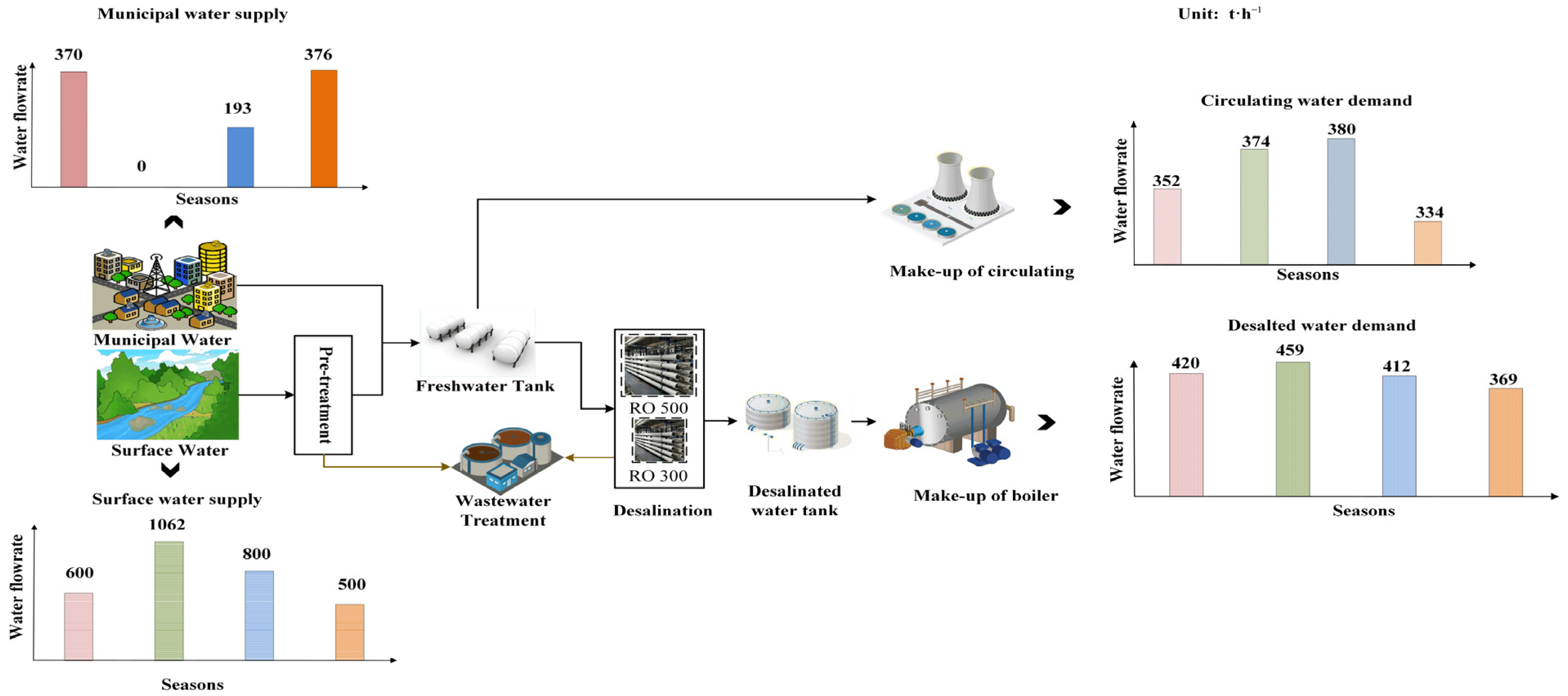
2.6. Case Description
3. Result and Discussion
3.1. Scenario 1—Ignoring Multi-Period Changes in Water Flowrate
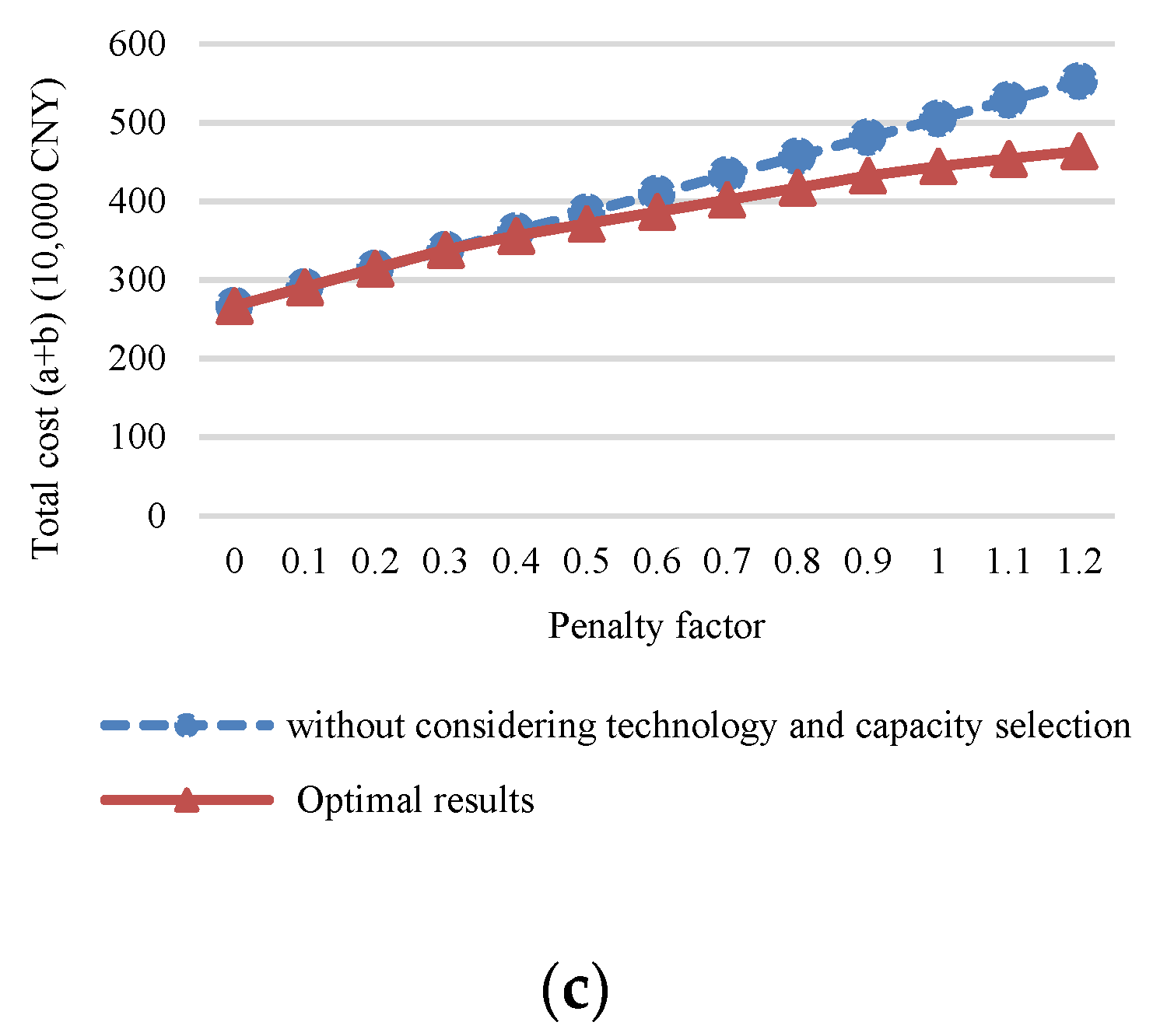
3.2. Scenario 2—Considering Multi-Period Changes in Water Flowrate
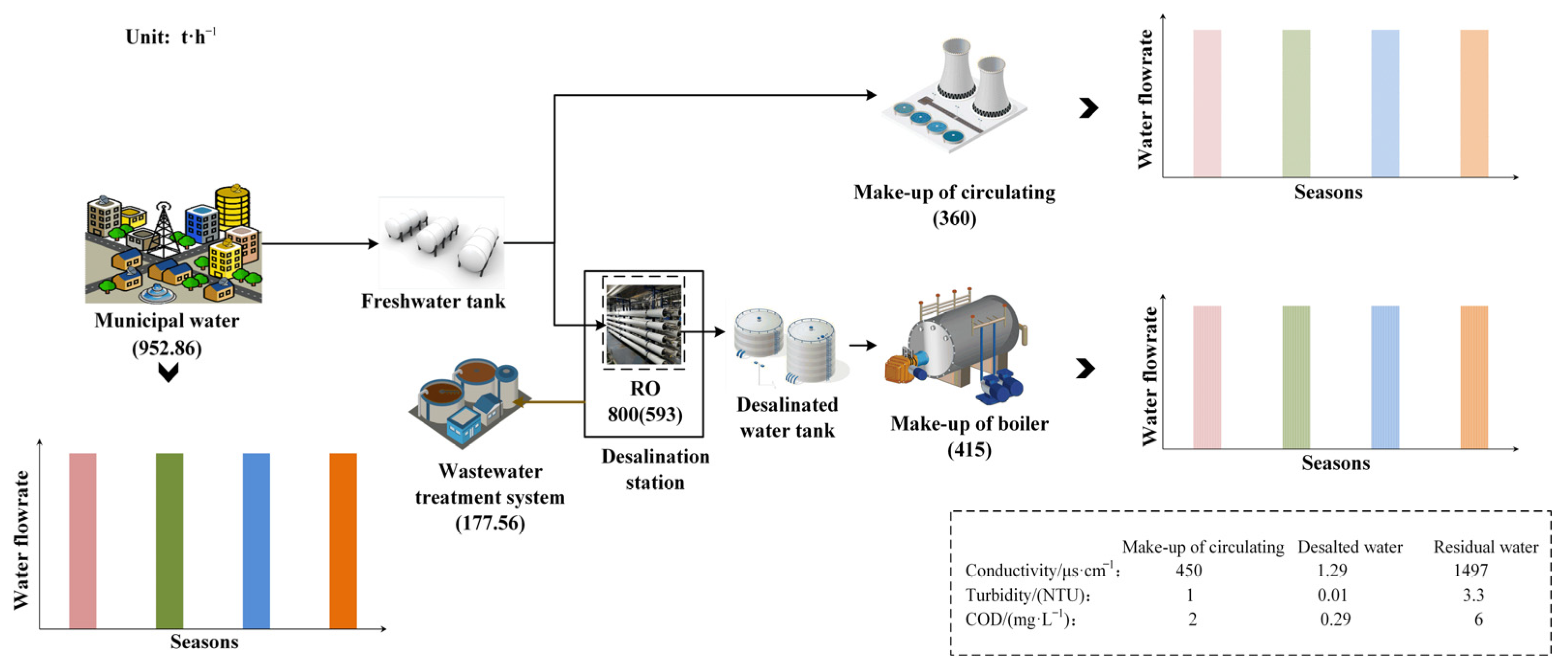
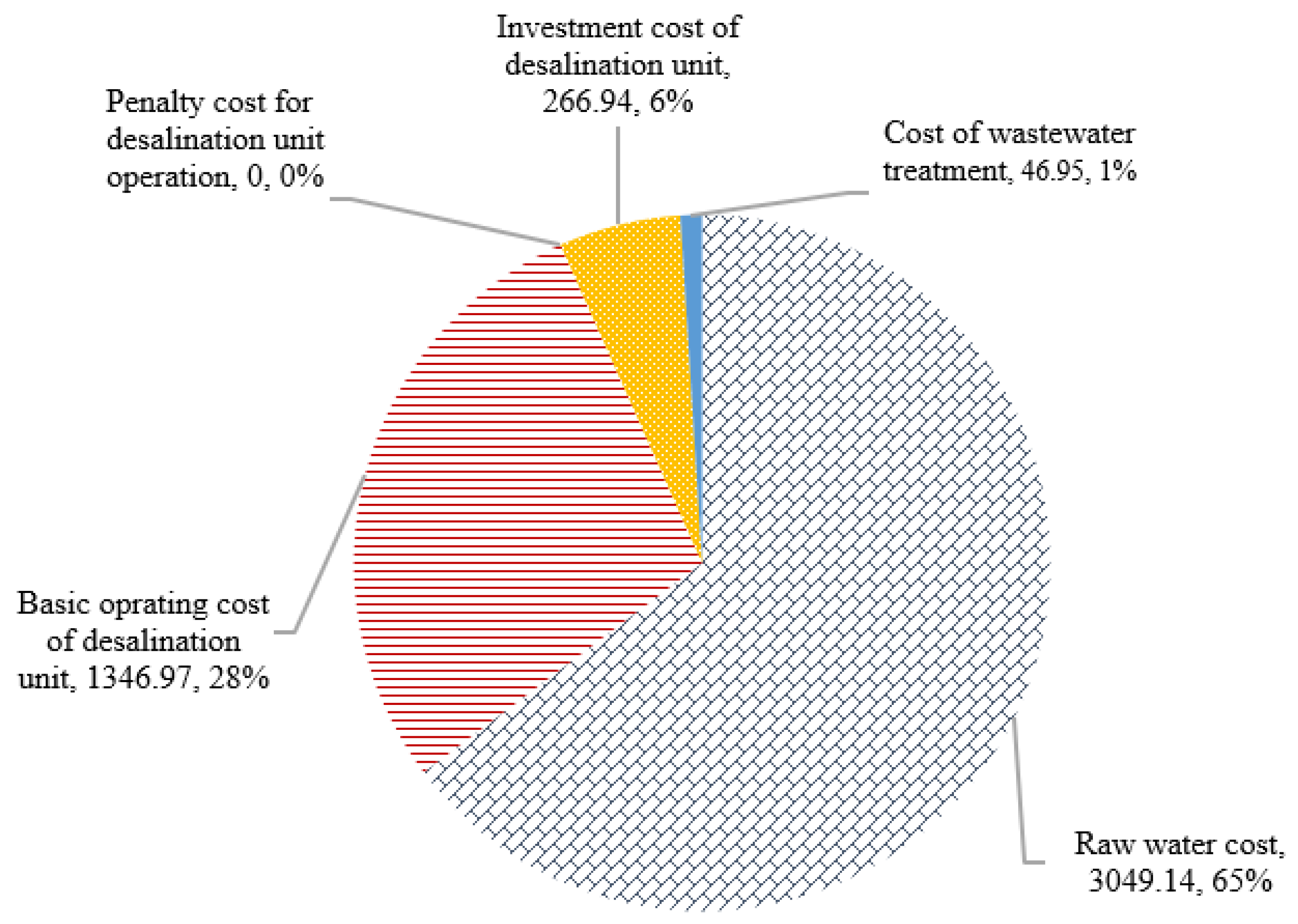
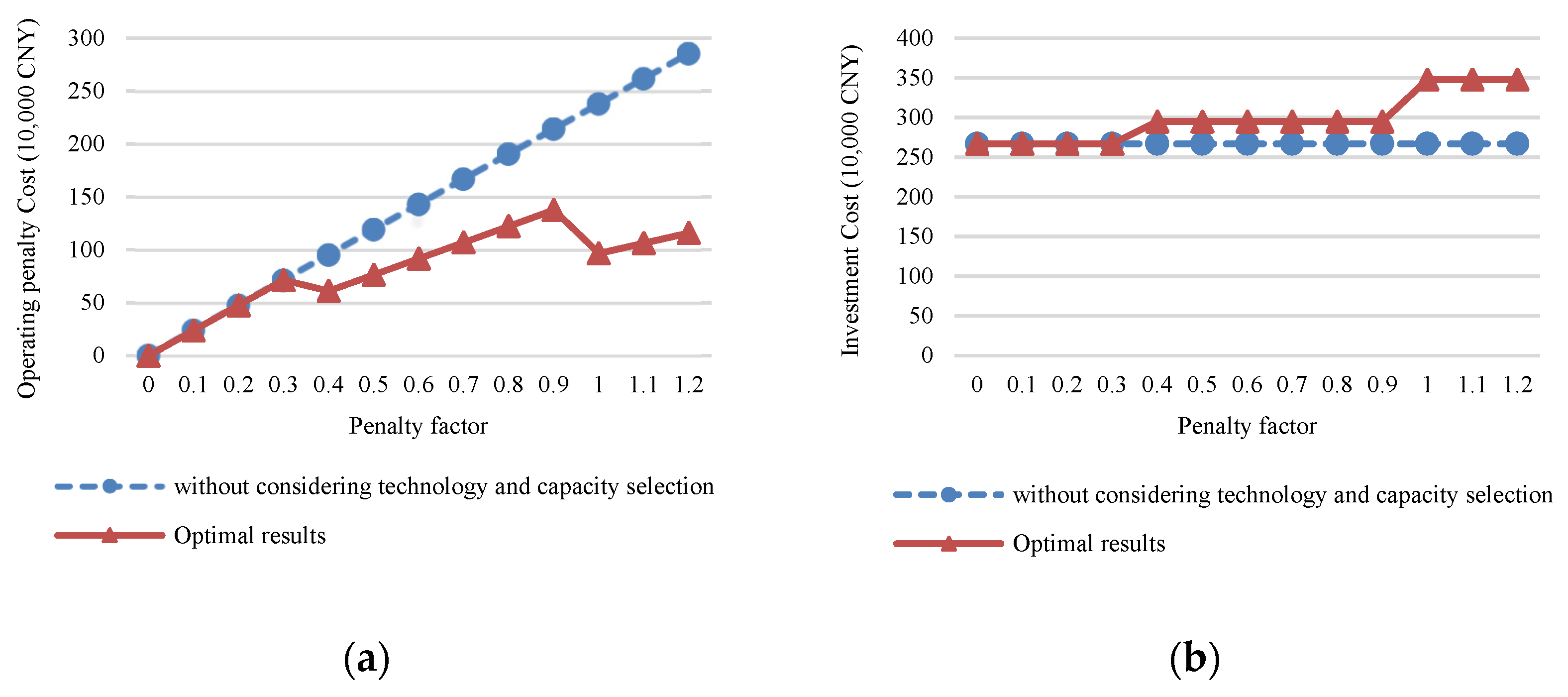
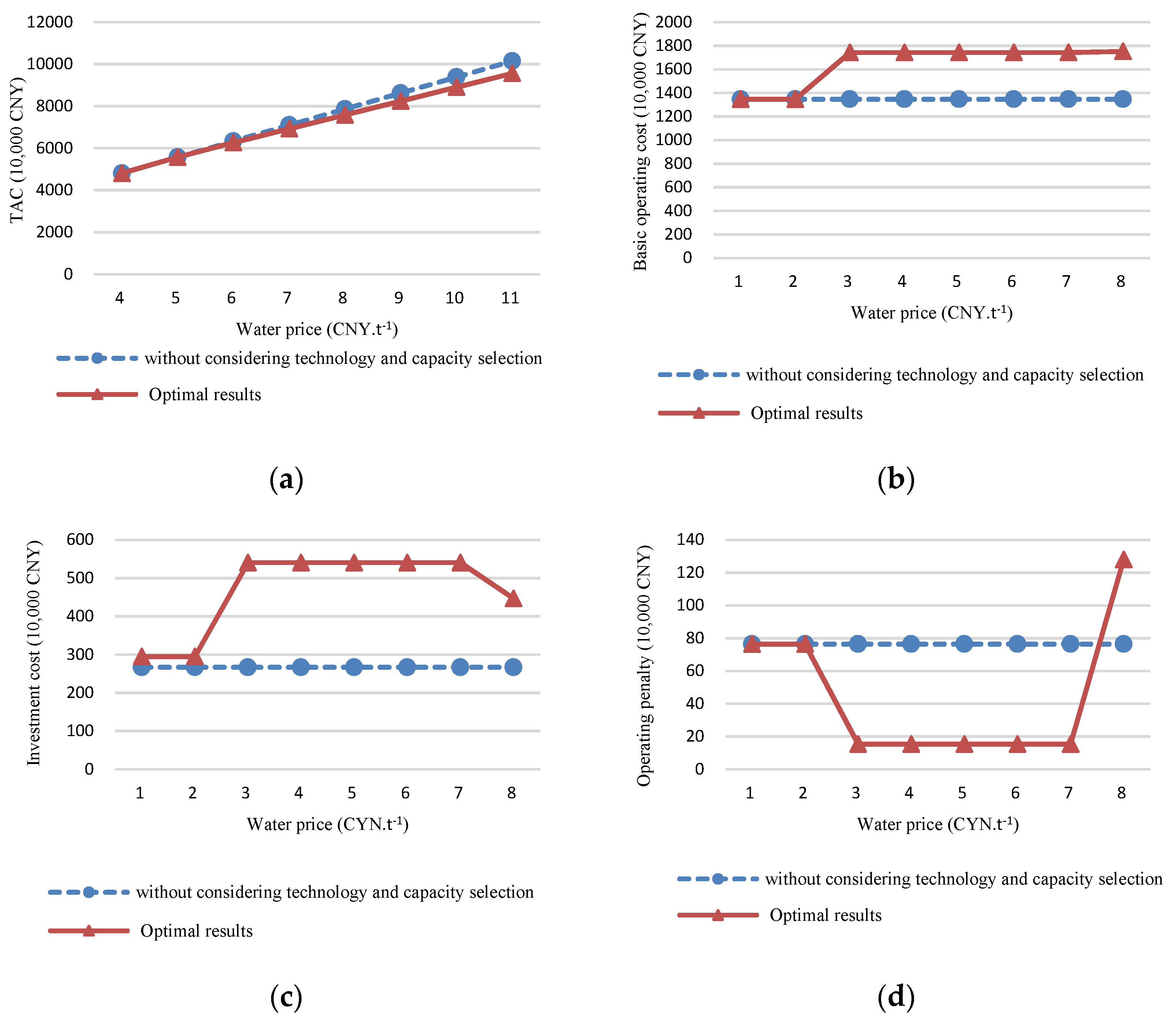
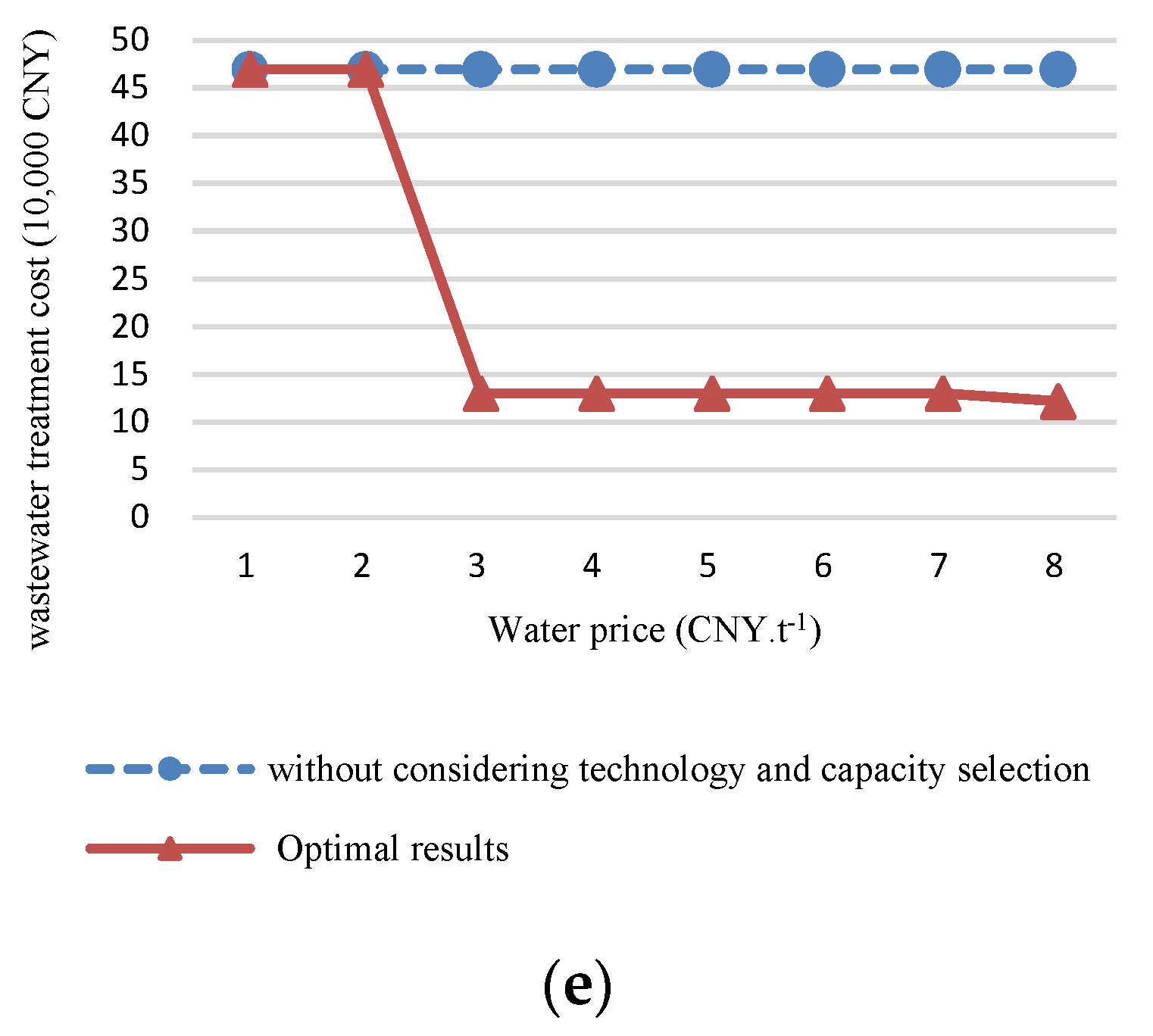
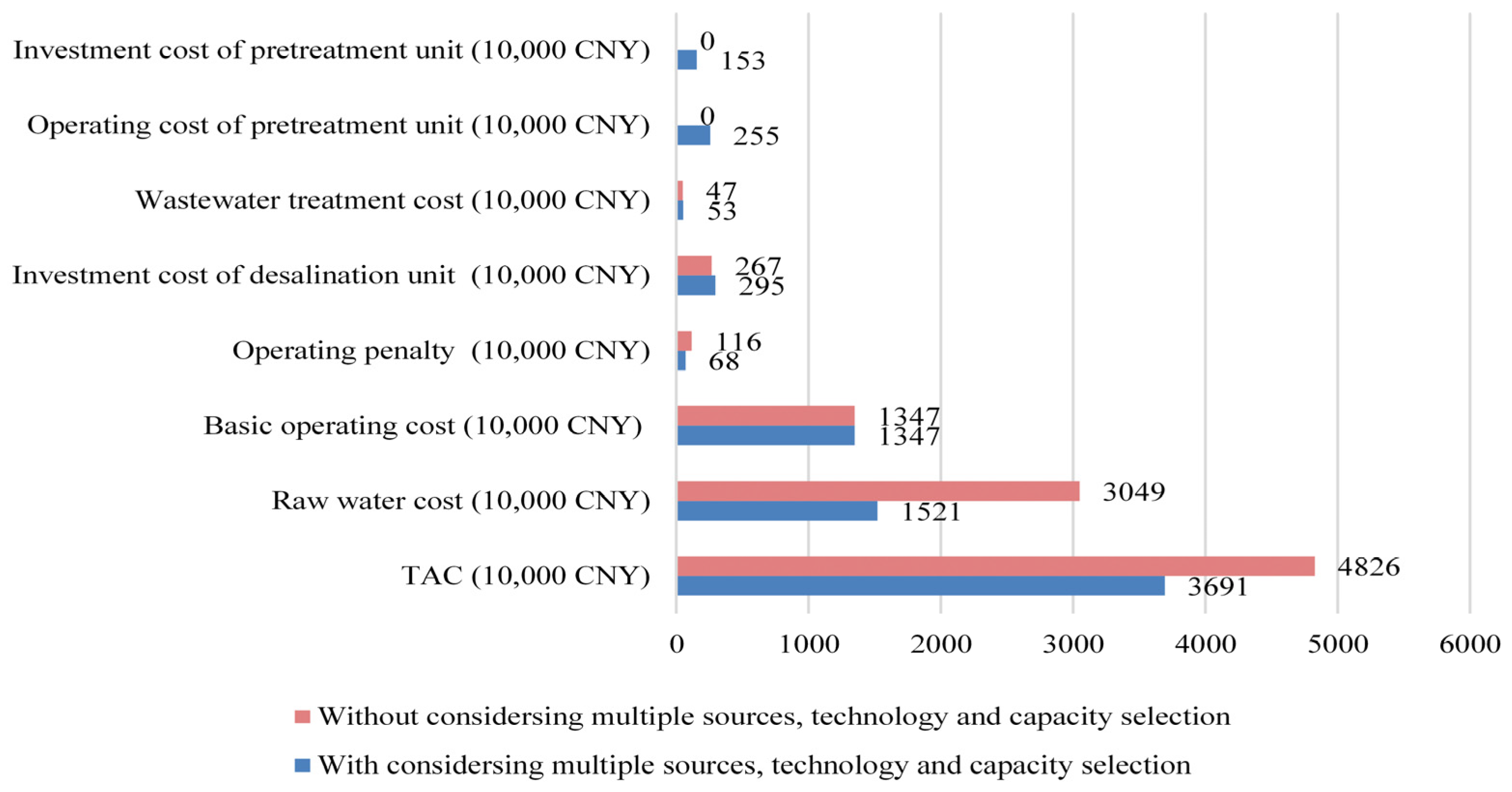
3.3. Scenario 3—Multi-Period Water Supply Network with Multiple Water Sources
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| Abbreviations | |
| COD | chemical oxygen demand |
| DWT | desalination water tank |
| FWT | freshwater tank |
| MW | municipal water |
| RWTS | raw water pre-treatment system |
| SFW | surface water |
| WTS | wastewater treatment system |
| Indexes | |
| dt | desalination system |
| k | water sinks |
| p | water properties |
| r | freshwater resources |
| s | storage tanks |
| t | different time periods |
| Parameters | |
| A | water production ratio |
| Af | annual factor |
| penalty factor | |
| CW | cost of raw water |
| EOC | operating cost |
| EIC | investment cost |
| Fmax | maximum water flowrate |
| M | big enough number |
| PR | installation cost as a percentage of total investment cost |
| RP | removal ratio |
| V | storage tank capacity |
| time length | |
| property operator | |
| β | depreciation factor |
| Set | |
| desalination system | |
| process water sinks | |
| water properties | |
| freshwater resources | |
| storage tanks | |
| different time periods | |
| Superscripts/Subscript | |
| CAP | water capacity |
| dt | desalination unit |
| in | inlet of water sink or treatment unit |
| k | water sink |
| max | maximum value |
| out | outlet of water sink or treatment unit |
| penalty | penalty factor |
| pt | pre-treatment unit |
| prod | product water |
| resd | residual water |
| s | storage tank |
| Variables | |
| water flowrate from r in different time periods, t/h | |
| water flowrate from r to s in different time periods, t/h | |
| inlet water flowrate of pt in different time periods, t/h | |
| product water flowrate from pt in different time periods, t/h | |
| residual water flowrate from pt in different time periods, t/h | |
| inlet water flowrate to s in different time periods, t/h | |
| outlet water flowrate from s in different time periods, t/h | |
| inlet water flowrate of dt in different time periods, t/h | |
| water flowrate from s to k in different time periods, t/h | |
| water flowrate from s to dt in different time periods, t/h | |
| product water flowrate from dt in different time periods, t/h | |
| inlet water flowrate in k in different time periods, t/h | |
| water flowrate from dt to s in different time periods, t/h | |
| residue water flowrate from pt to s in different time periods, t/h | |
| residue water flowrate from dt to k in different time periods, t/h | |
| water property operator at the inlet of pt in different time periods | |
| product water property operator of pt in different time periods | |
| residual water property operator of pt in different time periods | |
| inlet water property operator of s in different time periods | |
| outlet water property operator of s in different time periods | |
| water property operator from r in different time periods | |
| inlet water property operator of dt in different time period | |
| outlet water property operator of s in different time periods | |
| y | binary variable |
References
- Gleick, P.H. Global Freshwater Resources: Soft-Path Solutions for the 21st Century. Science 2003, 302, 1524–1528. [Google Scholar] [CrossRef]
- Hanjra, M.A.; Qureshi, M.E. Global Water Crisis and Future Food Security in an Era of Climate Change. Food Policy 2010, 35, 365–377. [Google Scholar] [CrossRef]
- Gu, S.; Jenkins, A.; Gao, S.-J.; Lu, Y.; Li, H.; Li, Y.; Ferrier, R.C.; Bailey, M.; Wang, Y.; Zhang, Y. Ensuring Water Resource Security in China; the Need for Advances in Evidence-Based Policy to Support Sustainable Management. Environ. Sci. Policy 2017, 75, 65–69. [Google Scholar] [CrossRef]
- Yuan, F.; Wei, Y.D.; Gao, J.; Chen, W. Water Crisis, Environmental Regulations and Location Dynamics of Pollution-Intensive Industries in China: A Study of the Taihu Lake Watershed. J. Clean. Prod. 2019, 216, 311–322. [Google Scholar] [CrossRef]
- Yu, W.; Haimes, Y.Y. Multilevel Optimization for Conjunctive Use of Groundwater and Surface Water. Water Resour. Res. 1974, 10, 625–636. [Google Scholar] [CrossRef]
- Ashwell, N.E.Q.; Peterson, J.M.; Hendricks, N.P. Optimal Groundwater Management under Climate Change and Technical Progress. Resour. Energy Econ. 2018, 51, 67–83. [Google Scholar] [CrossRef]
- Watkins, D.; McKinney, D.C. Robust Optimization for Incorporating Risk and Uncertainty in Sustainable Water Resources Planning. IAHS Publ.-Ser. Proc. Rep.-Intern Assoc Hydrol. Sci. 1995, 231, 225–232. [Google Scholar]
- Yu, L.; Xiao, Y.; Zeng, X.; Li, Y.; Fan, Y. Planning Water-Energy-Food Nexus System Management under Multi-Level and Uncertainty. J. Clean. Prod. 2020, 251, 119658. [Google Scholar] [CrossRef]
- Fu, Z.; Zhao, H.; Wang, H.; Lu, W.; Wang, J.; Guo, H. Integrated Planning for Regional Development Planning and Water Resources Management under Uncertainty: A Case Study of Xining, China. J. Hydrol. 2017, 554, 623–634. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, Y.; Wu, B.; Tian, Y.; Han, F.; Zheng, C. Optimizing Conjunctive Use of Surface Water and Groundwater for Irrigation to Address Human-Nature Water Conflicts: A Surrogate Modeling Approach. Agric. Water Manag. 2016, 163, 380–392. [Google Scholar] [CrossRef]
- Fazlollahi, S.; Bungener, S.L.; Mandel, P.; Becker, G.; Maréchal, F. Multi-Objectives, Multi-Period Optimization of District Energy Systems: I. Selection of Typical Operating Periods. Comput. Chem. Eng. 2014, 65, 54–66. [Google Scholar] [CrossRef]
- Bungener, S.; Hackl, R.; Van Eetvelde, G.; Harvey, S.; Marechal, F. Multi-Period Analysis of Heat Integration Measures in Industrial Clusters. Energy 2015, 93, 220–234. [Google Scholar] [CrossRef]
- Ahmad, M.I.; Zhang, N.; Jobson, M.; Chen, L. Multi-Period Design of Heat Exchanger Networks. Chem. Eng. Res. Des. 2012, 90, 1883–1895. [Google Scholar] [CrossRef]
- Almansoori, A.; Shah, N. Design and Operation of a Future Hydrogen Supply Chain: Multi-Period Model. Int. J. Hydrogen Energy 2009, 34, 7883–7897. [Google Scholar] [CrossRef]
- Ahmad, M.I.; Zhang, N.; Jobson, M. Modelling and Optimisation for Design of Hydrogen Networks for Multi-Period Operation. J. Clean. Prod. 2010, 18, 889–899. [Google Scholar] [CrossRef]
- Liang, X.; Kang, L.; Liu, Y. The Flexible Design for Optimization and Debottlenecking of Multiperiod Hydrogen Networks. Ind. Eng. Chem. Res. 2016, 55, 2574–2583. [Google Scholar] [CrossRef]
- Betancourt-Torcat, A.; Almansoori, A. Multi-Period Optimization Model for the UAE Power Sector. Energy Procedia 2015, 75, 2791–2797. [Google Scholar] [CrossRef][Green Version]
- Gupta, V.; Grossmann, I.E. An Efficient Multiperiod MINLP Model for Optimal Planning of Offshore Oil and Gas Field Infrastructure. Ind. Eng. Chem. Res. 2012, 51, 6823–6840. [Google Scholar] [CrossRef]
- Faria, D.C.; Bagajewicz, M.J. Planning Model for the Design and/or Retrofit of Industrial Water Systems. Ind. Eng. Chem. Res. 2011, 50, 3788–3797. [Google Scholar] [CrossRef]
- Burgara-Montero, O.; Ponce-Ortega, J.M.; Serna-González, M.; El-Halwagi, M.M. Incorporation of the Seasonal Variations in the Optimal Treatment of Industrial Effluents Discharged to Watersheds. Ind. Eng. Chem. Res. 2013, 52, 5145–5160. [Google Scholar] [CrossRef]
- Rojas-Torres, M.G.; Nápoles-Rivera, F.; Ponce-Ortega, J.M.; Serna-González, M.; El-Halwagi, M.M. Optimal Design of Sustainable Water Systems for Cities Involving Future Projections. Comput. Chem. Eng. 2014, 69, 1–15. [Google Scholar] [CrossRef]
- Lira-Barragán, L.F.; Ponce-Ortega, J.M.; Guillén-Gosálbez, G.; El-Halwagi, M.M. Optimal Water Management under Uncertainty for Shale Gas Production. Ind. Eng. Chem. Res. 2016, 55, 1322–1335. [Google Scholar] [CrossRef]
- Tosarkani, B.M.; Amin, S.H. A Robust Optimization Model for Designing a Wastewater Treatment Network under Uncertainty: Multi-Objective Approach. Comput. Ind. Eng. 2020, 146, 106611. [Google Scholar] [CrossRef]
- Boix, M.; Montastruc, L.; Pibouleau, L.; Azzaro-Pantel, C.; Domenech, S. Industrial Water Management by Multiobjective Optimization: From Individual to Collective Solution through Eco-Industrial Parks. J. Clean. Prod. 2012, 22, 85–97. [Google Scholar] [CrossRef]
- Bishnu, S.K.; Linke, P.; Alnouri, S.Y.; El-Halwagi, M. Multiperiod Planning of Optimal Industrial City Direct Water Reuse Networks. Ind. Eng. Chem. Res. 2014, 53, 8844–8865. [Google Scholar] [CrossRef]
- Arredondo-Ramírez, K.; Rubio-Castro, E.; Nápoles-Rivera, F.; Ponce-Ortega, J.M.; Serna-González, M.; El-Halwagi, M.M. Optimal Design of Agricultural Water Systems with Multiperiod Collection, Storage, and Distribution. Agric. Water Manag. 2015, 152, 161–172. [Google Scholar] [CrossRef]
- Leong, Y.T.; Lee, J.-Y.; Chew, I.M.L. Incorporating Timesharing Scheme in Ecoindustrial Multiperiod Chilled and Cooling Water Network Design. Ind. Eng. Chem. Res. 2016, 55, 197–209. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Song, H.; Du, J.; Yang, F. Multi-Period Water Network Management for Industrial Parks Considering Predictable Variations. Comput. Chem. Eng. 2017, 104, 172–184. [Google Scholar] [CrossRef]
- Ang, M.S.; Duyag, J.; Tee, K.C.; Sy, C.L. A Multi-Period and Multi-Criterion Optimization Model Integrating Multiple Input Configurations, Reuse, and Disposal Options for a Wastewater Treatment Facility. J. Clean. Prod. 2019, 231, 1437–1449. [Google Scholar] [CrossRef]
- Pérez-Uresti, S.I.; Ponce-Ortega, J.M.; Jiménez-Gutiérrez, A. A Multi-Objective Optimization Approach for Sustainable Water Management for Places with over-Exploited Water Resources. Comput. Chem. Eng. 2019, 121, 158–173. [Google Scholar] [CrossRef]
- Nápoles-Rivera, F.; Ponce-Ortega, J.M.; El-Halwagi, M.M.; Jiménez-Gutiérrez, A. Global Optimization of Mass and Property Integration Networks with In-Plant Property Interceptors. Chem. Eng. Sci. 2010, 65, 4363–4377. [Google Scholar] [CrossRef]
- El-Halwagi, M.M.; Glasgow, I.M.; Qin, X.; Eden, M.R. Property Integration: Componentless Design Techniques and Visualization Tools. AIChE J. 2004, 50, 1854–1869. [Google Scholar] [CrossRef]
| Item | IX | RO |
|---|---|---|
| Investment economy scale factor | 0.85 | |
| Annual factor of investment costs | 0.094 | |
| PR (%) | 40 | 25 |
| Cost factor IC (104 CNY) | 14.77 | 7.74 |
| Water production ratio | 0.9 | 0.7 |
| Conductivity removal rate | 0.995 | 0.998 |
| Turbidity removal rate | 0 | 0.99 |
| COD removal rate | 0 | 0.9 |
| Rated ton water treatment cost (CNY·t−1) | 4.75 | 2.84 |
| Available treatment capacities (t·h−1) | 250, 400, 600 | 300, 500, 800 |
| Season | First | Second | Third | Fourth | Mean |
|---|---|---|---|---|---|
| Minimum demand of desalted water (t·h−1) | 420 | 459 | 412 | 369 | 415 |
| Minimum demand of circulating water (t·h−1) | 352 | 374 | 380 | 334 | 360 |
| Maximum supply of municipal water (t·h−1) | - | - | - | - | - |
| Maximum supply of surface water (t·h−1) | 600 | 1500 | 800 | 500 | 925 |
| Properties | MW | SFW | FW | DW |
|---|---|---|---|---|
| Upper Bound | Upper Bound | |||
| Turbidity/(NTU) | 1 | 7 | 3 | 1 |
| Conductivity/μs·cm−1 | 450 | 590 | 1000 | 5 |
| COD/(mg·L−1) | 2 | 12 | 5 | 5 |
| Penalty Factor α | 0–0.3 | ||||
|---|---|---|---|---|---|
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 800 | Actual intake (t·h−1) | 592.86 | 592.86 | 592.86 | 592.86 |
| Penalty factor α | 0.4–0.9 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 500 | Actual intake (t·h−1) | 450 | 450 | 450 | 450 |
| RO, 300 | 142.86 | 142.86 | 142.86 | 142.86 | |
| Penalty factor α | ≥1.0 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 300 | Actual intake (t·h−1) | 270 | 270 | 270 | 270 |
| RO, 300 | 270 | 270 | 270 | 270 | |
| RO, 300 | 52.86 | 52.86 | 52.86 | 52.86 | |
| Municipal Water Price (CNY·t−1) | 4–5 | ||||
|---|---|---|---|---|---|
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 500 | Actual intake (t·h−1) | 450 | 450 | 450 | 450 |
| RO, 300 | 142.86 | 142.86 | 142.86 | 142.86 | |
| Municipal water price (CNY·t−1) | 6–10 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| IX, 250 | Actual intake (t·h−1) | 225 | 225 | 225 | 225 |
| IX, 250 | 225 | 225 | 225 | 225 | |
| RO, 300 | 14.29 | 14.29 | 14.29 | 14.29 | |
| Municipal water price (CNY·t−1) | ≥11 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| IX, 600 | Actual intake (t·h−1) | 461.11 | 461.11 | 461.11 | 461.11 |
| Penalty Factor α | 0–0.2 | ||||
|---|---|---|---|---|---|
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 800 | Actual intake (t·h−1) | 600 | 655.71 | 588.57 | 527.14 |
| Penalty factor α | 0.3–1.2 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 500 | Actual intake (t·h−1) | 450 | 450 | 450 | 450 |
| RO, 300 | 150 | 205.71 | 138.57 | 77.14 | |
| Penalty factor α | ≥1.3 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 300 | Actual intake (t·h−1) | 270 | 270 | 270 | 270 |
| RO, 300 | 270 | 270 | 270 | 270 | |
| RO, 300 | 60 | 115.71 | 48.57 | 0 | |
| Municipal Water Price (CNY·t−1) | 4–5 | ||||
|---|---|---|---|---|---|
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| RO, 500 | Treatment capacity (t·h−1) | 450 | 450 | 450 | 450 |
| RO, 300 | 150 | 205.71 | 138.57 | 77.14 | |
| Municipal water price (CNY·t−1) | 6 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| IX, 400 | Treatment capacity (t·h−1) | 360 | 360 | 360 | 360 |
| RO, 300 | 137.14 | 192.86 | 125.71 | 64.29 | |
| Municipal water price (CNY·t−1) | ≥7 | ||||
| Technology, design capacity (t·h−1) | Period | T1 | T2 | T3 | T4 |
| IX, 600 | Treatment capacity (t·h−1) | 466.67 | 510 | 457.78 | 410 |
| Period | T1 | T2 | T3 | T4 | |
|---|---|---|---|---|---|
| Makeup of circulating water | Conductivity (μs·cm−1) | 546.74 | 608.25 | 576.79 | 539.13 |
| Turbidity (NTU) | 0.48 | 0.14 | 0.31 | 0.52 | |
| COD (mg·L−1) | 2.29 | 2.47 | 2.38 | 2.27 | |
| Desalted water | Conductivity (μs·cm−1) | 1.56 | 1.74 | 1.65 | 1.54 |
| Turbidity (NTU) | 0.01 | 0.00 | 0.00 | 0.01 | |
| COD (mg·L−1) | 0.33 | 0.35 | 0.34 | 0.32 | |
| Wastewater | Conductivity (μs·cm−1) | 1653.49 | 1741.50 | 1689.17 | 1638.12 |
| Turbidity (NTU) | 22.22 | 32.27 | 28.28 | 21.37 | |
| COD (mg·L−1) | 35.34 | 50.98 | 44.58 | 33.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Iqbal, K.; Lv, X.; Deng, C. Optimal Design and Operation of Multi-Period Water Supply Network with Multiple Water Sources. Processes 2021, 9, 2143. https://doi.org/10.3390/pr9122143
Zhou W, Iqbal K, Lv X, Deng C. Optimal Design and Operation of Multi-Period Water Supply Network with Multiple Water Sources. Processes. 2021; 9(12):2143. https://doi.org/10.3390/pr9122143
Chicago/Turabian StyleZhou, Wenjin, Kashif Iqbal, Xiaoming Lv, and Chun Deng. 2021. "Optimal Design and Operation of Multi-Period Water Supply Network with Multiple Water Sources" Processes 9, no. 12: 2143. https://doi.org/10.3390/pr9122143
APA StyleZhou, W., Iqbal, K., Lv, X., & Deng, C. (2021). Optimal Design and Operation of Multi-Period Water Supply Network with Multiple Water Sources. Processes, 9(12), 2143. https://doi.org/10.3390/pr9122143







