Parameter Identification of a Quasi-3D PEM Fuel Cell Model by Numerical Optimization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model and Governing Equations
2.1.1. Governing Equations
Species Transport in Gas Channels
Species Transport in GDLs
Electrochemical Reactions
Ionic Conductivity
2.2. Numerical Optimization
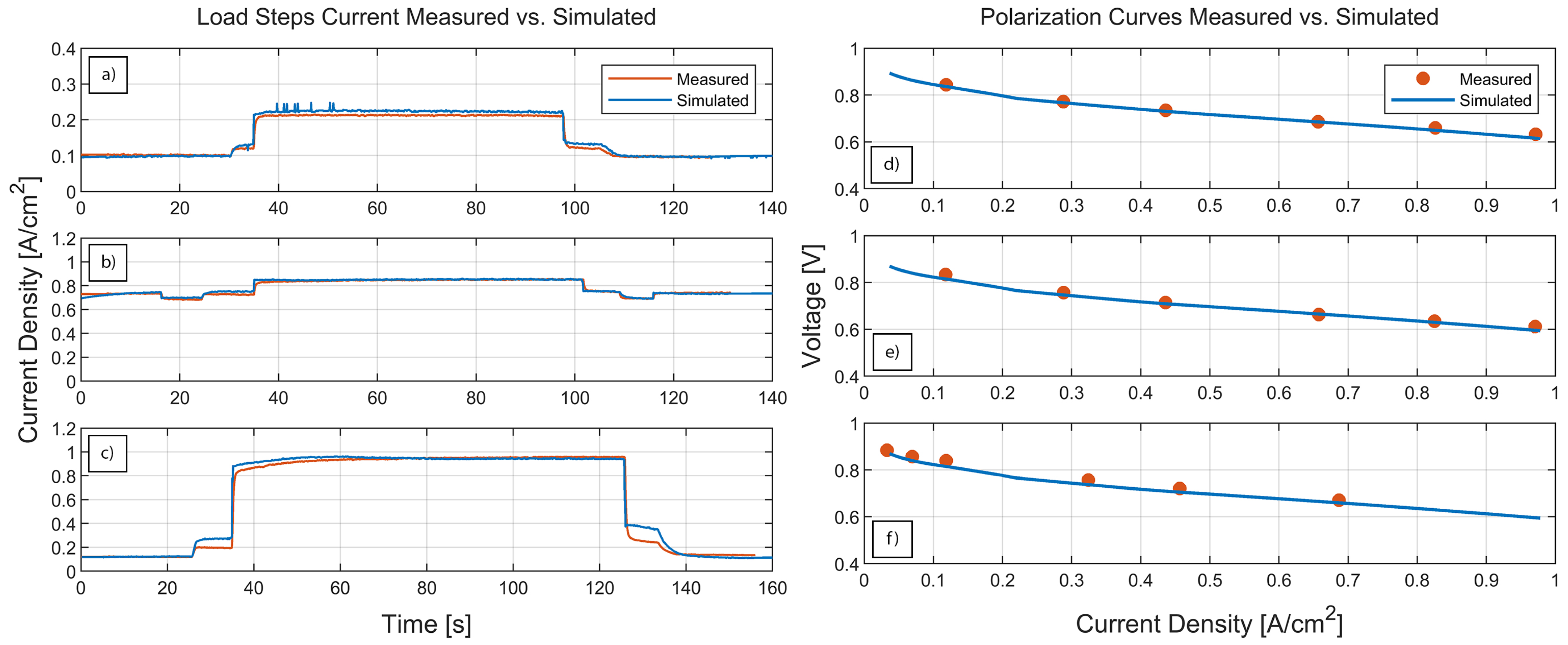
2.3. Experimental Results
- L1 is recorded with cell potential from 844 to 792 to 844
- L2 is recorded with cell potential from 666 to 640 to 666
- L3 is recorded with cell potential from 834 to 630 to 834
3. Results
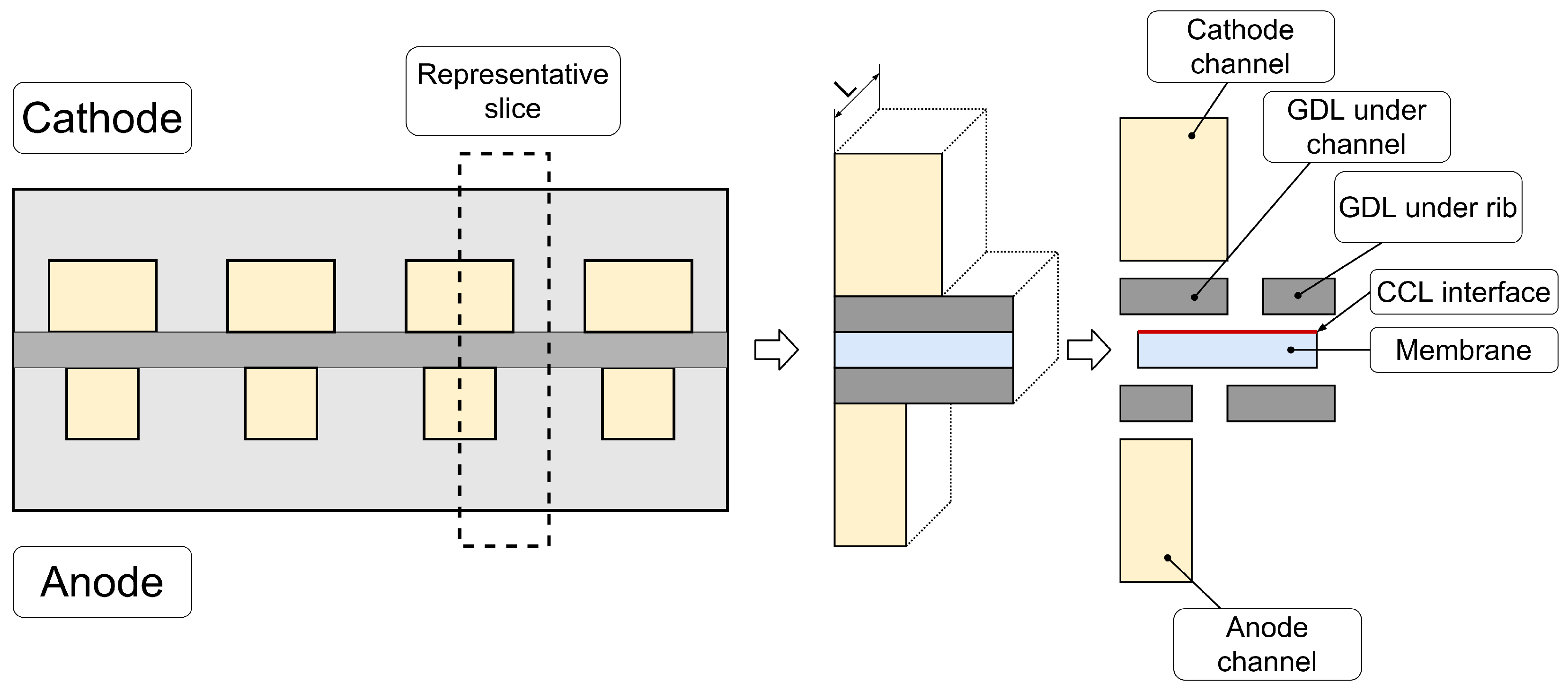
3.1. Hybrid 3D Model Details
Parameterization
3.2. Optimization
3.2.1. Activation Energies
3.2.2. Reference Exchange Current Density and Transfer Coefficient
Ionic Conductivity
3.2.3. GDL Electrical Conductivity
3.2.4. GDL Porosity and Tortuosity
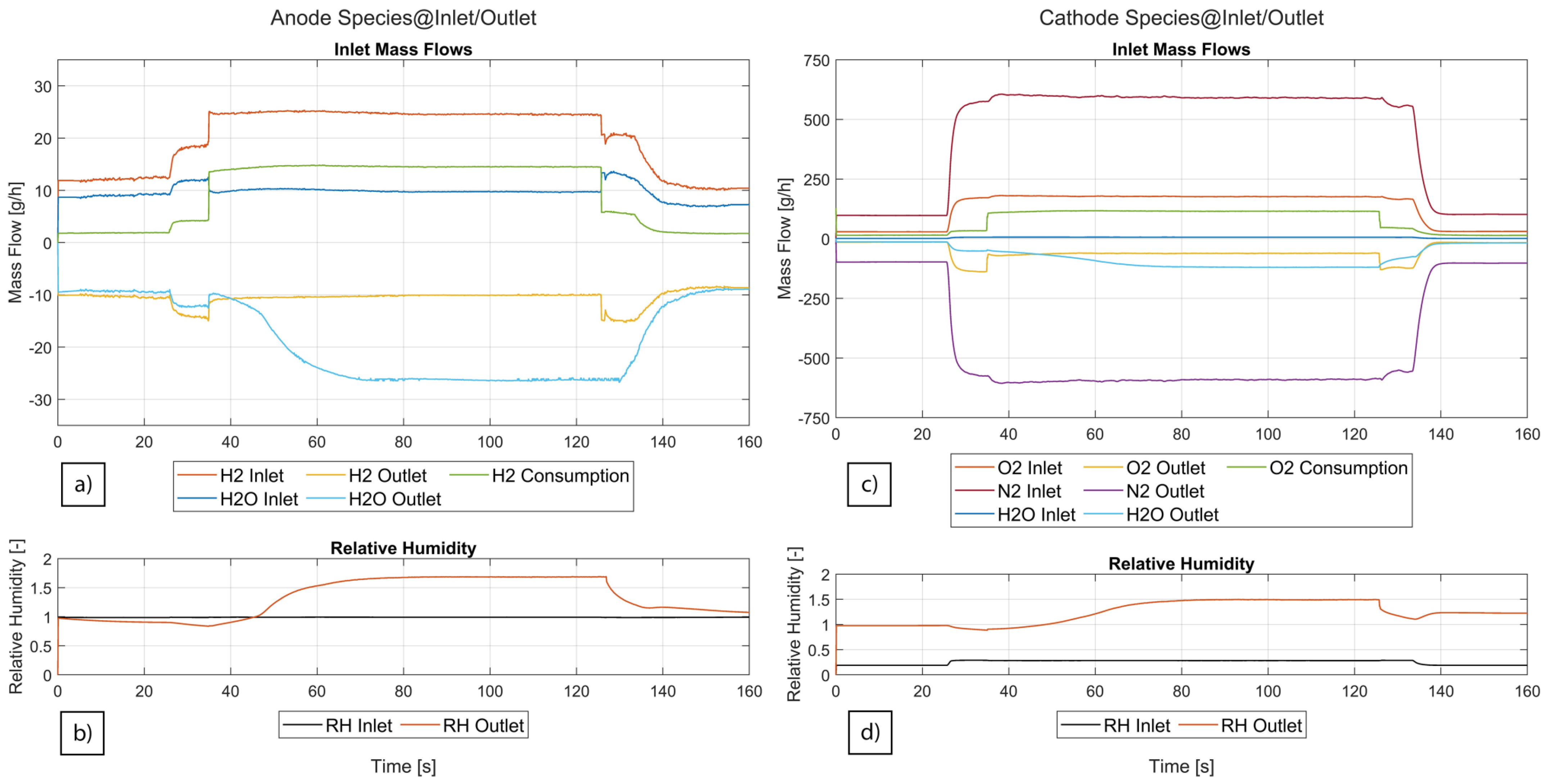
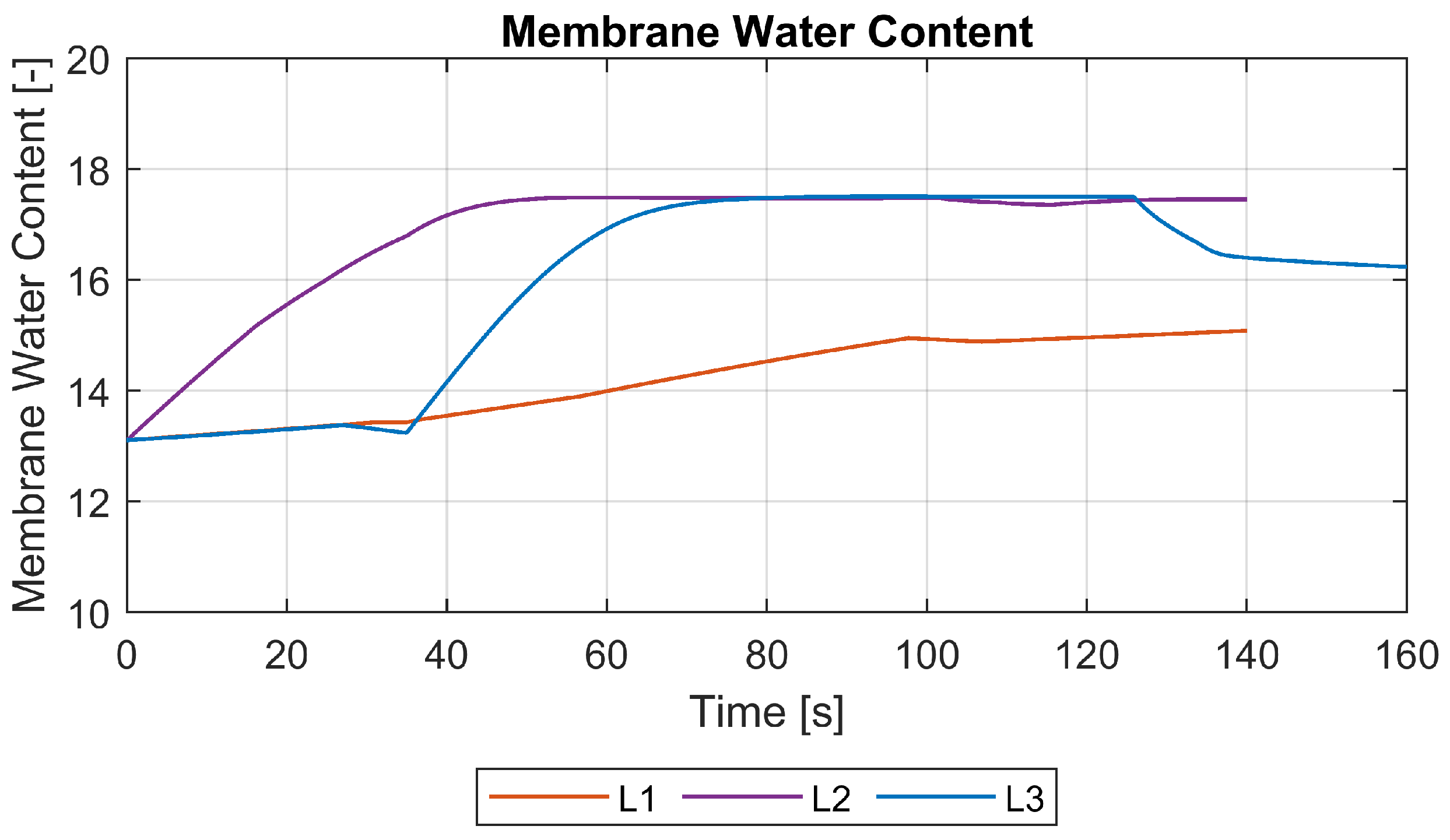
3.3. Species Mass Flows and Membrane Water Content
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACL | Anode Catalyst Layer |
| BPP | Bipolar Plate |
| BVE | Butler–Volmer Equation |
| CCL | Cathode Catalyst Layer |
| CL | Catalyst Layer |
| FC | Fuel Cell |
| GDL | Gas Diffusion Layer |
| GHG | Greenhouse Gases |
| LHS | Latin Hypercube Sampling |
| LSC | Long Side Chain |
| NMSA | Nelder–Mead Simplex Algorithm |
| PEM | Polymer Electrolyte Membrane |
| PEMFC | Polymer Electrolyte Membrane Fuel Cell |
| PFSA | Perfluoronated Sulfonic Acid |
| RECD | Reference Exchange Current Density |
| SSC | Short Side Chain |
| Reference ionic conductivity | |
| Activation energy ionic conductivity | |
| RECD CCL | |
| Activation energy RECD | |
| Transfer coefficient CCL | |
| GDL porosity | |
| GDL tortuosity | |
| Electrical conductivity | |
| Stoichiometric factor | |
| D | Diffusion coefficient |
| Membrane water content | |
| U | Electric potential |
References
- Bethoux, O. Hydrogen Fuel Cell Road Vehicles: State of the Art and Perspectives. Energies 2020, 13, 5843. [Google Scholar] [CrossRef]
- Ritzberger, D.; Hametner, C.; Jakubek, S. A Real-Time Dynamic Fuel Cell System Simulation for Model-Based Diagnostics and Control: Validation on Real Driving Data. Energies 2020, 13, 3148. [Google Scholar] [CrossRef]
- Cheddie, D.; Munroe, N. Review and comparison of approaches to proton exchange membrane fuel cell modeling. J. Power Sources 2005, 147, 72–84. [Google Scholar] [CrossRef]
- Demuren, A.; Edwards, R.L. Modeling Proton Exchange Membrane Fuel Cells—A Review. In 50 Years of CFD in Engineering Sciences; Runchal, A., Ed.; Springer: Singapore, 2020; pp. 513–547. [Google Scholar] [CrossRef]
- Springer, T.E. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Verbrugge, M.W. A Mathematical Model of the Solid-Polymer-Electrolyte Fuel Cell. J. Electrochem. Soc. 1992, 139, 2477. [Google Scholar] [CrossRef]
- Maggio, G.; Recupero, V.; Pino, L. Modeling polymer electrolyte fuel cells: An innovative approach. J. Power Sources 2001, 101, 275–286. [Google Scholar] [CrossRef]
- Wohr, M. Dynamic modelling and simulation of a polymer membrane fuel cell including mass transport limitation. Int. J. Hydrogen Energy 1998, 23, 213–218. [Google Scholar] [CrossRef]
- Gao, F.; Blunier, B.; Miraoui, A.; El Moudni, A. A Multiphysic Dynamic 1-D Model of a Proton-Exchange-Membrane Fuel-Cell Stack for Real-Time Simulation. IEEE Trans. Ind. Electron. 2010, 57, 1853–1864. [Google Scholar] [CrossRef]
- Murschenhofer, D.; Kuzdas, D.; Braun, S.; Jakubek, S. A real-time capable quasi-2D proton exchange membrane fuel cell model. Energy Convers. Manag. 2018, 162, 159–175. [Google Scholar] [CrossRef]
- Futter, G.A.; Gazdzicki, P.; Friedrich, K.A.; Latz, A.; Jahnke, T. Physical modeling of polymer-electrolyte membrane fuel cells: Understanding water management and impedance spectra. J. Power Sources 2018, 391, 148–161. [Google Scholar] [CrossRef]
- Goshtasbi, A.; Pence, B.L.; Chen, J.; DeBolt, M.A.; Wang, C.; Waldecker, J.R.; Hirano, S.; Ersal, T. A Mathematical Model toward Real-Time Monitoring of Automotive PEM Fuel Cells. J. Electrochem. Soc. 2020, 167, 024518. [Google Scholar] [CrossRef]
- Tavčar, G.; Katrašnik, T. An Innovative Hybrid 3D Analytic-Numerical Approach for System Level Modelling of PEM Fuel Cells. Energies 2013, 6, 5426–5485. [Google Scholar] [CrossRef] [Green Version]
- Tavčar, G.; Katrašnik, T. A computationally efficient hybrid 3D analytic-numerical approach for modelling species transport in a proton exchange membrane fuel cell. J. Power Sources 2013, 236, 321–340. [Google Scholar] [CrossRef]
- Pant, L.M.; Gerhardt, M.R.; Macauley, N.; Mukundan, R.; Borup, R.L.; Weber, A.Z. Along-the-channel modeling and analysis of PEFCs at low stoichiometry: Development of a 1+2D model. Electrochim. Acta 2019, 326, 134963. [Google Scholar] [CrossRef] [Green Version]
- Berning, T.; Djilali, N. A 3D, Multiphase, Multicomponent Model of the Cathode and Anode of a PEM Fuel Cell. J. Electrochem. Soc. 2003, 150, A1589. [Google Scholar] [CrossRef]
- Wu, H.; Berg, P.; Li, X. Steady and unsteady 3D non-isothermal modeling of PEM fuel cells with the effect of non-equilibrium phase transfer. Appl. Energy 2010, 87, 2778–2784. [Google Scholar] [CrossRef]
- Fink, C.; Fouquet, N. Three-dimensional simulation of polymer electrolyte membrane fuel cells with experimental validation. Electrochim. Acta 2011, 56, 10820–10831. [Google Scholar] [CrossRef]
- d’Adamo, A.; Haslinger, M.; Corda, G.; Höflinger, J.; Fontanesi, S.; Lauer, T. Modelling Methods and Validation Techniques for CFD Simulations of PEM Fuel Cells. Processes 2021, 9, 688. [Google Scholar] [CrossRef]
- Dickinson, E.J.F.; Smith, G. Modelling the Proton-Conductive Membrane in Practical Polymer Electrolyte Membrane Fuel Cell (PEMFC) Simulation: A Review. Membranes 2020, 10, 310. [Google Scholar] [CrossRef]
- Vetter, R.; Schumacher, J.O. Experimental parameter uncertainty in proton exchange membrane fuel cell modeling. Part I: Scatter in material parameterization. J. Power Sources 2019, 438, 227018. [Google Scholar] [CrossRef] [Green Version]
- Karpenko-Jereb, L.; Sternig, C.; Fink, C.; Hacker, V.; Theiler, A.; Tatschl, R. Theoretical study of the influence of material parameters on the performance of a polymer electrolyte fuel cell. J. Power Sources 2015, 297, 329–343. [Google Scholar] [CrossRef]
- Vetter, R.; Schumacher, J.O. Experimental parameter uncertainty in proton exchange membrane fuel cell modeling. Part II: Sensitivity analysis and importance ranking. J. Power Sources 2019, 439, 126529. [Google Scholar] [CrossRef] [Green Version]
- Laoun, B.; Naceur, M.W.; Khellaf, A.; Kannan, A.M. Global sensitivity analysis of proton exchange membrane fuel cell model. Int. J. Hydrogen Energy 2016, 41, 9521–9528. [Google Scholar] [CrossRef]
- Du, Z.P.; Steindl, C.; Jakubek, S. Efficient Two-Step Parametrization of a Control-Oriented Zero-Dimensional Polymer Electrolyte Membrane Fuel Cell Model Based on Measured Stack Data. Processes 2021, 9, 713. [Google Scholar] [CrossRef]
- Kravos, A.; Ritzberger, D.; Hametner, C.; Jakubek, S.; Katrašnik, T. Methodology for efficient parametrisation of electrochemical PEMFC model for virtual observers: Model based optimal design of experiments supported by parameter sensitivity analysis. Int. J. Hydrogen Energy 2021, 46, 13832–13844. [Google Scholar] [CrossRef]
- Ritzberger, D.; Höflinger, J.; Du, Z.P.; Hametner, C.; Jakubek, S. Data-driven parameterization of polymer electrolyte membrane fuel cell models via simultaneous local linear structured state space identification. Int. J. Hydrogen Energy 2021, 46, 11878–11893. [Google Scholar] [CrossRef]
- Goshtasbi, A.; Chen, J.; Waldecker, J.R.; Hirano, S.; Ersal, T. Effective Parameterization of PEM Fuel Cell Models—Part II: Robust Parameter Subset Selection, Robust Optimal Experimental Design, and Multi-Step Parameter Identification Algorithm. J. Electrochem. Soc. 2020, 167, 044505. [Google Scholar] [CrossRef]
- Goshtasbi, A.; Chen, J.; Waldecker, J.R.; Hirano, S.; Ersal, T. Effective Parameterization of PEM Fuel Cell Models—Part I: Sensitivity Analysis and Parameter Identifiability. J. Electrochem. Soc. 2020, 167, 044504. [Google Scholar] [CrossRef]
- Abaza, A.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Optimal Estimation of Proton Exchange Membrane Fuel Cells Parameter Based on Coyote Optimization Algorithm. Appl. Sci. 2021, 11, 2052. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Rezazadeh, A.; Khoddam, M.; Zarean, N. Parameter Optimization for a Pemfc Model With Particle Swarm Optimization. Int. J. Eng. Appl. Sci. 2011, 3, 102–108. [Google Scholar]
- El-Fergany, A.A. Extracting optimal parameters of PEM fuel cells using Salp Swarm Optimizer. Renew. Energy 2018, 119, 641–648. [Google Scholar] [CrossRef]
- Salim, R.; Nabag, M.; Noura, H.; Fardoun, A. The parameter identification of the Nexa 1.2 kW PEMFC’s model using particle swarm optimization. Renew. Energy 2015, 82, 26–34. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Ashourian, M. Parameter identification of PEMFC based on Convolutional neural network optimized by balanced deer hunting optimization algorithm. Energy Rep. 2020, 6, 1572–1580. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Multi-verse optimizer for identifying the optimal parameters of PEMFC model. Energy 2018, 143, 634–644. [Google Scholar] [CrossRef]
- Mo, Z.J.; Zhu, X.J.; Wei, L.Y.; Cao, G.Y. Parameter optimization for a PEMFC model with a hybrid genetic algorithm. Int. J. Energy Res. 2006, 30, 585–597. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, N.; Bi, Y.; Srinivasan, D. Parameter identification of PEMFC model based on hybrid adaptive differential evolution algorithm. Energy 2015, 90, 1334–1341. [Google Scholar] [CrossRef]
- Gong, W.; Yan, X.; Liu, X.; Cai, Z. Parameter extraction of different fuel cell models with transferred adaptive differential evolution. Energy 2015, 86, 139–151. [Google Scholar] [CrossRef]
- Sun, Z.; Cao, D.; Ling, Y.; Xiang, F.; Sun, Z.; Wu, F. Proton exchange membrane fuel cell model parameter identification based on dynamic differential evolution with collective guidance factor algorithm. Energy 2021, 216, 119056. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barbir, F. PEM Fuel Cells: Theory and Practice, 2nd ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Boston, MA, USA, 2013. [Google Scholar]
- Kochenderfer, M.J.; Wheeler, T.A. Algorithms for Optimization; The MIT Press: Cambridge, MA, USA; London, UK, 2019. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- Hoeflinger, J.; Hofmann, P.; Geringer, B. Experimental PEM-Fuel Cell Range Extender System Operation and Parameter Influence Analysis; SAE Technical Paper Series; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Innerwinkler, P.; Kelterer, A.M.; Sternig, C.; Fink, C.; Prenninger, P.; Tatschl, R. A novel membrane transport model for polymer electrolyte fuel cell simulations. Int. J. Hydrogen Energy 2014, 39, 7077–7088. [Google Scholar] [CrossRef]
- Bednarek, T.; Tsotridis, G. Issues associated with modelling of proton exchange membrane fuel cell by computational fluid dynamics. J. Power Sources 2017, 343, 550–563. [Google Scholar] [CrossRef]
- Fink, C.; Karpenko-Jereb, L.; Ashton, S. Advanced CFD Analysis of an Air-cooled PEM Fuel Cell Stack Predicting the Loss of Performance with Time. Fuel Cells 2016, 16, 490–503. [Google Scholar] [CrossRef] [Green Version]
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Lattice Boltzmann simulations of anisotropic permeabilities in carbon paper gas diffusion layers. J. Power Sources 2009, 186, 104–114. [Google Scholar] [CrossRef]
- Goudos, S.K.; Baltzis, K.B.; Antoniadis, K.; Zaharis, Z.D.; Hilas, C.S. A comparative study of common and self-adaptive differential evolution strategies on numerical benchmark problems. Procedia Comput. Sci. 2011, 3, 83–88. [Google Scholar] [CrossRef] [Green Version]
- Weber, A.Z.; Newman, J. Transport in Polymer-Electrolyte Membranes. J. Electrochem. Soc. 2004, 151, A311. [Google Scholar] [CrossRef]
- O’Hayre, R.P.; Prinz, F.B.; Cha, S.W.; Colella, W.G. Fuel Cell Fundamentals, 2nd ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained, 2nd ed.; J. Wiley: Chichester, WS, USA, 2011. [Google Scholar] [CrossRef]
- Moukheiber, E.; de Moor, G.; Flandin, L.; Bas, C. Investigation of ionomer structure through its dependence on ion exchange capacity (IEC). J. Membr. Sci. 2012, 389, 294–304. [Google Scholar] [CrossRef]
- Giancola, S.; Zatoń, M.; Reyes-Carmona, Á.; Dupont, M.; Donnadio, A.; Cavaliere, S.; Rozière, J.; Jones, D.J. Composite short side chain PFSA membranes for PEM water electrolysis. J. Membr. Sci. 2019, 570–571, 69–76. [Google Scholar] [CrossRef]
- Li, T.; Shen, J.; Chen, G.; Guo, S.; Xie, G. Performance Comparison of Proton Exchange Membrane Fuel Cells with Nafion and Aquivion Perfluorosulfonic Acids with Different Equivalent Weights as the Electrode Binders. ACS Omega 2020, 5, 17628–17636. [Google Scholar] [CrossRef] [PubMed]
- Das, P.K.; Li, X.; Liu, Z.S. Effective transport coefficients in PEM fuel cell catalyst and gas diffusion layers: Beyond Bruggeman approximation. Appl. Energy 2010, 87, 2785–2796. [Google Scholar] [CrossRef]



| Name - | Type - | Anode Inlet Pressure mbar | Cooling Inlet Temperature |
|---|---|---|---|
| P1 | Polarization Curve | 1700 | 55 |
| P2 | Polarization Curve | 1700 | 52 |
| P3 | Polarization Curve | 1400 | 55 |
| L1 | Load Step | 1700 | 55 |
| L2 | Load Step | 1700 | 55 |
| L3 | Load Step | 1700 | 55 |
| Parameter | Unit | Value |
|---|---|---|
| Temperature | 23 | |
| Pressure | mbar | 983 |
| Relative Humidity | % | 48 |
| Cathode | Anode | Membrane | |||||
|---|---|---|---|---|---|---|---|
| Parameter | Unit | BPP | GDL | CL | BPP | GDL | |
| Thickness | 1.65 | 0.21 | 0.01 | 1.65 | 0.21 | 0.015 | |
| Channel width | 1.1 | 0.6 | |||||
| Channel height | 0.5 | 0.5 | |||||
| Parameter | Unit | BPP | GDL | CCL | Membrane | |
|---|---|---|---|---|---|---|
| Density | 1900 | 2000 | 1980 | |||
| Electrical Conductivity | 2000 | ⧫ | ||||
| Porosity | - | ⧫ | ||||
| Tortuosity | - | ⧫ | ||||
| Ionic Conductivity | ||||||
| ⧫ | ||||||
| - | 14 | |||||
| Reference Temperature | 55 | |||||
| Activation Energy | ⧫ | |||||
| Water Diffusion Coefficient | ||||||
| 2.16 × 10−11 | ||||||
| - | 1 | |||||
| Reference Temperature | 25 | |||||
| Activation Energy | 19,809 | |||||
| Electro-osmotic Drag Coef. | ||||||
| - | 0.1136 | |||||
| - | 1 | |||||
| Equilibrium Water Content | - | Springer | ||||
| Transfer Coefficient | - | ⧫ | ||||
| Exchange Current Density | ||||||
| RECD | ⧫ | |||||
| Reference Temperature | 55 | |||||
| Activation Energy | ⧫ | |||||
| Water Exponent | - | 1 | ||||
| Oxygen Exponent | - | 0.75 | ||||
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Unit | A/cm2 | J/mol | - | S/m | J/mol | S/m | - | - |
| Bound min | 2.00 × 10 −4 | 50,000 | 0.3 | 4 | 10,000 | 80 | 0.4 | 1 |
| Bound max | 2.00 × 10 −3 | 250,000 | 0.4 | 20 | 50,000 | 390 | 0.8 | 3 |
| DiffEvo | 4.884 × 10 −4 | 226,071 | 0.333 | 14.97 | 66,037 | 356.6 | 0.63 | 1.16 |
| NelderMead | 6.732 × 10 −4 | 213,475 | 0.32 | 14.03 | 35,486 | 355.8 | 0.69 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haslinger, M.; Steindl, C.; Lauer, T. Parameter Identification of a Quasi-3D PEM Fuel Cell Model by Numerical Optimization. Processes 2021, 9, 1808. https://doi.org/10.3390/pr9101808
Haslinger M, Steindl C, Lauer T. Parameter Identification of a Quasi-3D PEM Fuel Cell Model by Numerical Optimization. Processes. 2021; 9(10):1808. https://doi.org/10.3390/pr9101808
Chicago/Turabian StyleHaslinger, Maximilian, Christoph Steindl, and Thomas Lauer. 2021. "Parameter Identification of a Quasi-3D PEM Fuel Cell Model by Numerical Optimization" Processes 9, no. 10: 1808. https://doi.org/10.3390/pr9101808
APA StyleHaslinger, M., Steindl, C., & Lauer, T. (2021). Parameter Identification of a Quasi-3D PEM Fuel Cell Model by Numerical Optimization. Processes, 9(10), 1808. https://doi.org/10.3390/pr9101808







