A Discrete Element Method Study of Solids Stress in Cylindrical Columns Using MFiX
Abstract
:1. Introduction
2. Governing Equations
3. Simulation Methodology
- At the beginning, particles were placed in a funnel, from which they were gradually discharged into the column due to gravity. This was done to reproduce as closely as possible the way particles were inserted into the experimental column, rather than feeding them at a constant mass flow rate. Moreover, it is perhaps the simplest way in MFiX to provide a time-limited flow of particles from the top of the column, as employing a user-defined function to modify the particle flow rate is more cumbersome. In this way, instead, a certain number of particles were inserted by selecting a “region” of specified coordinates in which they “appear” at the start of the simulation.
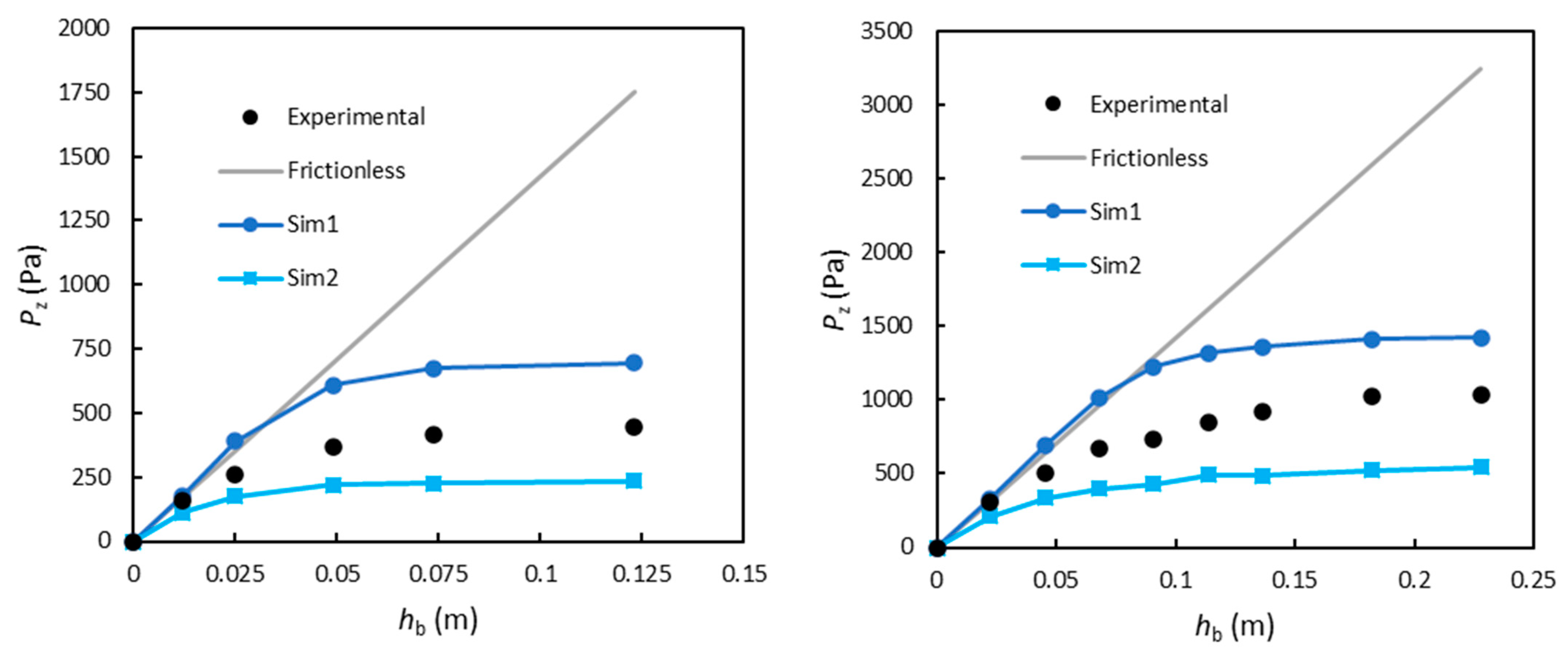
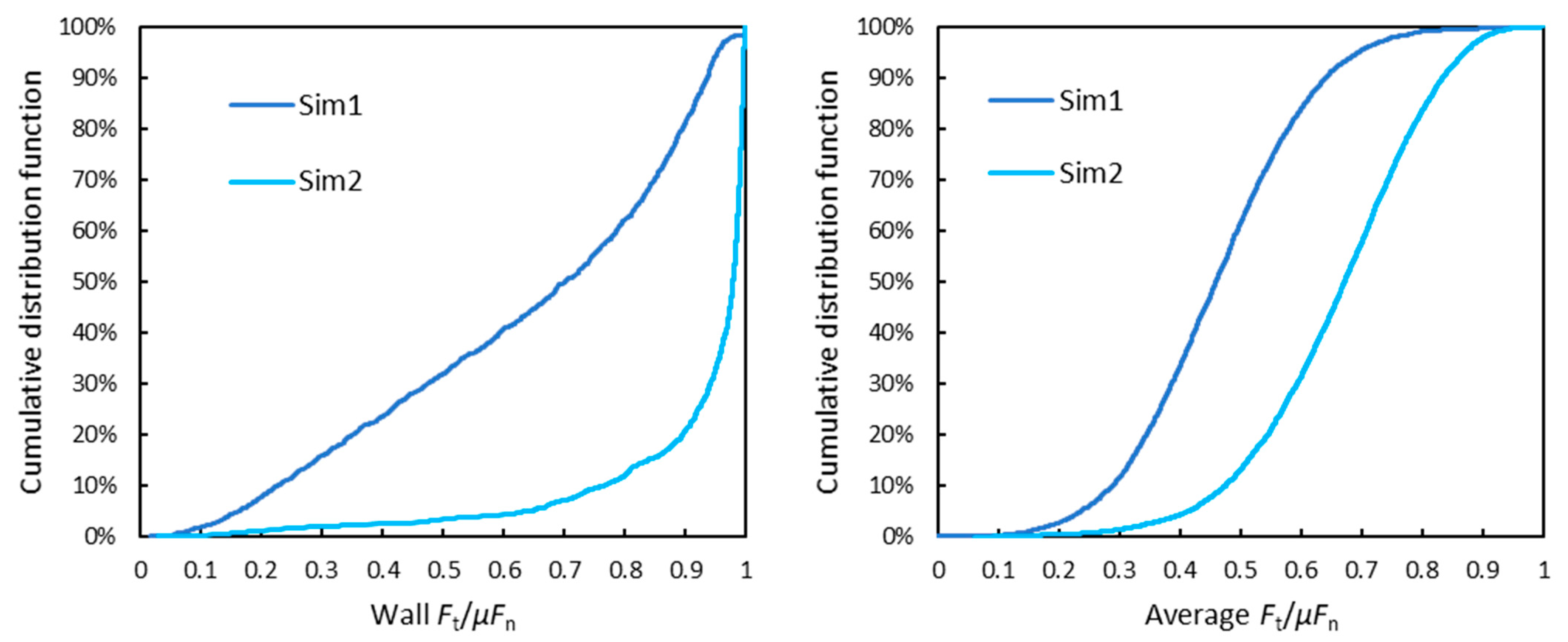
- When all particles had settled and stabilized, we extracted the values of Fn and Ft to analyze the internal stress distribution. The data related to this state are referred to as “Sim1”.
- Afterwards, the lateral wall was made move upwards with a speed of 1 mm/s for 1 s. This was done to partially reproduce two phenomena that may produce the same effect. The first is the expansion the wall in response to the pressure exerted by particles [8]. The second is the downward movement of the piston in contact with the balance, which was placed below the particles in the experiments [22]. Both phenomena make particles descend and reach the so‑called active state, thus increasing the particle-wall friction force, and reducing the pressure exerted on the bottom of the column. Increasing the particle-wall friction by moving the wall upwards is known as “friction mobilization” [17,18] and researchers have shown that wall movements in different directions lead to different friction variations. As Windows-Yule et al. [15] showed, the intensity of the wall vertical velocity is instead not very important, since even markedly different values produce rather similar results. Although this is clearly a simplified version of the physical phenomena, it can provide useful insights into the distribution of forces in the active state.
- After the wall had stopped moving and particles had stabilized, the values of Fn and Ft were investigated again. The data related to this state are referred to as “Sim2”.
4. Results and Discussion
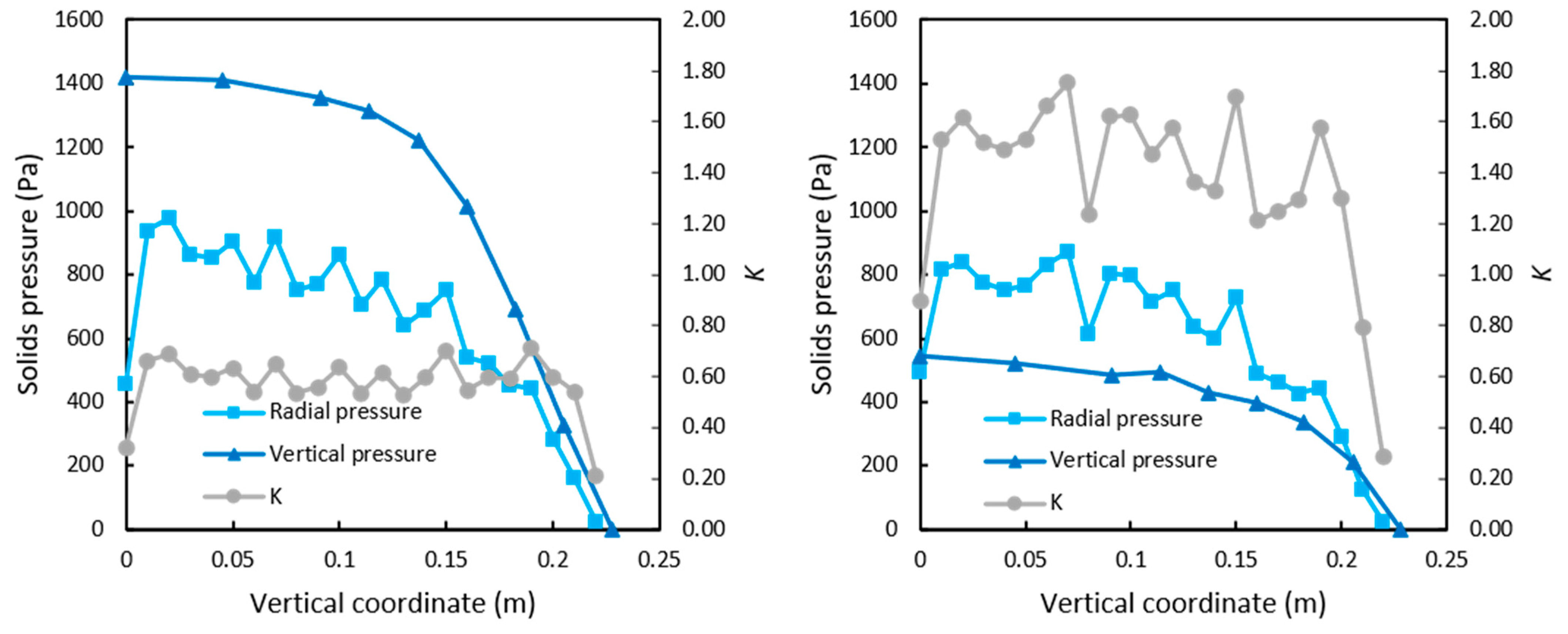
4.1. Analysis of the Stress Distribution
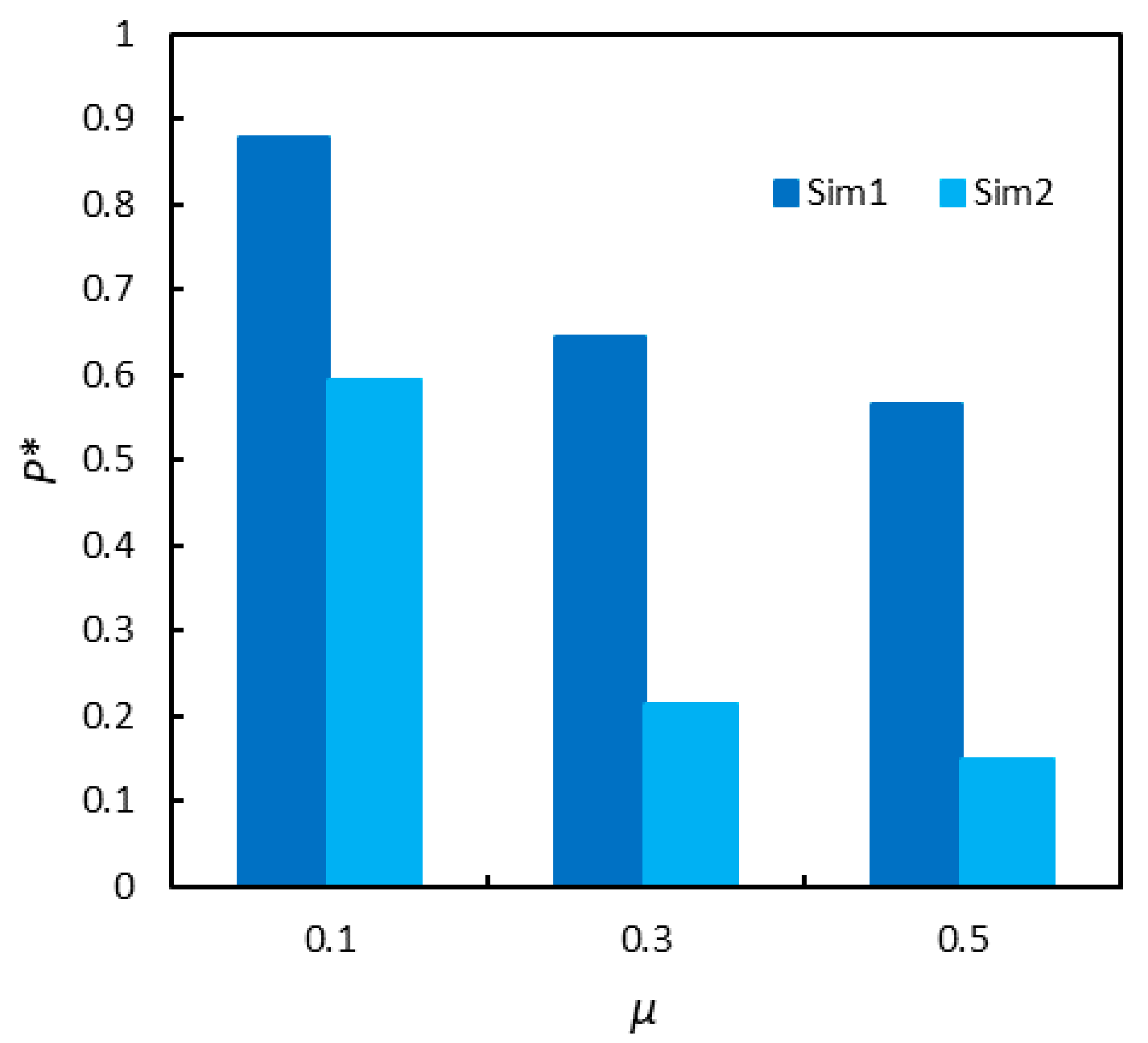
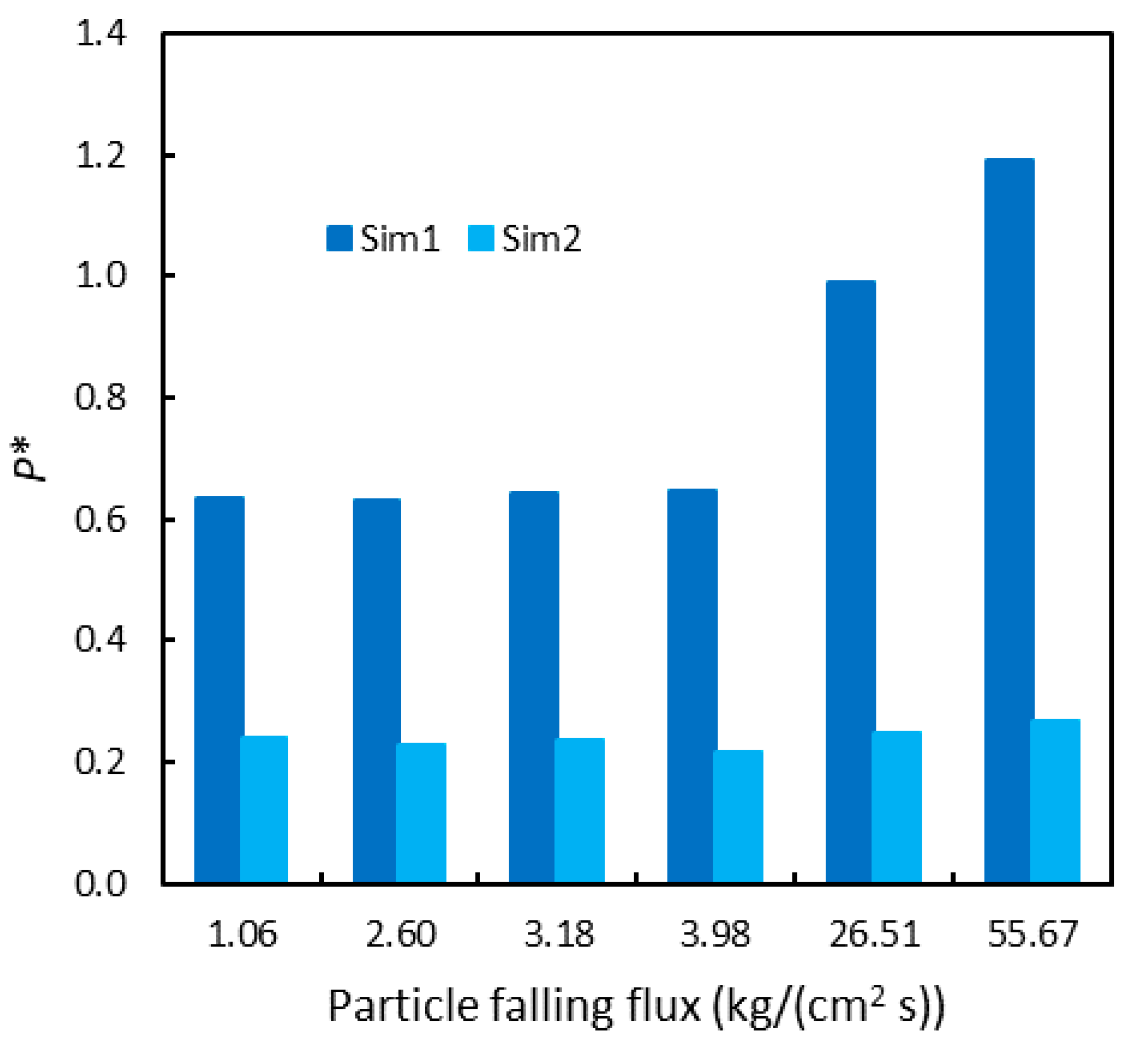
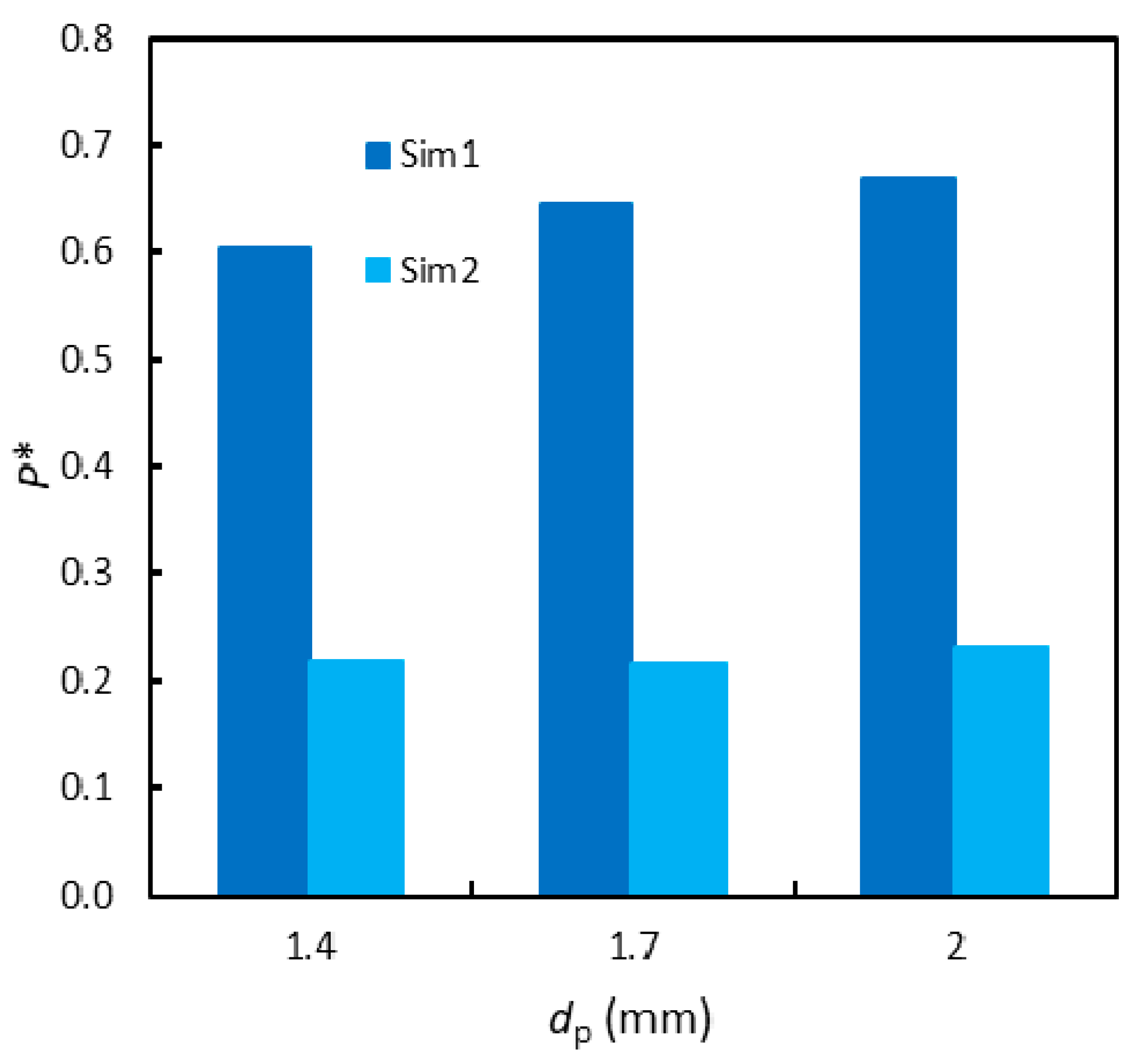
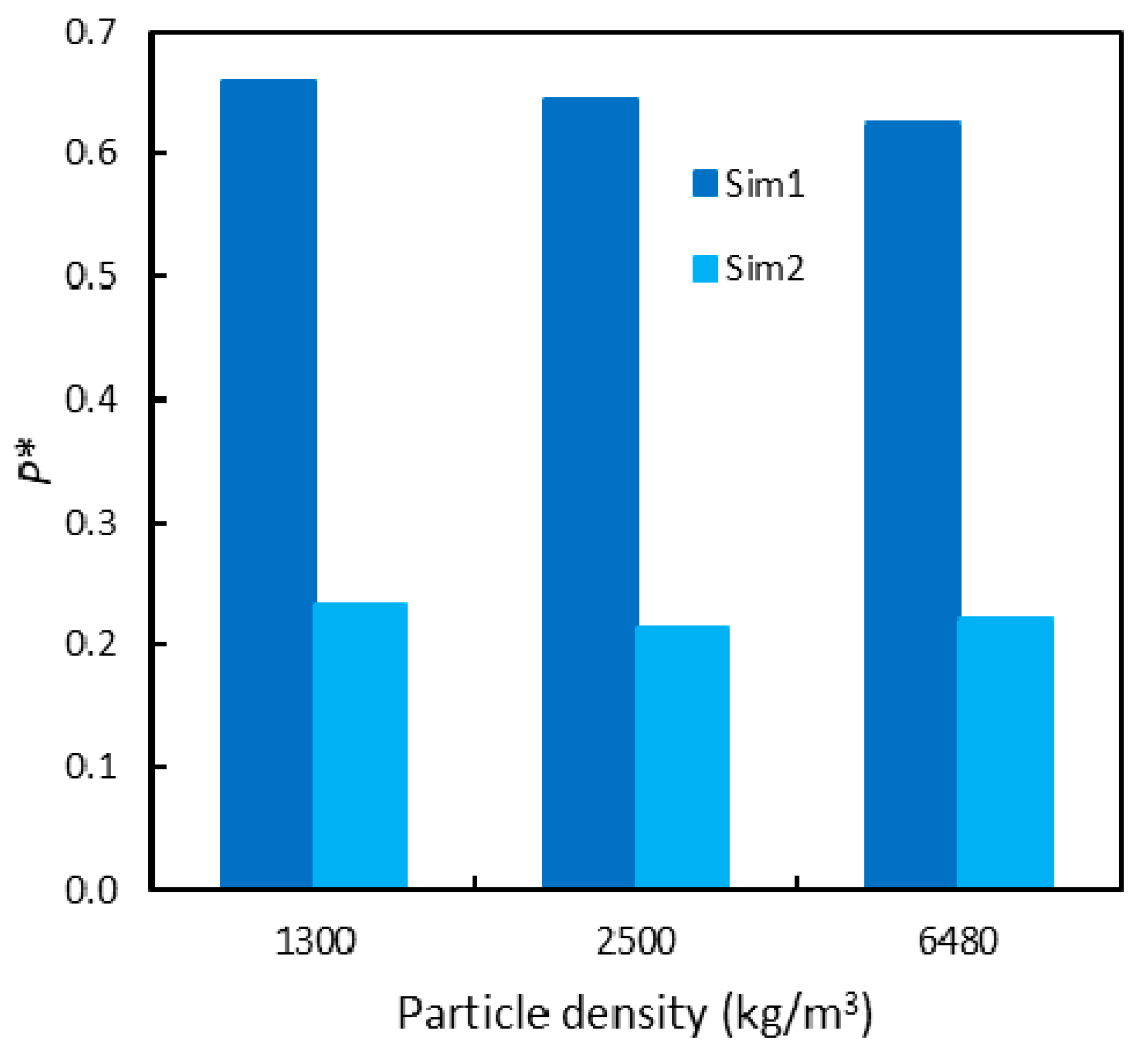
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding

Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Guo, Y.; Curtis, J.S. Discrete Element Method Simulations for Complex Granular Flows. Annu. Rev. Fluid Mech. 2015, 47, 21–46. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Kuang, S.B.; Chu, K.W.; Yu, A.B. Discrete particle simulation of particle–fluid flow: Model formulations and their applicability. J. Fluid Mech. 2010, 661, 482–510. [Google Scholar] [CrossRef]
- Ibrahim, A.; Meguid, M.A. Coupled Flow Modelling in Geotechnical and Ground Engineering: An Overview. Int. J. Geosynth. Ground Eng. 2020, 6, 39. [Google Scholar] [CrossRef]
- Di Felice, R.; Scapinello, C. The transition from the fixed to the fluidised state of binary-solid liquid beds. Chem. Eng. Sci. 2010, 65, 5187–5192. [Google Scholar] [CrossRef]
- Janssen, H.A. Versuche über Getreidedruck in Silozellen. Z. Ver. Dtsch. Ing. 1895, 39, 1045. [Google Scholar]
- Sperl, M. Experiments on corn pressure in silo cells—Translation and comment of Janssen’s paper from 1895. Granul. Matter 2006, 8, 59–65. [Google Scholar] [CrossRef] [Green Version]
- Nedderman, R.M. Statics and Kinematics of Granular Materials; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Peng, Z.; Li, R.; Jiang, Y. Stress distribution along sidewall of a granular column: Local fluctuation and global determination. Phys. A Stat. Mech. Its Appl. 2019, 526, 120865. [Google Scholar] [CrossRef]
- Zhao, H.; An, X.; Wu, Y.; Qian, Q. DEM modeling on stress profile and behavior in granular matter. Powder Technol. 2018, 323, 149–154. [Google Scholar] [CrossRef]
- Ramírez-Gómez, Á. The discrete element method in silo/bin research. Recent advances and future trends. Part. Sci. Technol. 2020, 38, 210–227. [Google Scholar] [CrossRef]
- Žurovec, D.; Hlosta, J.; Nečas, J.; Zegzulka, J. Monitoring bulk material pressure on bottom of storage using DEM. Open Eng. 2019, 9, 623–630. [Google Scholar] [CrossRef]
- Acevedo, M.; Zuriguel, I.; Maza, D.; Pagonabarraga, I.; Alonso-Marroquin, F.; Hidalgo, R.C. Stress transmission in systems of faceted particles in a silo: The roles of filling rate and particle aspect ratio. Granul. Matter 2014, 16, 411–420. [Google Scholar] [CrossRef]
- Qian, Q.; Wang, L.; An, X.; Wu, Y.; Wang, J.; Zhao, H.; Yang, X. DEM simulation on the vibrated packing densification of mono-sized equilateral cylindrical particles. Powder Technol. 2018, 325, 151–160. [Google Scholar] [CrossRef]
- Windows-Yule, C.R.K.; Mühlbauer, S.; Cisneros, L.A.T.; Nair, P.; Marzulli, V.; Pöschel, T. Janssen effect in dynamic particulate systems. Phys. Rev. E 2019, 100, 1–7. [Google Scholar] [CrossRef]
- Zhao, H.; An, X.; Wu, Y.; Yang, X. Microscopic analyses of stress profile within confined granular assemblies. AIP Adv. 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Horabik, J.; Parafiniuk, P.; Molenda, M. Stress profile in bulk of seeds in a shallow model silo as influenced by mobilisation of particle-particle and particle-wall friction: Experiments and DEM simulations. Powder Technol. 2018, 327, 320–334. [Google Scholar] [CrossRef]
- Vivanco, F.; Mercado, J.; Santibáñez, F.; Melo, F. Stress profile in a two-dimensional silo: Effects induced by friction mobilization. Phys. Rev. E 2016, 94, 022906. [Google Scholar] [CrossRef]
- Wiącek, J.; Stasiak, M.; Parafiniuk, P. Effective elastic properties and pressure distribution in bidisperse granular packings: DEM simulations and experiment. Arch. Civ. Mech. Eng. 2017, 17, 271–280. [Google Scholar] [CrossRef]
- Garg, R.; Galvin, J.; Li, T.; Pannala, S. Open-source MFiX-DEM software for gas-solids flows: Part I-Verification studies. Powder Technol. 2012, 220, 122–137. [Google Scholar] [CrossRef]
- Garg, R.; Galvin, J.; Li, T.; Pannala, S. Documentation of Open-Source MFiX–DEM Software for Gas-Solids Flows. Available online: https://mfix.netl.doe.gov/documentation/demdoc2010.pdf (accessed on 25 December 2020).
- Di Felice, R.; Scapinello, C. On the interaction between a fixed bed of solid material and the confining column wall: The Janssen approach. Granul. Matter 2010, 12, 49–55. [Google Scholar] [CrossRef]
- Lungu, M.; Siame, J.; Mukosha, L. Comparison of CFD-DEM and TFM approaches for the simulation of the small scale challenge problem 1. Powder Technol. 2020, 378, 85–103. [Google Scholar] [CrossRef]
- Garcia-Gutierrez, L.M.; Hernández-Jiménez, F.; Cano-Pleite, E.; Soria-Verdugo, A. Improvement of the simulation of fuel particles motion in a fluidized bed by considering wall friction. Chem. Eng. J. 2017, 321, 175–183. [Google Scholar] [CrossRef]
- Gao, X.; Li, T.; Rogers, W.A.; Smith, K.; Gaston, K.; Wiggins, G.; Parks, J.E. Validation and application of a multiphase CFD model for hydrodynamics, temperature field and RTD simulation in a pilot-scale biomass pyrolysis vapor phase upgrading reactor. Chem. Eng. J. 2020, 388, 124279. [Google Scholar] [CrossRef]
- Fullmer, W.D.; Musser, J. CFD-DEM solution verification: Fixed-bed studies. Powder Technol. 2018, 339, 760–764. [Google Scholar] [CrossRef]
- Zinani, F.; Philippsen, C.G.; Indrusiak, M.L.S. Numerical study of gas–solid drag models in a bubbling fluidized bed. Part. Sci. Technol. 2018, 36, 1–10. [Google Scholar] [CrossRef]
- Adepu, M.; Chen, S.; Jiao, Y.; Gel, A.; Emady, H. Wall to particle bed contact conduction heat transfer in a rotary drum using DEM. Comput. Part. Mech. 2020, 1–11. [Google Scholar] [CrossRef]
- Xu, Y.; Li, T.; Lu, L.; Tebianian, S.; Chaouki, J.; Leadbeater, T.W.; Jafari, R.; Parker, D.J.; Seville, J.; Ellis, N.; et al. Numerical and experimental comparison of tracer particle and averaging techniques for particle velocities in a fluidized bed. Chem. Eng. Sci. 2019, 195, 356–366. [Google Scholar] [CrossRef]
- Ansari, A.; Mohaghegh, S.D.; Shahnam, M.; Dietiker, J.F. Modeling Average Pressure and Volume Fraction of a Fluidized Bed Using Data-Driven Smart Proxy. Fluids 2019, 4, 123. [Google Scholar] [CrossRef] [Green Version]
- Miramontes, E.; Love, L.J.; Lai, C.; Sun, X.; Tsouris, C. Additively manufactured packed bed device for process intensification of CO2 absorption and other chemical processes. Chem. Eng. J. 2020, 388, 124092. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, L.; Li, Y.; Zhou, Q. A Model to Improve Granular Temperature in CFD-DEM Simulations. Energies 2020, 13, 4730. [Google Scholar] [CrossRef]
- Syamlal, M.; Rogers, W.; O’Brien, T.J. MFiX Documentation Theory Guide; Department of Energy: Oak Ridge, TN, USA, 1993; Volume 1004.
- Di Renzo, A.; Di Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Paulick, M.; Morgeneyer, M.; Kwade, A. Review on the influence of elastic particle properties on DEM simulation results. Powder Technol. 2015, 283, 66–76. [Google Scholar] [CrossRef]
- Alaci, S.; Muscă, I.; Pentiuc, Ș.-G. Study of the Rolling Friction Coefficient between Dissimilar Materials through the Motion of a Conical Pendulum. Materials 2020, 13, 5032. [Google Scholar] [CrossRef] [PubMed]
- Xiang, J.; McGlinchey, D.; Latham, J.P. An investigation of segregation and mixing in dense phase pneumatic conveying. Granul. Matter 2010, 12, 345–355. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Y.; Zhang, H.; Yu, H.-S. DEM and experimental study of bi-directional simple shear. Granul. Matter 2019, 21, 24. [Google Scholar] [CrossRef]
- Yang, R.Y.; Zou, R.P.; Yu, A.B. Numerical study of the packing of wet coarse uniform spheres. AIChE J. 2003, 49, 1656–1666. [Google Scholar] [CrossRef]
- Marchelli, F.; Moliner, C.; Bosio, B.; Arato, E. A CFD-DEM sensitivity analysis: The case of a pseudo-2D spouted bed. Powder Technol. 2019, 353, 409–425. [Google Scholar] [CrossRef]
- Bakshi, A.; Shahnam, M.; Gel, A.; Li, T.; Altantzis, C.; Rogers, W.; Ghoniem, A.F. Comprehensive multivariate sensitivity analysis of CFD-DEM simulations: Critical model parameters and their impact on fluidization hydrodynamics. Powder Technol. 2018, 338, 519–537. [Google Scholar] [CrossRef]
- Coetzee, C.J. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Wu, Y.; Hou, Q.; Dong, K.; Yu, A. Effect of packing method on packing formation and the correlation between packing density and interparticle force. Particuology 2020, 48, 170–181. [Google Scholar] [CrossRef]
- Tixier, M.; Pitois, O.; Mills, P. Experimental impact of the history of packing on the mean pressure in silos. Eur. Phys. J. E 2004, 14, 241–247. [Google Scholar] [CrossRef] [PubMed]







| Variable | Equation |
|---|---|
| Linear motion equation | |
| Rotational motion equation | |
| Total contact force | |
| Total torque | |
| Normal overlap | |
| Normal versor | |
| Relative velocity | |
| Normal relative velocity | |
| Tangential relative velocity | |
| Tangential versor | |
| Tangential displacement | at the beginning of contact |
| thereafter | |
| Distance from contact point to particle center | |
| Elastic normal force | |
| Damping normal force | |
| Elastic tangential force | |
| Damping tangential force | |
| Damping coefficient | |
| Collision time | |
| Coulomb friction force | |
| Actual tangential force | |
| Normal spring constant | |
| Tangential spring constant | |
| Effective mass | |
| Effective radius | |
| Shear modulus |
| Parameter | Value |
|---|---|
| Young modulus (E) | 10 MPa |
| Poisson’s ratio (σ) | 0.29 |
| Particle-particle and particle-wall friction coefficients (µ) | 0.3 |
| Particle-particle and particle-wall restitution coefficients (e) | 0.9 |
| Particle density (ρp) | 2500 kg/m3 |
| Particle diameter (dp) | 1.7 or 5 mm |
| Average particle filling flux | 3.18 kg/(cm2·s) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchelli, F.; Di Felice, R. A Discrete Element Method Study of Solids Stress in Cylindrical Columns Using MFiX. Processes 2021, 9, 60. https://doi.org/10.3390/pr9010060
Marchelli F, Di Felice R. A Discrete Element Method Study of Solids Stress in Cylindrical Columns Using MFiX. Processes. 2021; 9(1):60. https://doi.org/10.3390/pr9010060
Chicago/Turabian StyleMarchelli, Filippo, and Renzo Di Felice. 2021. "A Discrete Element Method Study of Solids Stress in Cylindrical Columns Using MFiX" Processes 9, no. 1: 60. https://doi.org/10.3390/pr9010060
APA StyleMarchelli, F., & Di Felice, R. (2021). A Discrete Element Method Study of Solids Stress in Cylindrical Columns Using MFiX. Processes, 9(1), 60. https://doi.org/10.3390/pr9010060






