Abstract
Computational methods have become reliable tools in many disciplines for research and industrial design. There are, however, an ever-increasing number of details waiting to be included in the models and software, including, e.g., chemical reactions and many physical phenomena, such as particle and droplet behavior and their interactions. The dominant method for copper production, flash smelting, has been extensively investigated, but the settler part of the furnace containing molten high temperature melts termed slag and matte, still lacks a computational modeling tool. In this paper, two commercial modeling software programs have been used for simulating slag–matte interactions in the settler, the target being first to develop a robust computational fluid dynamics (CFD) model and, second, to apply a new approach for molten droplet behavior in a continuum. The latter is based on CFD coupled with the discrete element method (DEM), which was originally developed for modeling solid particle–particle interactions and movement, and is applied here for individual droplets for the first time. The results suggest distinct settling flow phenomena and the significance of droplet coalescence for settling velocity and efficiency. The computing capacity requirement for both approaches is the main limiting factor preventing full-scale geometry modeling with detailed droplet interactions.
1. Introduction
In the flash smelting (FS) process, a mixture of sulfide-based concentrate and flux is continuously fed to the reaction shaft through a concentrate burner. Additional recycled materials, such as copper scrap and waste electrical and electronic equipment (WEEE) scrap can be used in the flash smelting feed. With the solid feed, oxygen enriched air is also blown through the burner. The air is used to create the exothermic reaction of sulfide oxidation, which creates the energy needed to melt the feed. This forms molten slag and matte phases as separate layers in the settler, with the lighter slag layer on top of the matte layer. The main functions of the slag are to protect the matte from oxygen, collect impurities such as Zn, Co, Ni, Sb, As, and Mo [1,2,3], and thermally insulate the matte to minimize energy losses. The slag and matte are tapped through tapping holes in the furnace wall. Unlike the feed, the tapping takes place at regular intervals, which causes variations in the thickness of the melt layers. Besides the melts, SO2 gas is also formed. The gas exits through the uptake shaft carrying dust that is collected in gas cleaning, and the gas is then used in sulfuric acid production. In addition, the thermal energy of the gas is recovered and used for heating input gases and possibly for the local community. The collected dust is then circulated back to the process [4].
The slag and matte layers are not stagnant in this continuous process. More material constantly descends from the reaction shaft and matte droplets settle through the slag layer, creating flows in the matte and slag layers. Xia et al. studied the slag and matte flows in a FS settler [5,6,7]. They found that tapping of the slag and the matte creates complex turbulent flows in the settler. The flows are not uniform: the effect of the tapping flow is reduced as the distance to the tapping hole increases. Furthermore, the region affected by the tapping decreases as the flow velocity is reduced.
However, the area under the reaction shaft has strong flows as the majority of the droplets will be descending relatively directly from the concentrate burner. Similar trajectories have been reported in a study by Zhou et al. [8]. Studies by Khan and Jokilaakso, and Jylhä and Jokilaakso show a funneling effect created by drag flows in the slag [9,10]. These drag flows were caused by settling matte droplets.
Mechanical copper losses in the FS process can be traced to copper as flue dust or matte entrained in the slag. The settling of matte droplets through the slag phase in the FS furnace (FSF) as shown in Figure 1, is an important phenomenon and determines the overall copper yield in the smelting unit process. The copper losses during the settling process are due, in addition to the mechanical entrainment of the copper matte droplets, to the chemical dissolution of copper in the slag phase. This not only reveals the loss of matte droplets during the settling process, but also how quick the settling process is. The entrainment of matte droplets has been studied by many researchers [11,12,13,14,15,16,17] and it has been concluded that mostly droplets ≤100 μm in size are trapped in the slag phase and are ultimately carried away in the slag phase through the slag outlet.
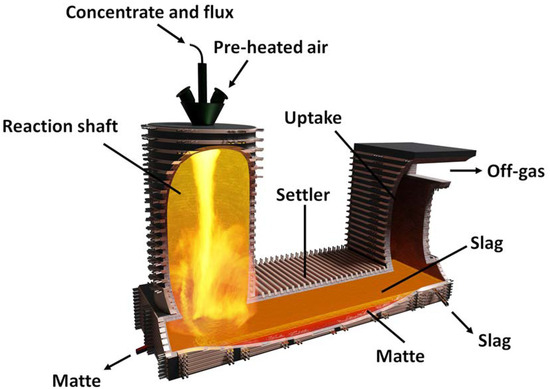
Figure 1.
Illustration of the Outotec flash smelting furnace.
The entrained copper losses to slag are due to, for example, solid spinels, small size, or droplets being lifted from the surface of the matte layer [18,19,20]. Spinels may be attached to a droplet or surround the droplet completely [21]. The attached spinel affects the settling of the droplet: the bulk density of the droplet–spinel entity is lower than that of a droplet without an attached spinel, but the size of the entity increases. Thus, the attached spinel may either increase or decrease the settling velocity of the droplet–spinel entity. However, as the droplet–spinel has better wetting with the slag than the matte, and has lower density than the matte, the droplet–spinel entity cannot enter the matte layer, and thus, droplets with spinel may be removed with the slag in tapping. Additionally, turbulence can lift parts of the surface layer of the matte to the slag [18]. Furthermore, the distance between the tapping hole and the slag–matte interface affects copper losses. In a study by Jiménez et al. [19], matte droplets were found to form a dispersion layer above the matte surface. With too short a distance between the matte surface and the tapping hole, droplets from the dispersion layer may be sucked upwards and removed through the tapping hole. According to their study, at least 20 cm distance is needed to minimize the quantity of droplets sucked from the dispersion layer.
To limit mechanical copper losses, several parameters should be optimized [22]. The density difference between the slag and the matte should be as high as possible, while the viscosity of the slag should be as low as possible. Also, the matte droplets should be as large as possible. These three factors decrease the residence time of the matte droplets in the slag. The density difference and the slag viscosity are greatly affected by slag chemistry and variations in solid content, oxygen levels, and temperature in the slag. The droplet size is affected by coalescence and reactions, which are also affected by the properties of the slag and droplets themselves.
Mathematical and computational modeling of pyrometallurgical processes and furnaces started decades ago, as there was an increasing need for better understanding of the phenomena occurring inside them. A significant increase in modeling development has been seen since the introduction of commercially available computational fluid dynamics (CFD) software. The development of the Outotec flash smelting furnace (FSF) and process modeling has been reviewed in a recent review paper [23]. The aim of the modeling studies reported here is to find a feasible computational method by using commercial simulation software packages for gaining a better understanding of the fluid dynamics of the settling matte droplets in the slag layer. After validating the fluid dynamics behavior with physical model results, additional droplet–droplet or droplet–spinel interactions and chemical reactions between matte droplets and slag will be included in the simulation. However, as the geometries and phenomena in the models are computationally extremely intensive, the additional features have to be included one by one as a longer-term target. Finally, the models and knowledge developed will be used to help find ways to reduce copper losses and develop processes and their operational efficiency in a similar manner as has been done with the FS reaction shaft models [23]. In this paper, the fluid dynamics modeling results are presented, and the results obtained with the two software packages are compared. The settling flow behavior of the molten matte phase has been revealed, and the results from statistical (or traditional) CFD modeling and from the new CFD–DEM coupling approach are consistent, suggesting a channeling or funneling kind of flow pattern.
The software used in this study was ANSYS® Fluent 19.2 and EDEM® 2019.1 with EDEM-Fluent coupling v2.2 provided by DEM Solutions Ltd., Edinburgh, Scotland, UK [24].
2. Methods
Information or research reports on the breakup or coalescence of matte droplets in the FS settler in the literature are scarce. Therefore, this study focused on this part of the process so that the entraining and settling behavior of matte droplets could be investigated thoroughly.
2.1. Population Balance Model
The high-volume fraction of the dispersed matte phase during the settling process in the FS settler was described by the population balance model (Eulerian–Eulerian approach). The dispersed phase model (DPM, Eulerian–Lagrange approach) method has limitations when the volume fraction is above 10%, since computational time becomes expensive. Several methods are available for droplet classifications using the population balance model. These include size class formation and the moment method. Size class formation divides the system into several size groups. Therefore, it is a more accurate way to estimate the system. Size classes are further classified into the homogeneous and inhomogeneous methods. The homogeneous method classifies the different size groups into a single velocity field, which means it treats all the size groups as one phase and, therefore, the results from this method are not as accurate. In contrast, the inhomogeneous method defines a velocity profile for each size group, so this method is more feasible for an accurate representation of a system that contains different size groups. The inhomogeneous method has been used for an oil, water and air system [25], and it accurately predicted the system. Therefore, this method was preferred for this study as well. However, defining the different size groups with the inhomogeneous method is not enough, since the model equations need to be parametrized to truly depict the scenario population balance, especially for coalescence efficiency and frequency, to capture the correct coalescence rate. Nonetheless, since it is not easy to obtain experimental data under the harsh conditions of the settler, these methods may give a good estimate of what is happening inside the settler.
The population balance model distributes different droplet sizes into various size groups. These groups represent a range of droplet sizes and the volume fraction of each droplet size is estimated through mathematical models. The equation representing the population balance model (PBE) in a control volume is shown in Equation (1) [26].
where f represents the density function with parameters: x, ξ, and t, where x represents the physical coordinates, and ξ represents the internal coordinates of the particle, for example, diameter. Internal coordinates could be either a scalar or a vector depending on how many properties of the droplet or particle you wish to include. Since in this work the focus is on the diameter of the droplet, ε is considered as a scalar. Finally, t represents the time, V represents velocity, and S an external source term.
If the death and birth of particles are not considered, then the number of particles in a control volume is constant, and
Two different schemes, the class method and the moment method, are available for estimating the particle size distribution (PSD) in the domain. The class method divides the PSD into various discrete size groups and each size group is represented by the PBE. For some applications, the multiple size groups (MUSIG) model has been developed, which uses a homogeneous and inhomogeneous approach to solve the PSD field.
Inhomogeneous particle size distribution was used for this work since homogeneous PSD schemes use a single velocity field for all particle sizes groups and therefore, may not be an accurate representation of the velocity fields for different size groups. In contrast, inhomogeneous PSD uses different velocity fields for the size groups [26].
2.2. Coalescence Model
The Luo coalescence model [27] over-predicts the coalescence frequency and requires adjustment of coefficients in the equation using sensitivity analysis and validation with experimental data [28]. Therefore, the turbulence model was used for detailed analysis. However, a few results from the Luo model are presented as well for comparison. The turbulence model is governed by the following empirical equations.
The droplet collision rate is determined by the local shear within the eddy in the suspension mixture and is represented by the following equation [29]
where is the shear rate of the droplet and ςT is the capture efficiency coefficient of turbulent collision. Finally, the aggregation or coalescence rate is determined by the equation presented below [30]. The Brownian effect is negligible in turbulent flows and on droplet scale, so it was excluded.
2.3. Coupled CFD–DEM
Matte settling through the slag was also investigated with CFD coupled to a discrete element method (DEM). With the CFD–DEM method, individual droplets can be simulated by approximating them as soft spheres that are affected by slag flow. In the coupling, CFD is used to calculate the slag flow and drag forces for each droplet, while DEM is used to solve the contact forces and movement of the droplets. Additional models can be used to take more complex phenomena, such as coalescence, into account. CFD and DEM are not computed simultaneously; instead, first CFD solves one time step and transfers the drag forces to DEM, which then calculates until the CFD time step is reached and returns the droplet locations to CFD. Generally, DEM calculates several time steps between each CFD time step as the CFD time steps are longer. The basic principle of CFD–DEM simulation is illustrated in Figure 2.
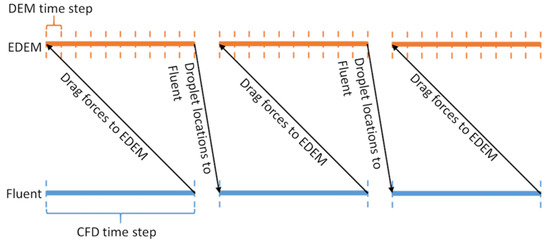
Figure 2.
Illustration of the computational fluid dynamics–discrete element method (CFD–DEM) calculation process.
In CFD–DEM simulation, coalescence was calculated using the bubble coalescence probability by Wang et al. [31], which was calculated for every droplet–droplet contact. If the probability was at least 50%, the droplets were considered to have coalesced.
2.4. Geometry Dimensions and Materials
As CFD–DEM is a computationally demanding method, the FS settler model had to be scaled down for studying the settling phenomenon. The high computational demand is caused by using two methods in parallel and solving interactions of a very large number of individual elements. The geometry for the slag was a cube with 20 cm sides, as presented in Figure 3. As both slag and matte descend from the reaction shaft, the droplet and slag inlet was set at the center of the top face of the cube, while the tapping hole was depicted with a small tube on one side. The inlet and tapping hole had diameters of 15 cm and 1.5 cm, respectively. The slag flow rate (70 t/h) was taken from the literature [6] and scaled down with the reaction shaft diameter (4.5 m) reported in the literature [32]. The matte droplet feed rate was set as 40% of the slag feed rate and varied in size according to a normal distribution. The values of the slag and matte parameters used in the simulation are listed in Table 1.
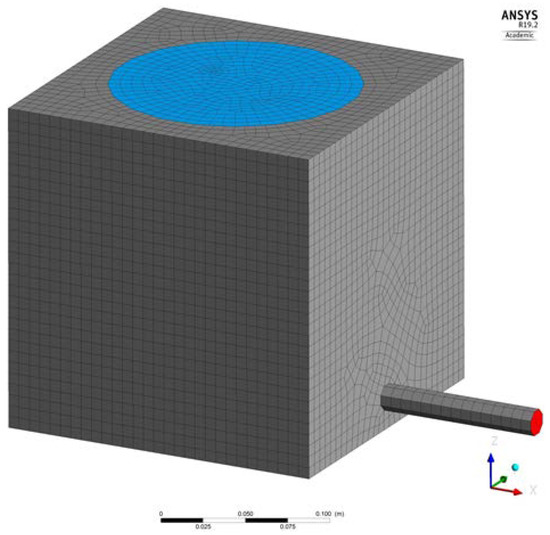
Figure 3.
Geometry and mesh of the CFD model for CFD–DEM simulation. Inlet (blue) on the top and tapping hole (red) on the right side.

Table 1.
Values of the slag and matte parameters.
An additional user-defined model was used to simulate coalescence of the matte droplets. Coalescence was approximated by deleting the coalescing droplets and creating a new one in their center of mass with a mass equal to the sum of the deleted ones. Due to the limitations of the model, coalescence was instantaneous. The maximum size for coalesced droplets was limited to 2 mm, as larger droplets caused the software to use all the available memory due to the coalescence affected too many droplets at once.
This scaled-down settler geometry with similar slag and matte physical properties was modeled with CFD software as well. However, in addition to the previous research in this regard (single particle size of 500 μm) [10] and the CFD–DEM modeling part, in this CFD modeling the particle size distribution (PSD) scheme was also applied. The final selection and distribution of different droplets present in the initial mixture (PSD) were taken from the work of Jun 2018 [33], which is presented in Table 2.

Table 2.
Size distribution of the droplets at the inlet.
Parallel with the development of these computational models, experimental investigations were ongoing on laboratory scale. The kinetics of slag–matte reactions [34,35] at temperatures prevailing in the FSF was studied in a vertical tube furnace in air and argon (oxygen-free) atmospheres simulating the settler area reactions between matte droplets and partly and nonreacted feed particles. Additionally, the main impurity elements (Sb, As, Bi) and pieces of waste electric and electronic equipment (WEEE) [36] were used in the experiments.
3. Results
3.1. CFD Simulation
Coalescence was studied using the Luo coalescence model [27] and the turbulence coalescence model [30]; however, the Luo model over-predicted the results. For example, the coalescence rate was quite high and almost all the smaller-sized droplets were coalesced into large size droplets, and therefore, the concentration of large droplets was high in the scaled-down settler. The results after 20 s are presented in Table 3. The results were obtained at a plane passing through the center of the scaled-down settler at x = 0.

Table 3.
Results for Luo [27] coalescence model.
From the above results it can be concluded that all the smaller size droplets had coalesced into large size droplets and were not present in the settler after 20 s, which reveals that the coalescence rate was unrealistic. However, even though the coalescence rate might not be accurate, the model shows similar flowing behavior as depicted in the CFD–DEM method below. Thus, it can be concluded that the flow is aligned more towards the center of the settler forming a conical shape. The turbulence model was also used in lieu of the Luo model to obtain a comparison, and the results are presented in Table 4.

Table 4.
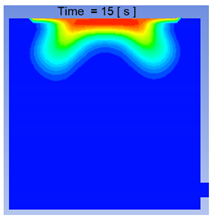
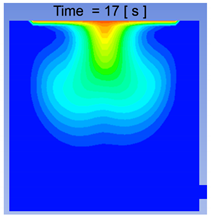
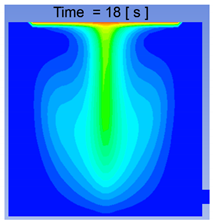
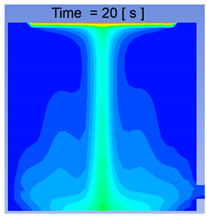
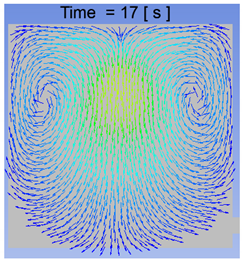
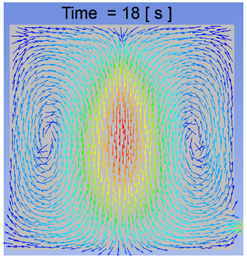
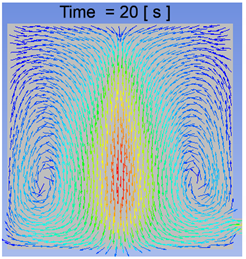
Volume Fraction Contours for 500 μm Droplets at 15, 17, 18, and 20 s.
The volume fraction contours for the small-sized settler, taken at a plane in the center of the settler at x = 0.1 for 500 μm droplets, are presented in Table 4. It can be deduced that coalescence mostly occurred near the top of the slag surface, and as the particles started to settle, they took their own path. Second, the volume fraction was decreasing towards the larger size droplets, which shows that a small number of droplets bigger than 900 μm were present in the settler. Almost all the droplets reached the bottom of the settler within 20 s. In the future, it would be good to focus the study of droplet coalescence on sizes between 500–1000 μm.
The velocity vector profiles for the small settler model with 500 μm droplets are presented in Table 5. The velocity vector profiles confirm the formation of a funnel-shaped flow. After entering the slag layer, the flow channels the droplets towards the center of the settler.

Table 5.
Velocity Vector Contours for 500 μm Droplets at 15, 17, 18, and 20 s.
The volume fraction contours for the full-sized settler taken at the center plane of the settler (x = 0.5) containing the settler inlet and slag outlet are presented in Table 6. These volume fraction contours reveal that most of the coalescence occurred at the surface of the slag. However, a small number of droplets also coalesced during the descending route because of the turbulence underneath the inlet. This chaotic behavior was created because of the reverse flows caused by vortices and slag movement in the upward direction due to the density difference. This phenomenon is presented in the velocity vector profiles in Table 7.

Table 6.
Volume fraction contours for 500 μm droplets.

Table 7.
Velocity Vector Contours for 500 μm Droplets (m/s).
Finally, when we compare the volume fraction contours of the smaller-sized settler presented in Table 4, and the volume fraction contours of the full-size settler presented in Table 6, we can observe a significant difference. This is because in the full-size settler instead of a single funnel-shaped flow, different locally channeled flows are formed, which is exhibited in the profile. The same phenomenon is depicted in the velocity vector profiles in Table 5 and Table 7.
The velocity vector profiles of 500 μm droplets are presented at a plane of the settler center (x = 0.5 m). This vector profile exhibits the development of 500 μm droplets and settling behavior. As the matte and slag mixture enters the settler, the matte droplets start settling, and after separation the slag circulates upwards. This creates a turbulent flow and vortices underneath the inlet illustrated by the vector profiles, which also confirm the formation of the local channeling flows aligned to their centers.
Compared to the 900 μm droplets, 1300 μm droplets are present in the settler in fairly low numbers, which is revealed by the number fraction of the different-sized matte droplets plot in Figure 4 and the volume fraction distribution in Figure 5. Figure 5 shows the volume fraction distribution of different-sized droplets present in the settler at different time intervals. Figure 4 also illustrates that a higher number of small droplets are present in the system, which suggests that their coalescence rate is low, and thus, the coalescence rate is low in general. The dominant droplet size is smaller than 300 μm.
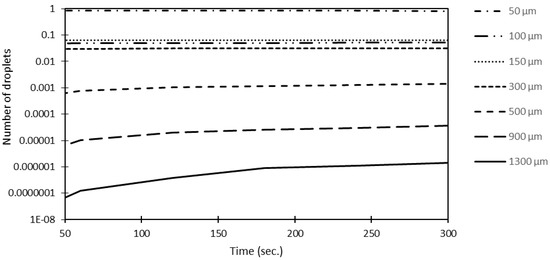
Figure 4.
Number fraction distribution of different-sized droplets inside the settler.
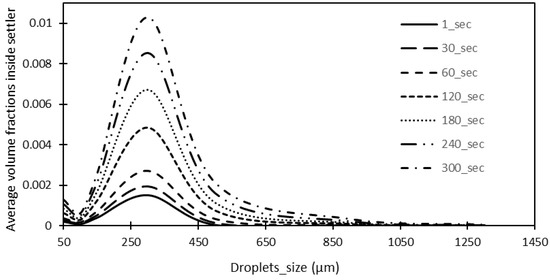
Figure 5.
Volume fraction distribution curves.
The volume fraction distribution curves presented in Figure 5 show that most of the droplets are between 200 μm to 400 μm. The peak of these curves is usually achieved at around 300 μm. This is also an indication that the transition to large droplets above 400 μm is significantly low.
3.2. Coupled CFD–DEM Simulation
The CFD–DEM simulation revealed a strong funneling effect in the settling droplet cloud. The effect was caused by the drag of the settling matte, pulling droplets towards the centerline of the cloud, and subsequently increasing the bulk density as the droplets became more closely packed. This caused an increased settling velocity which, in turn, increased the drag, and thus, created a self-sustaining funneling effect. However, the CFD–DEM simulation did not show the development of two light matte streams that can be seen at 15 s in Table 4. The development of the effect is shown in Figure 6.
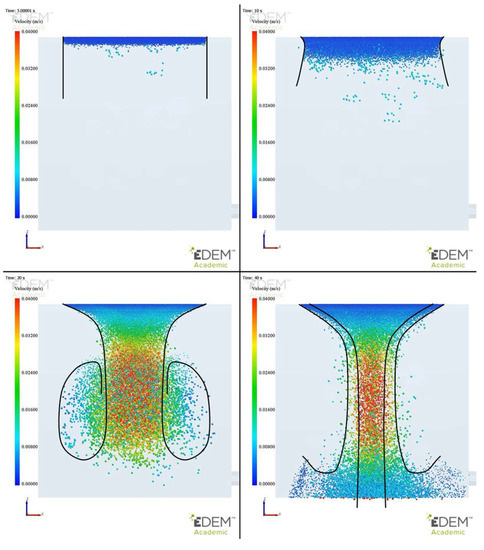
Figure 6.
Formation of the funneling effect in the slag at 5 s, 10 s, 20 s, and 40 s.
The funneling effect increased the settling efficiency of the matte by increasing the settling velocity, as presented in Figure 7. Also shown is a comparison to a calculated velocity. Stokes’s law was used to calculate the settling velocity for an average droplet size for every 0.5 s, while the function calculator in Ansys CFD-Post was used to calculate the average downward slag flow velocity. These were summed to obtain the calculated velocity, which was found to match well with the results from the simulation. The average velocity decreased as the cloud reached the slag–matte interface. The decrease was caused by the slag scattering droplets on the outer sides of the bottom cloud. The scattering was caused by downward flowing slag being deflected by the matte. As the droplets were scattered, some of the smaller droplets were pushed sideways and slightly upwards, prolonging the residence time of the droplets. Some of these droplets were removed through the tapping hole. Also, some of the droplets could have been trapped by the slag flows, preventing them from settling onto the matte layer and leading to copper losses.
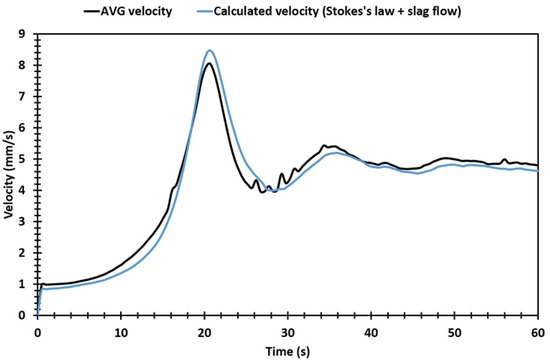
Figure 7.
Average velocity of droplets and calculated velocity.
In addition to the funneling effect, droplet size has a significant effect on settling. The droplet size increases as two droplets collide and coalesce. The droplet size can be seen to increase rapidly near the surface of the slag as drag decelerates the falling droplets. The average diameter of the droplets in the whole slag layer at 60 s was 627 µm. As the droplets started to settle and coalesce, the size increased rapidly, averaging around 1280 µm below a depth of 50 mm, as presented in Figure 8. However, the size distribution and the figure show that a significant number of the droplets coalesced very near the slag surface.
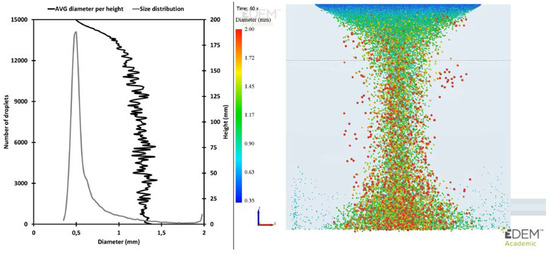
Figure 8.
Droplet sizes in the slag layer at 60 s. The 50 mm settling distance is marked with a line.
The total feed rate was around 25,000 droplets per second. The cloud penetrated the slag layer in around 23 s, during which time over 500,000 droplets were injected in the slag. However, the droplet numbers in the simulation are significantly lower due to the high coalescence rate; 72% of all droplets in the simulation had coalesced. As can be seen in Figure 9, the droplet number peaks at around 135,000 droplets at the 12 second mark, but then begins to decrease. The decrease can be accounted for by the start of the funnel formation, which pulls the droplets closer together and thus enhances coalescence. However, the number of coalesced droplets does not show a similar peak during the funnel formation period, which can be explained by the increasing droplet diameter as the coalesced droplets further coalesce with each other. The average diameter stabilized soon after the funnel effect had fully formed. Also, the number of droplets in the simulation stabilized at around 124,000 after 30 s.
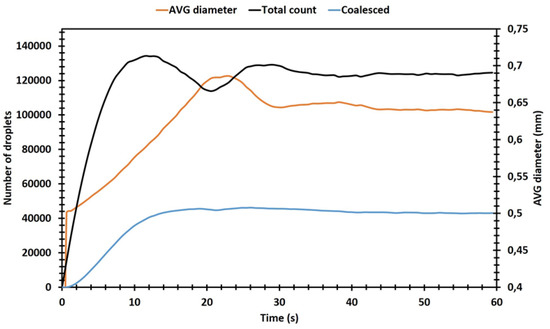
Figure 9.
Droplet count and diameter development during the simulation.
4. Discussion
In the literature, [5,7] research regarding matte droplets settling through the slag phase was conducted at steady state using the Eulerian–Eulerian approach. In addition, the Eulerian–Lagrangian approach has been used to study the paths of individual droplets during settling and the effect of the slag tapping position and velocity on settling [6]. The conclusion drawn in these studies was that mostly droplets of 100 μm and below remained suspended in the slag phase, and that a higher tapping velocity and tap position close to the inlet disturbed the settling and entrapped the matte droplets. Similar conclusions were later drawn when using the Eulerian–Eulerian approach and transition state conditions while studying 100 μm, 300 μm, and 500 μm sized droplets individually [10]. The current investigation continued by adding the coalescence of droplets. Furthermore, instead of mono-sized droplets at the inlet, a mixture of different-sized droplets as reported in literature [33] were used for the inlet conditions, and the results from the full-scale settler were consistent with those reported earlier [6,7,10].
As expected, large droplets settled quickly and droplets of 500 μm and above mostly settled within 90 s. However, small droplets below 500 μm were still settling after 90 s, especially the 100 μm and 50 μm droplets, which were mostly dispersed inside the slag. Additionally, the formation of a vortex under the inlet and chaotic flows due to opposing currents of matte droplets trying to settle [7], and the lighter slag phase moving upwards were likewise observed in this work. Nonetheless, the coalescence rate of large droplets was relatively low, as indicated by the low volume fraction of 900 μm and 1300 μm sized droplets. In the future work, more droplets with a wider size distribution will be used as the inlet condition to get closer to the real situation.
The results in the down-scaled model and industrial scale geometry suggested a funneling settling of the matte phase. However, in the industrial scale simulation, there were several funnels whereas in the small model, only one central funnel formed. Intuitively, it is quite obvious that the large inlet area of the industrial settler would not produce only one single channel for the whole matte phase, but rather, several localized “nucleation” sites from where the funneled settling would start.
The settling of individual matte droplets was simulated using CFD–DEM coupling. The funneling effect was also formed in the slag layer as the drag pulled the droplets towards the centerline of the settling cluster. The funneling effect increased the settling velocity of the droplets, and thus, increased the settling efficiency.
A user-defined model for coalescence was also included in the CFD–DEM simulation. The behavior of the droplets, and consequently, coalescence is practically impossible to observe in a real FS process due to the extreme environment in the furnace. However, the effects of the coalescence in the simulations seemed reasonable: the settling velocity of the droplets increased due to the increasing size of the droplets. Also, coalesced droplets created a relatively large size distribution in the slag layer. Compared to the Eulerian–Eulerian method, the coalescence rate was higher in the CFD–DEM simulation. This difference could have been caused by different methods for solving the droplet–droplet contact or coalescence criteria. Nonetheless, some of the smaller droplets did not coalesce and never settled, and consequently, they were entrained in the slag and would have caused copper losses.
Due to computational instabilities, the maximum droplet size had to be limited to 2 mm. This could have had some effect on settling, as some droplets could have grown more, leading to a smaller number of droplets with a larger average size. They would cause stronger drag, and thus strengthen the funneling effect. However, the number of such large droplets would most likely be relatively low, limiting their effect. Also, very large droplets could break into smaller ones due to inertial forces. Furthermore, a significant majority of the droplets would most likely be much smaller.
The funneling effect and coalescence together formed a kind of feedback loop. Coalescence increased the droplet size which increased drag, and subsequently strengthened the funneling effect. The effect caused the droplets to move closer to each other, which consequently increased the coalescence rate. Both phenomena increased the settling velocity. The results were in good agreement with the values calculated by combining the average slag flow velocity and Stokes’s law velocity of an average-sized droplet.
The slag flow deflecting from the matte surface created a kind of dispersion layer above the slag–matte interface, as some of the smaller droplets were pushed sideways with the slag. This kind of layer has also been reported in the literature [20]. Some droplets from the dispersion layer were sucked by the tapping hole, leading to copper losses. Such a situation can be seen in Figure 6; however, the effect in the simulation is likely over-emphasized by the small geometry as the tapping hole is much closer to the matte–slag interface than it would be in a real settler.
The use of well-established CFD modeling with the commercial and widely used tool ANSYS Fluent, together with a coupled CFD–DEM modeling with EDEM software was the first computational attempt to understand the settling of matte droplets in the FS settler. The results of the scaled-down geometry obtained with both computational approaches suggest that droplet coalescence plays a crucial role in the resulting flow pattern. The matte droplets entering the slag surface layer coalesce rapidly causing accelerated settling which, in turn, drags the droplets towards a central path or channel down to the underlaying matte layer. In the full-scale geometry, in contrast, the flow of matte droplets, although quickly coalescing, seems to follow a more complicated settling pattern. This is believed to be due to the more complicated flow of the continuous slag phase induced by the input material flow.
A comparison of the two computational approaches for the matte settling phenomena can be seen in Figure 10, where the small-scale model results from the CFD and CFD–DEM models are shown. Based on the computational results of the small-scale model of the matte droplets settling through the slag layer, it seems to be fair to conclude that the two approaches used, CFD and coupled CFD–DEM, both predict the settling pattern to be channeled or funneled to a central “trail” of coalescing droplets. However, these results have to be validated by a physical model before this can be confirmed.
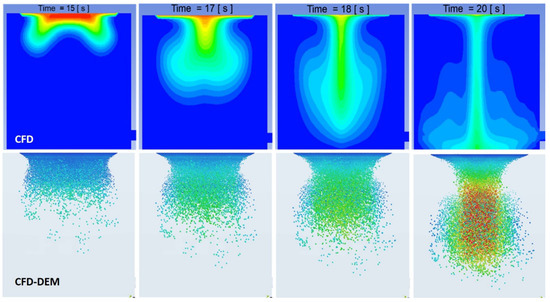
Figure 10.
A comparison of the CFD and CFD–DEM results for matte settling in the small-scale settler model, revealing a similar funneling flow pattern at 15, 17, 18, and 20 s. Upper row: CFD, lower row: CFD–DEM.
The relation of the funneling effect and size of the settling cloud requires further study. In a real FS furnace, the area corresponding to the inlet in the model is significantly larger. The diameter of the reaction shaft can be, for example, 4.5 m compared to the 15 cm of the scaled-down model in this study. Additionally, the inlet area would not be as well defined as in the computational study. Instead, there would be a gradient in the feed density. Further research is needed to evaluate the effect of these factors on the formation and strength of the funneling effect. Moreover, the small geometry of the model may affect the ease of forming the funneling effect as walls close to the cloud may create stronger turbulence in the slag. Thus, larger model geometry should also be studied and the funneling effect experimentally validated with a physical water–oil model. The results of the validation will be presented in a future article.
Further development is needed to improve the accuracy of the coalescence model. An improved coalescence model could decrease memory issues (especially with the CFD–DEM computation), if the droplet size limit were increased. In addition, simulating the formation and effect of spinel particles should be considered. DEM is capable of simulating spinel particles too, but their attachment to droplets and formation require an additional model. The spinel model would also be supplemented by a reaction kinetics model. However, development of these two models would require further development in the software used as well. Additionally, a more powerful computer is required until full-scale settler simulations with CFD–DEM can be considered as even small-scale simulations take a long time. For example, the small cube simulation took over a month of computing and the larger model [9] took over two months with Intel Xeon E3-1230 v5 @ 3.4 GHz.
5. Conclusions
A comparison of two computational approaches, CFD and CFD–DEM, was carried out for the matte settling phenomena in settler geometries. The results of the small-scale model of matte droplets settling through a slag layer suggest that the settling flow pattern is channeled or funneled as a central trail of coalescing droplets. For a sounder conclusion, these results still have to be validated by a physical model. Nevertheless, as a conclusion, the applicability of the coupled CFD–DEM software equal to CFD software for the liquid–liquid system used in this study can be confirmed.
One conclusion regarding the settling pattern of matte droplets in the industrial scale settler geometry, is that it is plausible that the droplets coalesce and form centralized funnels instead of settling uniformly across the whole inlet area. This phenomenon is beneficial for the efficient separation of the slag and matte phases, and thus, for the recovery of the metal. Consistently with industrial reality, the smallest droplets were very slow to settle, and consequently they require a very long time or a very thin slag layer to reach the matte layer before the slag leaves the settler through the tapping hole. One option could be to operate with continuous tapping and a thin slag layer.
The studied case clearly indicated that the current computing power is still the limiting step in computer modeling of a full-scale industrial settler with realistic droplet coalescence calculation. Although there are some similarities in the settling pattern in the small- and full-scale models, they are too different for conclusions to be made based on the small-scale model. This poses a challenge for the validation of the full-scale model results as there are no possibilities for direct observations of the flow phenomena in the molten slag layer inside the settler. So far, the only option is to compare copper losses from the CFD model with industrial data [10].
Author Contributions
Conceptualization, all; methodology, J.-P.J. and N.A.K.; analysis, all; investigation, J.-P.J. and N.A.K.; resources, A.J.; writing the manuscript, J.-P.J. and N.A.K.; review and editing, A.J.; supervision, A.J.; funding acquisition, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
The funding from the Steel and Metal Producers’ Fund in Finland, and from the Aalto University School of Chemical Engineering is greatly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Arslan, C.; Arslan, F. Recovery of copper, cobalt, and zinc from copper smelter and converter slags. Hydrometallurgy 2002, 67, 1–7. [Google Scholar] [CrossRef]
- Sarfo, P.; Das, A.; Wyss, G.; Young, C. Recovery of metal values from copper slag and reuse of residual secondary slag. Waste Manag. 2017, 70, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Kambham, K.; Sangameswaran, S.; Datar, S.R.; Kura, B. Copper slag: Optimization of productivity and consumption for cleaner production in dry abrasive blasting. J. Clean. Prod. 2007, 15, 2007. [Google Scholar] [CrossRef]
- Kojo, I.V.; Storch, H. Copper production with Outokumpu Flash Smelting: An Update. In International Symposium on Sulfide Smelting, Proceedings of the Sohn International Symposium: Advanced Processing of Metals and Materials, San Diego, California, 27–31 August 2006; TMS: Warrendale, PA, USA, 2006; Volume 8. [Google Scholar]
- Xia, J.L.; Ahokainen, T.; Kankaanpää, T.; Järvi, J. Numerical Modeling of Flow and Heat Transfer in the Settler of a Copper Flash Smelting. In Proceedings of the 6th International Symposium on Heat Transfer, Beijing, China, 15–19 June 2004. [Google Scholar]
- Xia, J.L.; Ahokainen, T.; Kankaanpää, T.; Järvi, J.; Taskinen, P. Numerical modelling of copper droplet setting behavior in the settler of a flash smelting furnace. In Proceedings of the European Metallurgical Conference, EMC 2005, Dresden, Germany, 18–21 September 2005. [Google Scholar]
- Xia, J.L.; Ahokainen, T.; Kankaanpää, T.; Järvi, J.; Taskinen, P. Flow and heat transfer performance of slag and matte in the settler of a copper flash smelting furnace. Steel Res. Int. 2007, 78, 155–159. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, J.; Chen, Z.; Mao, Y. Influence Analysis of Air Flow Momentum on Concentrate Dispersion and Combustion in Copper Flash Smelting Furnace by CFD Simulation. JOM 2014, 66, 1629–1637. [Google Scholar] [CrossRef]
- Jylhä, J.-P.; Jokilaakso, A. CFD-DEM modelling of matte droplet behaviour in a flash smelting settler. In Proceedings of the 58th Conference of Metallurgists Hosting Copper 2019, Vancouver, BC, Canada, 18–21 August 2019. [Google Scholar]
- Khan, N.A.; Jokilaakso, A. Dynamic Modelling of Molten Slag-Matte Interactions in an Industrial Flash Smelting Furnace Settler. In Proceedings of the Extraction 2018, Ottawa, ON, Canada, 26–29 August 2018. [Google Scholar]
- Niemi, T. Particle Size Distribution in CFD Simulation of Gas-Particle Flows; Aalto University: Espoo, Finland, 2012. [Google Scholar]
- Warczok, A.; Utigard, A.T. Settling of copper drops in molten slags. Met. Materi. Trans. B 1995, 26, 1165–1173. [Google Scholar] [CrossRef]
- Yu, D.; Mambakkam, V.; Rivera, H.A.; Li, D.; Chattopadhyay, K. Spent Potlining (SPL): A myriad of opportunities. In Aluminium International Today; Quartz Business Media Ltd.: Redhill, Surrey, UK, 2015. [Google Scholar]
- Elliott, F.J.; Mounier, M. Surface and Interfacial Tensions in Copper Matte-Slag Systems, 1200 °C. Can. J. Met. Mat. Sci. 2013, 21, 415–428. [Google Scholar] [CrossRef]
- Phelan, D. The Modelling of Matte Droplet Coalescence in the Vanykov Process. Master’s thesis, University of Wollongong, Wollongong, Australia, 1999. [Google Scholar]
- Cheng, X.; Cui, Z.; Contreras, L.; Chen, M.; Nguyen, A.; Zhao, B. Introduction of Matte Droplets in Copper Smelting Slag. In Proceedings of the 8th International Symposium on High-Temperature Metallurgical Processing, Gewerbestrasse, Switzerland, 9 February 2017; pp. 385–394. [Google Scholar]
- Iwamasa, P.K.; Fruehan, R.J. Separation of Metal Droplets from Slag. ISIJ Int. 1996, 36, 1319–1327. [Google Scholar] [CrossRef][Green Version]
- Miettinen, E. Thermal Conductivity and Characteristics of Copper Flash Smelting Flue Dust Accretions. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2008. [Google Scholar]
- De Wilde, E.; Bellemans, I.; Campforts, M.; Guo, M.; Blanpain, B.; Moelans, N.; Verbeken, K. Investigation of High-Temperature Slag/Copper/Spinel Interactions. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2016, 47, 3421–3434. [Google Scholar] [CrossRef]
- Jiménez, F.; Ríos, G.; Martinez, J.; Fernández-Caliani, J. Speciation of copper in flash, converter and slag-cleaning furnace slags. In Proceedings of the Copper 2013, Santiago, Chile, 1–4 December 2013. [Google Scholar]
- De Wilde, E.; Bellemans, I.; Zheng, L.; Campforts, M.; Guo, M.; Blanpain, B.; Moelans, N.; Verbeken, K. Origin and sedimentation of Cu-droplets sticking to spinel solids in pyrometallurgical slags. Mater. Sci. Tech. 2016, 32, 1911–1924. [Google Scholar] [CrossRef]
- Bellemans, I.; De Wilde, E.; Moelans, N.; Verbeken, K. Metal losses in pyrometallurgical operations—A review. Adv. Colloid Interface Sci. 2018, 255, 47–63. [Google Scholar] [CrossRef] [PubMed]
- Taskinen, P.; Jokilaakso, A.; Lindberg, D.; Xia, J. Modelling copper smelting–the flash smelting plant, process and equipment. Min. Proc. Ext. Met. 2019. [Google Scholar] [CrossRef]
- DEM Solutions Ltd. EDEM 2019.1 User Guide; DEM Solutions Ltd.: Edinburgh, UK, 2019. [Google Scholar]
- Fagerlund, O.K.; Jalkanen, H. Microscale Simulation of Settler Processes in Copper Matte Smelting. Met. Materi. Trans. B 2000, 31, 439–451. [Google Scholar]
- De Wilde, E. Methodology Development and Experimental Determination of the Origin of Sticking Copper Droplets in Pyrometallurgical Slags. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2015. [Google Scholar]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. Am. Inst. Chem. Eng. J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Z.; Zhou, P.; Yu, J.; Liu, A. Numerical simulation of flow characteristics in settler of flash furnace. Trans. Nonf. Met. Soc. China 2012, 22, 1517–1525. [Google Scholar] [CrossRef]
- Ping, Z.; Ping, J.Y.; Rong, H.C.; Chi, M. Settling mechanism and influencing factors on matte droplets in settler slag of copper flash smelting furnace. Chin. J. Nonf. Met. 2006, 16, 2032–2037. [Google Scholar]
- Kamp, A.M.; Chesters, A.K.; Colin, C.; Fabre, J. Bubble coalescence in turbulent flows: A mechanistic model for turbulence-induced coalescence applied to microgravity bubbly pipe flow. Int. J. Multip. Flow 2001, 27, 1363–1396. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Jin, Y. Theoretical prediction of flow regime transition in bubble columns by the population balance model. Chem. Eng. Sci. 2005, 60, 6199–6209. [Google Scholar] [CrossRef]
- Davenport, W.G.; Partelpoeg, E.H. Flash Smelting: Analysis, Control and Optimization, 1st ed.; Pergamon Press: New York, NJ, USA, 1987; pp. 22–28. [Google Scholar]
- Jun, Z.; Zhuo, C. Smelting Mechanism in the Reaction Shaft of a Commercial Copper Flash Furnace. In Proceedings of the Extraction 2018, Ottawa, ON, Canada, 26–29 August 2018. [Google Scholar]
- Guntoro, P.I.; Jokilaakso, A.; Hellstén, N.; Taskinen, P. Copper matte—Slag reaction sequences and separation processes in matte smelting. J. Min. Metall. B 2018, 54, 301–311. [Google Scholar] [CrossRef]
- Wan, X.; Shen, L.; Jokilaakso, A.; Eriç, H.; Taskinen, P. Experimental approach to matte-slag reactions in the flash smelting process. Min. Proc. Ext. Met. Rev 2020, in press. [Google Scholar] [CrossRef]
- Wan, X.; Fellman, J.; Jokilaakso, A.; Klemettinen, L.; Marjakoski, M. Behavior of waste printed circuit board (WPCB) materials in the copper matte smelting process. Metals 2018, 8, 887. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).