1. Introduction
Over the last decade, smart meters have been rapidly deployed around the world. Around 86 million and 11 million smart meters have been installed by large and small suppliers in the US and UK respectively by the end of 2018 [
1,
2]. Almost 90% of these meters were installed for residential customers. One of the main objectives of smart metering in residential sectors is to encourage users to consume less energy by raising awareness about their consumption levels. Smart meters provide information on cost and amount of energy consumption in near real-time for both suppliers and consumers. Regarding the households, huge amounts of fine-grained data on the use of energy not only provide them with more accurate bills but also with valuable information on their electricity consumption habits and time-based pricing rates. This information through demand response and incentivization programs would help them to reduce their energy usage during peak hours and schedule their appliances according to electricity prices. High-resolution data generated by smart meters, on the other hand, provide suppliers with several controlling functions such as power quality monitoring and power loss identification. Moreover, it opens many doors of opportunities in electricity load analysis such as load forecasting with high accuracy at lower aggregation levels [
3,
4].
Electrical load forecasting is the prediction of the load demand that an electricity consumer will have in the future. Load forecasts help suppliers to balance supply and demand and to ensure the reliability of power grids at the time of power deficiency. Load forecasts are also important for electricity traders to balance their electricity purchase and sales [
5]. Load forecasting is performed in a wide range of time horizons aiming at different targets: short-term load forecast (a few minutes to 1 day ahead) to adjust supply and demand; medium-term load forecast (1 day to 1 year ahead) to plan outage and maintenance and long-term load forecast (more than 1 year ahead) to plan the development of power infrastructures. Load forecasting is also performed in various aggregation levels when it is applied to the areas with different geographical scales such as a country, city, small communities or a building. The forecasting task becomes more challenging when it comes to lower aggregation levels such as a building level since, many fluctuating factors affect a building’s energy consumption with varying degrees such as weather parameters, building properties, Heating, Ventilating and Air-Conditioning (HAVC) facilities and the consumption behavior of occupants [
6,
7].
A large number of studies on accurate short-term load forecasting has been reported in recent years due to its impact on the efficient operation of power systems and the economy. Furthermore, many studies have benefited from smart metering data to develop more advanced models for load forecasting at individual building levels. The methods for predicting building energy consumption generally are classified into two categories: engineering (physical) and data-driven techniques. Engineering methods use mathematical equations to present the physical components and thermal performance of buildings. However, they need high details about different parameters of the buildings that are not always available. Moreover, a high level of expertise is required to perform expensive and elaborate computations. On the other hand, data-driven approaches do not need such detailed data about the simulated building and instead learns from real-time or historical data. These approaches are further classified into two groups: statistical and AI-based techniques [
8,
9].
Statistical methods use historical data as an aim for correlating energy consumption with the most important variables as inputs. Therefore, a larger amount of historical data with high quality plays an important role in the effectiveness of statistical models. Traditional linear statistical models such as Gaussian mixture models (GMM), Conditional demand analysis (CDA), Regression models and auto autoregressive moving average (ARMA) and ARIMA, have remained the baseline for time series prediction with widespread use in many applications [
10]. Although it is easy to use statistical techniques, the basic assumption of such models is based on the fact that time series are considered linear and therefore follow a specifically known distribution of statistics. Numerous machine learning models have been developed to overcome these limitations. The models based on Support Vector Machines (SVM), as well as Classification and Regression Trees (CART), are among the successful machine learning techniques used in time series forecasting and energy applications.
Over the past decades, many researchers have investigated the application of AI-based techniques in forecasting problems. Among AI-based techniques, Artificial Neural Networks (ANNs) with different structures have been widely applied in the load forecasting domain [
11]. ANNs similar to statistical methods use historical data to build a model. However, with hidden layer structures and learning ability offer several advantages over statistical and classical machine learning techniques for time series forecasting. They are considered data-driven and self- adaptive methods which can capture subtle and functional patterns through a training process on historical records of data, even if the underlying relationship between input and output variables is complex or unknown. Nevertheless, the neural networks with shallow structures have the disadvantage of assuming that all inputs and outputs are independent of each other, even when dealing with sequential data [
12].
Recent studies in time series forecasting have shown the better performance of prediction models using neural networks with deep architecture. Long Short-Term Memory (LSTM) network which was first proposed by [
13], is a variation of deep learning concept which was designed specifically to learn the short-term and long-term dependencies present in sequential data. LSTM has been popular with excellent accuracy in the realm of sequence learning like natural language translation and speech recognition [
14]. In recent years there has been an increase in the number of studies on the application of LSTM networks and their variants in short-term load forecasting.
According to the literature, most classical and AI-based methods specifically deep techniques developed for load forecasting, require sufficient historical load data for training. At the building level, they mainly have access to the historical energy consumption of the building under study and utilize it for training the model. Subsequently, for performance evaluation, they use the future profile of the same house or building. Similarly, in higher aggregation levels such as a community or a substation level, the models are trained on aggregated historical consumption of buildings and are tested on the future profile of the same buildings. Typically, the low testing error of the models guarantees the precise prediction and the small difference between train and test error ensures the models’ generalization ability. Moreover, many of the studies use additional information and build multivariate models based on consumer behavior [
15], weather and calendar parameters [
16] appliance measurements [
17], etc. to improve the forecasting accuracy.
However, there are still some issues about the forecasting accuracy and generalization ability of such models which have not been largely addressed. For example, to what extent the generalization ability can be expanded or trusted and what happens to the model forecasting accuracy if we only provide them with consumption data. The first question focuses on the scalability of the models; how successful the forecasting models are when tested on a different profile that they are not previously trained on. The test profiles could be quite different from the trained ones in terms of consumption patterns or average daily and yearly consumption. This may happen in scenarios when historical information on a building’s energy consumption is not accessible and we can still rely on predictive models trained on available historical profiles. For instance, if a new house profile is added to a community, or a new smart meter has been installed. The model developed in these situations can also be less expensive in terms of complexity and computation time. The second question focuses on how powerful a model can be if we only have access to anonymized data on historical energy consumption due to privacy issues or lack of other data sources.
This paper investigates the mentioned scenarios with a focus on short-term load forecasting at an individual building level. For this purpose, we develop four baseline models to predict hourly residential load demand and evaluates their predictive accuracy and generalization ability in the given scenarios. The models are chosen from the category of most-widely used machine learning methods for energy prediction known as ANNs, Support vector Machines, regression trees (CART) and LSTM with standard architecture. They are trained on consumption data of various load profiles and tested on unseen houses with different levels of hourly load volatility. Furthermore, the sensitivity of the models on the size of training data and the number of input variables will be tested and a comprehensive analysis of forecasting results will be provided. The developed models are expected to learn various load profiles relying on the built-in information in time series data and are aimed at improving generalization ability and increasing model robustness. The models that produce low-prediction errors on multiple houses can further be used as representative predictive models for a group of houses in a community. In demand response applications, this can potentially remove the need to build separate forecasting models per house profile within the community of houses.
The paper is structured as follows.
Section 2 provides an overview of the literature.
Section 3 and
Section 4 briefly presents the architecture and design considerations of the implemented forecasting techniques. Then,
Section 5 introduces the performance metrics for model evaluations. The dataset used in our analysis is described in
Section 6. The experimental results and discussion are provided in
Section 7. The paper ends with a conclusion in
Section 8.
2. Related Work
There are many forecasting models that have been investigated and proposed since the 1970’s for energy predation. Among them, statistical techniques have been extensively applied in load demand forecasting problems. For example, in [
18] the authors developed one-day-ahead forecasts on hourly and daily electricity loads of a house using both simple and multiple regression analyses. They utilized weather parameters as the predictor variables and concluded that models trained on the daily dataset provide more accurate forecasting results. S.Sp. Pappas et al. in [
19], proposed a method for electricity consumption and price forecasting using AutoRegressive Moving Average (ARMA) models based on adaptive multi-model partitioning theory. Their results show that the proposed method could apply to online modeling and noisy input data.
There have been some hybrid load forecasting approaches that are based on statistical techniques. For instance, XiaoshuLü et al. [
20] presented a hybrid model based on a physical–statistical approach to improve forecast accuracy in energy and building applications. The physical model was developed to define the physical concepts of energy streams while the statistical technique was designed to consider model inconsistencies and specific diversity of buildings.
Support Vector Regression has also been applied in time series prediction as well as power load demand forecasting. In [
21] three Support Regression Models and an improved SVR variant utilizing optimization algorithms were used to predict the day-ahead electricity load. The models’ effectiveness centered on the small size of training data and their online learning functionality. In [
22] we can find a comprehensive overview of SVR applications in time series prediction as well as power load demand forecasting. Many researchers have also attempted to apply the Classification and Regression Trees (CART) techniques to improve the load forecast accuracy. For instance, Lahouar.A. et al. [
23] proposed a model based on random forests for short term load forecast with special attention to load profile, holidays and customer behavior. Similarly, researchers in [
7,
24] utilized environmental and calendar features to develop a method for electric load forecasting based on Decision Tree and algorithms.
Recent studies have shown the better performance of prediction models using AI-based techniques due to their ability to learn nonlinearities between inputs and outputs. Among AI-based techniques, artificial neural networks have been successfully applied in the forecasting domain. Nasreen K. Ahmed et al. [
25] performed an empirical comparison of machine learning models for time series forecasting. In addition to the classical techniques, they analyzed several variations of artificial neural networks. The experiments demonstrated that multilayer perceptron and the gaussian process regression outperform other state-of-the-art models. There are also some studies that discuss the hybridization of different ANN approaches and are successfully applied to short-term load forecasting. In [
26] Hamid R. Khosravani et al. developed hybrid models based on different neural network architectures and genetic algorithms with several optimization parameters to predict electric power demand at the Solar Energy Research Center. The comparison results with an autoregressive baseline model reveal that the models based on the multi-objective genetic algorithm outperformed the model based on computational and empirical methods with lower complicity. Kuihe Yang et al. [
27] proposed an ANN-based method with fuzzy logic to develop models with fewer complexities and to improve the accuracy of forecasts.
There have been numerous studies that utilized optimization algorithms to optimize the structural and training parameters of ANNs in forecasting problems. For example, Chaturvedi et al. [
28] have demonstrated the effectiveness of training neural networks with a Genetic algorithm as an optimization strategy. A review study on different variants of artificial neural networks in the field of short-term load forecasting emphasizes that a combination of neural networks with evolutionary algorithms could outperform the singles models in terms of forecasting accuracy [
29].
Over the last decade, neural networks with deep structure have increasingly attracted the attention of researches in prediction problems. Compared to shallow networks, they benefit from many hidden layers, exponentially fewer neurons, better activation functions, and parameter initialization techniques as well as effective learning algorithms. Different versions of deep neural networks are recently being employed in energy prediction context, especially LSTM networks and their variance due to their capability to capture the temporal behavior of time series data. Daniel. M et al. [
30] investigated the effectiveness of LSTM-based architectures for building level energy load forecasting. They applied two standard and Sequence to Sequence (S2S) architectures for the hourly forecast of a residential load dataset with one-minute and one-hour resolutions. Experimental results showed that the standard LSTM performing better in one-hour resolution data while S2S performed well on both datasets. In another study by Kong et al. [
31] on short-term residential load forecasting an LSTM-based framework has been assessed for both individual and aggregated prediction levels. The comparison results with several state-of-the-work approaches demonstrated the superiority of LSTM for individual residential load forecasting. In terms of aggregated (substation) level, the aggregation of all individual forecasts yielded better results than the direct forecast of aggregated loads. Agrawal et al. [
32] Introduced a deep-structure RNN-LSTM network at a higher aggregation level; ISO New England energy market using daily, monthly and weekly features to produce hourly predictions over a one-year period. Similar to the approaches using shallow ANNs, some studies explored the combination of LSTM with other models or optimization algorithms. For instance, in [
33] a CNN-LSTM neural network was proposed to predict the energy consumption of residential buildings with higher accuracy. The CNN layer was used to extract complex features influencing energy consumption and the LSTM layer was fed with the features to model the temporal information in time series components. Mamun et al. [
34] and Bouktif et al. [
35] investigated the effectiveness of hybrid deep neural networks based on LSTM and genetic algorithms for load forecasting on the energy market and metropolitan’s electricity consumption data sets. Application of feature selection in [
35] proved that using only optimal lagged features as the input to the LSTM model produces the lowest forecasting error for both medium-term and long-term horizons.
3. Modeling Techniques
In this paper, four modeling techniques are used for energy load forecasting: Support Vector Regression (SVR) with Radial Basis Function kernel, Gradient Boosting Regression Trees (GBRT) driven from Classification and Regression Tree (CART) analysis, feedforward neural networks (FFNNs) and LSTM networks. The first two methods belong to the category of classical machine learning techniques and the other two belong to AI-based machine learning techniques with shallow and deep structures respectively. In the following, the detailed information about each model is provided.
3.1. Support Vector Regression (SVR)
SVR is an extension of the support vector machine (SVM) algorithm for numeric prediction or regression tasks. SVM is one of the popular machine learning algorithms used for classification tasks. The SVR identifies and optimizes the generalization bounds given for regression [
36]. The formulation of SVR for time series prediction is expressed as follows. Given training data
where
are input vectors and
are the associated output value of
, then the SVR is an optimization problem as follows:
where
maps to a higher dimensional space and
is the upper training error (
is the lower) subject to the
-insensitive tube
. The parameters that control the output of the regression are the error cost C, the width of tube
, and the mapping function,
[
37]. The constraints imply that most data
are put in the tube
. If
is not in the tube, there is an error
or
which we would like to minimize the objective function.
is always zero in traditional least-square regression and data is not mapped to higher dimensional spaces. The SVR formulation theory is similar concerning SVM, and once equipped, the SVR will produce predictions using the following formula:
We used a Radial Basis Function (RBF) as the kernel function due to its ability to capture non-linear relationships between inputs and outputs. The RBF kernel on two samples
and
, represented as feature vectors in the input space, is defined as:
where
is the squared Euclidean distance between the two feature vectors and
is a free parameter.
3.2. Gradient Boosted Regression Tree
Gradient Boosted Regression Trees (GBRT) is a powerful data-driven technique based on a constructive ensemble strategy and is widely used in non-parametric prediction problems. The GBRT algorithm is a variant of Gradient Boosting Machine (GBM) for regression trees which was originally derived by Friedman (2002) [
38].
Two main algorithms define the GBRT model: the decision tree models as the base (weak) learners and gradient boosting algorithm to consecutively fit new models aiming at reaching to more accurate estimation [
39].
The target of GBM algorithm is to find an approximation
to a function
that minimizes a loss function
; where
is the real output, and
is the target value. The loss function that is selected in our problem, is the squared error
function as the commonly used loss functions for continuous targets and expressed as follows:
The negative gradient is simply computed as follows:
The simplicity of the gradient computation will facilitate the residual refitting of the GBM algorithm. The concept behind this loss function is to put penalties on large residuals while neglecting small deviations from the target outputs.
In the GBM algorithm with decision trees as the base learners, the first step is to construct a base tree
using a training dataset
with size
. Then for the iterations from 1 to
, the negative gradients are computed and a new tree
is fitted. Each tree is further updated according to the best gradient step
and is added to the ensemble. After
iterations, all the regression trees which added sequentially to the ensemble form the output of the algorithm as a combination of weak learners [
40].
3.3. Feed Forward Neural Network (FFNN)
An ANN is a system of processing units (neurons) that can be linked together in different ways and estimate various non-linear and arbitrary patterns. In a feed-forward architecture (FFNN), there is no feedback and intra-layer connections between neurons. The weights and bias of the network are estimated using a training algorithm such as the back-propagation algorithm. This algorithm measures the error of output every time and feeds back this information to the network to reduce the error up to an acceptable predefined value. Further, more details on back-propagation algorithms are described in [
41].
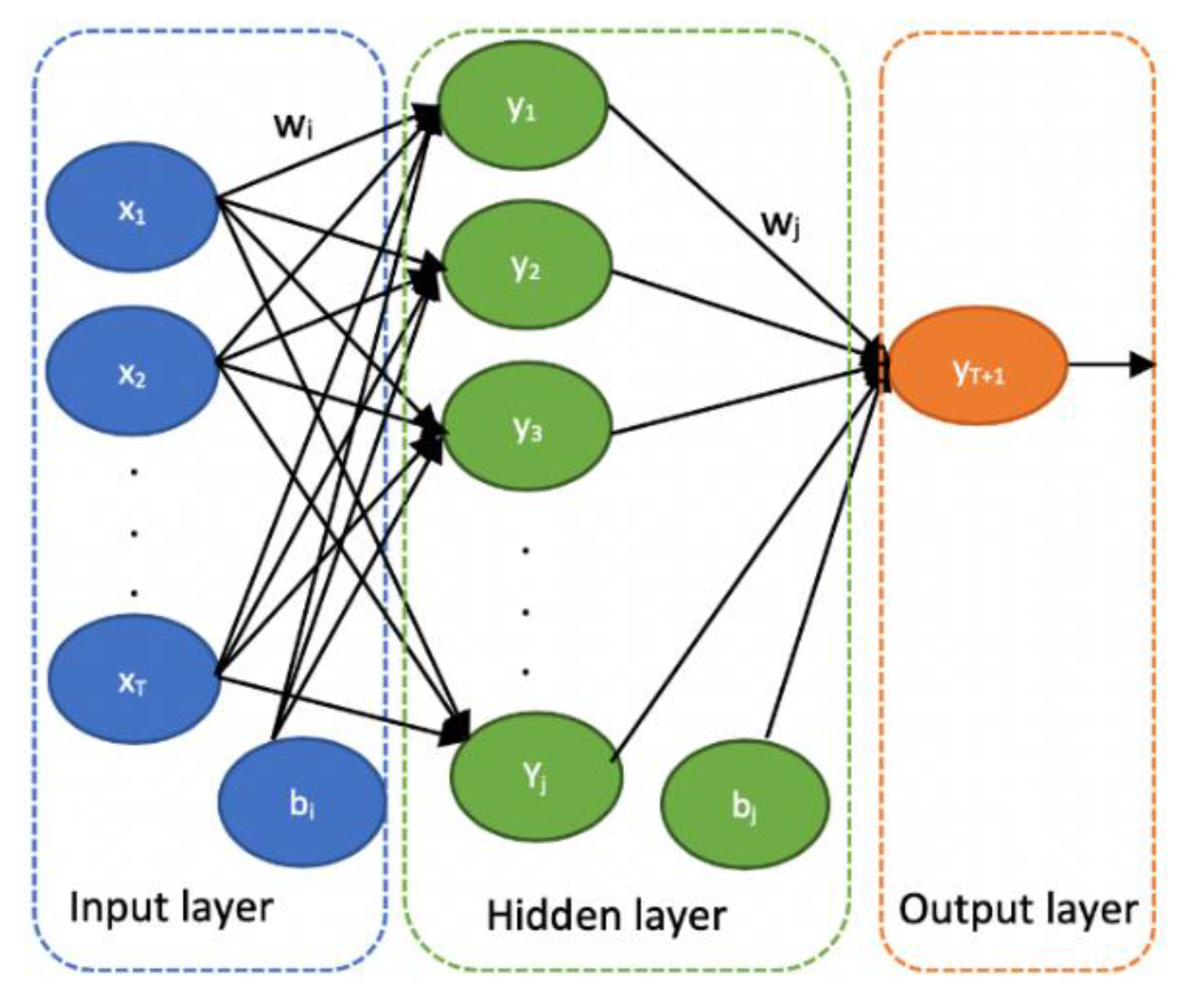
The input values in an MLP structure are weighed through weight matrices and the output of neurons is determined through an activation function. The structure of the Artificial Neural network that we used in our study illustrated in
Figure 1. In the Feed Forward Neural Network illustrated above, given an input sequence
indicating consumption values from previous T time steps, it computes output y at the next time step
by the following equations:
where
denotes the input to hidden weight vector,
denotes hidden to output weight vector,
and
denote bias vectors,
refers to a non-linear hidden activation function while
refers to a linear function and
is the number of neurons in the hidden layer.
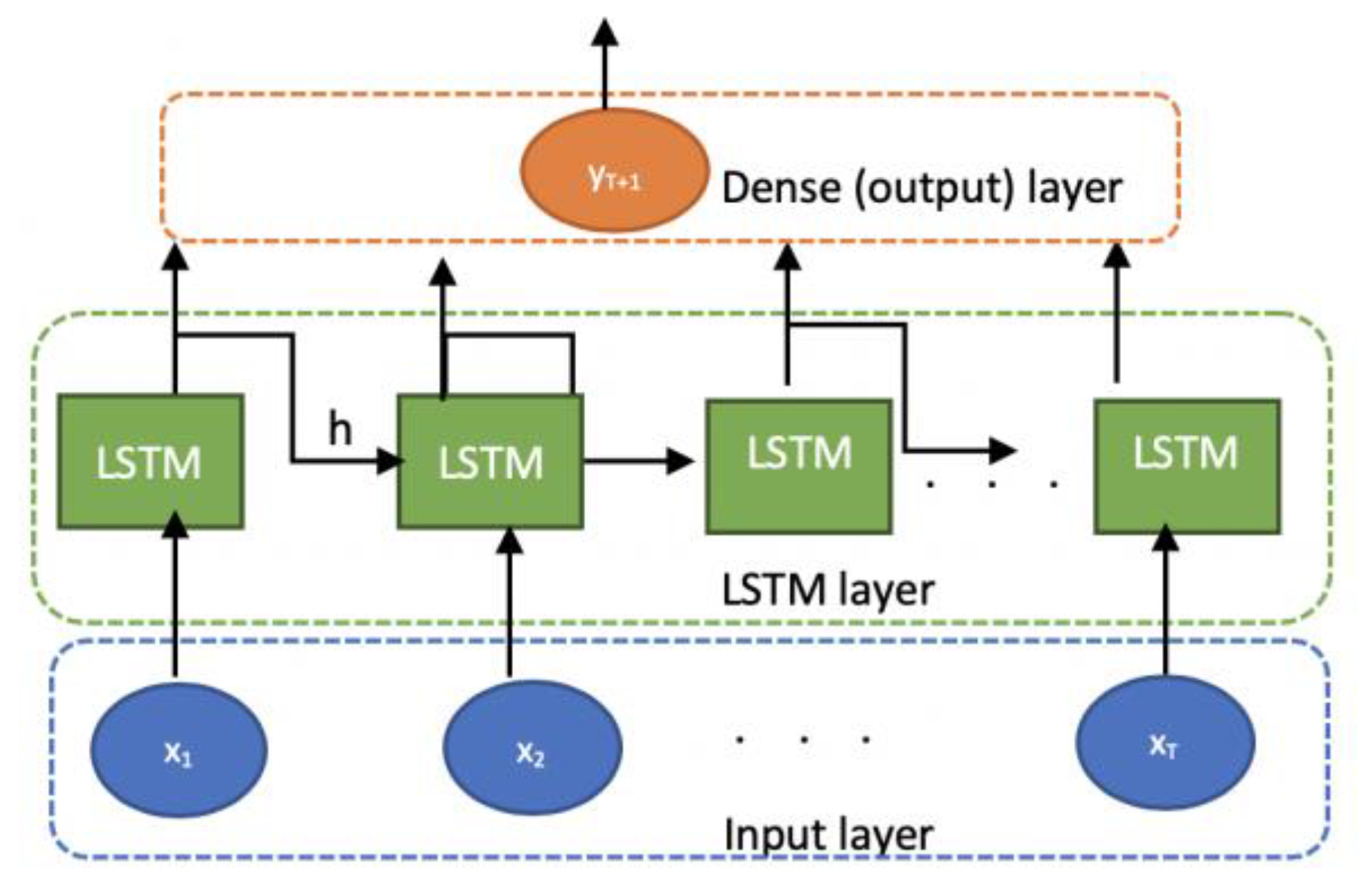
3.4. Long-Short Term Memory Network (LSTM)
The LSTM is a variant of Recurrent Neural Network (RNN) which is specially designed for time series data. The RNNs are neural networks that use feedback connections among the nodes to remember the values from previous time steps. Therefore, they will be able to capture the temporal behavior of time series data. Each neuron, in a conventional RNN, receives the input and its output from the previous step
However, on long sequences, they have the problems of vanishing or exploding of gradients over many time steps. The LSTM addresses this problem and empowers RNNs algorithms using internal memory cells [
31,
42]. They converge faster and utilize memory cells to store information for long and short periods of time. Regarding power data showing obvious characteristics of time series data with cycles, the history information from LSTM can be advantageous to load forecasting. The structure of the LSTM Network applied to our problem is illustrated in
Figure 2.
In an LSTM network, given an input sequence
, it computes an output as follows:
where
denotes the hidden-output weight matrix,
denotes bias vector and
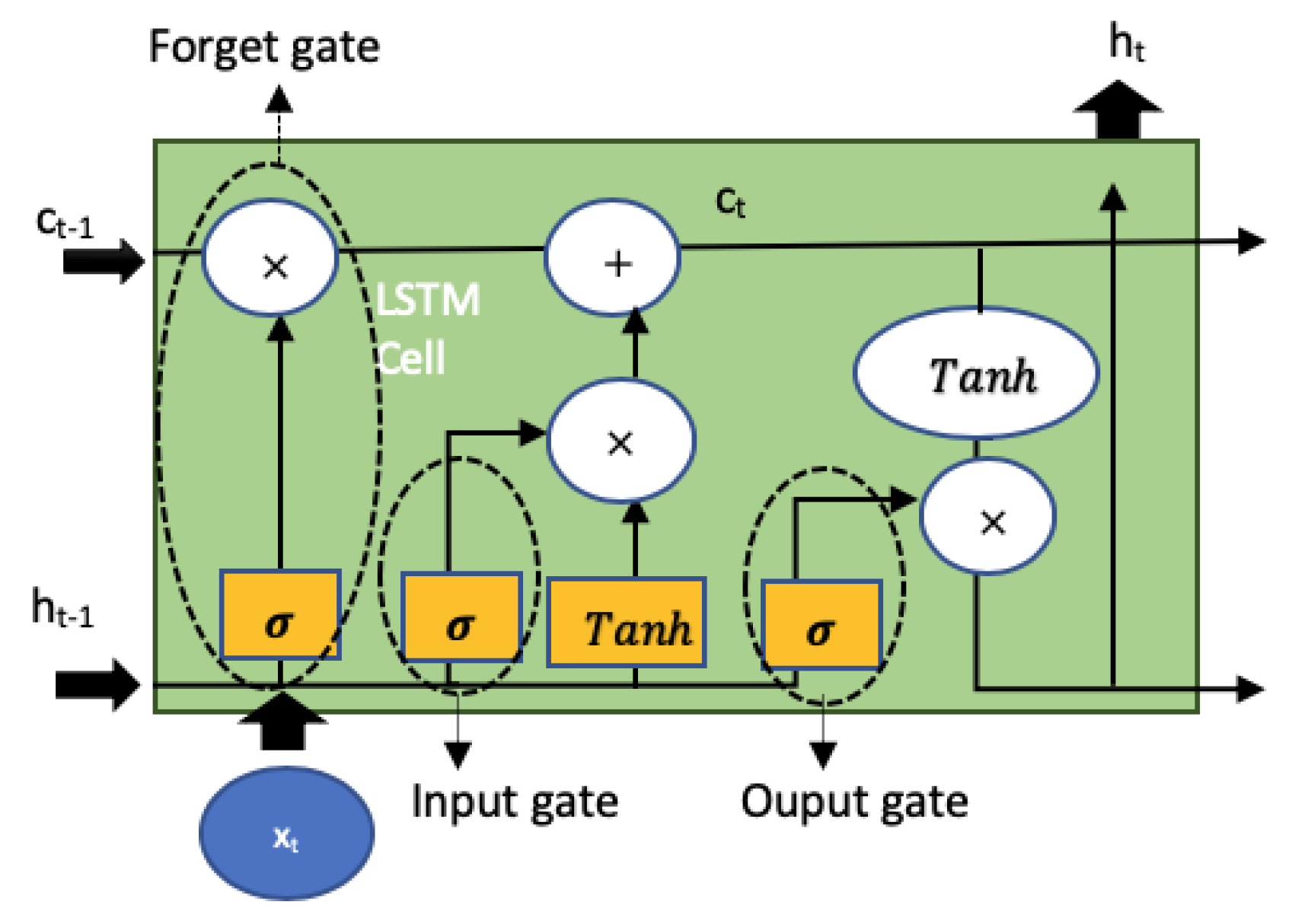
denotes the hidden vector and is computed from the LSTM cell (block). A common LSTM block illustrated in
Figure 3. An LSTM cell has three gates: an input gate to identify important information and preserve it in a long-term memory called the cell state
, an forget gate to decide what information needs to be forgotten from the previous cell sate
and an output gate to decide what to send to the next sequence.
Once an input
enters the LSTM cell, it is passed through a logistic sigmoid function
and input gate
[
42]:
Then the output of forget gate is computed as:
To scale the output of LSTM activation function, the output gate
is expressed as:
The transient ‘memory’ value of the activation function,
is given as:
where
in the input vector of input gate and computed as:
Here
denotes the element-vise multiplication of the vectors. The LSTM output
at time step
finally is computed as:
During the training process, the weight matrices and and bias vectors and are learned by an optimization algorithm.
4. Data Normalization and Parameter Tuning
As mentioned in
Section 1, the purpose of this research is to implement the models which are independent of external factors. Therefore, we feed all the models with the past load consumption values in the previous time steps known as load lags. Although all lag variables (features) have the same scale, we scaled data for the FFNN and LSTM networks using Minmax normalization, however, for the other two algorithms (SVR and GBRT) we used the original data. The main reason is that in the AI-based networks normalizing or standardizing the input data usually prevents computational problems and improves the functionality of training algorithms. The scaling method transforms the value of each variable between zero and one as follows:
For ANN and LSTM as AI-based networks, this transformation is highly recommended to prevent computational problems and improve the functionality of training algorithms. While the choice of scaling for the other two models depends on the problem and the scale of features. After testing the performance of SVR and GBRT on the validation set, with and without data normalization we found that SVR performs better without scaling while GBRT was not significantly affected, with and without data normalization. Therefore, we decided to use the scaled data for all models except for the SVR. The forecasts were rescaled to the initial scale after the prediction process. For the SVR, with RBF kernel function we tuned the parameters of C, epsilon, and, gamma through a grid search approach. We considered four candidate values for each parameter; 1,10,50,100 for C, 0.001, 0.01, 0.1, 0.2 for gamma and 0.1, 0.2, 0.3, 0.4 for epsilon. In total, for each given scenario in the experiments, we tested 4 ∗ 4 ∗ 4 = 64 SVR models on the validation set.
For the GBRT model, one of the important parameters that need to be regularized is the number of weak learners (trees). The development of a model with a large number of weak learners would lead to lower regression error, but higher complexity and risk of overfitting. Furthermore, the speed of learning which scales the contribution of each learner is another influential parameter that needs to be set to reduce complexity and computation time. The lower learning rate would normally require fewer learners, thus making the ensemble model simpler with higher generalization ability [
40]. To determine the optimum number of trees and the learning rate we employed a grid search strategy to compare the generalization error under each combination of these parameters. According to that, for each variant of the GBRT model, the number of trees was set among the range of 150,200 and 300 and the learning rate was chosen among a range between 0.04 and 0.1.
The tree depth is also another parameter that requires tuning to avoid the overfitting problem. The maximum number of variables for decision splits and the minimum number of records for leaf nodes are the characterizing parameters for defining the tree depth. Generally, the tree depth has a high impact on the overfitting problem, when decision trees are trained on a few observations with a large number of attributes. For our problem, the training set has a large number of records and a few numbers of features which reduces the chance of overfitting. Therefore, we set the maximum number of features for the best split to the input size and set the leaf size as the default value of ‘one’ considered in the SkLearn library. Nevertheless, to compute the optimal value for the maximum depth of each tree we again used a grid search algorithm and set the candidate values in a range of 2 to 4.
Regarding the FFNN we considered a single hidden layer with
n input nodes corresponding to the number of input (lag) variables. To reduce the computation time, we did not tune the number of nodes in the hidden layer, instead, we considered it as twice as the number of input nodes plus one as discussed and suggested in [
43]. However, we tuned two parameters related to the training process by grid search: the optimization algorithm and weight initialization technique. We selected ‘Adam’, ‘NAdam’ and ‘RMSprop’ as the candidate values of optimization algorithm along with ‘Uniform’, ‘normal’, ’Golrot Normal’ as the candidates for weight initialization technique. The linear activation function is used in the Dense layer and The Rectified Linear Units (ReLU) [
44] function is used in the hidden layer. A batch size of 128 training samples and a number of 70 epochs (iterations) were chosen for the learning process of each variant. Finally, a learning ratio of 0.001 was set in each iteration for the convergence.
For the LSTM, we did not tune various hyperparameters because of the high computational costs. However, the number of LSTM units as one of the most important hyperparameters related to the network structure was tuned using the validation dataset. The optimal value of this parameter for each LSTM variant was chosen among the candidate values of 5, 10, 15 and 20. The number of features was set to one and the number of timesteps was chosen as the number of lag variables. Adaptive Moment Estimation (ADAM) function was used for optimization due to its computational efficiency and its ability to optimize models with a large number of parameters [
45]. The linear activation function is used in the Dense layer before the output of all units and the ReLU activation function was used for the recurrent step. ReLU function is monotonic and half rectified, which assigns zero to any negative values. This has the advantage of not generating vanishing or exploding gradients. However, it can cause dead neurons; therefore, we used the dropout layer between LSTM and Dense (output) layer with the rate of 0.2 to reduce the negative effect of dead neurons which may hurt the training phase. Since LSTM has stronger learning ability than a shallow neural network, higher batch size of 256 and fewer number of epochs (50) was set for training the network.
5. Error Metrics
To evaluate the performance of a forecasting technique, forecasting error is calculated. The lower the forecasting error, the higher the performance of the model. The forecasting error is the difference between the actual observation and the predicted value. There are many error metrics that are proposed for calculating the forecasting error and comparing the performance of time-series forecasting techniques. In this study, we used three such metrics—Mean Absolute Error (MAE), Root Mean Square Error (RMSE) and Mean Average Scaled Error (MASE).
If
is the prediction value and
is the actual value at time t and
is the number of test observations, we can define the three metrics as the following:
The MAE calculates the magnitude of the errors on average and ignores whether the prediction values are higher or lower than the real values. Thus, MAE gives equal importance (weight) to all individual differences. The RMSE on the other hand, penalizes large errors by calculating the squared error before averaging them.
The MASE was proposed by [
46] is introduced as a more applicable error metric and as an alternative to some metrics like Mean Absolute Percentage Error (MAPE) when the observation or prediction values are zero. The MAPE is commonly used as a loss function in model evaluation because it can interpret the relative error. However, the problem with MAPE can occur when there are zero values in the series and there will be a division by zero. For such sequences, MASE is appropriate as it never produces infinite or unknown values. In this alternative, each actual value of the series in the MAPE formula can be replaced by the average of all actual values of that series. In addition to these metrics, we added another error metric to our evaluation which is particularly defined for demand forecasting problems, applied in [
47]—Daily Peak Mean Average Percentage Error (DpMAPE). The DpMAPE measures how accurate is the model in forecasting daily peak consumption. The information about peak time and peak consumption values is highly important for energy management systems for saving grid costs through peak shaving services. The DpMAPE computes the relative difference (percentage) between the daily peak consumption and predicted daily peak value expressed by the following equation:
Finally, since each forecasting model is tested under different scenarios and produces different values for the defined measures, we need to have a combined metric to assess the best variant of each model. This metric is also adopted from [
47] and calculates a cumulative weighted error (CWE) based on four defined metrics as follows:
The CWE is further used to compare the prediction performance of the best variants among different predictive models.
6. Smart Metering Data and Statistical Analysis
The introduced models are evaluated on a subset of energy consumption data set for short-term load forecasting. The original dataset is collected from smart meters installed in 5567 households in London, that took part in the UK Power Networks led Low Carbon London project between November 2011 and February 2014 [
48]. The participants in the project were chosen as a representative sample of the greater London population. The dataset includes recordings from 110 blocks of houses containing energy consumption (in kWh) with the frequency of half-hour, unique household identifier, as well as date and time. The blocks are grouped into 18 categories known as the ACORN (acorn) groups. The social factors and population behavior of each type and category provide precise and valuable information about the households in the given category. A comprehensive and detailed report on the ACORN classification can be found in [
49]. For this study, we have chosen seven blocks belonging to five acorn categories known as A, B, C, D and E.
According to the definitions in [
49], consumers in groups A, B and C are referred to as ‘Affluent achievers’; they live in big houses located in the wealthy and suburban region. Group C is called ‘Mature money’ and belongs to the retired couples who live in rural towns and villages mainly in detached or semidetached houses. On the other hand, households in groups D and E which are called ‘Rising prosperity’, are not that wealthy, but younger, educated and living in major cities.
In the preprocessing step, we discarded the houses with a large number of missing records and unusual information. To be precise, among the 347 house profiles existing in the seven blocks, we primarily chose 220 buildings with missing records fewer than a week. From the remaining, the houses with zero mean consumption, indicating no consumption and those with zero standard deviation implying flat consumption were filtered out. Furthermore, the house profiles with unusual total annual consumptions, over 20,000 KWh and less than 2000 KWh as well as total daily consumption of fewer than 3 KWh for more than a month, were discarded. Finally, from the 180 remaining houses, we randomly selected 15 houses from 5 acorn groups, and therefore a total of 75 house profiles were picked for further study. In the final preprocessing step, linear interpolation was performed on the house profiles containing small gaps from 1 to 24 h. For each building, the energy reading for the year 2013, due to the fewer number of missing records was chosen. Accordingly, the number of observations in each dataset turned to 356 days ∗ 24 h = 8760 and the total number of observations in all 75 houses turned to 75 ∗ 8760 = 657,000.
Figure 4 illustrates the energy readings of fifteen sample houses in the dataset belonging to different acorn groups over one-year. As we can see they demonstrate different amounts of hourly consumption (ranging between zero and five KW/h), as well as various consumption patterns over the same year (2013).
It is obvious that the short-term load forecasting models are aimed at predicting accurate peak load or energy consumption. However, one of the main influential factors in short-term load forecasting at the household level is the load volatility which simply means deviations from the average consumption. These deviations arise frequently in a residential house because its energy consumption is usually influenced by various factors such as temperature, utilized appliances and consumption habits. In the context of load forecasting, higher load violation increases the complexity of the load profile, thereby making an accurate load forecasting more complicated. Load analysis of the existing profiles in terms of load volatility will assess in advance which house profiles are potentially more challenging to forecast.
Figure 5 and
Figure 6 provide more insight into the load volatility of the house profiles using box-plots statistics [
50]. The boxplots provide information on the median value and variability of the consumption values.
Figure 5 shows how the hourly energy load of one house changes during different days of a week. For example, this house has experienced high variations in hourly consumption during the weekend and on Thursday than the other weekdays. Moreover, the median value of energy consumption has been increased over the weekend. The bobbles in the plot indicate that a few consumption values are out of the maximum range; Q3 + 1.5 ∗ (Q3 − Q1) [
50] which can be considered as outliers. For instance, on Saturday, there have been recordings higher than 1 + 1.5 ∗ (1.0 − 0.3) = 2.05 KW/h showing by bobbles.
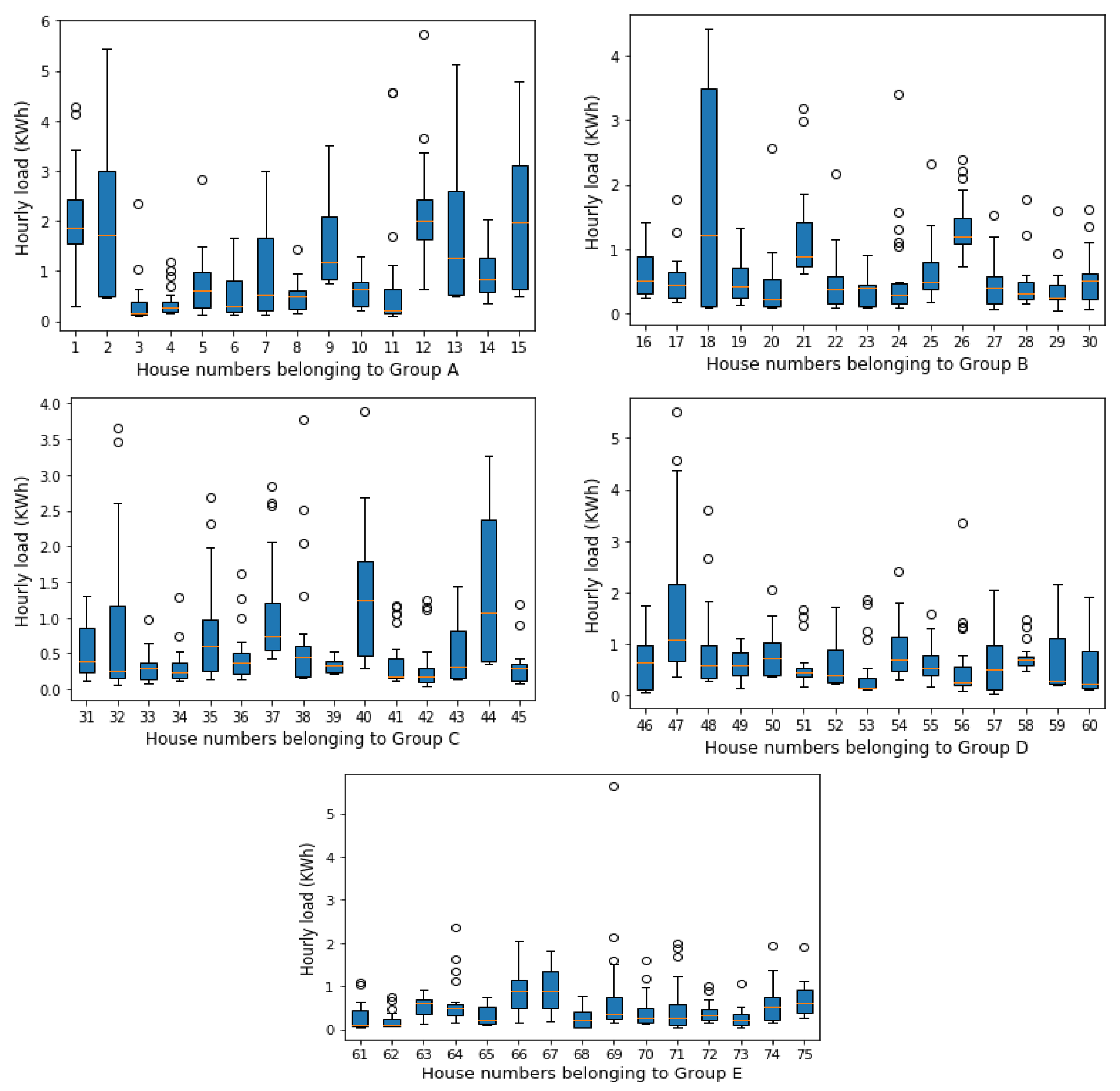
Figure 6 similarly illustrates the hourly load volatility of houses in each customer group over one working day. We can see that there are certain houses where their hourly consumption patterns change very little, such as houses 3, 4 and 8 in group A; potentially easier to predict while there are some houses (such as House 15 in group A or House 18 in group B) experiencing major changes in their hourly load profiles which can make them difficult to forecast.
Table 1 provides summary statistics of house profiles per customer group for the whole test period. The buildings in group A on average, have the highest mean electricity load over different time slots (hour, day and week) with the highest deviations from the mean values (standard deviation values of 0.72, 6.5 and 34). Similarly, customers in group D consume high energy but with lower deviations. On the other hand, the customers in groups B and C behave similarly and on average consume less electricity over a year. However, the lowest average values and smallest volatilities are recorded for the households in group E.
7. Forecasting Experiments and Results
In this work, we performed two separate experiments; one for developing and fine-tuning of the models on the validation set and another for the performance evaluation on the test set. To do the experiments, all the time series models were implemented using Keras and Scikit-learn libraries [
51,
52]. Total computations were conducted in Python 3 on a MacBook Pro machine @3,1 GHz, Intel Core i5 and 16 GB RAM.
The data set including 75 house profiles with hourly intervals was split into three separate subsets: trainset with 60% of data (45 houses), validation set with 20% of data (15 houses) and test set with the rest 20% (15 houses). The selection of validation and test sets was not performed randomly, instead, from each acorn group we selected 3 house profiles as the validation set and three house profiles as the test set with various levels of yearly consumption and average hourly load variations. This selection approach would help us to assess the model performance on a variety of house profiles with different statistical characteristics and consumption behaviors. The random selection might lead us to choose biased datasets either simple or complicated profiles which may cause overestimation or underestimation of the models’ forecasting capabilities.
7.1. Model Development and Tuning
In this step, we implemented the models based on the architecture design explained in
Section 3 and tuned the parameters according to
Section 4. One of the aims of these experiments was to understand how the model’s accuracy is affected by the size of training data and the number of input variables. The number of predictor variables and the size of input data can be influential on the performance of machine learning algorithms. If we build a model with an insufficient number of variables and training records, the model will be too simple and is not able to learn the relation between input and output variable(s). In contrast, the model complexity and computation time would increase if it is fed with too many features and redundant information.
As mentioned earlier, for all models, the input variables were considered as the load lags from previous time steps. The number of lags that were tested in our experiments varies from 1 to 9 e.g., the load consumption for the previous 1 to 3 h and the load consumption at the previous 1 to 6 and 1 to 9 h. Regarding the size of the training set, four subsets of training data were considered for the evaluation: 25%, 50%, 75% and 100% of the total train size represented by D1, D2, D3, and D4 respectively.
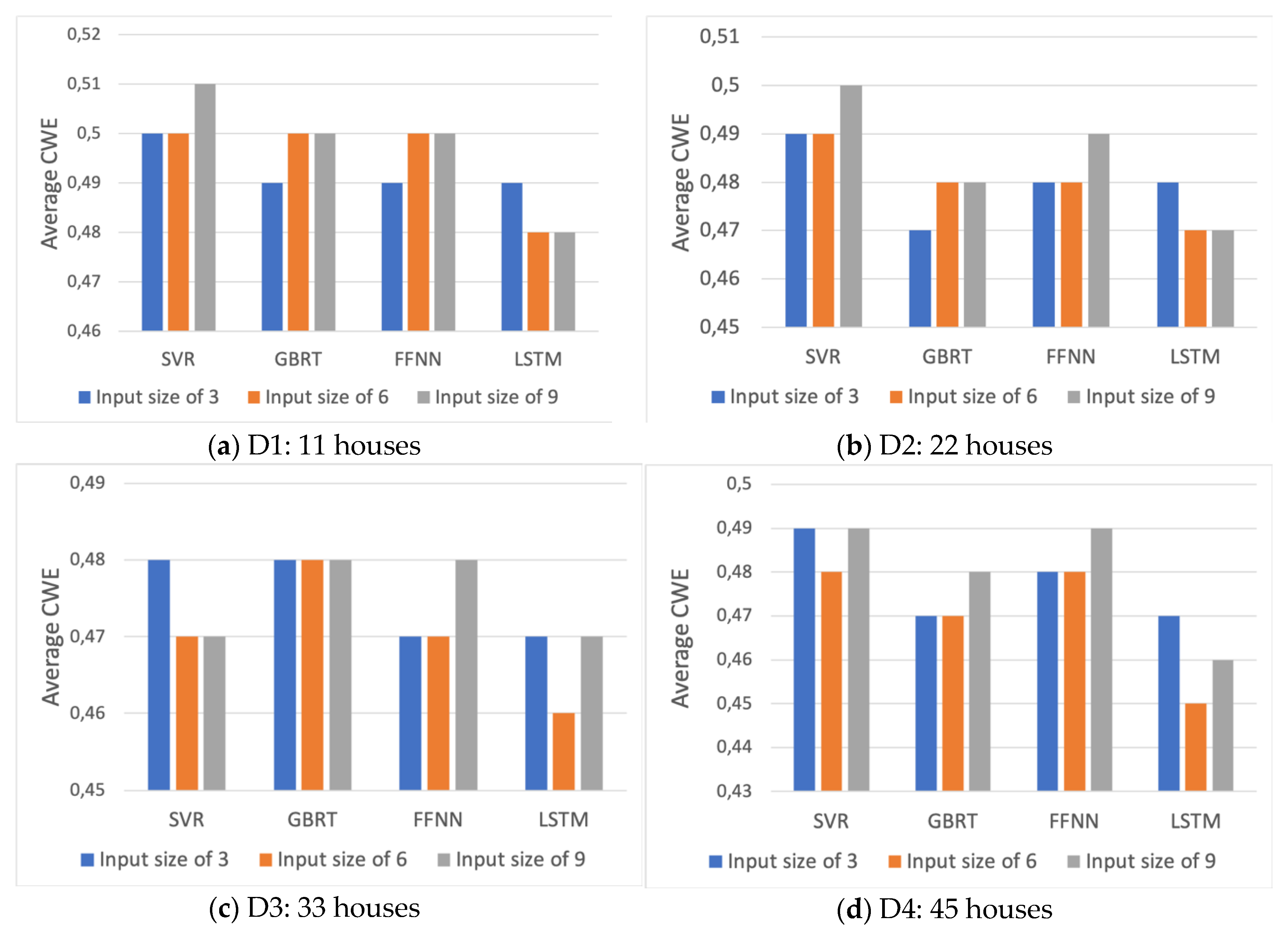
Figure 7 shows the evolution of the average prediction error on the validation set versus the number of input variables and the size of the training set for each of the four models studied.
According to the bar plots, the average prediction errors of all models decreased between 1% to 3% when the size of the training set increased from D1 to D3. However, a further increase in the training size has not affected the accuracy of all models similarly. The SVR and FFNN have shown the highest accuracy when they are trained on D3 dataset while GBRT and LSTM performed the best with the largest size of input data (D4).
Furthermore, the prediction error does not follow a clear trend regarding the number of input lags. For the GBRT and FFNN, it is observed that with the increase of the input number from 6 to 9 the errors tend to rise. This suggests that the hourly consumption pattern can be captured by the smaller number of input lags. Thus, in some cases, more load lags can be discarded in order to reduce the computation cost and complexity of the model. The likely reason is that although the input to the model (past consumption variables) is highly correlated with the target variable (one-hour ahead consumption), they are also highly correlated with each other as they are consecutive lags. The mutual dependence between consecutive lags indicates redundancy of information they convey to the model which would not boost the learning ability, rather it could increase the training time.
However, for the LSTM on average more lag variables seem more informative to the model. For the SVR the forecasting error does not show a clear pattern concerning the input size.
7.2. Model Evaluation
In this section, we selected the final models (best variants) based on the minimum CWE obtained in the previous section. In the cases where the CWE results were the same, we picked the variant with smaller daily peak MAPE error.
Table 2 provides information about the best variants; the size of training data, the number of input variables, the parameters and the training time.
The best variants are then tested on the test profiles. To understand the generalization ability of each model to different profiles, we computed the average error metrics over 15 houses. To estimate how much the error values, vary from the average, the corresponding standard deviation (SD) for each error metric and model is further reported. The lower standard deviation values for a model indicates a narrower range of errors and implicitly more robustness and consistency of the model.
Table 3 reports the average forecasting errors for one-hour ahead predictions. The reported CWE values prove that, on average, the GBRT, FFNN and LSTM slightly outperform SVR in hourly load predictions.
The AI-based models compared to the CART algorithm (GBRT) obtain better performance considering the average CWE (0.44 and 0.43 versus 0.45). However, GBRT and LSTM detect better the daily peak with an average DpMAPE of 17.8 and 17.7 KW/h respectively. In general, all models scale well and demonstrates robustness with average MAE of at most 0.24 KW/h and standard deviation of at most 0.06.
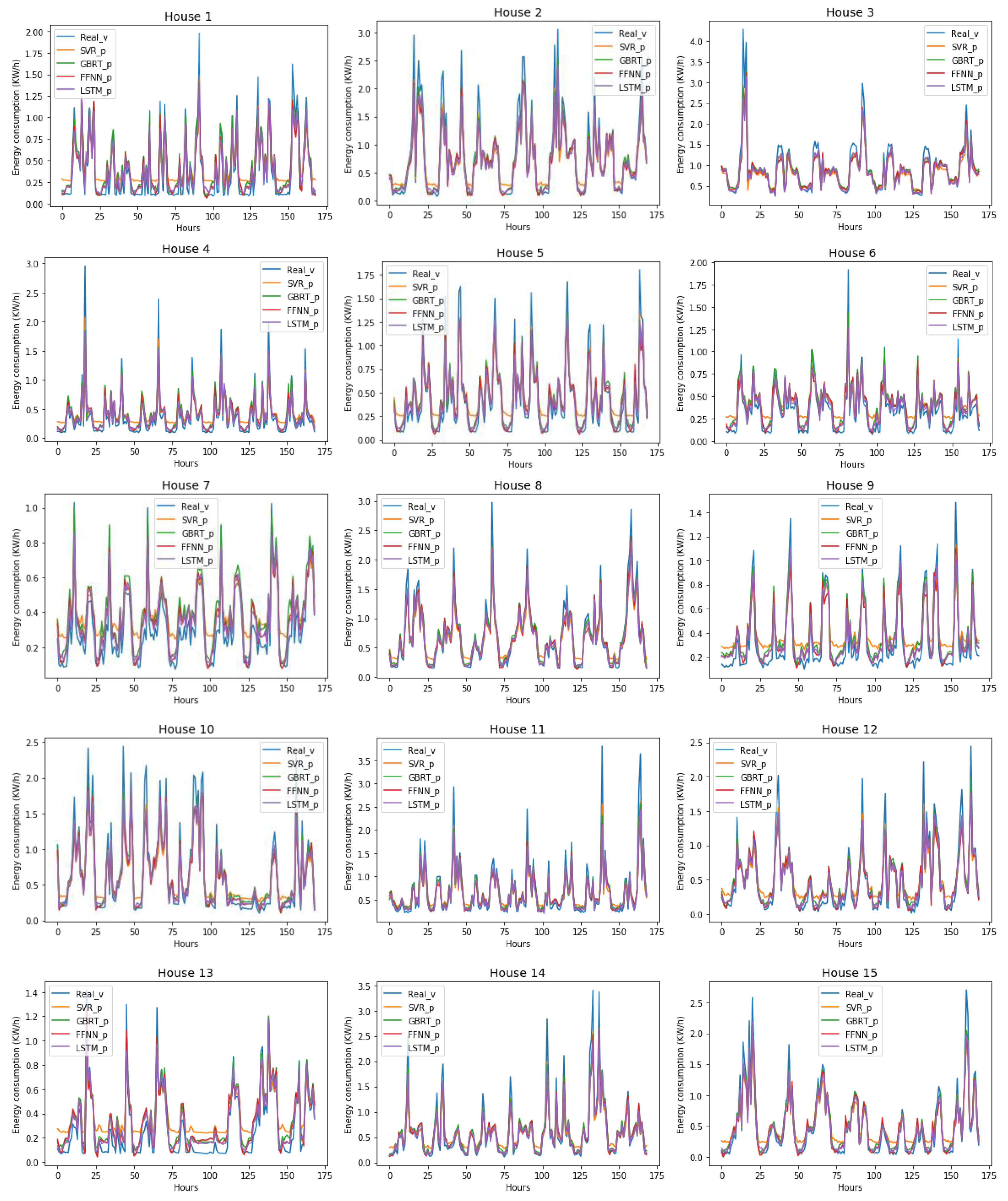
Figure 8 illustrates how the models predicted the energy consumption of each test house over one week during the spring season.
Except for the SVR which slightly overestimates the real consumption values in most houses, the other three models mainly demonstrate a good match and steady weekly prediction for the one-hour ahead estimation.
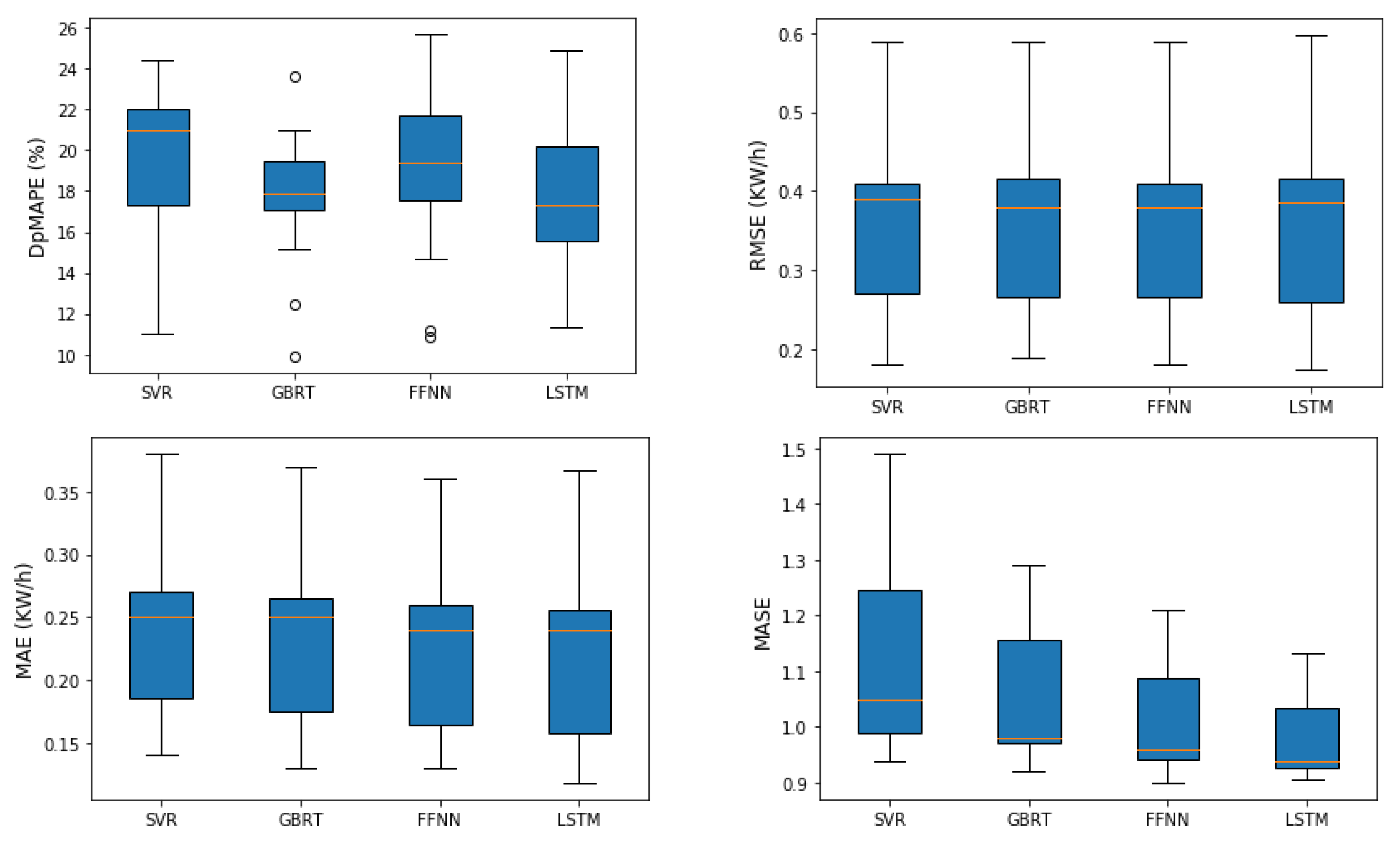
Figure 9 provides more insights into the variability or dispersion of error metrics which were averaged over all profiles and compared among different ML models.
The distribution of average DpMAPE errors proves that the median value of the peak prediction errors of GBRT and LSTM is less than the ones in other techniques. This means that these models adapt better to changes in daily peak consumption and achieve low perdition errors. The small size of the boxplot for the GBRT algorithm even shows the least variability in the peak errors, thus higher robustness. The ability of these models in obtaining high accuracy is also visible through boxplot statistics of average MASE. The median values in the plots of RMSE and MAE indicate that for all the models, half of the errors are around or less than 0.4 and 0.25 KW/h respectively. However, these plots are not informative enough for comparative analysis.
Another comparison is carried out by considering the diversity of consumer groups.
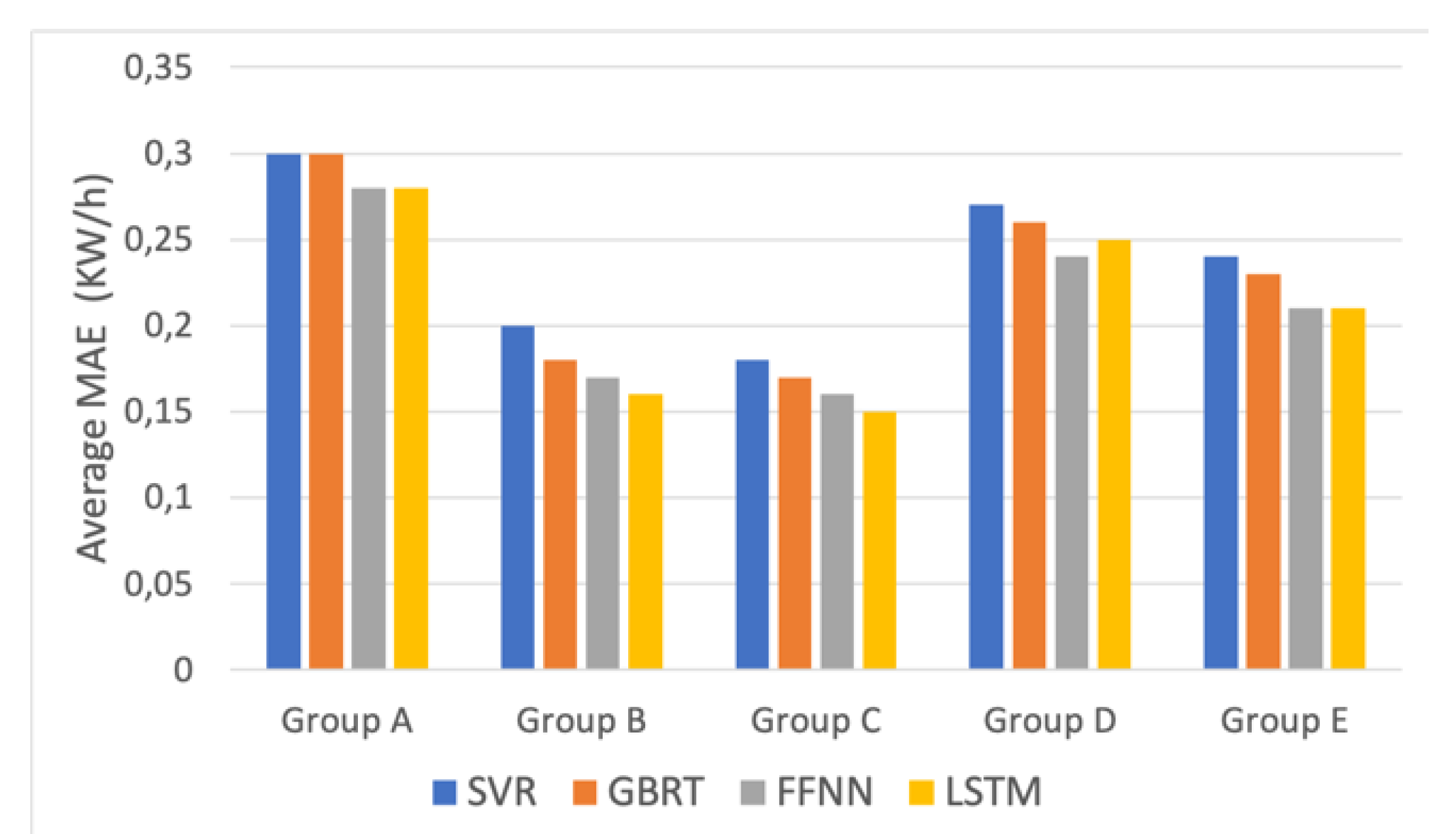
Figure 10 shows the average mean absolute error in five distinct customer groups. The prediction error for the house profiles belonging to group A was the highest, while in the other categories it reduced between 2% and 15%. Groups B and C show the lowest values for different models out of all the other groups. It also confirms the lower average prediction error as FFNN, and LSTM were used as the prediction algorithms. The superiority of these models in hourly prediction is also visible for the test houses in other customer groups. Overall, we can conclude that the forecasting task in group A and group D is more challenging due to high average consumption over a year as well as high hourly load variations. The models in groups B and C, on the other hand, obtained higher accuracy due to the lower load volatility and lower average yearly consumption of the house profiles. These customers have shown the most predictable profiles. The interesting finding is that the consumption behavior of the houses belonging to group E with the lowest average consumption and the lowest daily variations were still difficult to predict. The probable reason is that the majority of houses in the training phase, on average, have experienced higher hourly energy consumption than these test profiles. Therefore, the trained models could not learn their consumption behavior properly.
The final analysis was performed to evaluate the effect of temperature and seasonal events on the prediction accuracy of various techniques.
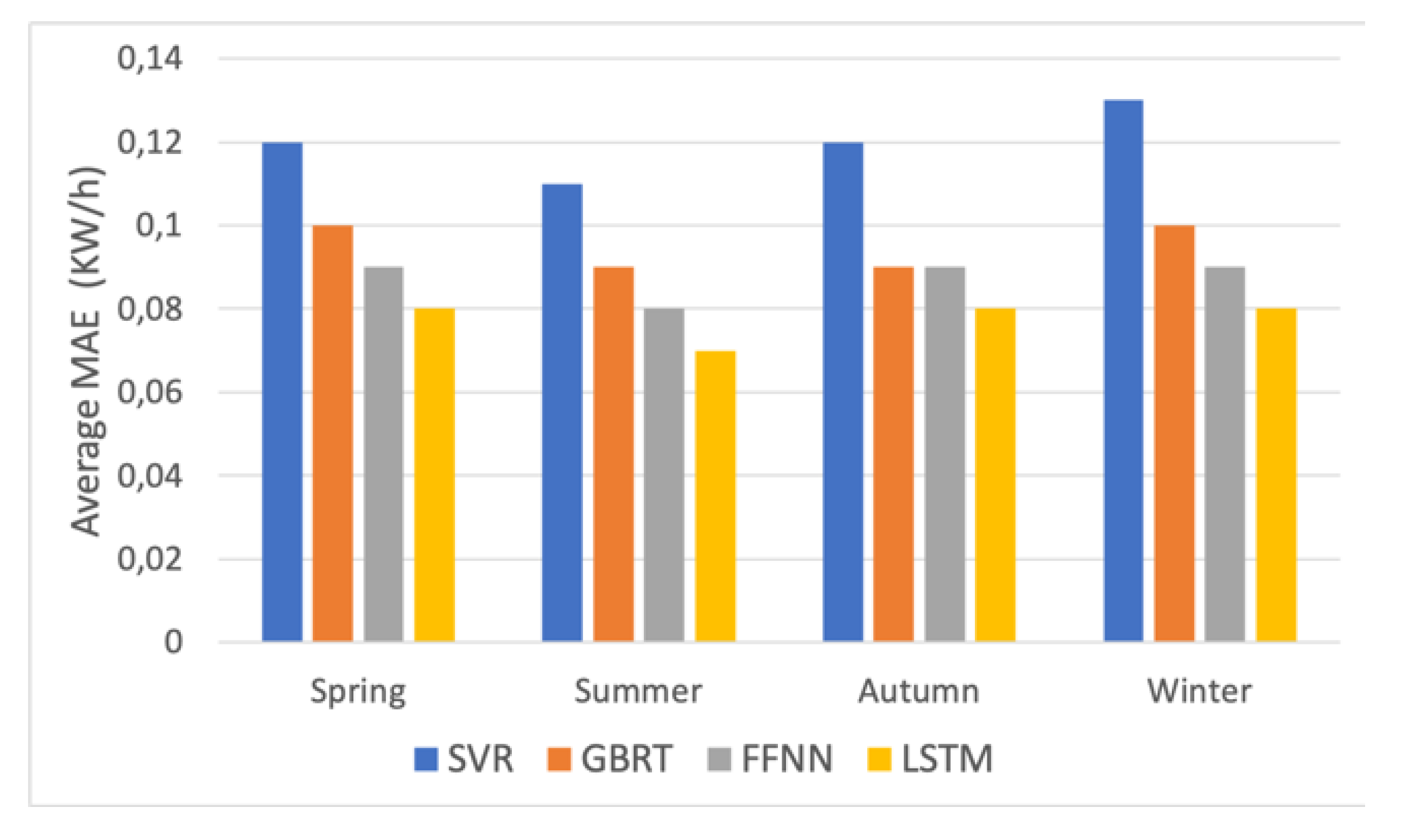
Figure 11 shows the average MAE of four techniques over all test houses in four consecutive seasons of the Year 2013. It is evident from the chart the SVR produced the highest error than the other three models over the seasons, though its estimation error reached the lowest (around 0.07 KW/h) in the summer. The other three models also predict summer load with the highest accuracy. The forecasting error during spring and autumn increased for the most models by around 10%. In winter the SVR and GBRT had another 10% increase, while FFNN and LSTM seemed more adaptable to seasonal change and their error remained unchanged.
8. Conclusions
This paper presents analysis and comparison of hour-ahead load forecasting over one-year period with four data-driven models known as SVR, GBRT, FFNN and LSTM. They were trained on historical load data provided by the UK residential smart meters. Their generalization ability was evaluated on the house profiles which were not previously trained on. The test houses were chosen from five customer groups with different levels of load volatility and average yearly consumption. The sensitivity of each algorithm was also tested to the number of training houses and the number of input lag variables. The main findings are summarized as follows:
Although the models were merely fed with consumption values as the predictors, in general, they could provide stable one-hour ahead prediction over a one-year period.
The AI methodologies; LSTM and FFNN compared to the other two techniques, adapted better to changes while performing predictions, following the trend of real consumption and on average, achieving lower prediction errors.
With regard to daily peak load estimations of various profiles, the GBRT in addition to LSTM outperformed other techniques.
As for the computation cost, the GBRT is the fastest algorithm to be trained and fine-tuned among the others. On the contrary, the training times of the SVR and LSTM are significantly high, especially when the training size for the SVR grows or the number of variables for tuning in the LSTM network increases.
Increasing the number of training houses could improve the accuracy of forecasts as long as the additional profile(s) raise the model knowledge about the test profile. This implies a larger training set does not necessarily boost the model performance.
Increasing the number of inputs does not have a similar effect on the performance of different variants. Some models perform better with recent information about past consumption and some need more knowledge on past consumption values.
A comparative study among the five customer groups shows that the customers with the lower average amount of yearly consumption and smaller hourly load volatility generate more predictable profiles.
An analysis of seasonal predictions reveals that the seasons with lower temperatures usually come with more load violations, thus making forecasting more difficult for almost all models.
Future lines of research in short-term load forecasting at the individual building level aim to customize forecasting techniques for the consumer groups with large variations in their consumption patterns. performance evaluation of the studied techniques on the dataset with higher resolution and for longer forecasting horizons can also be another research direction for the future work.