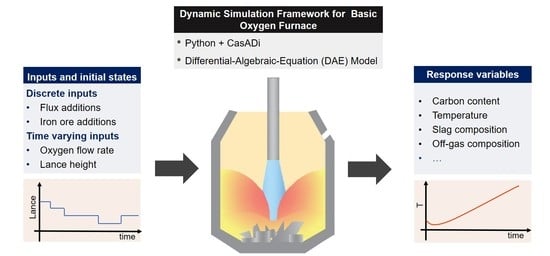
Dynamic Modeling and Simulation of Basic Oxygen Furnace (BOF) Operation
Abstract
1. Introduction
2. Mathematical Model
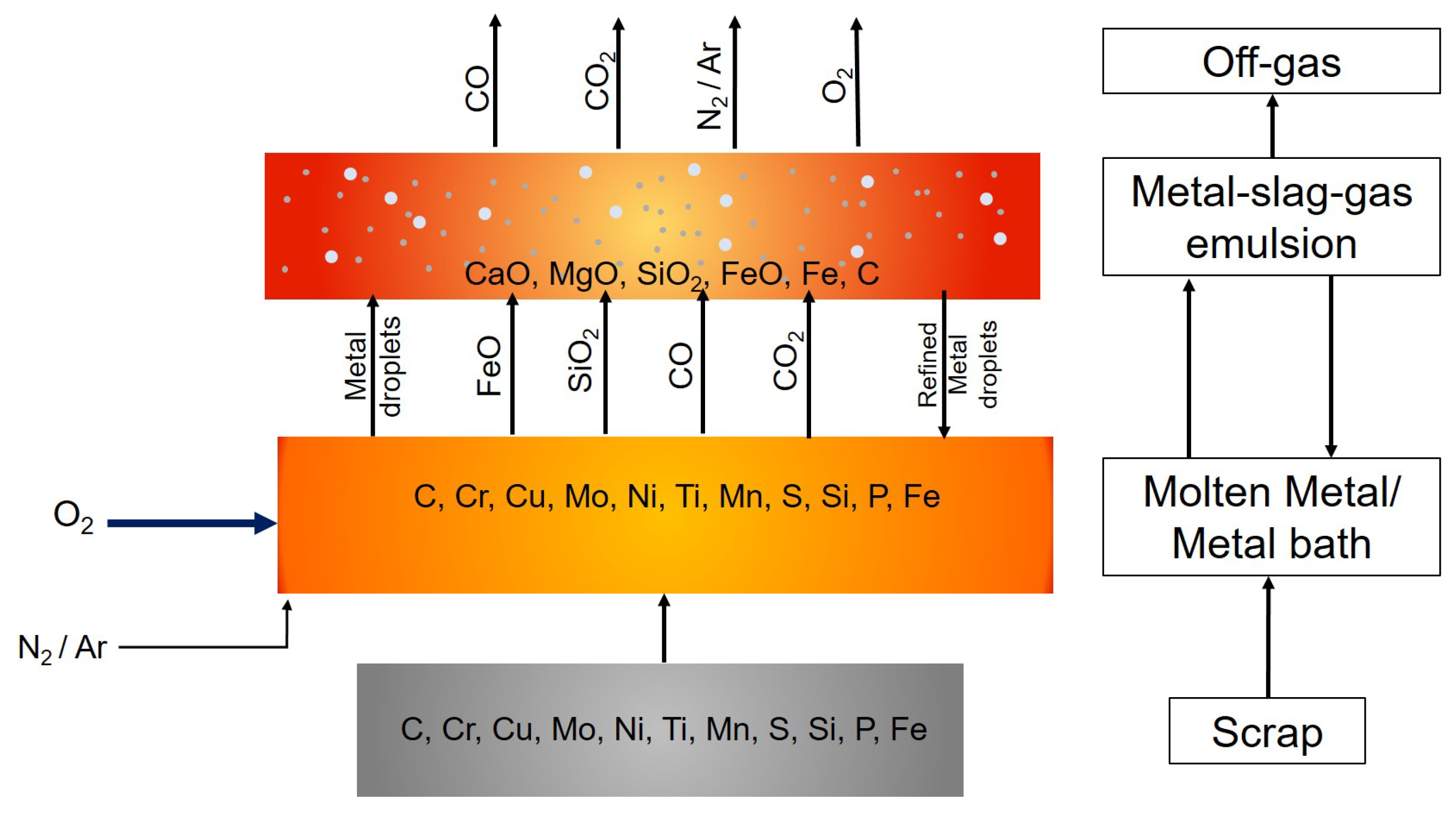
2.1. Mass and Energy Balances
- The gas hold up in the slag and metal bath is negligible
- The gas exits the furnace at the slag temperature
- The temperature of the slag-metal-emulsion and metal bath is uniform
- A fraction of all the heat generated is assumed to be lost to the environment and the remainder is assumed to be absorbed by the slag.
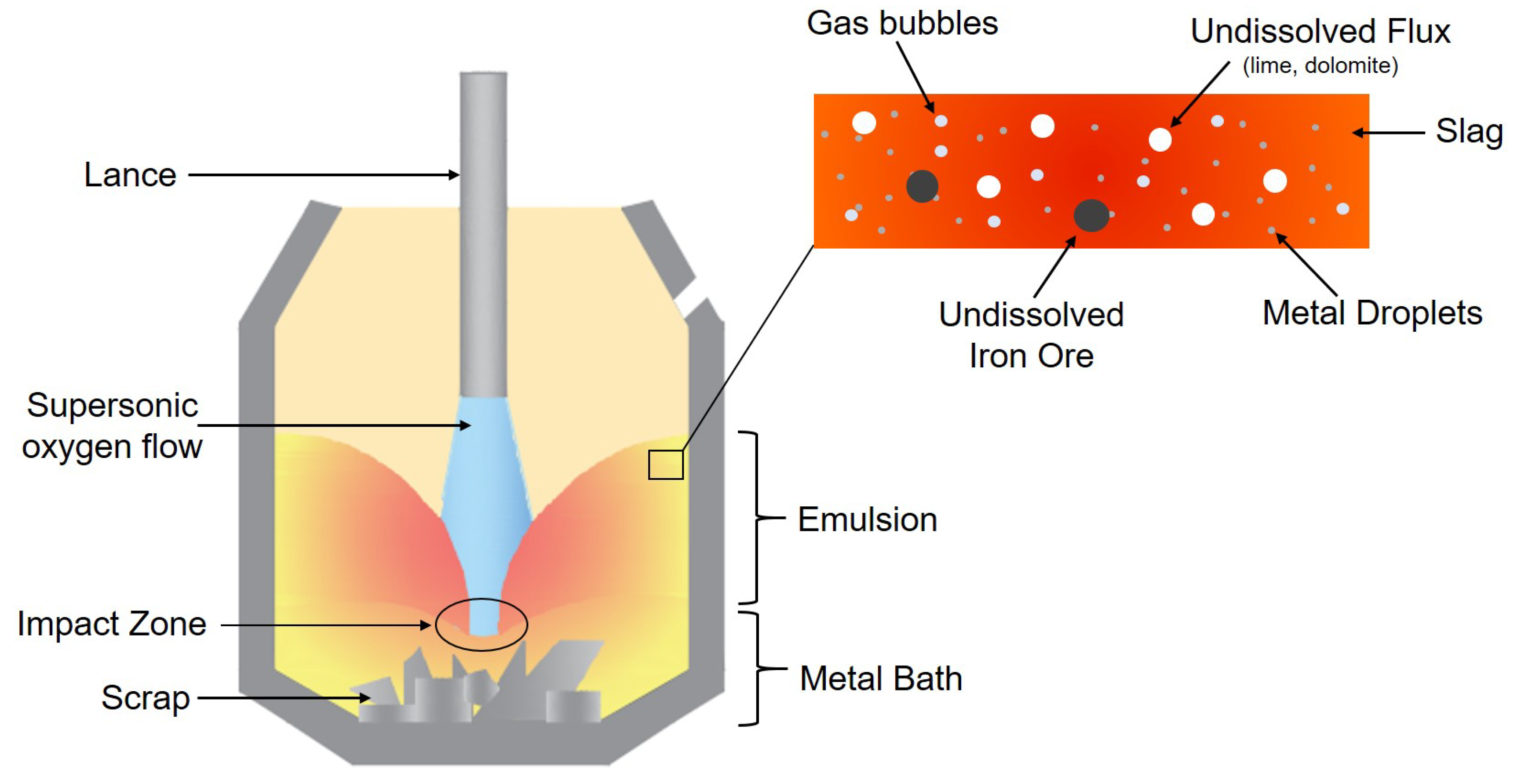
2.2. The Impact Zone
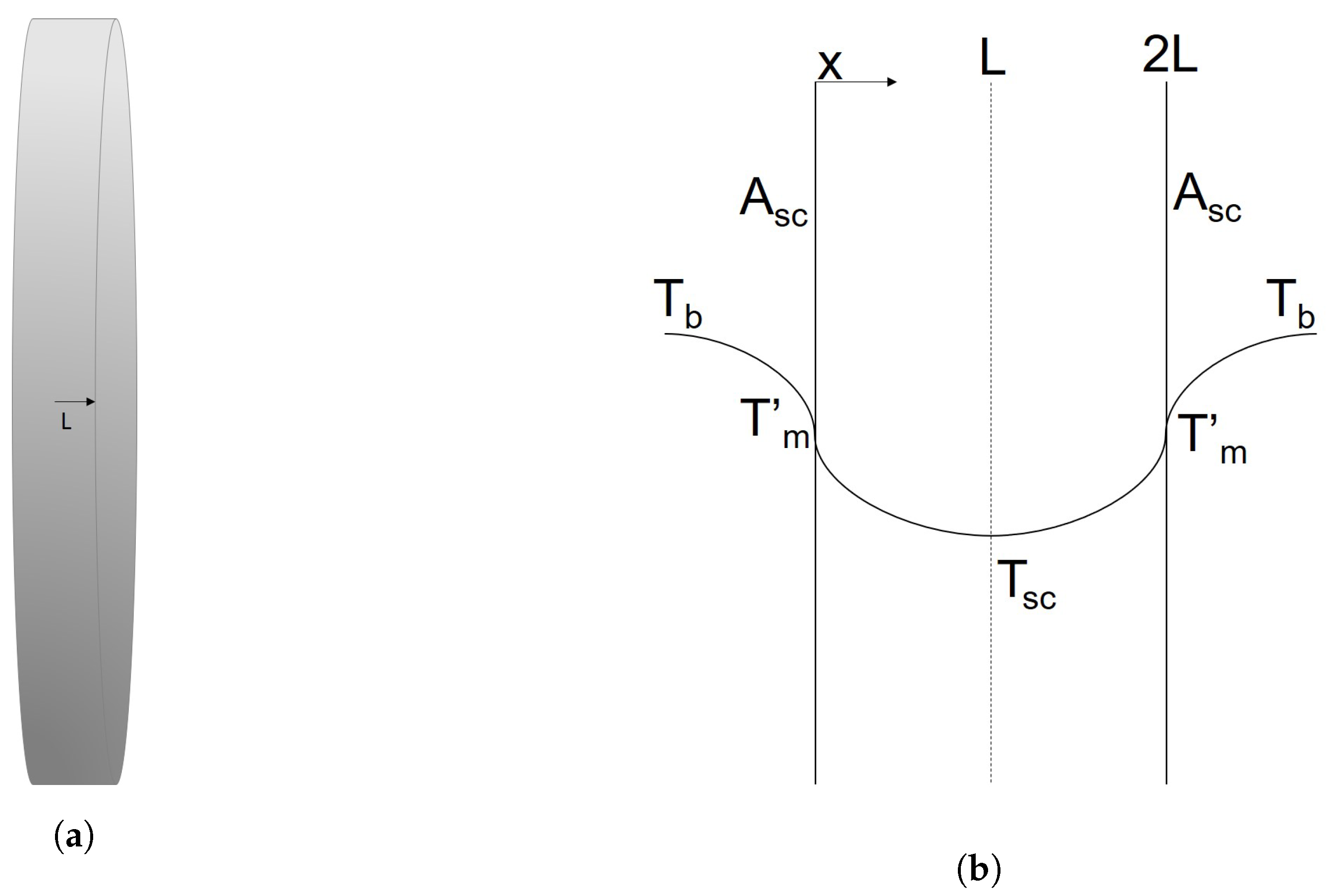
2.3. Scrap Melting
2.4. Iron Ore Dissolution
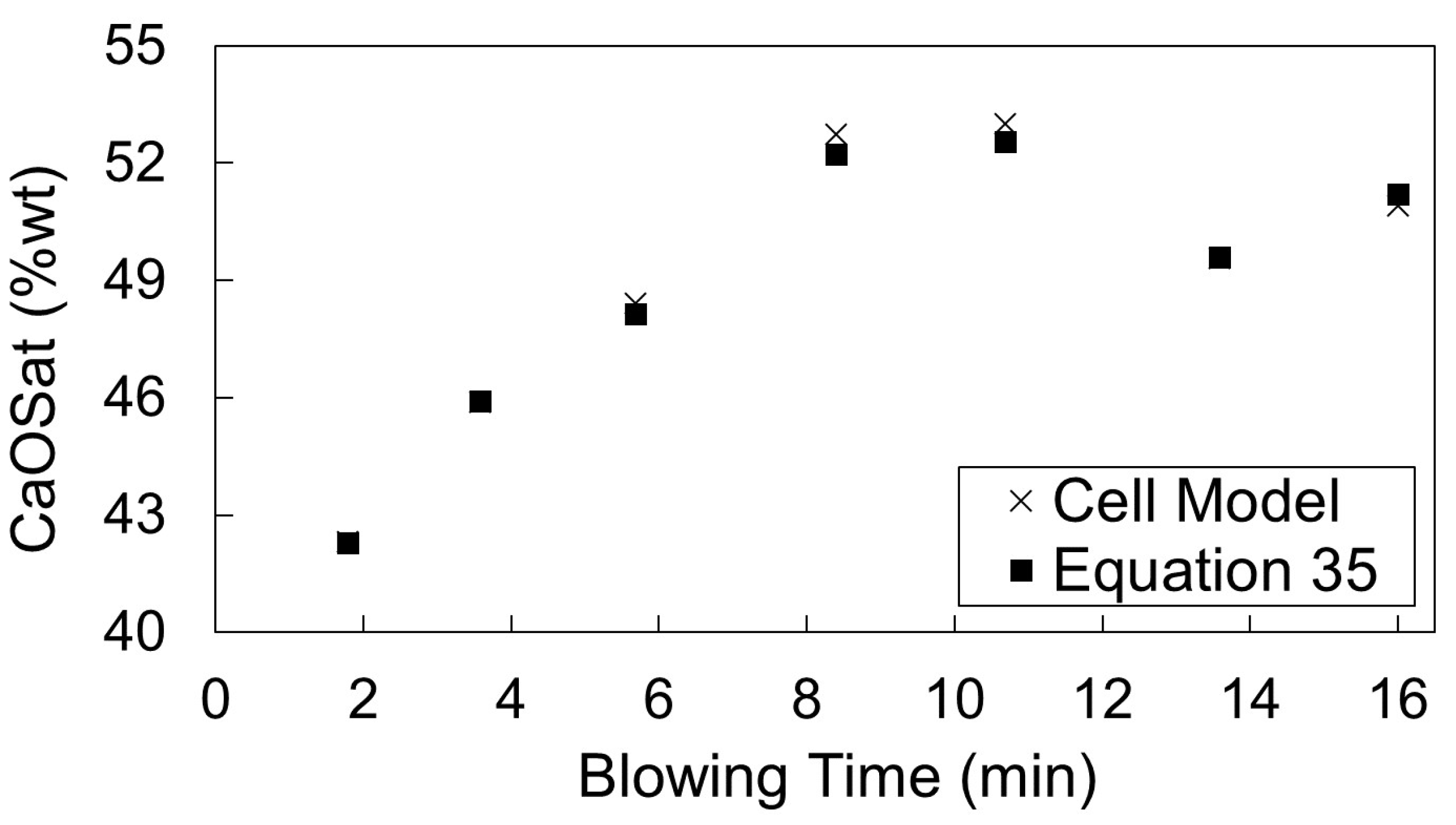
2.5. Flux Dissolution
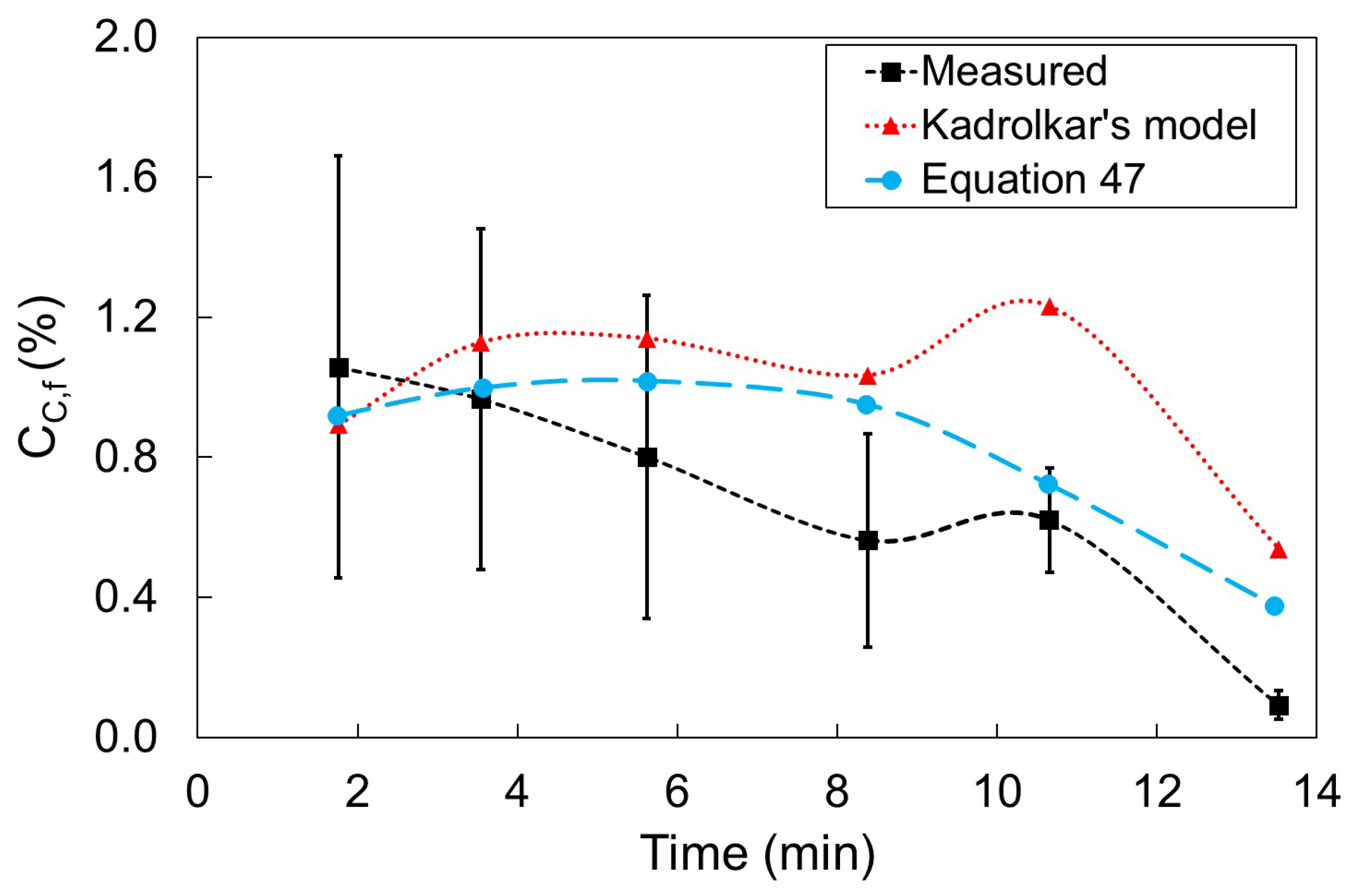
2.6. Decarburization in the Emulsion Zone
- All droplets decarburize immediately after they are ejected from the impact zone
- The carbon content of the metal droplets in the emulsion zone is approximated as the average carbon content of the individual metal droplets
- Except for carbon, the mass of other elements in the metal droplets stays constant whilst the droplet travels through the emulsion zone
2.7. Implementation
- Equations of the form:where , were rewritten as:where is a positive small number. This strategy was used on the submodels for flux dissolution, iron ore and scrap melting to prevent division by zero since either the radius or thickness of the particles continuously decreases with time and can eventually equal zero.
- Piecewise functions of the form:were rewritten using hyperbolic tangent functions:where is an adjustable parameter that controls the steepness of the continuous switching function approximation. This was used for flux dissolution (Equation (42)), scrap melting (Equation (29)), decarburization in the emulsion zone (Equations (47) and (48)), among others for a smooth transition and to ensure differentiability.
- Flux additions: Flux and iron ore can be added at anytime during a blow, and each individual addition is modeled as shown in Section 2.5. To model the indiviudal flux additons a new variable , where i is the flux type (lime, dolomite, iron ore) and j is the addition number (first, second, third), is defined for the flux addition time. Given the radius of the flux added at time , Equation (41) for lime dissolution rate can be reformulated as:which was implemented using a hyperbolic tangent function.
3. Results and Discussion
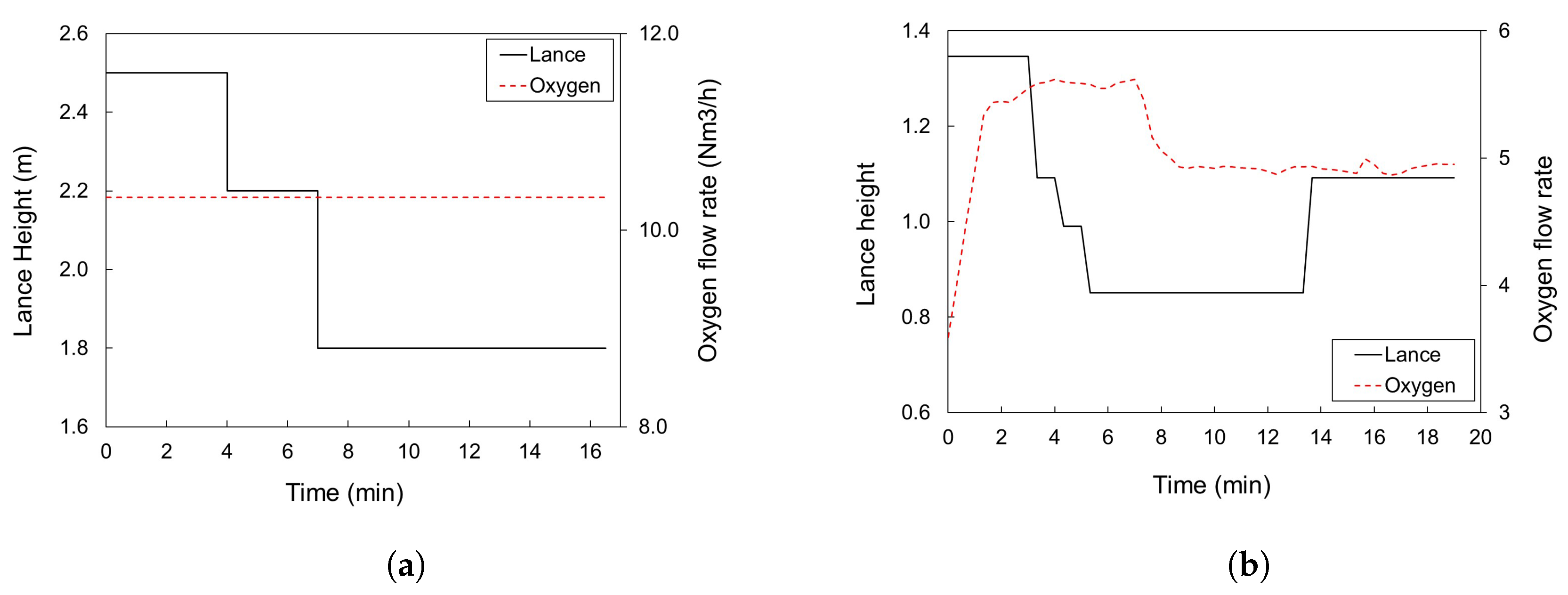
3.1. System Parameters and Input Data
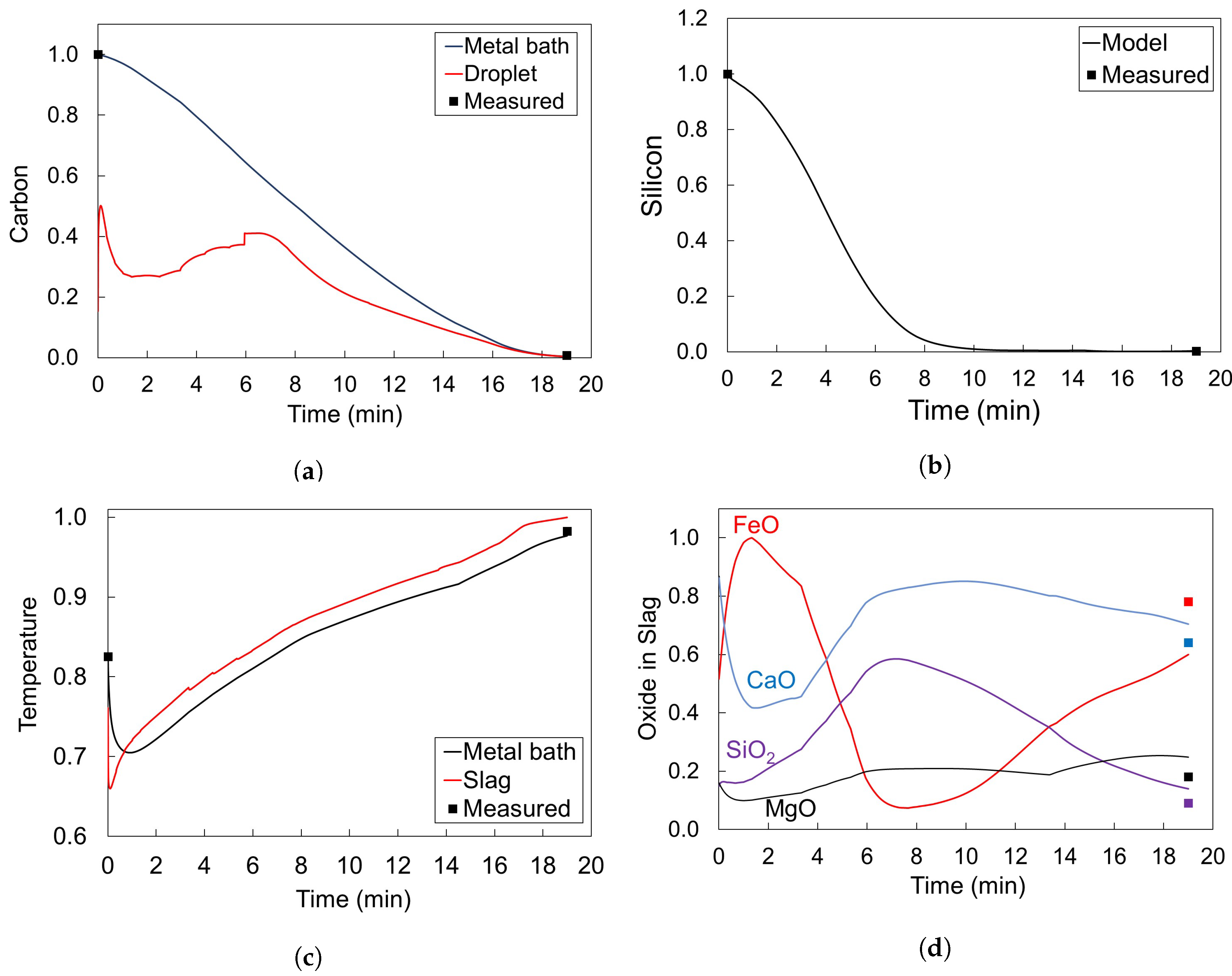
3.2. Simulation Results for Cicutti’s Operations
- Period I: As the silicon content of the metal bath decreases, the decarburization rate increases
- Period II: Decarburization rate stays approximately constant
- Period III: Decarburization rate is controlled by mass transfer of carbon in the metal bath
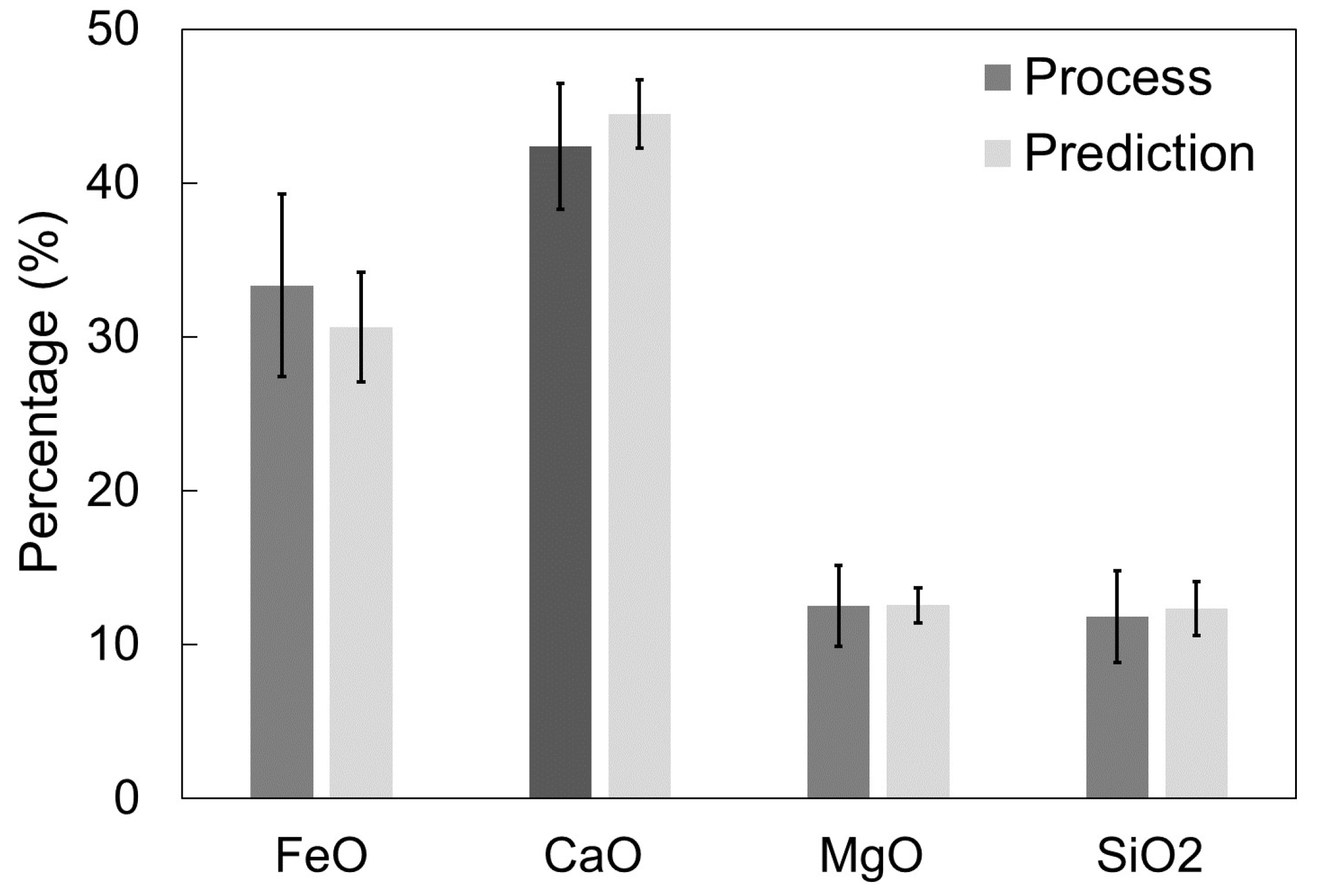
3.3. Simulation Results for Plant A Operations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Steel Association. Fact Sheet: Steel and Raw Materials. 2016. Available online: https://www.worldsteel.org/publications/fact-sheets.html (accessed on 27 March 2019).
- Molloseau, C.; Fruehan, R. The reaction behavior of Fe-CS droplets in CaO-SiO 2-MgO-FeO slags. Metall. Mater. Trans. B 2002, 33, 335–344. [Google Scholar] [CrossRef]
- Chen, E.; Coley, K.S. Kinetic study of droplet swelling in BOF steelmaking. Ironmaking Steelmaking 2010, 37, 541–545. [Google Scholar] [CrossRef]
- Jalkanen, H. Experiences in physicochemical modelling of oxygen converter process (BOF). Adv. Process. Met. Mater. 2006, 2, 541–554. [Google Scholar]
- Kattenbelt, C.; Roffel, B. Dynamic modeling of the main blow in basic oxygen steelmaking using measured step responses. Metall. Mater. Trans. B 2008, 39, 764–769. [Google Scholar] [CrossRef]
- Dogan, N.; Brooks, G.A.; Rhamdhani, M.A. Comprehensive model of oxygen steelmaking part 1: Model development and validation. ISIJ Int. 2011, 51, 1086–1092. [Google Scholar] [CrossRef]
- Lytvynyuk, Y.; Schenk, J.; Hiebler, M.; Sormann, A. Thermodynamic and Kinetic Model of the Converter Steelmaking Process. Part 1: The Description of the BOF Model. Steel Res. Int. 2014, 85, 537–543. [Google Scholar] [CrossRef]
- Sarkar, R.; Gupta, P.; Basu, S.; Ballal, N.B. Dynamic modeling of LD converter steelmaking: Reaction modeling using Gibbs’ free energy minimization. Metall. Mater. Trans. B 2015, 46, 961–976. [Google Scholar] [CrossRef]
- Rout, B.K.; Brooks, G.; Rhamdhani, M.A.; Li, Z.; Schrama, F.N.; Sun, J. Dynamic Model of Basic Oxygen Steelmaking Process Based on Multi-zone Reaction Kinetics: Model Derivation and Validation. Metall. Mater. Trans. B 2018, 49, 537–557. [Google Scholar] [CrossRef]
- Kadrolkar, A.; Dogan, N. The Decarburization Kinetics of Metal Droplets in Emulsion Zone. Metall. Mater. Trans. B 2019, 50, 2912–2929. [Google Scholar] [CrossRef]
- Shukla, A.K.; Deo, B.; Robertson, D.G.C. Scrap Dissolution in Molten Iron Containing Carbon for the Case of Coupled Heat and Mass Transfer Control. Metall. Mater. Trans. B 2013, 44, 1407–1427. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Cicutti, C.; Valdez, M.; Pérez, T.; Petroni, J.; Gomez, A.; Donayo, R.; Ferro, L. Study of slag-metal reactions in an LD-LBE converter. In Proceedings of the 6th International Conference on Molten Slags, Fluxes and Salts, Helsinki, Finland, 12–17 June 2000. [Google Scholar]
- Deo, B.; Boom, R. Fundamentals of Steelmaking Metallurgy; Prentice Hall International: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Koria, S.C.; Lange, K.W. Penetrability of impinging gas jets in molten steel bath. Steel Res. 1987, 58, 421–426. [Google Scholar] [CrossRef]
- Kitamura, S.y.; Kitamura, T.; Shibata, K.; Mizukami, Y.; Mukawa, S.; Nakagawa, J. Effect of stirring energy, temperature and flux composition on hot metal dephosphorization kinetics. ISIJ Int. 1991, 31, 1322–1328. [Google Scholar] [CrossRef]
- Rout, B.K.; Brooks, G.; Rhamdhani, M.A.; Li, Z.; Schrama, F.N.; Overbosch, A. Dynamic Model of Basic Oxygen Steelmaking Process Based on Multizone Reaction Kinetics: Modeling of Decarburization. Metall. Mater. Trans. B 2018, 49, 1022–1033. [Google Scholar] [CrossRef]
- O’Malley, R.J. The Heating and Melting of Metallic DRI Particles in Steelmaking Slags. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, CA, USA, 1983. [Google Scholar]
- Zhang, L. Modeling on melting of sponge iron particles in iron-bath. Steel Res. 1996, 67, 466–474. [Google Scholar] [CrossRef]
- Pineda-Martínez, E.; Hernández-Bocanegra, C.A.; Conejo, A.N.; Ramirez-Argaez, M.A. Mathematical Modeling of the Melting of Sponge Iron in a Bath of Non-reactive Molten Slag. ISIJ Int. 2015, 55, 1906–1915. [Google Scholar] [CrossRef]
- Shukla, A.K. Dissolution of Steel Scrap in Molten Metal During Steelmaking. Ph.D. Dissertation, Indian Institute of Technology, Kanpur, India, 2011. [Google Scholar]
- Dogan, N. Mathematical Modelling of Oxygen Steelmaking. Ph.D. Dissertation, Swinburne University of Technology, Melbourne, Australia, 2011. [Google Scholar]
- Caffery, G.; Rafiei, P.; Honeyands, T.; Trotter, D.; Marketing, B.B. Understanding the Melting Characteristics of HBI in Iron and Steel Melts. In Proceedings of the Asssociation for Iron & Steel Technology, Nashville, TN, USA, 15–17 September 2004; Volume 1, p. 503. [Google Scholar]
- Gaye, H.; Wanin, M.; Gugliermina, P.; Schittly, P. Kinetics of scrap dissolution in the converter: Theoretical model and plant experimentation. In Proceedings of the 68th Steelmaking Conference, Detroit, MI, USA, 14–17 April 1985; pp. 91–103. [Google Scholar]
- MacRosty, R.D.; Swartz, C.L. Dynamic optimization of electric arc furnace operation. AIChE J. 2007, 53, 640–653. [Google Scholar] [CrossRef]
- Bekker, J.G.; Craig, I.K.; Pistorius, P.C. Modeling and Simulation of an Electric Arc Furnace Process. ISIJ Int. 1999, 39, 23–32. [Google Scholar] [CrossRef]
- Dogan, N.; Brooks, G.A.; Rhamdhani, M.A. Kinetics of flux dissolution in oxygen steelmaking. ISIJ Int. 2009, 49, 1474–1482. [Google Scholar] [CrossRef]
- Hamano, T.; Horibe, M.; Ito, K. The dissolution rate of solid lime into molten slag used for hot-metal dephosphorization. ISIJ Int. 2004, 44, 263–267. [Google Scholar] [CrossRef]
- Umakoshi, M.; Mort, K.; Kawai, Y. Dissolution rate of burnt dolomite in molten FetO-CaO-SiO2 slags. Trans. Iron Steel Inst. Jpn. 1984, 24, 532–539. [Google Scholar] [CrossRef]
- Kadrolkar, A.; Andersson, N.Å.; Dogan, N. A Dynamic Flux Dissolution Model for Oxygen Steelmaking. Metall. Mater. Trans. B 2017, 48, 99–112. [Google Scholar] [CrossRef]
- Subagyo; Brooks, G.A.; Coley, K.S.; Irons, G.A. Generation of Droplets in Slag-Metal Emulsions through Top Gas Blowing. ISIJ Int. 2003, 43, 983–989. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Lytvynyuk, Y.; Schenk, J.; Hiebler, M.; Sormann, A. Thermodynamic and kinetic model of the converter steelmaking process. Part 2: The model validation. Steel Res. Int. 2014, 85, 544–563. [Google Scholar] [CrossRef]
- Brooks, G.; Pan, Y.; Subagyo; Coley, K. Modeling of trajectory and residence time of metal droplets in slag–metal–gas emulsions in oxygen steelmaking. Metall. Mater. Trans. B 2005, 36, 525–535. [Google Scholar] [CrossRef]
- Rout, B.K.; Brooks, G.; Subagyo; Rhamdhani, M.A.; Li, Z. Modeling of droplet generation in a top blowing steelmaking process. Metall. Mater. Trans. B 2016, 47, 3350–3361. [Google Scholar] [CrossRef]
- Mills, K.C. Viscosities of Molten Slags in Slag Atlas, 2nd ed.; Verlag Stahleisen: Düsseldorf, Germany, 1995; p. 353. [Google Scholar]






| Parameters | Cicutti | Plant A |
|---|---|---|
| 0.2 | 0.07 | |
| 1 | 1.16 | |
| 10 | 2 | |
| 1 | 1 | |
| 3 | 3.07 | |
| 1 | 1 | |
| 7 × 10 | 2.0 × 10 | |
| 7 | 7 | |
| 30 | 30 | |
| 20 | 20 | |
| 0.5 | 0.5 | |
| , | 1000 | 1000 |
| 2500 | 2500 | |
| 80,000 | 80,000 |
| Input | Hot Metal | Heavy Scrap | Light Scrap | Pig Iron | External Scrap |
|---|---|---|---|---|---|
| Mass (kg) | 170,000 | 3570 | 10,000 | 12,140 | 4284 |
| Thickness (mm) | - | 100 | 25 | 200 | 500 |
| C (%) | 4 | 0.08 | 0.08 | 4.5 | 0.05 |
| Si (%) | 0.33 | 0.05 | 0.05 | 0.5 | 0.001 |
| Mn (%) | 0.52 | 0.3 | 0.3 | 0.5 | 0.2 |
| P (%) | 0.066 | - | - | - | - |
| S (%) | 0.015 | - | - | - | - |
| Model | Computer | Software | Solution Time |
|---|---|---|---|
| Dogan et al. [6] | Pentium (R) 4 CPU 3.00 GHz and 3GB of RAM | Scilab | 240 min |
| Sarkar et al. [8] | Not given | Matlab | 27 min |
| Rout et al. [9] | Intel(R) Core(TM) i5-4570 CPU @3.20 GHz and 8 GB RAM | Matlab | 20 min |
| Present study | Intel(R) Core(TM) i7-7700 CPU @3.16GHz and 16.0 GB RAM | Python 3.7 | 0.036 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dering, D.; Swartz, C.; Dogan, N. Dynamic Modeling and Simulation of Basic Oxygen Furnace (BOF) Operation. Processes 2020, 8, 483. https://doi.org/10.3390/pr8040483
Dering D, Swartz C, Dogan N. Dynamic Modeling and Simulation of Basic Oxygen Furnace (BOF) Operation. Processes. 2020; 8(4):483. https://doi.org/10.3390/pr8040483
Chicago/Turabian StyleDering, Daniela, Christopher Swartz, and Neslihan Dogan. 2020. "Dynamic Modeling and Simulation of Basic Oxygen Furnace (BOF) Operation" Processes 8, no. 4: 483. https://doi.org/10.3390/pr8040483
APA StyleDering, D., Swartz, C., & Dogan, N. (2020). Dynamic Modeling and Simulation of Basic Oxygen Furnace (BOF) Operation. Processes, 8(4), 483. https://doi.org/10.3390/pr8040483