A Geometric Observer-Assisted Approach to Tailor State Estimation in a Bioreactor for Ethanol Production
Abstract
1. Introduction
2. Process Model
3. Estimation Problem
3.1. Robust Estimability and Robust Detectability
3.2. Selection of the Estimator Structure
3.3. Algorithms for the Estimation Problem
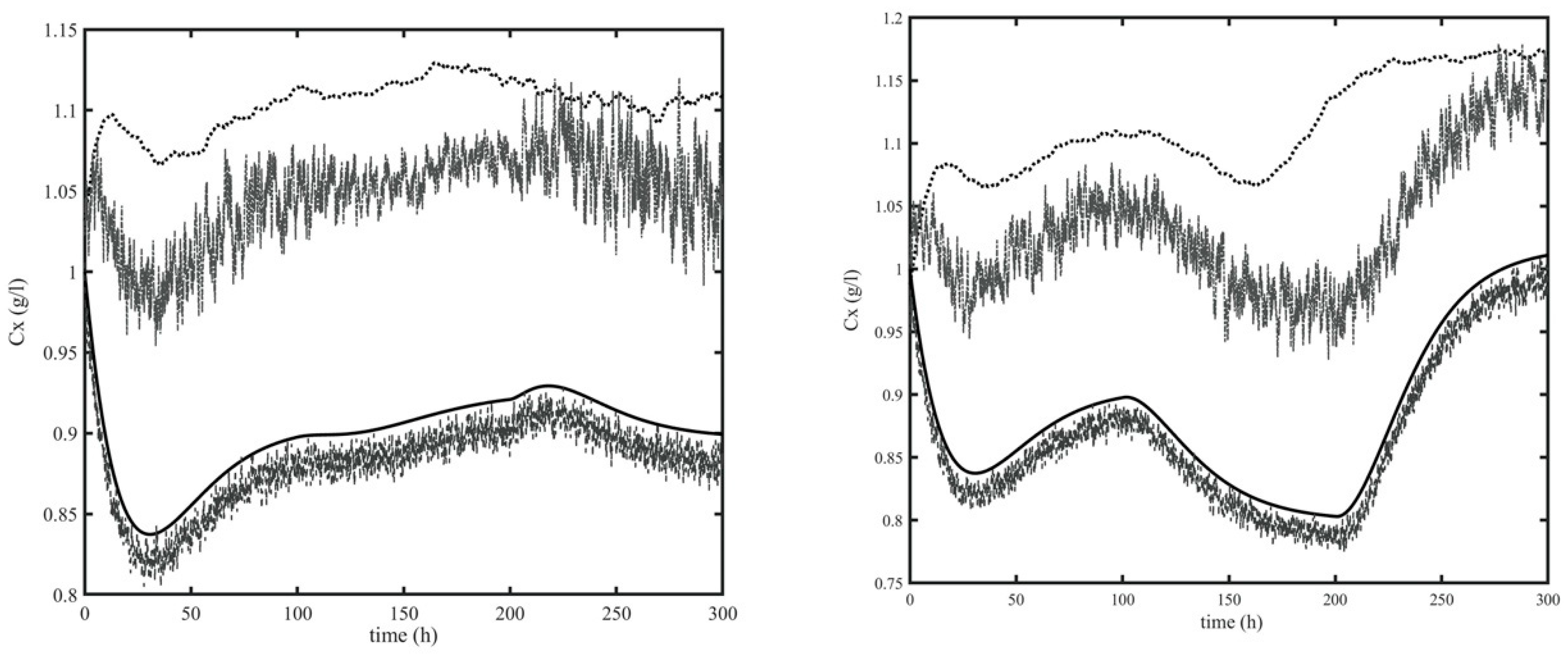
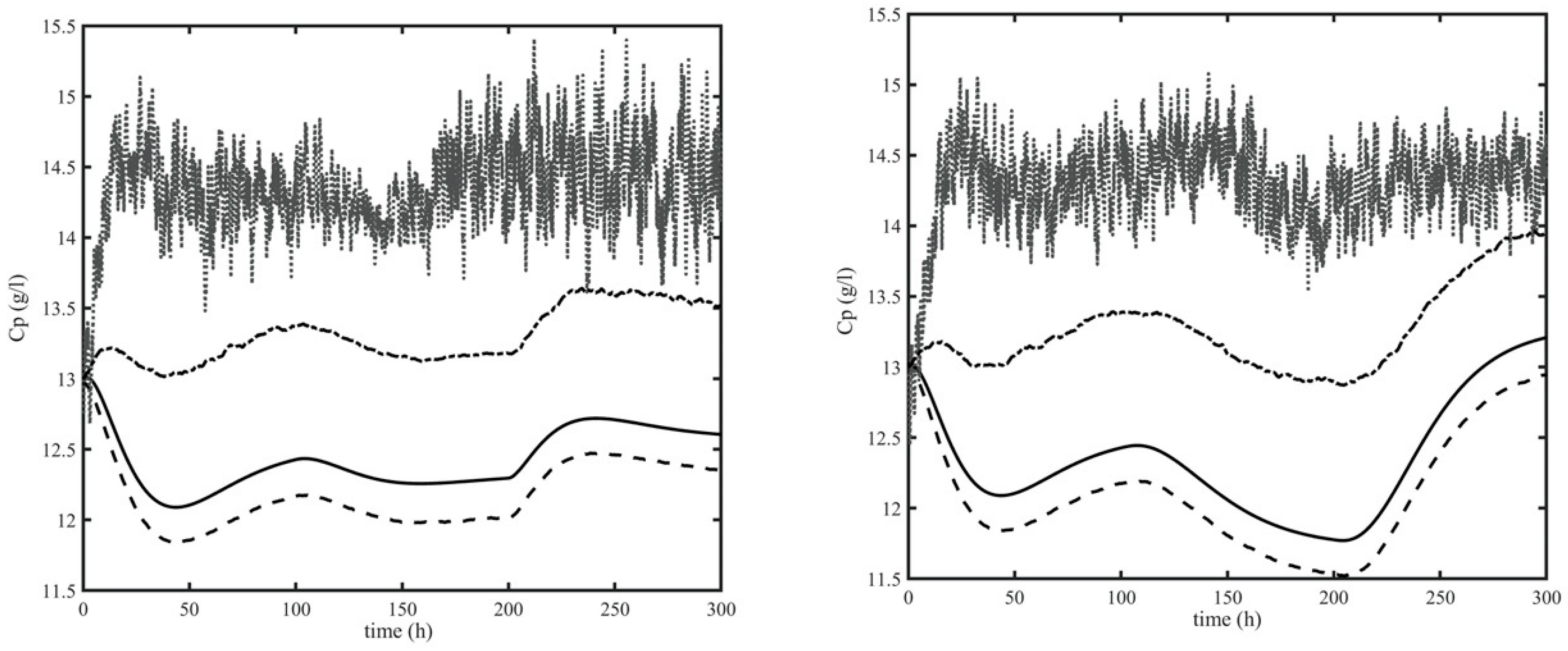
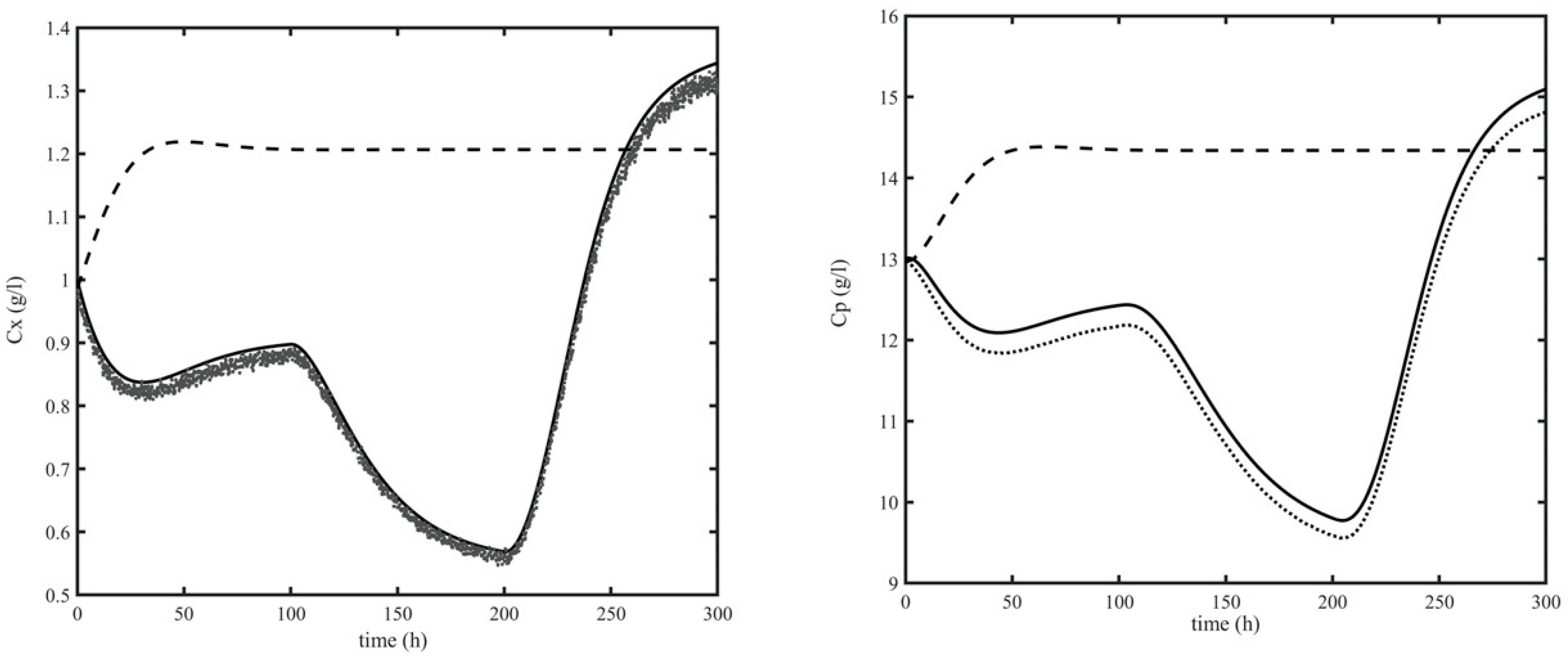
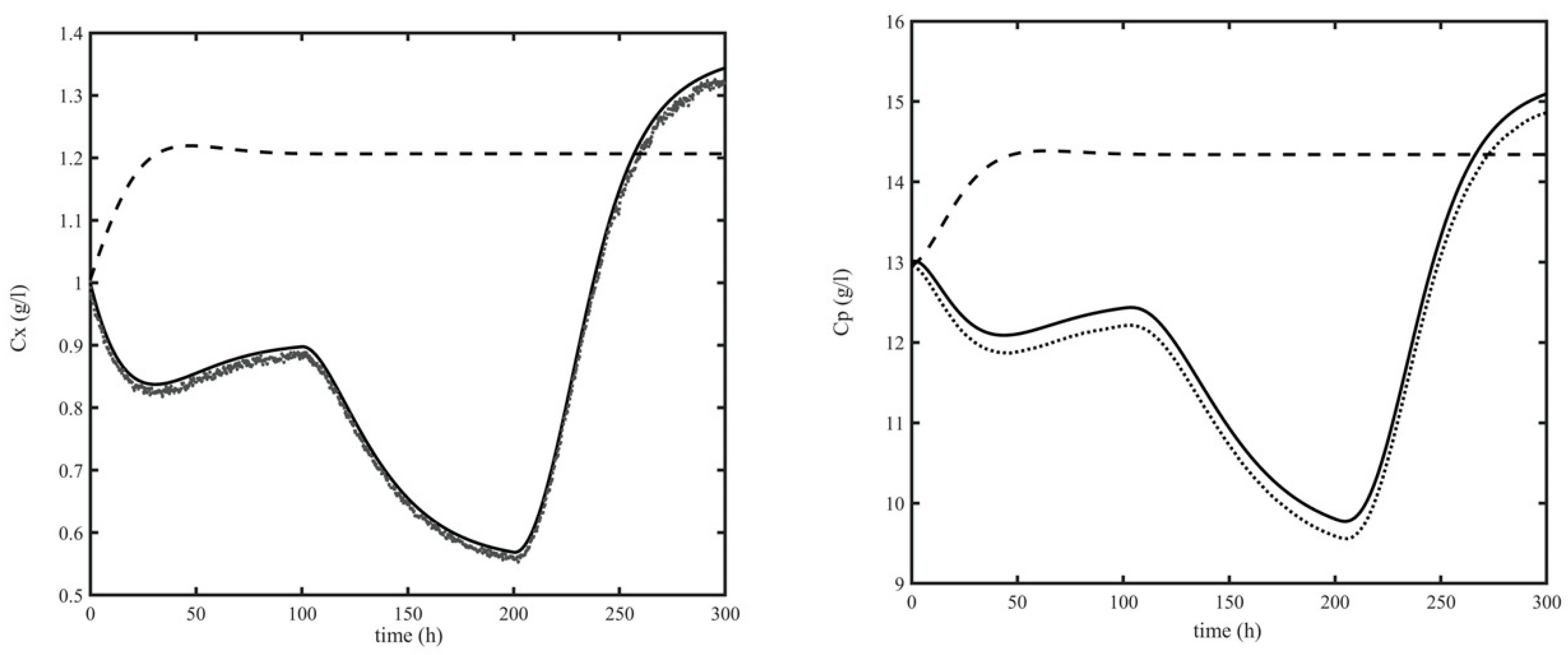
4. Results
4.1. Estimation Structure
4.2. Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ramaswamy, S.; Cutright, T.J.; Qammar, H.K. Control of a continuous bioreactor using model predictive control. Process Biochem. 2005, 40, 2763–2770. [Google Scholar] [CrossRef]
- Imtiaz, U.; Assadzadeh, A.; Jamuar, S.S.; Sahu, J.N. Bioreactor temperature profile controller using inverse neural network (INN) for production of ethanol. J. Process Control 2013, 23, 731–742. [Google Scholar] [CrossRef]
- Holzberg, T.R.; Watson, V.; Brown, S.; Andar, A.; Ge, X.; Kostov, Y.; Tolosa, L.; Rao, G. Sensors for biomanufacturing process development: Facilitating the shift from batch to continuous manufacturing. Curr. Opin. Chem. Eng. 2018, 22, 115–127. [Google Scholar] [CrossRef]
- Cabaneros Lopez, P.; Feldman, H.; Mauricio-Iglesias, M.; Junicke, H.; Huusom, J.K.; Gernaey, K.V. Benchmarking real-time monitoring strategies for ethanol production from lignocellulosic biomass. Biomass Bioenergy 2019, 127, 105296. [Google Scholar] [CrossRef]
- Pachauri, N.; Singh, V.; Rani, A. Two degree of freedom PID based inferential control of continuous bioreactor for ethanol production. Isa Trans. 2017, 68, 235–250. [Google Scholar] [CrossRef]
- Tronci, S.; Grosso, M.; Alvarez, J.; Baratti, R. On the global nonlinear stochastic dynamical behavior of a class of exothermic CSTRs. J. Process Control 2011, 21, 1250–1264. [Google Scholar] [CrossRef]
- Baratti, R.; Tronci, S.; Schaum, A.; Alvarez, J. Open and closed-loop stochastic dynamics of a class of nonlinear chemical processes with multiplicative noise. J. Process Control 2018, 66, 108–121. [Google Scholar] [CrossRef]
- Moreno, J.A.; Alvarez, J. On the estimation problem of a class of continuous bioreactors with unknown input. J. Process Control 2015, 30, 34–49. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Ciccarella, G.; Dalla Mora, M.; Germani, A. A Luenberger-like observer for nonlinear systems. Int. J. Control 1993, 57, 537–556. [Google Scholar] [CrossRef]
- Wang, G.B.; Peng, S.S.; Huang, H.P. A sliding observer for nonlinear process control. Chem. Eng. Sci. 1997, 52, 787–805. [Google Scholar] [CrossRef]
- Zeitz, M. The extended Luenberger observer for nonlinear systems. Syst. Control Lett. 1987, 9, 149–156. [Google Scholar] [CrossRef]
- Alvarez, J.; López, T. Robust dynamic state estimation of nonlinear plants. Aiche J. 1999, 45, 107–123. [Google Scholar] [CrossRef]
- Dewasme, L.; Goffaux, G.; Hantson, A.L.; Wouwer, A.V. Experimental validation of an Extended Kalman Filter estimating acetate concentration in E. coli cultures. J. Process Control 2013, 23, 148–157. [Google Scholar] [CrossRef]
- Longhi, L.G.S.; Marcon, S.M.; Trierweiler, J.O.; Secchi, A.R. State estimation of an experimental bioreactor using the extended Kalman filtering technology. Ifac Proc. Vol. 2002, 35, 379–382. [Google Scholar] [CrossRef]
- Nagy, Z.K. Model based control of a yeast fermentation bioreactor using optimally designed artificial neural networks. Chem. Eng. J. 2007, 127, 95–109. [Google Scholar] [CrossRef]
- Álvarez, J.; Fernández, C. Geometric estimation of nonlinear process systems. J. Process Control 2009, 19, 247–260. [Google Scholar] [CrossRef]
- Porru, M.; Özkan, L. Monitoring of Batch Industrial Crystallization with Growth, Nucleation, and Agglomeration. Part 2: Structure Design for State Estimation with Secondary Measurements. Ind. Eng. Chem. Res. 2017, 56, 9578–9592. [Google Scholar] [CrossRef]
- Alvarez, J. Nonlinear state estimation with robust convergence. J. Process Control 2000, 10, 59–71. [Google Scholar] [CrossRef]
- Bela, S. Bioengineering Operations; Tankonykiado: Budapest, Hungary, 1992. [Google Scholar]
- Spigno, G.; Tronci, S. Development of hybrid models for a vapor-phase fungi bioreactor. Math. Probl. Eng. 2015, 2015, 801213. [Google Scholar] [CrossRef]
- Salas, S.D.; Romagnoli, J.A.; Tronci, S.; Baratti, R. A geometric observer design for a semi-batch free-radical polymerization system. Comput. Chem. Eng. 2019, 126, 391–402. [Google Scholar] [CrossRef]
- Dochain, D.; Tali-Maamar, N.; Babary, J.P. On modelling, monitoring and control of fixed bed bioreactors. Comput. Chem. Eng. 1997, 21, 1255–1266. [Google Scholar] [CrossRef]
- Long, R.; Qin, Y.Y.; Jia, J.C. Observable degree analysis of SINS initial alignment based on singular value decomposition. In Proceedings of the 2008 IEEE International Symposium on Knowledge Acquisition and Modeling Workshop, Wuhan, China, 21–22 December 2008; pp. 444–448. [Google Scholar]
- Leu, G.; Baratti, R. An extended Kalman filtering approach with a criterion to set its tuning parameters; application to a catalytic reactor. Comput. Chem. Eng. 2000, 23, 1839–1849. [Google Scholar] [CrossRef]
- Salas, S.D.; Ghadipasha, N.; Zhu, W.; Mcafee, T.; Zekoski, T.; Reed, W.F.; Romagnoli, J.A. Framework design for weight-average molecular weight control in semi-batch polymerization. Control Eng. Pract. 2018, 78, 12–23. [Google Scholar] [CrossRef]




| Virtual Plant | Estimator | |
|---|---|---|
| µp | 1.790 | 1.7465 |
| Ks | 1.030 | 1.0248 |
| Kp | 0.139 | 0.1281 |
| Ks1 | 1.680 | 1.8090 |
| Kp1 | 0.070 | 0.0692 |
| Rsx | 0.607 | 0.6274 |
| Rsp | 0.435 | 0.4549 |
| CO2 = 2.5 mg/L | pH = 6 |
|---|---|
| CP = 13 g/L | Tag = 29 °C |
| CS = 27 g/L | Tin = 25 °C |
| CS,in = 60 g/L | Tin,ag = 15 °C |
| CX = 1 g/L | Tr = 26 °C |
| Fag = 18 L/h | V = 1000 L |
| Fi = Fe = 51 L/h | - |
| CX | CS | CO2 | Tr | Tag |
|---|---|---|---|---|
| ±2.5% | ±2.5% | ±2.5% | ±0.1 °C | ±0.1 °C |
| Input | t = 0 h | t = 100 h | t = 200 h | |
|---|---|---|---|---|
| T1 | CS,in (g/L) | 60 | 45 | 75 |
| T2 | Tin,ag (°C) | 15 | 10 | 20 |
| T3 | Tin (°C) | 25 | 20 | 30 |
| 1802.6 | 71.37 | |
| 0.086 | 0.03 |
| 2.15 | 8.75 | 1.53 | |
| 0.47 | 0.12 | 0.99 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisci, S.; Grosso, M.; Tronci, S. A Geometric Observer-Assisted Approach to Tailor State Estimation in a Bioreactor for Ethanol Production. Processes 2020, 8, 480. https://doi.org/10.3390/pr8040480
Lisci S, Grosso M, Tronci S. A Geometric Observer-Assisted Approach to Tailor State Estimation in a Bioreactor for Ethanol Production. Processes. 2020; 8(4):480. https://doi.org/10.3390/pr8040480
Chicago/Turabian StyleLisci, Silvia, Massimiliano Grosso, and Stefania Tronci. 2020. "A Geometric Observer-Assisted Approach to Tailor State Estimation in a Bioreactor for Ethanol Production" Processes 8, no. 4: 480. https://doi.org/10.3390/pr8040480
APA StyleLisci, S., Grosso, M., & Tronci, S. (2020). A Geometric Observer-Assisted Approach to Tailor State Estimation in a Bioreactor for Ethanol Production. Processes, 8(4), 480. https://doi.org/10.3390/pr8040480






