Temperature Distribution Estimation in a Dwight–Lloyd Sinter Machine Based on the Combustion Rate of Charcoal Quasi-Particles
Abstract
1. Introduction
2. Experimental Sample and Procedure
3. Results
4. Kinetic Analysis
4.1. Unreacted Core Model for Coke
- 1.
- O2 transport from the gas phase to the particle surface through the gas film:
- 2.
- O2 transport from the particle surface to the reaction interface through the alumina powder layer after coke combustion:
- 3.
- The combustion reaction at the reaction interface:
- 4.
- CO2 transport from the reaction interface to the particle surface through the alumina powder layer after coke combustion:
- 5.
- CO2 transport from the particle surface to the gas phase through the gas film:
| Coke | (−125 μm) | kc = 6.02 × 10−2 exp(−9.32 × 103/RT) | (m/s) |
| (125~250 µm) | kc = 4.51 × 10−2 exp(−5.12 × 103/RT) | (m/s) |

| Coke | (−125 μm) | De = 1.79 × 10−3 exp(−36.4 × 103/RT) | (m/s) |
| (125~250 µm) | De = 3.06 × 10−3 exp(−36.6 × 103/RT) | (m/s) |

4.2. Chemical Reaction Control Step for Charcoal
| Coke | (−125 μm) | kc = | (m/s) |
| (125~250 µm) | kc = | (m/s) |

5. Sintering Simulation Model
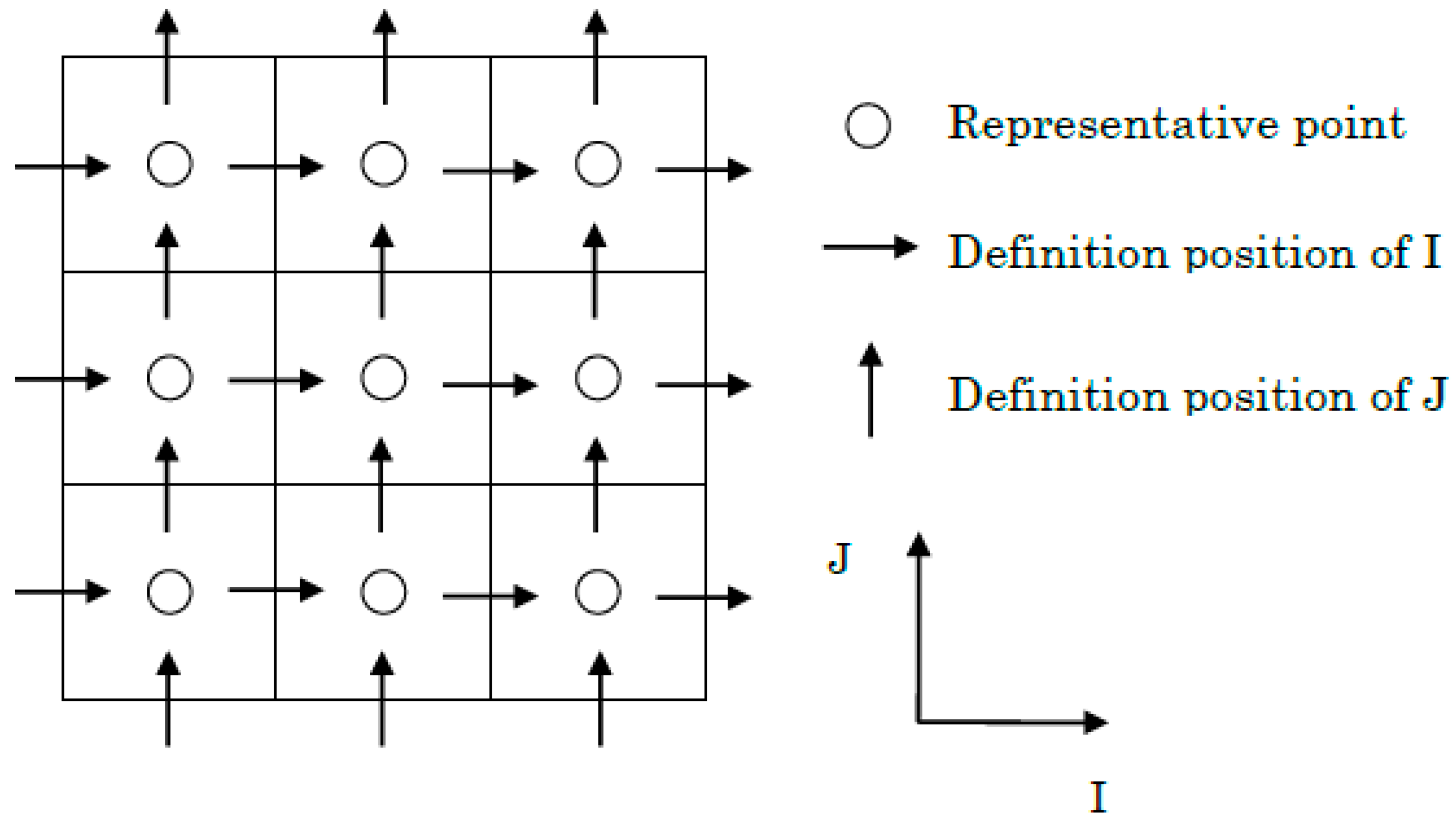
5.1. Simulation Method
5.2. Calculation Conditions
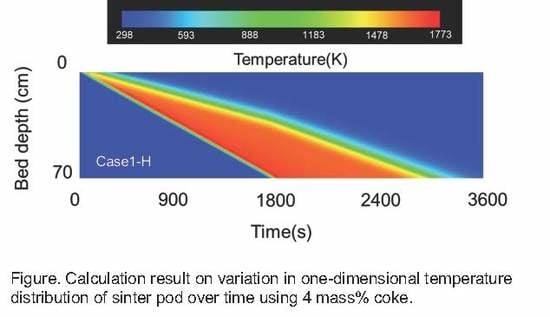
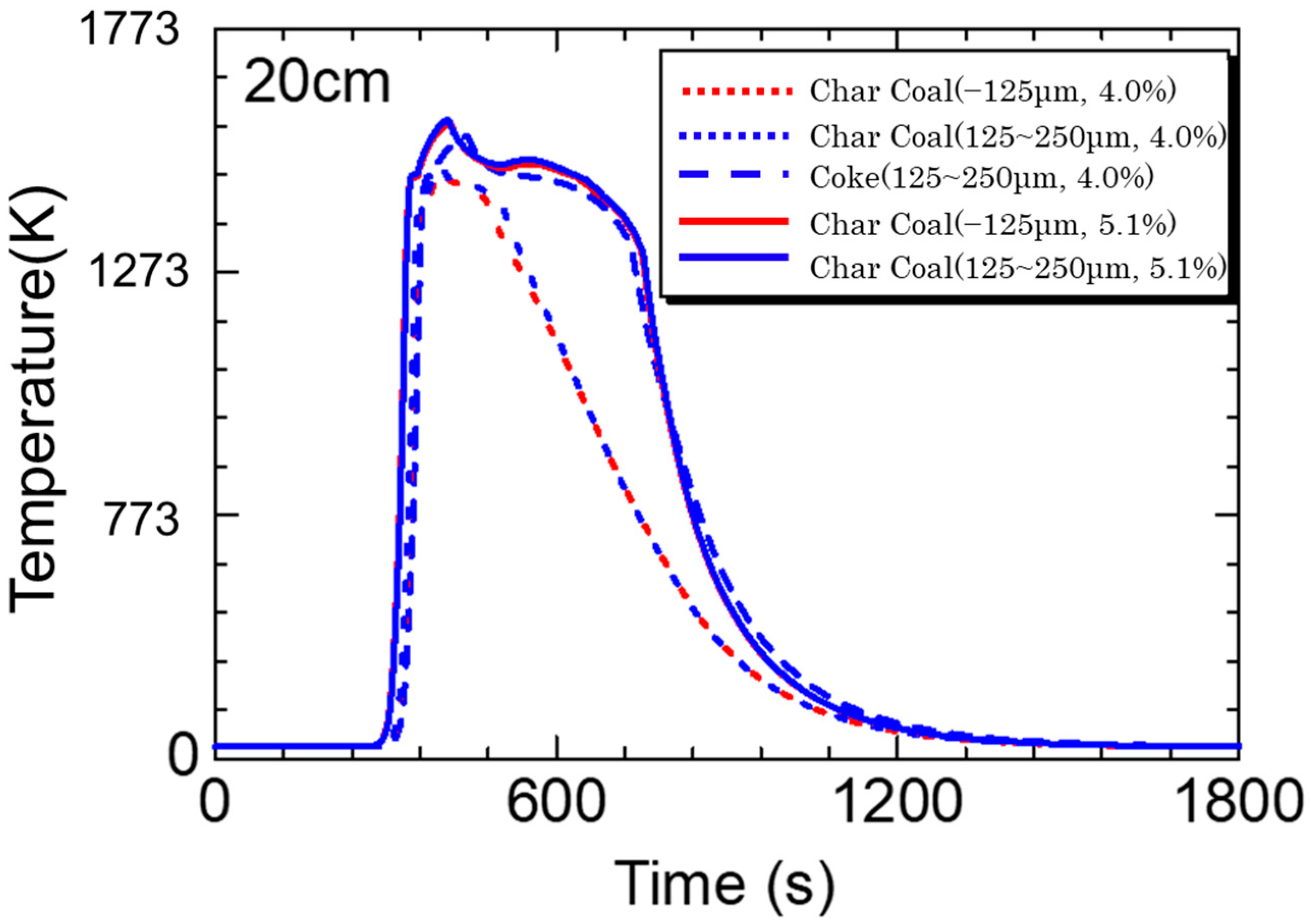
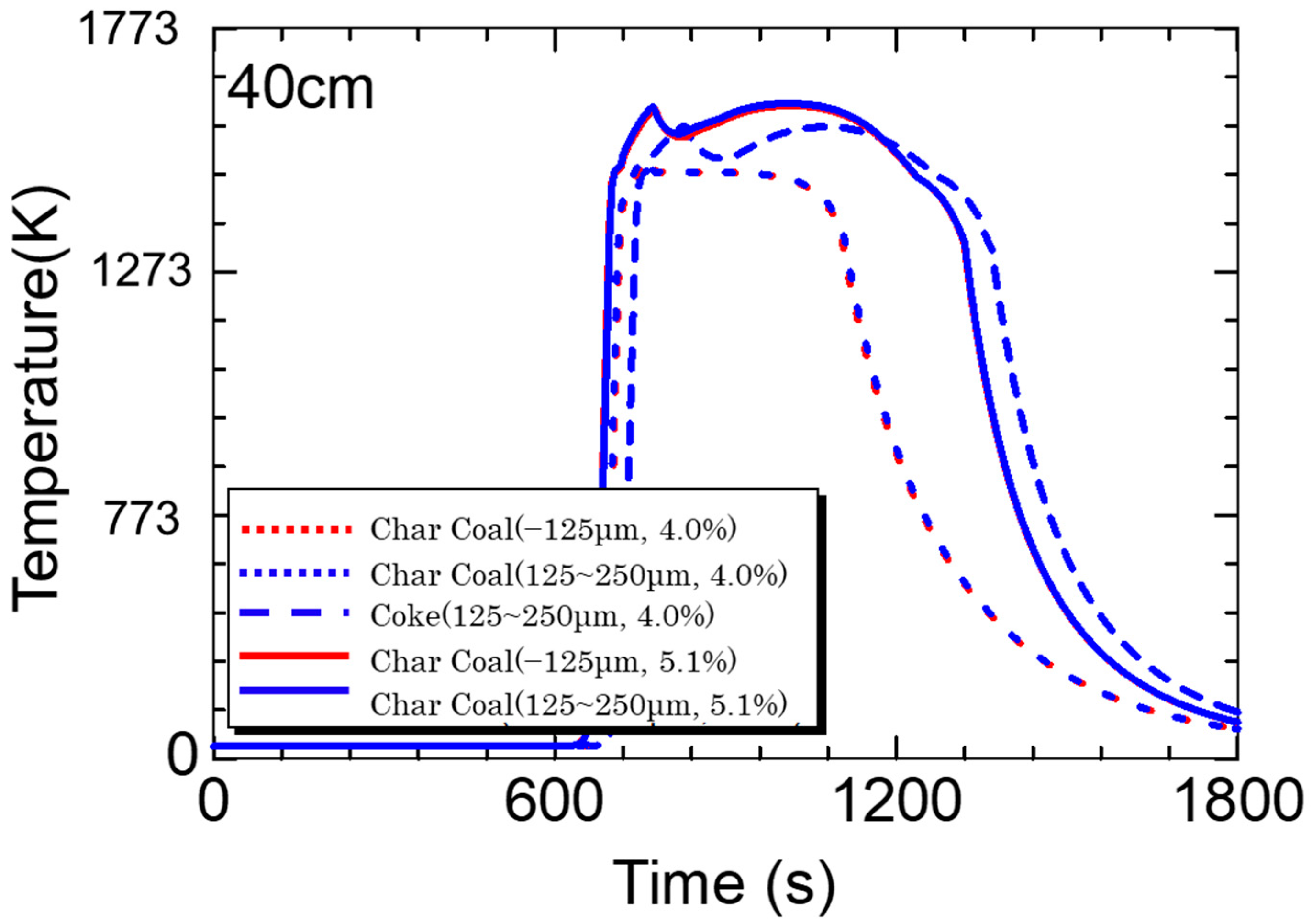
5.3. Calculation Results
6. Conclusions
- Compared with coke, the reaction curves of charcoal combustion show that the combustion reaction of charcoal is faster.
- The interfacial chemical reaction rate coefficient of charcoal for the experimental data was calculated as follows:
| Coke | (−125 μm) | kc = | (m/s) |
| (125~250 µm) | kc = | (m/s) |
- Calculations using the rate equation obtained in the sintering simulation model found that the high temperature range of charcoal is smaller than that of coke due to charcoal’s low fixed carbon content and density.
- If the fixed carbon content of charcoal is the same as that of coke, which means that the combustion heat of carbon materials is the same, a temperature profile of the same level can be obtained.
- The sintering simulation results suggest that there are probabilities that biomass carbon materials can replace coke in the sintering process.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A(kc,De) | Frequency factor (m/s) |
| C(O2, CO2) | O2 or CO2 concentration in the gas phase (mol/m3) |
| C(O2, CO2)·i | O2 or CO2 concentration at the reaction interface (mol/m3) |
| C(O2, CO2)·s | O2 or CO2 concentration at the particle surface (mol/m3) |
| Cp | Specific heat (J/kg/K) |
| d | Particle size (m) |
| De | Effective diffusion coefficient in the Al2O3 powder layer (m2/s) |
| (DO2, CO2)eff | Effective diffusion coefficient of O2 or CO2 in the Al2O3 powder layer (m2/s) |
| Ea(kc,De) | Activation energy (J/mol) |
| F | Reaction ratio (–) |
| H | Reaction heat of each reaction (J/mol) |
| h | Convection heat transfer coefficient (J/m2/s/K) |
| K | Equilibrium constant (–) |
| kC | Interfacial chemical reaction rate coefficient (m/s) |
| kf | Mass transfer coefficient in the gas film (m/s) |
| k | Heat conductivity (J/m/s/K) |
| k’ | Overall reaction rate (m/s) |
| n(Coke, Quasi-particle, Lime, Ore) | The amount of coke, quasi-particle, lime and ore among unit volume (-) |
| ΔP | Pressure loss (atm) |
| r0 | Initial radius (m) |
| ri | Radius of the non-reaction nucleus (m) |
| ri,x * | Generation rate of the component x in the number i cell (kg/s/m3) |
| rQuasi-particle | Distance from the left of the particle to the reaction interface of the quasi-particle (m) |
| r * | Reaction ratio of the component in the sample (–) |
| r *Quasi-particle | Reaction rate per one particle of the quasi-particle (mol/s) |
| Tg | Temperature of gas in the control volume (K) |
| Ts | Temperature of solid in the control volume (K) |
| Δwt | Sample weight change (kg) |
| U | Superficial velocity (m/s) |
| u | Gas flow rate (m/s) |
| W | Weight change of the sample during the experiment (kg) |
| ΔZ | Length of the control volume (m) |
| Px | Density of component x (kg/m3) |
| ρCm | Carbon concentration in the sample (mol/m3) |
| ρN2, O2,CO2, H2O | Density of gas in the sample(kg/m3) |
| εa | Porosity (-) |
| Φ | (Surface area of a ball which has the same volume with the particle)/(Surface area of the particle) (-) |
| μg | Viscosity of gas (Pa·s) |
References
- Japan’s National Greenhouse Gas Emissions in Fiscal Year 2017 (Final Figures); Ministry of the Environment: Tokyo, Japan, 2019.
- Takeshima, S. Biomass, Carbon-neutral and Renewable Energy. K. J. JIME 2012, 47, 133. [Google Scholar] [CrossRef][Green Version]
- Lovel, R.R.; Vining, K.R.; Dell’Amico, M. The influence of fuel reactivity on iron ore sintering. ISIJ Int. 2009, 49, 195–202. [Google Scholar] [CrossRef]
- Zandi, M.; Martinez-Pacheco, M.; Fray, T. Biomass for iron ore sintering. Miner. Eng. 2010, 23, 1139–1145. [Google Scholar] [CrossRef]
- Ooi, T.; Aries, E.; Ewan, B.; Thompson, D.; Anderson, D.R.; Fisher, R.; Fray, T.; Tognarelli, D. The study of sunflower seed husks as a fuel in the iron ore sintering process. Miner. Eng. 2008, 21, 167–177. [Google Scholar] [CrossRef]
- Gan, M.; Fan, X.; Chen, X.; Ji, Z.; Lv, W.; Wang, Y.; Yu, Z.; Jiang, T. Reduction of pollutant emission in iron ore sintering process by applying biomass fuels. ISIJ Int. 2012, 52, 1574–1578. [Google Scholar] [CrossRef]
- Yagi, T.; Ono, Y. A method of analysis for reduction of iron oxide in mixed-control kinetics. Trans. ISIJ 1968, 8, 377. [Google Scholar]
- Ohno, K.; Noda, K.; Nisioka, K.; Maeda, T.; Shimizu, M. Combustion rate of coke in quasi-particle at iron ore sintering process. ISIJ Int. 2013, 53, 1588–1593. [Google Scholar] [CrossRef]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Ohno, K.; Noda, K.; Nisioka, K.; Maeda, T.; Shimizu, M. Effect of coke combustion rate equation on numerical simulation of temperature distribution in iron ore sintering process. ISIJ Int. 2013, 53, 1642–1647. [Google Scholar] [CrossRef]
- Tu, C.M.; Davis, H.; Hottel, H.C. Combustion rate of carbon-combustion of spheres in flowing gas streams. Ind. Eng. Chem. 1934, 26, 749–757. [Google Scholar] [CrossRef]
- Davis, H.; Hottel, H.C. Combustion rate of carbon-combustion at a surface overlaid with stagnant gas. Ind. Eng. Chem. 1934, 26, 889–892. [Google Scholar] [CrossRef]
- Parker, A.S.; Hottel, H.C. Combustion rate of carbon study of gas-film structure by microsampling. Ind. Eng. Chem. 1936, 28, 1334–1341. [Google Scholar] [CrossRef]
- Oyama, N.; Iwami, Y.; Yamamoto, T.; Machida, S.; Higuchi, T.; Sato, H.; Sato, M.; Takeda, K.; Watanabe, Y.; Shimizu, M.; et al. Development of secondary-fuel injection technology for energy reduction in the iron ore sintering process. ISIJ Int. 2011, 51, 913–921. [Google Scholar] [CrossRef]
- Hida, Y.; Sasaki, M.; Enokido, T.; Umezu, Y.; Iida, T.; Uno, S. Effect of the existing state of coke breeze in quasi-particles of raw mix on coke combustion in the sintering process. Tetsu-to-Hagané 1982, 68, 400–409. [Google Scholar] [CrossRef]

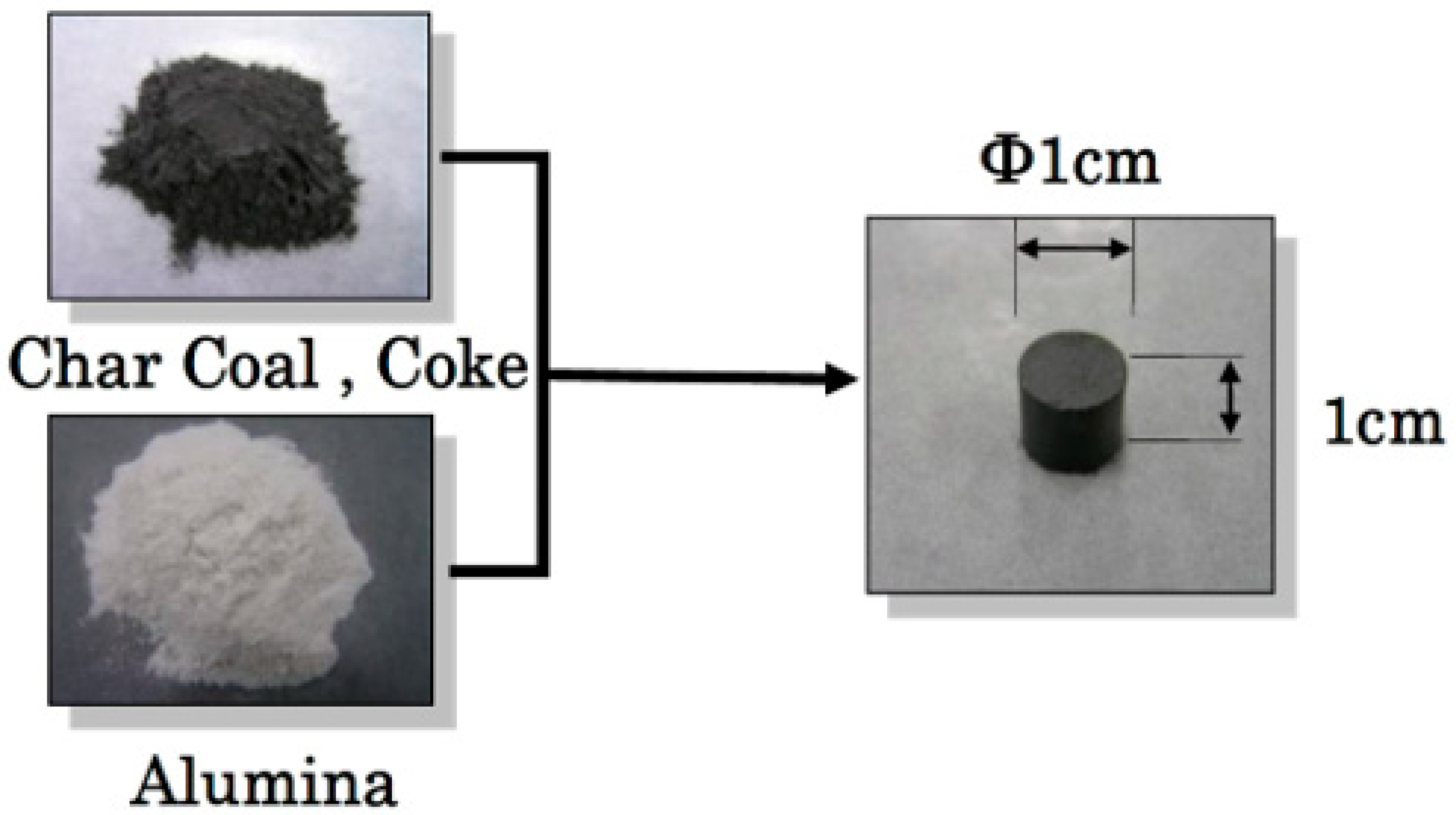




| Ash (mass %) | V.M. (mass %) | Fix.C. (mass %) | Specific Surface Area (m2/g) | |
|---|---|---|---|---|
| Charcoal (−125 μm) | 1.84 | 29.2 | 69.0 | 61.0 |
| Charcoal (125~250 μm) | 28.5 | |||
| Coke (−125 μm) | 10.1 | 1.71 | 88.2 | 2.59 |
| Coke (125~250 μm) | 0.92 |
| ▪Sinter Bed | |
| Bed depth | 450 mm |
| Porosity of sinter bed | 35% |
| ▪Composition of Raw materials | |
| Hematite | 85.0 mass % |
| Lime (CaO) | 10.0 mass % |
| Moisture | 5.0 mass % |
| Coke, Charcoal | 4.0 mass % (additionally) |
| Charcoal | 5.1 mass % (additionally) |
| ▪Diameter of Raw Materials | |
| Hematite | 2.5 mm:0.25 mm ≈ 88.6:11.4 |
| Lime (CaO) | 2.0 mm |
| ▪Others | |
| Initial temperature | 298 K |
| Ignition temperature | 1573 K |
| Ignition time | 90 s |
| Gas flow rate (outlet) | 0.6 m/s |
| Calculation cell | 5 mm |
| Time step | 0.001 s |
| Courant number | 0.2 |
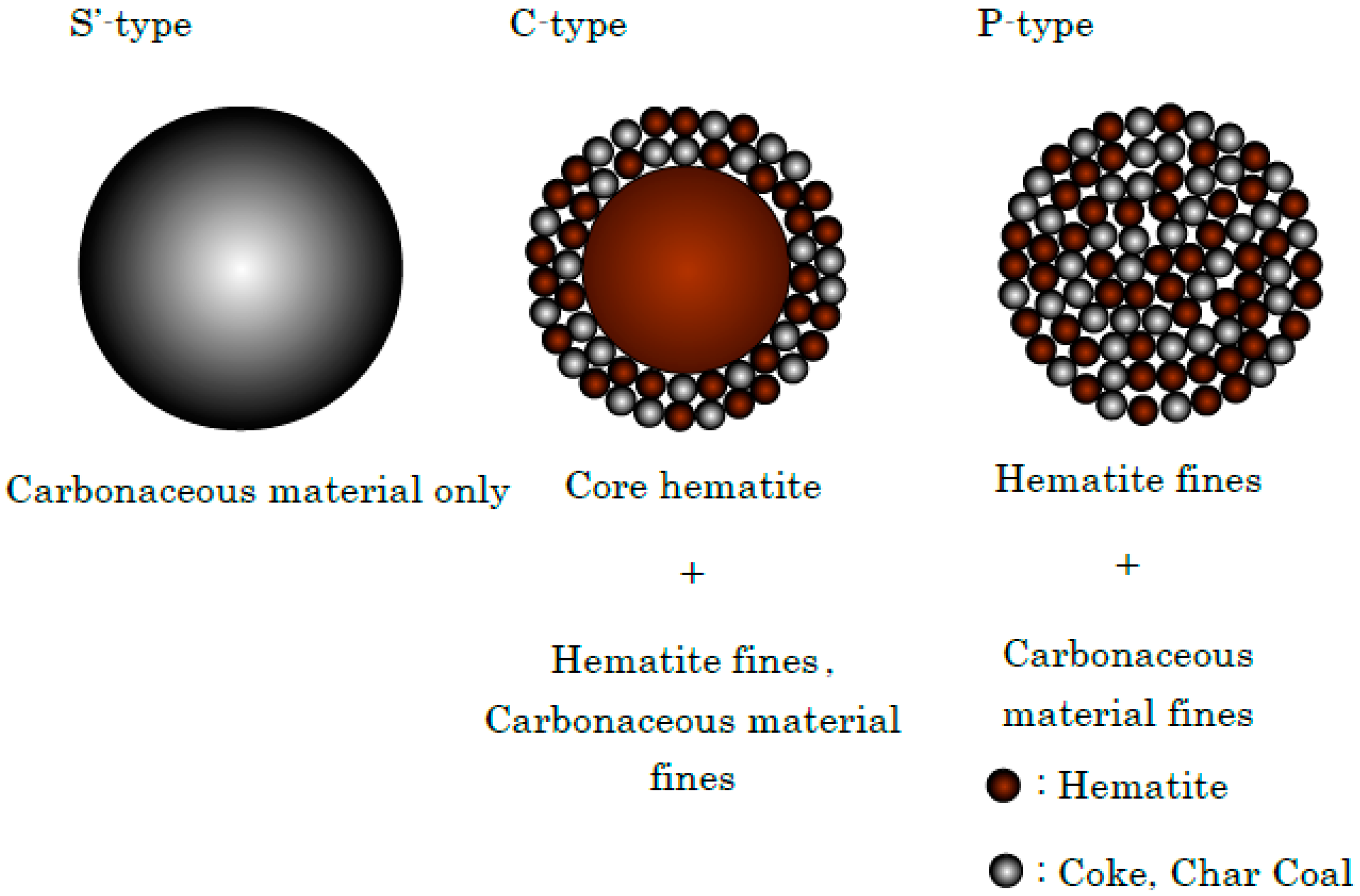
| Existing State of Coke (%) | Total | Amount of Coke and Charcoal in Sinter Bed (%) | ||
|---|---|---|---|---|
| S’-Type | C-Type | P-Type | ||
| 40.0 | 30.0 | 30.0 | 100 | 4.0, 5.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Ohno, K.-i.; Nonaka, S.; Maeda, T.; Kunitomo, K. Temperature Distribution Estimation in a Dwight–Lloyd Sinter Machine Based on the Combustion Rate of Charcoal Quasi-Particles. Processes 2020, 8, 406. https://doi.org/10.3390/pr8040406
Wang Z, Ohno K-i, Nonaka S, Maeda T, Kunitomo K. Temperature Distribution Estimation in a Dwight–Lloyd Sinter Machine Based on the Combustion Rate of Charcoal Quasi-Particles. Processes. 2020; 8(4):406. https://doi.org/10.3390/pr8040406
Chicago/Turabian StyleWang, Ziming, Ko-ichiro Ohno, Shunsuke Nonaka, Takayuki Maeda, and Kazuya Kunitomo. 2020. "Temperature Distribution Estimation in a Dwight–Lloyd Sinter Machine Based on the Combustion Rate of Charcoal Quasi-Particles" Processes 8, no. 4: 406. https://doi.org/10.3390/pr8040406
APA StyleWang, Z., Ohno, K.-i., Nonaka, S., Maeda, T., & Kunitomo, K. (2020). Temperature Distribution Estimation in a Dwight–Lloyd Sinter Machine Based on the Combustion Rate of Charcoal Quasi-Particles. Processes, 8(4), 406. https://doi.org/10.3390/pr8040406