Simulation of Solid Oxide Fuel Cell Anode in Aspen HYSYS—A Study on the Effect of Reforming Activity on Distributed Performance Profiles, Carbon Formation, and Anode Oxidation Risk
Abstract
1. Introduction
2. Simulation Methodology
3. Results and Discussion
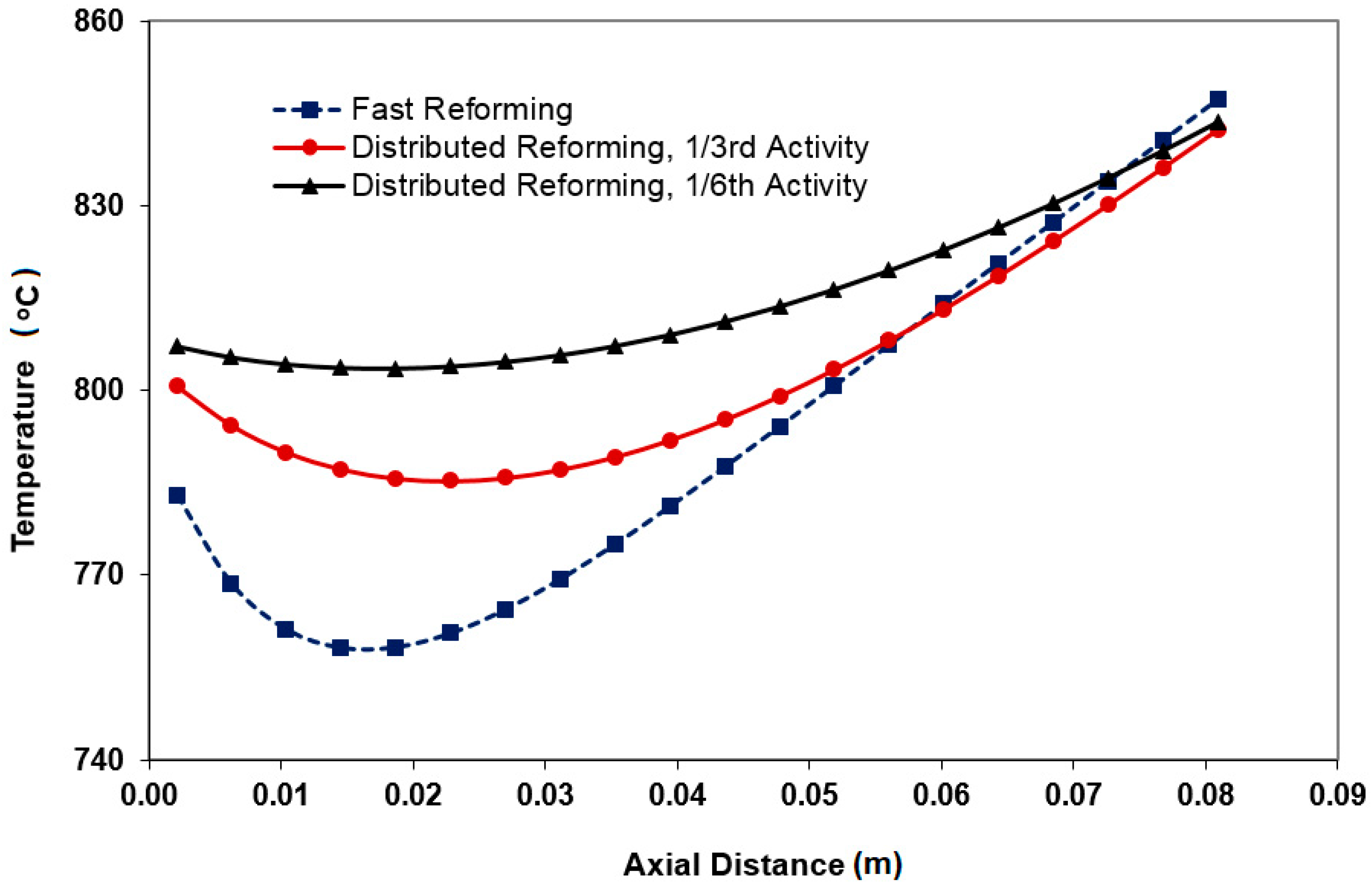
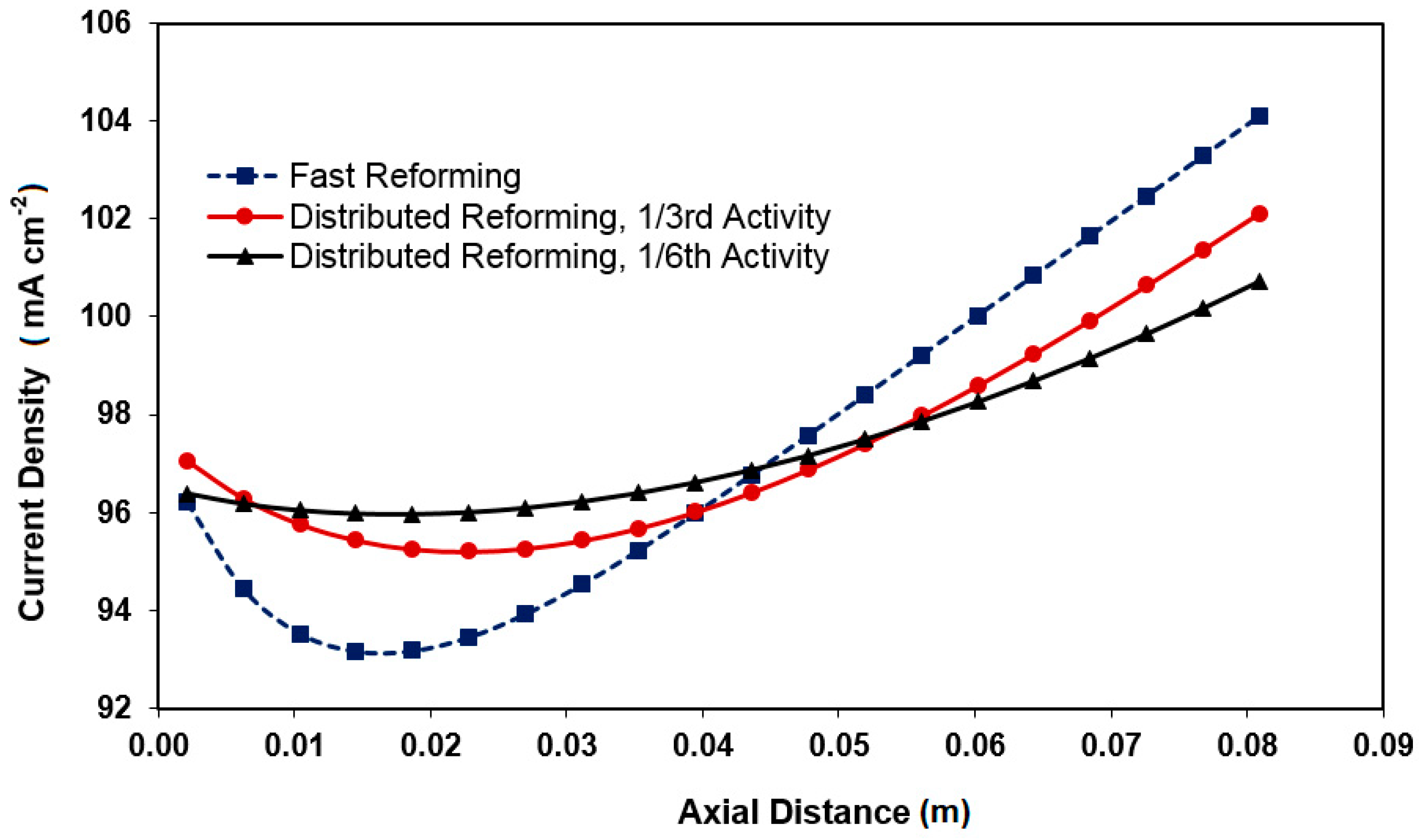
3.1. Distributed Profiles
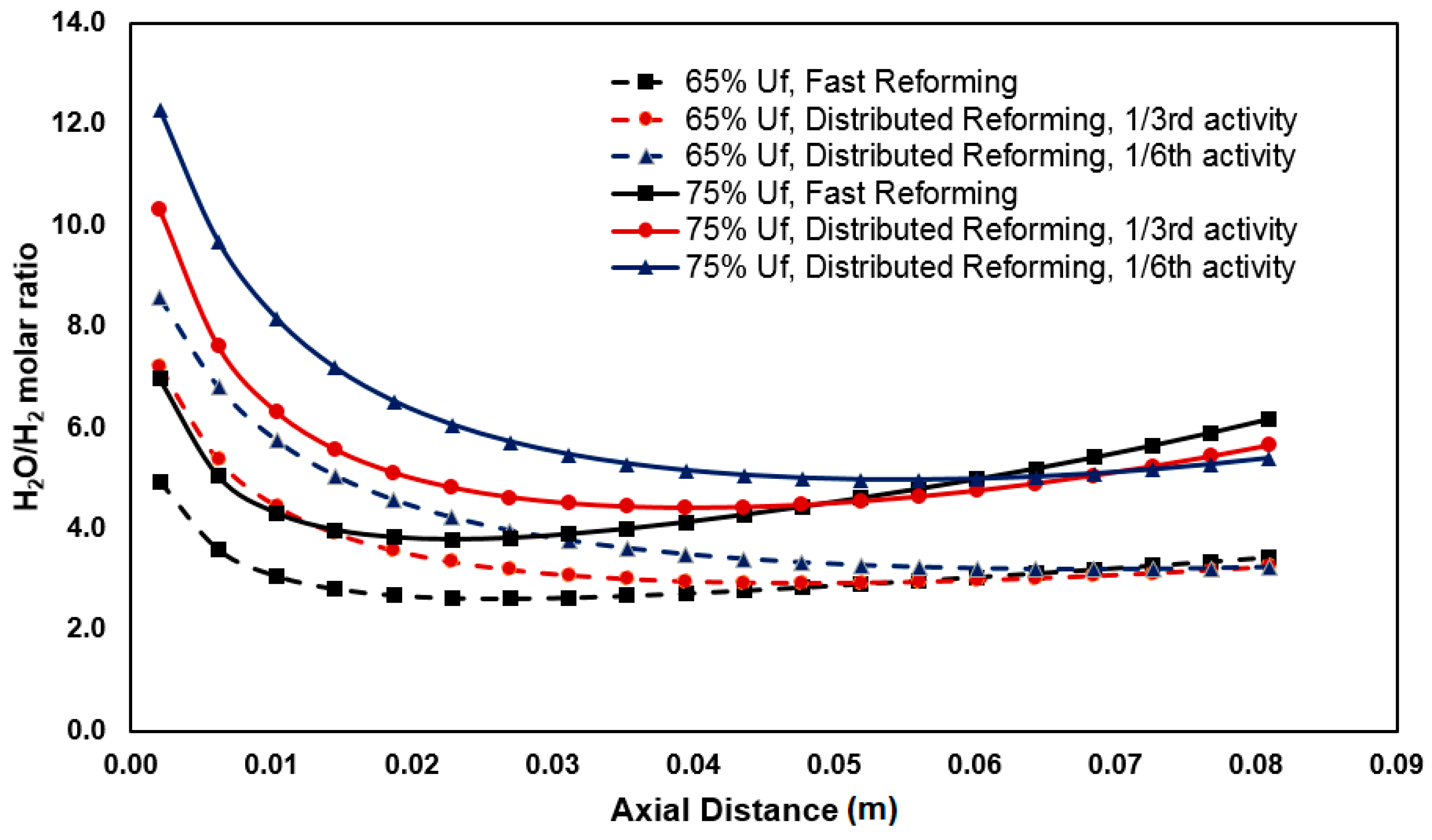
3.2. Anode Oxidation
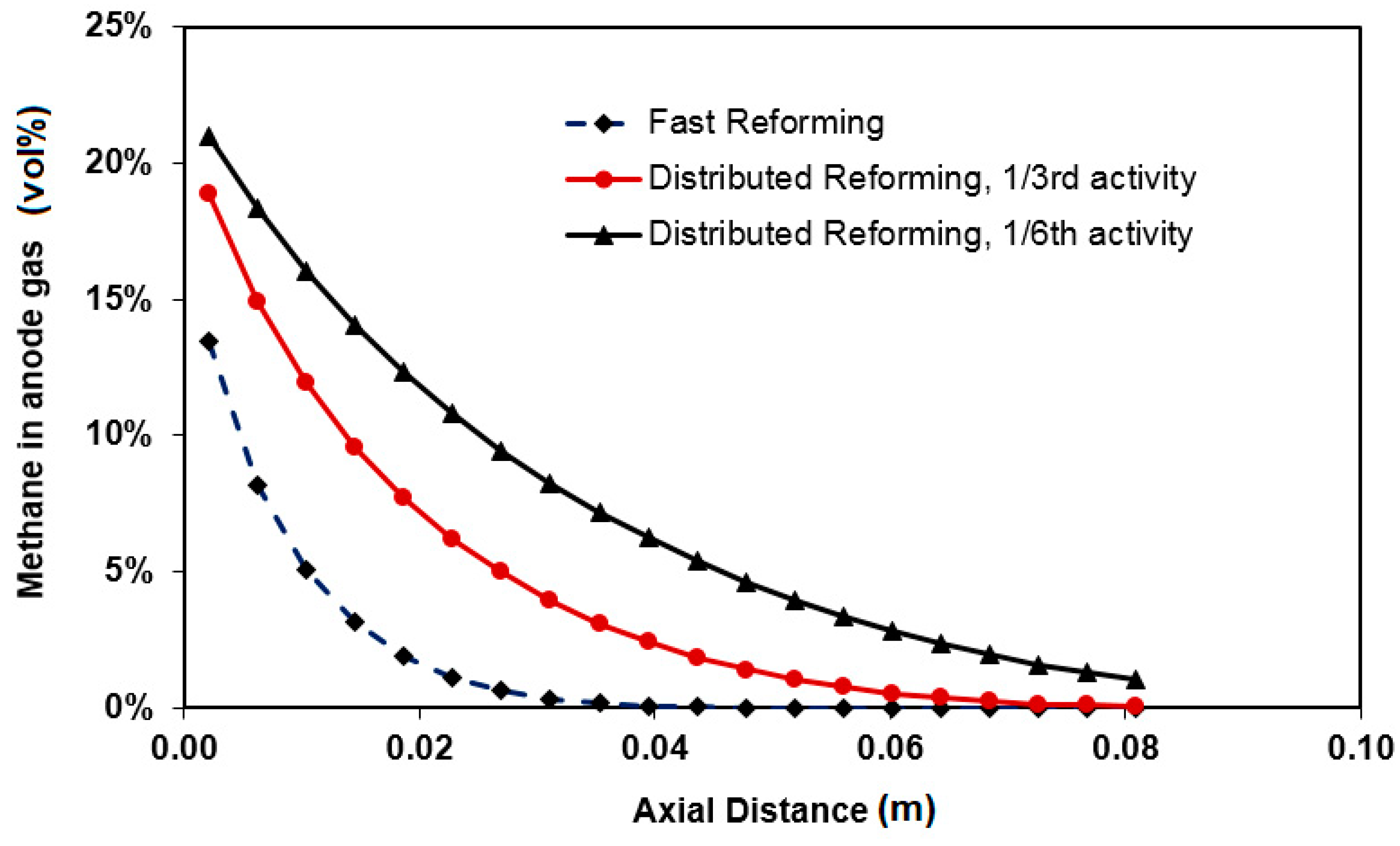
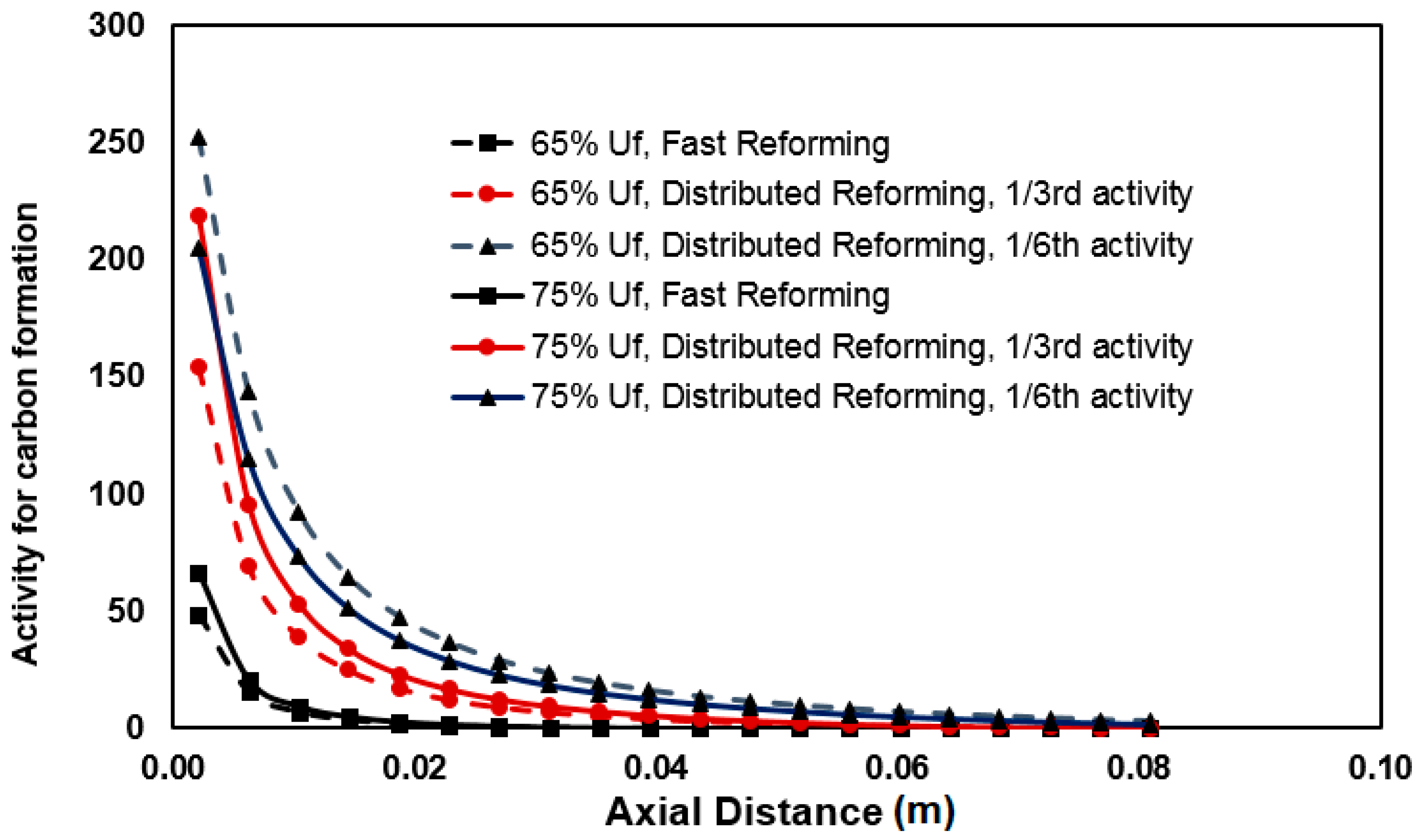
3.3. Carbon Formation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gasik, M. Materials for Fuel Cells; Woodhead Publishing: Sawston, Cambridge, UK, 2008. [Google Scholar]
- Cooper, S.J.; Brandon, N.P. Chapter 1—An Introduction to Solid Oxide Fuel Cell Materials, Technology and Applications. In Solid Oxide Fuel Cell Lifetime and Reliability; Brandon, N.P., Ruiz-Trejo, E., Boldrin, P., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 1–18. [Google Scholar]
- Wang, J.; Wang, H.; Fan, Y. Techno-Economic Challenges of Fuel Cell Commercialization. Engineering 2018, 4, 352–360. [Google Scholar] [CrossRef]
- Ahmed, K.; Föger, K. Perspectives in Solid Oxide Fuel Cell-Based Microcombined Heat and Power Systems. J. Electrochem. Energy Convers. Storage 2017, 14, 031005. [Google Scholar] [CrossRef]
- Lanzini, A.; Ferrero, D.; Santarelli, M. Energy System Analysis of SOFC Systems. In Advances in Medium and High Temperature Solid Oxide Fuel Cell Technology; Boaro, M., Salvatore, A.A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 223–264. [Google Scholar]
- Van Biert, L.; Visser, K.; Aravind, P.V. Intrinsic methane steam reforming kinetics on nickel-ceria solid oxide fuel cell anodes. J. Power Sources 2019, 443, 227261. [Google Scholar] [CrossRef]
- Van Biert, L.; Godjevac, M.; Visser, K.; Aravind, P.V. Dynamic modelling of a direct internal reforming solid oxide fuel cell stack based on single cell experiments. Appl. Energy 2019, 250, 976–990. [Google Scholar] [CrossRef]
- CFCL Delivers Fuel Cell Components for 40 Integrated m-CHP Units. Available online: http://www.fuelcelltoday.com/news-archive/2013/october/cfcl-delivers-fuel-cell-components-for-40-integrated-m-chp-units/ (accessed on 20 May 2019).
- Amiri, A.; Vijay, P.; Tadé, M.O.; Ahmed, K.; Ingram, G.D.; Pareek, V.; Utikar, R. Solid oxide fuel cell reactor analysis and optimisation through a novel multi-scale modelling strategy. Comput. Chem. Eng. 2015, 78, 10–23. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D. Simulation of a tubular solid oxide fuel cell stack operating on biomass syngas using aspen plus. J. Electrochem. Soc. 2010, 157, B975–B981. [Google Scholar] [CrossRef]
- Kupecki, J.; Badyda, K. SOFC-based micro-CHP system as an example of efficient power generation unit. Arch. Thermodyn. 2011, 32, 33. [Google Scholar] [CrossRef]
- Riensche, E.; Meusinger, J.; Stimming, U.; Unverzagt, G. Optimization of a 200 kW SOFC cogeneration power plant. Part II: Variation of the flowsheet. J. Power Sources 1998, 71, 306–314. [Google Scholar] [CrossRef]
- Tanim, T.; Bayless, D.J.; Trembly, J.P. Modeling a 5 kWe planar solid oxide fuel cell based system operating on JP-8 fuel and a comparison with tubular cell based system for auxiliary and mobile power applications. J. Power Sources 2014, 245, 986–997. [Google Scholar] [CrossRef]
- Amiri, A.; Vijay, P.; Tadé, M.O.; Ahmed, K.; Ingram, G.D.; Pareek, V.; Utikar, R. Planar SOFC system modelling and simulation including a 3D stack module. Int. J. Hydrogen Energy 2016, 41, 2919–2930. [Google Scholar] [CrossRef]
- Tang, S.; Amiri, A.; Tadé, M.O. System Level Exergy Assessment of Strategies Deployed for Solid Oxide Fuel Cell Stack Temperature Regulation and Thermal Gradient Reduction. Ind. Eng. Chem. Res. 2019, 58, 2258–2267. [Google Scholar] [CrossRef]
- Zhang, W.; Croiset, E.; Douglas, P.L.; Fowler, M.W.; Entchev, E. Simulation of a tubular solid oxide fuel cell stack using AspenPlusTM unit operation models. Energy Convers. Manag. 2005, 46, 181–196. [Google Scholar] [CrossRef]
- Anderson, T.; Vijay, P.; Tade, M.O. An adaptable steady state Aspen Hysys model for the methane fuelled solid oxide fuel cell. Chem. Eng. Res. Des. 2014, 92, 295–307. [Google Scholar] [CrossRef]
- Ahmed, K.; Foger, K. Kinetics of internal steam reforming of methane on Ni/YSZ-based anodes for solid oxide fuel cells. Catal. Today 2000, 63, 479–487. [Google Scholar] [CrossRef]
- Tingey, G.L. Kinetics of the Water—Gas Equilibrium Reaction. I. The Reaction of Carbon Dioxide with Hydrogen. J. Phys. Chem. 1966, 70, 1406–1412. [Google Scholar] [CrossRef]
- Aguiar, P.; Chadwick, D.; Kershenbaum, L. Modelling of an indirect internal reforming solid oxide fuel cell. Chem. Eng. Sci. 2002, 57, 1665–1677. [Google Scholar] [CrossRef]
- Ahmed, K.; Foger, K. An experimental and modelling study of the performance of a single-cell SOFC stack operating on mixtures of H2-CO-H2O-CO2. In Proceedings of the 4th European SOFC Forum, Oberrohrdorf, Switzerland, 30 June–3 July 2000; pp. 315–324. [Google Scholar]
- Twigg, M.V. Catalyst Handbook. CRC: Boca Raton, FL, USA, 1989. [Google Scholar]
- Ahmed, K.; Föger, K. Analysis of equilibrium and kinetic models of internal reforming on solid oxide fuel cell anodes: Effect on voltage, current and temperature distribution. J. Power Sources 2017, 343, 83–93. [Google Scholar] [CrossRef]
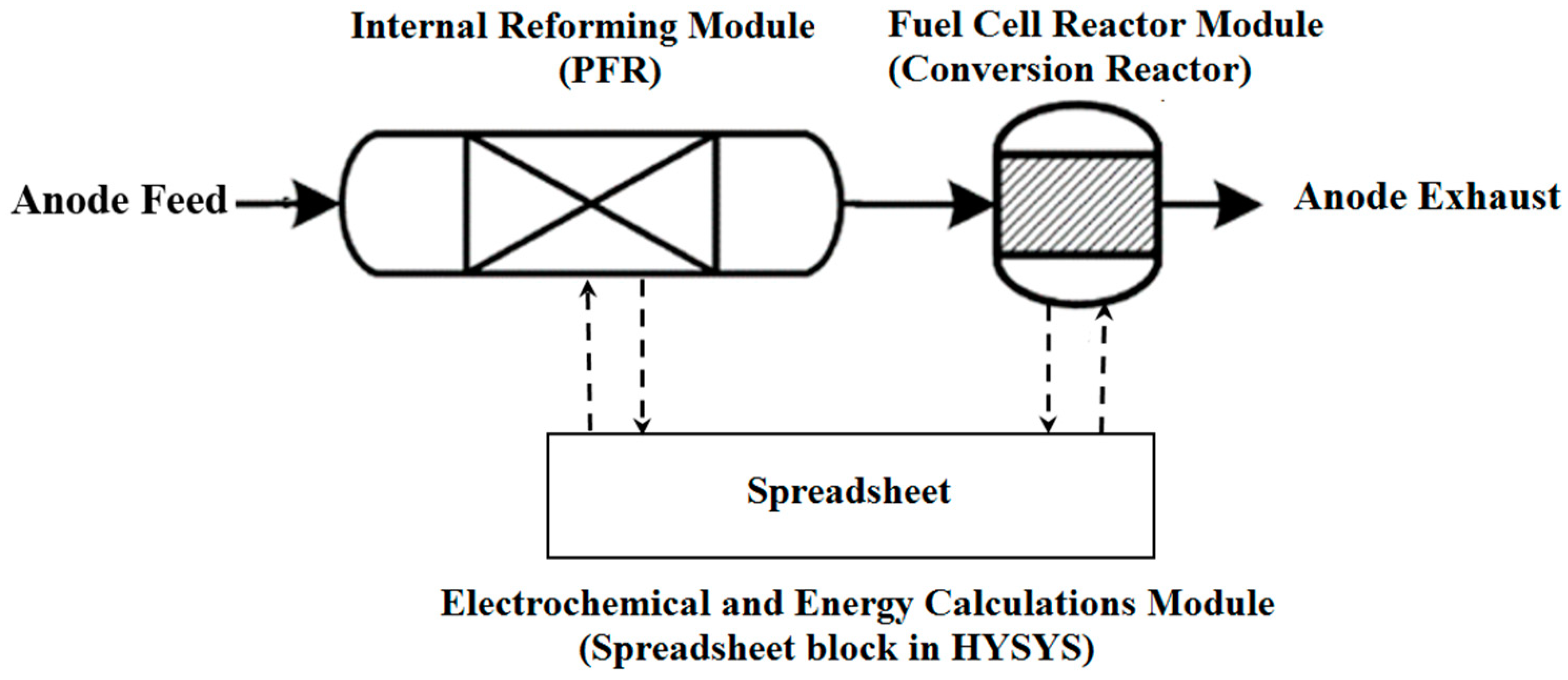


| Equations/Parameters | Comment |
|---|---|
| Constant fuel utilization. | |
| Average current drawn based on given fuel rate and desired fuel utilization. | |
| Heat of electrochemical reaction for given fuel consumption, calculated in the spreadsheet block. | |
| Temperature change due to heat release from fuel oxidation. | |
| , x ={H2, H2O, CO, CO2, CH4}, | Open-circuit operation (OCO) composition and temperature profiles from the internal reforming module (PFR) based on MSR and WGS reaction kinetics. |
| Temperature profile for closed-circuit operation from corresponding open-circuit operation data. | |
| Closed-circuit operation (CCO) composition profiles using fuel utilization. | |
| Current density profile estimation from temperature distribution and open-circuit hydrogen concentration profile. | |
| Kinetics of MSR; ko = 8542 mol/(m2bar1/2s), α = 0.85, β = −0.35, and Ea = 95 kJ/mol [18]. | |
| Kinetics of the reverse WGS reaction reported by Tingey [19]. | |
| The cell voltage was calculated by deducting the voltage losses from the open-circuit Nernst voltage. | |
| Open-circuit Nernst voltage. | |
| Overpotential losses were calculated using an empirical equation [21]; a = 4.43, y = 0.77, z = -0.15, and Eb = 10,560 kJ/mol, determined by regression analysis of experimental measurement of cell overpotential at various current densities and fuel utilization at the three temperatures 750, 800, and 850 °C. | |
| The cell ohmic resistance is independent of fuel utilization as expected [21], where te is the electrolyte thickness (µm) and A = 21,428 µm/Ω and B = 7776 K are constants, with their values determined empirically [21]. |
| Variable | Value |
|---|---|
| NG Flow Rate | 5.4 SLM |
| Air Flow Rate | 300 SLM |
| Air Inlet Temperature to Stack | 810 °C |
| Fuel Utilization | 65% |
| S/C Ratio (at reformer inlet) | 2.25 |
| Fuel Inlet Temperature to Stack | 810 °C |
| Note: SLM—Standard litres per minute, at 0 °C, 1 atm | |
| Variable | Value |
|---|---|
| Net Power | 1.3 kW |
| Net Electrical Efficiency | 38.6% |
| Stack Operating Current | 40.7 A |
| Operating Voltage | 0.67 V |
| Air Utilization | 11.4% |
| Average Stack Temperature | 792.7 °C |
| Stack Exhaust Temperature | 847.4 °C |
| Nernst Voltage (Open-Circuit) | 0.993 V |
| Nernst Voltage (65% Uf) | 0.900 V |
| Overpotential Losses | 0.173 V |
| Ohmic Resistance | 1.547 ohm-cm2 |
| Methane Slip | 0.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, K.; Amiri, A.; O. Tadé, M. Simulation of Solid Oxide Fuel Cell Anode in Aspen HYSYS—A Study on the Effect of Reforming Activity on Distributed Performance Profiles, Carbon Formation, and Anode Oxidation Risk. Processes 2020, 8, 268. https://doi.org/10.3390/pr8030268
Ahmed K, Amiri A, O. Tadé M. Simulation of Solid Oxide Fuel Cell Anode in Aspen HYSYS—A Study on the Effect of Reforming Activity on Distributed Performance Profiles, Carbon Formation, and Anode Oxidation Risk. Processes. 2020; 8(3):268. https://doi.org/10.3390/pr8030268
Chicago/Turabian StyleAhmed, Khaliq, Amirpiran Amiri, and Moses O. Tadé. 2020. "Simulation of Solid Oxide Fuel Cell Anode in Aspen HYSYS—A Study on the Effect of Reforming Activity on Distributed Performance Profiles, Carbon Formation, and Anode Oxidation Risk" Processes 8, no. 3: 268. https://doi.org/10.3390/pr8030268
APA StyleAhmed, K., Amiri, A., & O. Tadé, M. (2020). Simulation of Solid Oxide Fuel Cell Anode in Aspen HYSYS—A Study on the Effect of Reforming Activity on Distributed Performance Profiles, Carbon Formation, and Anode Oxidation Risk. Processes, 8(3), 268. https://doi.org/10.3390/pr8030268






